| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
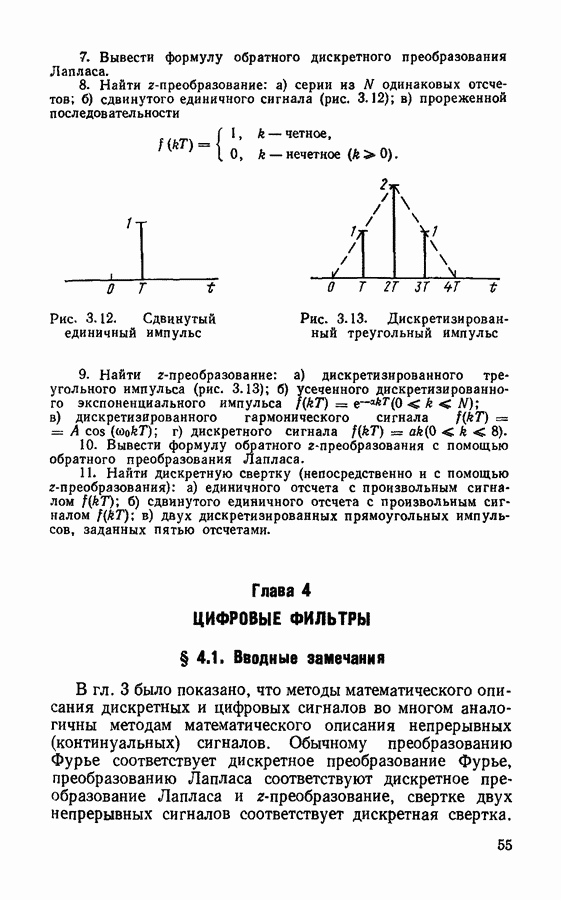
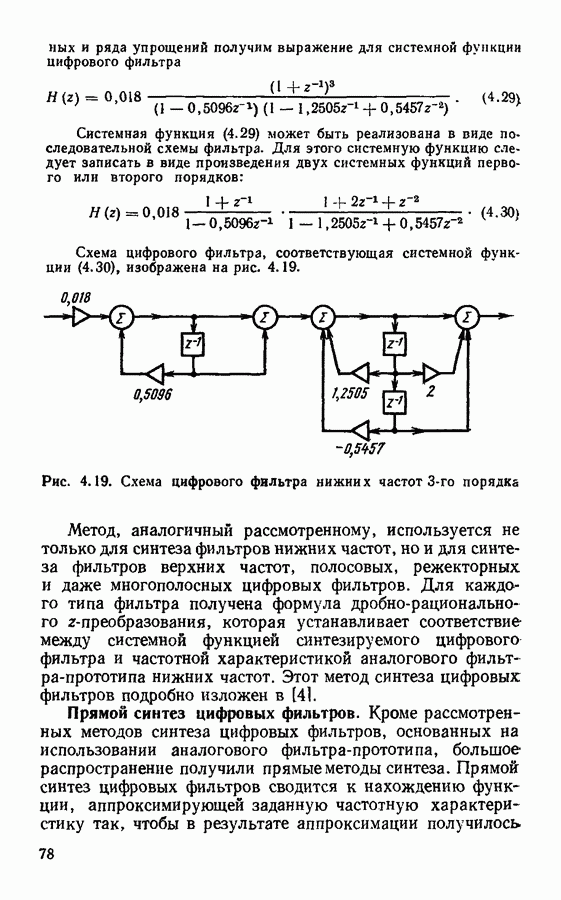
§ 3.3. Быстрое преобразование Фурье
Недостатком дискретного преобразования Фурье является большое количество математических операций, которые необходимо произвести при применении формулы (3.4) или (3.14). Если число степеней свободы сигнала равно  то для расчета по формулам дискретного преобразования Фурье необходимо выполнить
то для расчета по формулам дискретного преобразования Фурье необходимо выполнить  умножений и
умножений и  сложений комплексных чисел — всего
сложений комплексных чисел — всего  арифметических операций. При большом
арифметических операций. При большом  такая обработка сигналов оказывается слишком трудоемкой.
такая обработка сигналов оказывается слишком трудоемкой.
Для облегчения вычисления дискретного преобразования Фурье применяют специальные алгоритмы, которые позволяют во много раз сократить объем необходимых вычислений. Такие алгоритмы называют быстрым преобразованием Фурье.
Существует несколько различных алгоритмов быстрого преобразования Фурье [2,4]. Каждый из них применяют в определенной ситуации, в зависимости от того, на какие множители может быть разложено число степеней свободы  Наиболее простые алгоритмы получаются, если
Наиболее простые алгоритмы получаются, если  является степенью числа 2. Рассмотрим один из таких алгоритмов, основанный на так называемом прореживании по времени.
является степенью числа 2. Рассмотрим один из таких алгоритмов, основанный на так называемом прореживании по времени.
Пусть требуется вычислить дискретное преобразование Фурье числовой последовательности 

Поскольку число отсчетов сигнала  четное, исходную последовательность можно разбить на две:
четное, исходную последовательность можно разбить на две:  куда войдут все
куда войдут все  с четными номерами, и
с четными номерами, и  куда войдут все
куда войдут все  с нечетными номерами (рис. 3.2), так что
с нечетными номерами (рис. 3.2), так что

Применим дискретное преобразование Фурье к последовательностям  при этом учтем, что последовательности
при этом учтем, что последовательности  содержат по
содержат по  членов:
членов:

Для сокращения записи обозначим  Тогда
Тогда

Нашей конечной целью является вычисление значений  Учитывая, что все члены последовательности
Учитывая, что все члены последовательности  принадлежат
принадлежат  или
или  можно записать
можно записать


Рис. 3.2. К выводу алгоритма быстрого преобразования Фурье
Таким образом, значения  можно вычислить по известным значениям
можно вычислить по известным значениям  Однако формула (3.17) справедлива только для
Однако формула (3.17) справедлива только для  так как
так как  не определены для больших значений
не определены для больших значений  Поэтому для
Поэтому для  значения
значения  можно вычислить, используя свойство периодичности дискретного преобразования Фурье:
можно вычислить, используя свойство периодичности дискретного преобразования Фурье:

Учитывая,  получим
получим
окончательную расчетную формулу для  при
при 

Процесс вычисления дискретного преобразования Фурье по формулам (3.17), (3.18) схематически изображен на рис. 3.3 с помощью направленного сигнального графа. Здесь каждое из умножений на  представлено в виде стрелки, под которой записан соответствующий множитель. Кружочки схематически обозначают сложение (вычитание), причем линия, отходящая от кружочка вправо вверх, соответствует сумме, а отходящая вправо вниз — разности двух значений, подводимых к кружочку слева. Например, сумма значений
представлено в виде стрелки, под которой записан соответствующий множитель. Кружочки схематически обозначают сложение (вычитание), причем линия, отходящая от кружочка вправо вверх, соответствует сумме, а отходящая вправо вниз — разности двух значений, подводимых к кружочку слева. Например, сумма значений  и равна
и равна  а разность этих значений равна
а разность этих значений равна 

Рис. 3.3 Замена восьмиточечного дискретного преобразования Фурье двумя четырехточечными
Для вычисления значений  нужно выполнить два дискретных преобразования Фурье, однако число дискретных значений в каждом из этих преобразований оказывается в 2 раза меньше, чем в исходном преобразовании Фурье и равно
нужно выполнить два дискретных преобразования Фурье, однако число дискретных значений в каждом из этих преобразований оказывается в 2 раза меньше, чем в исходном преобразовании Фурье и равно  При этом для вычисления
При этом для вычисления  необходимо выполнить по
необходимо выполнить по  арифметических операций, и еще
арифметических операций, и еще  операций необходимо произвести в процессе расчетов значений
операций необходимо произвести в процессе расчетов значений  по формулам (3.17), (3.18). Таким образом, общее число арифметических операций, необходимых для вычисления дискретного преобразования Фурье, будет равно
по формулам (3.17), (3.18). Таким образом, общее число арифметических операций, необходимых для вычисления дискретного преобразования Фурье, будет равно  что при большом
что при большом  оказывается значительно меньше, чем при вычислении
оказывается значительно меньше, чем при вычислении  по общей формуле дискретного преобразования Фурье (3.14).
по общей формуле дискретного преобразования Фурье (3.14).
Если число степеней свободы сигнала  является степенью числа 2, то число
является степенью числа 2, то число  тоже будет четным. В этом случае для вычисления значений
тоже будет четным. В этом случае для вычисления значений  вместо общей формулы дискретного преобразования Фурье можно применить алгоритм, аналогичный только что рассмотренному. При этом общая процедура расчета может быть схематически представлена сигнальным графом, представленным на рис. 3.4.
вместо общей формулы дискретного преобразования Фурье можно применить алгоритм, аналогичный только что рассмотренному. При этом общая процедура расчета может быть схематически представлена сигнальным графом, представленным на рис. 3.4.
Процесс упрощения алгоритма расчета можно продолжать до тех пор, пока не останутся только простейшие двухточечные дискретные преобразования Фурье. В результате получим сигнальный граф для  изображенный на рис. 3.5. Детальное рассмотрение этого рисунка позволяет точно определить число арифметических операций, необходимых для вычисления дискретного преобразования Фурье.
изображенный на рис. 3.5. Детальное рассмотрение этого рисунка позволяет точно определить число арифметических операций, необходимых для вычисления дискретного преобразования Фурье.

Рис. 3.4. Замена четырехточечных дискретных преобразований Фурье двухточечными

Рис. 3.6. Схематическое изображение алгоритма быстрого преобразования Фурье
Число умножений определяется числом стрелок на рис. 3.5, а число сложений (вычитаний) — числом кружочков, умноженным на 2. В рассмотренном случае восьмиточечного дискретного преобразования Фурье в соответствии с рис. 3.5 необходимо выполнить  т. е.
т. е.  сложений (вычитаний) и
сложений (вычитаний) и  т. е.
т. е.  умножений. Фактическое число умножений оказывается несколько меньше, так как часть из них оказывается тривиальными умножениями на
умножений. Фактическое число умножений оказывается несколько меньше, так как часть из них оказывается тривиальными умножениями на 
Таким образом, при применении данного алгоритма для вычисления дискретного преобразования Фурье последовательности из  точек требуется выполнить
точек требуется выполнить  сложений и самое большее
сложений и самое большее  умножений. Для сравнения напомним, что при использовании обычной формулы дискретного преобразования Фурье необходимо выполнить
умножений. Для сравнения напомним, что при использовании обычной формулы дискретного преобразования Фурье необходимо выполнить  арифметических операций. Применение быстрого преобразования Фурье при
арифметических операций. Применение быстрого преобразования Фурье при  позволяет сократить объем вычислений более чем в 100 раз.
позволяет сократить объем вычислений более чем в 100 раз.
Кроме рассмотренного алгоритма быстрого преобразования Фурье существует ряд других, которые применяют в тех случаях, когда N не является степенью числа 2, а раскладывается на другие простые сомножители. Все эти алгоритмы подробно рассмотрены в [7].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
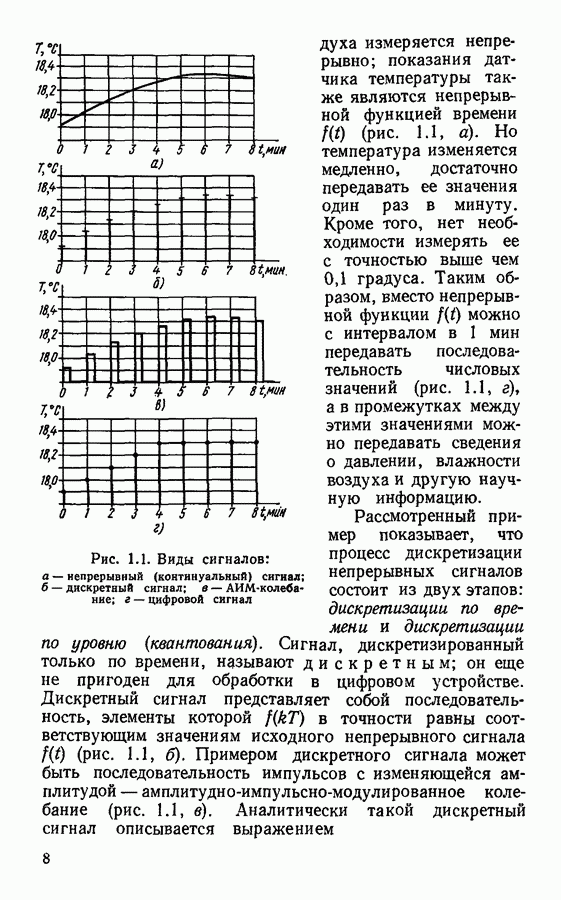
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
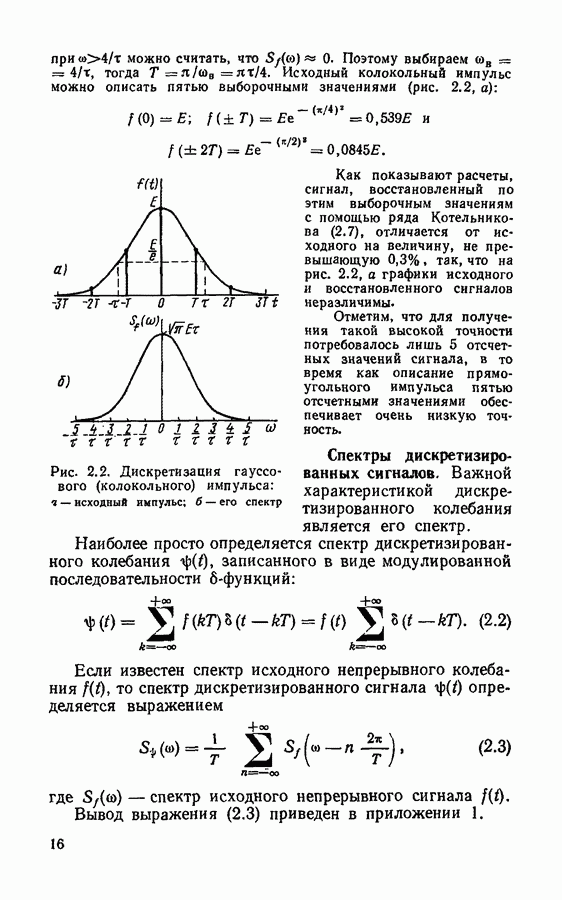
- § 2.1. Основы дискретизации непрерывных сигналов
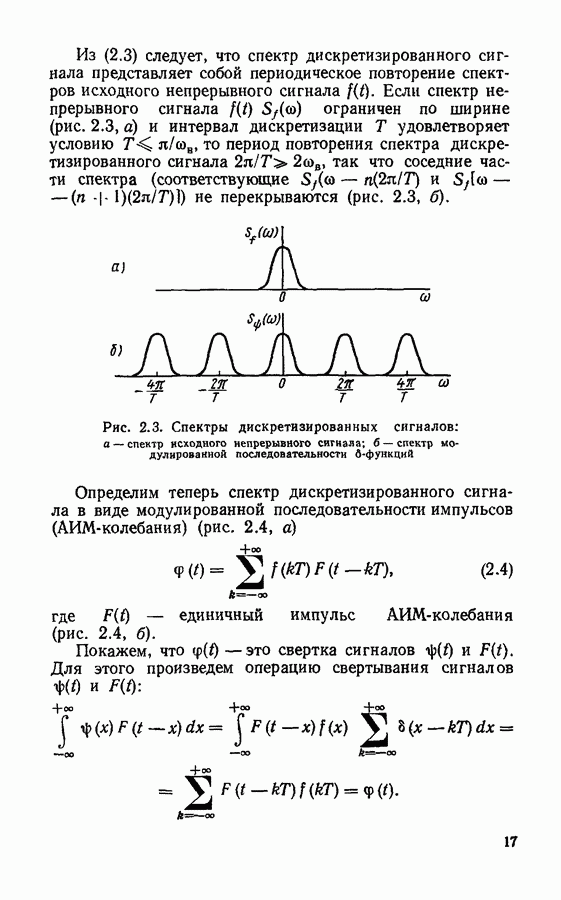
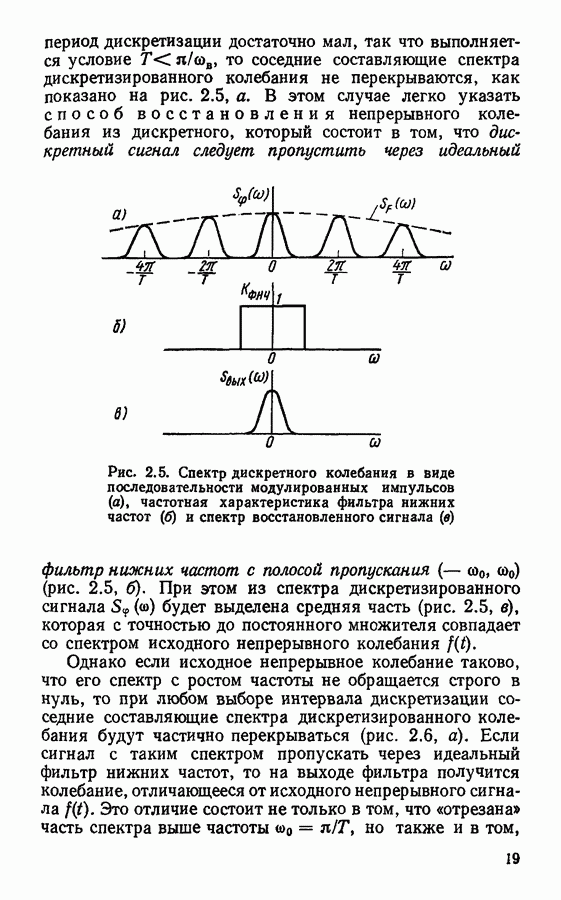
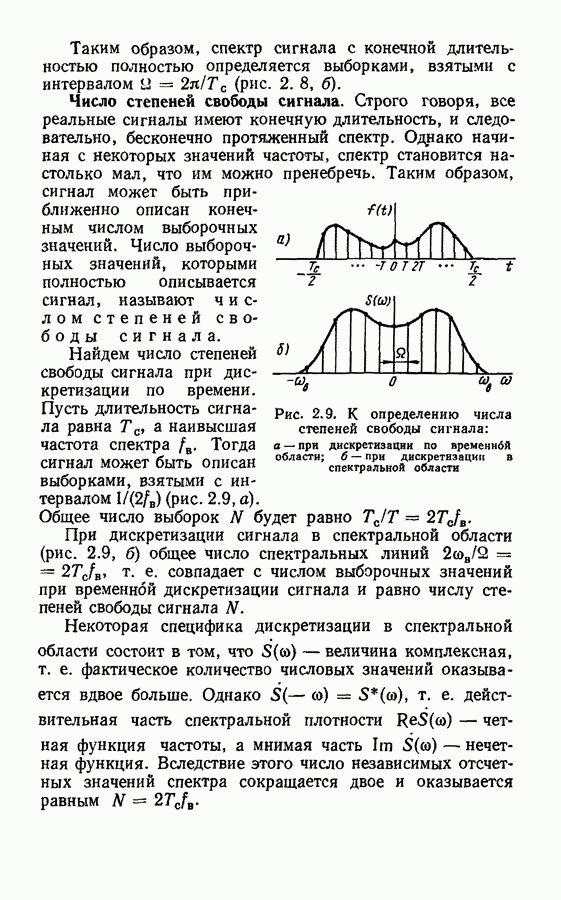
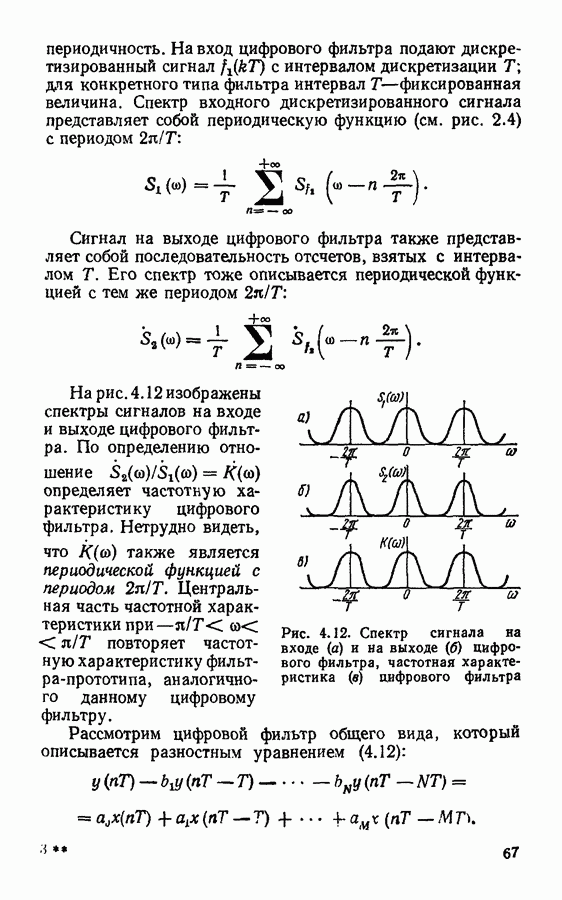
- Спектры дискретизированных сигналов.
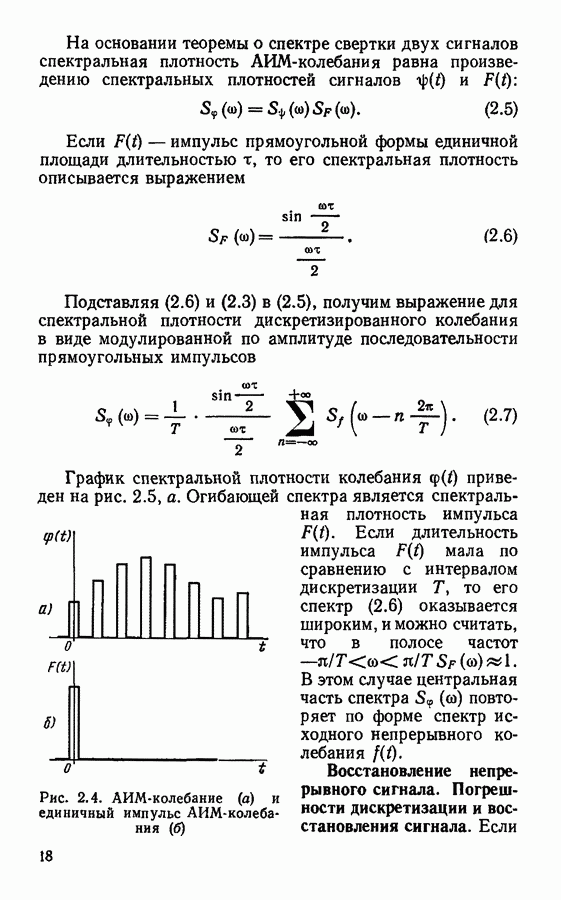
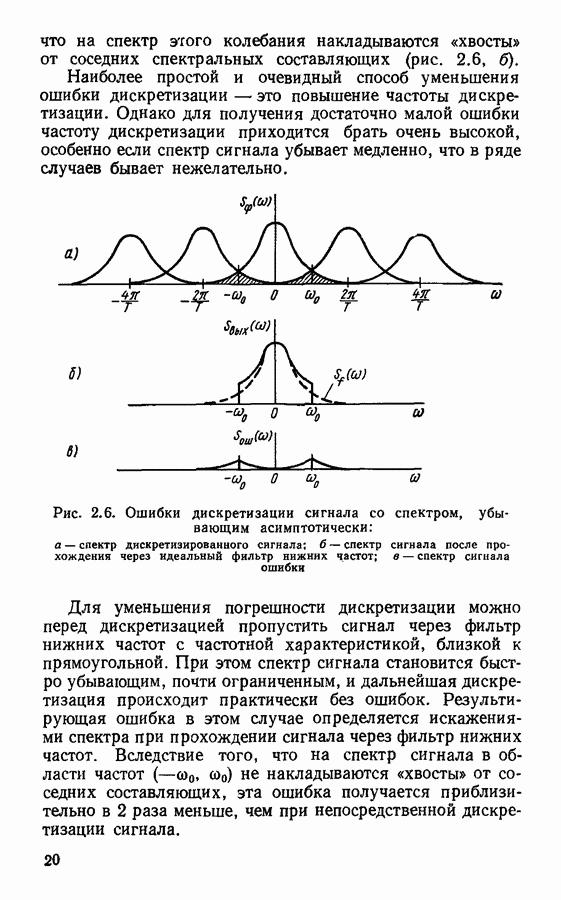
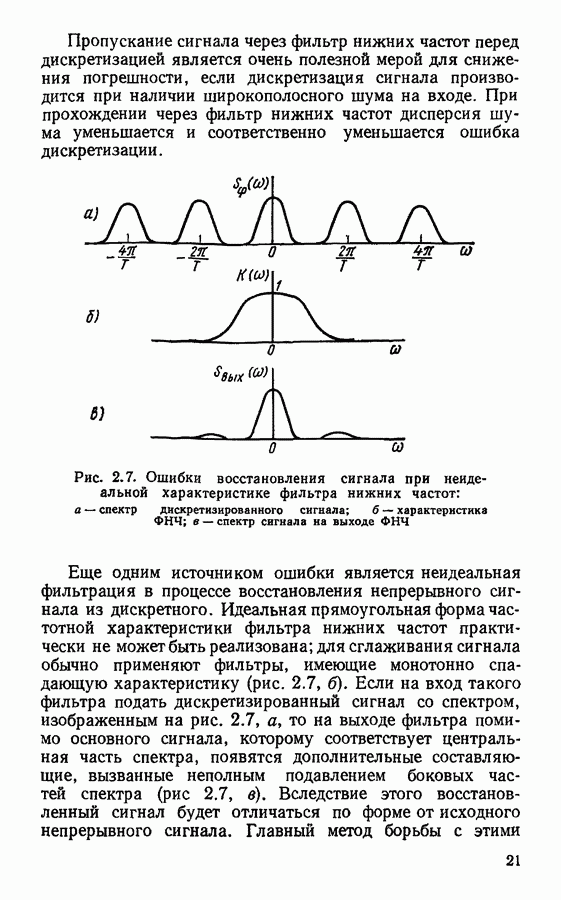
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
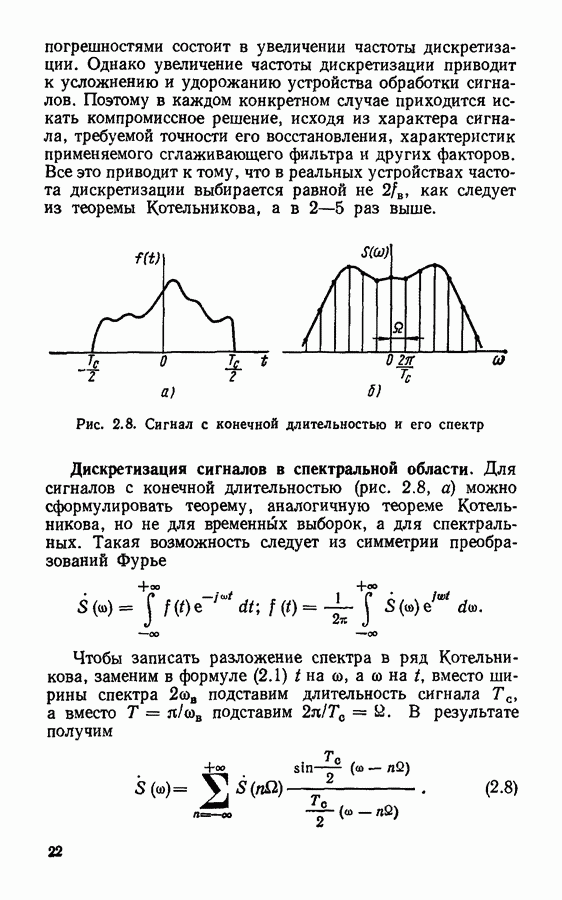
- Дискретизация сигналов в спектральной области.
- Число степеней свободы сигнала.
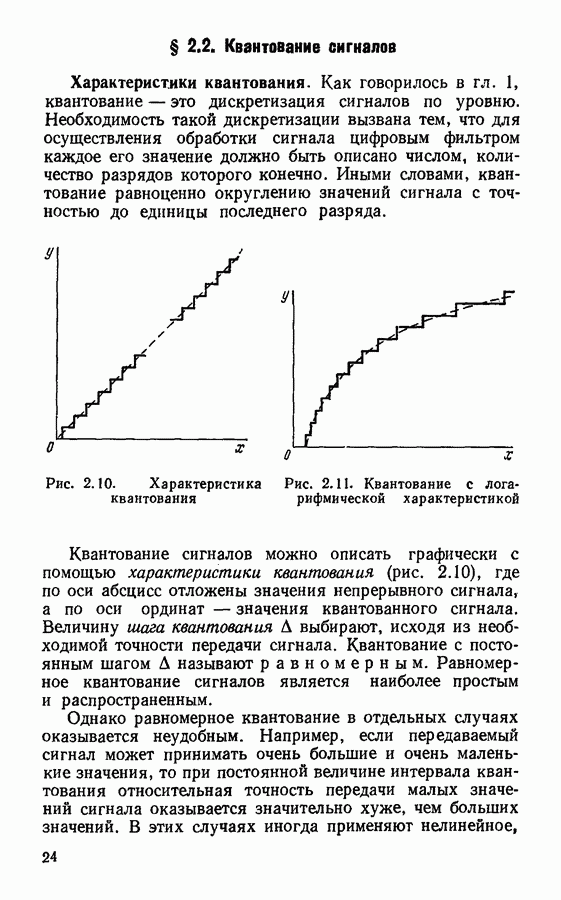
- § 2.2. Квантование сигналов
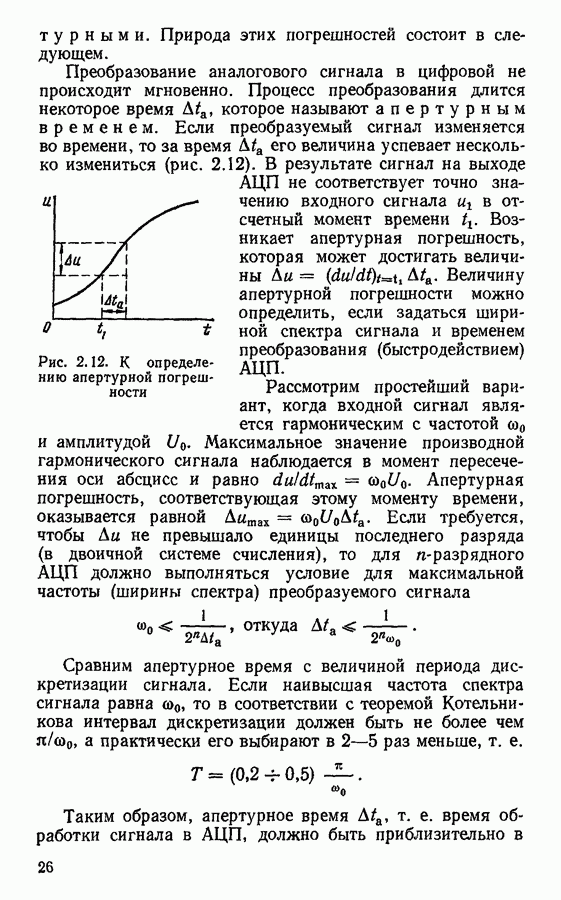
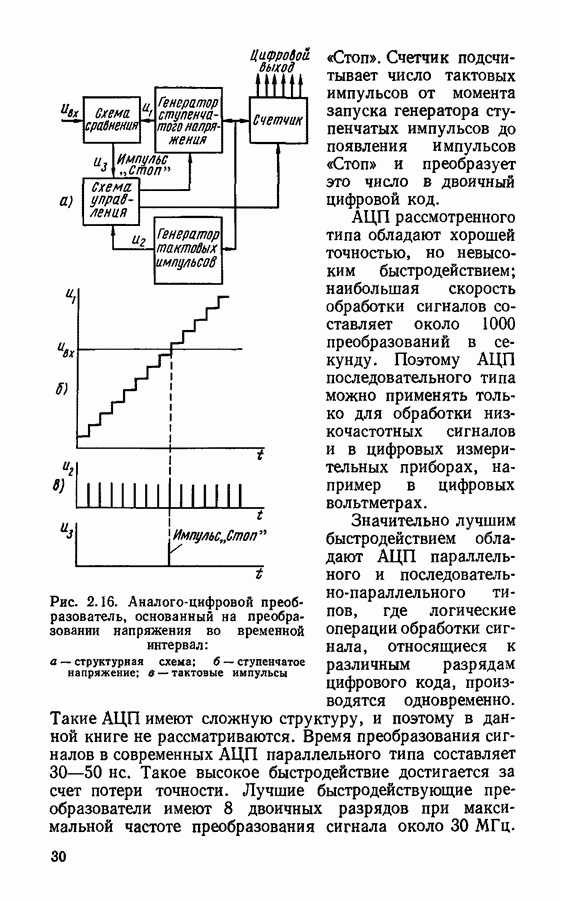
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
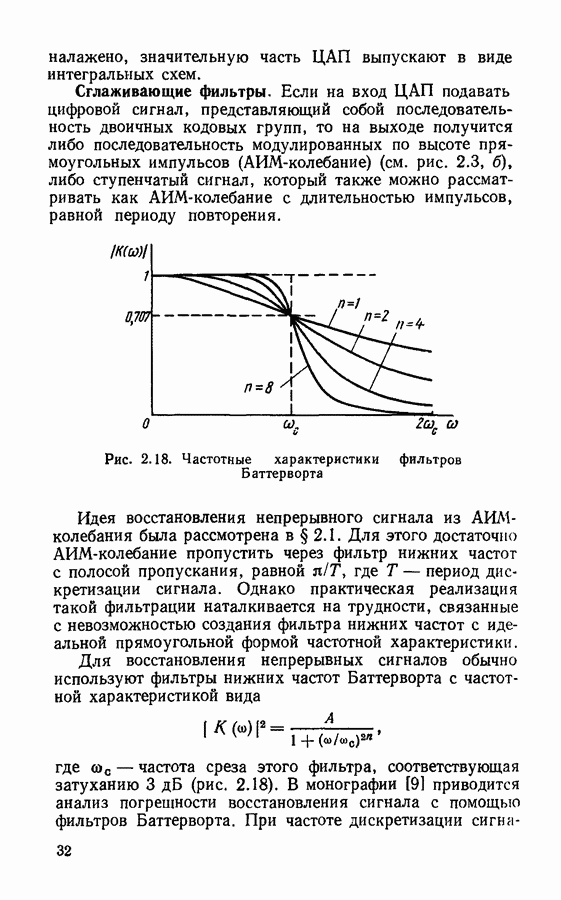
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
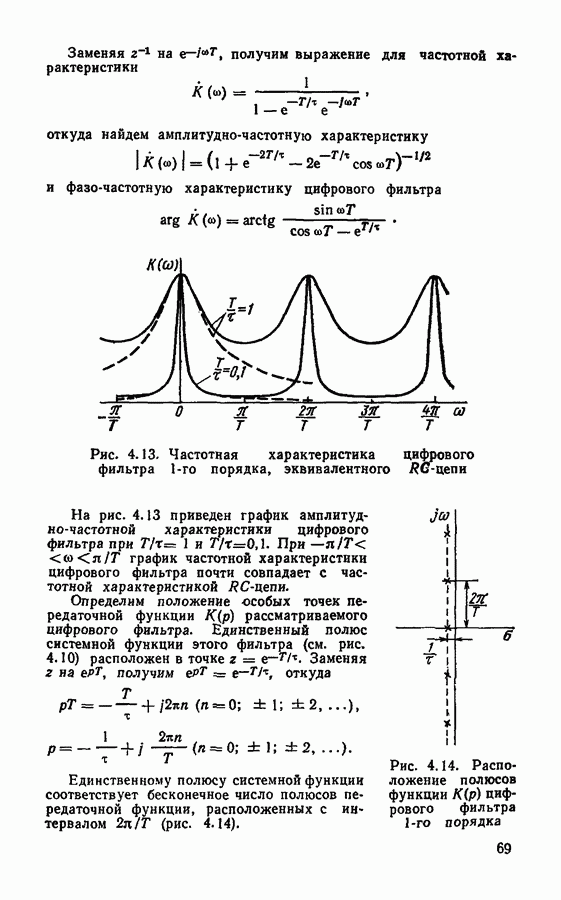
- § 4.3. Частотные характеристики цифровых фильтров
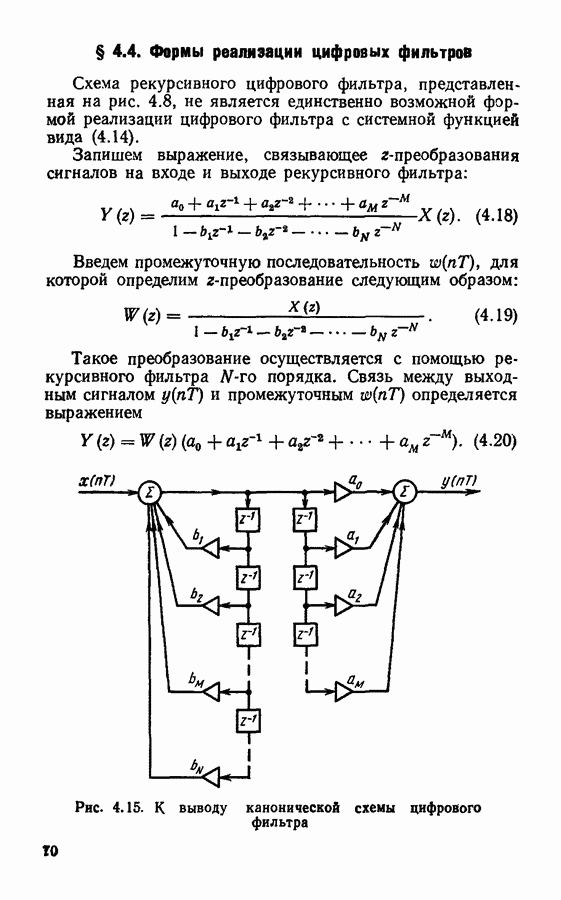
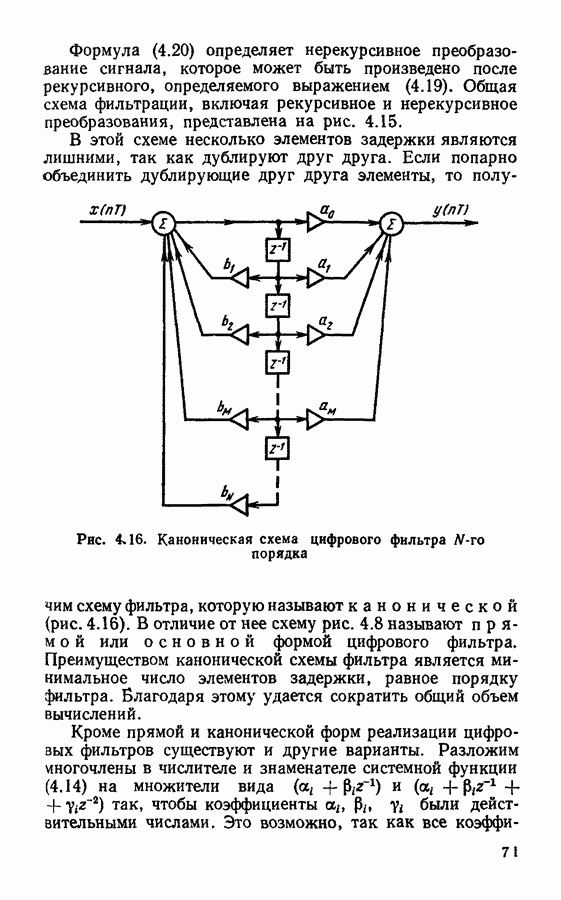
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
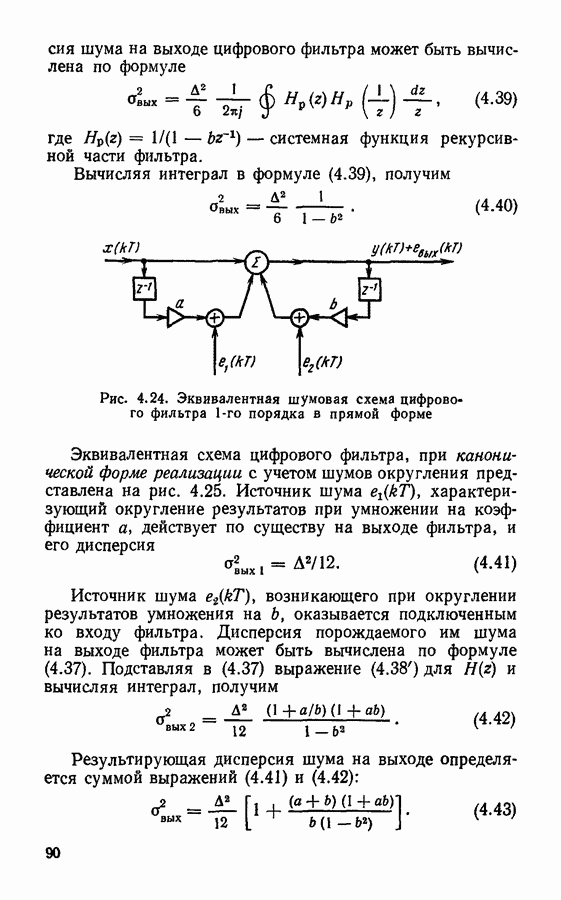
- Ошибки, вызванные квантованием результатов вычислений.
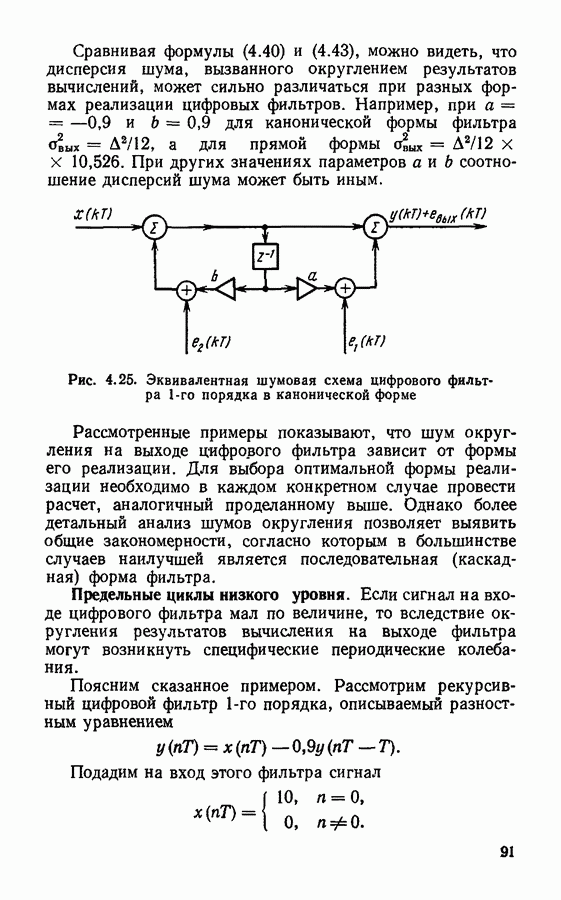
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА