| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3.2. Дискретное преобразование Фурье
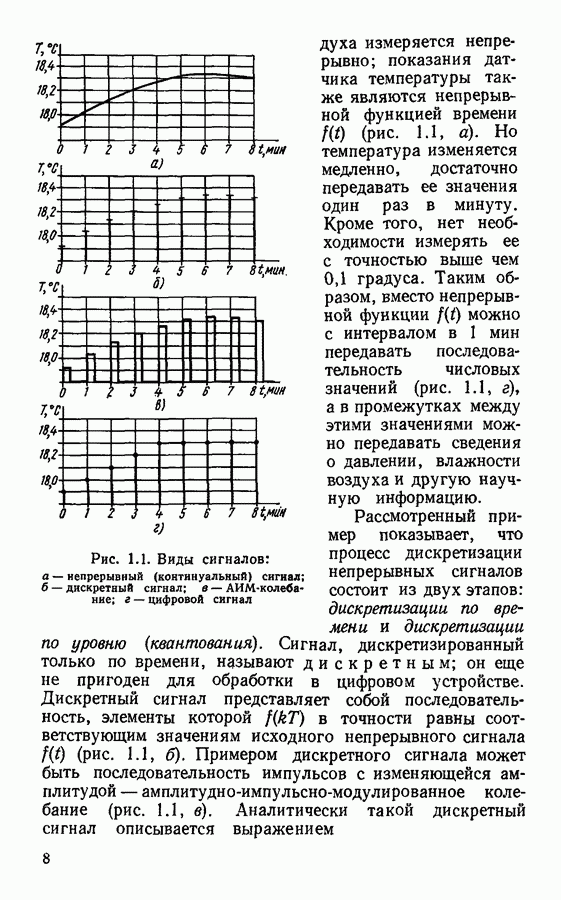
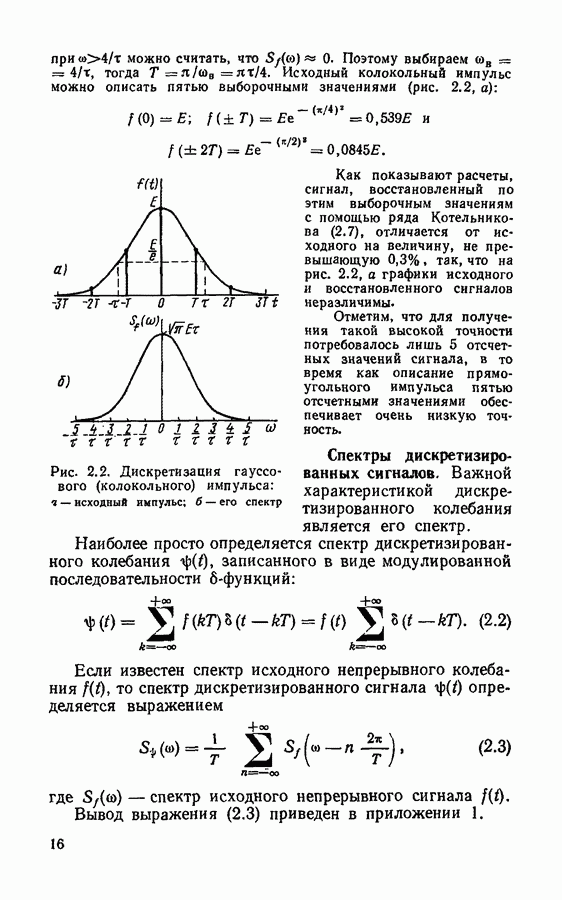
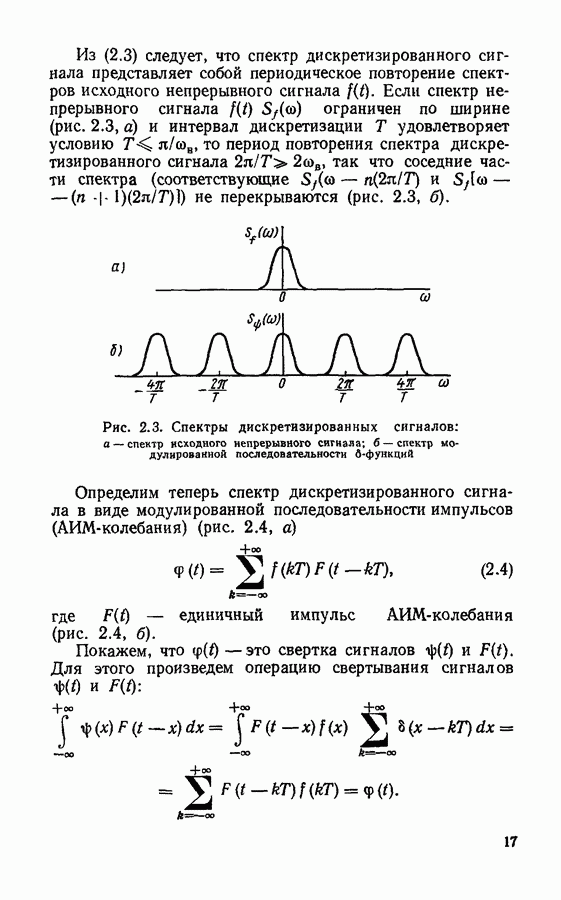
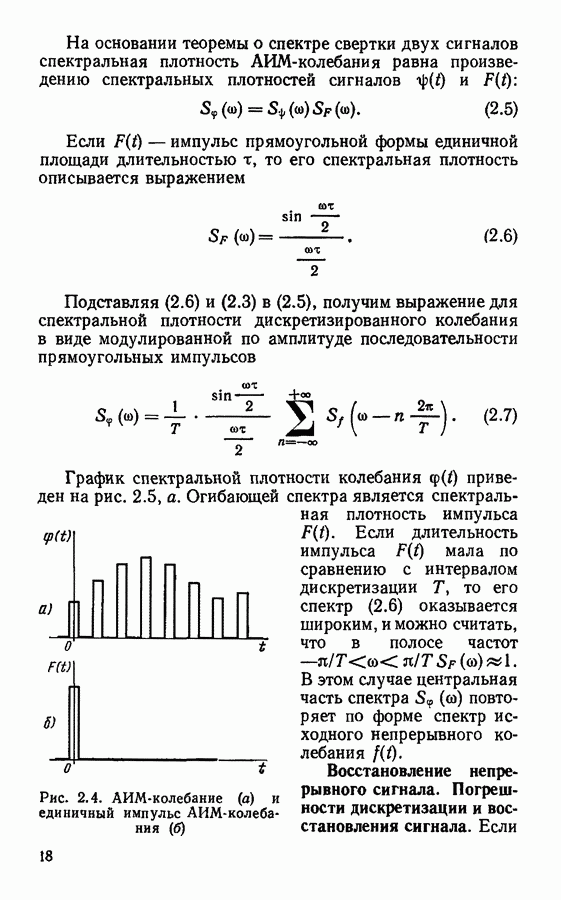
Из предыдущего раздела о дискретизации непрерывных сигналов следует, что реальные сигналы могут быть описаны выборками как в спектральной, так и во временной области. И дискретный спектр, и дискретный сигнал полностью описывают исходный непрерывный (континуальный) сигнал. Однако чтобы найти дискретный спектр по заданному дискретному сигналу, надо проделать трудоемкие расчеты: сначала по дискретному сигналу восстановить непрерывный сигнал, затем с помощью преобразования Фурье найти непрерывный спектр, затем его дискретизировать. Аналогичную процедуру необходимо проделать для обратного преобразования. Непосредственный переход от дискретного сигнала к дискретному спектру и наоборот возможен с использованием дискретного преобразования Фурье.
Рассмотрим непрерывный сигнал  конечной длительности
конечной длительности  с числом степеней свободы, равным
с числом степеней свободы, равным  Для этого сигнала можно записать разложение в ряд Котельникова:
Для этого сигнала можно записать разложение в ряд Котельникова:

С помощью обычного преобразования Фурье найдем спектр этого сигнала:

Непосредственное вычисление интеграла в этой формуле — процедура трудоемкая. Однако это нетрудно сделать другим способом.
Рассмотрим спектр  который определяется выражением
который определяется выражением

Применив к нему обратное преобразование Фурье, получим, что ему соответствует временная функция

Очевидно, справедливо и обратное соотношение

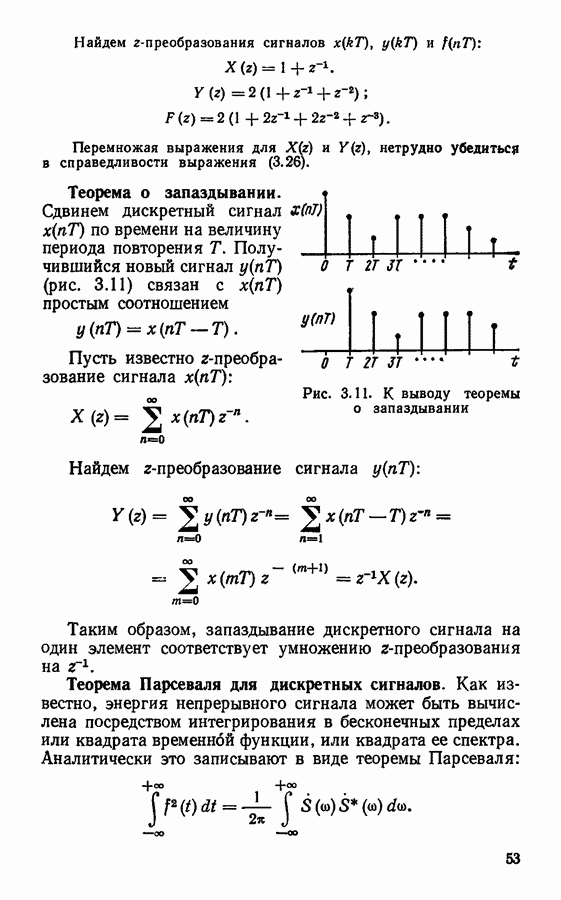
Применяя теорему о запаздывании, можно записать

Подставляя (3.2) в (3.1), получим окончательное выражение для спектра

Чтобы перейти к дискретному преобразованию Фурье, значения спектра в выражении (3.3) нужно вычислять не для всех значений частоты, а для дискретных (выборочных):

В результате получим окончательную формулу для дискретного преобразования Фурье

или

Свойства дискретного преобразования Фурье во многом аналогичны свойствам обычного преобразования Фурье. Отметим только одно специфическое свойство, которое
можно назвать периодичностью дискретного преобразования Фурье.
Рассмотрим значение  определяемое формулой (3.4) для
определяемое формулой (3.4) для  где
где  целое число:
целое число:

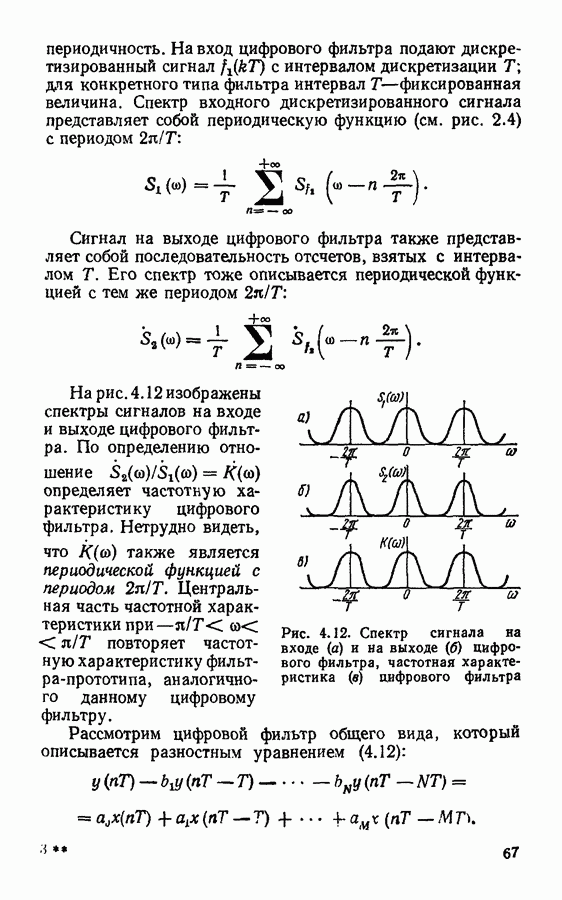
Таким образом, дискретное преобразование Фурье является периодической функцией частоты с периодом, равным  Это свойство аналогично свойству периодичности спектра дискретизированных сигналов, которое рассматривалось в гл. 2.
Это свойство аналогично свойству периодичности спектра дискретизированных сигналов, которое рассматривалось в гл. 2.
Перейдем теперь к выводу обратного дискретного преобразования Фурье, позволяющего определять выборки сигнала по выборкам спектра. Для этого воспользуемся обычным обратным преобразованием Фурье

Спектральную плотность сигнала  запишем в виде ряда Котельникова
запишем в виде ряда Котельникова

и подставим в интеграл обратного преобразования Фурье

Интеграл в выражении  аналогичен вычисленному ранее интегралу (3.2). Пользуясь этой аналогией, запишем
аналогичен вычисленному ранее интегралу (3.2). Пользуясь этой аналогией, запишем

Подставляя (3.6) в (3.5), получим выражение для временной функции 

Полагая в соотношении  получим формулу для определения значений дискретного сигнала
получим формулу для определения значений дискретного сигнала  т. е. приходим к обратному дискретному преобразованию Фурье
т. е. приходим к обратному дискретному преобразованию Фурье

где А принимает значения от 0 до 
Иногда для удобства записи, используя свойство периодичности дискретного преобразования Фурье, изменяют пределы суммирования в выражении (3.8) и обратное дискретное преобразование Фурье записывают в виде

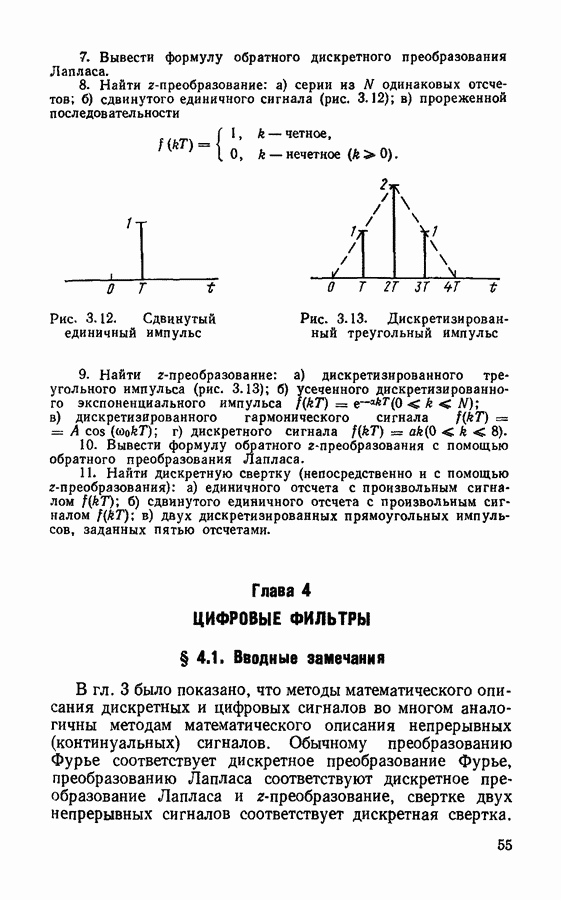
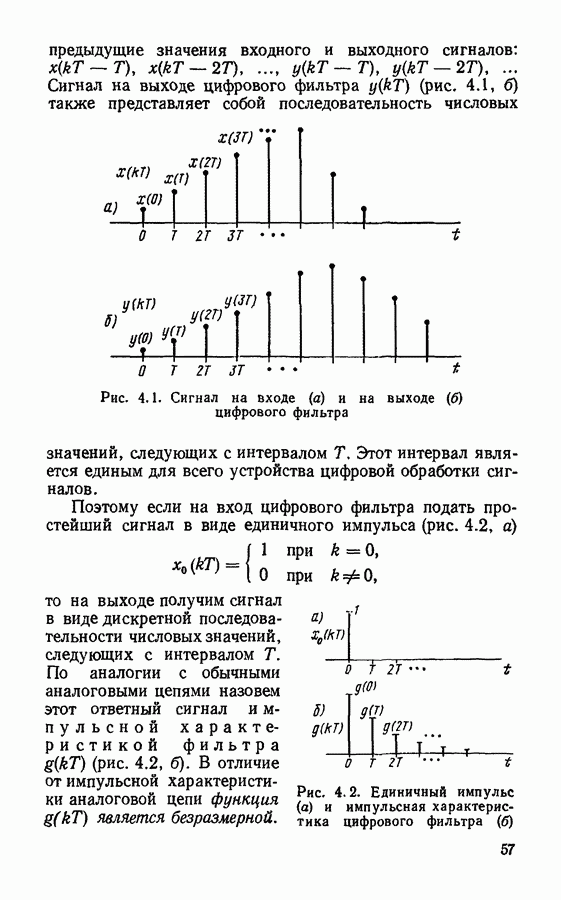
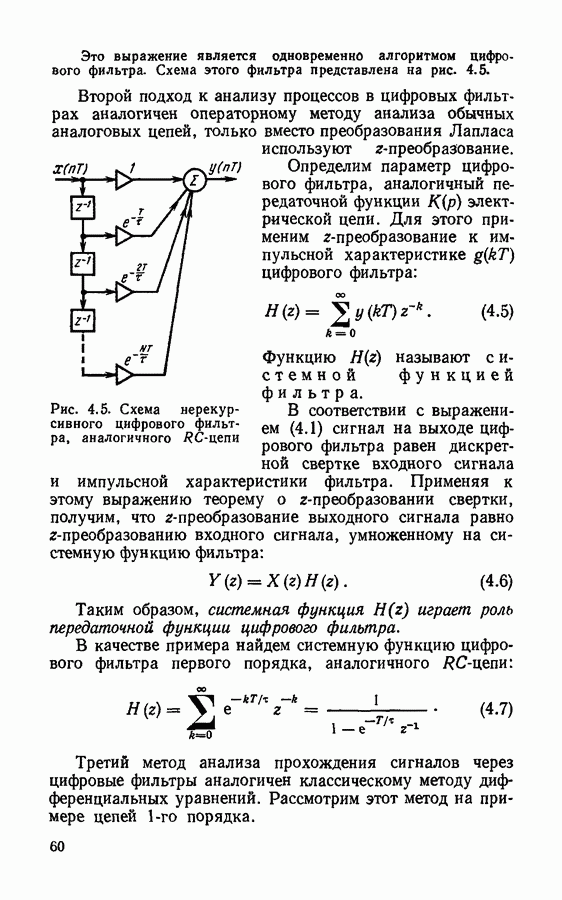
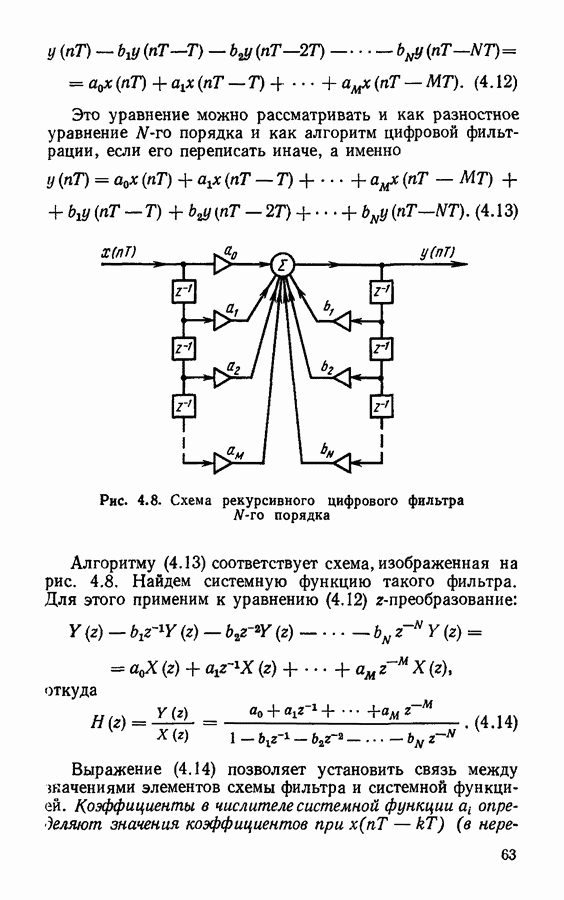
Для иллюстрации применим дискретное преобразование Фурье к дискретизированному треугольному импульсу (рис.  описываемому пятью выборочными значениями
описываемому пятью выборочными значениями

Подставим это выражение дискретного сигнала в формулу дискретного преобразования Фурье (3.4)

откуда

где 
Для сравнения найдем спектральную плотность исходного треугольного импульса:

причем

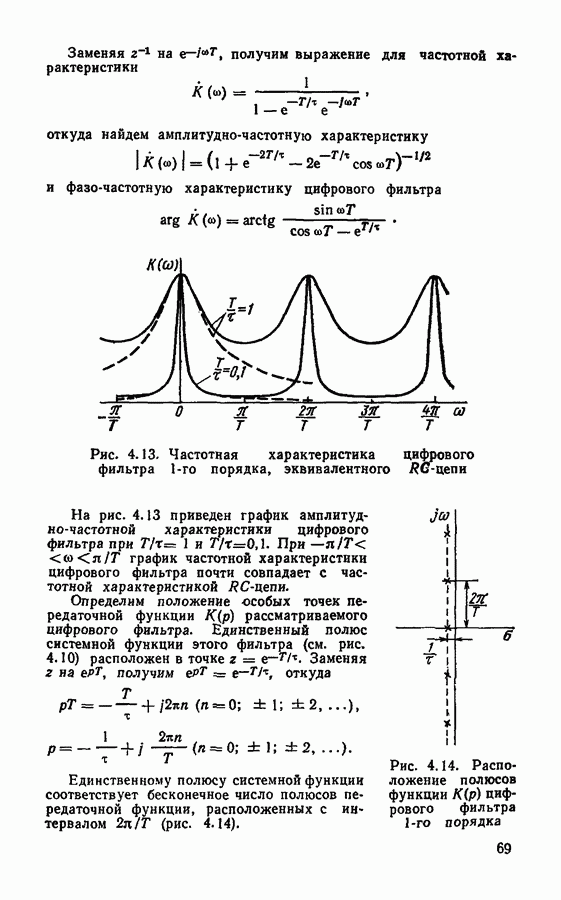
Легко видеть, что дискретный спектр (3.11) неточно описывает спектральную плотность треугольного импульса (3.12). Значения  несколько отличаются от соответствующих значений спектра треугольного импульса
несколько отличаются от соответствующих значений спектра треугольного импульса  (рис. 3.1, б).
(рис. 3.1, б).
Теперь подставим дискретные значения спектра (3.11) в выражение для обратного дискретного преобразования Фурье (3.8):

откуда

Несмотря на отличие значений дискретного спектра от значений непрерывного, полученный результат полностью совпадает с формулой исходного дискретного сигнала (3.11).
Рассмотренный пример показывает, что дискретное преобразование Фурье не всегда точно описывает спектр исходного непрерывного сигнала, подобно тому, как

Рис. 3.1. Дискретное преобразование Фурье дискретизированного треугольного импульса
дискретизированный сигнал не всегда точно описывает исходный непрерывный сигнал. Однако связь между дискретным сигналом и его дискретным преобразованием Фурье всегда носит взаимно однозначный характер и формулу прямого и обратного преобразований Фурье являются строгими при любом числе дискретных значений. Поэтому аппарат дискретных преобразований Фурье имеет самостоятельное значение и может быть применен к любым числовым последовательностям.
В этом случае формулы дискретного преобразования Фурье должны быть несколько изменены, так как для абстрактной числовой последовательности значения интервала дискретизации  и длительности сигнала
и длительности сигнала  не имеют смысла. Поэтому коэффициент
не имеют смысла. Поэтому коэффициент  перед суммой в формуле (3.4) опускают,
перед суммой в формуле (3.4) опускают,  заменяют на
заменяют на  отсчетные значения сигнала и спектра обозначают через
отсчетные значения сигнала и спектра обозначают через  и формулу дискретного преобразования Фурье записывают в виде
и формулу дискретного преобразования Фурье записывают в виде

При этом обратное дискретное преобразование Фурье имеет вид

Значения  вычисленные по формуле (3.14), отличаются от выборочных значений спектра
вычисленные по формуле (3.14), отличаются от выборочных значений спектра  непрерывного колебания
непрерывного колебания  в
в  раз. Для определения выборочных значений
раз. Для определения выборочных значений  надо значения
надо значения  вычисленные по формуле (3.14), умножить на величину интервала дискретизации по времени
вычисленные по формуле (3.14), умножить на величину интервала дискретизации по времени  :
:

Покажем, что преобразования (3.14), (3.15) являются взаимно обратными. Для этого возьмем произвольную числовую последовательность  с помощью дискретного преобразования Фурье (3.14) найдем последовательность
с помощью дискретного преобразования Фурье (3.14) найдем последовательность  и применим к ней обратное дискретное преобразование
и применим к ней обратное дискретное преобразование
Фурье (3.15). Получившуюся при этом последовательность обозначим 

Поменяем порядок суммирования и несколько преобразуем это выражение:

Внутренняя сумма выражения (3,16) равна нулю, если  и равна
и равна  если
если  Следовательно,
Следовательно,  при
при  т. е. числовые последовательности
т. е. числовые последовательности  совпадают друг с другом. Таким образом, при последовательном применении к любой числовой последовательности прямого и обратного дискретного преобразования Фурье получают в результате ту же последовательность.
совпадают друг с другом. Таким образом, при последовательном применении к любой числовой последовательности прямого и обратного дискретного преобразования Фурье получают в результате ту же последовательность.
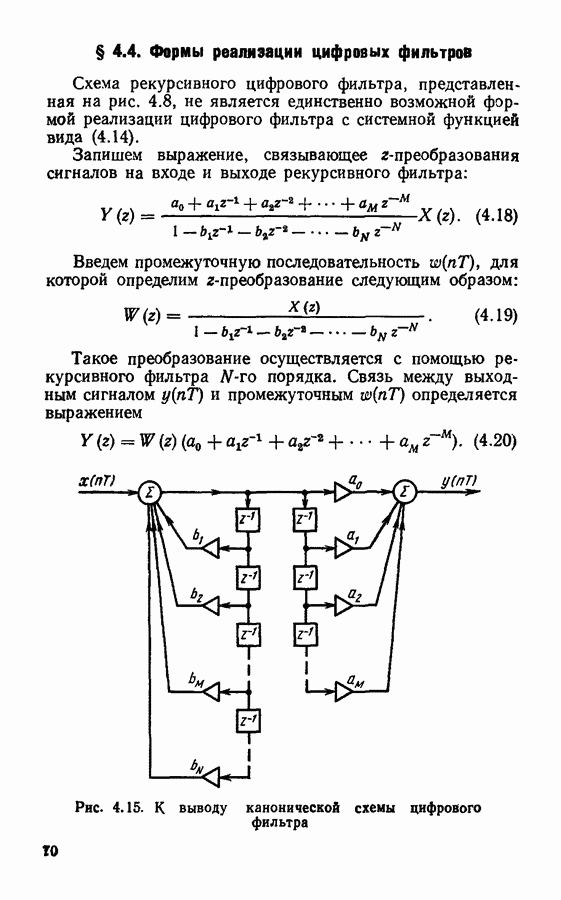
Проиллюстрируем это положение простейшими примерами.
1. Рассмотрим простейший дискретный сигнал, состоящий из одного отсчетного значения, равного а. Подставляя эту простейшую последовательность в формулу дискретного преобразования Фурье (3.14), получим  Таким образом, дискретное преобразование Фурье отдельного числового значения равно этому же значению.
Таким образом, дискретное преобразование Фурье отдельного числового значения равно этому же значению.
Подставим  в формулу обратного дискретного преобразования Фурье
в формулу обратного дискретного преобразования Фурье  . В результате, как и следовало ожидать, получим исходное значение
. В результате, как и следовало ожидать, получим исходное значение 
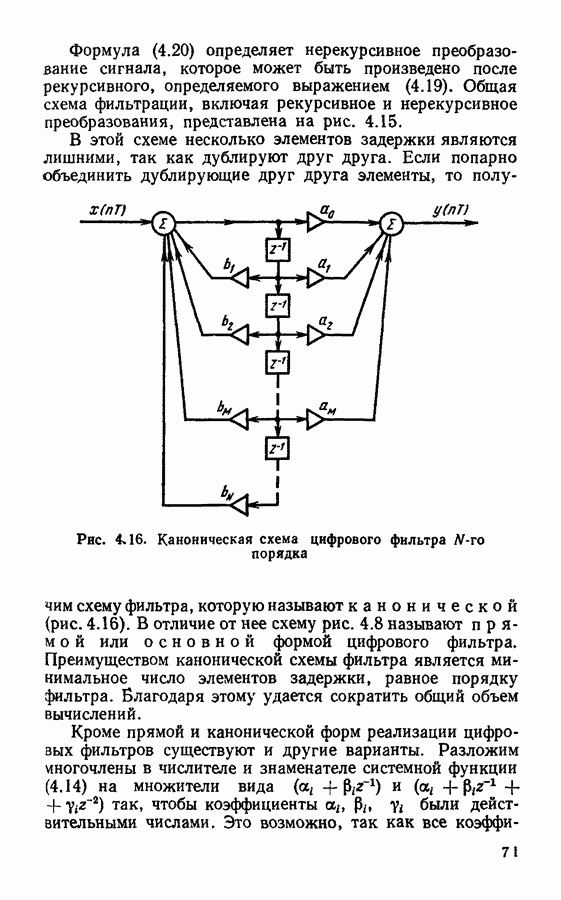
2. Рассмотрим более сложный сигнал, состоящий из двух отсчетных значений  и Применим к нему дискретное преобразование Фурье
и Применим к нему дискретное преобразование Фурье 

Следовательно, 
Применяя к этому результату обратное преобразование Фурье (3.14), получим

Одно из основных применений дискретного преобразования Фурье — это вычисление спектров функций, заданных графически или таблично. Дискретное преобразование Фурье можно применять при обработке экспериментальных данных, например в тех случаях, когда надо найти энергетический спектр по корреляционной функции сигнала.
Другое важное применение дискретного преобразования Фурье — вычисление сигнала на выходе фильтра с заданной частотной характеристикой. Если задан входной сигнал  то для него можно вычислить дискретное преобразование Фурье
то для него можно вычислить дискретное преобразование Фурье  Если теперь умножим на частотную характеристику фильтра, то получим дискретное преобразование Фурье выходного сигнала:
Если теперь умножим на частотную характеристику фильтра, то получим дискретное преобразование Фурье выходного сигнала:  После этого с помощью обратного дискретного преобразования Фурье можно найти сигнал на выходе фильтра.
После этого с помощью обратного дискретного преобразования Фурье можно найти сигнал на выходе фильтра.
Если входной сигнал имеет большую длительность, его обработку с помощью дискретного преобразования Фурье можно производить по частям. Для этого берут первые N отсчетов входного сигнала, вычисляют их дискретное преобразование Фурье и после умножения на частотную характеристику фильтра с помощью обратного дискретного преобразования Фурье вычисляют первые N отсчетов выходного сигнала. После этого аналогичным путем обрабатывают следующие N отсчетов входного сигнала и т. д. Для повышения точности обработки сигнала обрабатываемые серии отсчетов могут частично перекрываться.
Преимуществом такого метода обработки сигналов является отсутствие каких-либо ограничений на вид частотной характеристики фильтра. Например, частотная характеристика может быть идеальной прямоугольной формы, что невозможно реализовать с помощью обычных фильтров.
Обработку сигналов с помощью дискретного преобразования Фурье нельзя назвать цифровой фильтрацией в полном смысле слова. Обычные цифровые фильтры, работающие в реальном масштабе времени, производят обработку сигнала непрерывно по мере его поступления, а вычисление выходного сигнала с помощью дискретного преобразования Фурье может быть произведено лишь после того, как станет известным полностью входной сигнал или хотя бы первая серия из N его отсчетов. Поэтому при использовании дискретного преобразования Фурье выходной сигнал может быть получен только с некоторым
запаздыванием по отношению к входному сигналу. Однако в ряде практических применений такое запаздывание выходного сигнала не играет существенной роли, и тогда обработка сигналов с использованием дискретного преобразования Фурье оказывается целесообразной.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
- Спектры дискретизированных сигналов.
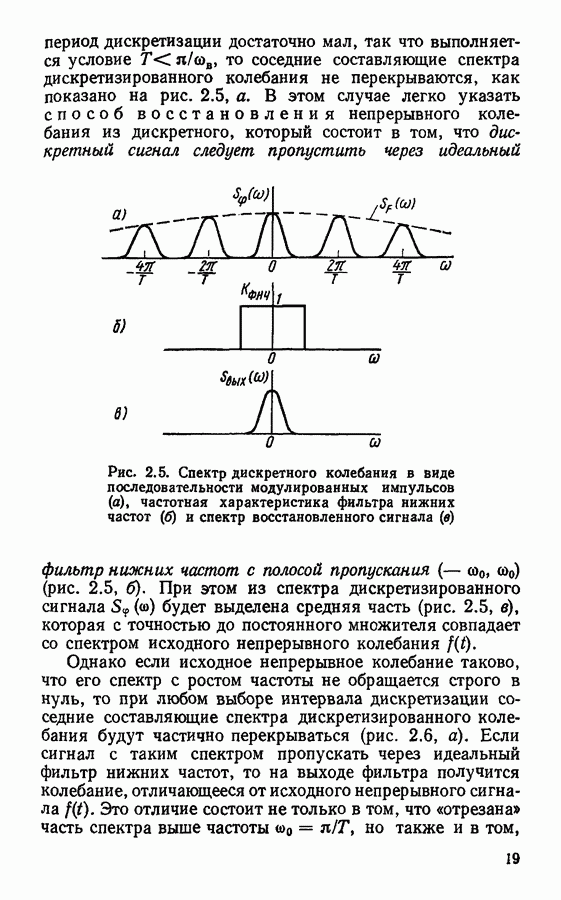
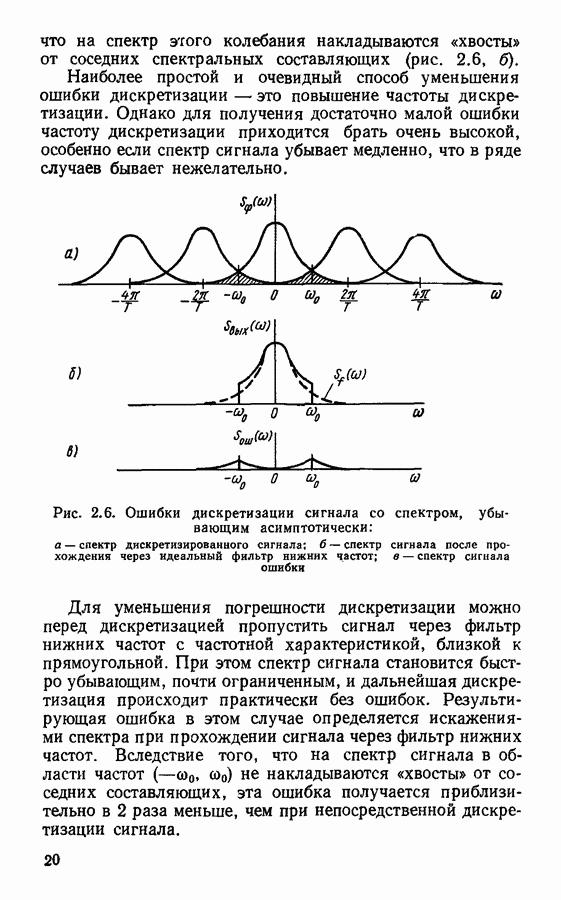
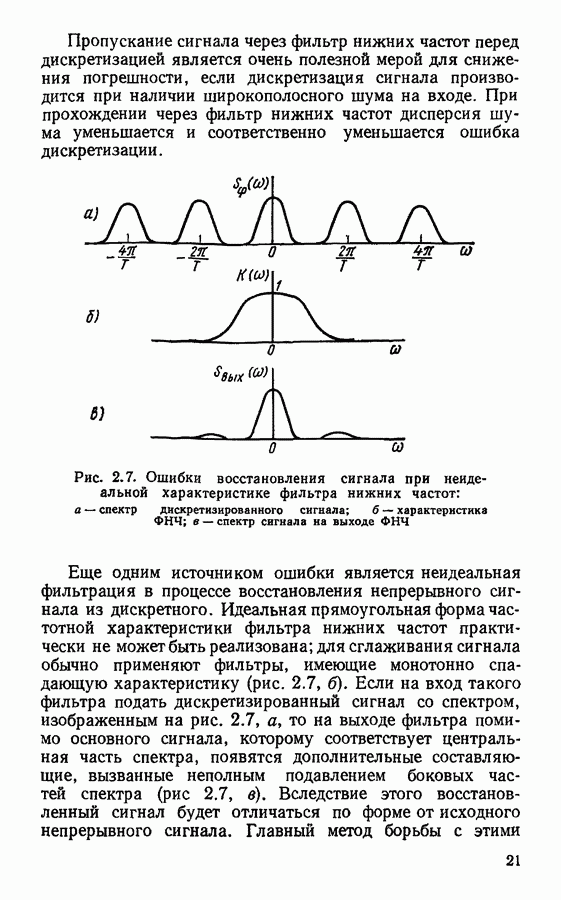
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
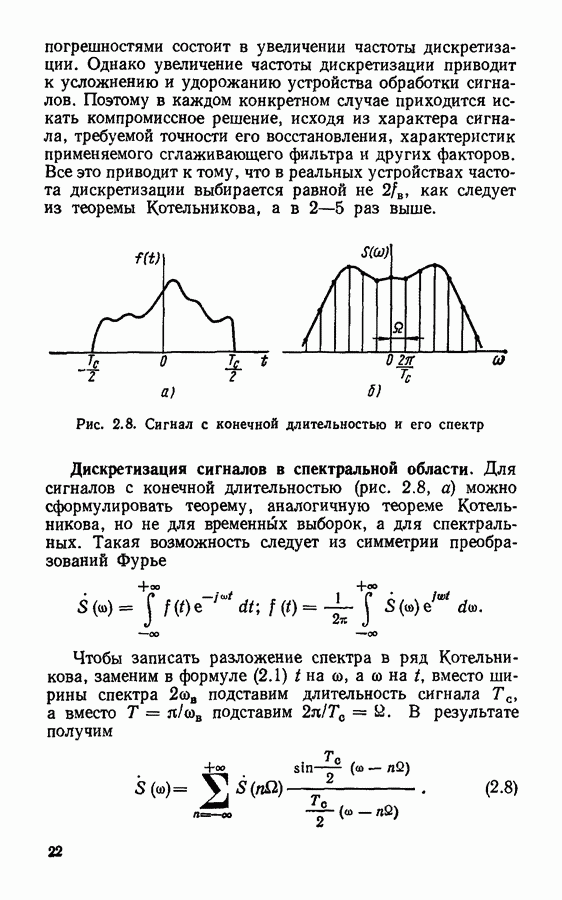
- Дискретизация сигналов в спектральной области.
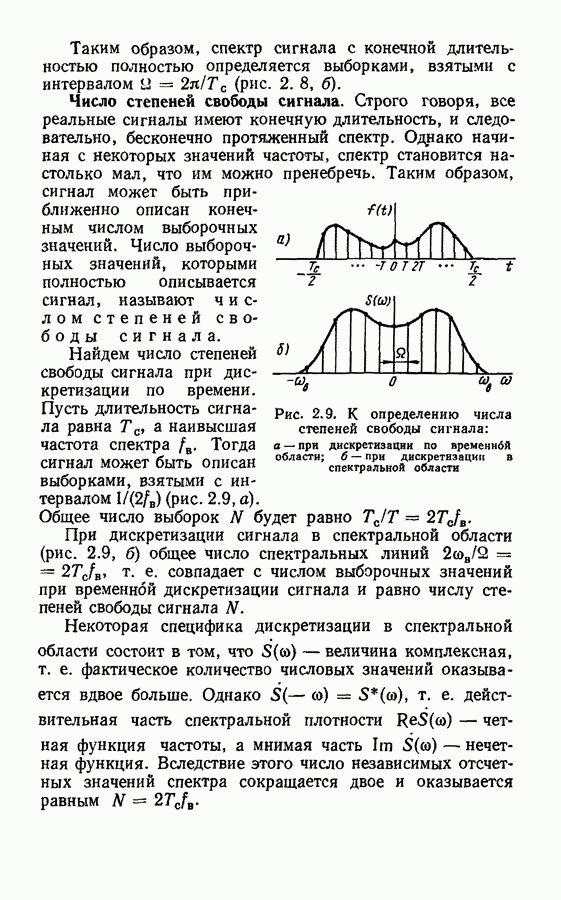
- Число степеней свободы сигнала.
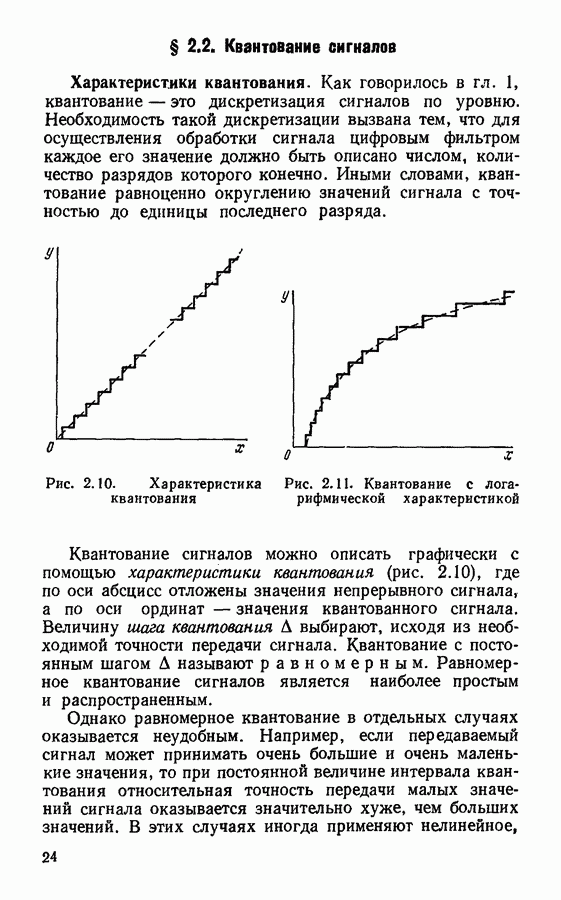
- § 2.2. Квантование сигналов
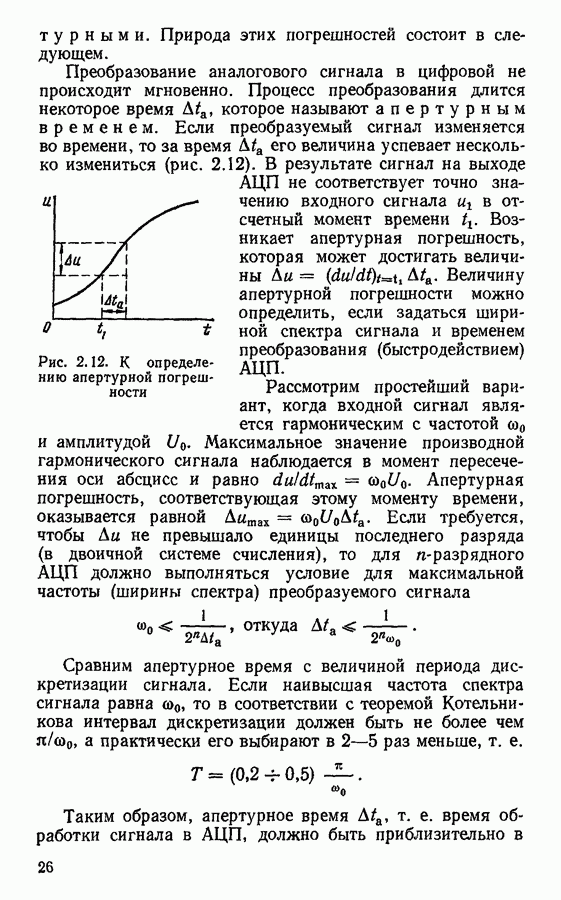
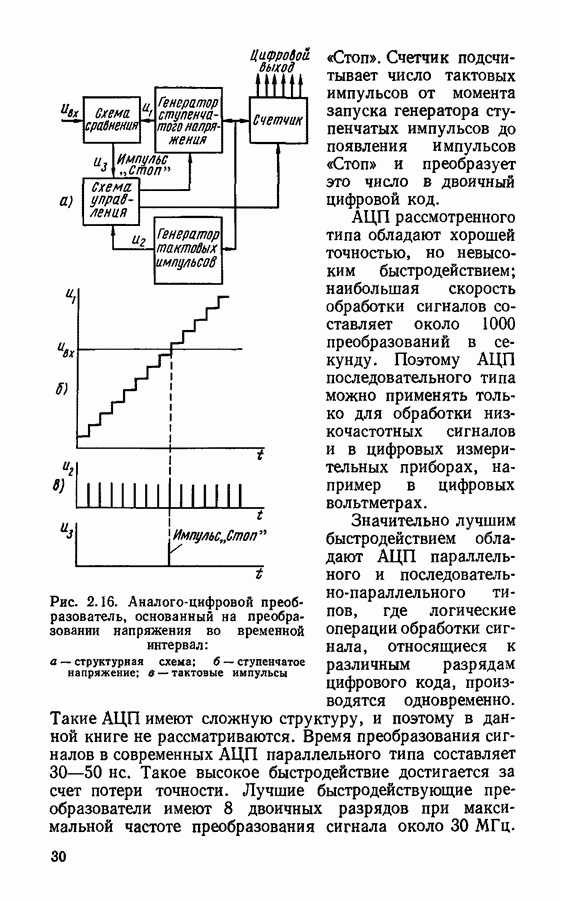
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
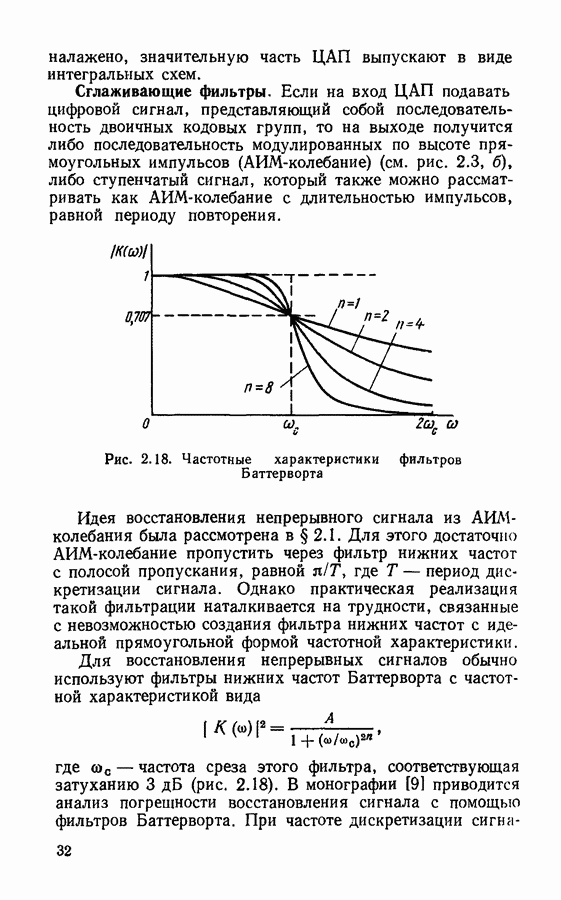
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
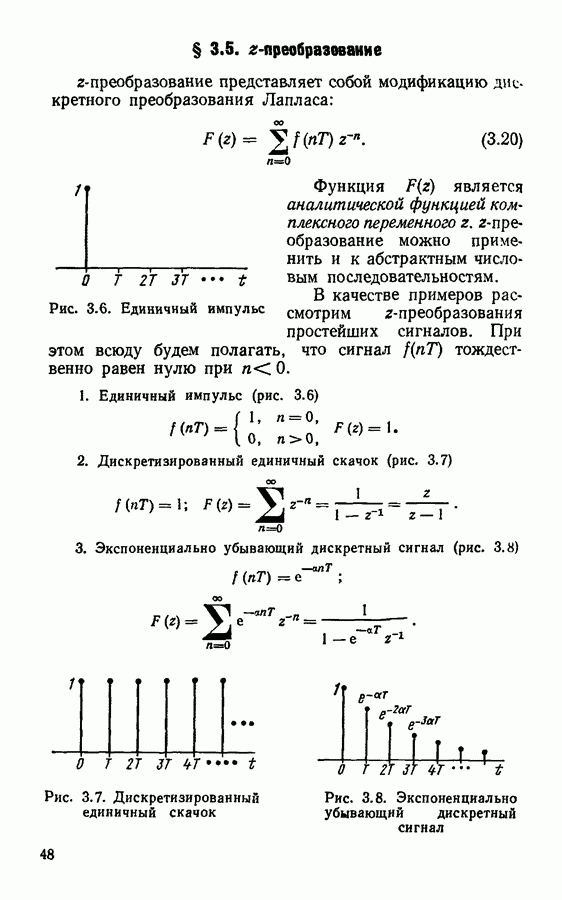
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
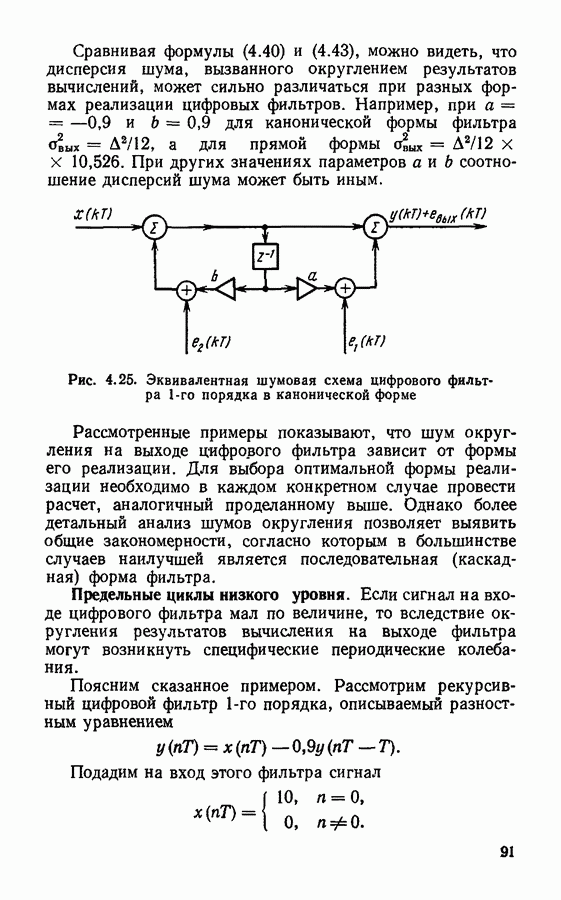
- § 4.4. Формы реализации цифровых фильтров
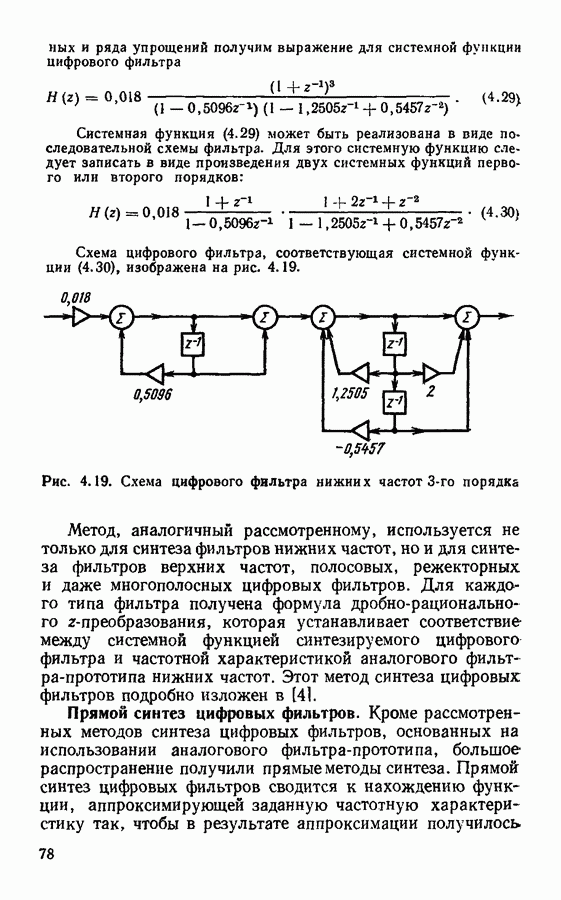
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
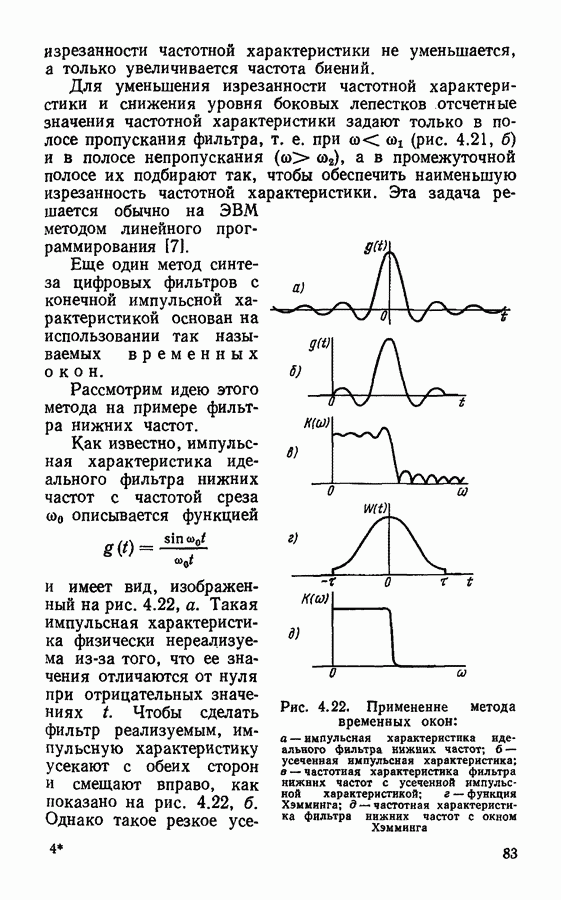
- Методы синтеза фильтров с конечной импульсной характеристикой.
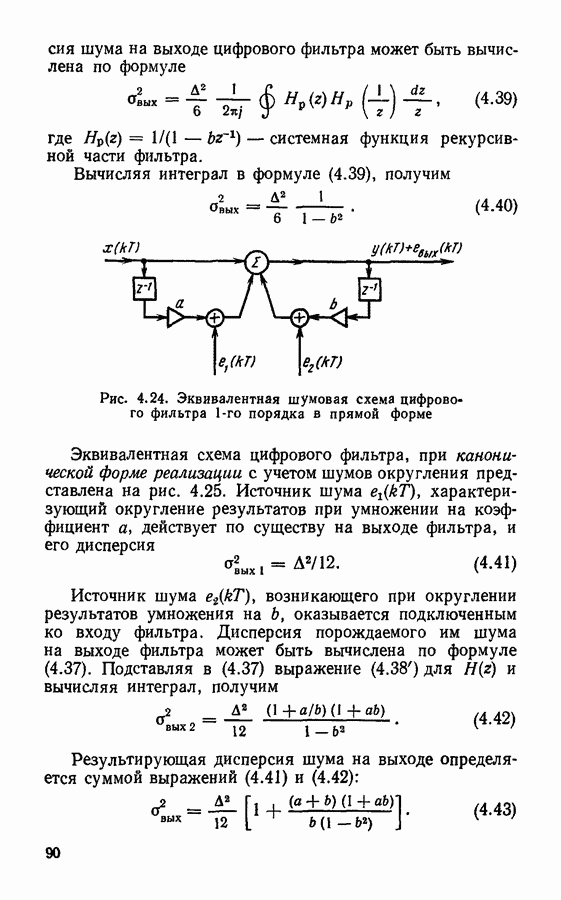
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА