| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
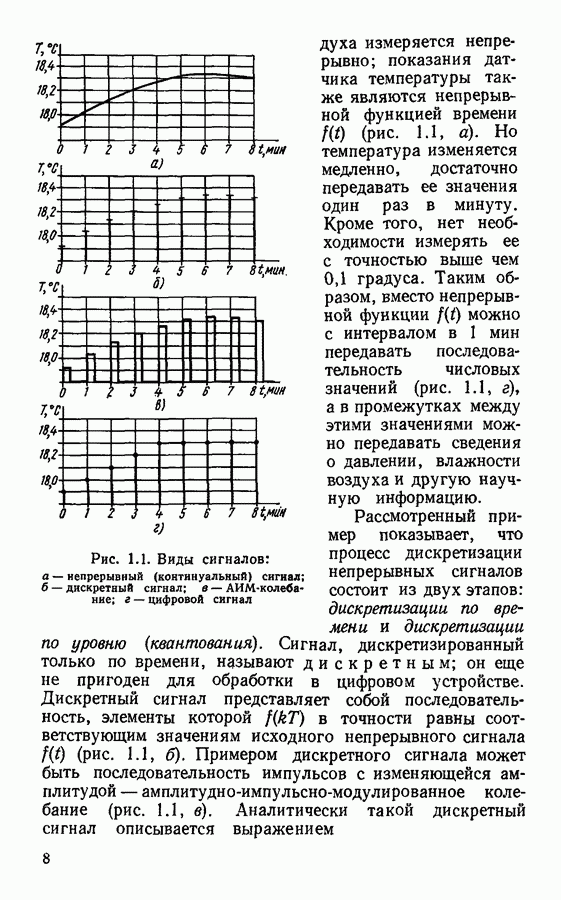
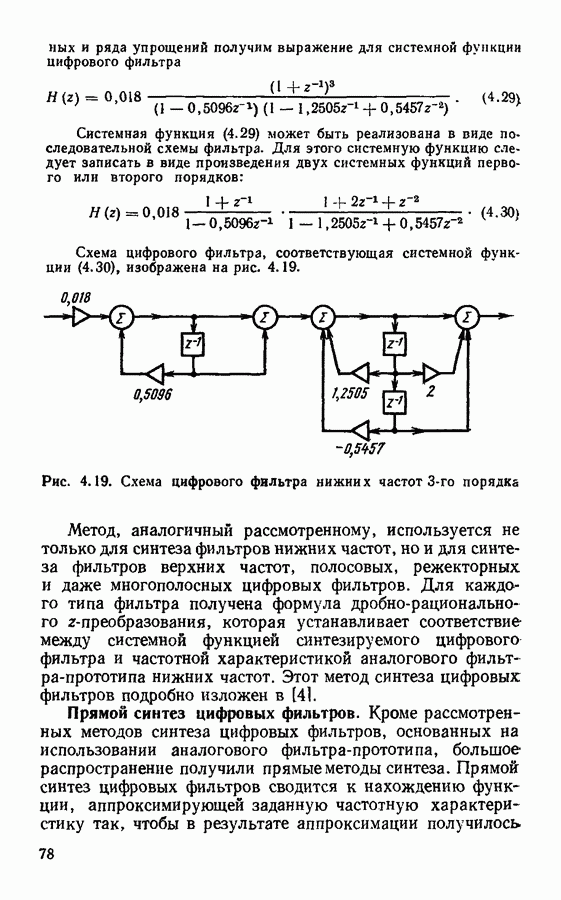
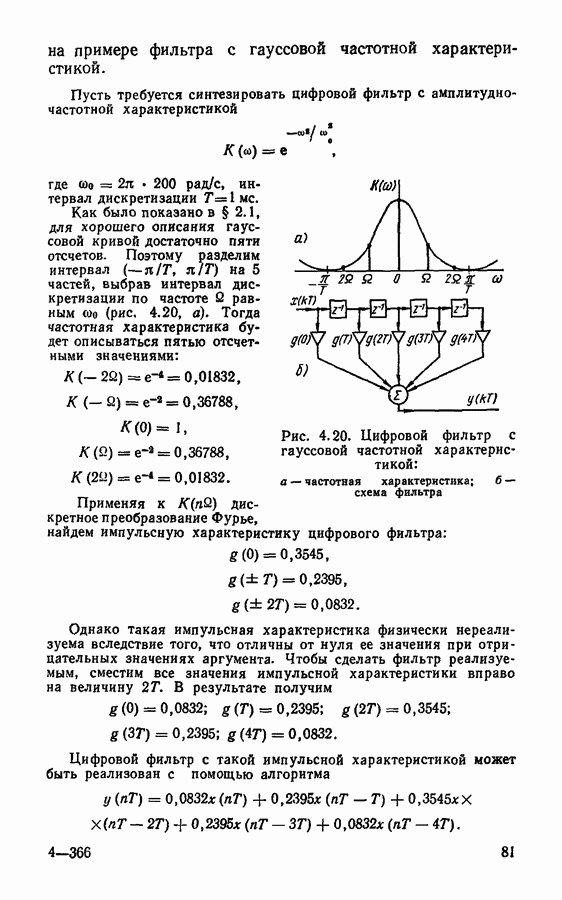
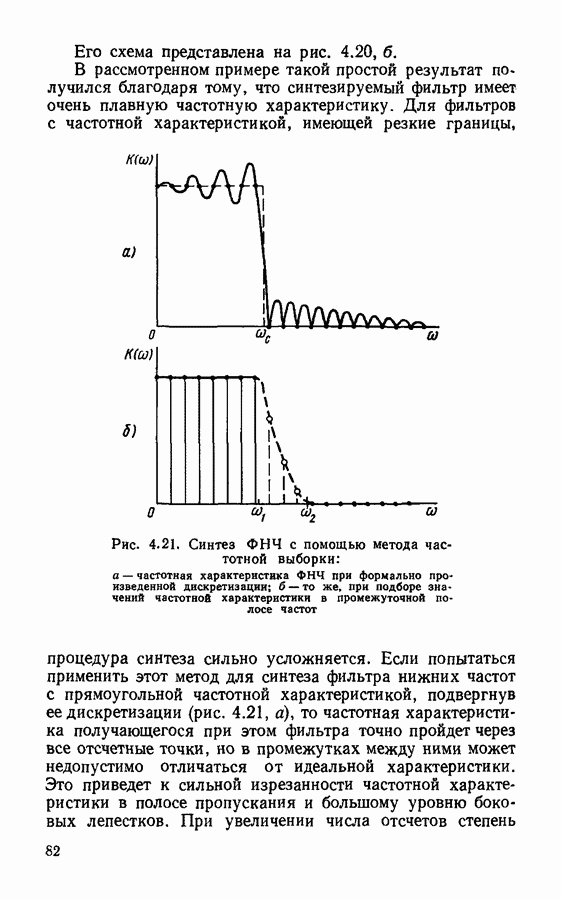
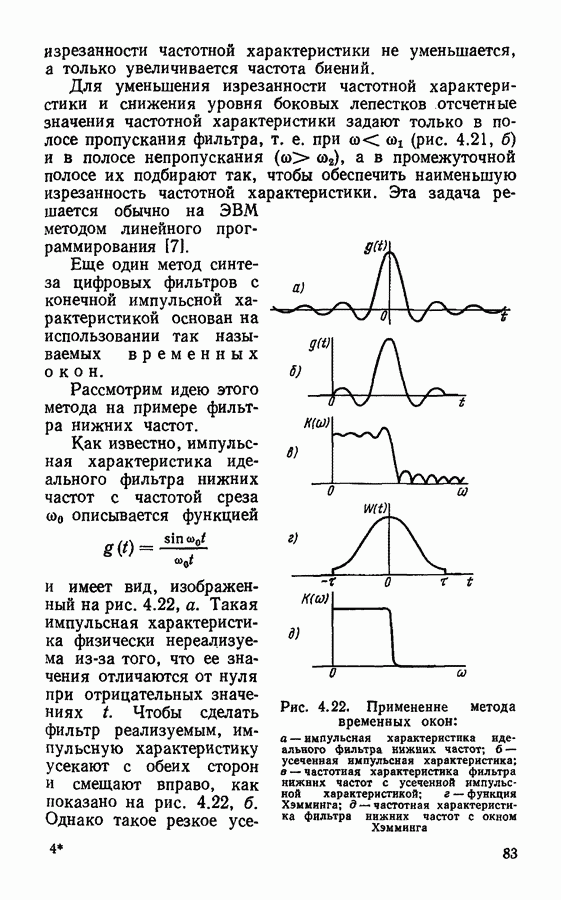
§ 4.3. Частотные характеристики цифровых фильтров
До сих пор мы не рассматривали такую важную характеристику цифрового фильтра, как частотная, В какой-то мере роль частотной характеристики играет системная функция. Однако использовать только системную функцию не всегда удобно, особенно при рассмотрении цифровых систем обработки сигналов, аналогичных фильтрам верхних частот, фильтрам нижних частот, полосовым и режекторным фильтрам. Как известно, для описания аналоговых фильтров часто используют частотную характеристику (частотный коэффициент передачи). Поскольку система цифровой обработки сигналов должна выполнять те же функции, что и аналоговый фильтр, для такой системы в целом и для входящих в нее цифровых фильтров также следует определить частотную характеристику.
Частотная характеристика (частотный коэффициент передачи) аналогового фильтра может быть определена как отношение спектра сигнала на выходе фильтра  при некотором воздействии к спектру входного сигнала
при некотором воздействии к спектру входного сигнала 

В качестве входного сигнала удобно использовать обобщенный гармонический сигнал  тогда сигнал на выходе имеет вид
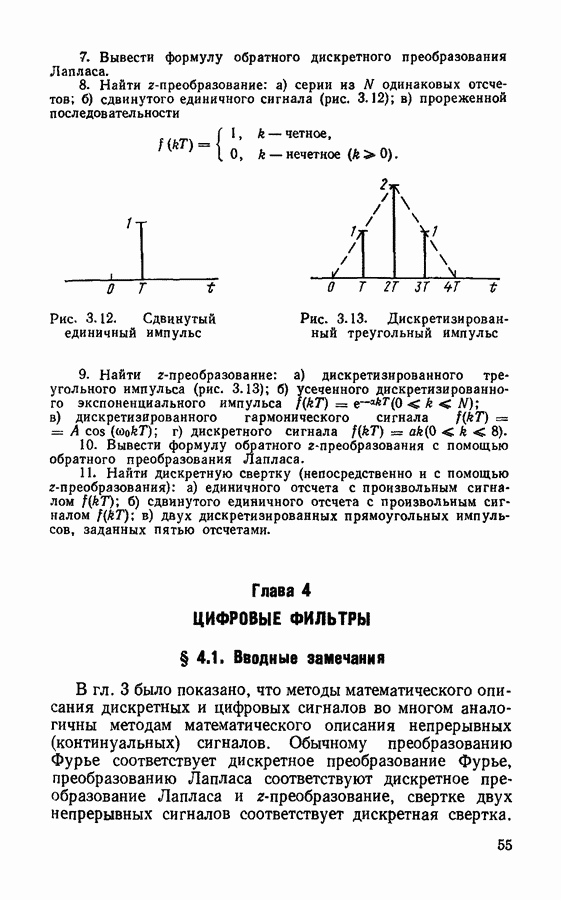
тогда сигнал на выходе имеет вид 
Для определения частотной характеристики цифрового фильтра на его вход (точнее говоря, на вход дискретного фильтра, так как эффекты квантования мы не учитываем) подают дискретизированный сигнал  . Тогда сигнал на выходе будет иметь вид
. Тогда сигнал на выходе будет иметь вид 
Частотная характеристика цифрового фильтра имеет некоторые специфические свойства. Главное из них — это
периодичность. На вход цифрового фильтра подают дискретизированный сигнал  с интервалом дискретизации
с интервалом дискретизации  для конкретного типа фильтра интервал
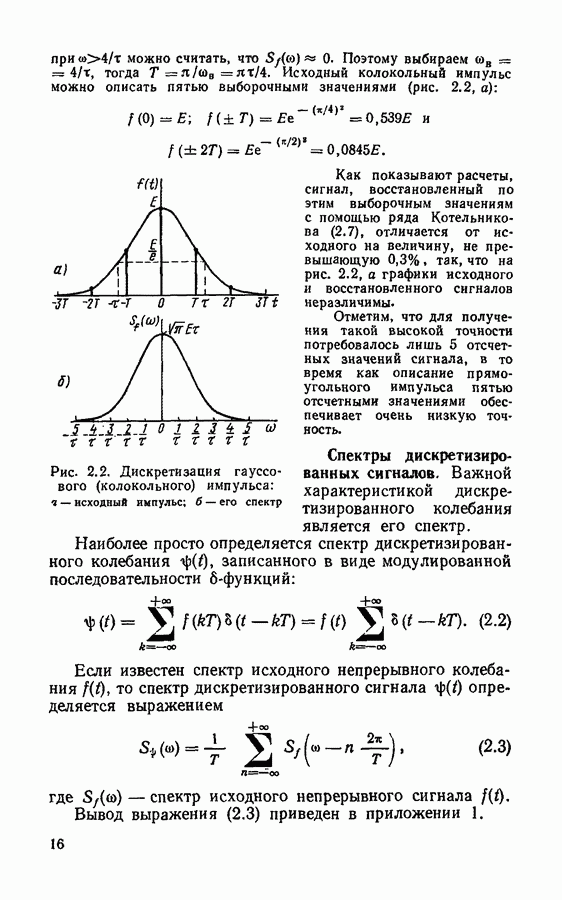
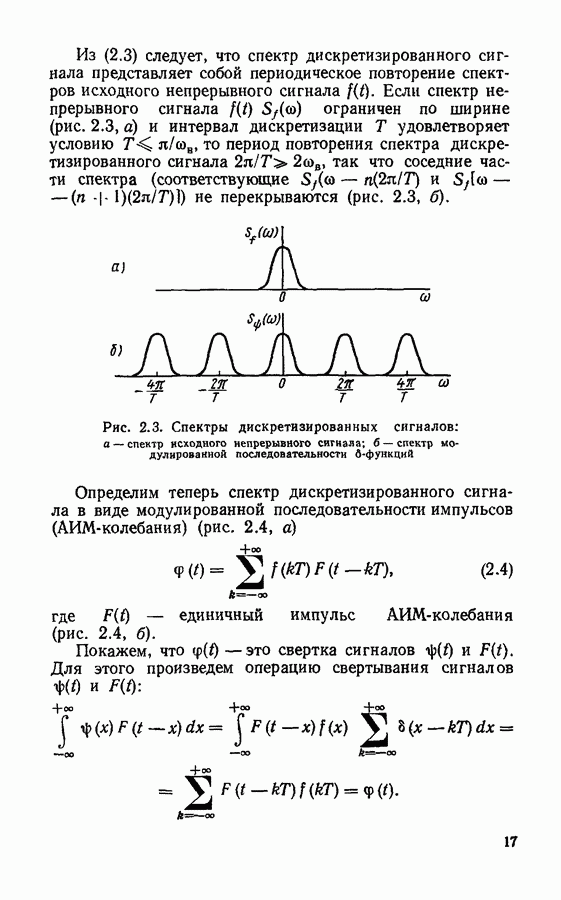
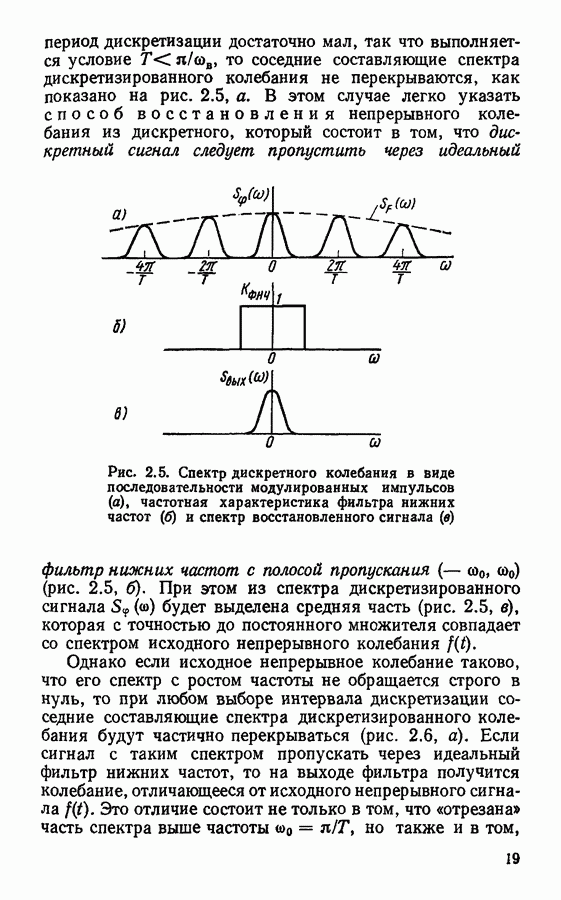
для конкретного типа фильтра интервал  —фиксированная величина. Спектр входного дискретизированного сигнала представляет собой периодическую функцию (см. рис. 2.4) с периодом
—фиксированная величина. Спектр входного дискретизированного сигнала представляет собой периодическую функцию (см. рис. 2.4) с периодом 

Сигнал на выходе цифрового фильтра также представляет собой последовательность отсчетов, взятых с интервалом  Его спектр тоже описывается периодической функцией с тем же периодом
Его спектр тоже описывается периодической функцией с тем же периодом 


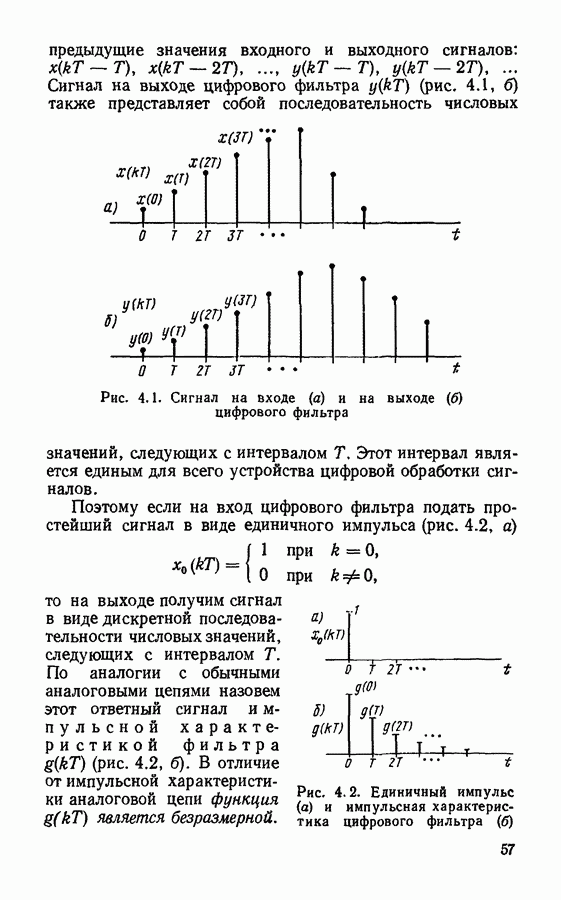
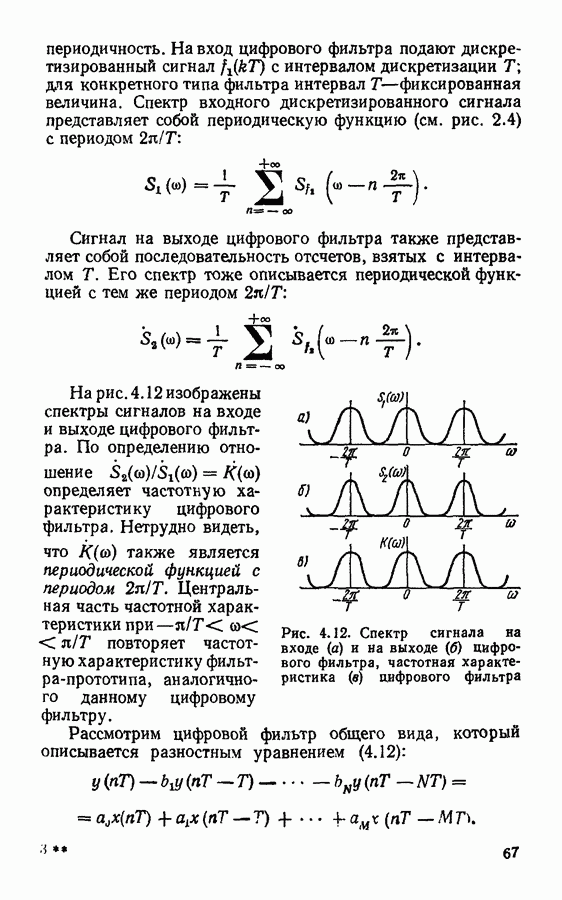
Рис. 4.12. Спектр сигнала на входе  и на выходе
и на выходе  цифрового фильтра, частотная характеристика
цифрового фильтра, частотная характеристика  цифрового фильтра
цифрового фильтра
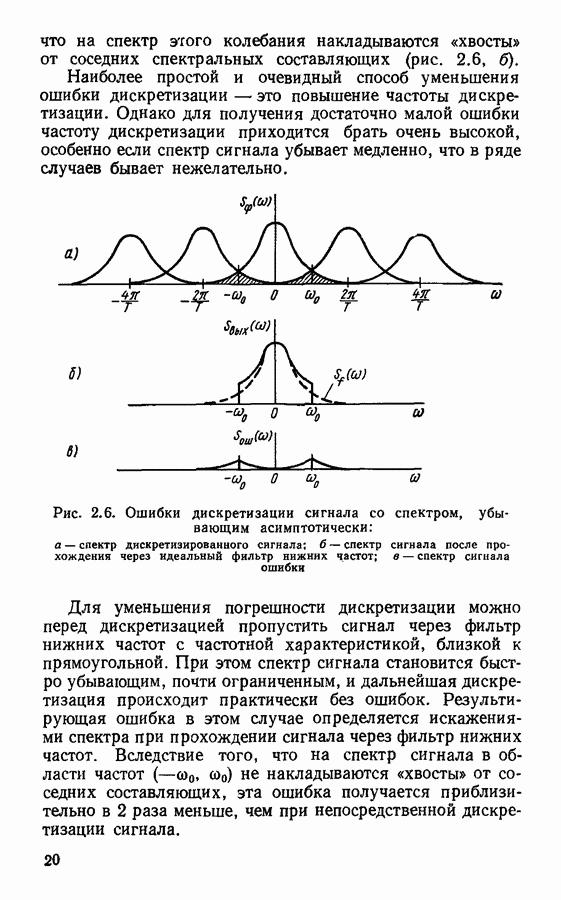
На рис. 4.12 изображены спектры сигналов на входе и выходе цифрового фильтра. По определению отношение  определяет частотную характеристику цифрового фильтра. Нетрудно видеть, что
определяет частотную характеристику цифрового фильтра. Нетрудно видеть, что  также является периодической функцией с периодом
также является периодической функцией с периодом  Центральная часть частотной характеристики при
Центральная часть частотной характеристики при  повторяет частотную характеристику фильтра-прототипа, аналогичного данному цифровому фильтру.
повторяет частотную характеристику фильтра-прототипа, аналогичного данному цифровому фильтру.
Рассмотрим цифровой фильтр общего вида, который описывается разностным уравнением (4.12):

Пусть входной сигнал  Тогда, по определению, сигнал на выходе фильтра
Тогда, по определению, сигнал на выходе фильтра  Подставляя выражения для
Подставляя выражения для  в уравнение (4.12), получим
в уравнение (4.12), получим

откуда

Выражение (4.15) совпадает с выражением (4.14) для системной функции фильтра, если  заменить на
заменить на  Таким образом, установлена простая связь между частотной характеристикой фильтра и его системной функцией:
Таким образом, установлена простая связь между частотной характеристикой фильтра и его системной функцией:

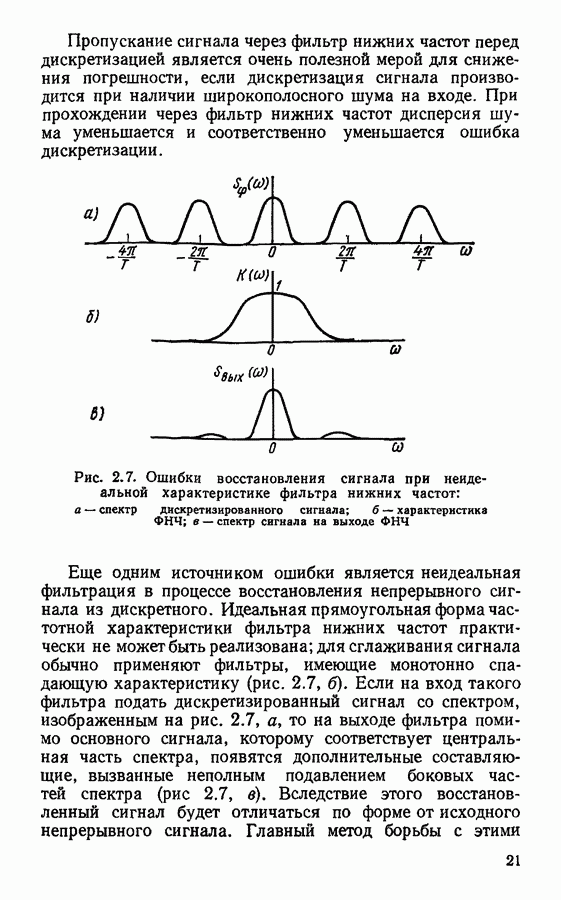
Из выражения (4.16) следуют многие свойства частотной характеристики цифровых фильтров, в частности периодичность. Соотношение (4.16) позволяет определить положение нулей и полюсов частотной характеристики  по известному положению особых точек системной функции
по известному положению особых точек системной функции  . И наконец, формула (4.16) позволяет записать связь между частотной характеристикой цифрового фильтра и его импульсной характеристикой. Заменяя в формуле
. И наконец, формула (4.16) позволяет записать связь между частотной характеристикой цифрового фильтра и его импульсной характеристикой. Заменяя в формуле  на
на  получим
получим

Таким образом, частотная характеристика цифрового фильтра связана с импульсной характеристикой соотношением, подобным дискретному преобразованию Фурье (3.3).
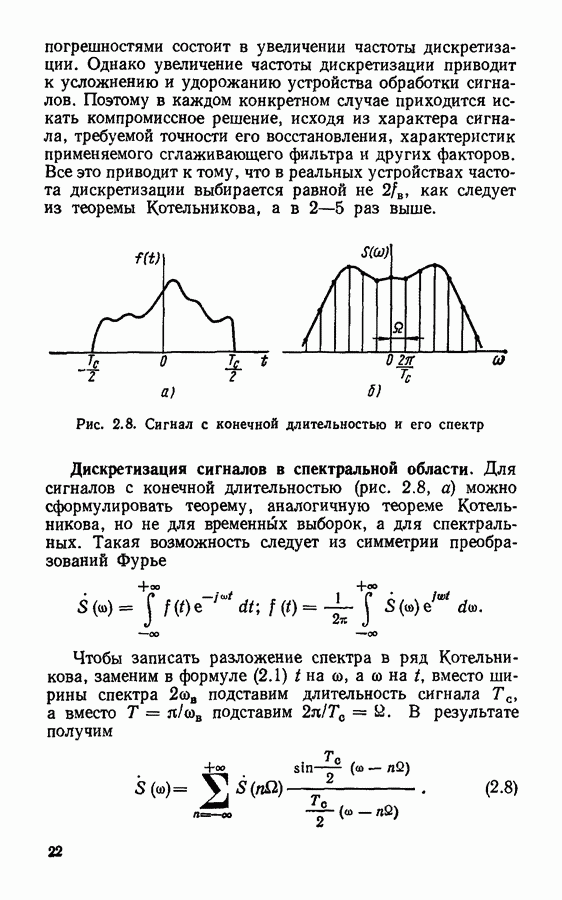
В качестве примера рассмотрим цифровой фильтр  порядка, аналогичный
порядка, аналогичный  -цепи, с импульсной характеристикой
-цепи, с импульсной характеристикой  Системная функция такого фильтра определяется выражением
Системная функция такого фильтра определяется выражением

Заменяя  на
на  получим выражение для частотной характеристики
получим выражение для частотной характеристики

откуда найдем амплитудно-частотную характеристику

и фазо-частотную характеристику цифрового фильтра


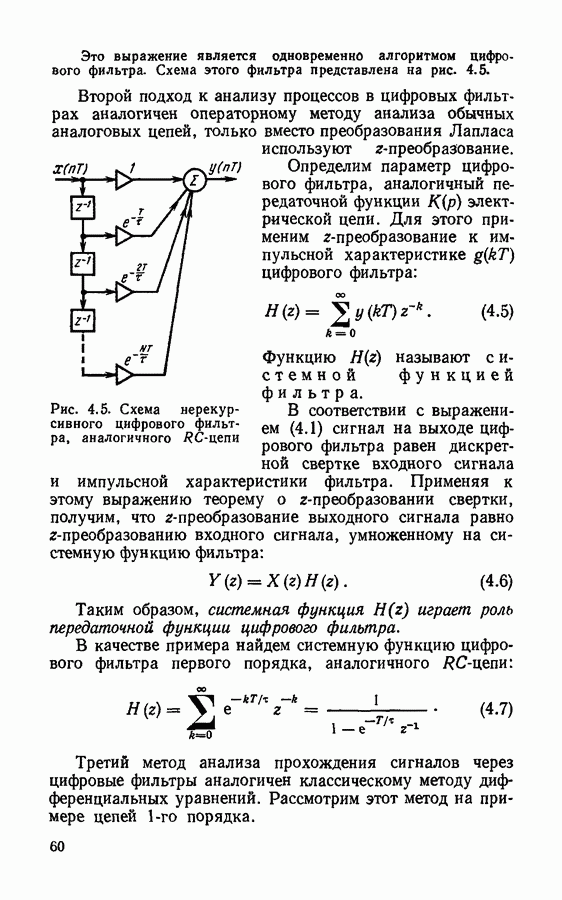
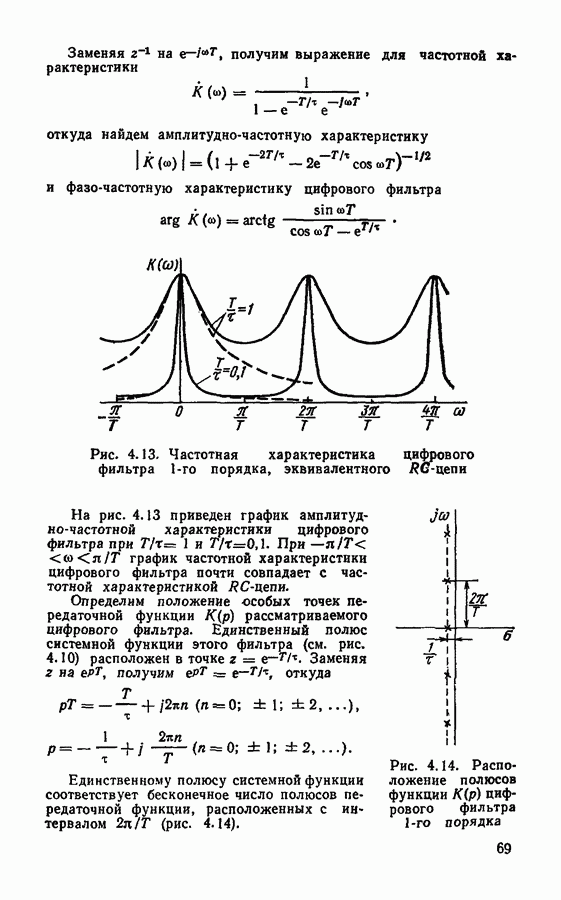
Рис. 4.13, Частотная характеристика цифрового фильтра  порядка, эквивалентного
порядка, эквивалентного  -цепи
-цепи
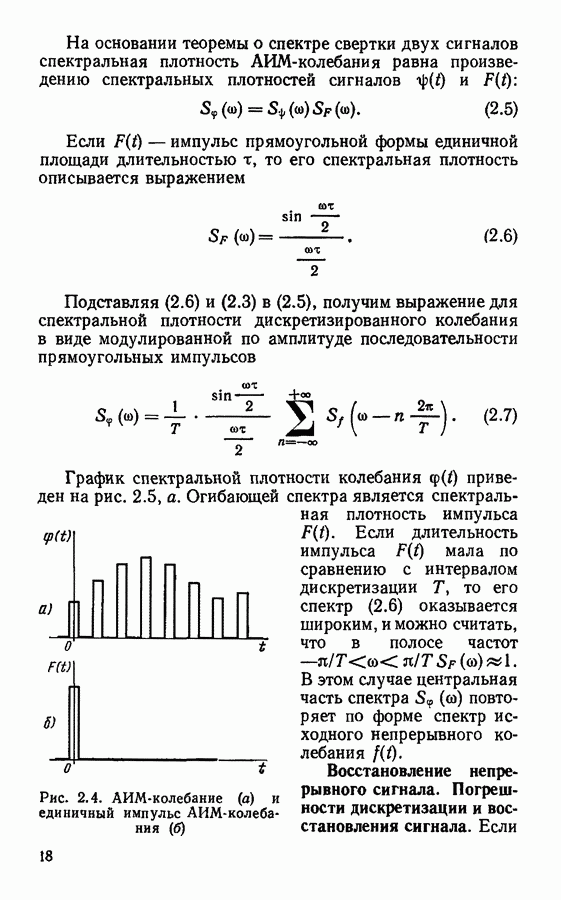
На рис. 4.13 приведен график амплитудно-частотной характеристики цифрового фильтра при  При
При  график частотной характеристики цифрового фильтра почти совпадает с частотной характеристикой
график частотной характеристики цифрового фильтра почти совпадает с частотной характеристикой  -цепи.
-цепи.
Определим положение особых точек передаточной функции  рассматриваемого цифрового фильтра. Единственный полюс системной функции этого фильтра
рассматриваемого цифрового фильтра. Единственный полюс системной функции этого фильтра  рис. 4.10) расположен в точке
рис. 4.10) расположен в точке  Заменяя
Заменяя  на
на  получим
получим  откуда
откуда

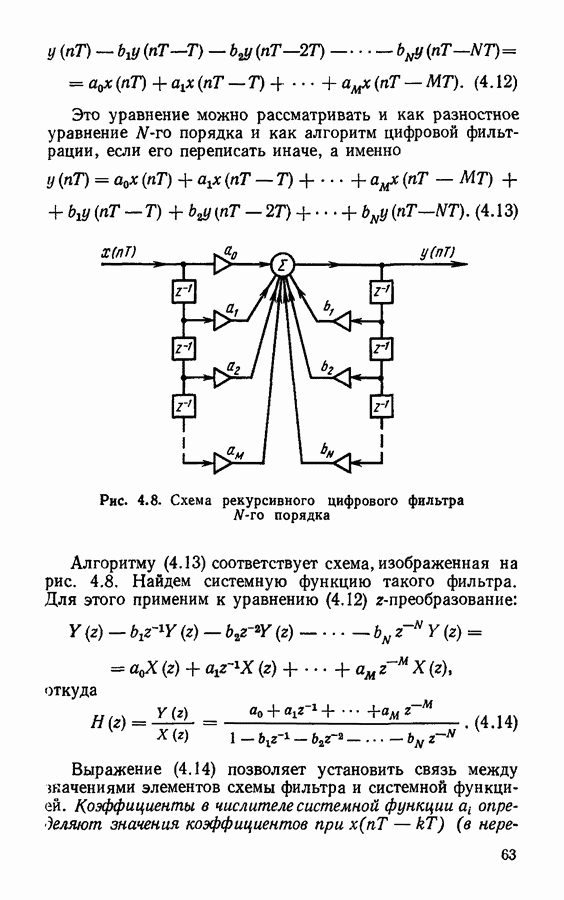
Единственному полюсу системной функции соответствует бесконечное число полюсов передаточной функции, расположенных с интервалом  (рис. 4.14).
(рис. 4.14).

Рис. 4.14. Расположение полюсов функции  цифрового фильтра
цифрового фильтра  порядка
порядка
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
- Спектры дискретизированных сигналов.
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
- Дискретизация сигналов в спектральной области.
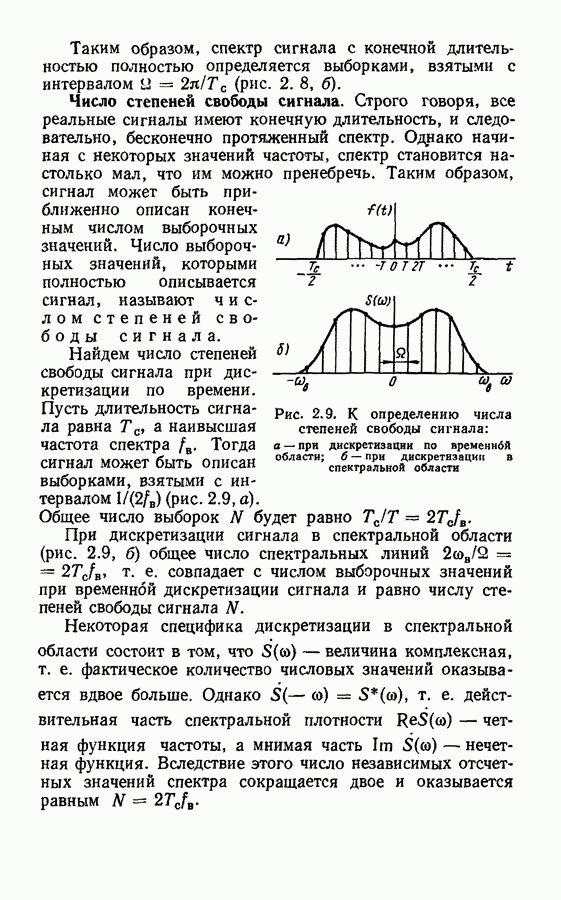
- Число степеней свободы сигнала.
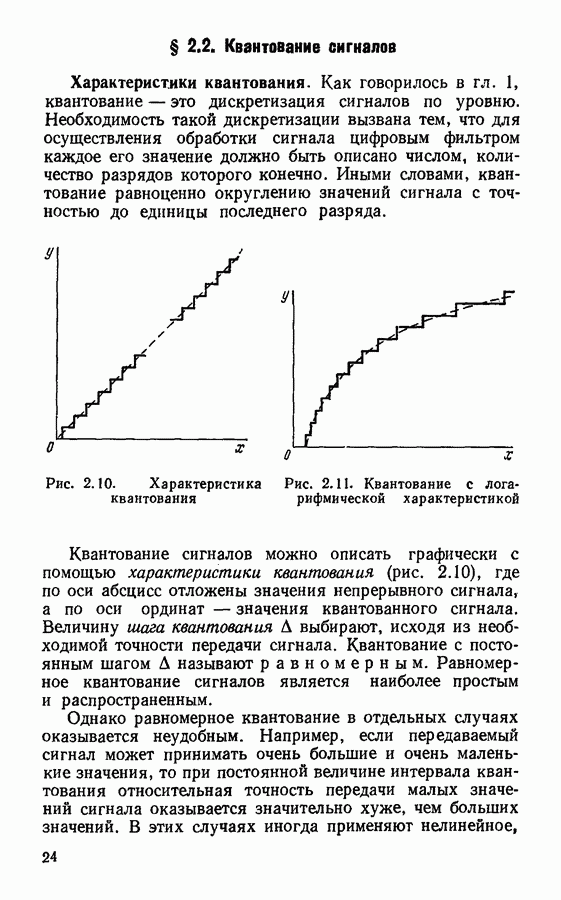
- § 2.2. Квантование сигналов
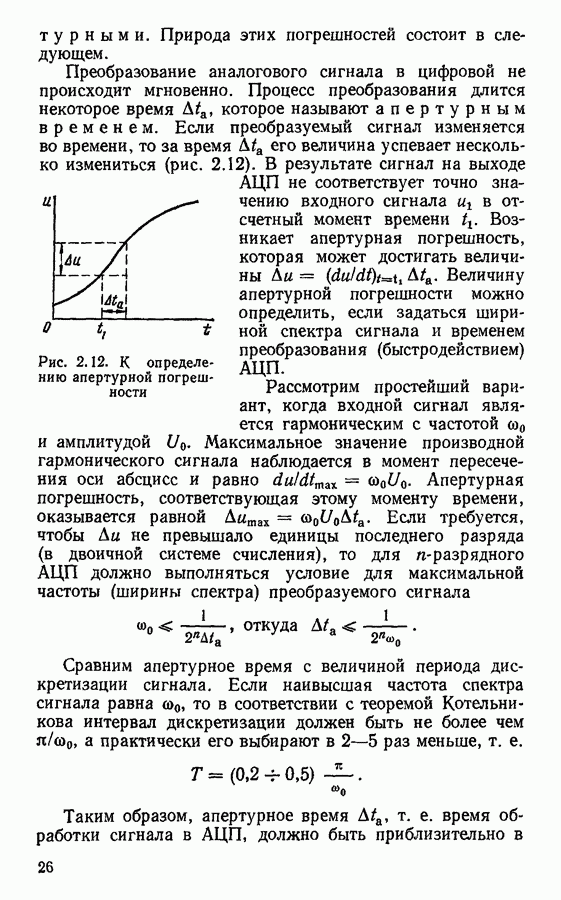
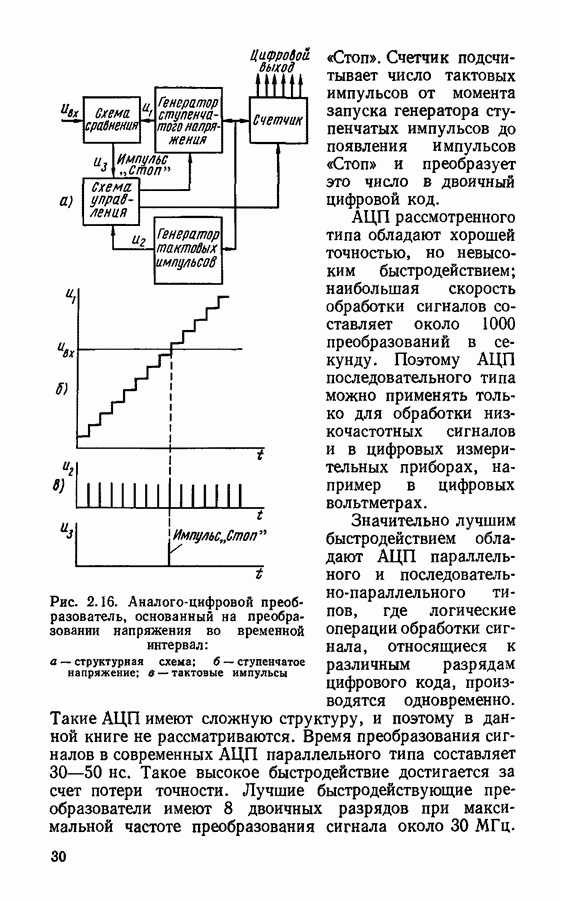
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
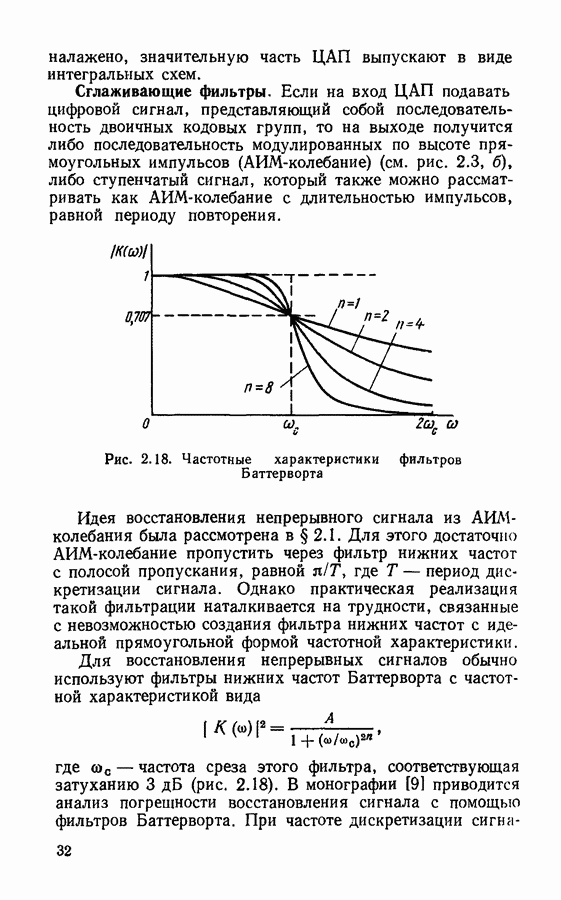
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
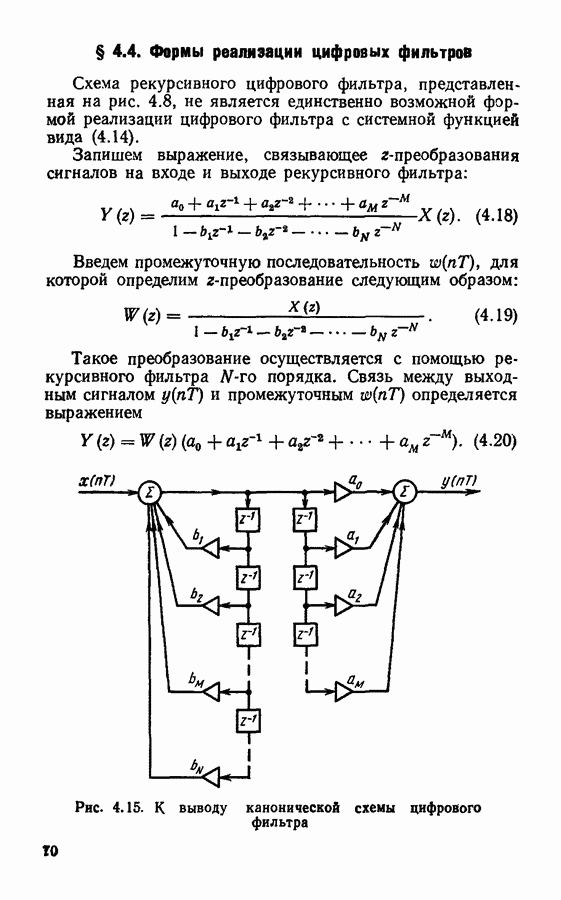
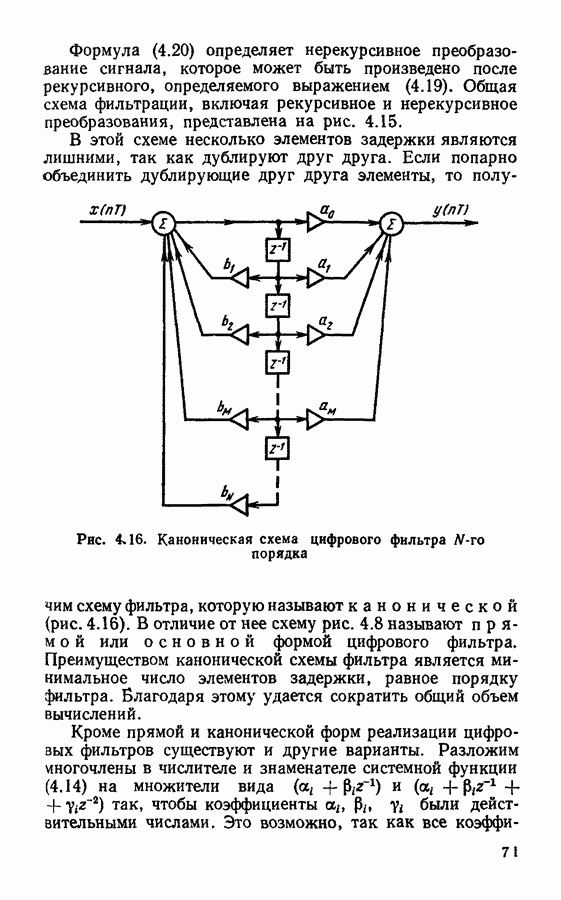
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
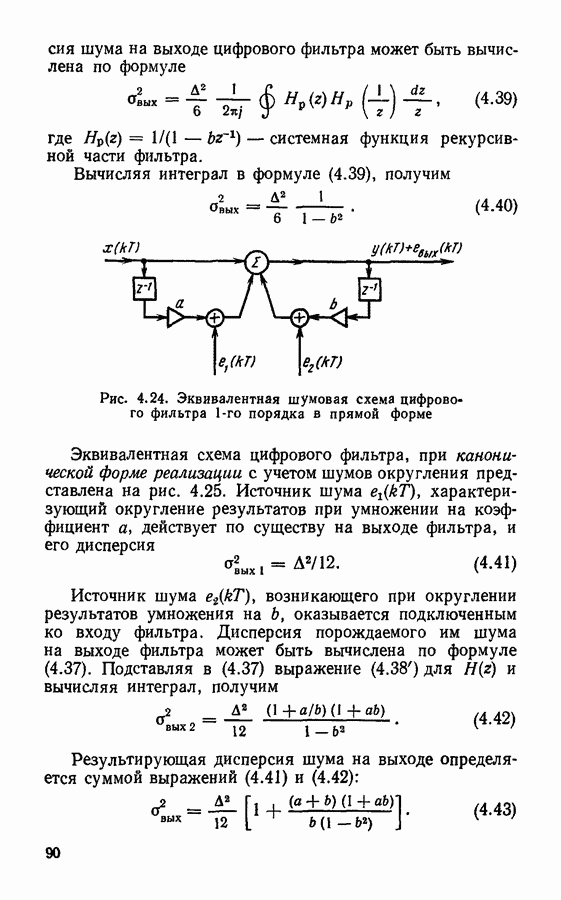
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
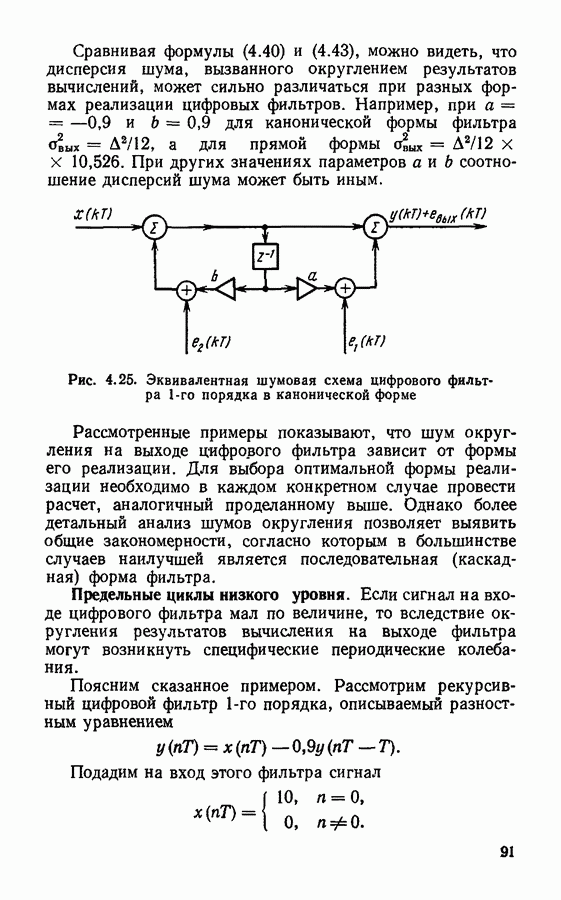
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА