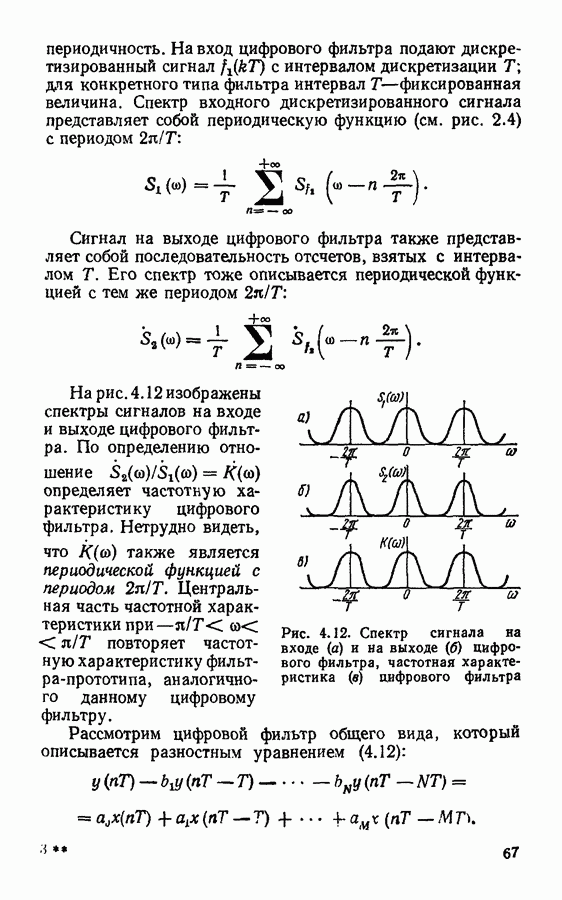
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
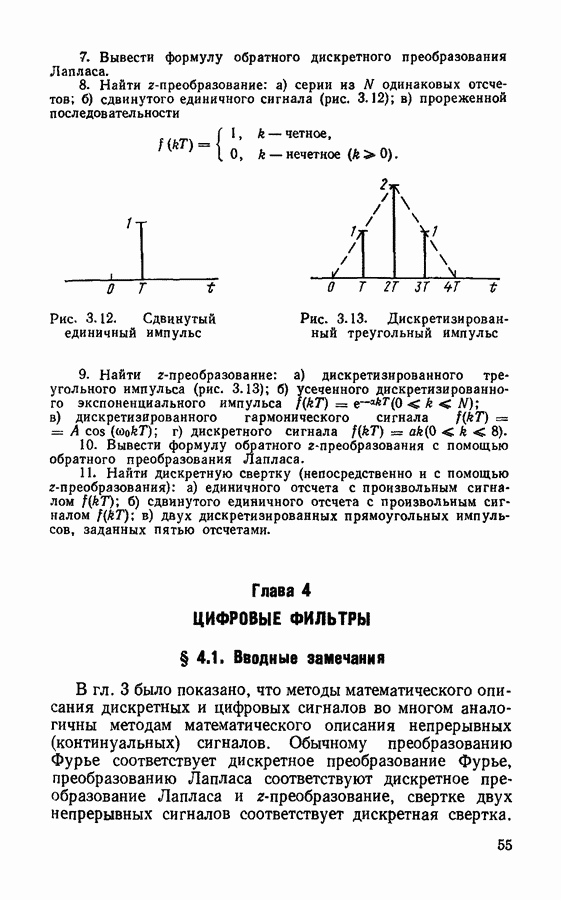
Ошибки, вызванные квантованием результатов вычислений.
При обработке сигналов в цифровых фильтрах производится ряд арифметических операций: умножение значений сигнала на постоянные коэффициенты и суммирование. В арифметических устройствах, в которых используются числа с фиксированной запятой, сложение чисел не приводит к увеличению числа разрядов, а при умножении число разрядов возрастает и возникает необходимость округления результатов вычисления. Каждое такое округление приводит к появлению ошибки, аналогичной шуму квантования.
Для анализа ошибок округления результатов вычисления каждый из источников ошибок заменяется на схеме цифрового фильтра источником шума  включенным в соответствующую часть схемы. Общее число таких источников должно быть равно числу умножений.
включенным в соответствующую часть схемы. Общее число таких источников должно быть равно числу умножений.
Рассмотрим расчет шумов округления на примере цифрового фильтра  порядка с системной функцией
порядка с системной функцией

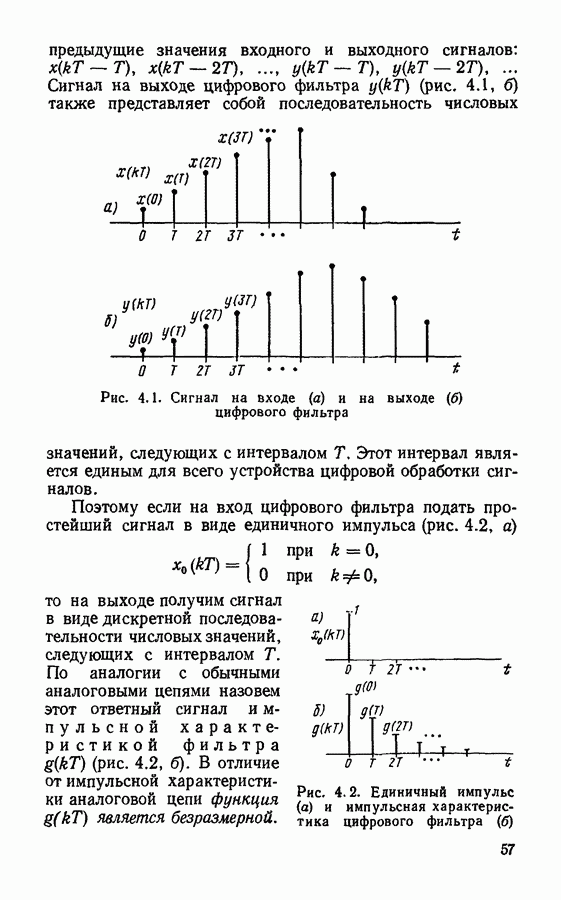
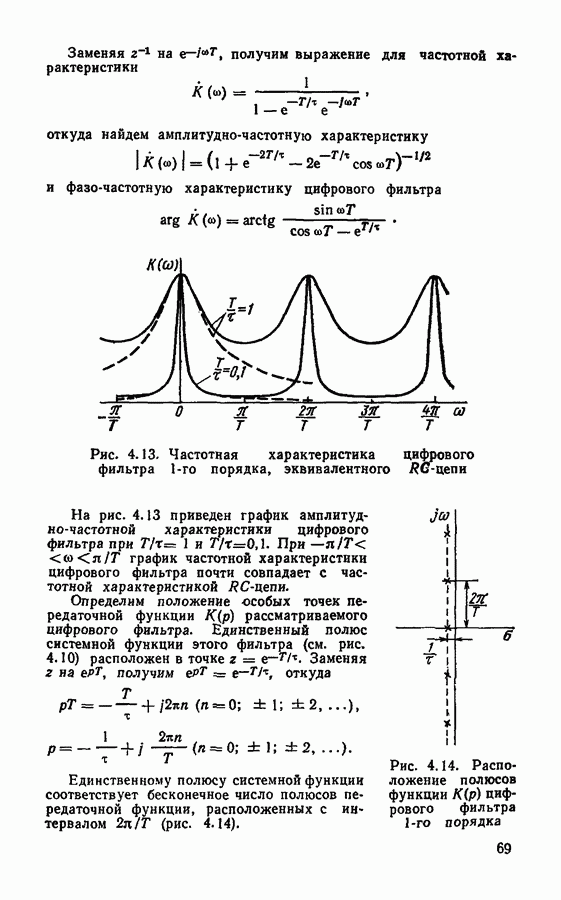
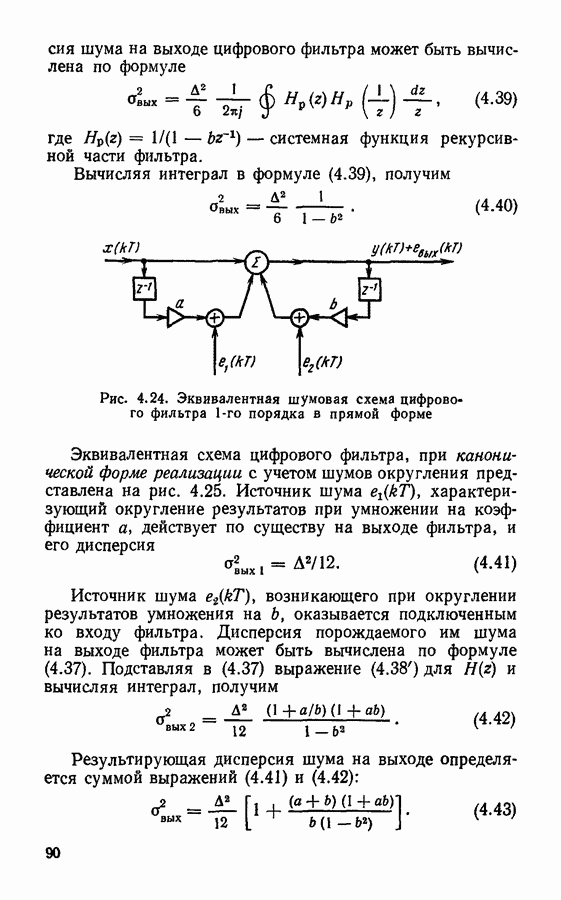
Цифровой фильтр с системной функцией (4.38) может быть реализован в прямой и канонической формах. Эквивалентная схема фильтра при прямой форме реализации с учетом шумов округления имеет вид, изображенный на рис. 4.24. Источники шума  имеют одинаковую дисперсию
имеют одинаковую дисперсию  причем величина А определяется числом используемых разрядов. Оба источника действуют по существу на входе общего сумматора и создают суммарный шум округления. Если считать источники шума независимыми, то дисперсия суммарного шума на входе сумматора
причем величина А определяется числом используемых разрядов. Оба источника действуют по существу на входе общего сумматора и создают суммарный шум округления. Если считать источники шума независимыми, то дисперсия суммарного шума на входе сумматора

Этот шум, проходя через оставшуюся рекурсивную часть фильтра, создает выходной шум 
Дисперсия шума на выходе цифрового фильтра может быть вычислена по формуле

где  системная функция рекурсивной части фильтра.
системная функция рекурсивной части фильтра.
Вычисляя интеграл в формуле (4.39), получим


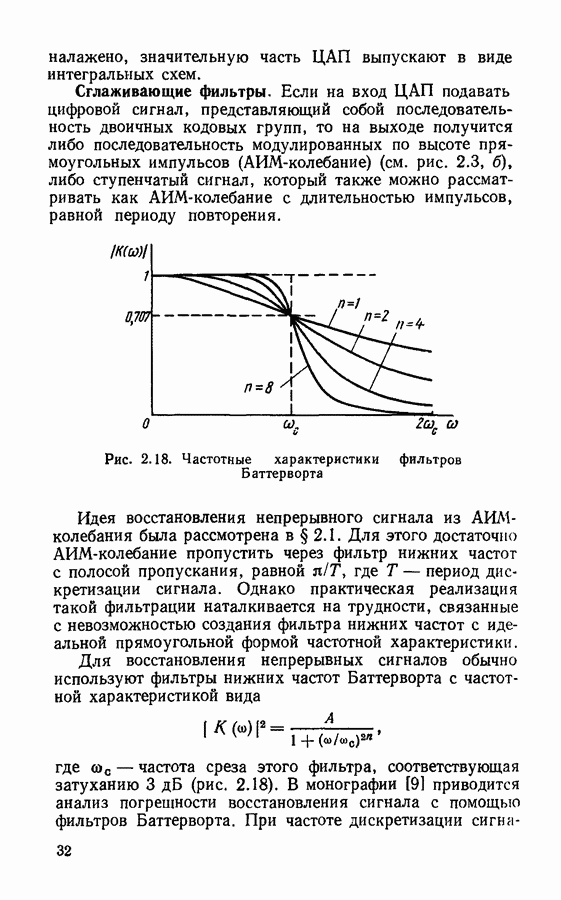
Рис. 4.24. Эквивалентная шумовая схема цифрового фильтра  порядка в прямой форме
порядка в прямой форме
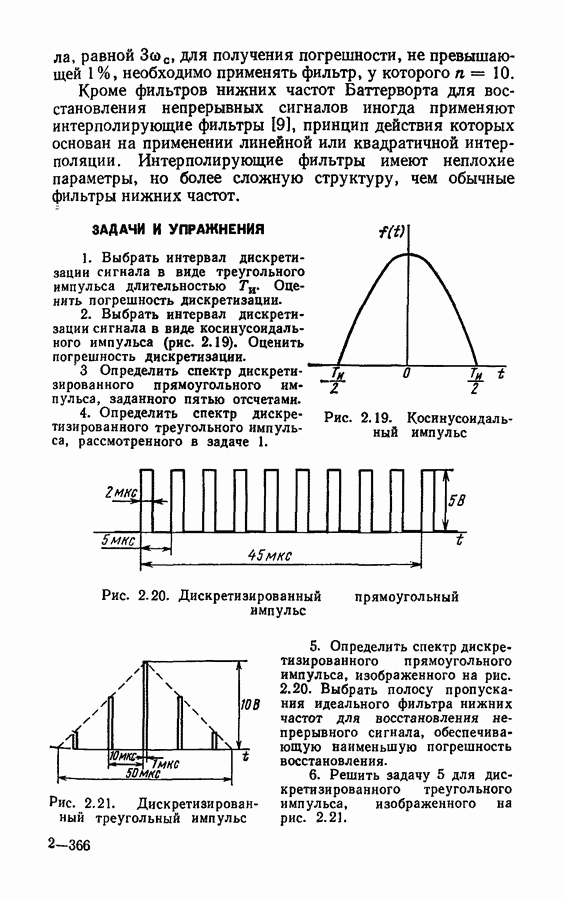
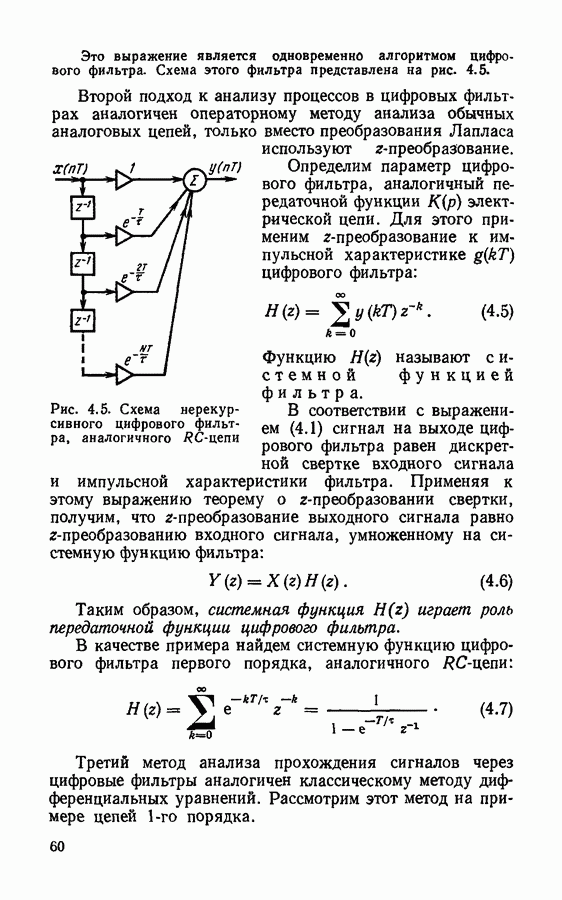
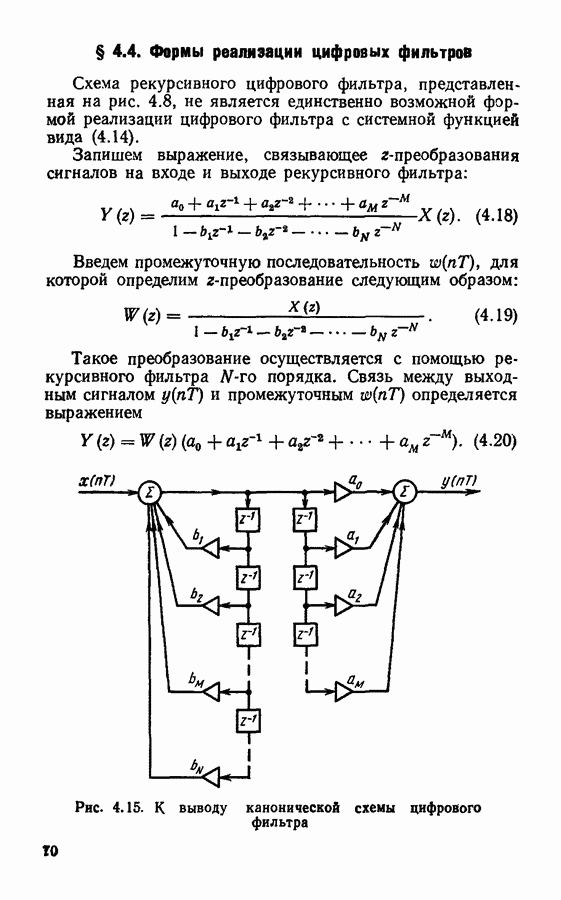
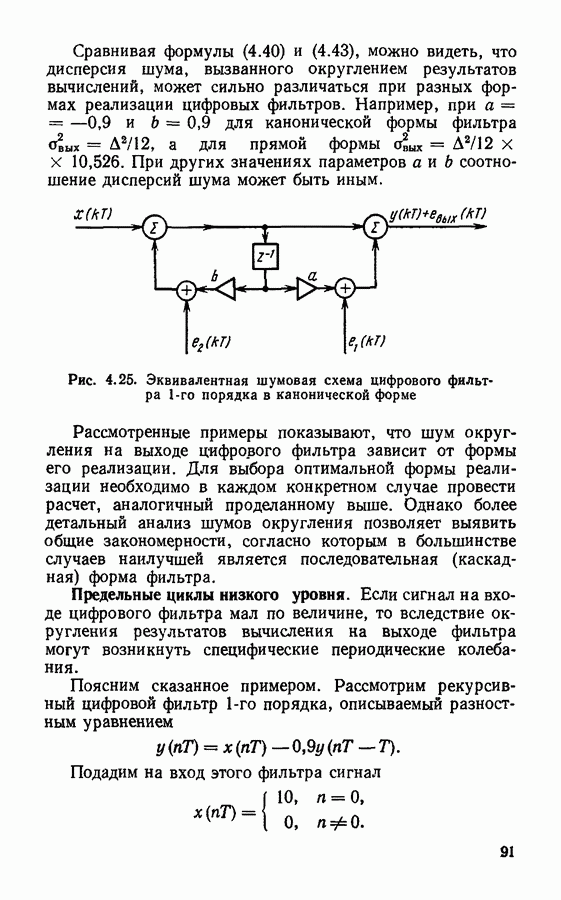
Эквивалентная схема цифрового фильтра, при канонической форме реализации с учетом шумов округления представлена на рис. 4.25. Источник шума  характеризующий округление результатов при умножении на коэффициент а, действует по существу на выходе фильтра, и его дисперсия
характеризующий округление результатов при умножении на коэффициент а, действует по существу на выходе фильтра, и его дисперсия

Источник шума  возникающего при округлении результатов умножения на
возникающего при округлении результатов умножения на  оказывается подключенным ко входу фильтра. Дисперсия порождаемого им шума на выходе фильтра может быть вычислена по формуле (4.37). Подставляя в (4.37) выражение (4.38) для
оказывается подключенным ко входу фильтра. Дисперсия порождаемого им шума на выходе фильтра может быть вычислена по формуле (4.37). Подставляя в (4.37) выражение (4.38) для  и вычисляя интеграл, получим
и вычисляя интеграл, получим

Результирующая дисперсия шума на выходе определяется суммой выражений (4.41) и (4.42):

Сравнивая формулы (4.40) и (4.43), можно видеть, что дисперсия шума, вызванного округлением результатов вычислений, может сильно различаться при разных формах реализации цифровых фильтров. Например, при  и
и  для канонической формы фильтра
для канонической формы фильтра  , а для прямой формы
, а для прямой формы  При других значениях параметров а и
При других значениях параметров а и  соотношение дисперсий шума может быть иным.
соотношение дисперсий шума может быть иным.

Рис. 4.25. Эквивалентная шумовая схема цифрового фильтра 1-го порядка в канонической форме
Рассмотренные примеры показывают, что шум округления на выходе цифрового фильтра зависит от формы его реализации. Для выбора оптимальной формы реализации необходимо в каждом конкретном случае провести расчет, аналогичный проделанному выше. Однако более детальный анализ шумов округления позволяет выявить общие закономерности, согласно которым в большинстве случаев наилучшей является последовательная (каскадная) форма фильтра.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
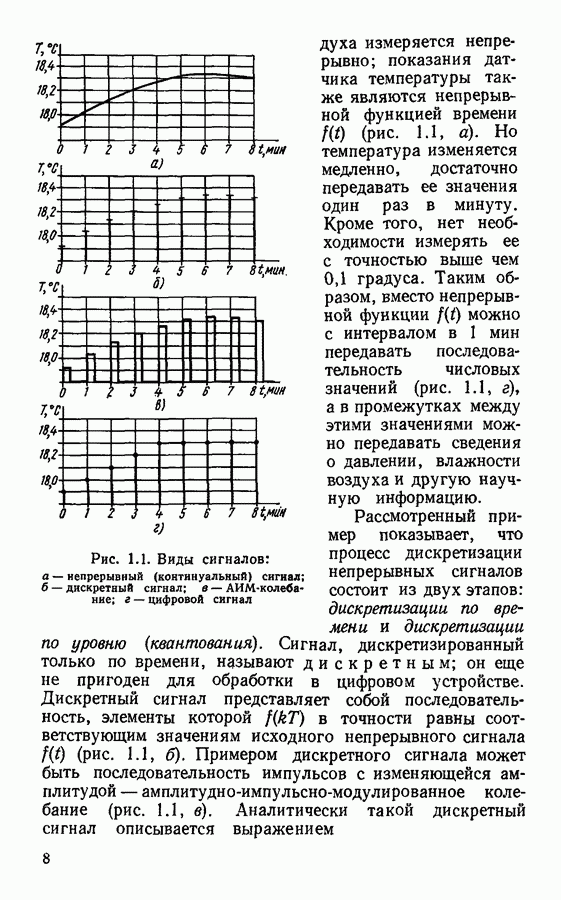
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
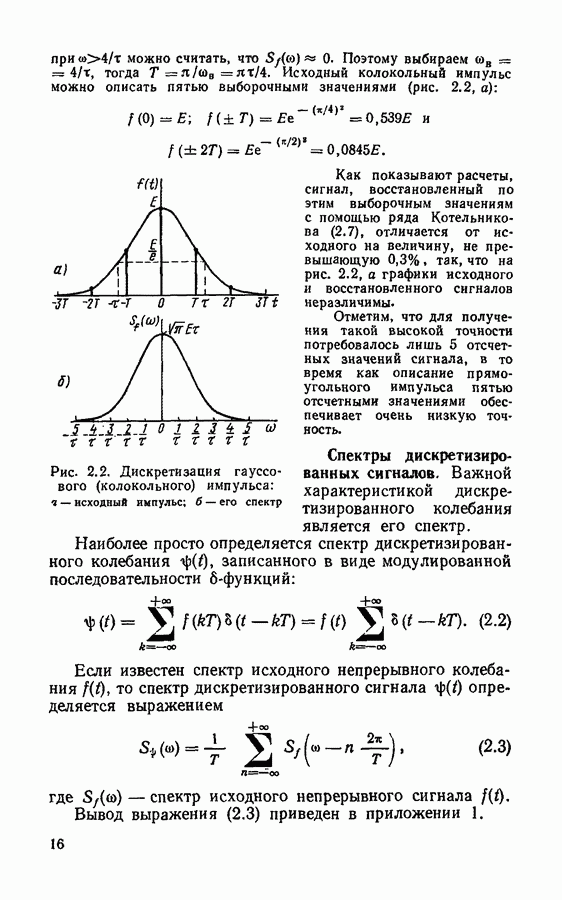
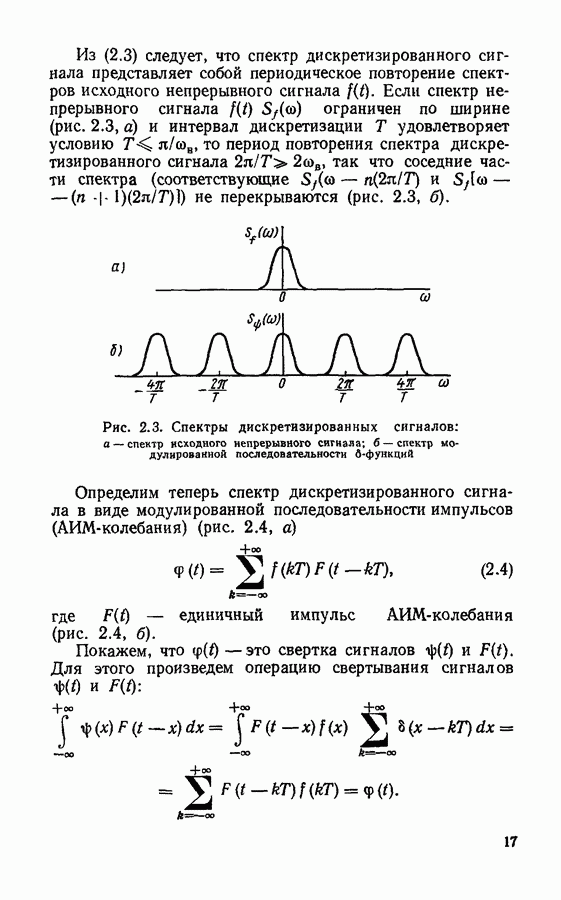
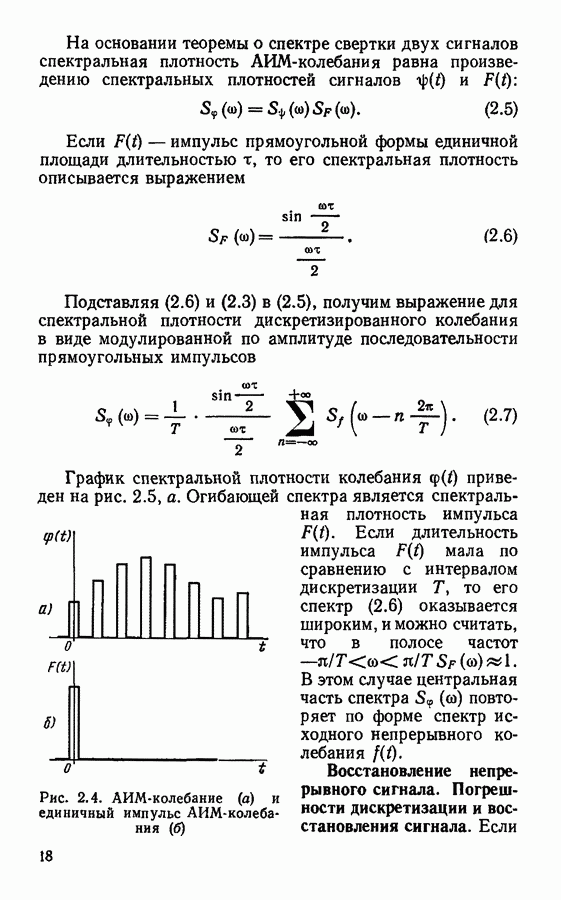
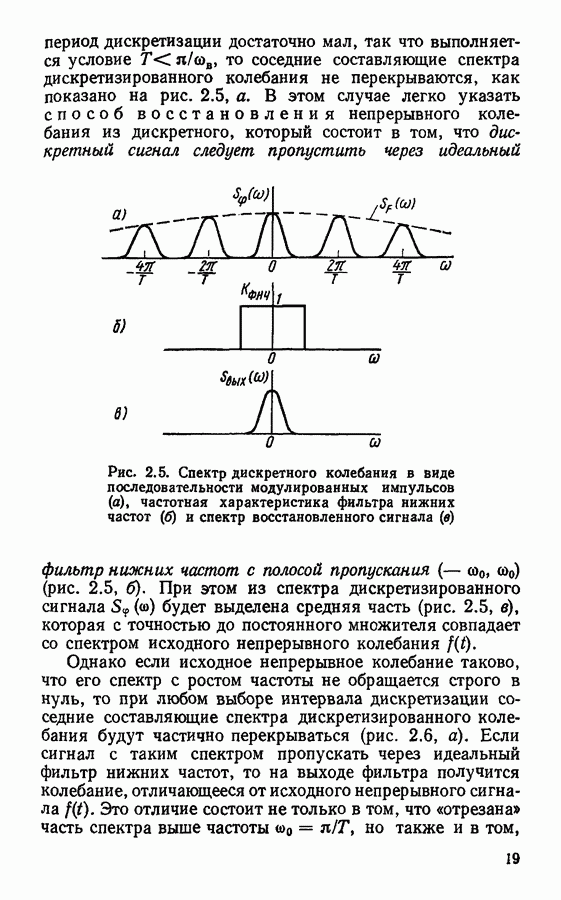
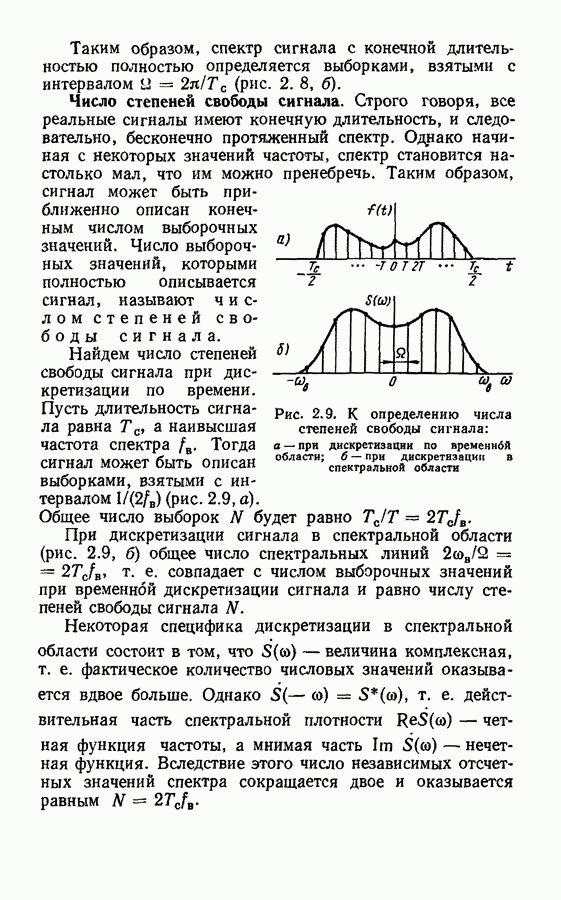
- Спектры дискретизированных сигналов.
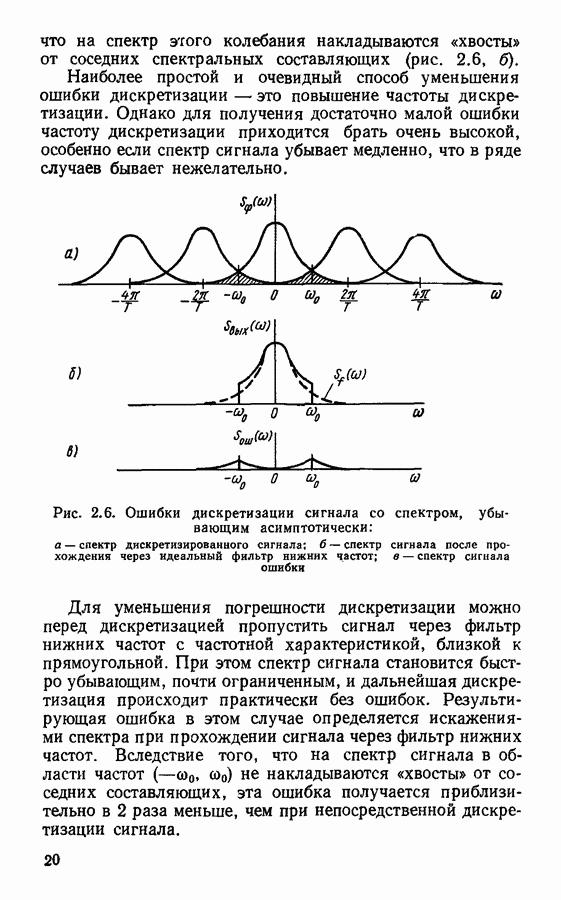
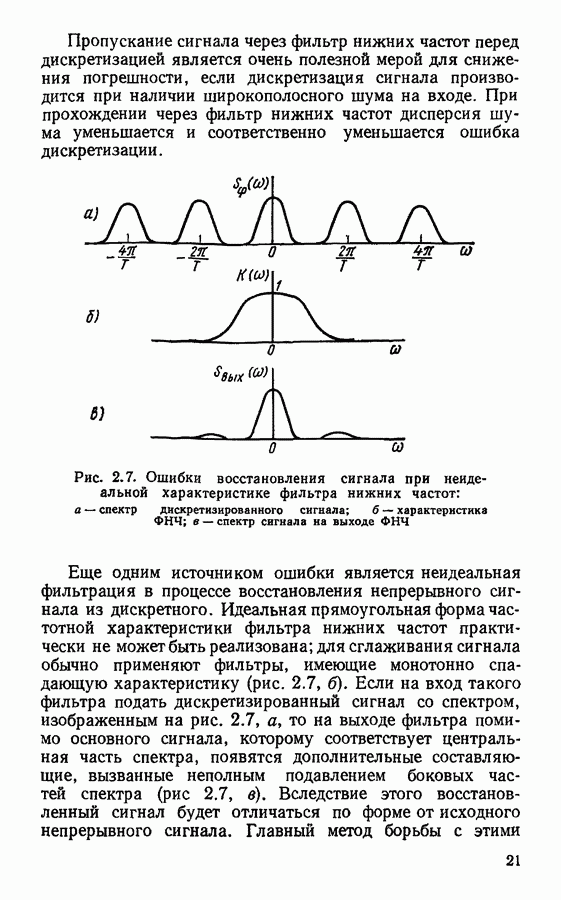
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
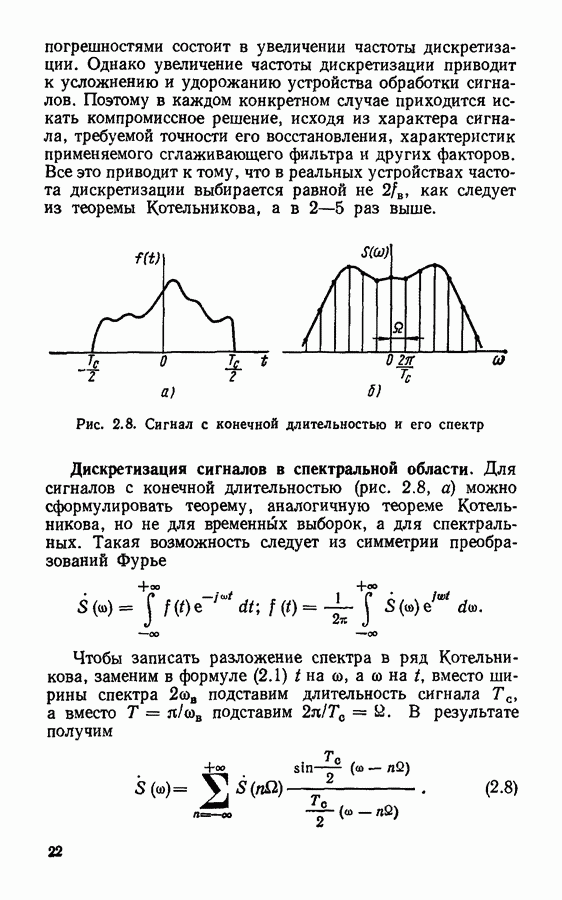
- Дискретизация сигналов в спектральной области.
- Число степеней свободы сигнала.
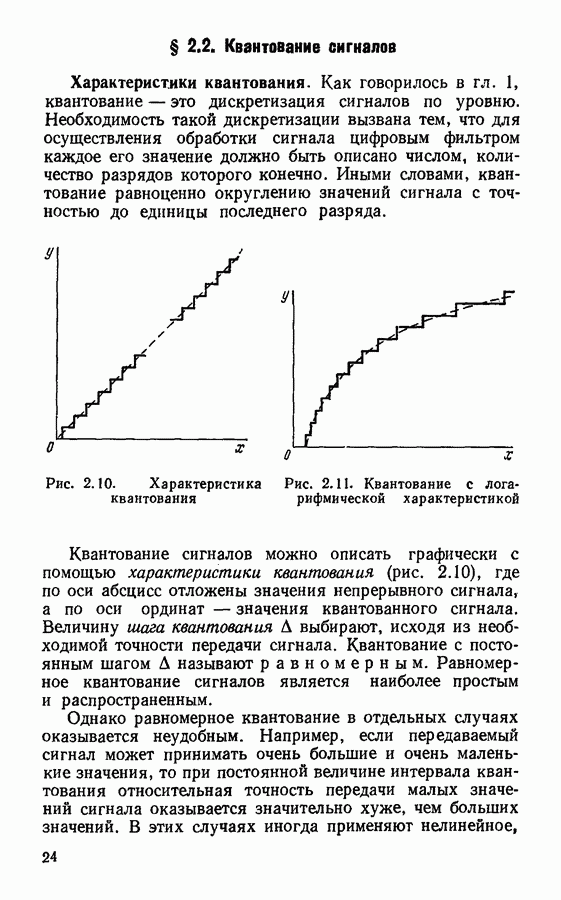
- § 2.2. Квантование сигналов
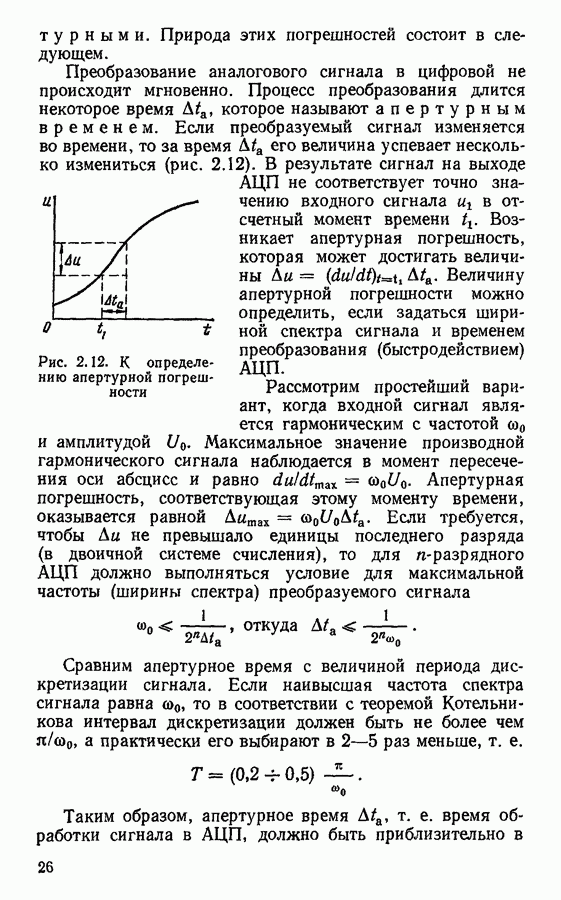
- Аналого-цифровое преобразование.
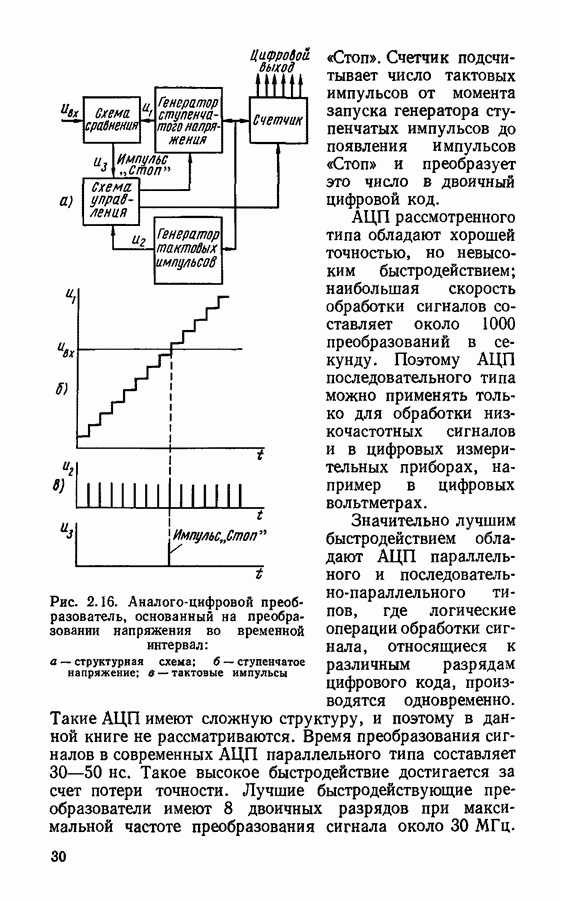
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА