| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4.6. Эффекты квантования в цифровых фильтрах
До сих пор мы не учитывали эффекты квантования, предполагая, что сигнал на входе цифрового фильтра может принимать любые значения. Иначе говоря, вместо цифровых сигналов и фильтров мы рассматривали дискретные.
В цифровых фильтрах сигнал задается последовательностью чисел с конечным числом разрядов, т. е. значения сигнала округляются с заданной точностью. Это приводит к появлению ряда специфических эффектов, не встречающихся в аналоговых и дискретных устройствах. Главными из этих эффектов являются: а) квантование сигналов на входе (шум квантования), о котором говорилось в § 2.2; б) неточные (округленные) значения постоянных параметров фильтров; в) округление результатов промежуточных вычислений; г) предельные циклы малого уровня.
Анализ эффектов квантования — это один из самых сложных вопросов теории цифровых фильтров. Величина погрешности обработки сигналов, вызванной эффектами квантования, зависит от многих факторов: структуры фильтра, способа представления чисел в машине, характера входного сигнала и др. Общий анализ погрешностей цифровой обработки сигналов не входит в задачи данной книги. Ограничимся лишь краткой характеристикой различных эффектов квантования. Более подробно вопросы эффектов квантования и погрешностей цифровой обработки сигналов изложены в [2, 3, 5].
В цифровых вычислительных устройствах применяют два способа представления чисел: с фиксированной запятой и с плавающей запятой.
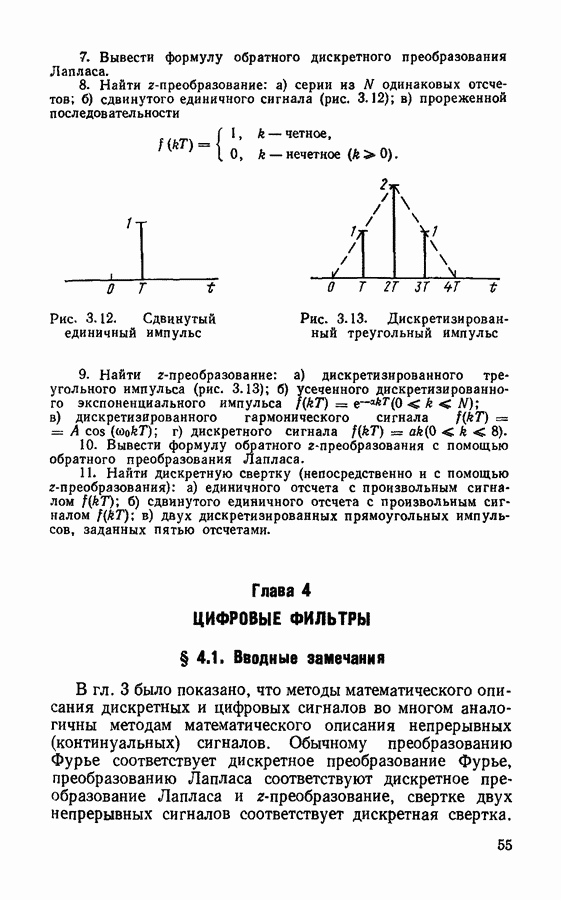
При представлении числа с фиксированной запятой (в двоичном коде) его можно записать в форме

где 
Недостатком устройств, в которых используются числа с фиксированной запятой, является небольшой динамический диапазон. Например, максимальное значение числа, записанного в виде (4.33), не превышает 2. В то же время арифметические устройства с фиксированной запятой проще по структуре; их легче анализировать.
Числа с плавающей запятой обычно представляются в виде, изображенном на рис. 4.23. Арифметические устройства, в которых используются числа с плавающей запятой, обладают значительно большим динамическим диапазоном, однако анализ ошибок квантования в них достаточно сложен. Например, величина ошибок округления зависит не только от числа разрядов, но и от порядка округляемого числа.

Рис. 4.23. Представление числа в арифметическом устройстве с плавающей запятой
В рамках данной книги анализ эффектов квантования будем проводить только для вычислительных устройств, в которых используются числа с фиксированной запятой. Анализ эффектов квантования в цифровых фильтрах с плавающей запятой приведен в [31.
Погрешности, вызываемые квантованием входного сигнала. Одним из источников погрешности цифровой обработки сигналов является шум квантования, возникающий при квантовании (округлении) значений входного сигнала в аналого-цифровом преобразователе.
Как отмечалось, квантованный сигнал на входе цифрового фильтра можно представить в виде суммы исходного неквантованного сигнала и шума квантования  Если фильтр линейный, то прохождение через него сигнала и шума квантования можно рассматривать независимо друг от друга.
Если фильтр линейный, то прохождение через него сигнала и шума квантования можно рассматривать независимо друг от друга.
Определим шум на выходе цифрового фильтра, вызванный прохождением через него шума квантования. Шум квантования представляет собой последовательность дискретных значений  не превышающих по модулю половины шага квантования
не превышающих по модулю половины шага квантования  и распределенных по равномерному закону. Статистическая связь между соседними дискретными значениями обычно бывает невелика, и можно приближенно считать, что они некоррелированы. В этом случае можно найти дисперсию шума на выходе фильтра. Обозначим через
и распределенных по равномерному закону. Статистическая связь между соседними дискретными значениями обычно бывает невелика, и можно приближенно считать, что они некоррелированы. В этом случае можно найти дисперсию шума на выходе фильтра. Обозначим через  шум на выходе цифрового фильтра,
шум на выходе цифрового фильтра,
т. е. реакцию фильтра на входное воздействие  Очевидно, что
Очевидно, что  можно записать как
можно записать как

Поскольку соседние отсчеты входного шума некоррелированы, дисперсия шума на входе фильтра равна сумме дисперсий отдельных слагаемых в выражении (4.34). Учитывая, что дисперсия равномерного закона распределения шириной  равна
равна  получим
получим

Поскольку все  положительны, дисперсия отсчетов шума на выходе фильтра растет с увеличением числа отсчетов, стремясь к предельному значению
положительны, дисперсия отсчетов шума на выходе фильтра растет с увеличением числа отсчетов, стремясь к предельному значению

Обычно для цифровых фильтров выполняется условие  и дисперсия
и дисперсия  конечна.
конечна.
Для расчета дисперсии шума квантования на выходе цифрового фильтра можно получить еще одну формулу. Учитывая, что системная функция цифрового фильтра является  -преобразованием импульсной характеристики, запишем для нее теорему Парсеваля
-преобразованием импульсной характеристики, запишем для нее теорему Парсеваля

Подставляя выражение (4.36) в (4.35), получим

Формулу (4.37) удобно применять для расчета дисперсии шума на выходе цифрового фильтра в тех случаях,
когда импульсная характеристика неизвестна, а задана системная функция фильтра.
В качестве примера найдем дисперсию шума квантования на выходе цифрового фильтра  порядка с системной функцией
порядка с системной функцией

если дисперсия шума квантования на входе равна 
Расчет дисперсии шума на выходе можно произвести двумя способами: с помощью формулы (4.37) и путем непосредственного суммирования ряда (4.35). Воспользуемся первым способом.
Подставляя выражение (4.38) для системной функции в формулу (4.37), получим

Подынтегральная функция имеет два полюса: 
Внутри контура интегрирования  расположен лишь полюс
расположен лишь полюс  Вычет в этой точке равен
Вычет в этой точке равен  следовательно
следовательно

Такой же результат можно получить, вычисляя импульсную характеристику цифрового фильтра с помощью формулы обратного  -преобразования и суммируя ряд (4.36).
-преобразования и суммируя ряд (4.36).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
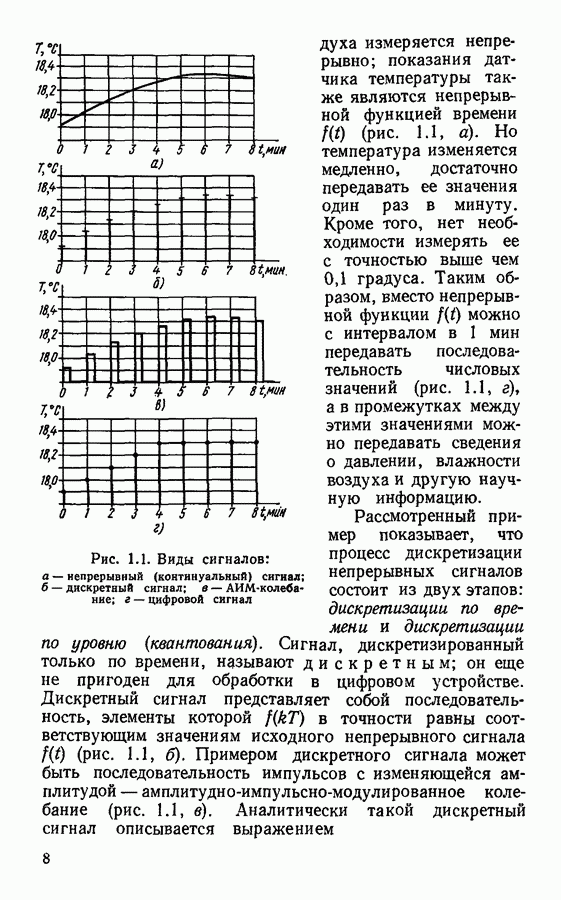
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
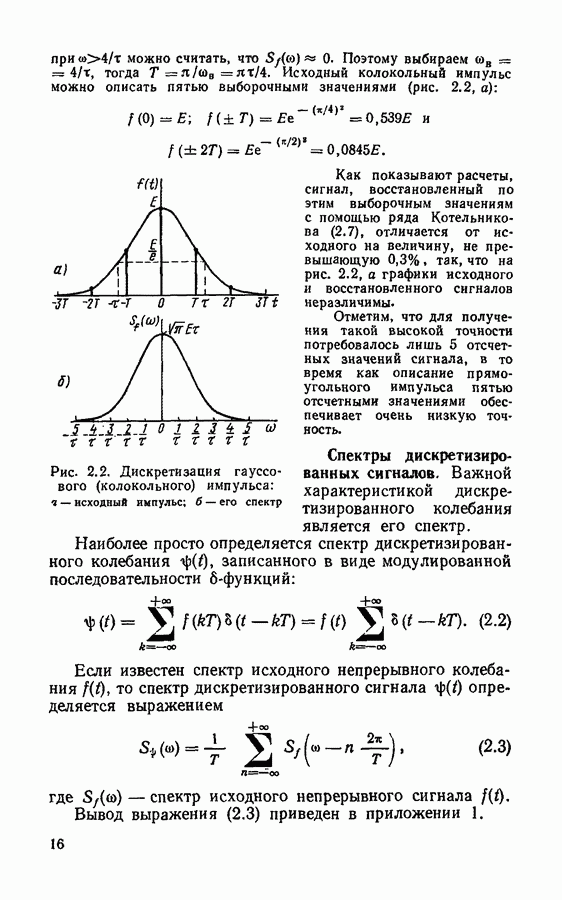
- § 2.1. Основы дискретизации непрерывных сигналов
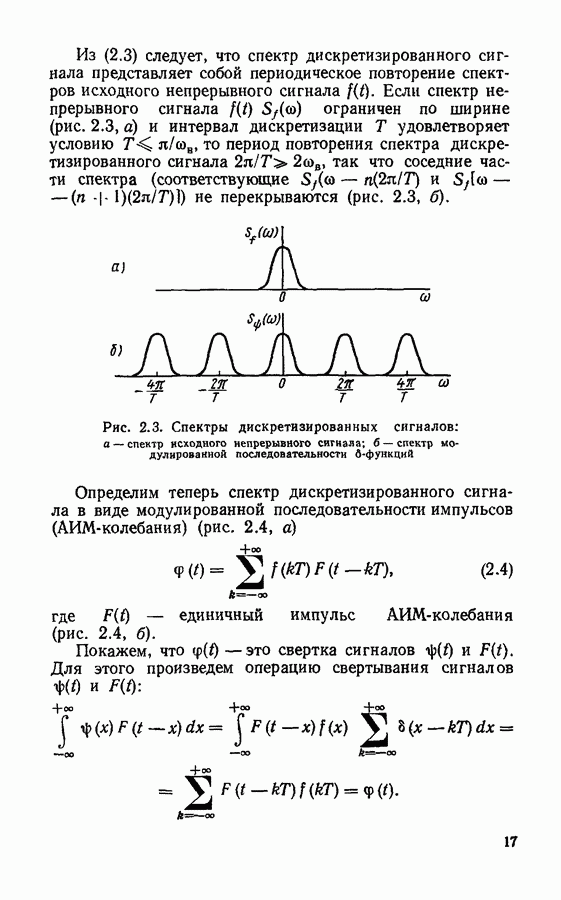
- Спектры дискретизированных сигналов.
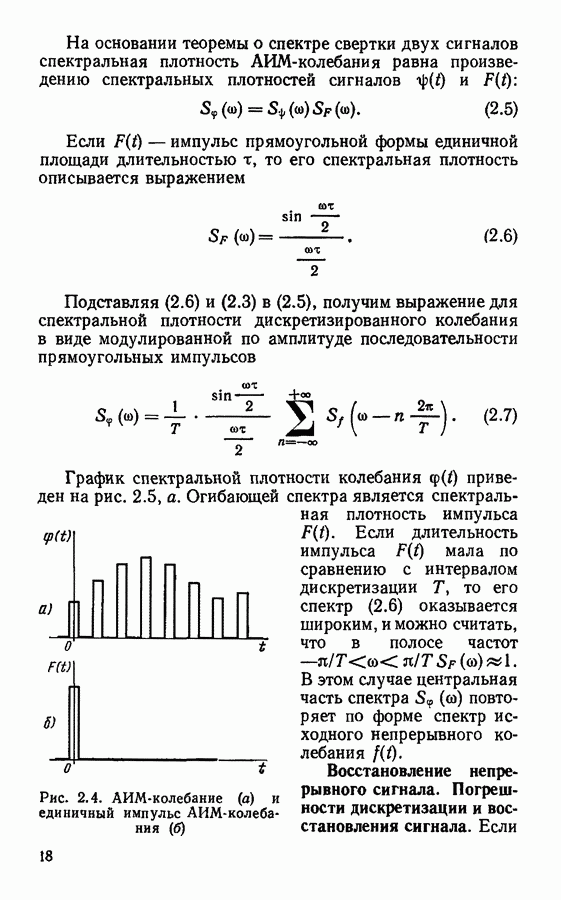
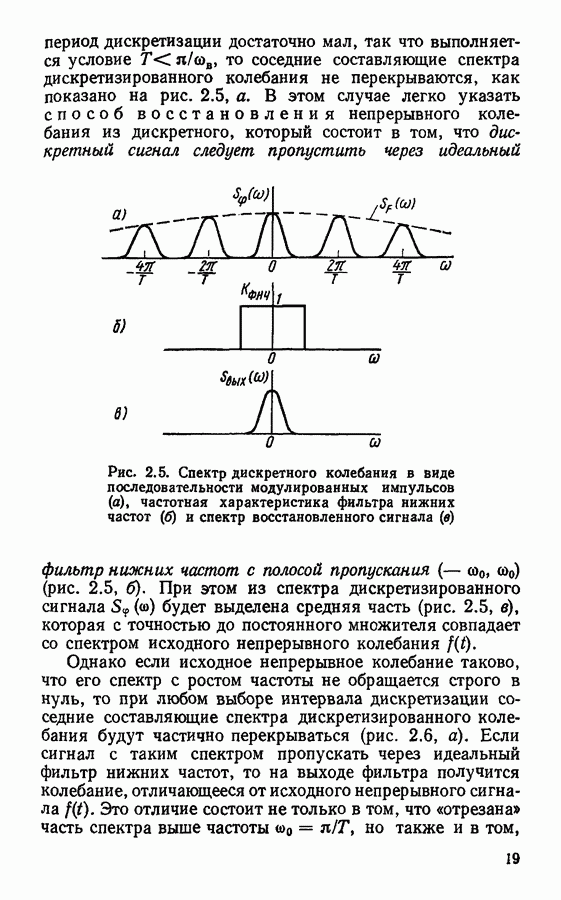
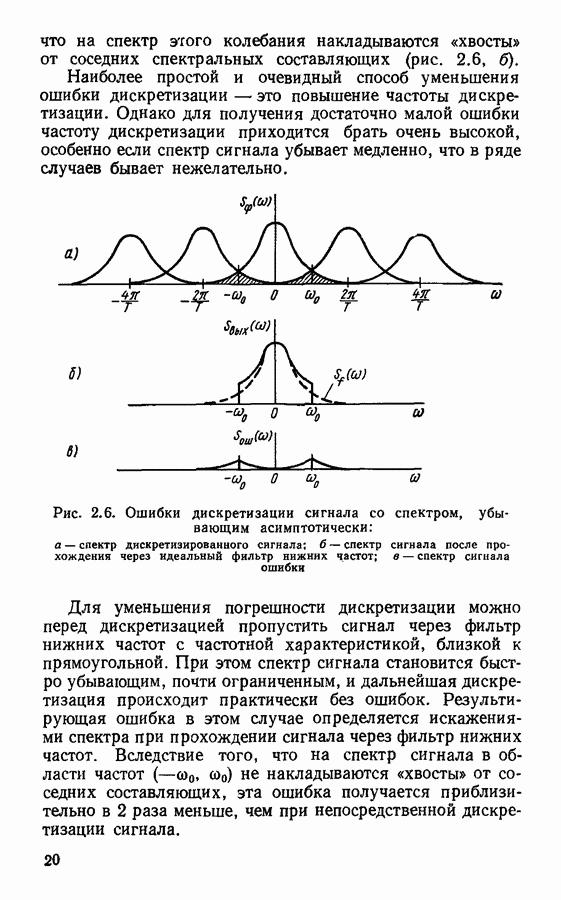
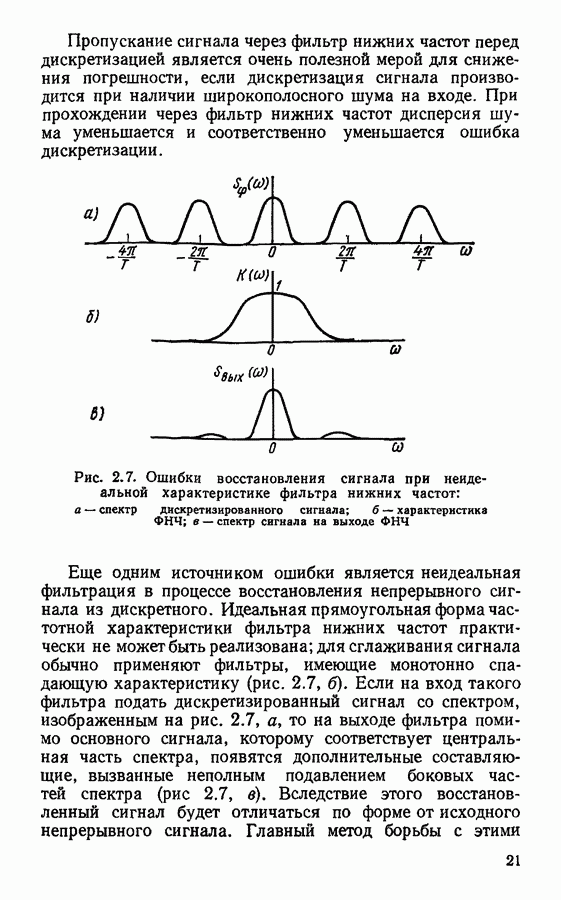
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
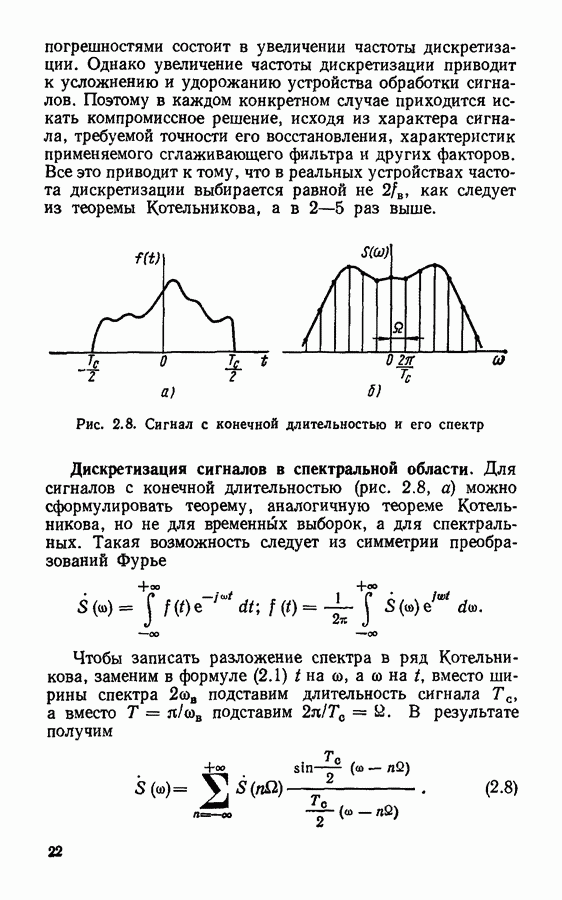
- Дискретизация сигналов в спектральной области.
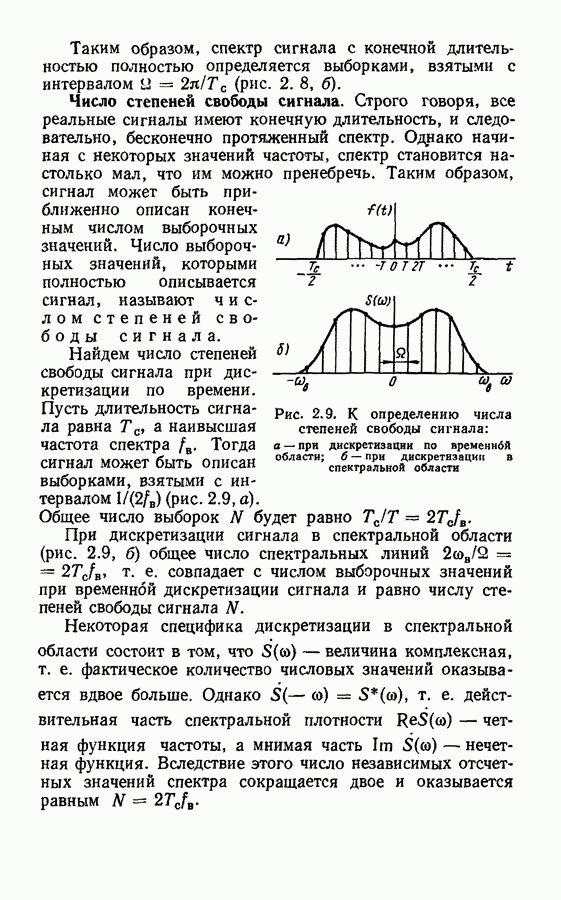
- Число степеней свободы сигнала.
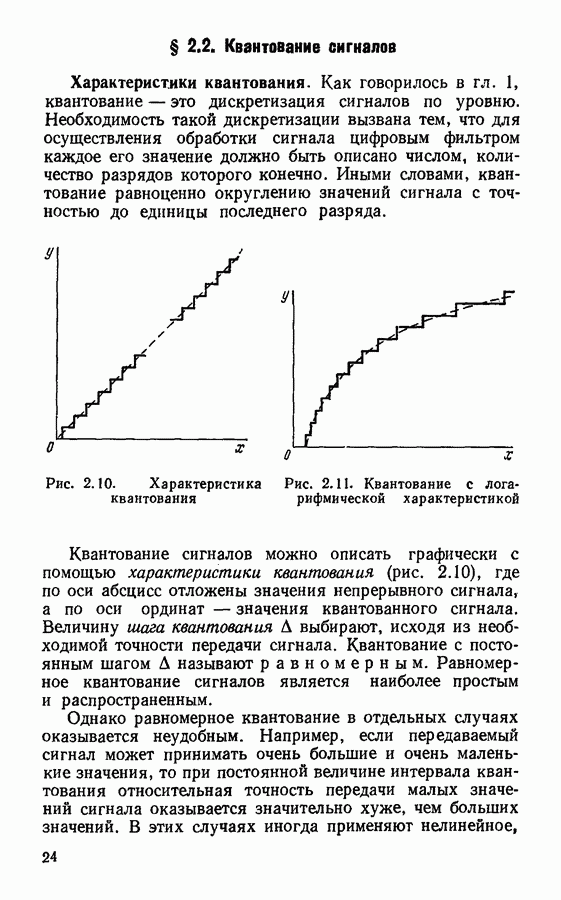
- § 2.2. Квантование сигналов
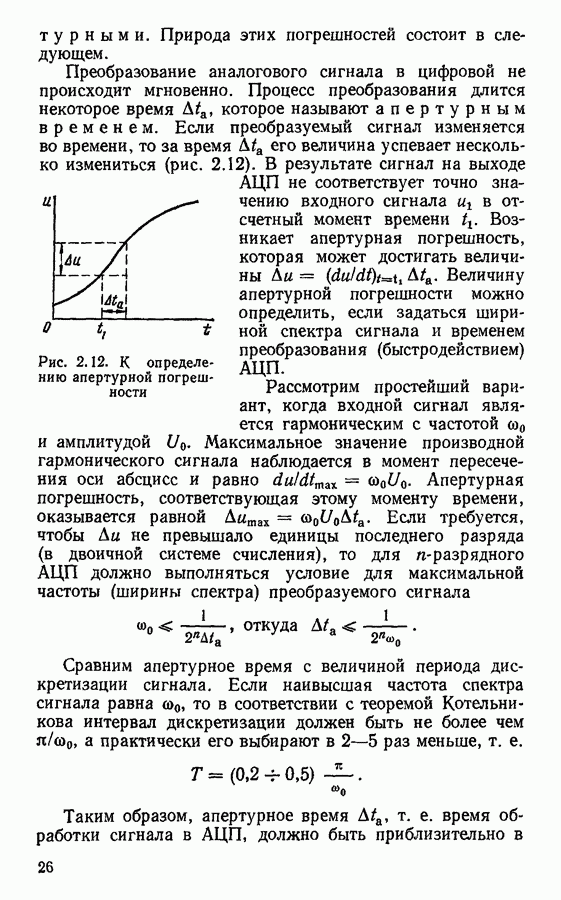
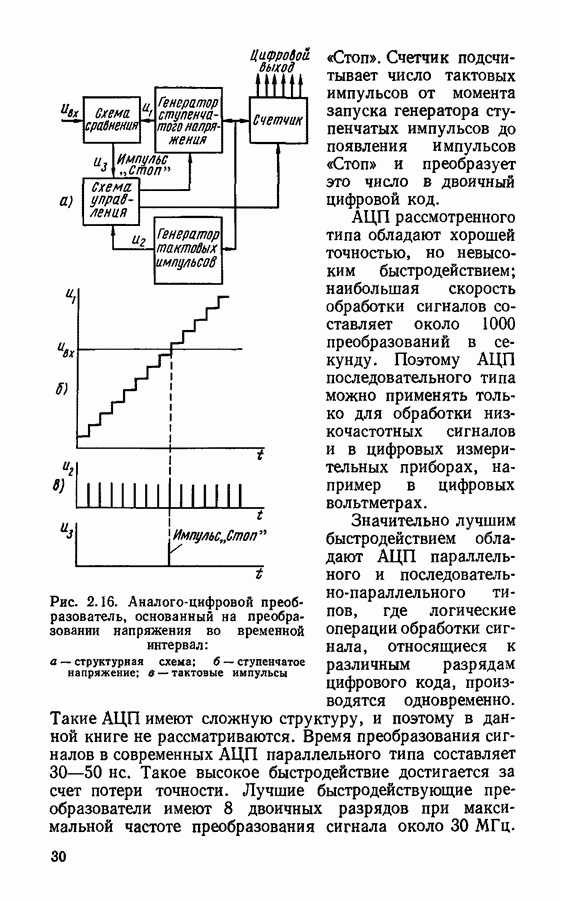
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
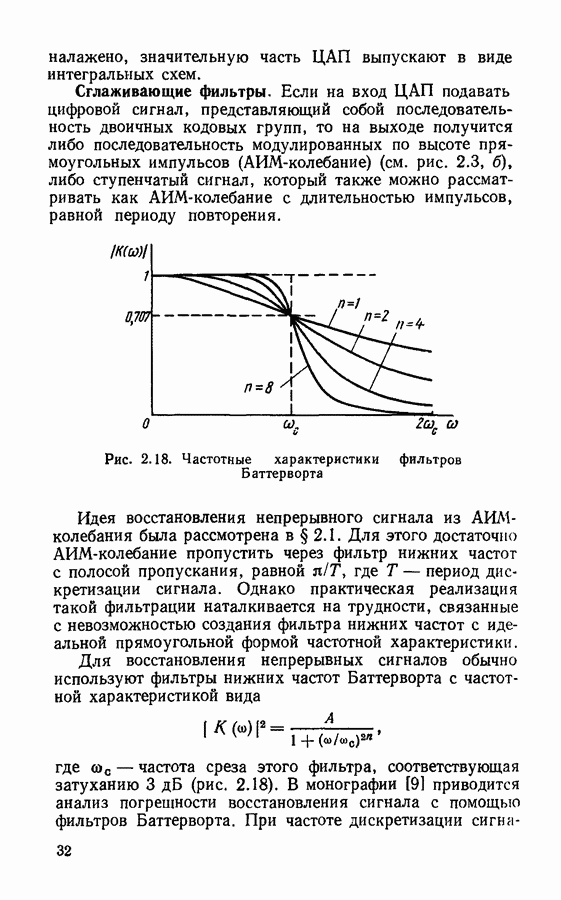
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
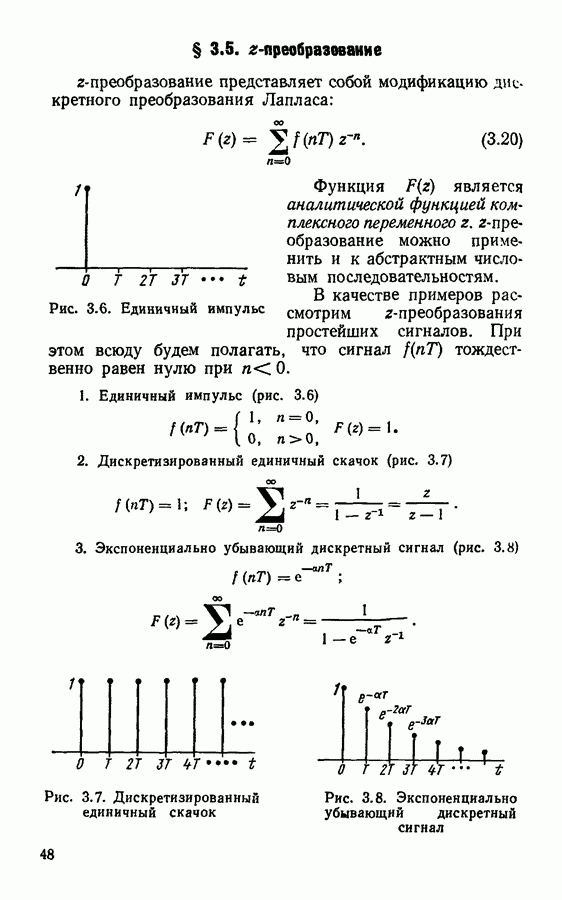
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
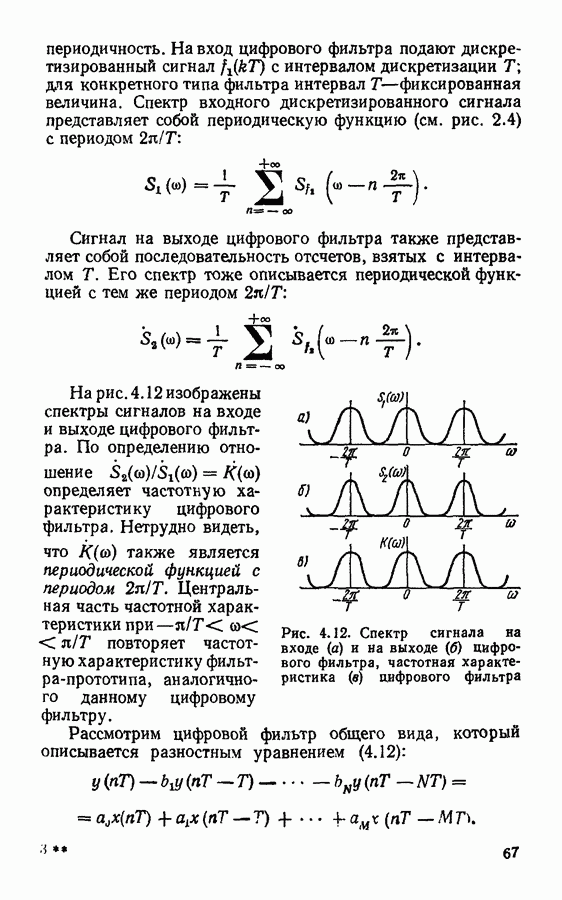
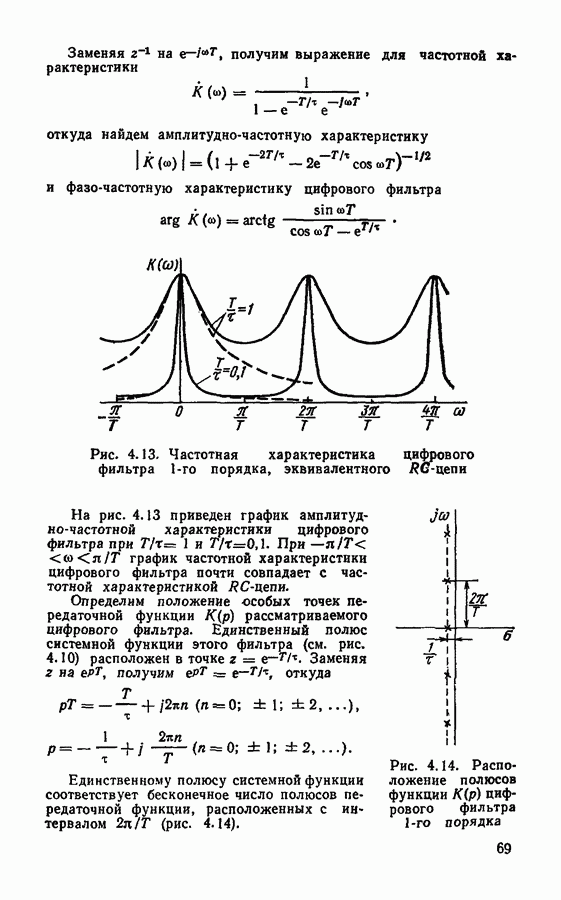
- § 4.3. Частотные характеристики цифровых фильтров
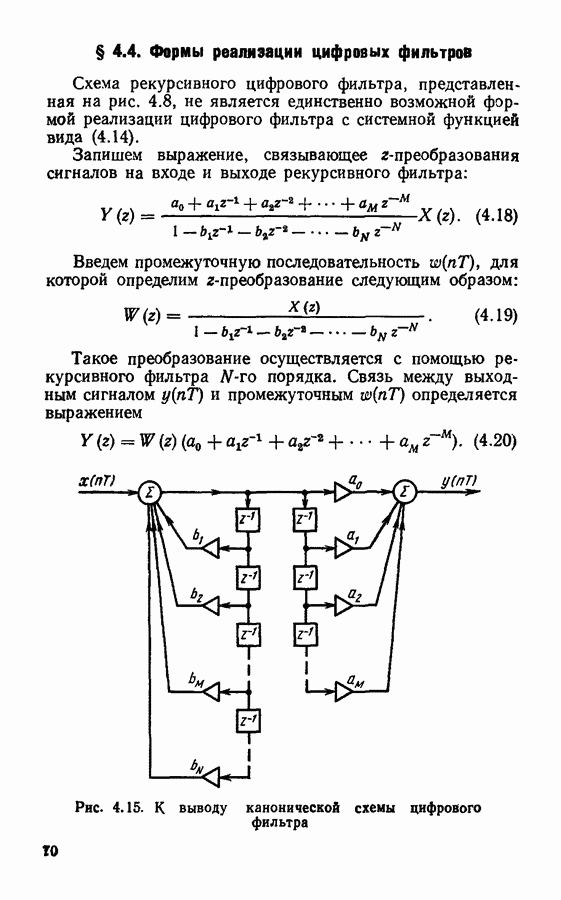
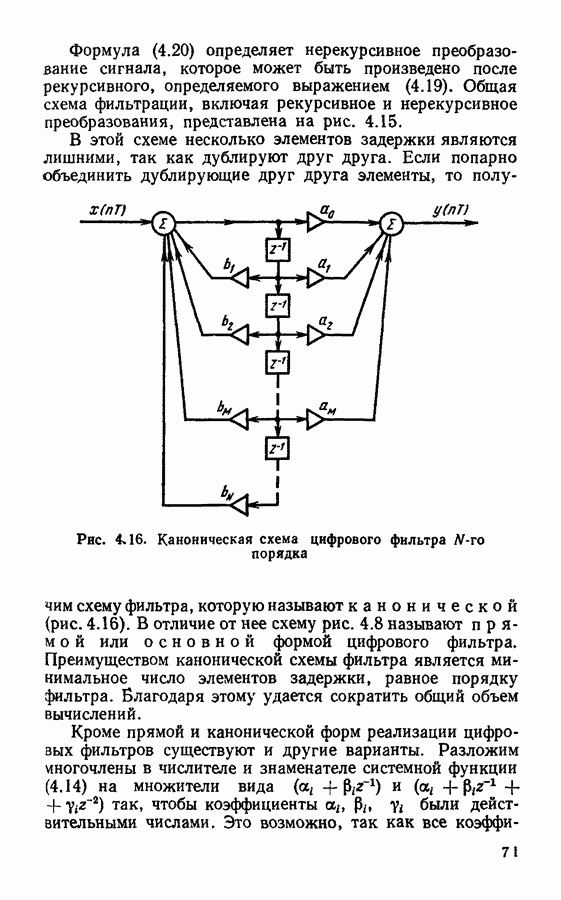
- § 4.4. Формы реализации цифровых фильтров
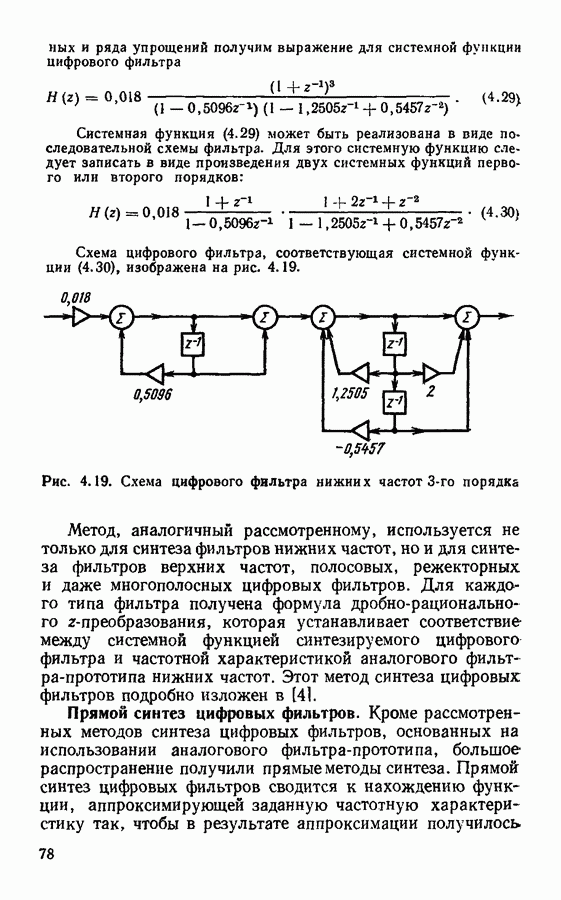
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
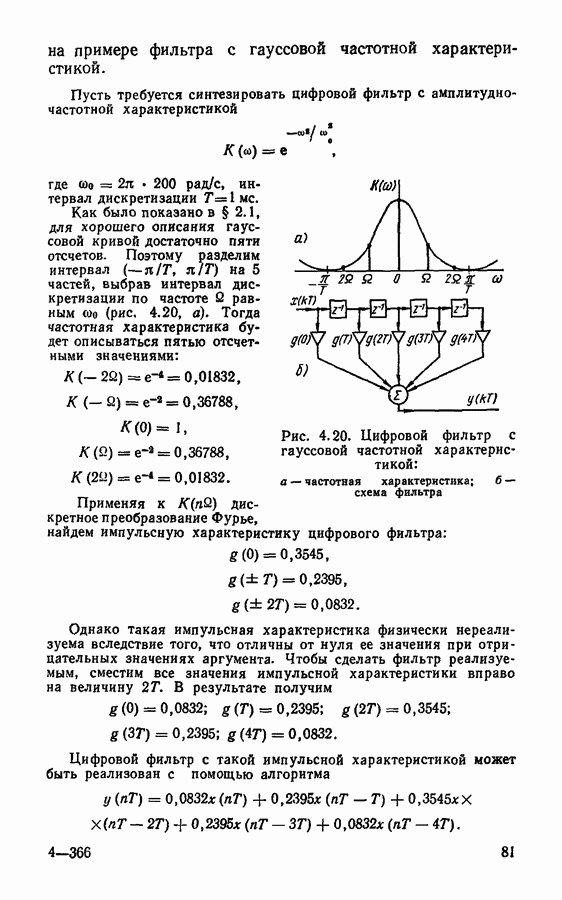
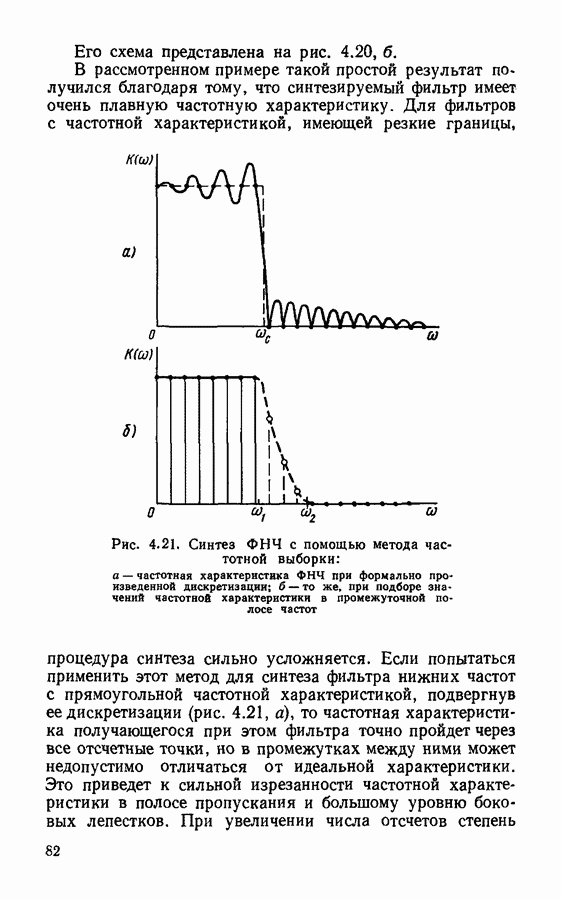
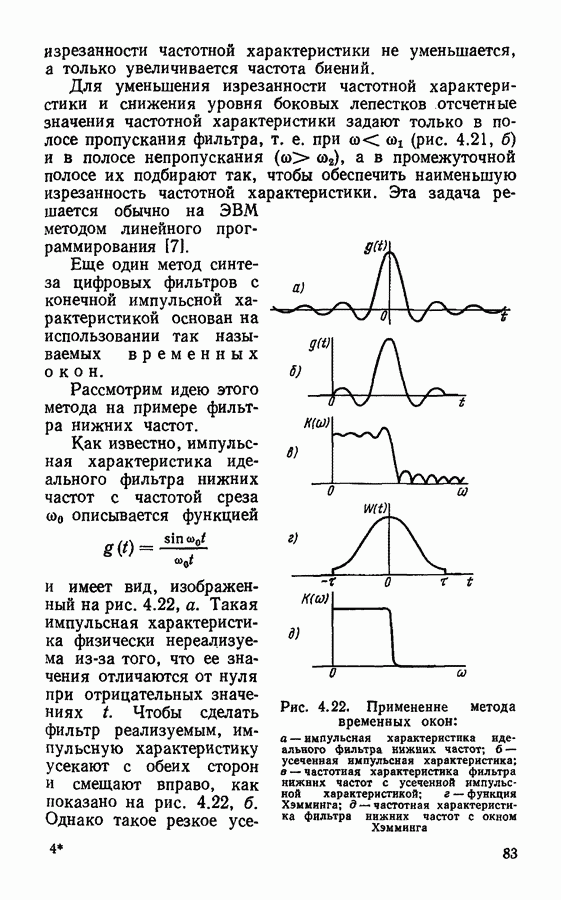
- Методы синтеза фильтров с конечной импульсной характеристикой.
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
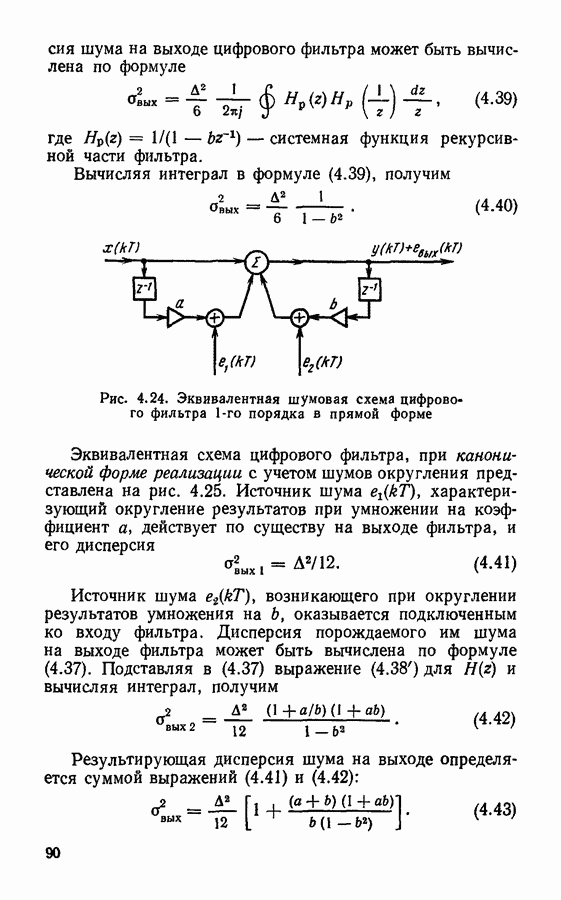
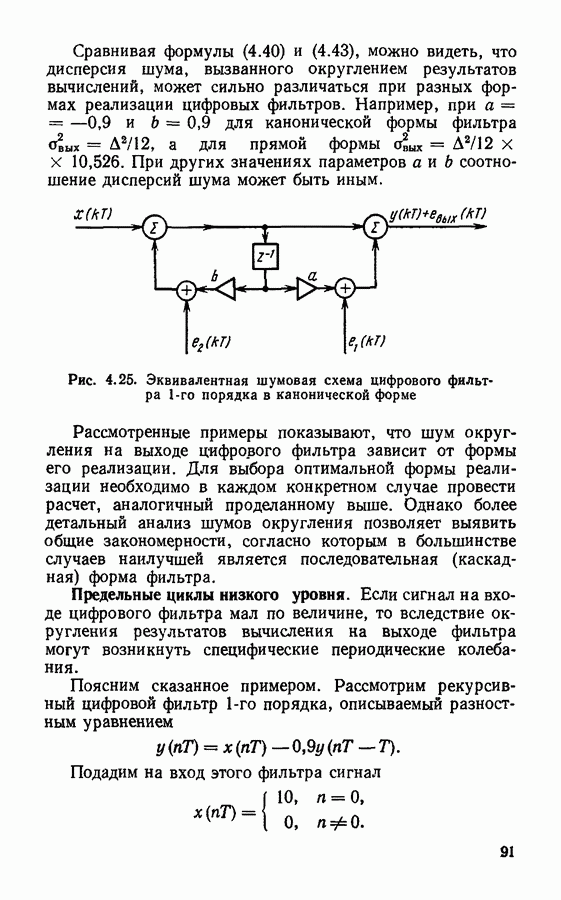
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА