| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
§ 3.1. Постановка задачи
При теоретическом исследовании процессов цифровой фильтрации при малых ошибках квантования для упрощения анализа обычно пренебрегают эффектами квантования, т. е. при таком анализе вместо цифровых сигналов рассматривают дискретные.
В тех случаях, когда нужно учесть эффекты квантования, обычно поступают следующим образом. Входной квантованный сигнал представляют в виде суммы неквантованного дискретного сигнала и шума квантования. Далее, поскольку фильтр линеен, рассматривают прохождение отдельно неквантованного дискретного сигнала и шума квантования и потом на выходе фильтра их аддитивно суммируют.
Таким образом, дискретные неквантованные сигналы играют важную роль в теории цифровой фильтрации. В этой и следующей главах будут рассмотрены в основном дискретные сигналы.
Теория дискретных сигналов во многом похожа на теорию непрерывных (аналоговых) сигналов. Это связано с тем, что дискретное колебание при правильно выбранной частоте дискретизации несет в себе всю или почти всю информацию об исходном непрерывном колебании. Такая глубокая связь между дискретными и непрерывными сигналами, возможность их взаимного преобразования объясняют аналогию их свойств, схожесть методов математического описания. Практически каждому методу математического описания непрерывного сигнала соответствует свой аналог в теории дискретных сигналов. Обычному преобразованию Фурье непрерывных сигналов соответствует дискретное преобразование Фурье, преобразованию Лапласа соответствуют дискретное преобразование Лапласа и  -преобразование. Поэтому при анализе методов математического описания дискретных сигналов постоянно пользуются этой аналогией.
-преобразование. Поэтому при анализе методов математического описания дискретных сигналов постоянно пользуются этой аналогией.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
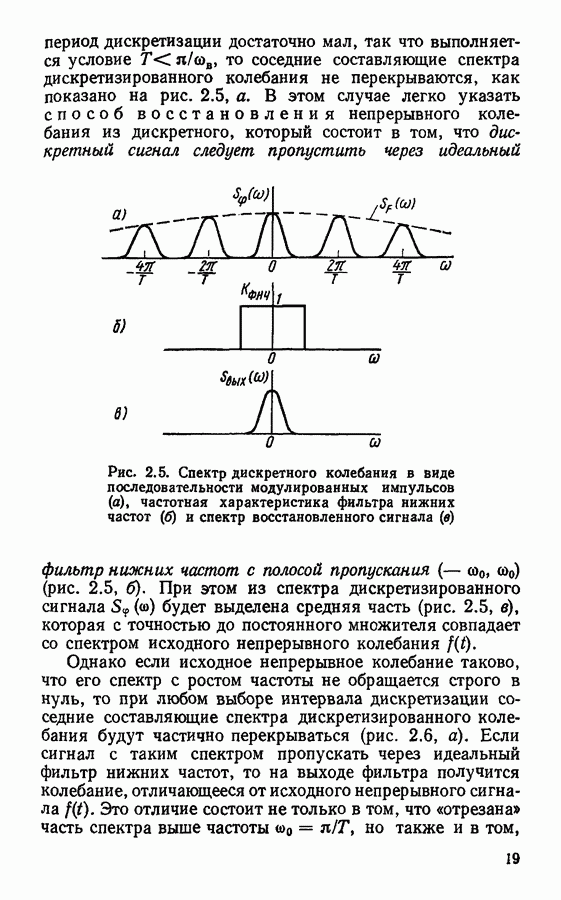
- Спектры дискретизированных сигналов.
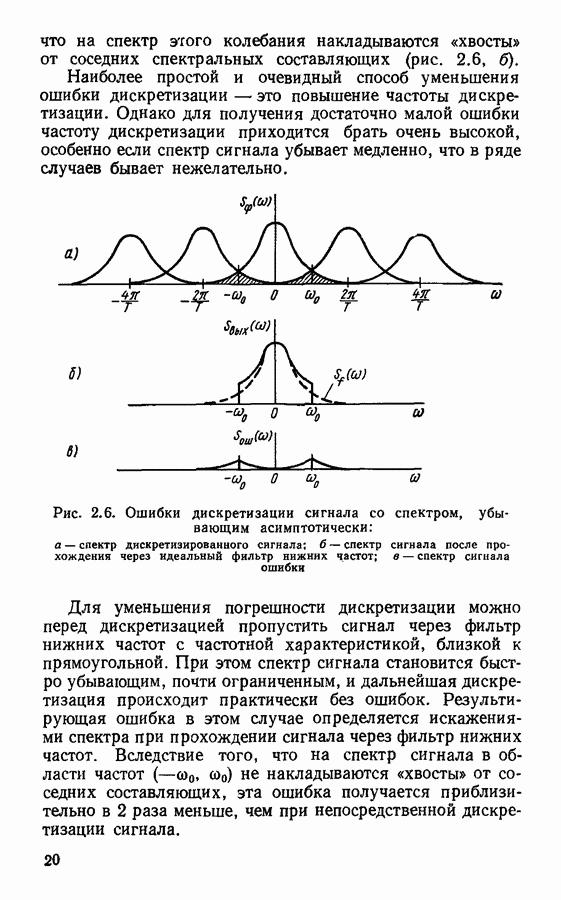
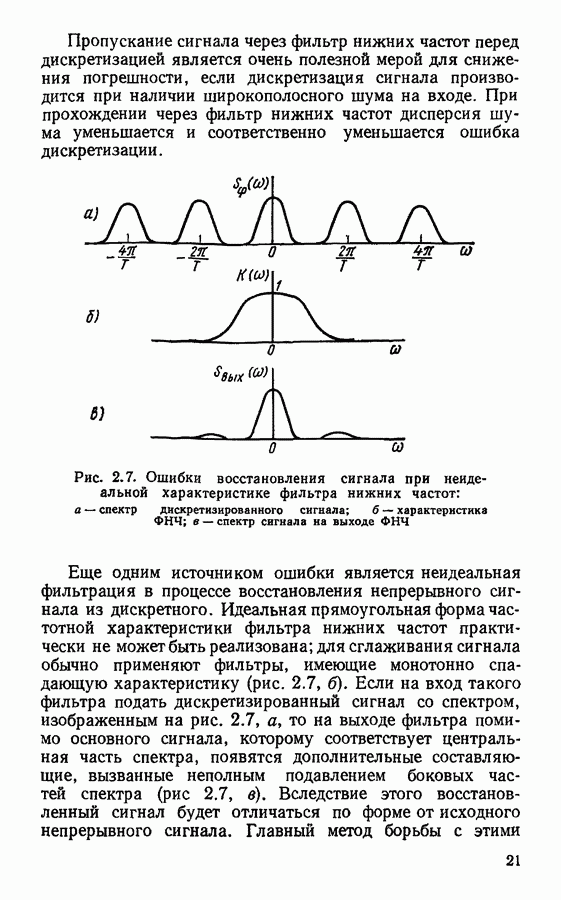
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
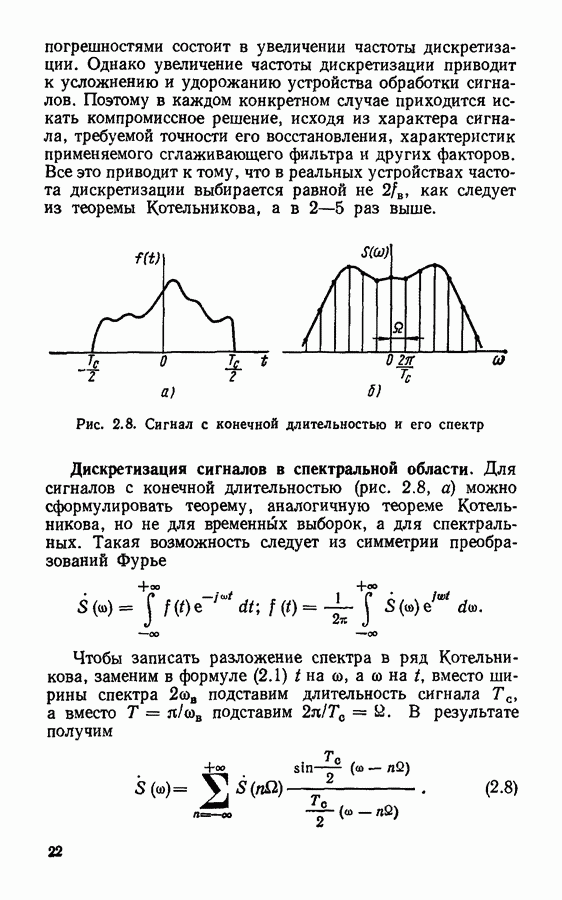
- Дискретизация сигналов в спектральной области.
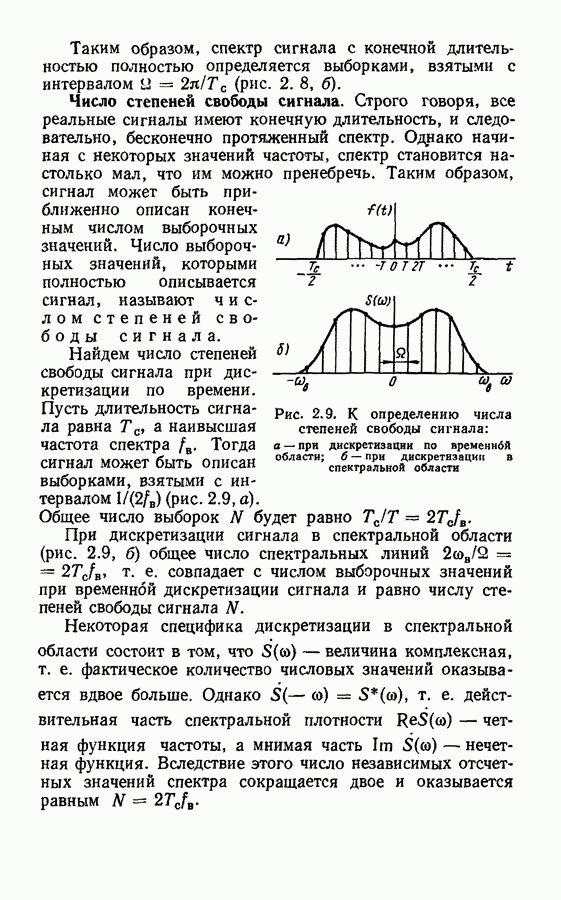
- Число степеней свободы сигнала.
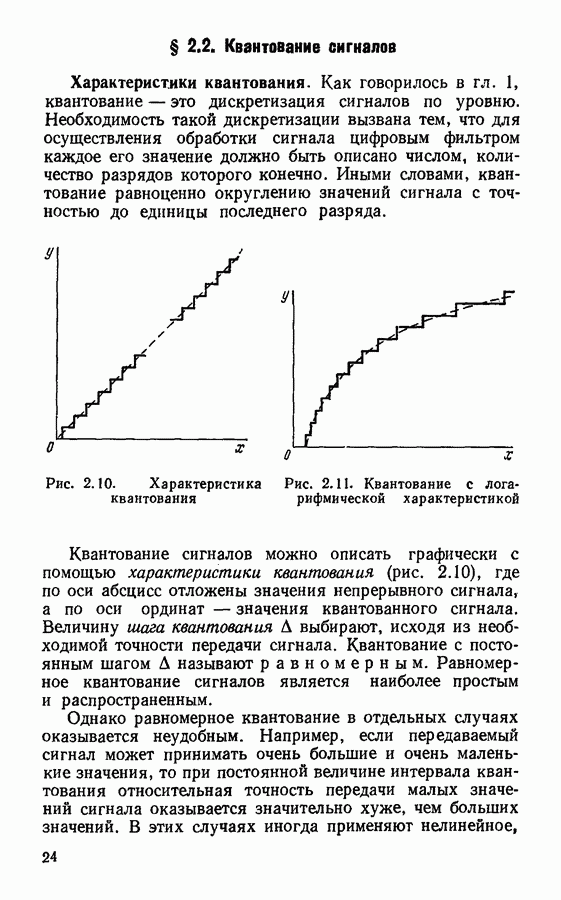
- § 2.2. Квантование сигналов
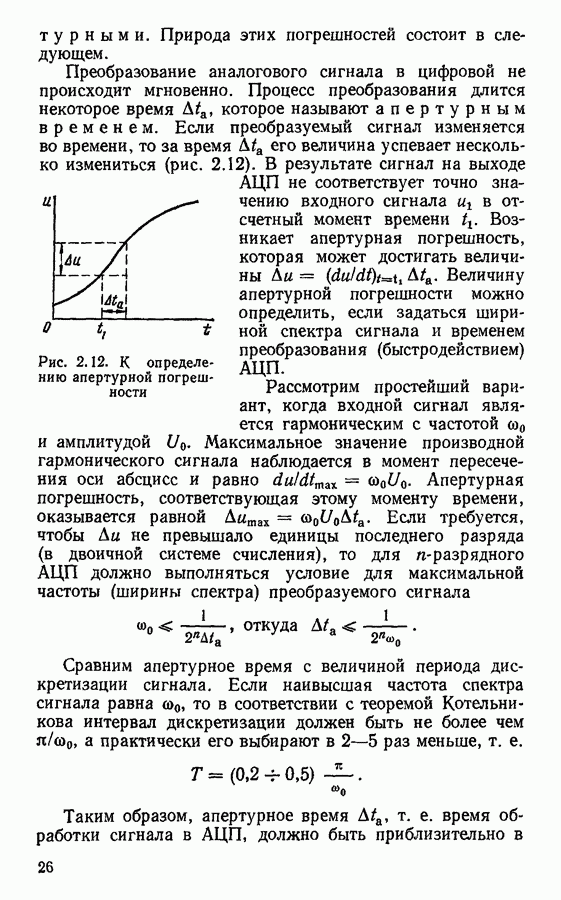
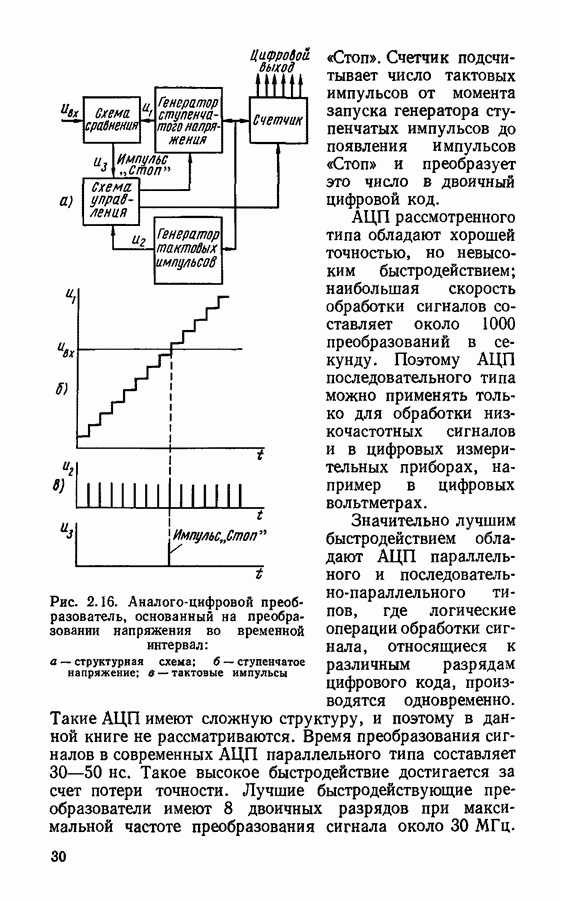
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
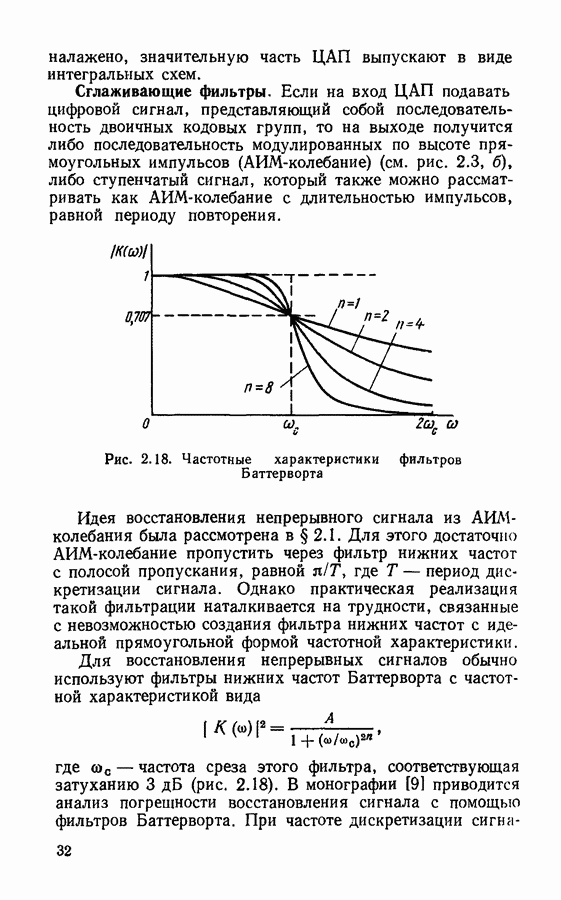
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
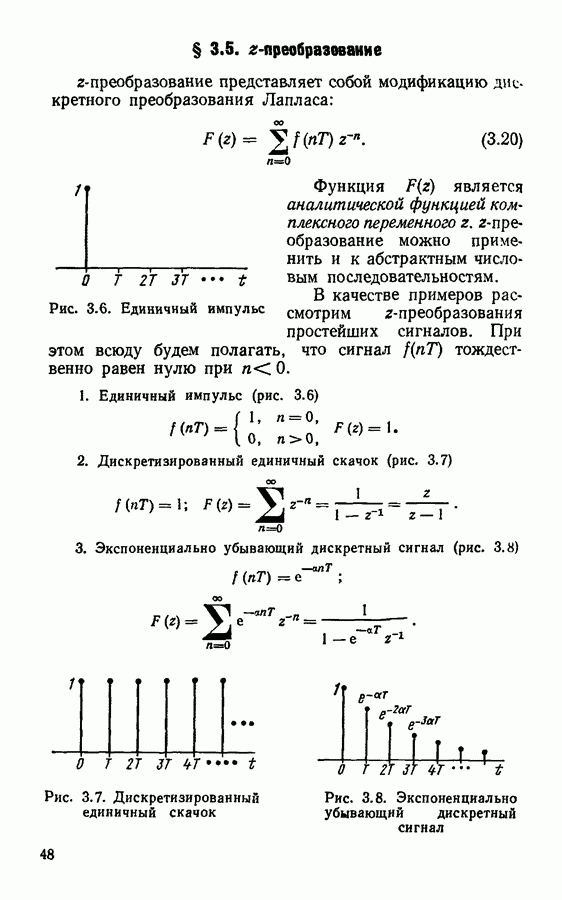
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
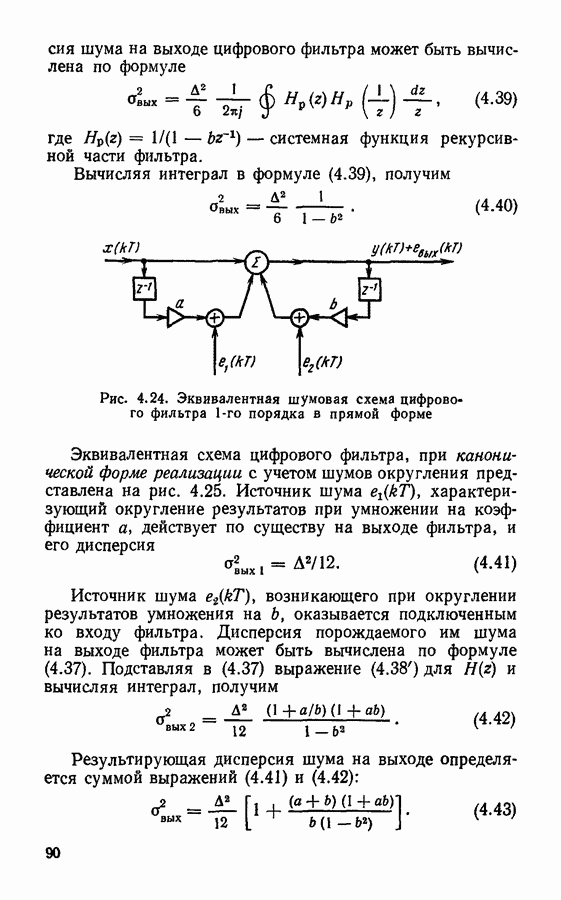
- Ошибки, вызванные квантованием результатов вычислений.
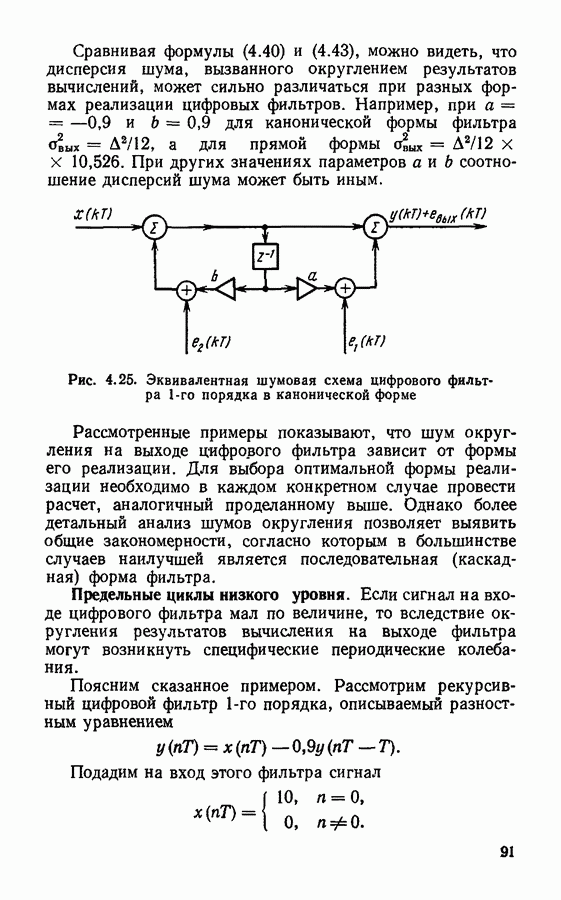
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА