| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3.5. z-преобразование
z-преобразование представляет собой модификацию дискретного преобразования Лапласа:


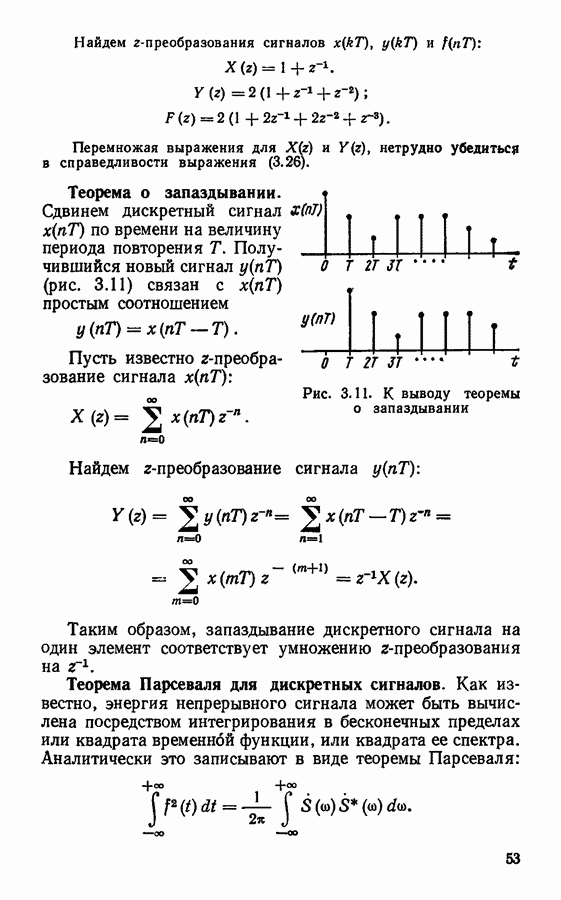
Рис. 3.6. Единичный импульс
Функция  является аналитической функцией комплексного переменного
является аналитической функцией комплексного переменного  -преобразование можно применить и к абстрактным числовым последовательностям.
-преобразование можно применить и к абстрактным числовым последовательностям.
В качестве примеров рассмотрим  -преобразования простейших сигналов. При этом всюду будем полагать, что сигнал
-преобразования простейших сигналов. При этом всюду будем полагать, что сигнал  тождественно равен нулю при
тождественно равен нулю при 
1. Единичный импульс (рис. 3.6)

2. Дискретизированный единичный скачок (рис, 3.7)

3. Экспоненциально убывающий дискретный сигнал (рис 3.8)


Рис. 3.7. Дискретизированный единичный скачок

Рис. 3.8. Экспоненциально убывающий дискретный сигнал
4. Комплексная экспонента

5. Гармоническая функция

6. Степенная функция

Поскольку  -преобразование — это степенной ряд переменной 2-1, то важно рассмотреть вопрос о его сходимости.
-преобразование — это степенной ряд переменной 2-1, то важно рассмотреть вопрос о его сходимости.
Ряд (3.20), определяющий  -преобразование, сходится для
-преобразование, сходится для  где
где  радиус сходимости, зависящий от вида функции
радиус сходимости, зависящий от вида функции  Наиболее просто радиус сходимости определяется для последовательности
Наиболее просто радиус сходимости определяется для последовательности  . В этом случае
. В этом случае  Эта функция имеет полюс при
Эта функция имеет полюс при  Вне окружности
Вне окружности  функция
функция  является аналитической функцией комплексной переменной
является аналитической функцией комплексной переменной  и описывающий ее ряд (3.20) сходится. Следовательно, для
и описывающий ее ряд (3.20) сходится. Следовательно, для  радиус сходимости
радиус сходимости 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
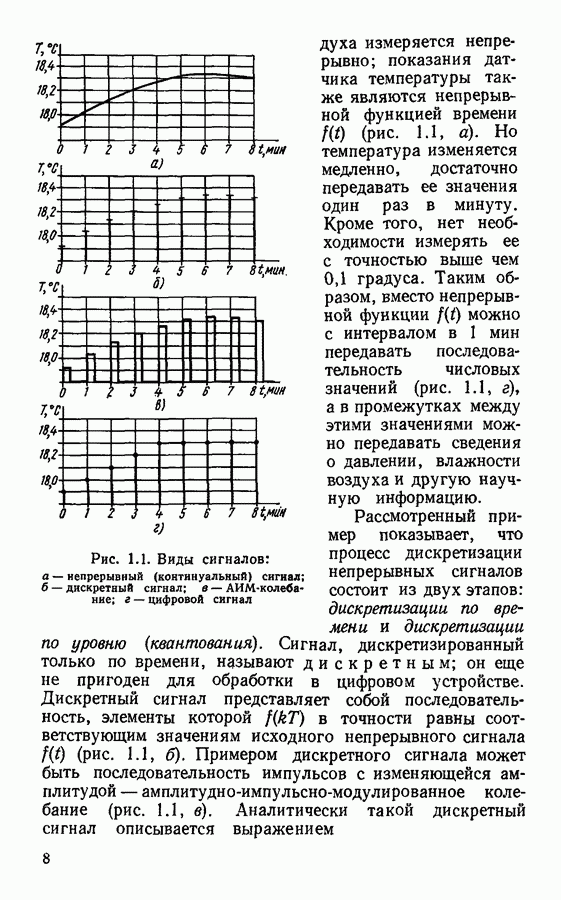
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
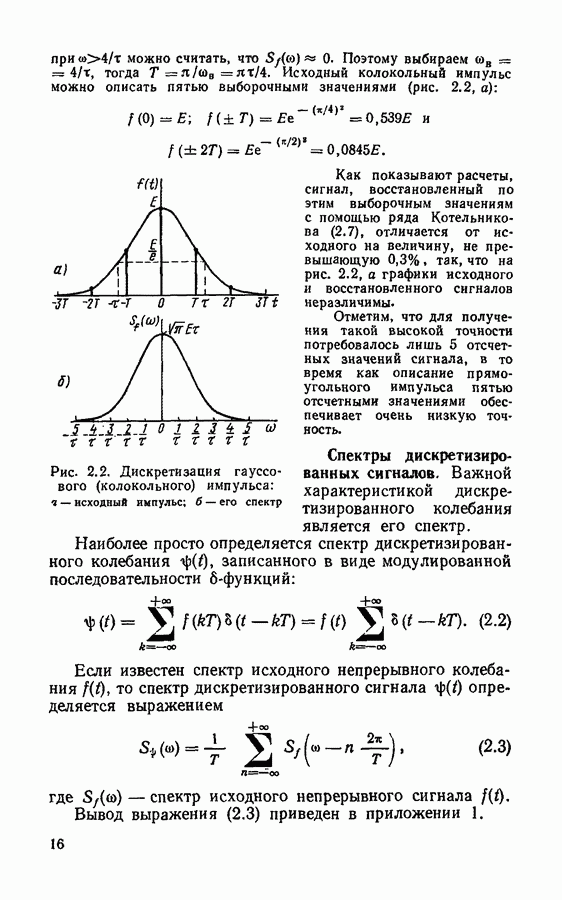
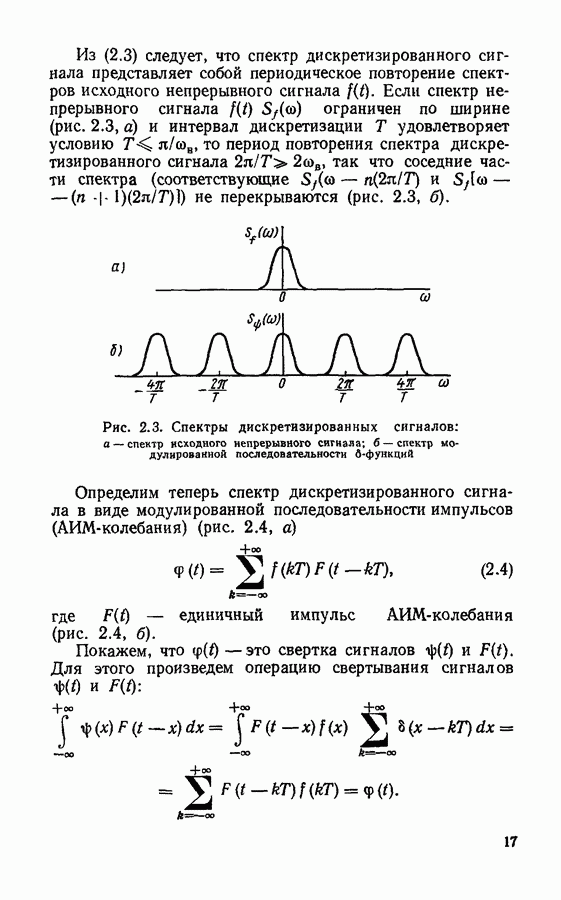
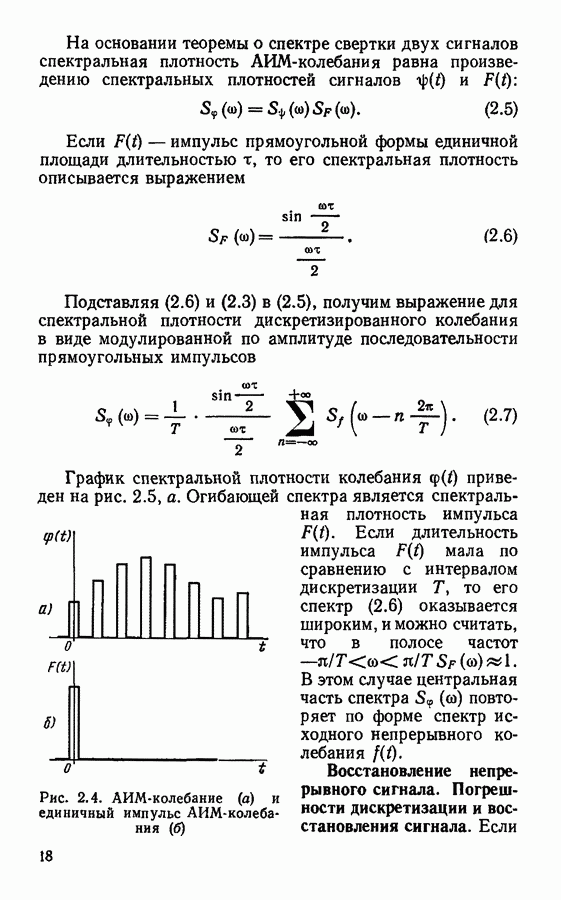
- Спектры дискретизированных сигналов.
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
- Дискретизация сигналов в спектральной области.
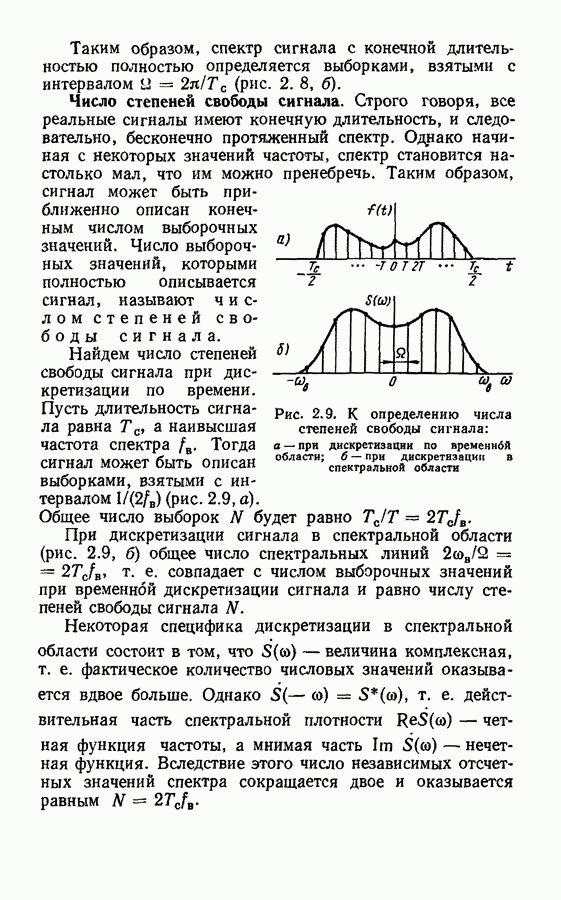
- Число степеней свободы сигнала.
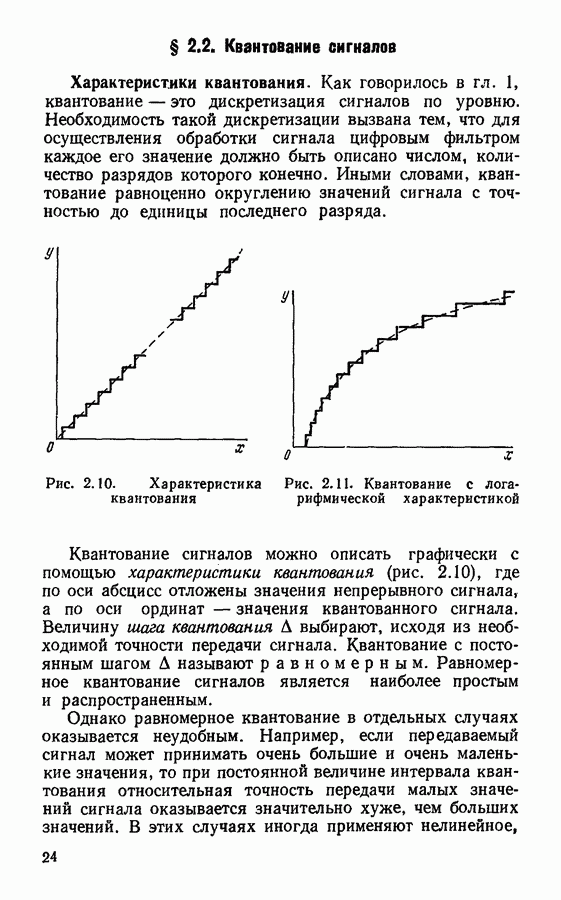
- § 2.2. Квантование сигналов
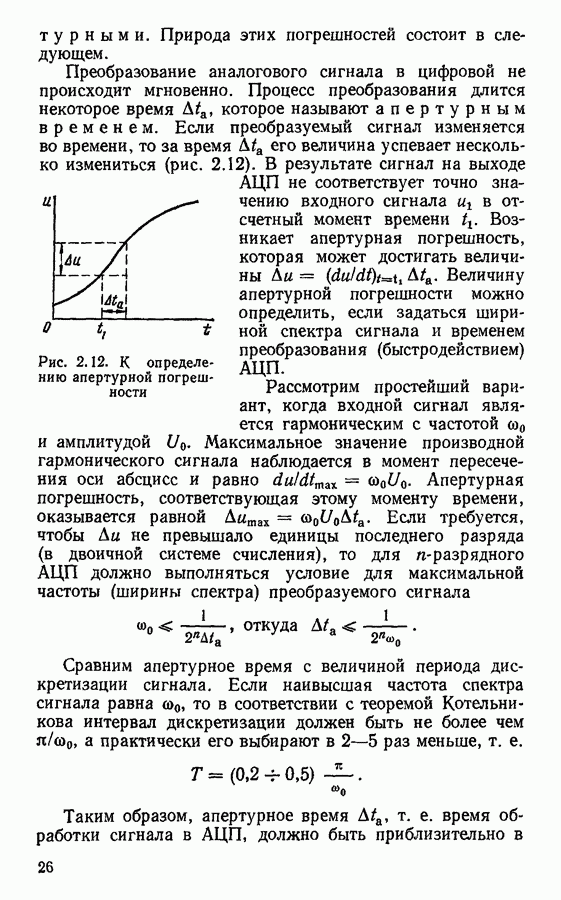
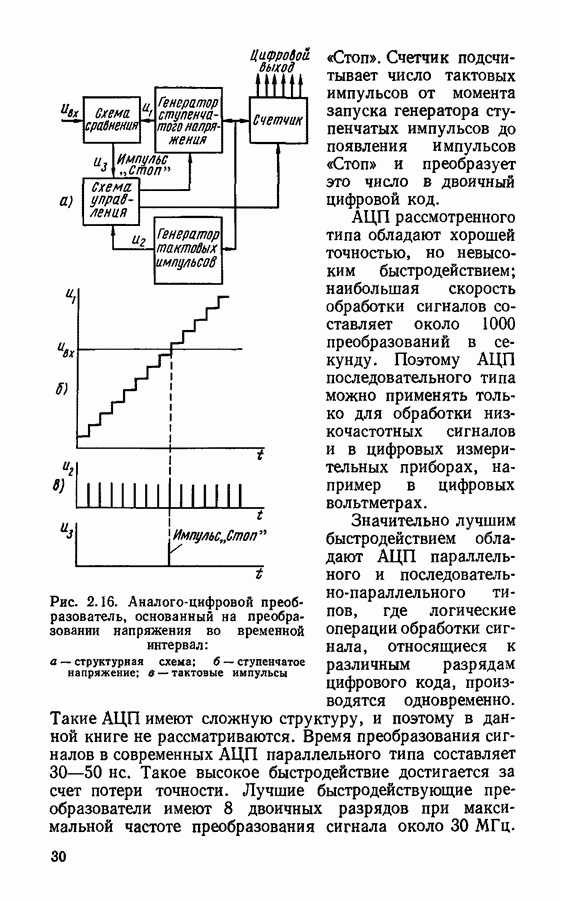
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
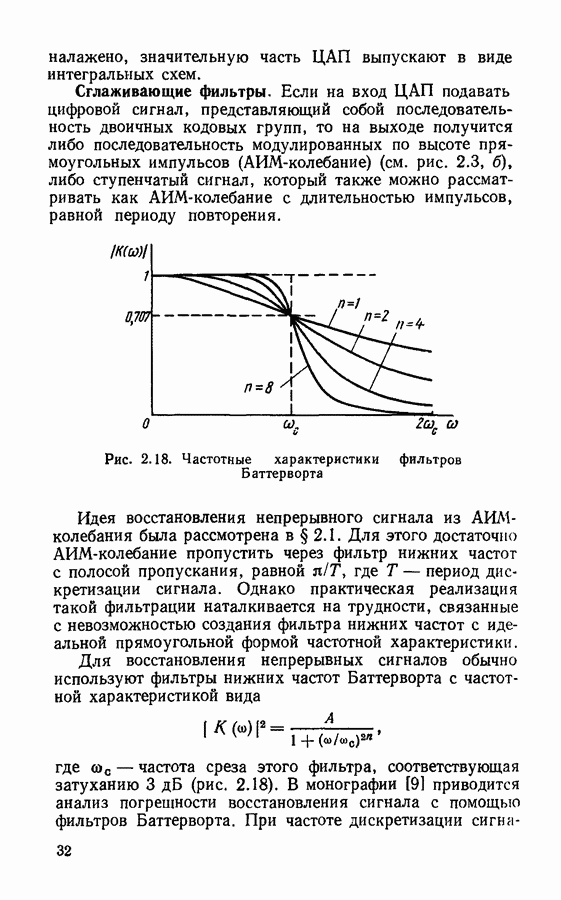
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
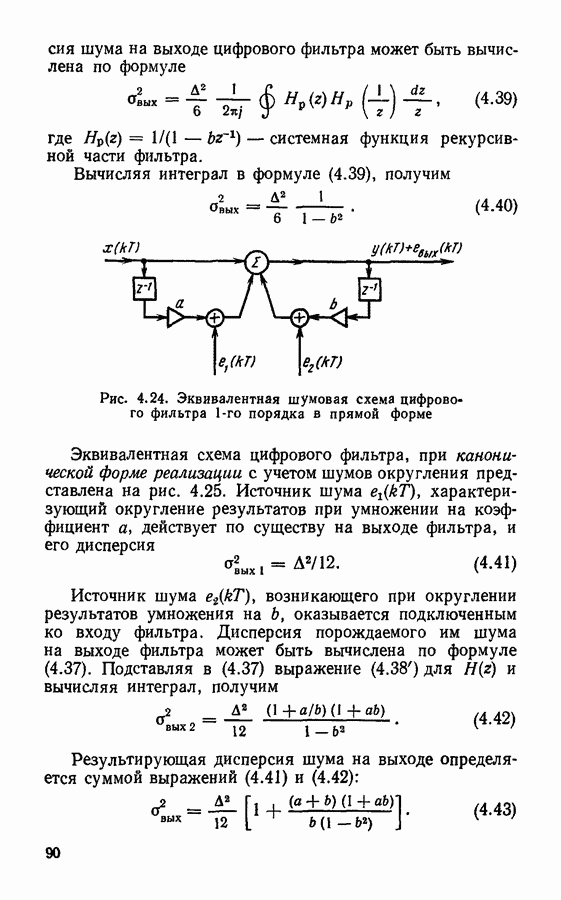
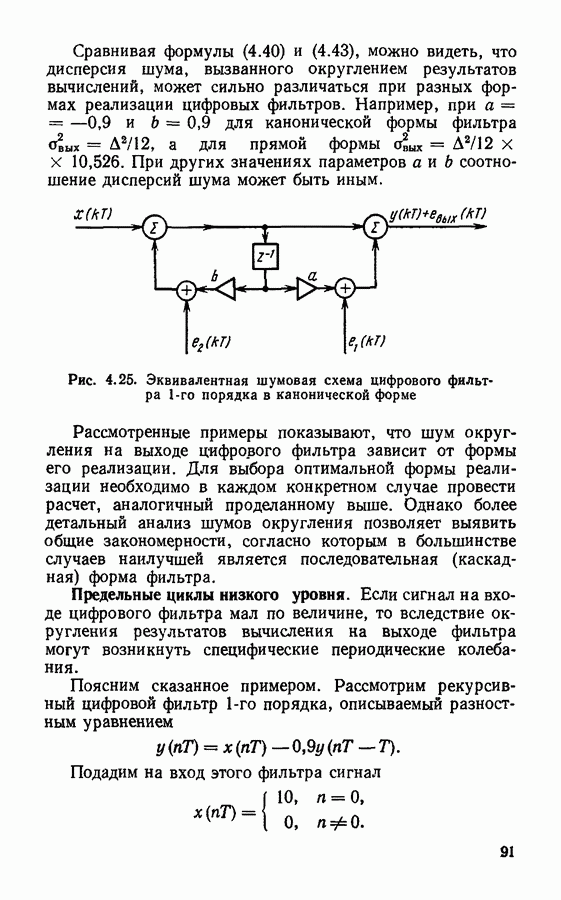
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА