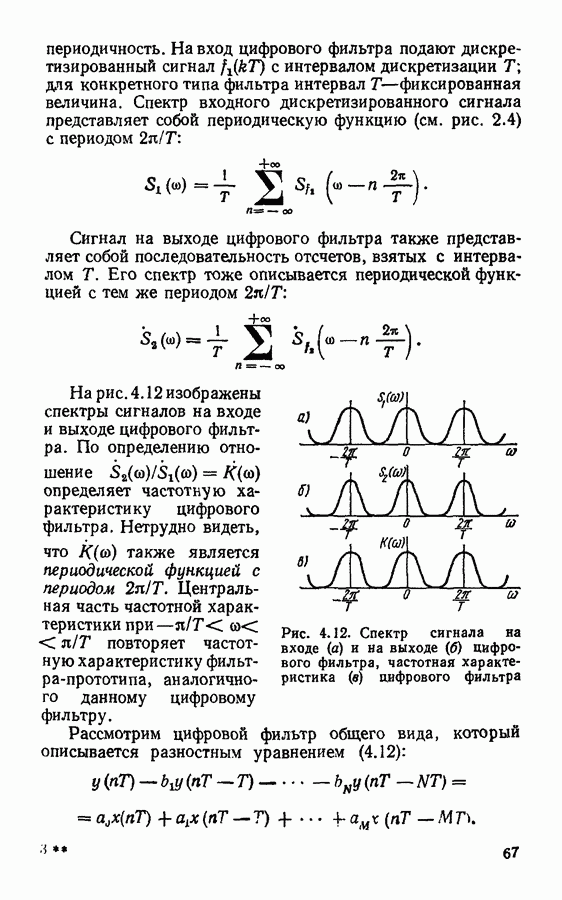
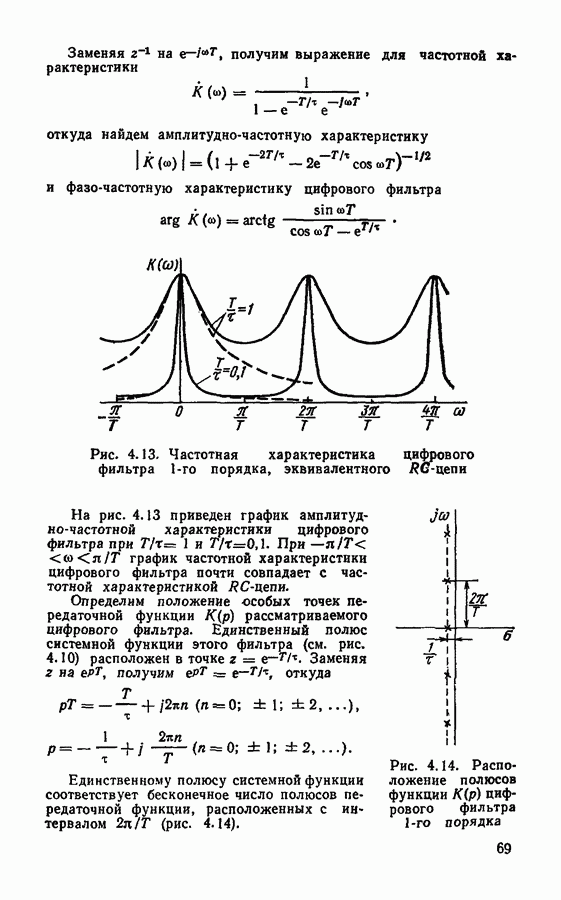
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
§ 2.1. Основы дискретизации непрерывных сигналов
Выбор частоты дискретизации.
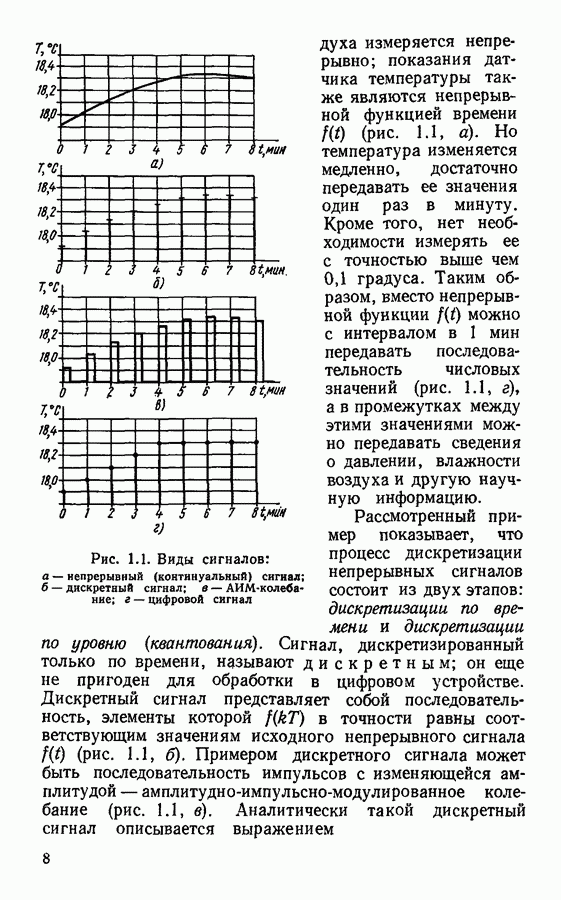
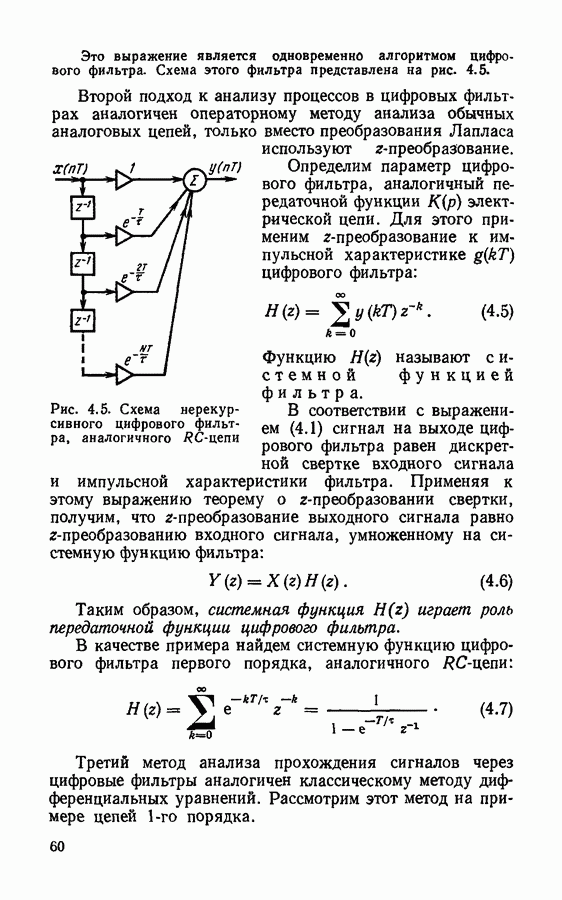
Как указывалось, процедура превращения непрерывных, или континуальных, сигналов в цифровые состоит из двух этапов: дискретизации и квантования. В результате первого этапа непрерывный сигнал заменяется дискретными отсчетными значениями, взятыми через определенные интервалы времени. Очень важен правильный выбор интервала дискретизации. Если отсчеты сигнала брать слишком редко, то быстрые изменения, скачки дискретизируемого сигнала могут остаться незамеченными. Если отсчеты брать слишком часто, то это исключит ошибки, но будет неэкономно, так как придется передавать слишком много значений сигнала.
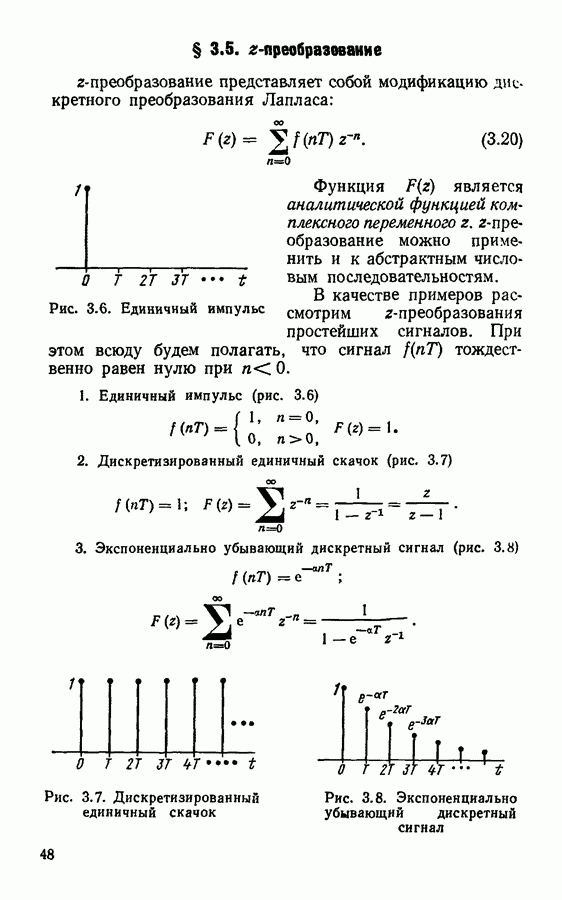
Задача о выборе интервала дискретизации наиболее просто решается для сигналов с ограниченным спектром на основании теоремы Котельникова, или теоремы отсчетов.
В соответствии с теоремой Котельникова непрерывный сигнал  в спектре которого не содержится частот выше
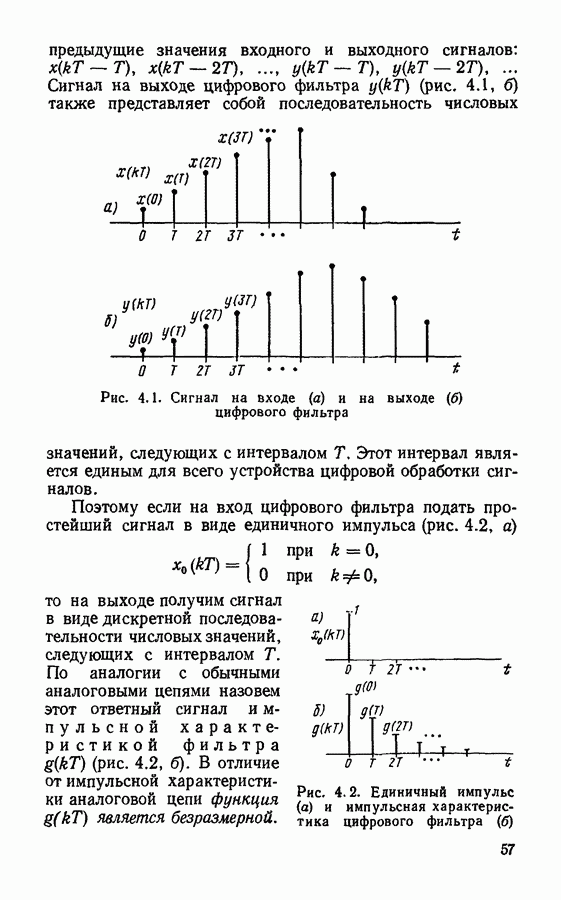
в спектре которого не содержится частот выше  полностью описывается выборочными значениями
полностью описывается выборочными значениями  отсчитанными через интервалы времени
отсчитанными через интервалы времени  Аналитически это выражается в виде ряда Котельникова
Аналитически это выражается в виде ряда Котельникова

Интервал времени  между соседними отсчетами называют интервалом Котельникова или интервалом Найквиста.
между соседними отсчетами называют интервалом Котельникова или интервалом Найквиста.
В соответствии с теоремой Котельникова вместо непрерывного сигнала  с ограниченным спектром можно передавать дискретную последовательность значений
с ограниченным спектром можно передавать дискретную последовательность значений  причем интервал дискретизации
причем интервал дискретизации  должен быть не более чем
должен быть не более чем  Если отсчеты взять слишком редко, то это может привести к грубым ошибкам.
Если отсчеты взять слишком редко, то это может привести к грубым ошибкам.
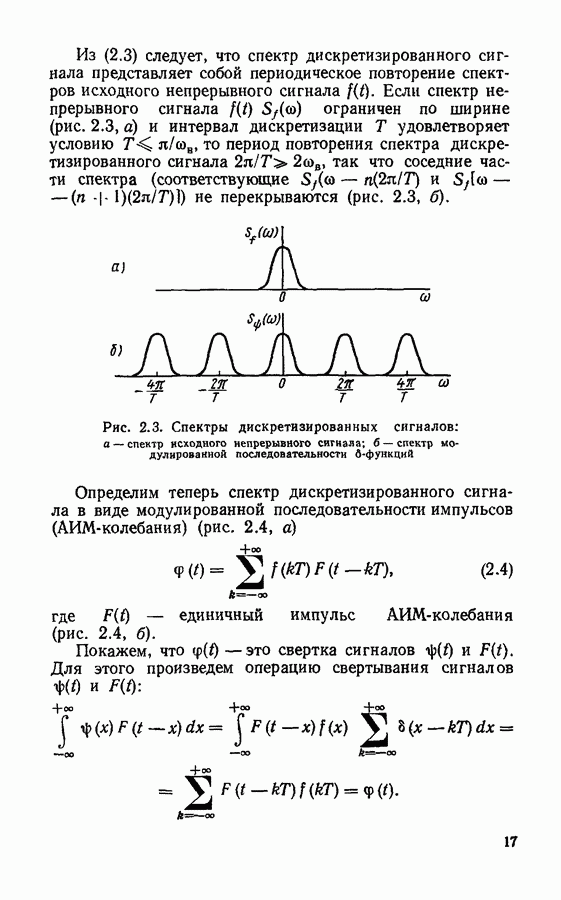
Практически все реальные сигналы имеют конечную длительность, и поэтому спектр их безграничен (см., например, рис. 2.1). Для таких сигналов оказывается невозможным указать значение частоты  выше которого спектр тождественно равен нулю. Это означает, что при любом значении интервала дискретизации
выше которого спектр тождественно равен нулю. Это означает, что при любом значении интервала дискретизации  последовательность дискретных отсчетов описывает исходный непрерывный сигнал с некоторой ошибкой. Величина этой ошибки определяется частью спектра сигнала, соответствующей частотам выше
последовательность дискретных отсчетов описывает исходный непрерывный сигнал с некоторой ошибкой. Величина этой ошибки определяется частью спектра сигнала, соответствующей частотам выше  Более подробно ошибки дискретизации сигнала рассмотрены далее, при анализе ошибок восстановления непрерывного сигнала.
Более подробно ошибки дискретизации сигнала рассмотрены далее, при анализе ошибок восстановления непрерывного сигнала.
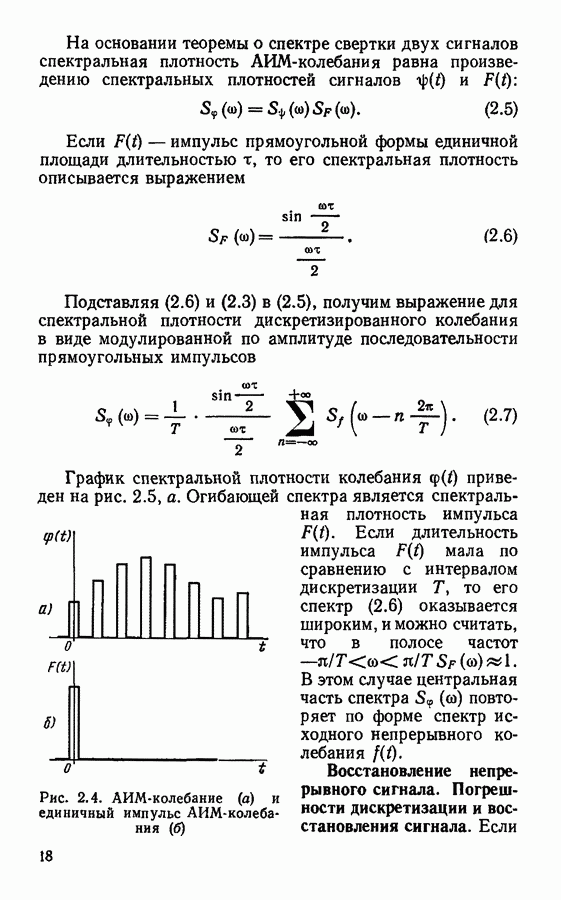
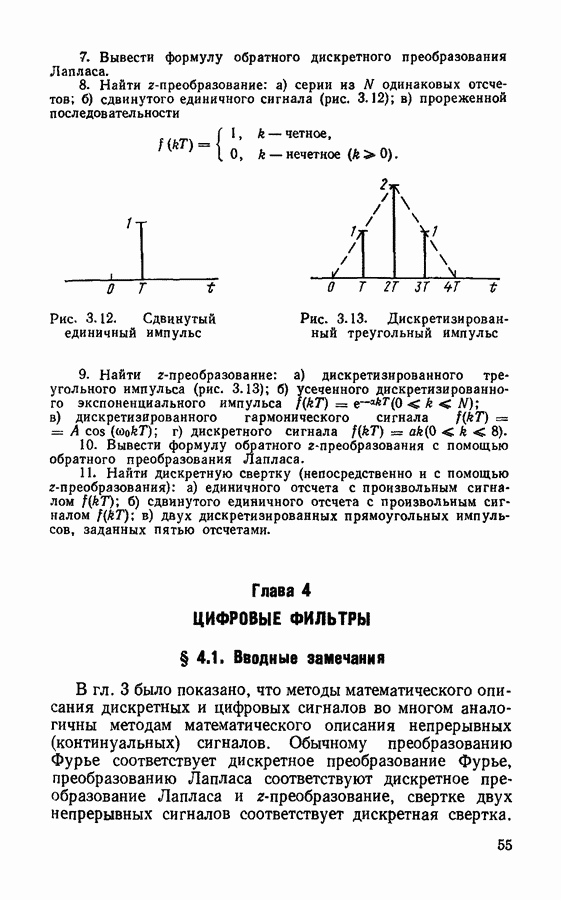
Рассмотрим в качестве примера дискретизацию прямоугольного импульса с амплитудой  и длительностью
и длительностью  (рис. 2.1, а). Спектральная плотность такого импульса описывается выражением
(рис. 2.1, а). Спектральная плотность такого импульса описывается выражением

График спектральной плотности  приведен на рис. 2.1, б.
приведен на рис. 2.1, б.  ростом частоты величина
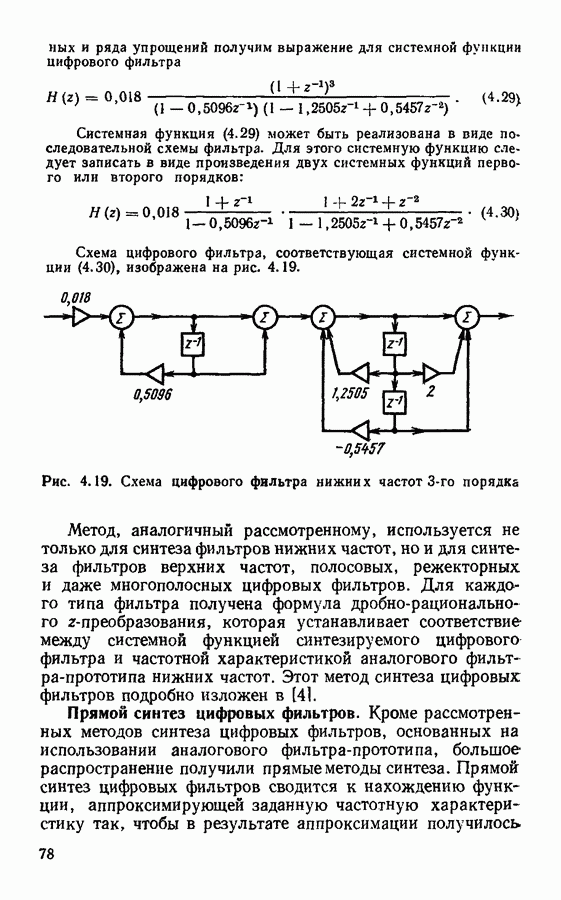
ростом частоты величина  убывает медленно и не обращается строго в нуль, так что при любом значении частоты дискретизации дискретный сигнал описывает исходный прямоугольный импульс с некоторой ошибкой, и эта ошибка убывает медленно с ростом частоты дискретизации.
убывает медленно и не обращается строго в нуль, так что при любом значении частоты дискретизации дискретный сигнал описывает исходный прямоугольный импульс с некоторой ошибкой, и эта ошибка убывает медленно с ростом частоты дискретизации.
Пусть, например,  Тогда
Тогда  При этом импульс описывается пятью отсчетными значениями; крайние отсчетные значения попадают на границы импульсов. Если эти отсчетные значения принять равными
При этом импульс описывается пятью отсчетными значениями; крайние отсчетные значения попадают на границы импульсов. Если эти отсчетные значения принять равными  и затем попытаться восстановить исходный сигнал с помощью ряда Котельникова (2.1), то получим график, изображенный на рис. 2.1, в. Восстановленный сигнал имеет сглаженную форму и несколько большую
и затем попытаться восстановить исходный сигнал с помощью ряда Котельникова (2.1), то получим график, изображенный на рис. 2.1, в. Восстановленный сигнал имеет сглаженную форму и несколько большую
длительность, чем исходный прямоугольный импульс. Сглаженный характер восстановленного сигнала является следствием отбрасывания высокочастотных частей спектра, а несоответствие длительностей исходного и восстановленного сигналов можно устранить путем более тщательного подбора величины интервала дискретизации 
Выберем  Тогда
Тогда  и граница импульса
и граница импульса  будет находиться точно посередине между отсчетными моментами времени
будет находиться точно посередине между отсчетными моментами времени  При этом сигнал, восстановленный с помощью ряда Котельникова (2.1), (рис. 2. 1,г), будет иметь такую же длительность, как и исходный прямоугольный импульс.
При этом сигнал, восстановленный с помощью ряда Котельникова (2.1), (рис. 2. 1,г), будет иметь такую же длительность, как и исходный прямоугольный импульс.

Рис. 2.1. Дискретизация прямоугольного импульса: а — исходный прямоугольный импульс;  его спектр; дискретизация прямоугольного импульса при
его спектр; дискретизация прямоугольного импульса при  то же, при
то же, при 
Рассмотренный пример позволяет сделать следующий вывод. Импульсы с резкими границами типа прямоугольного имеют медленно убывающий спектр, и поэтому их дискретизация затруднительна. Так, при описании прямоугольного импульса пятью выборочными значениями сигнал, восстановленный по этим значениям с помощью ряда Котельникова, сильно отличается от исходного сигнала.
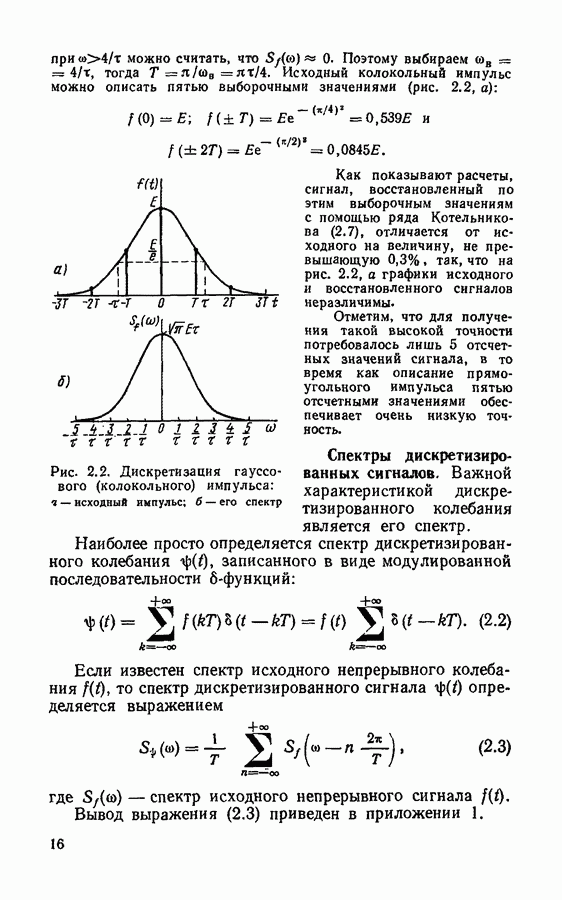
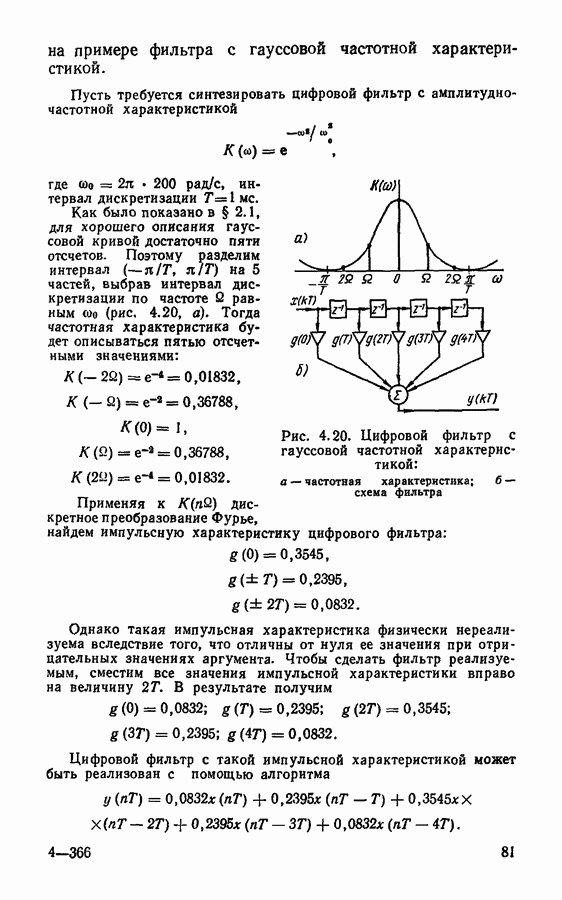
Совсем иные результаты получаются при дискретизации сигналов сглаженной формы. В качестве примера рассмотрим дискретизацию импульса гауссовой (колокольной) формы (рис. 2.2, а)

Спектральная плотность такого импульса также описывается гауссовой кривой

График спектральной плотности  приведен на рис. 2.2, б Функция
приведен на рис. 2.2, б Функция  имеет быстро убывающий характер, так что уже
имеет быстро убывающий характер, так что уже
 можно считать, что
можно считать, что  Поэтому выбираем
Поэтому выбираем  тогда
тогда  Исходный колокольный импульс можно описать пятью выборочными значениями (рис. 2.2, а):
Исходный колокольный импульс можно описать пятью выборочными значениями (рис. 2.2, а):


Рис 2.2, Дискретизация гауссового (колокольного) импульса: а — исходный импульс; б - его спектр
Как показывают расчеты, сигнал, восстановленный по этим выборочным значениям с помощью ряда Котельникова (2.7), отличается от исходного на величину, не превышающую 0,3%, так, что на рис. 2.2, а графики исходного и восстановленного сигналов неразличимы
Отметим, что для получения такой высокой точности потребовалось лишь 5 отсчетных значений сигнала, в то время как описание прямоугольного импульса пятью отсчетными значениями обеспечивает очень низкую точность.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
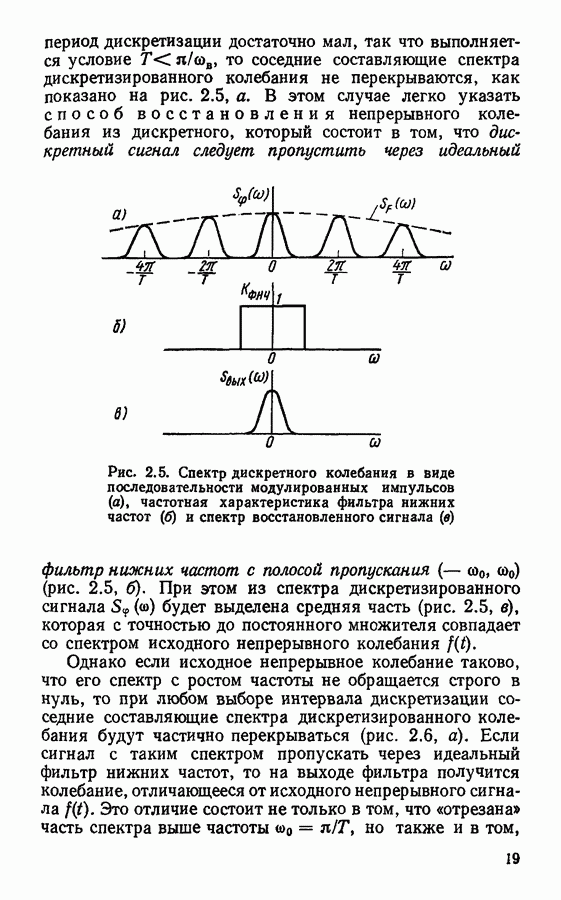
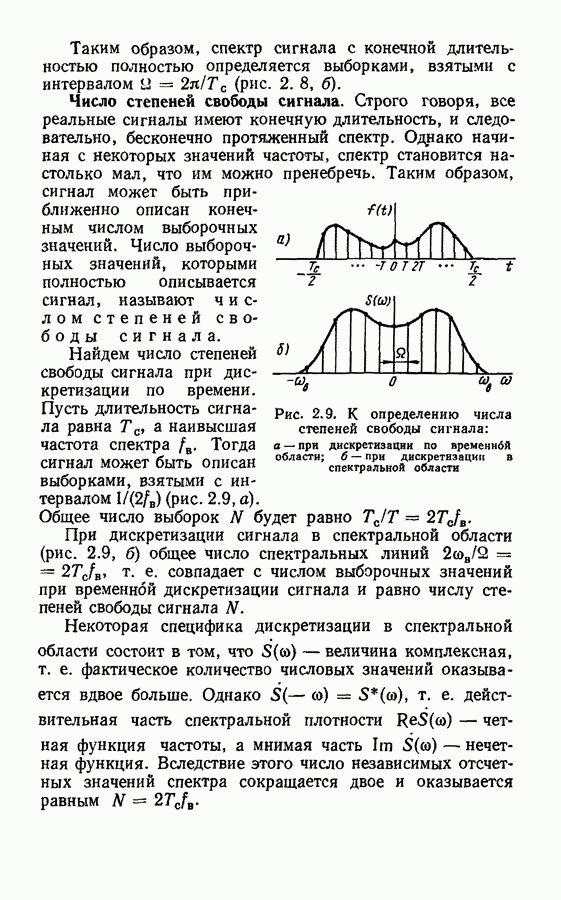
- Спектры дискретизированных сигналов.
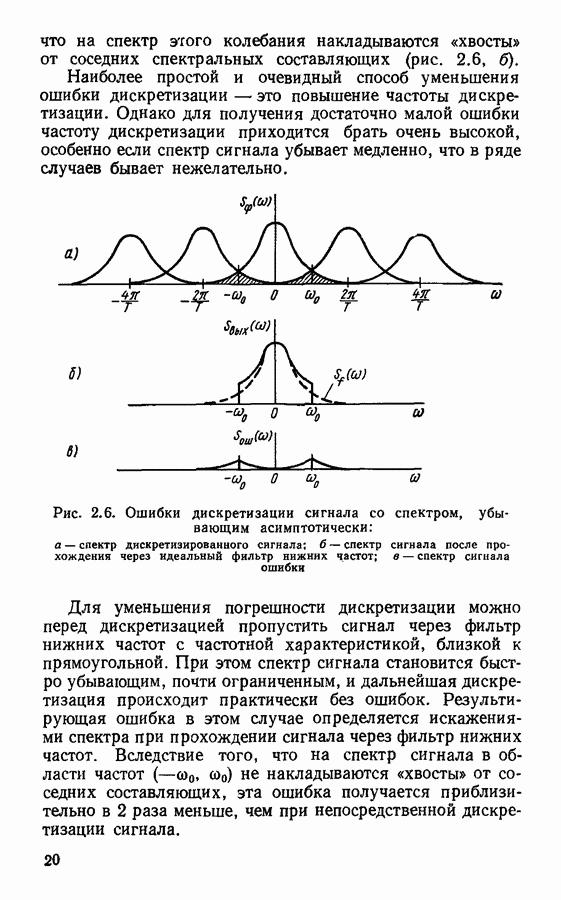
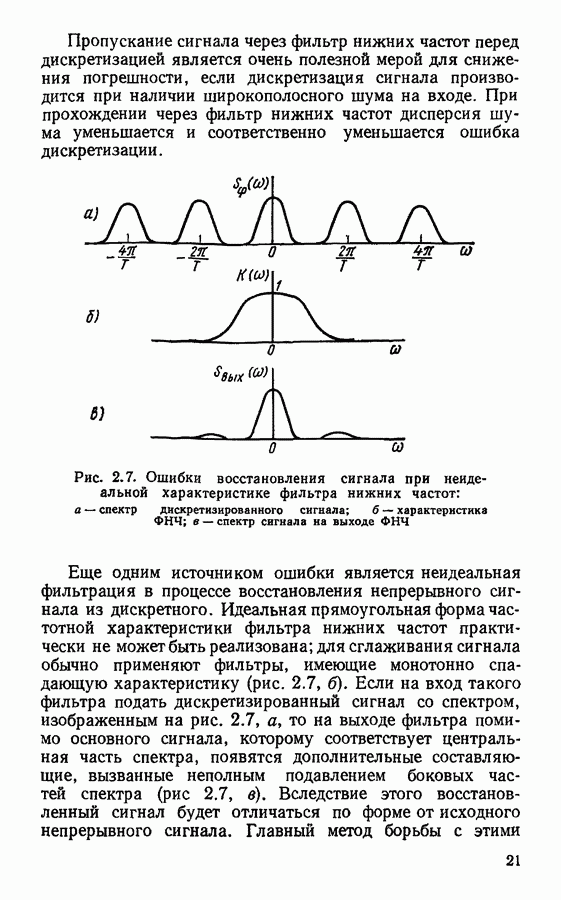
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
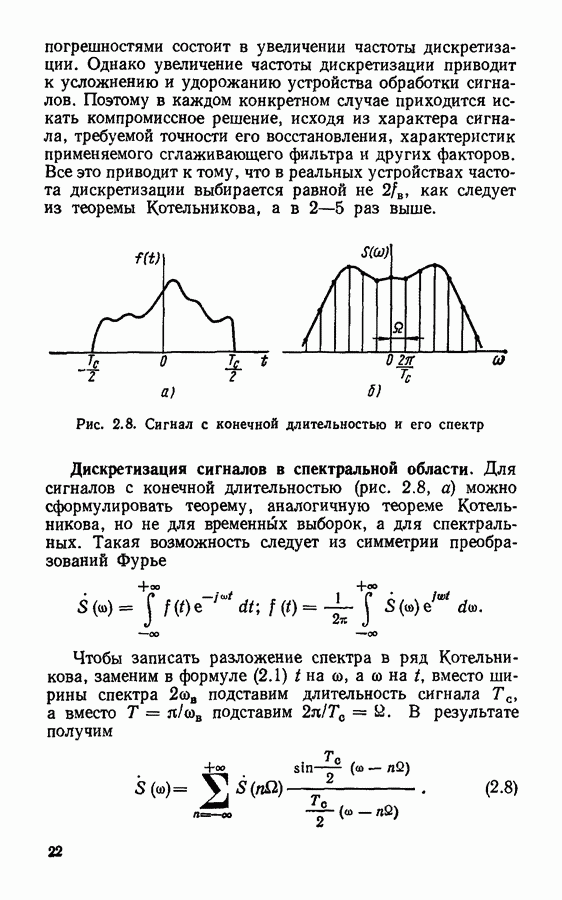
- Дискретизация сигналов в спектральной области.
- Число степеней свободы сигнала.
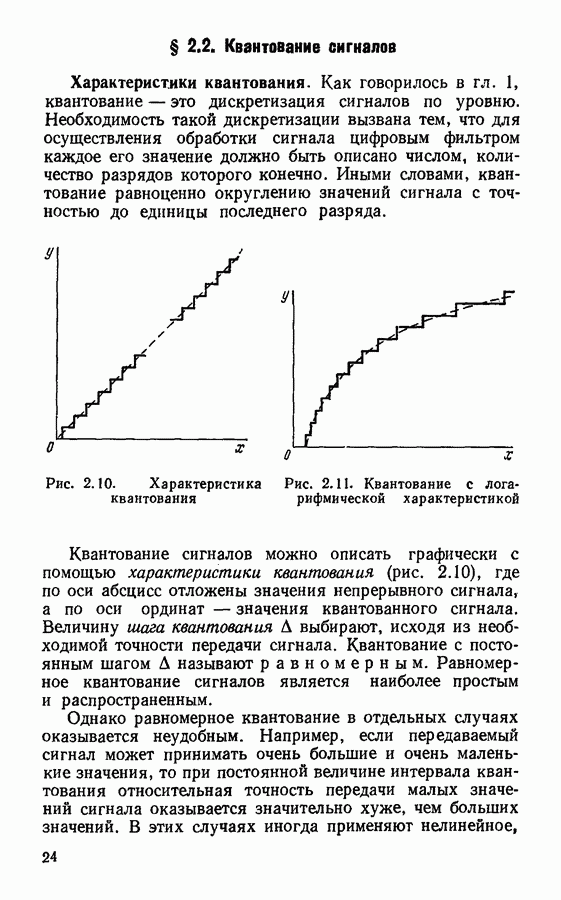
- § 2.2. Квантование сигналов
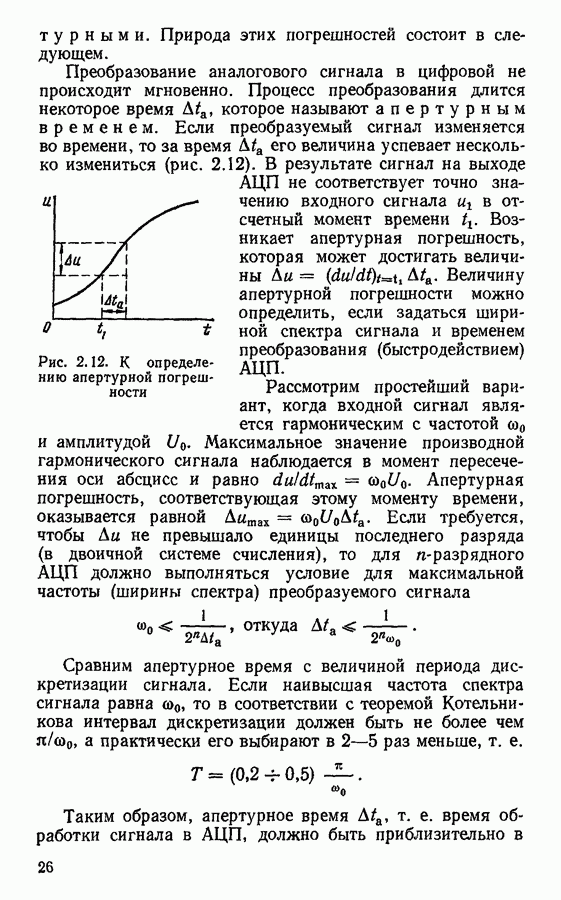
- Аналого-цифровое преобразование.
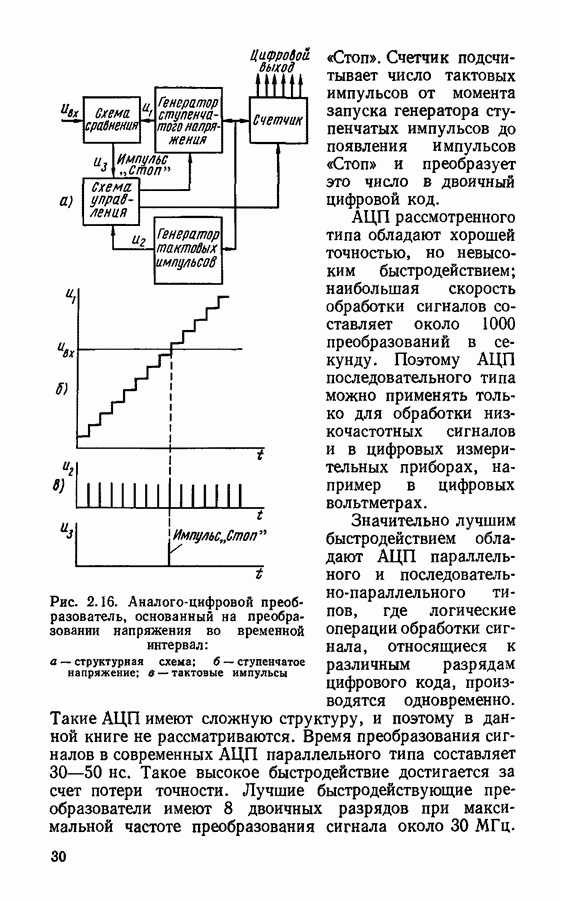
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
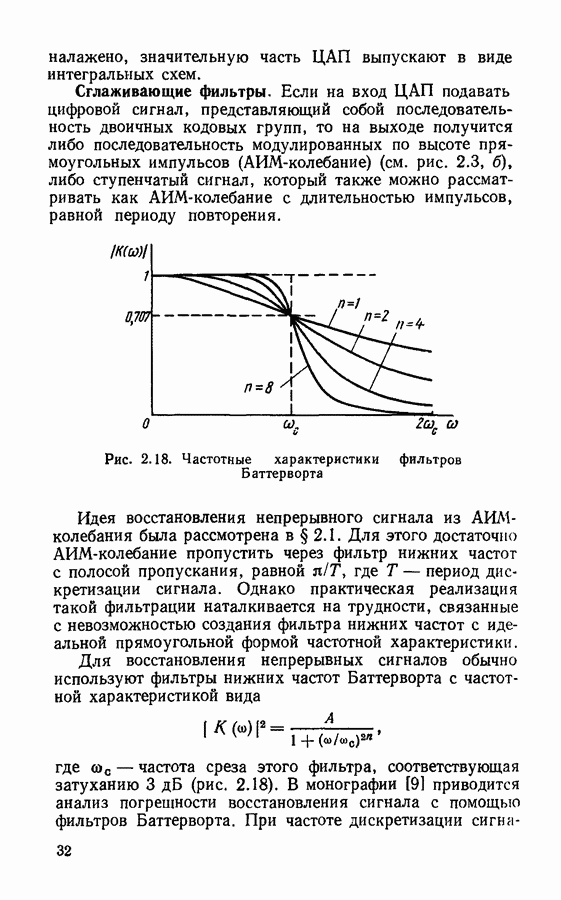
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
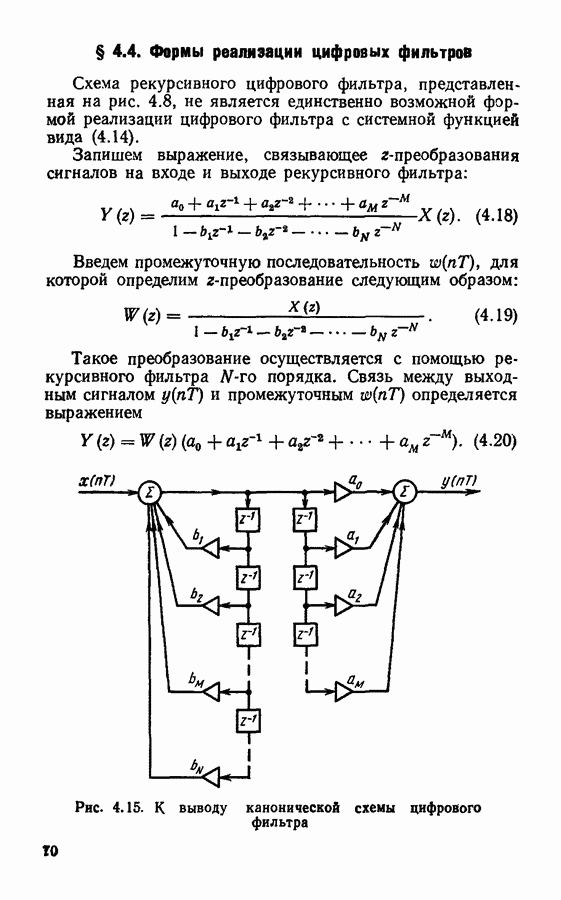
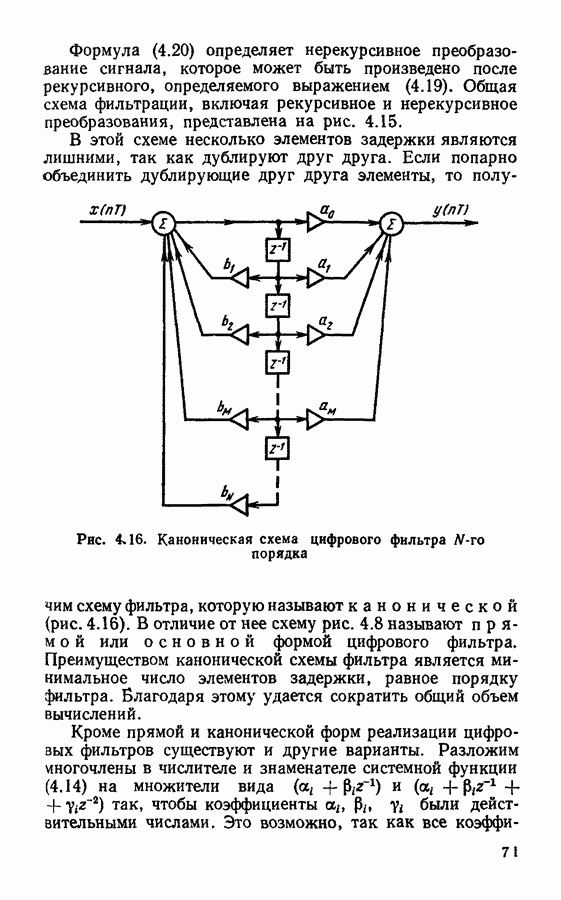
- § 4.4. Формы реализации цифровых фильтров
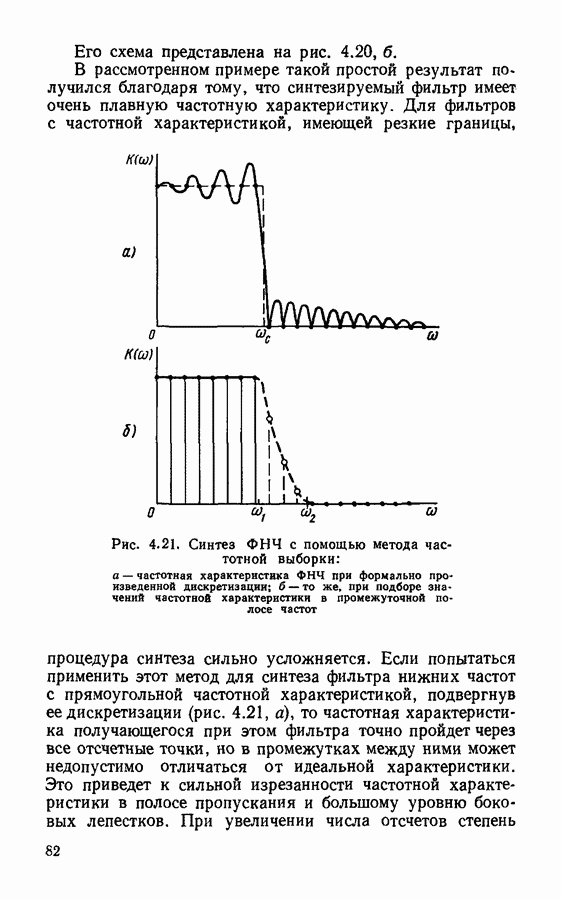
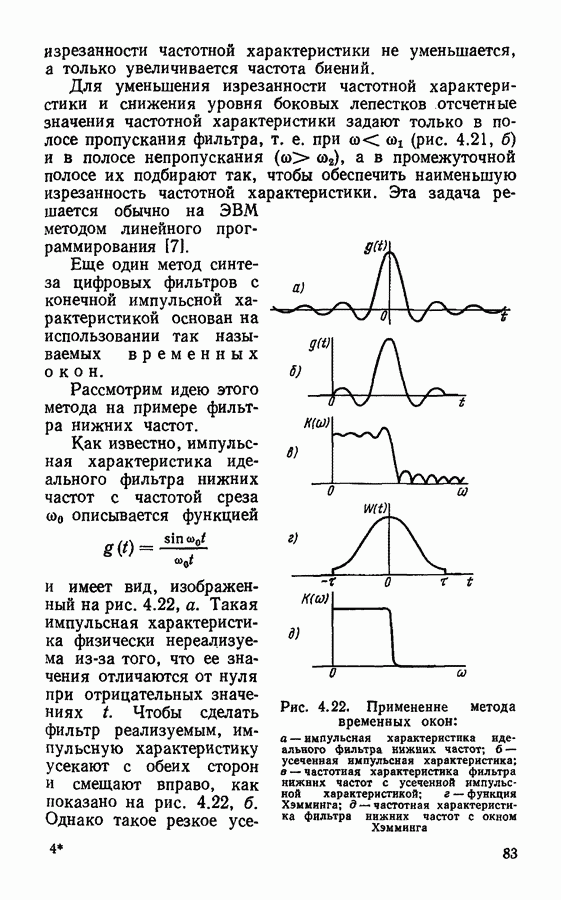
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
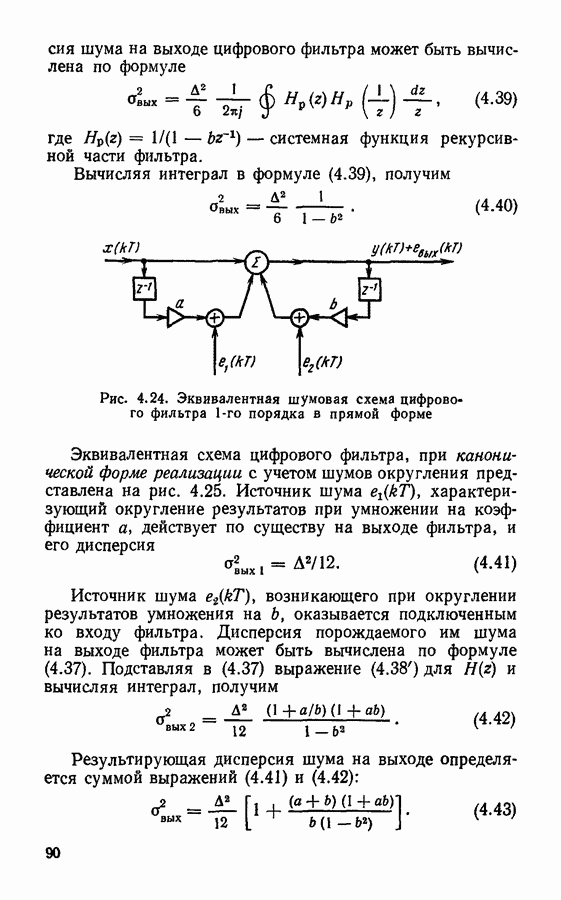
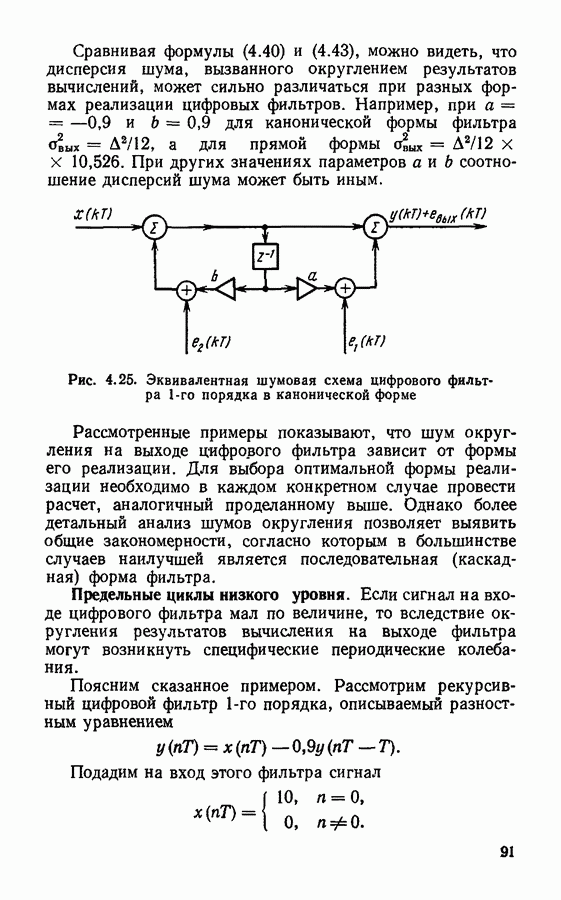
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА