| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
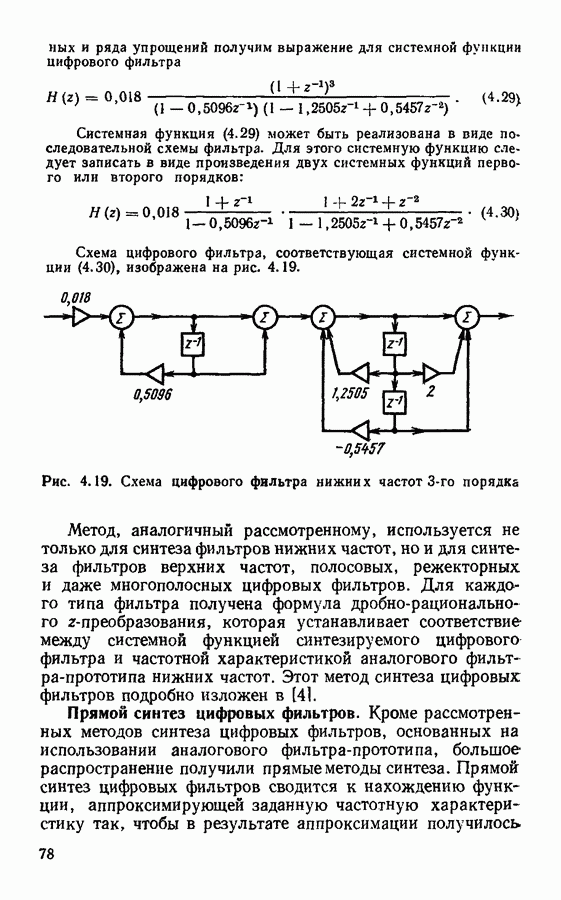
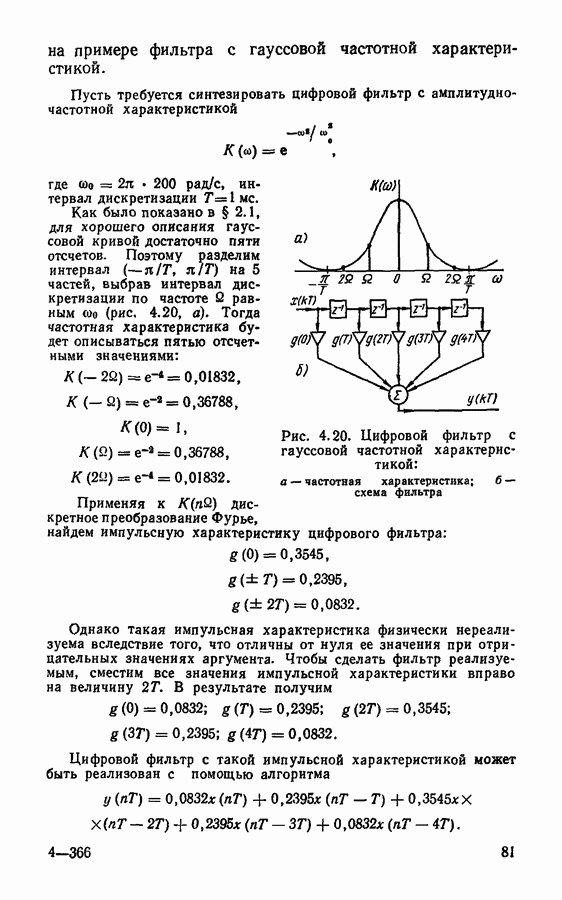
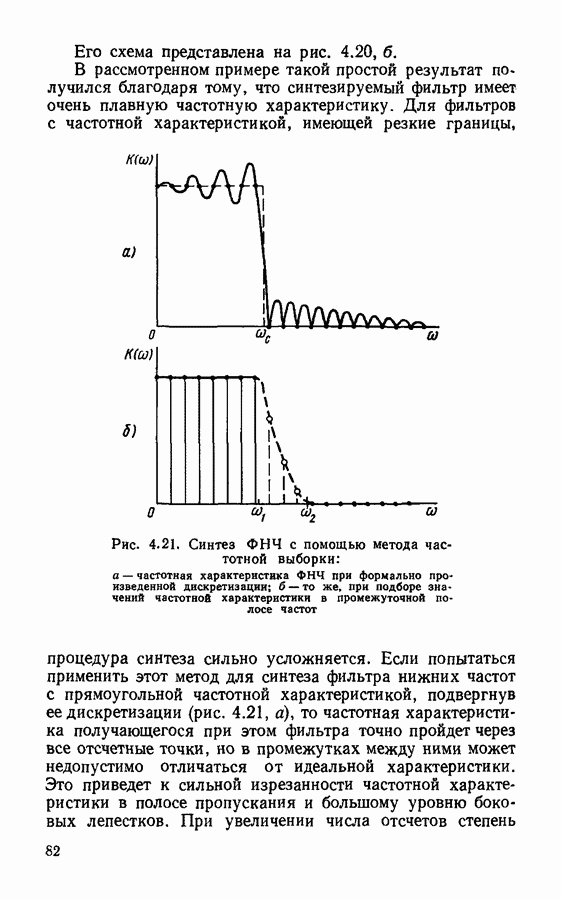
Прямой синтез цифровых фильтров.
Кроме рассмотренных методов синтеза цифровых фильтров, основанных на использовании аналогового фильтра-прототипа, большое распространение получили прямые методы синтеза. Прямой синтез цифровых фильтров сводится к нахождению функции, аппроксимирующей заданную частотную характеристику так, чтобы в результате аппроксимации получилось.
дробно-рациональное выражение для системной функции цифрового фильтра.
Соответствие между частотной характеристикой и системной функцией цифрового фильтра устанавливается соотношением (4.16). Для перехода от частотной характеристики к системной функции надо в выражении для частотной характеристики  заменить на
заменить на  Чтобы получающееся при этом выражение
Чтобы получающееся при этом выражение  для системной функции было дробно-рациональным, исходное выражение для
для системной функции было дробно-рациональным, исходное выражение для  должно быть дробно-рациональным относительно
должно быть дробно-рациональным относительно  Поиск подходящей аппроксимации для
Поиск подходящей аппроксимации для  является главной трудностью прямого метода синтеза цифровых фильтров.
является главной трудностью прямого метода синтеза цифровых фильтров.
Обычно задачу аппроксимации решают, подбирая для  рациональное выражение относительно тригонометрических функций от
рациональное выражение относительно тригонометрических функций от  Каждая из тригонометрических: функций может быть представлена в виде комбинации комплексных экспонент
Каждая из тригонометрических: функций может быть представлена в виде комбинации комплексных экспонент  в результате чего можно получить выражение для частотной характеристики
в результате чего можно получить выражение для частотной характеристики  в требуемой форме.
в требуемой форме.
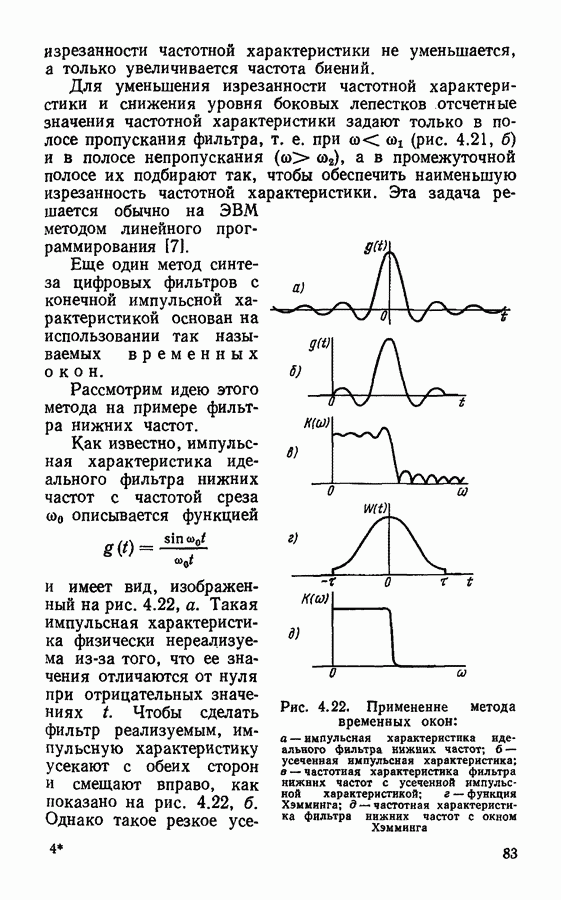
Например, для фильтра нижних частот с частотой среза  частотная характеристика может быть аппроксимирована выражением
частотная характеристика может быть аппроксимирована выражением

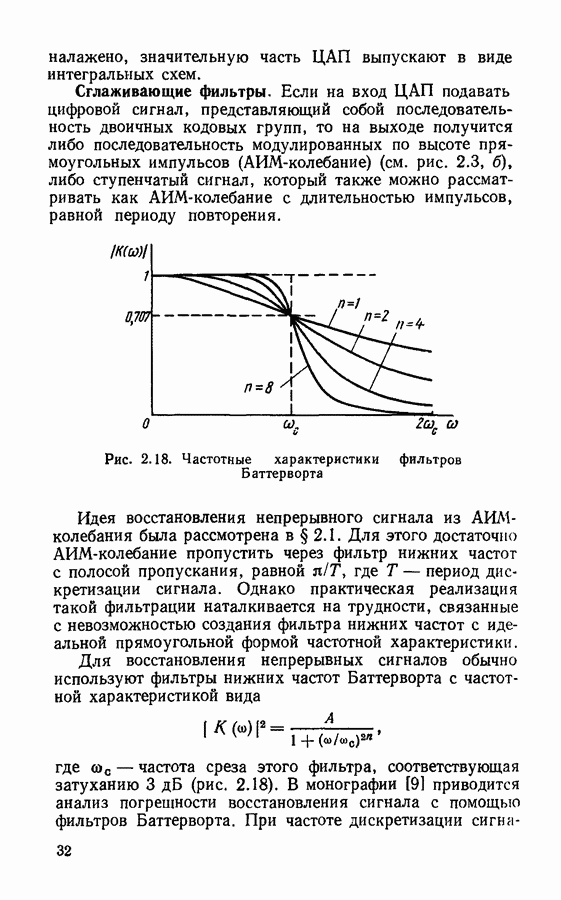
График функции (4.31) почти не отличается от частот  характеристик фильтров Баттерворта, изображенных на рис. 2.18.
характеристик фильтров Баттерворта, изображенных на рис. 2.18.
Дальнейшая процедура синтеза цифрового фильтра сводится к следующему: 1) по заданным характеристикам рассчитывают порядок фильтра  заменяя в выражении для
заменяя в выражении для  на
на  находят квадрат системной функции
находят квадрат системной функции  определяют положение полюсов функции
определяют положение полюсов функции  и с помощью процедуры, изложенной в [2], находят положение полюсов функции
и с помощью процедуры, изложенной в [2], находят положение полюсов функции  исходя из положения полюсов, находят выражение для системной функции
исходя из положения полюсов, находят выражение для системной функции  и записывают алгоритм цифровой фильтрации.
и записывают алгоритм цифровой фильтрации.
Более подробно прямые методы синтеза цифровых фильтров, включая вопросы устойчивости, изложены в [4] и [7].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
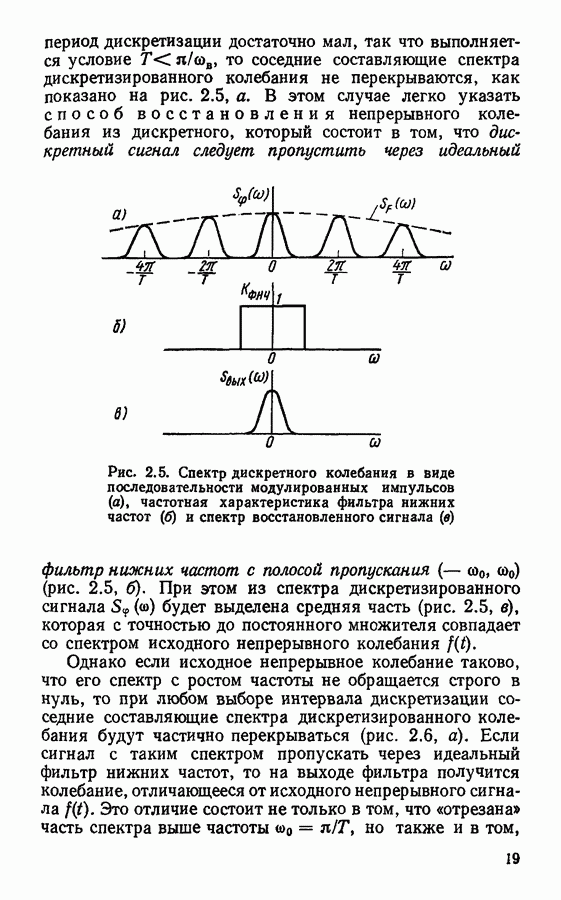
- Спектры дискретизированных сигналов.
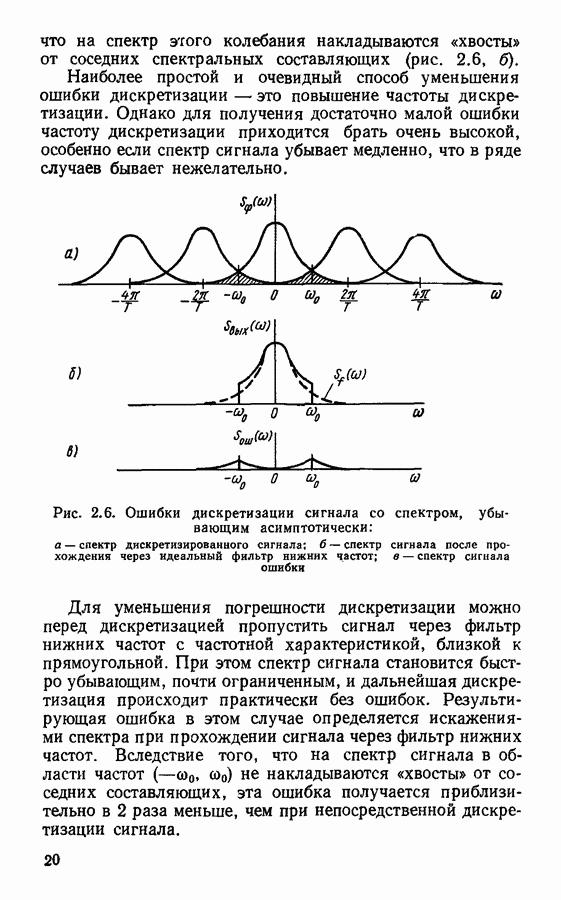
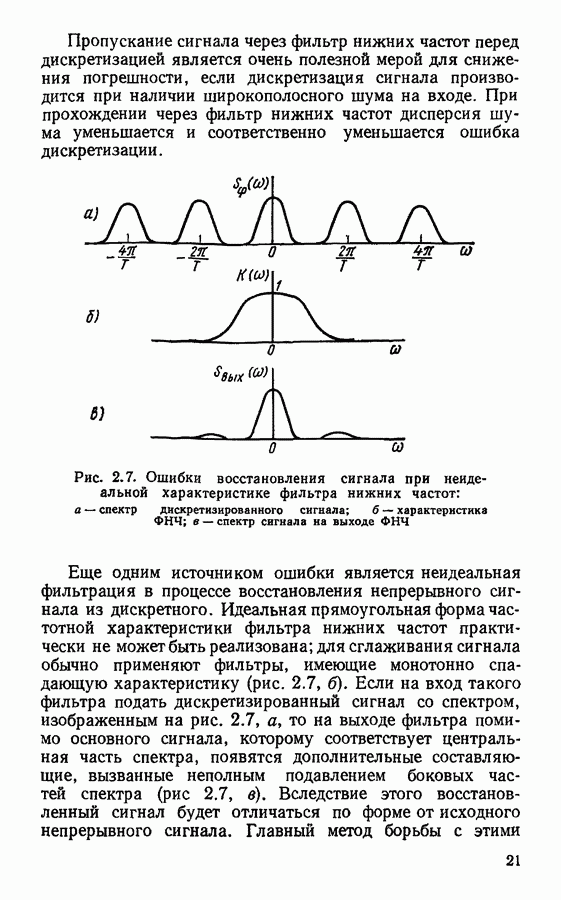
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
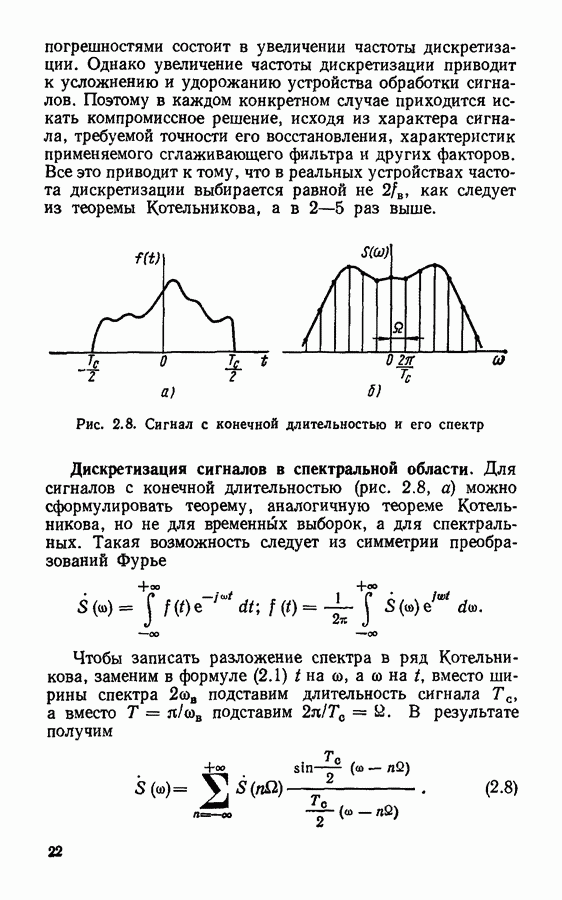
- Дискретизация сигналов в спектральной области.
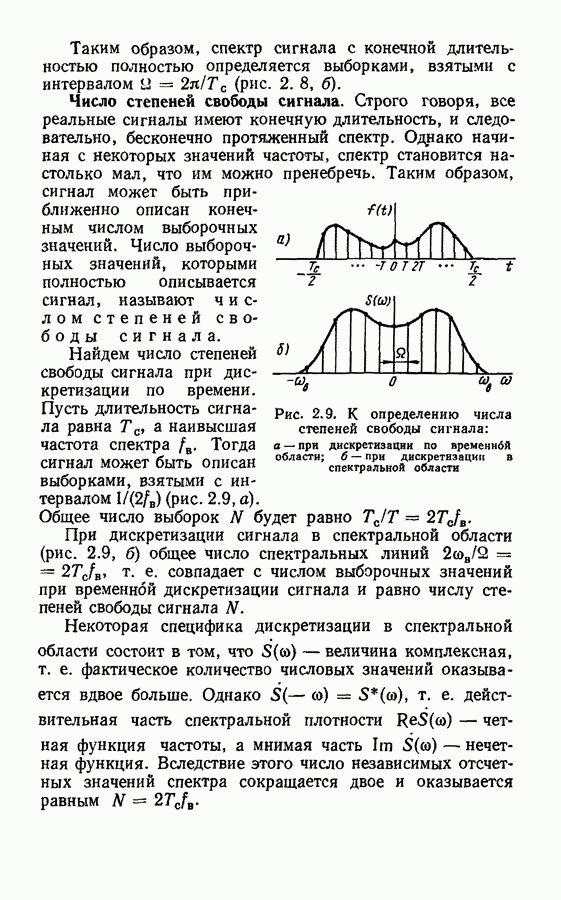
- Число степеней свободы сигнала.
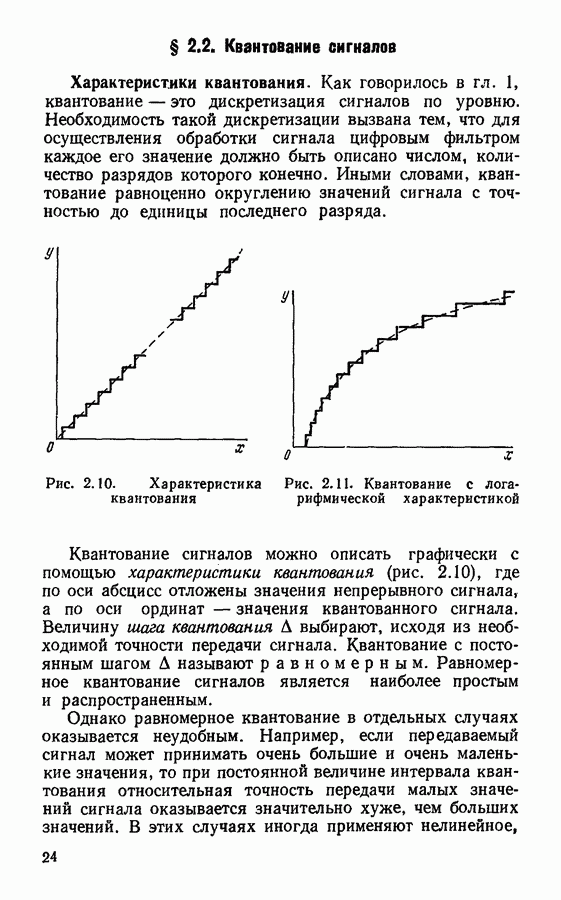
- § 2.2. Квантование сигналов
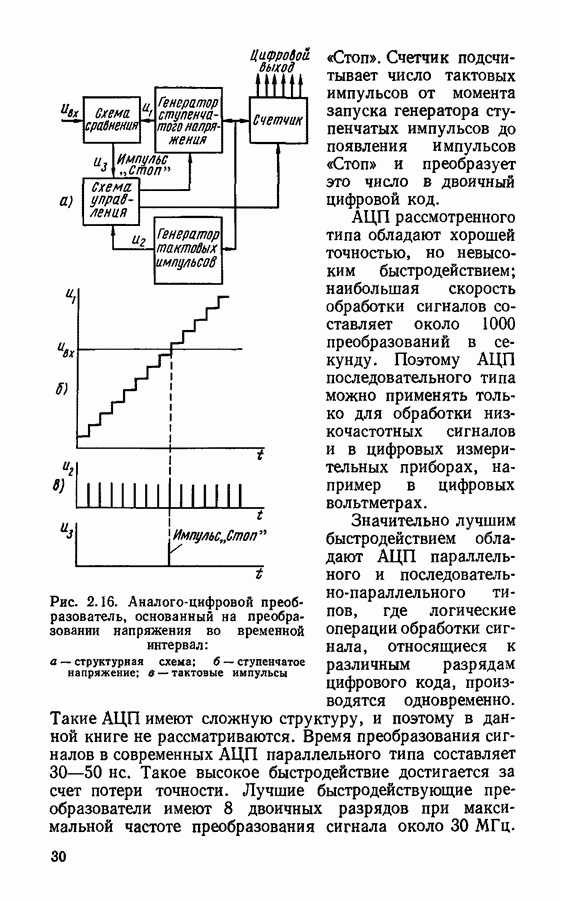
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА