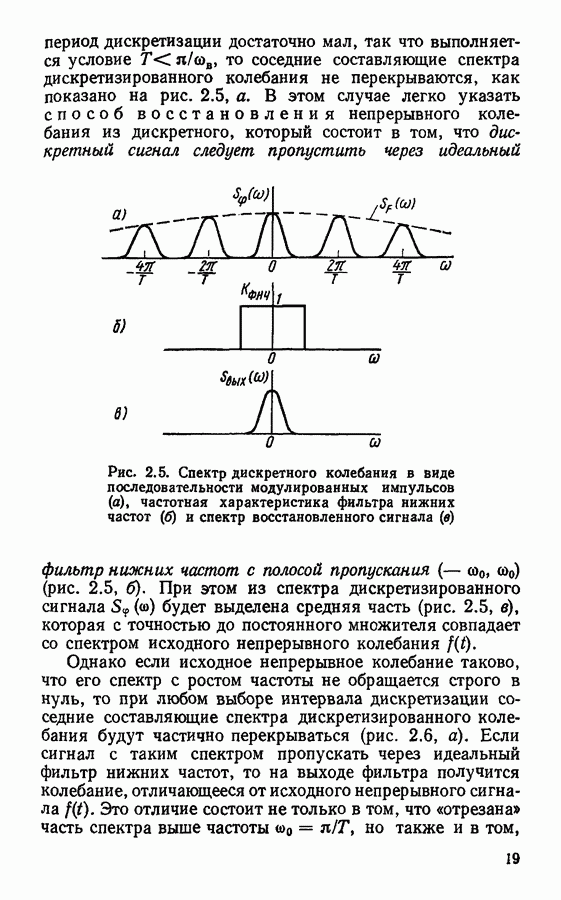
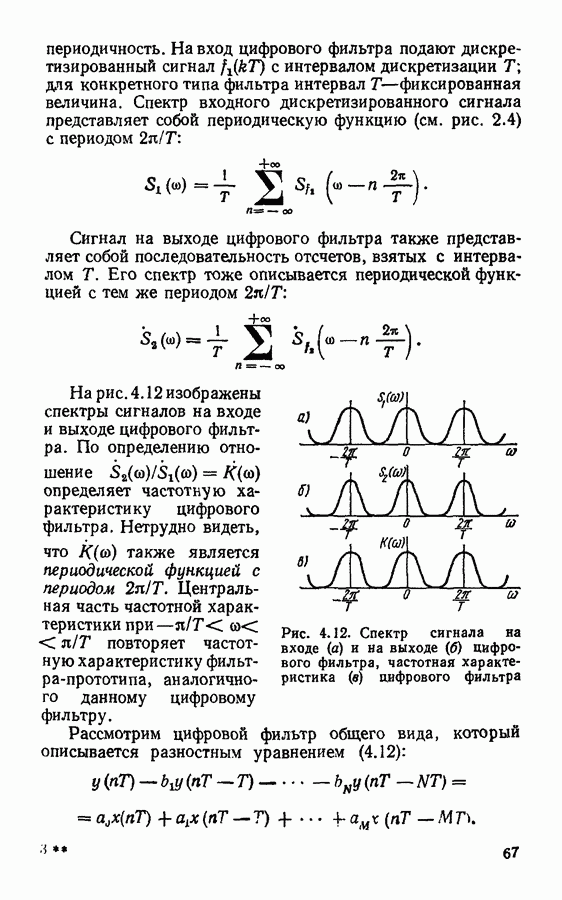
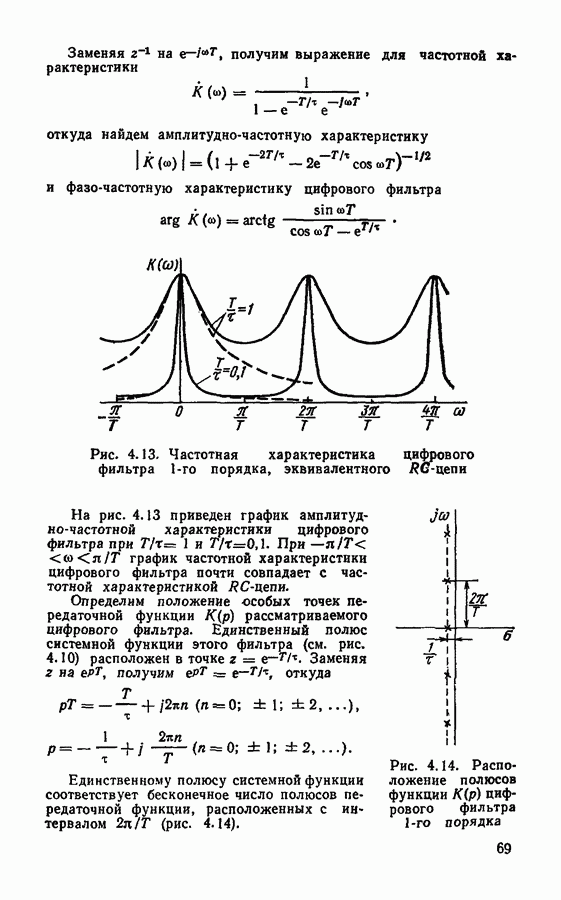
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4.4. Формы реализации цифровых фильтров
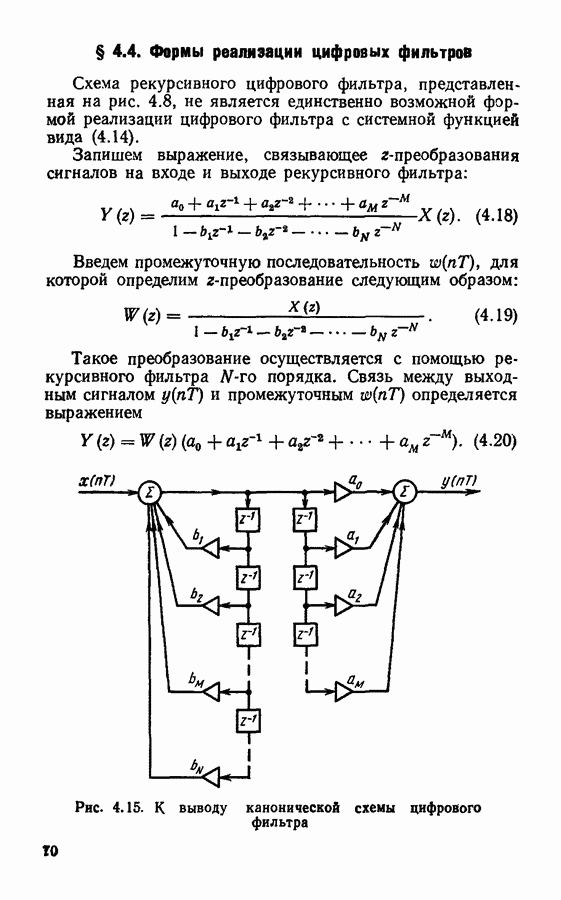
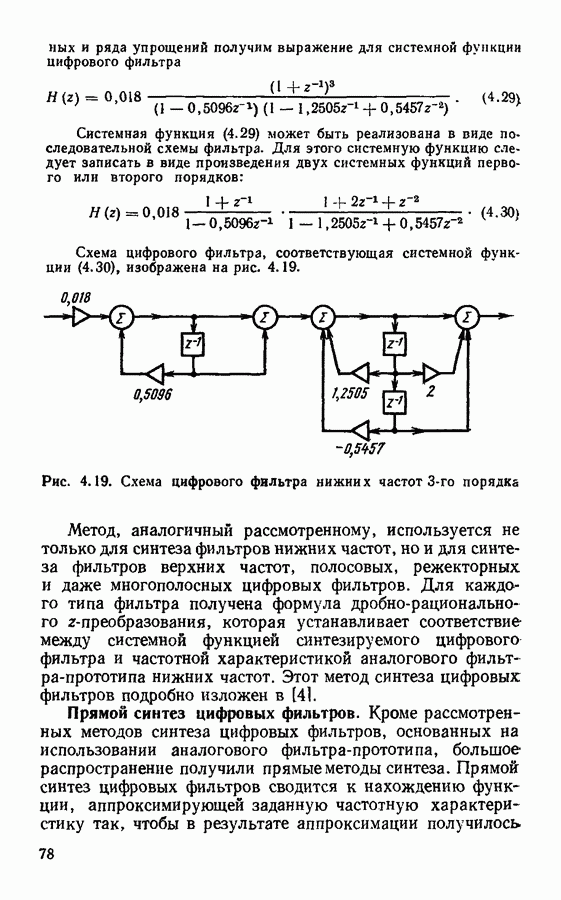
Схема рекурсивного цифрового фильтра, представленная на рис. 4.8, не является единственно возможной формой реализации цифрового фильтра с системной функцией вида (4.14).
Запишем выражение, связывающее  -преобразования сигналов на входе и выходе рекурсивного фильтра:
-преобразования сигналов на входе и выходе рекурсивного фильтра:

Введем промежуточную последовательность  для которой определим
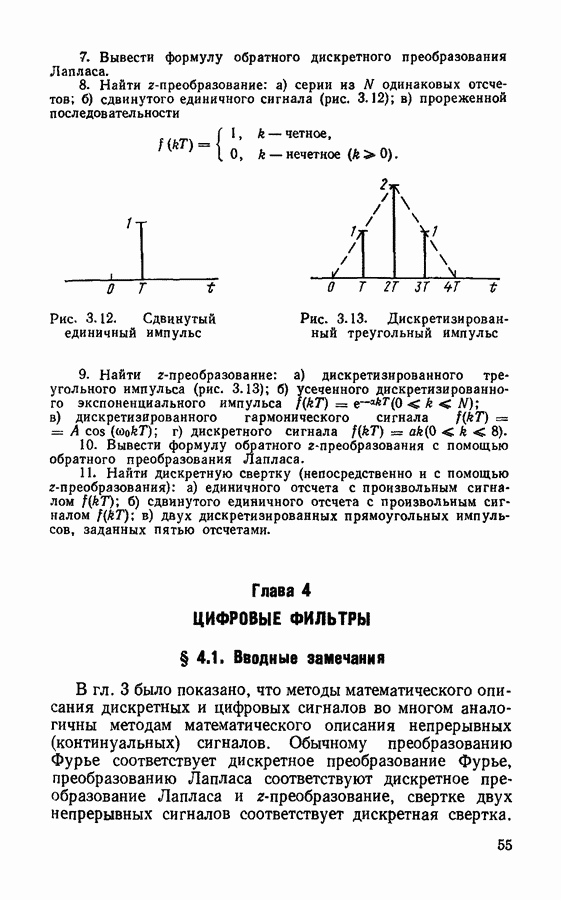
для которой определим  -преобразование следующим образом:
-преобразование следующим образом:

Такое преобразование осуществляется с помощью рекурсивного фильтра  порядка. Связь между выходным сигналом
порядка. Связь между выходным сигналом  и промежуточным
и промежуточным  определяется выражением
определяется выражением


Рис. 4.15. К выводу канонической схемы цифрового фильтра
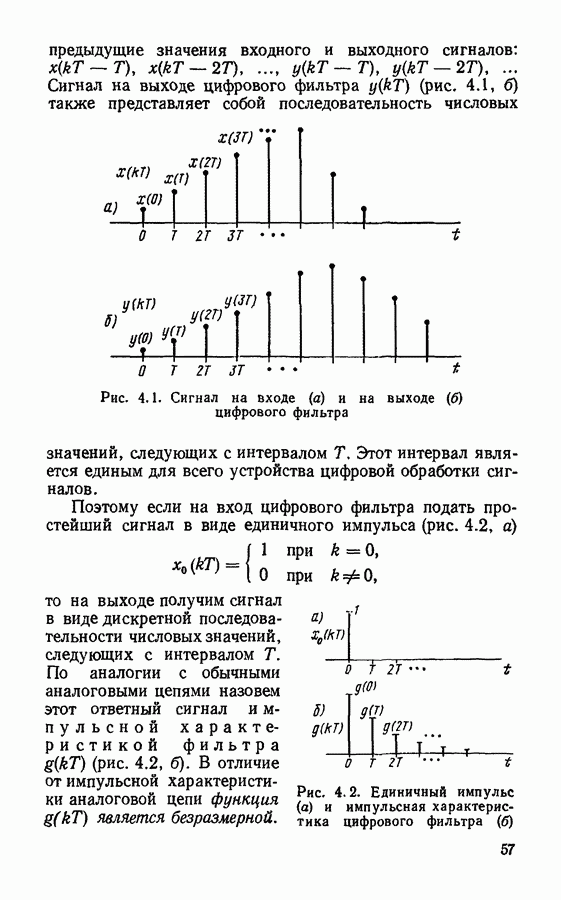
Формула (4.20) определяет нерекурсивное преобразование сигнала, которое может быть произведено после рекурсивного, определяемого выражением (4.19). Общая схема фильтрации, включая рекурсивное и нерекурсивное преобразования, представлена на рис. 4.15.

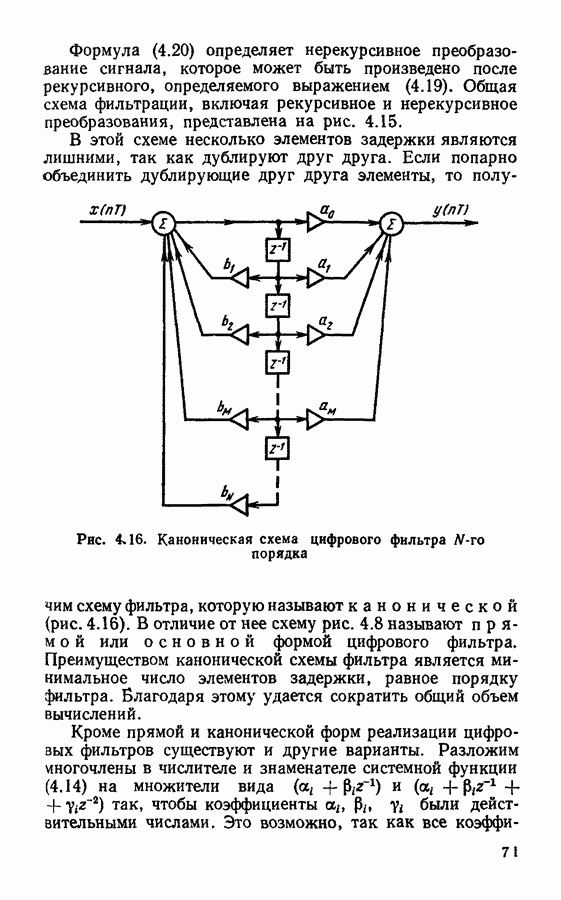
Рис. 4.16. Каноническая схема цифрового фильтра  порядка
порядка
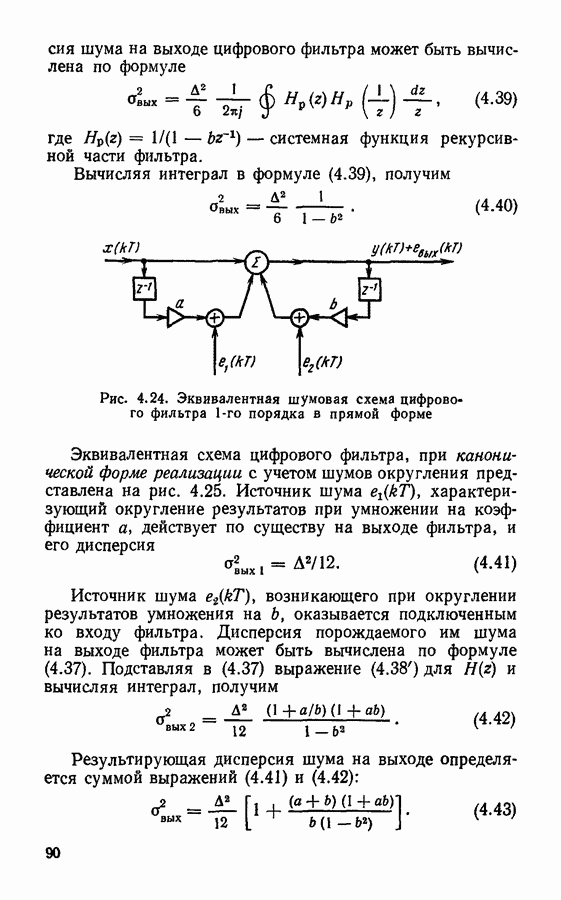
В этой схеме несколько элементов задержки являются лишними, так как дублируют друг друга. Если попарно объединить дублирующие друг друга элементы, то получим схему фильтра, которую называют канонической (рис. 4.16). В отличие от нее схему рис. 4.8 называют прямой или основной формой цифрового фильтра. Преимуществом канонической схемы фильтра является минимальное число элементов задержки, равное порядку фильтра. Благодаря этому удается сократить общий объем вычислений.
Кроме прямой и канонической форм реализации цифровых фильтров существуют и другие варианты. Разложим многочлены в числителе и знаменателе системной функции (4.14) на множители вида  чтобы коэффициенты
чтобы коэффициенты  были действительными числами. Это возможно, так как все
были действительными числами. Это возможно, так как все
коэффициенты  в числителе и знаменателе выражения (4.14) также являются действительными числами. Затем, группируя соответствующим образом эти множители, представим системную функцию фильтра в виде произведения
в числителе и знаменателе выражения (4.14) также являются действительными числами. Затем, группируя соответствующим образом эти множители, представим системную функцию фильтра в виде произведения

где сомножители  имеют вид
имеют вид  или
или  и являются, таким образом, системными функциями цифровых фильтров
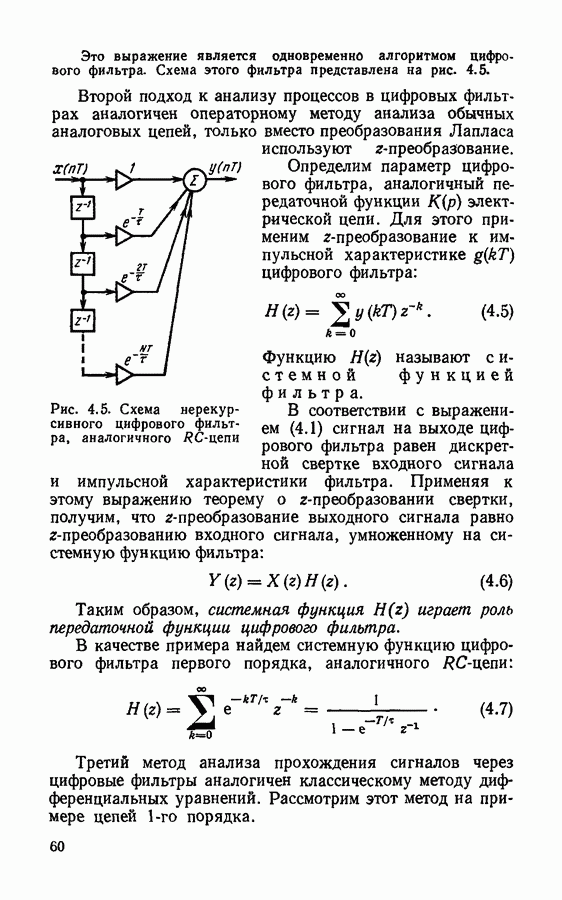
и являются, таким образом, системными функциями цифровых фильтров  порядков. Таким образом, цифровой фильтр с системной функцией вида (4.21) может быть реализован посредством каскадного соединения цифровых фильтров
порядков. Таким образом, цифровой фильтр с системной функцией вида (4.21) может быть реализован посредством каскадного соединения цифровых фильтров  порядков, как показано на рис. 4.17. Такую форму реализации цифровых фильтров называют последовательной или каскадной.
порядков, как показано на рис. 4.17. Такую форму реализации цифровых фильтров называют последовательной или каскадной.
Системную функцию фильтра (4.21), представленную в виде произведения элементарных сомножителей, можно посредством разложения на простые дроби преобразовать к виду

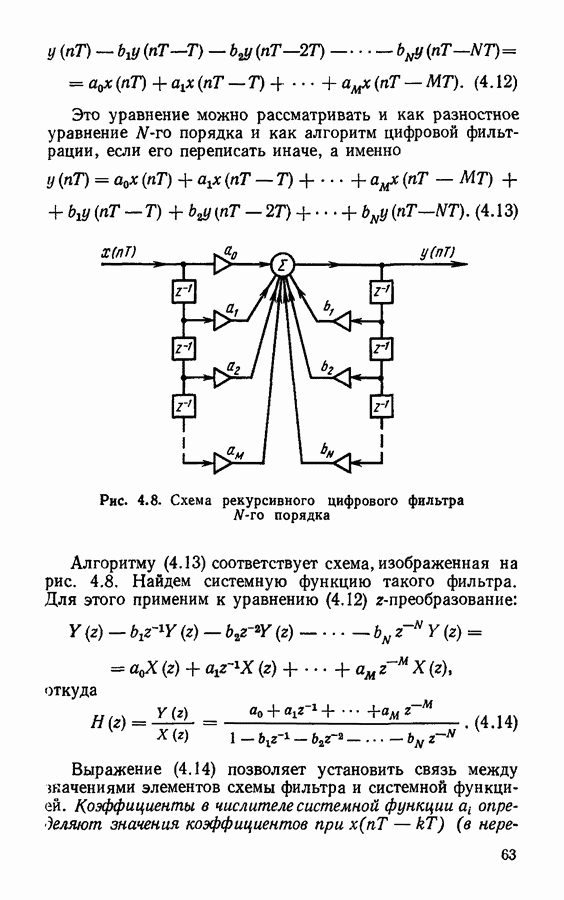
где  системные функции цифровых фильтров
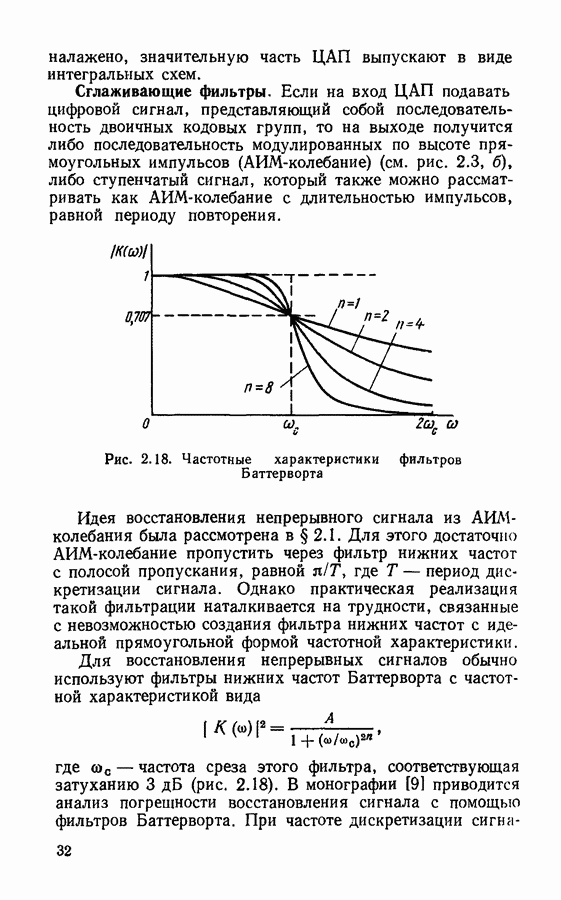
системные функции цифровых фильтров  порядков. Такое представление системной функции соответствует схемной реализации в виде параллельного соединения элементарных цифровых фильтров (рис. 4.18).
порядков. Такое представление системной функции соответствует схемной реализации в виде параллельного соединения элементарных цифровых фильтров (рис. 4.18).
Рис. 4.17. Последовательная схема цифрового фильтра

Рис. 4.18. Параллельная схема цифрового фильтра
Рассмотренные четыре типа фильтров совершенно эквивалентны друг другу и дают один и тот же результат, если не учитывать квантование сигналов и считать, что параметры фильтров т. е. коэффициенты  и другие,
и другие,

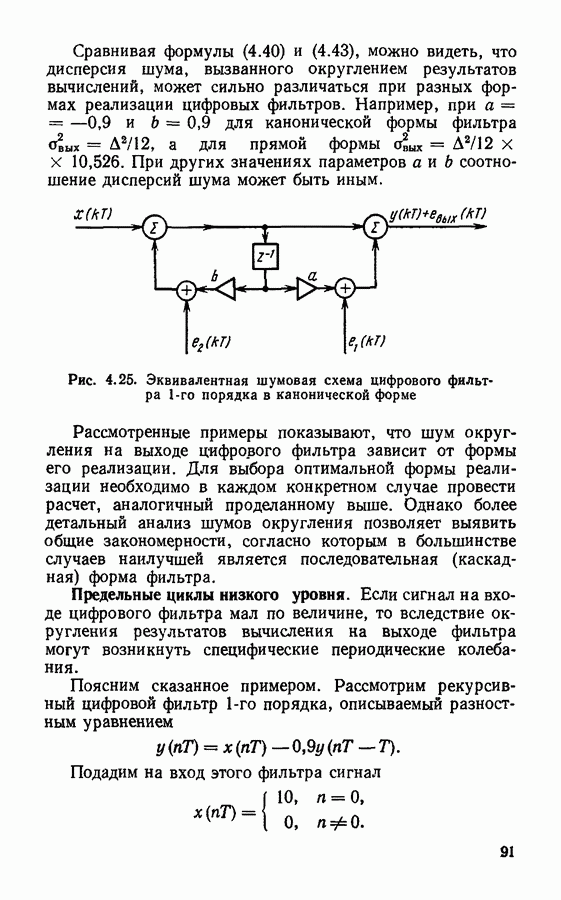
заданы абсолютно точно. В реальных цифровых фильтрах происходит округление значений входного сигнала и результатов промежуточных вычислений, а параметры фильтров задаются с конечной точностью. В результате этого возникают погрешности обработки сигналов, а в отдельных случаях нарушается устойчивость фильтров. Наиболее сильно эти нежелательные эффекты проявляются при реализации фильтров в виде прямой и канонической форм; применение последовательной или параллельной форм позволяет несколько снизить ошибки обработки сигналов. Более подробно вопрос о погрешностях цифровой фильтрации будет рассмотрен далее.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
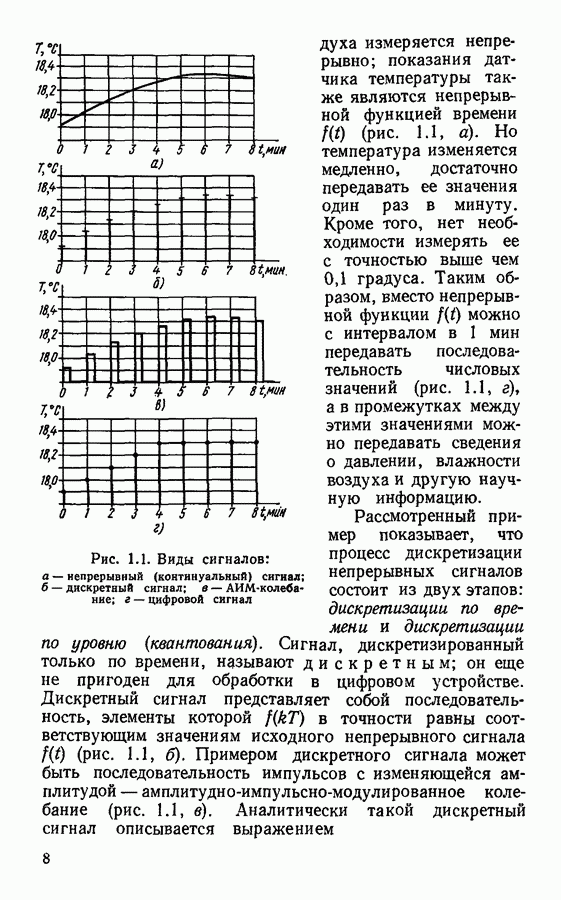
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
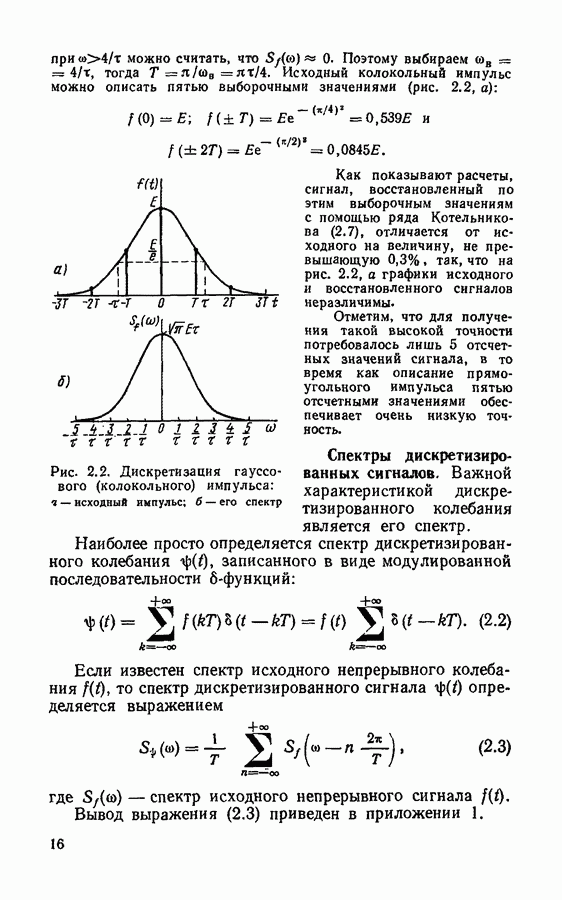
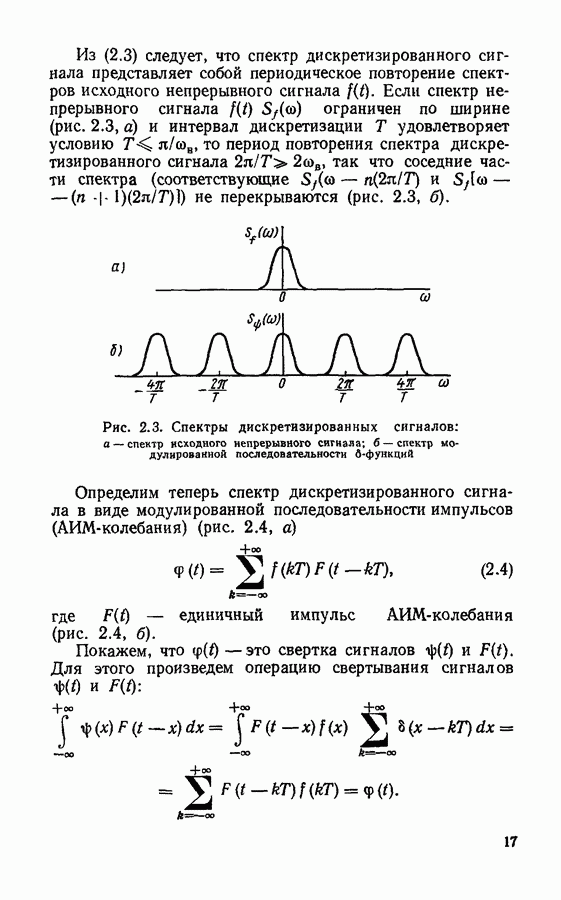
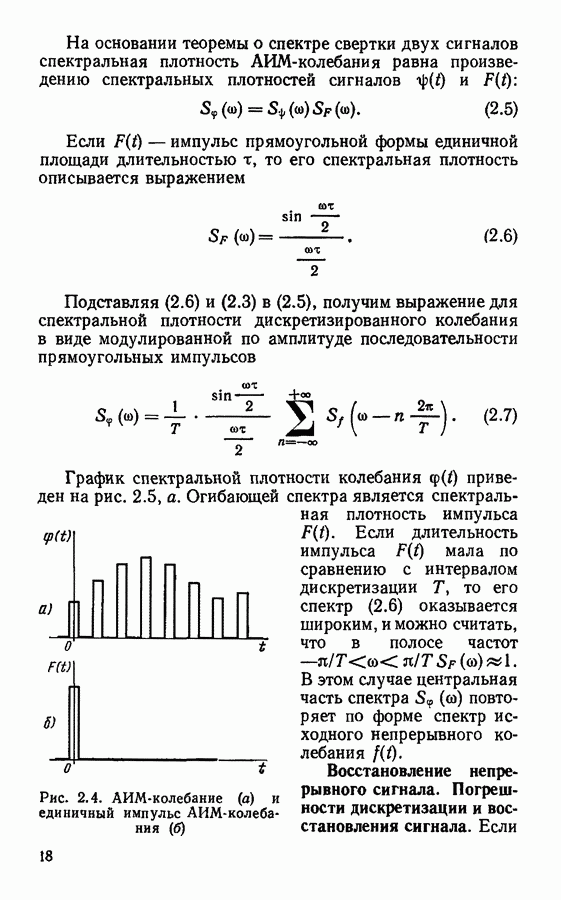
- § 2.1. Основы дискретизации непрерывных сигналов
- Спектры дискретизированных сигналов.
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
- Дискретизация сигналов в спектральной области.
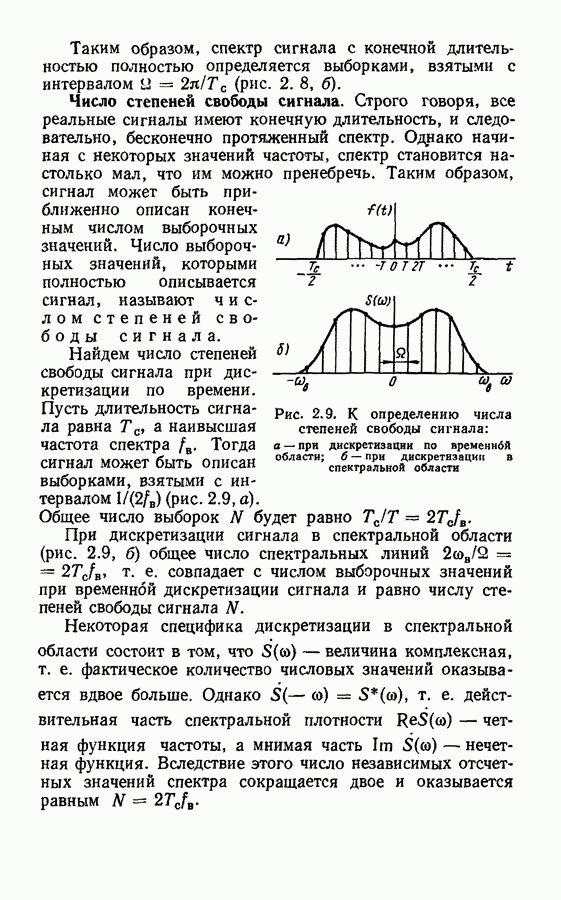
- Число степеней свободы сигнала.
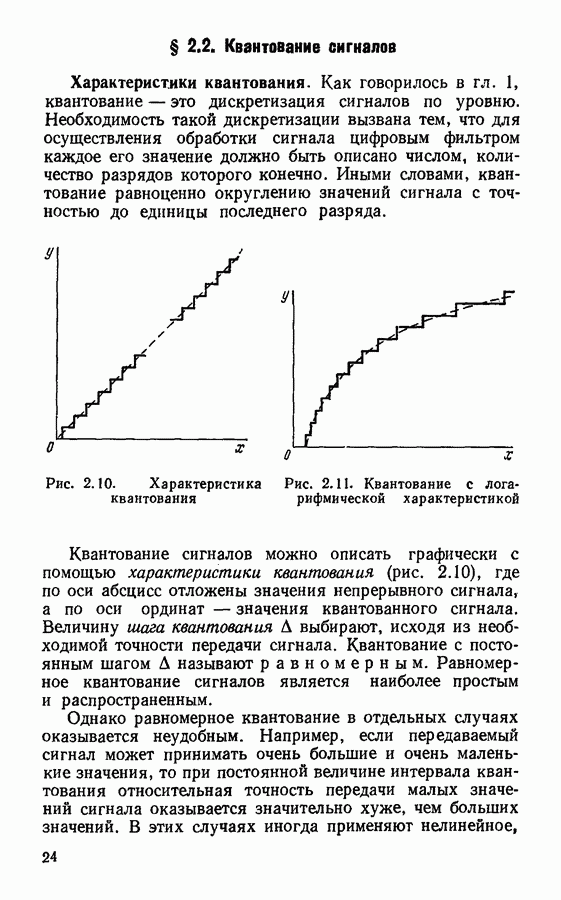
- § 2.2. Квантование сигналов
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
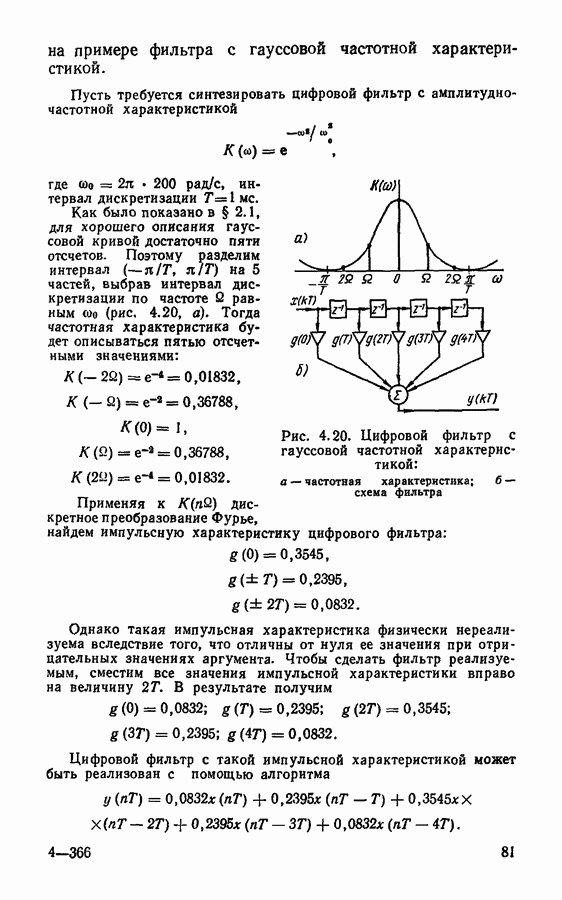
- Прямой синтез цифровых фильтров.
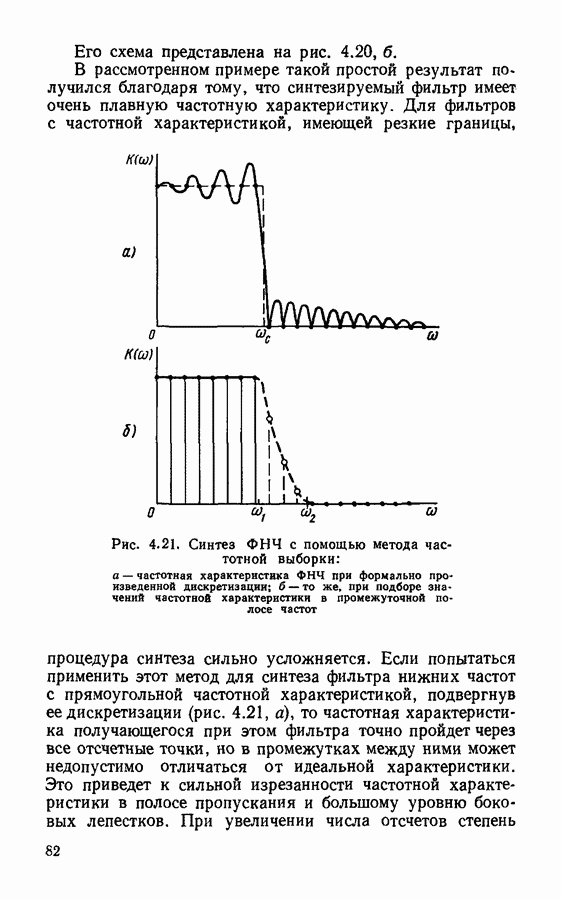
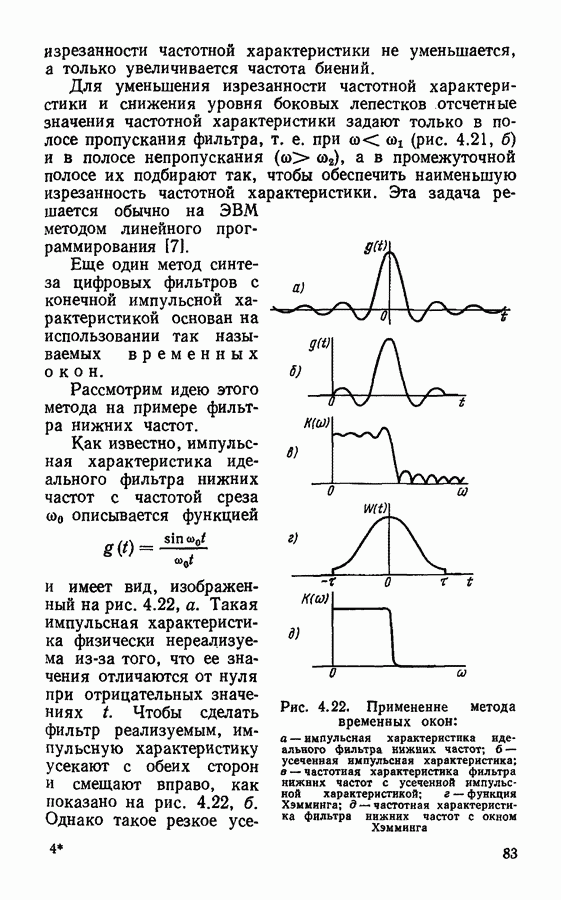
- Методы синтеза фильтров с конечной импульсной характеристикой.
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА