| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
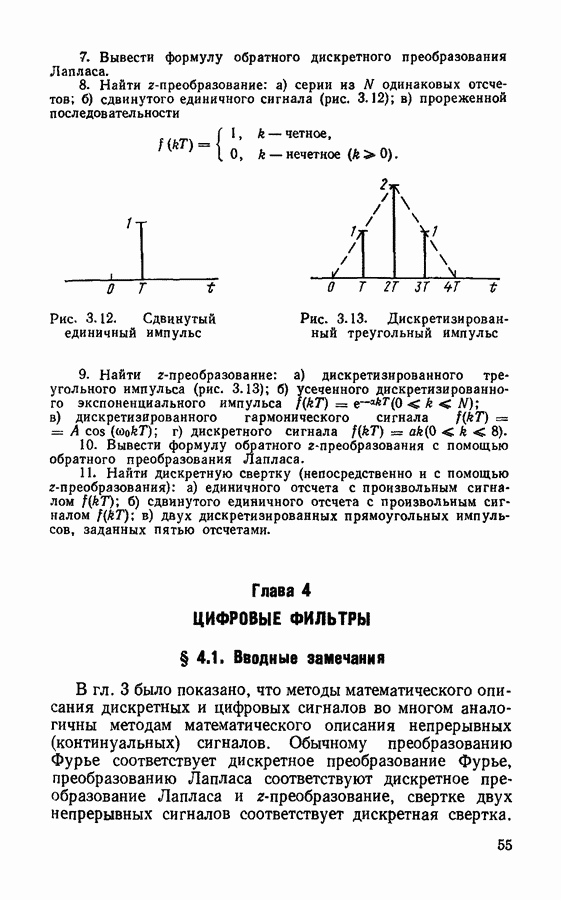
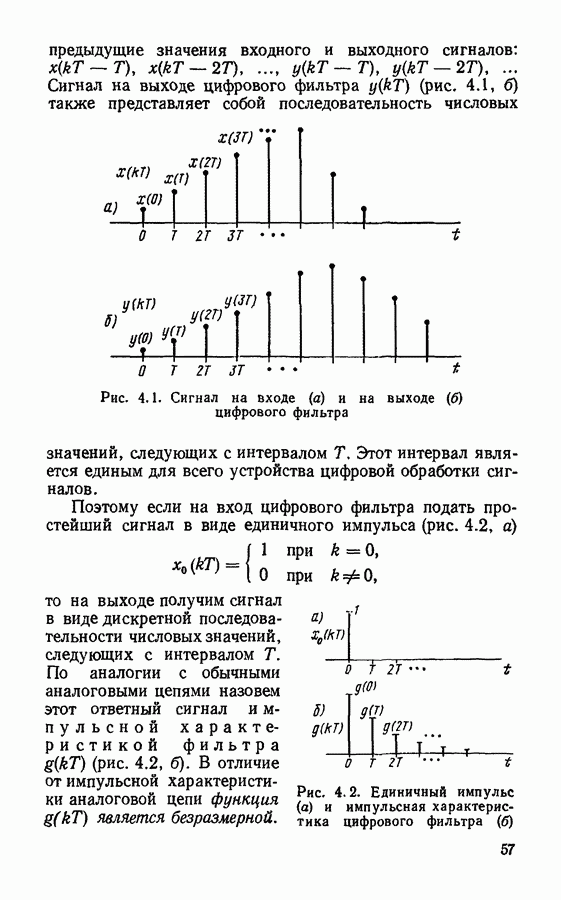
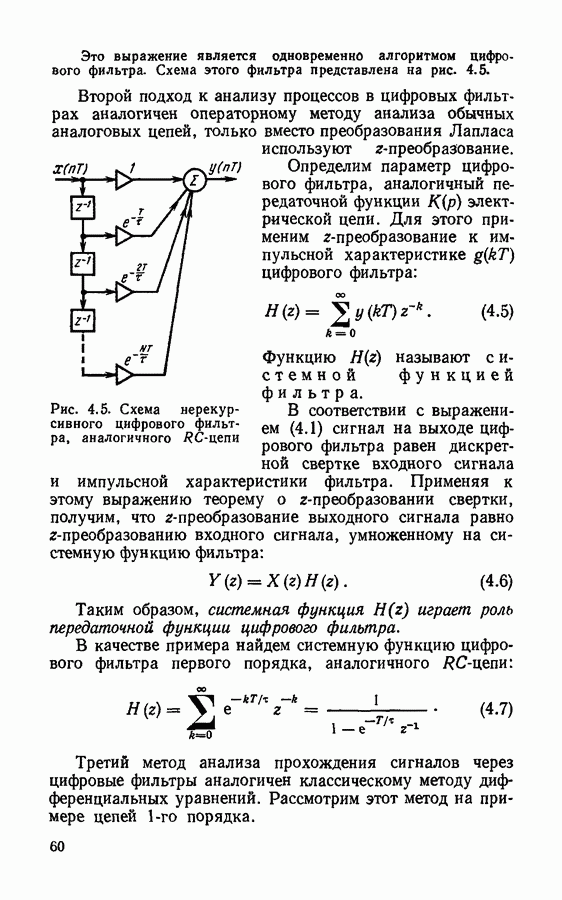
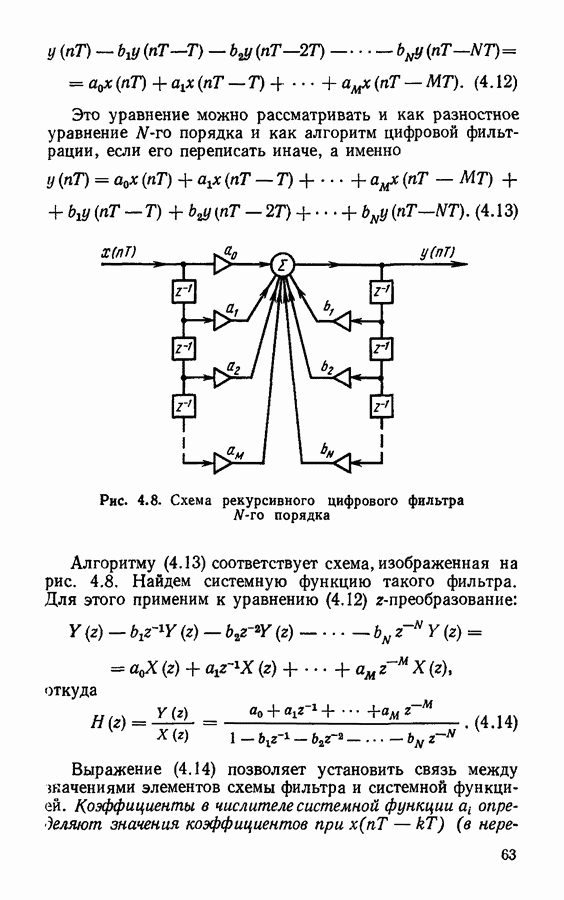
Спектры дискретизированных сигналов.
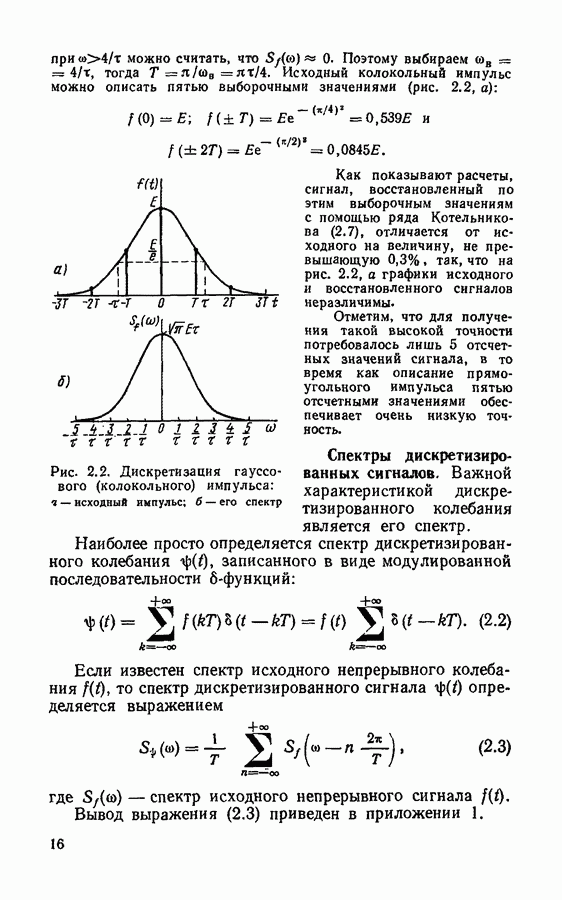
Важной характеристикой дискретизированного колебания является его спектр. Наиболее просто определяется спектр дискретизированного колебания записанного в виде модулированной последовательности  -функций:
-функций:

Если известен спектр исходного непрерывного колебания  то спектр дискретизированного сигнала
то спектр дискретизированного сигнала  определяется выражением
определяется выражением

где  спектр исходного непрерывного сигнала
спектр исходного непрерывного сигнала  -Вывод выражения (2.3) приведен в приложении 1.
-Вывод выражения (2.3) приведен в приложении 1.
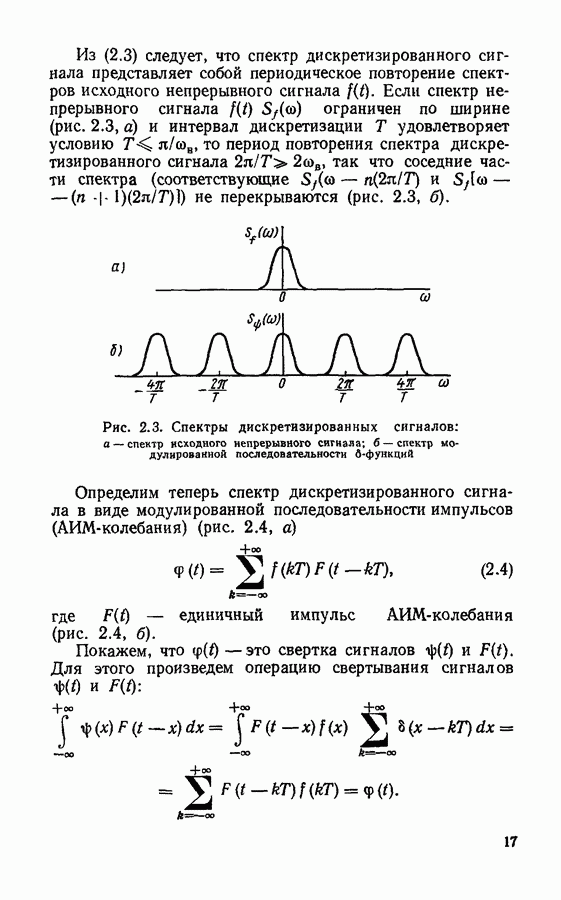
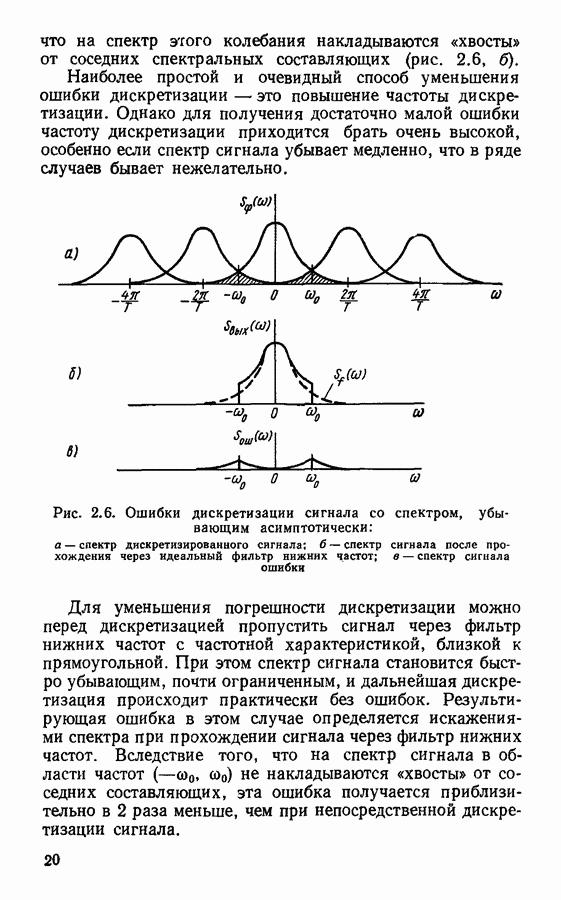
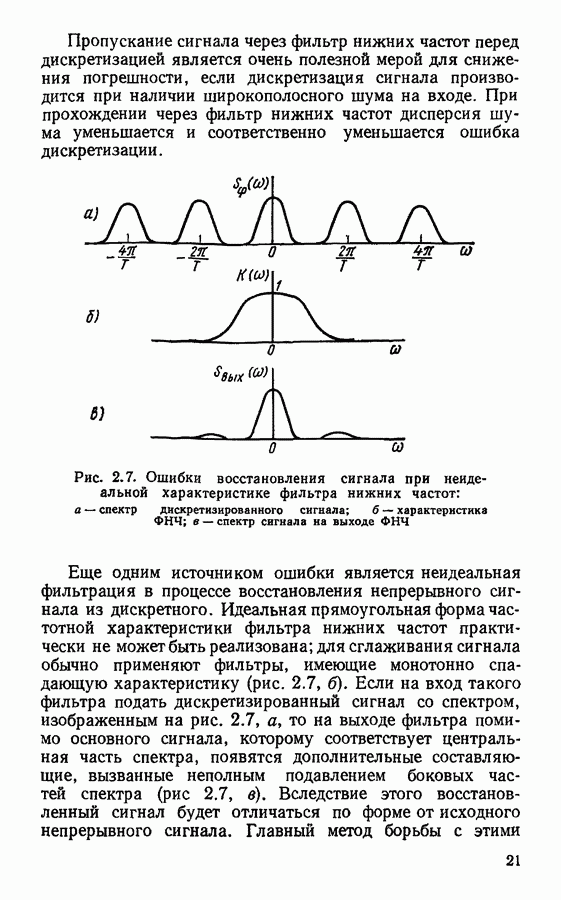
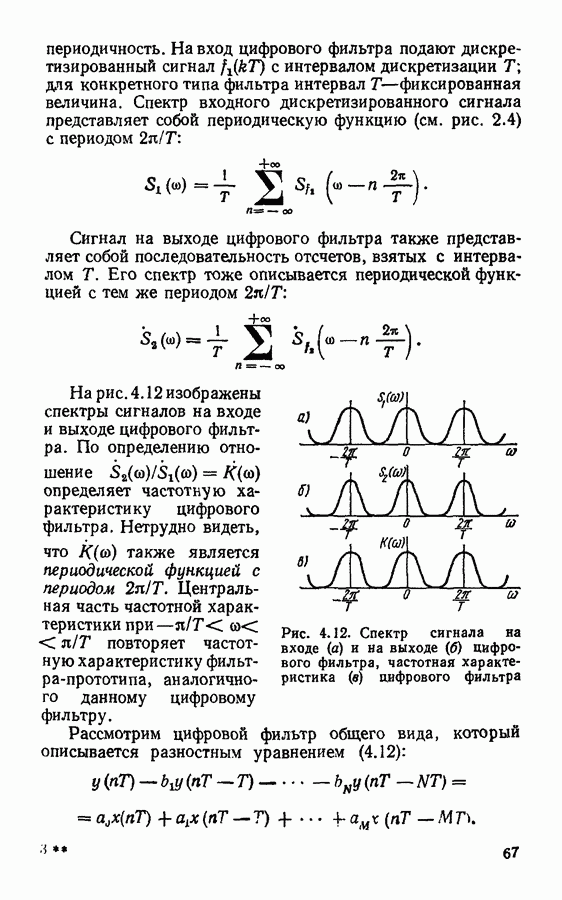
Из (2.3) следует, что спектр дискретизированного сигнала представляет собой периодическое повторение спектров исходного непрерывного сигнала  Если спектр непрерывного сигнала
Если спектр непрерывного сигнала  ограничен по ширине (рис. 2.3, а) и интервал дискретизации
ограничен по ширине (рис. 2.3, а) и интервал дискретизации  удовлетворяет условию
удовлетворяет условию  то период повторения спектра дискретизированного сигнала
то период повторения спектра дискретизированного сигнала  так что соседние части спектра (соответствующие
так что соседние части спектра (соответствующие  не перекрываются (рис. 2.3, б).
не перекрываются (рис. 2.3, б).

Рис. 2.3. Спектры дискретизированных сигналов: а — спектр исходного непрерывного сигнала;  спектр модулированной последовательности
спектр модулированной последовательности  -функций
-функций
Определим теперь спектр дискретизированного сигнала в виде модулированной последовательности импульсов (АИМ-колебания) (рис. 2.4, а)

где  единичный импульс АИМ-колебания (рис. 2.4, б).
единичный импульс АИМ-колебания (рис. 2.4, б).
Покажем, что  — это свертка сигналов
— это свертка сигналов  Для этого произведем операцию свертывания сигналов
Для этого произведем операцию свертывания сигналов 

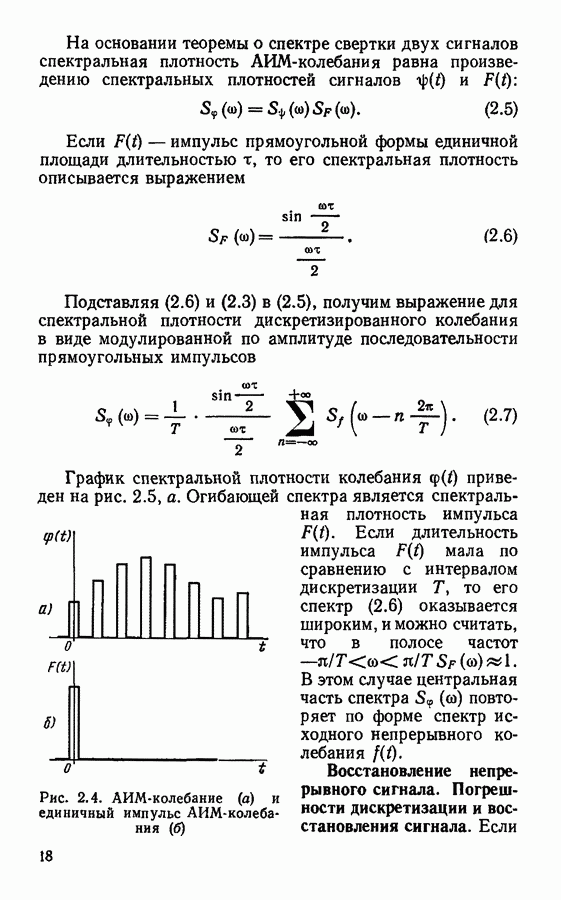
На основании теоремы о спектре свертки двух сигналов спектральная плотность АИМ-колебания равна произведению спектральных плотностей сигналов (

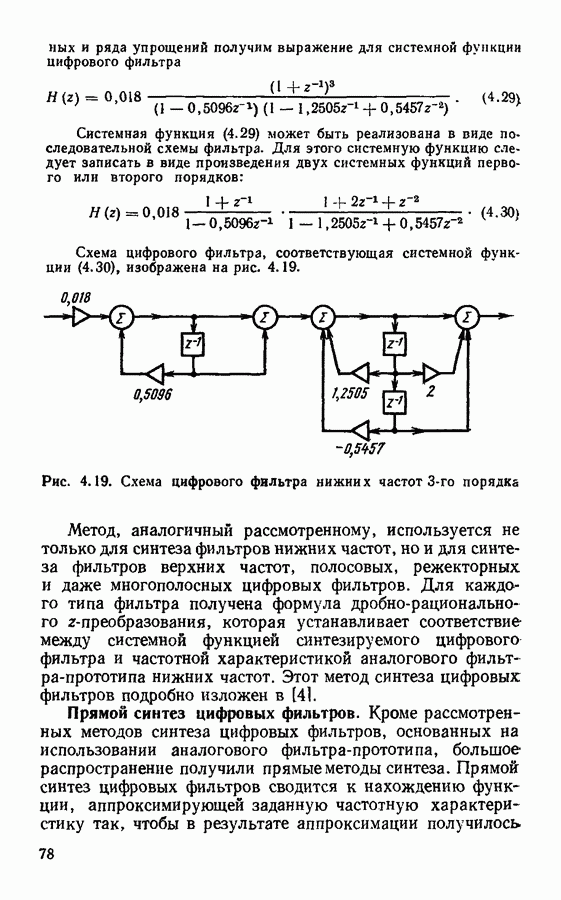
Если  импульс прямоугольной формы единичной площади длительностью
импульс прямоугольной формы единичной площади длительностью  то его спектральная плотность описывается выражением
то его спектральная плотность описывается выражением

Подставляя (2.6) и (2.3) в (2.5), получим выражение для спектральной плотности дискретизированного колебания в виде модулированной по амплитуде последовательности прямоугольных импульсов

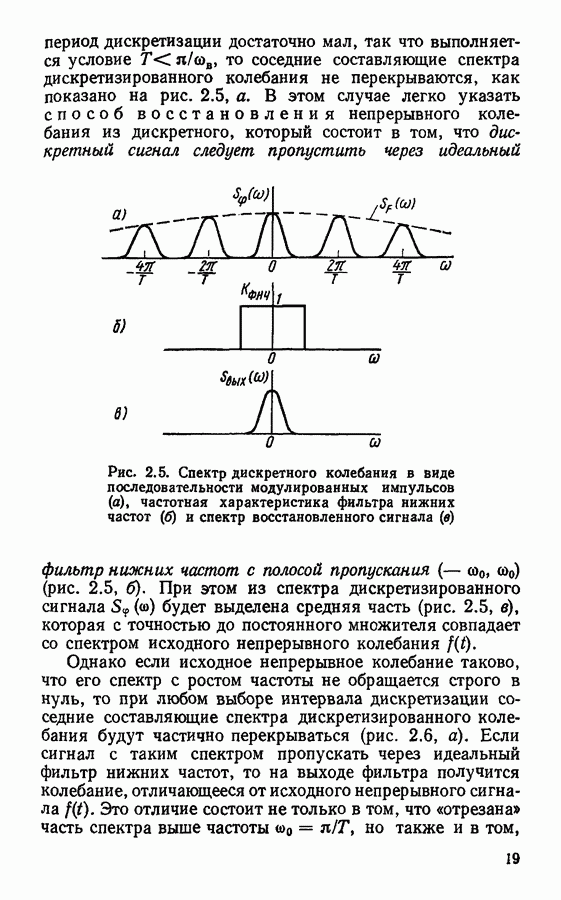
График спектральной плотности колебания  приведен на рис. 2.5, а. Огибающей спектра является спектральная плотность импульса
приведен на рис. 2.5, а. Огибающей спектра является спектральная плотность импульса  Если длительность импульса
Если длительность импульса  мала по сравнению с интервалом дискретизации
мала по сравнению с интервалом дискретизации  то его спектр (2.6) оказывается широким, и можно считать, что в полосе частот
то его спектр (2.6) оказывается широким, и можно считать, что в полосе частот  . В этом случае центральная часть спектра
. В этом случае центральная часть спектра  повторяет по форме спектр исходного непрерывного колебания
повторяет по форме спектр исходного непрерывного колебания 

Рис. 2.4. АИМ-колебание (а) и единичный импульс АИМ-колебания (б)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
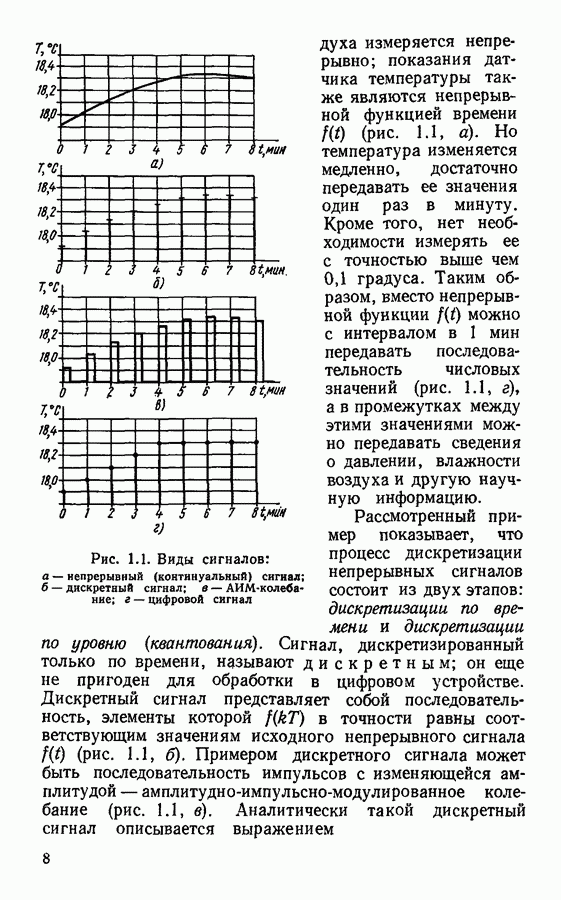
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
- Спектры дискретизированных сигналов.
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
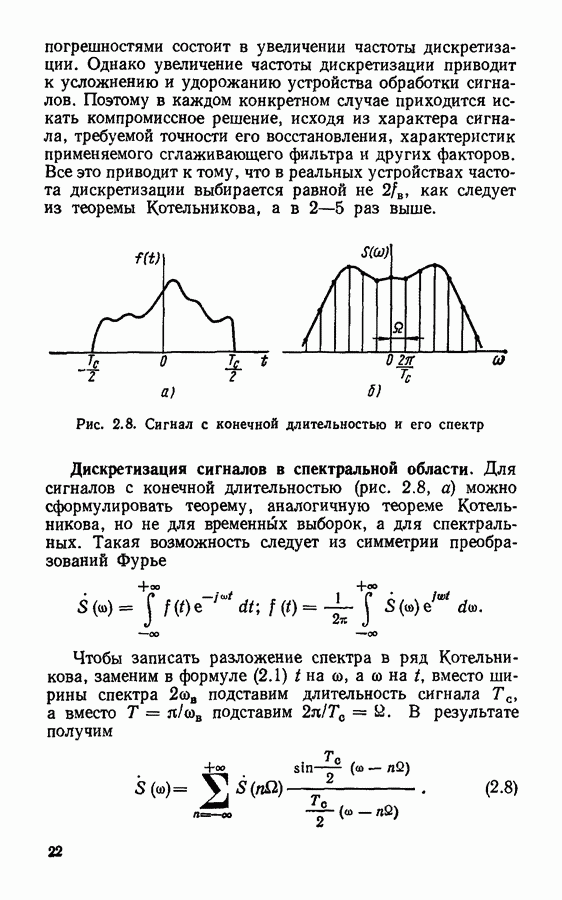
- Дискретизация сигналов в спектральной области.
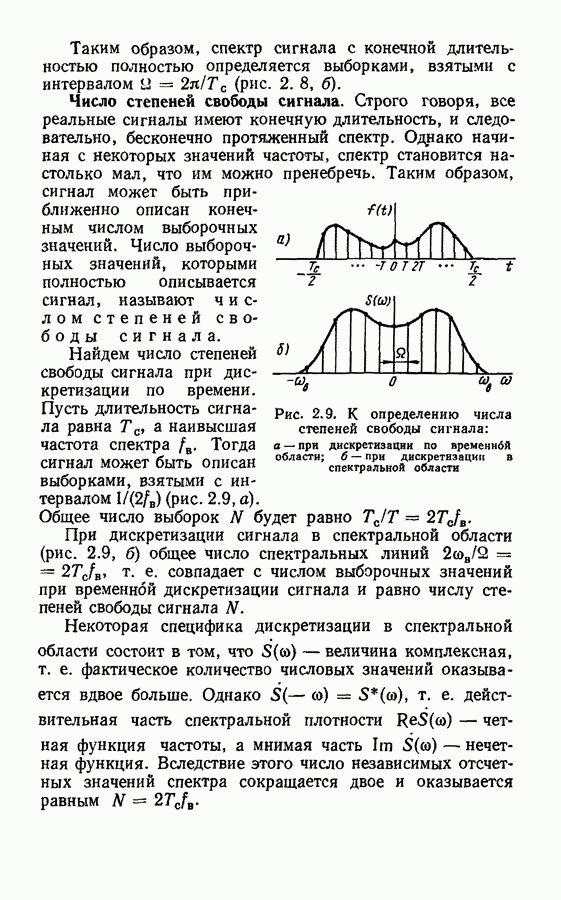
- Число степеней свободы сигнала.
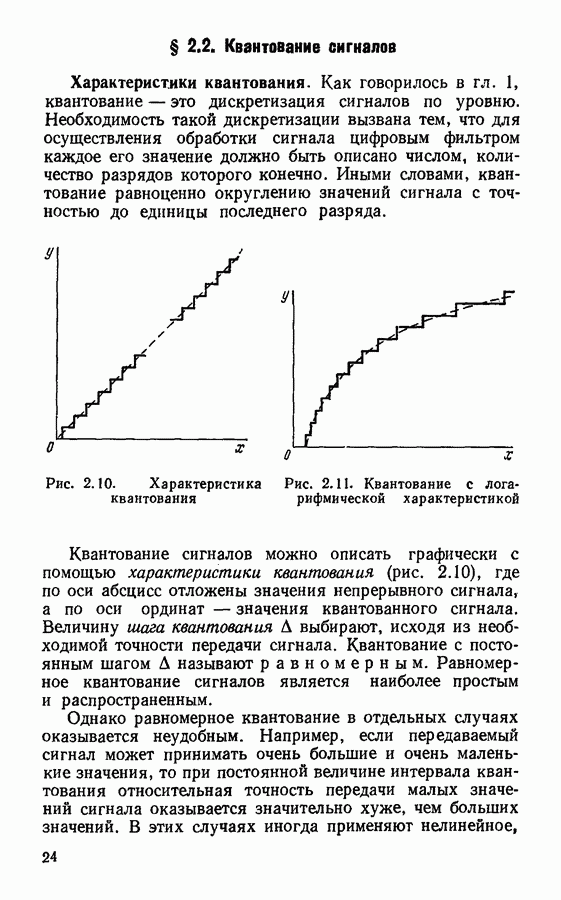
- § 2.2. Квантование сигналов
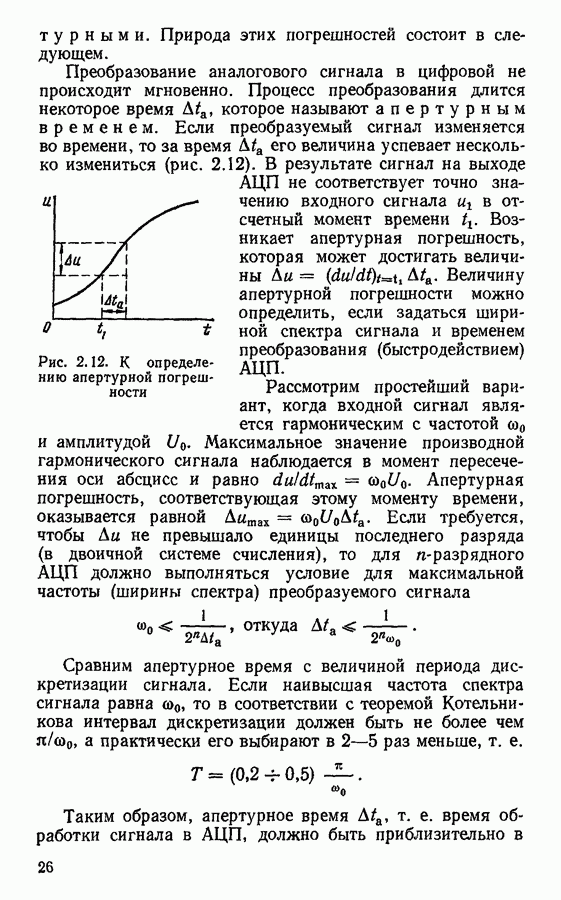
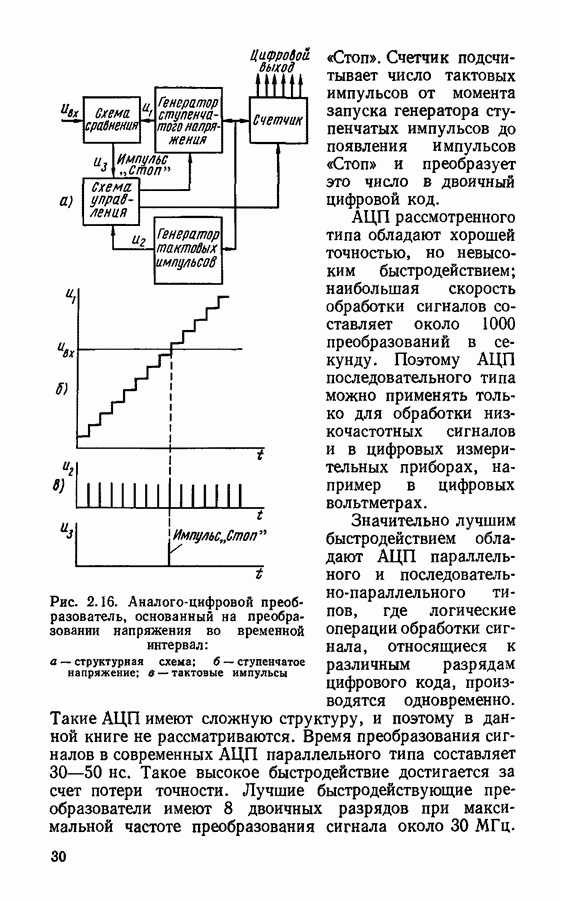
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
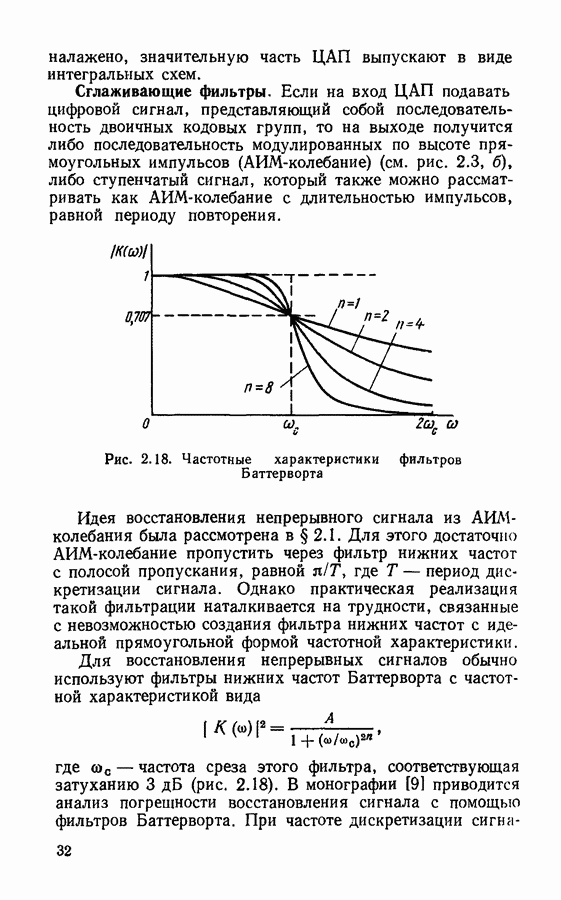
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
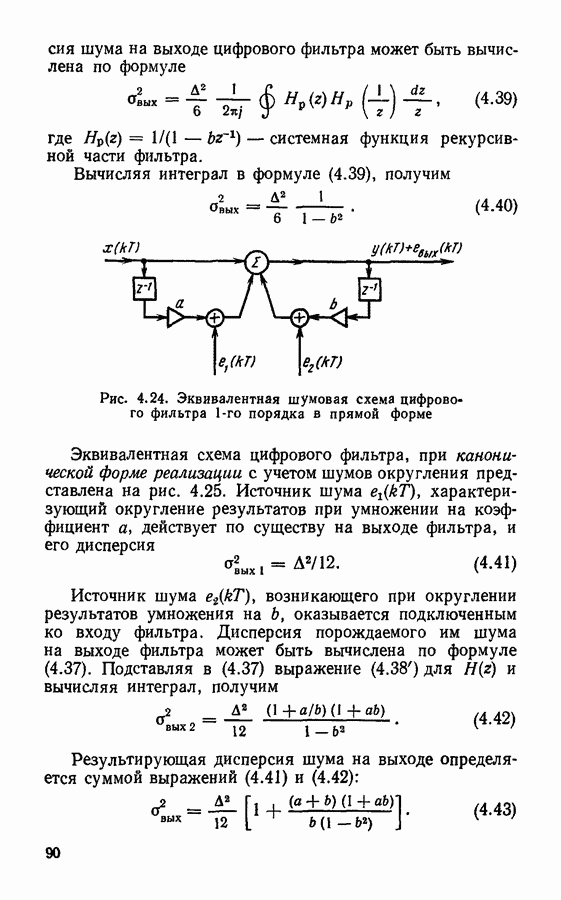
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
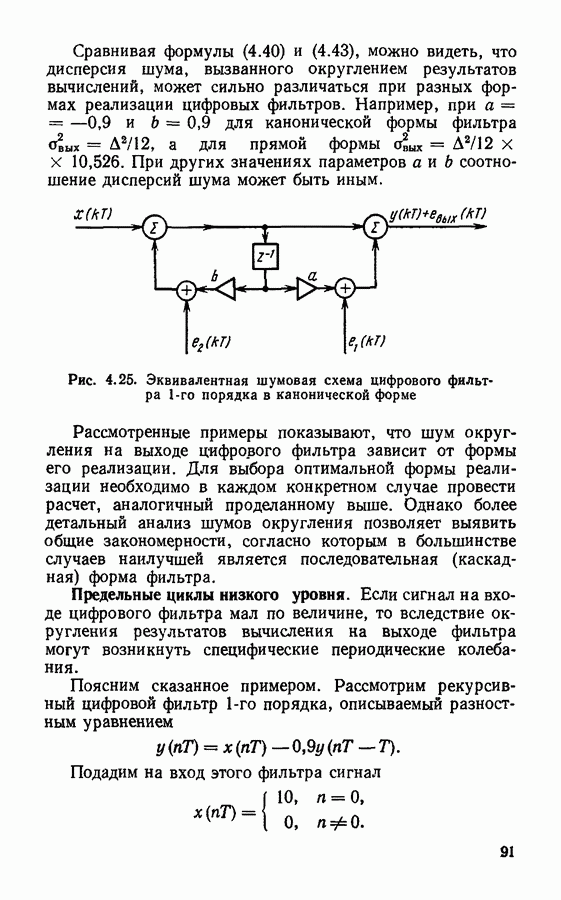
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА