| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
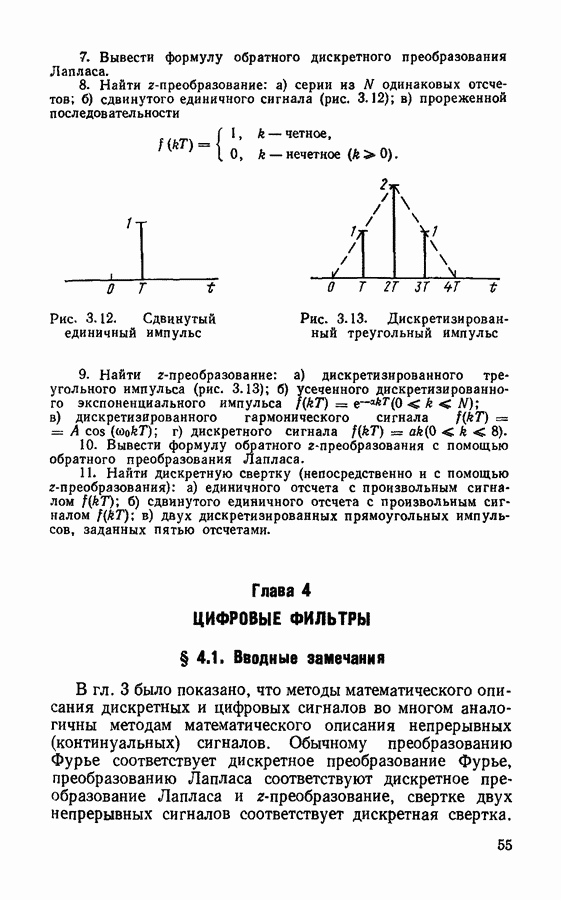
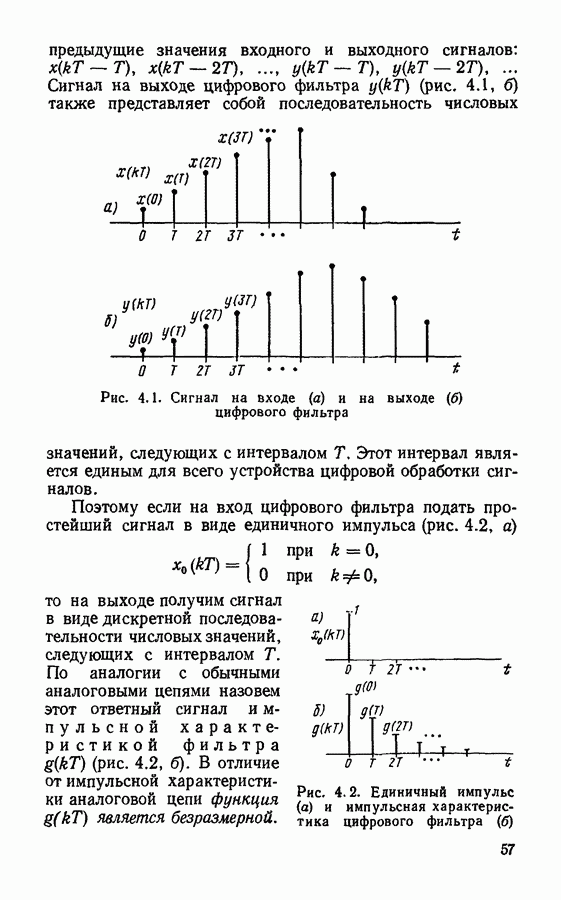
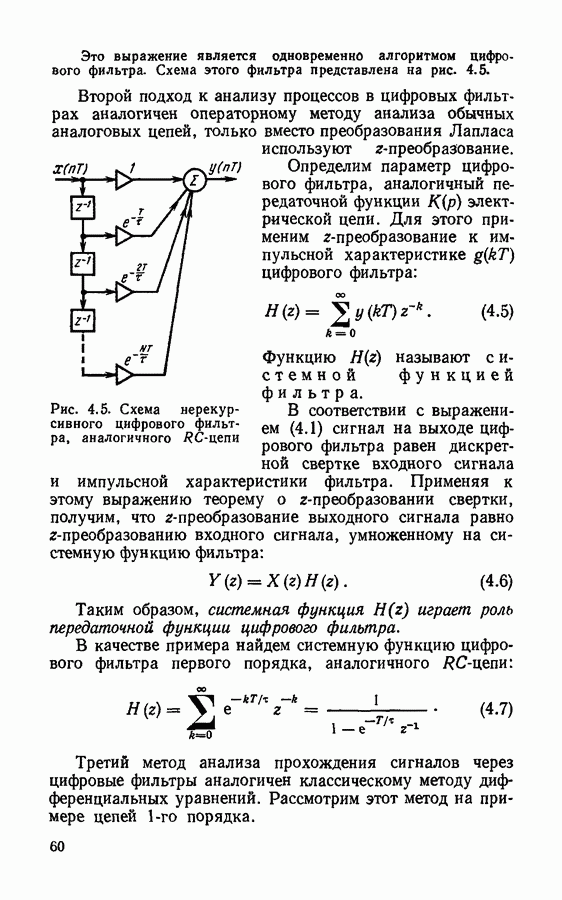
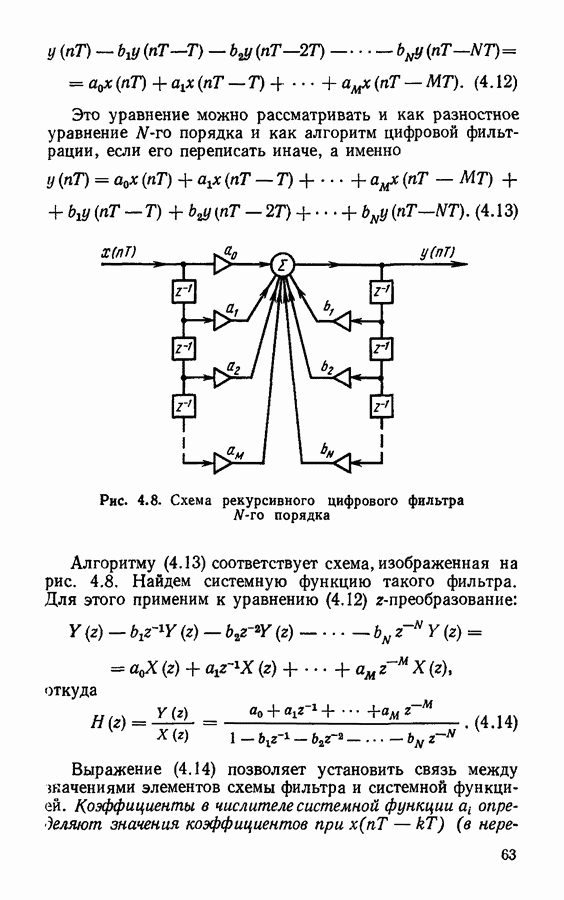
Методы синтеза фильтров с конечной импульсной характеристикой.
До сих пор мы рассматривали в основном цифровые фильтры, длительность импульсной характеристики которых была неограничена — так называемые фильтры с бесконечной импульсной характеристикой, или БИХ-фильтры. Однако наряду с БИХ-фильтрами широкое распространение получили цифровые фильтры с импульсной характеристикой конечной длительности, называемые иначе КИХ-фильтрами. Фильтры с конечной импульсной характеристикой реализуются, как правило, по нерекурсивной схеме и обладают рядом положительных качеств, основное из которых состоит в том, что благодаря отсутствию обратных связей КИХ-фильтры всегда устойчивы.
Фильтры с конечной импульсной характеристикой не имеют непосредственных аналогов среди пассивных электрических фильтров, поэтому методы их синтеза относятся к прямым методам. Одним из наиболее употребительных методов синтеза КИХ-фильтров является метод частотной выборки.
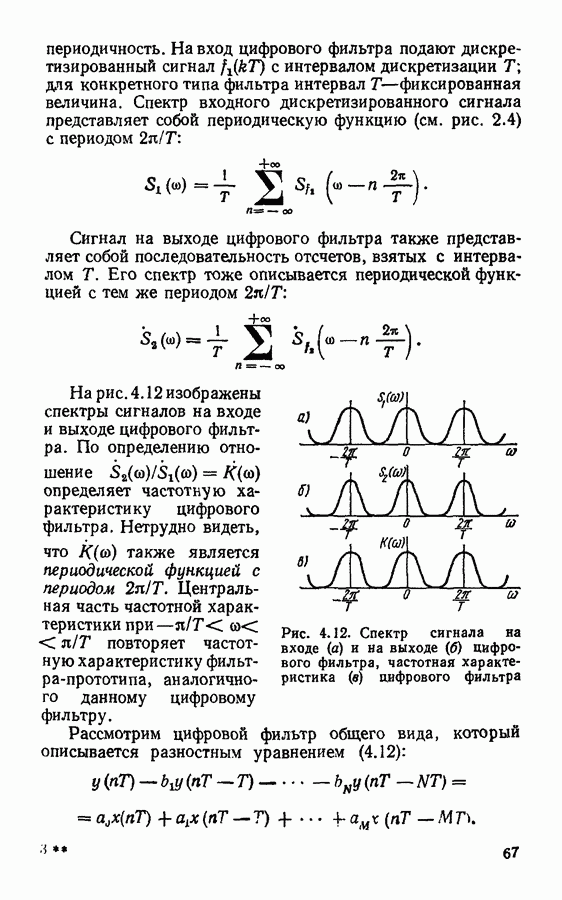
Идея метода очень проста. Частотную характеристику цифрового фильтра подвергают дискретизации как периодическую функцию, разбивая интервал  на
на  равных частей. Интервал дискретизации 2 должен быть таким, чтобы передать характерные подробности частотной характеристики. К образовавшейся последовательности значений
равных частей. Интервал дискретизации 2 должен быть таким, чтобы передать характерные подробности частотной характеристики. К образовавшейся последовательности значений  применяют дискретное преобразование Фурье или быстрое преобразование Фурье и находят импульсную характеристику
применяют дискретное преобразование Фурье или быстрое преобразование Фурье и находят импульсную характеристику  Значения
Значения  являются коэффициентами нерекурсивного фильтра.
являются коэффициентами нерекурсивного фильтра.
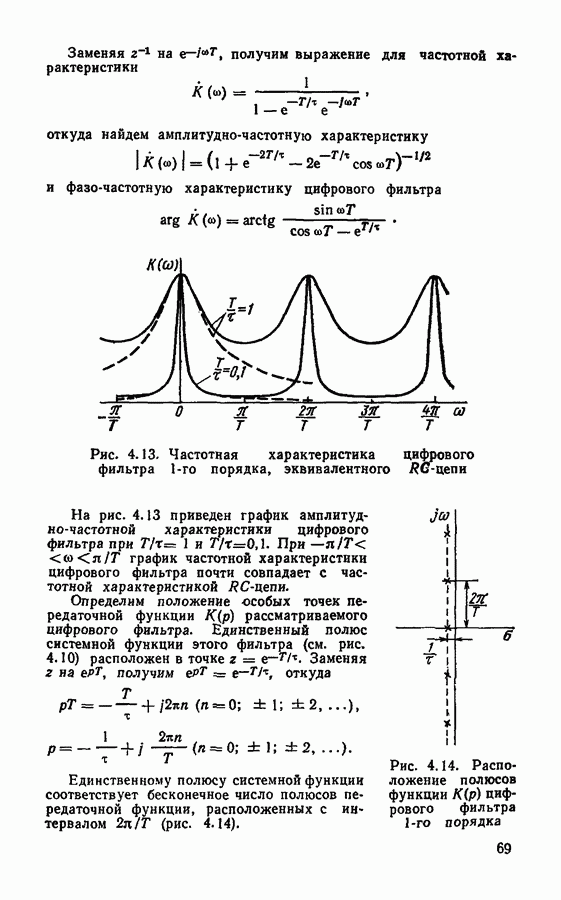
Иногда получающаяся в процессе синтеза импульсная характеристика цифрового фильтра оказывается физически нереализуемой, так как отличны от нуля ее значения  при отрицательных
при отрицательных  Фильтр можно сделать физически реализуемым, если его импульсную характеристику сместить вправо так, чтобы для моментов времени
Фильтр можно сделать физически реализуемым, если его импульсную характеристику сместить вправо так, чтобы для моментов времени  она тождественно равнялась нулю. При таком смещении изменяется фазо-частотная характеристика цифрового фильтра, а его амплитудно-частотная характеристика остается неизменной. Поэтому метод частотной выборки позволяет синтезировать фильтры с заданной амплитудно-частотной характеристикой при неконтролируемой фазочастотной характеристике.
она тождественно равнялась нулю. При таком смещении изменяется фазо-частотная характеристика цифрового фильтра, а его амплитудно-частотная характеристика остается неизменной. Поэтому метод частотной выборки позволяет синтезировать фильтры с заданной амплитудно-частотной характеристикой при неконтролируемой фазочастотной характеристике.
Метод частотной выборки хорошо работает при плавных частотных характеристиках. Продемонстрируем его
на примере фильтра с гауссовой частотной характеристикой.
Пусть требуется синтезировать цифровой фильтр с амплитудно-частотной характеристикой

где  интервал дискретизации
интервал дискретизации 

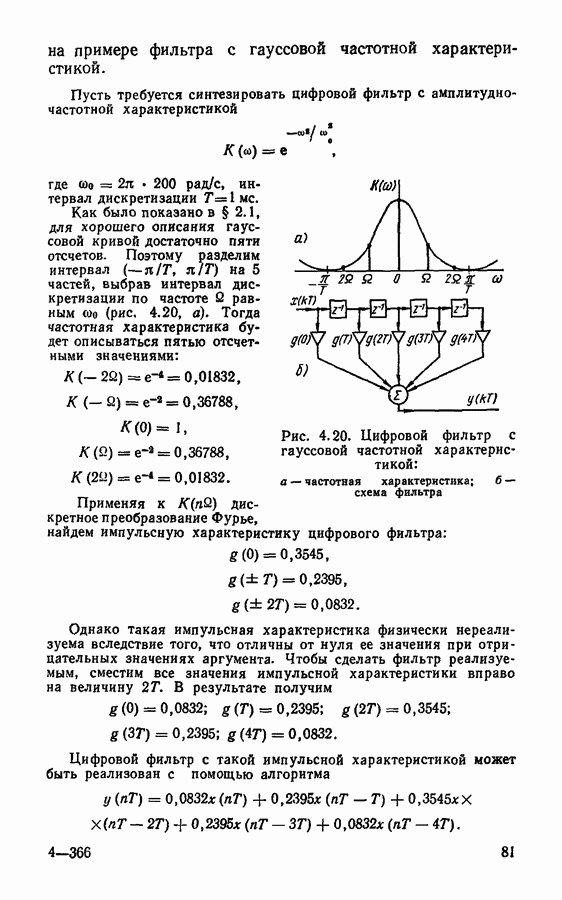
Рис. 4.20 Цифровой фильтр с гауссовой частотной характеристикой: а — частотная характеристика; 6 — схема фильтра
Как было показано в § 2.1, для хорошего описания гауссовой кривой достаточно пяти отсчетов. Поэтому разделим интервал  на 5 частей, выбрав интервал дискретизации по частоте
на 5 частей, выбрав интервал дискретизации по частоте  равным
равным  (рис, 4.20, а). Тогда частотная характеристика будет описываться пятью отсчетными значениями:
(рис, 4.20, а). Тогда частотная характеристика будет описываться пятью отсчетными значениями:

Применяя к  дискретное преобразование Фурье, найдем импульсную характеристику цифрового фильтра:
дискретное преобразование Фурье, найдем импульсную характеристику цифрового фильтра:

Однако такая импульсная характеристика физически нереализуема вследствие того, что отличны от нуля ее значения при отрицательных значениях аргумента. Чтобы сделать фильтр реализуемым, сместим все значения импульсной характеристики вправо на величину  . В результате получим
. В результате получим

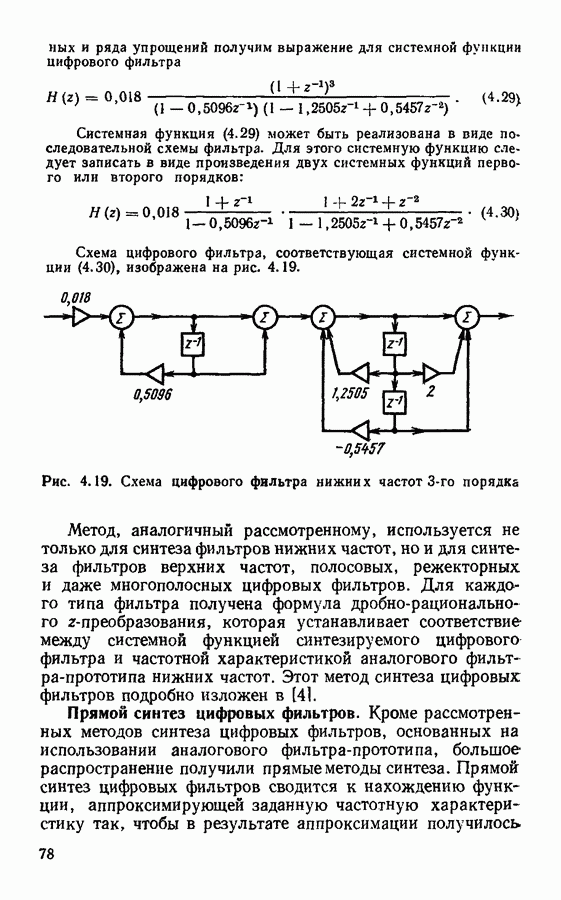
Цифровой фильтр с такой импульсной характеристикой может быть реализован с помощью алгоритма

Его схема представлена на рис. 4.20, б.
В рассмотренном примере такой простой результат по. лучился благодаря тому, что синтезируемый фильтр имеет очень плавную частотную характеристику. Для фильтров с частотной характеристикой, имеющей резкие границы, процедура синтеза сильно усложняется.

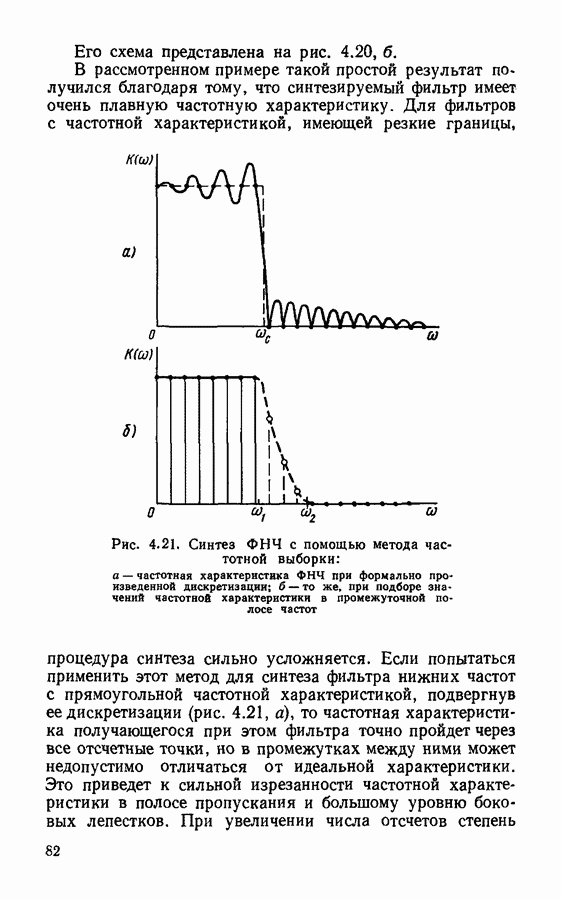
Рис. 4.21. Синтез ФНЧ с помощью метода частотной выборки: а — частотная характеристика ФНЧ при формально произведенной дискретизации; б — то же, при подборе значений частотной характеристики в промежуточной полосе частот
Если попытаться применить этот метод для синтеза фильтра нижних частот с прямоугольной частотной характеристикой, подвергнув ее дискретизации (рис. 4.21, а), то частотная характеристика получающегося при этом фильтра точно пройдет через все отечетные точки, но в промежутках между ними может недопустимо отличаться от идеальной характеристики. Это приведет к сильной изрезанности частотной характеристики в полосе пропускания и большому уровню боковых лепестков. При увеличении числа отсчетов степень
изрезанности частотной характеристики не уменьшается, а только увеличивается частота биений.
Для уменьшения изрезанности частотной характеристики и снижения уровня боковых лепестков отсчетные значения частотной характеристики задают только в полосе пропускания фильтра, т. е. при  (рис. 4.21, б) и в полосе непропускания
(рис. 4.21, б) и в полосе непропускания  а в промежуточной полосе их подбирают так, чтобы обеспечить наименьшую изрезанность частотной характеристики. Эта задача решается обычно на ЭВМ методом линейного программирования [71.
а в промежуточной полосе их подбирают так, чтобы обеспечить наименьшую изрезанность частотной характеристики. Эта задача решается обычно на ЭВМ методом линейного программирования [71.
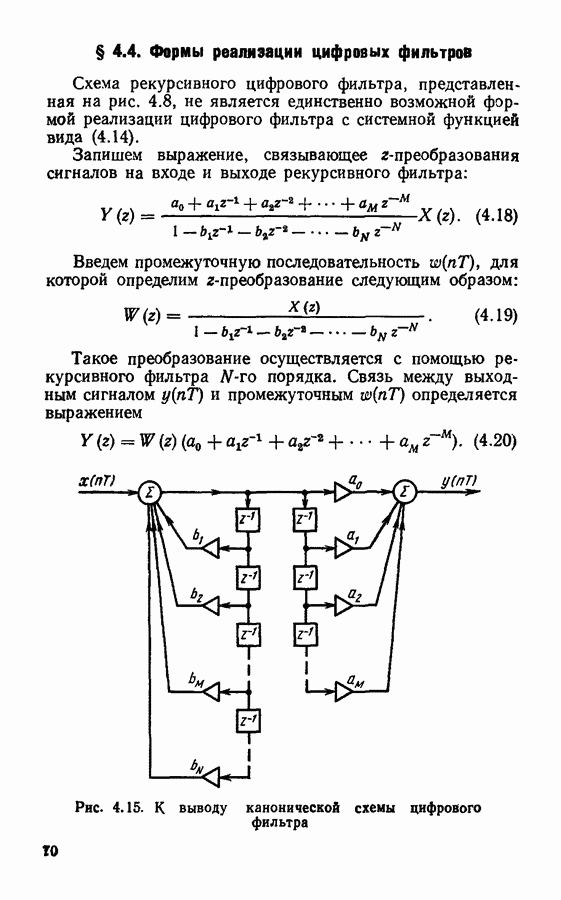
Еще один метод синтеза цифровых фильтров с конечной импульсной характеристикой основан на использовании так называемых временных окон.
Рассмотрим идею этого метода на примере фильтра нижних частот.
Как известно, импульсная характеристика идеального фильтра нижних частот с частотой среза  описывается функцией
описывается функцией

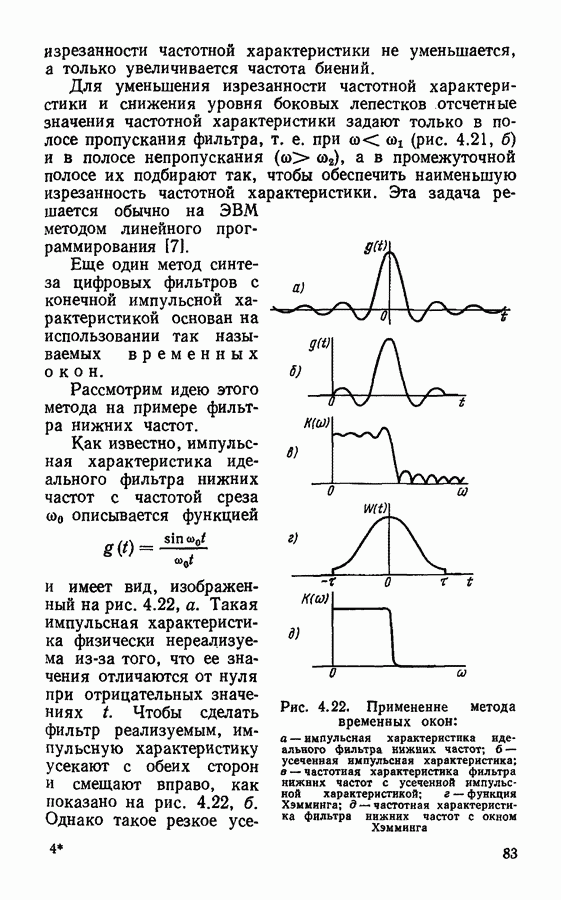
и имеет вид, изображенный на рис. 4.22, а. Такая импульсная характеристика физически нереализуема из-за того, что ее значения отличаются от нуля при отрицательных значениях  Чтобы сделать фильтр реализуемым, импульсную характеристику усекают с обеих сторон и смещают вправо, как показано на рис. 4.22, б.
Чтобы сделать фильтр реализуемым, импульсную характеристику усекают с обеих сторон и смещают вправо, как показано на рис. 4.22, б.
Однако такое резкое

Рис. 4.22. Применение метода временных окон: а — импульсная характеристика идеального фильтра нижних частот б — усеченная импульсная характеристика; в — частотная характеристика фильтра нижннх частот с усеченной импульсной характеристикой;  функция Хэмминга;
функция Хэмминга;  частотная характеристика фильтра нижних частот с окном Хэмминга
частотная характеристика фильтра нижних частот с окном Хэмминга
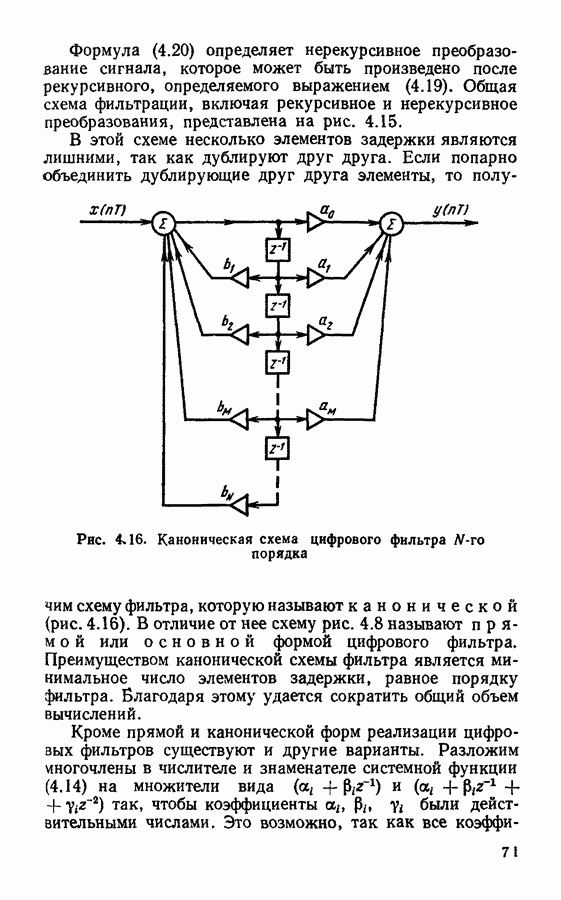
усечение импульсной характеристики приводит к сильной изрезанности частотной характеристики в полосе пропускания и недопустимо большому уровню боковых лепестков в полосе непропускания (рис. 4.22, в). Чтобы улучшить вид частотной характеристики, импульсную характеристику умножают на весовую функцию (так называемое «временное окно»), которая близка к единице в середине и плавно убывает к краям. В результате форма импульсной характеристики становится более плавной и, как следствие этого, улучшается вид частотной характеристики.
Существует несколько различных типов временных окон. Одним из наиболее распространенных является окно Хэмминга (рис. 4.22, г), которое описывается функцией

Окно Хэмминга позволяет получить частотную характеристику, близкую к прямоугольной, с уровнем боковых лепестков  (рис. 4.22, д).
(рис. 4.22, д).
Однако наилучшие результаты получаются при использовании окна Кайзера, которое описывается выражением

где  модифицированная функция Бесселя мнимого аргумента;
модифицированная функция Бесселя мнимого аргумента;  параметр окна, который выбирают, исходя из того, какое требование к частотной характеристике является более важным. При увеличении
параметр окна, который выбирают, исходя из того, какое требование к частотной характеристике является более важным. При увеличении  уменьшается уровень боковых лепестков частотной характеристики и пульсации в полосе пропускания и в то же время уменьшается крутизна скатов частотной характеристики. С помощью окна Кайзера можно синтезировать фильтры, имеющие практически прямоугольную форму частотной характеристики.
уменьшается уровень боковых лепестков частотной характеристики и пульсации в полосе пропускания и в то же время уменьшается крутизна скатов частотной характеристики. С помощью окна Кайзера можно синтезировать фильтры, имеющие практически прямоугольную форму частотной характеристики.
Обзор методов синтеза цифровых фильтров, приведенный в данном параграфе, является далеко не полным и не охватывает всех разновидностей методов, применяемых в инженерной практике. Более подробно этот вопрос рассмотрен в [2, 3, 4, 7].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
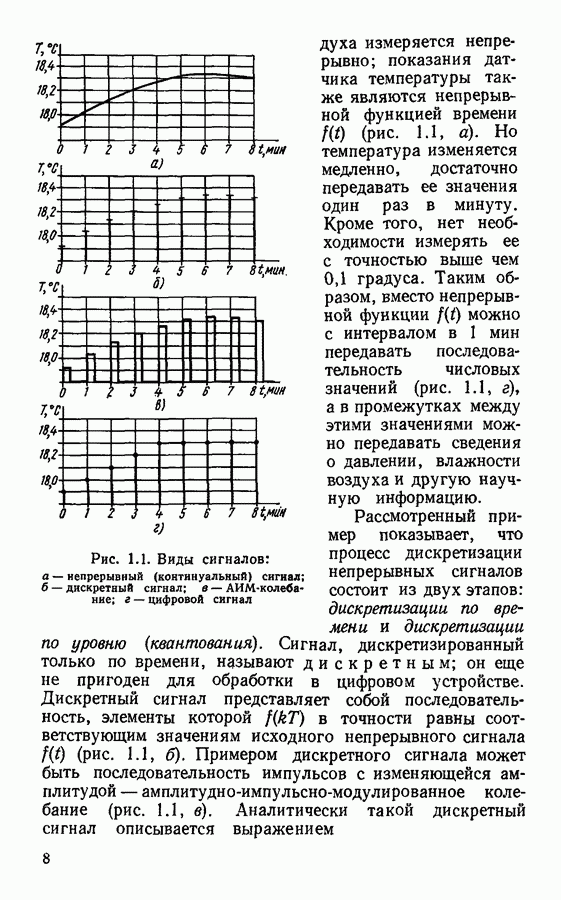
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
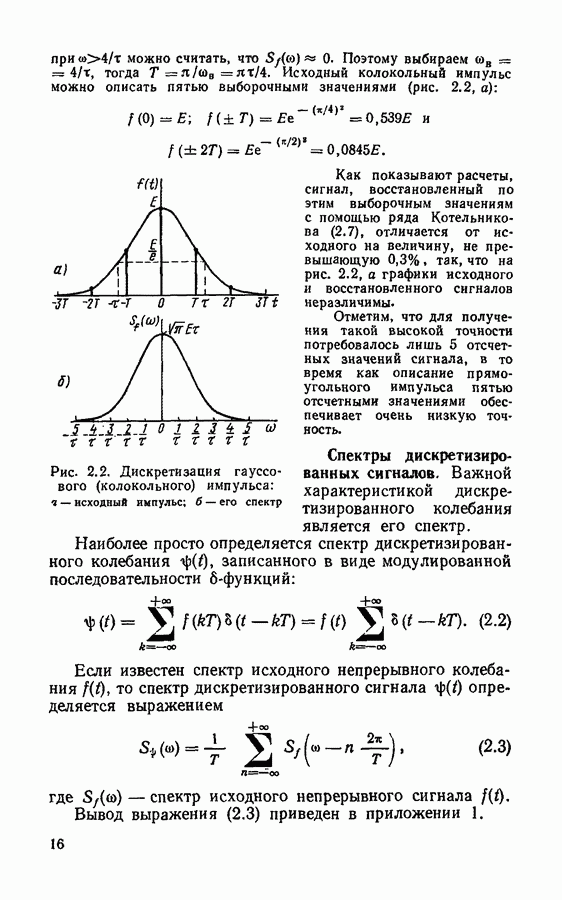
- § 2.1. Основы дискретизации непрерывных сигналов
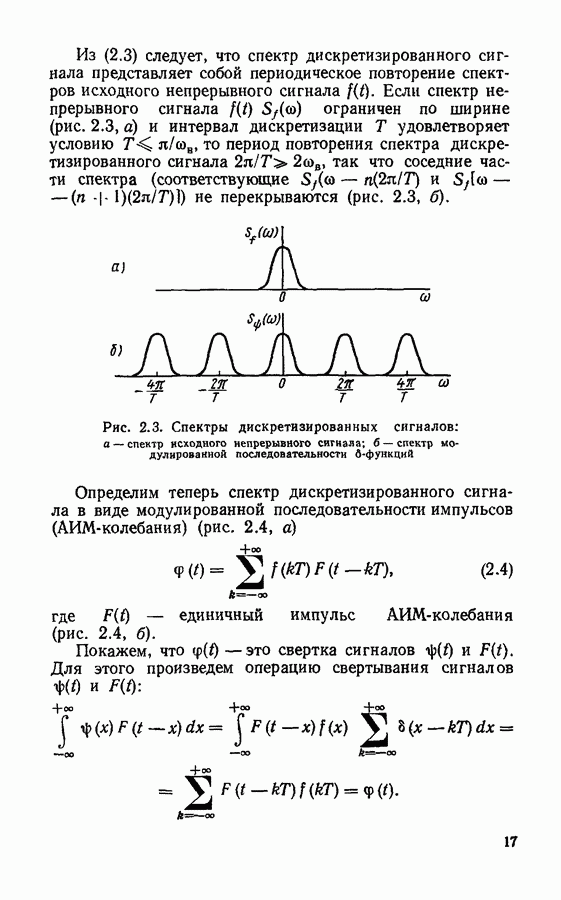
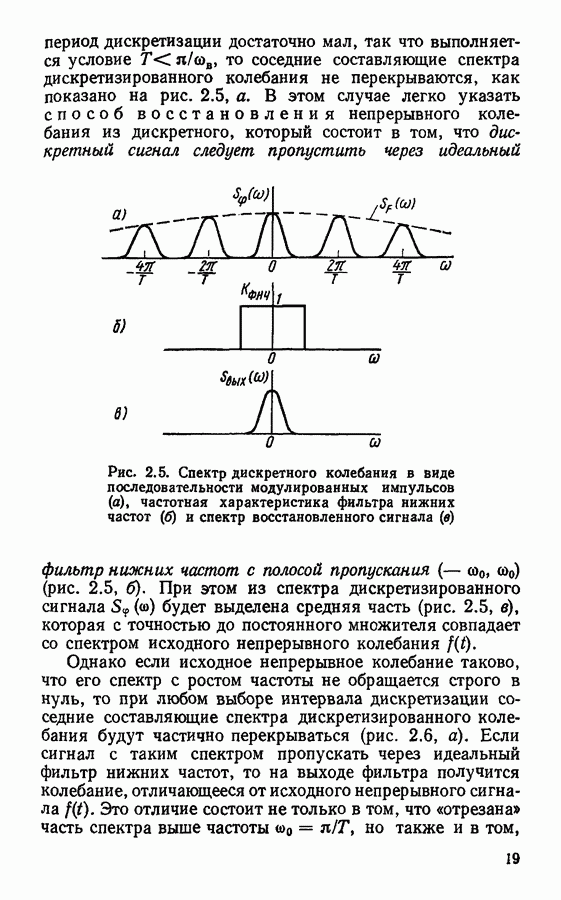
- Спектры дискретизированных сигналов.
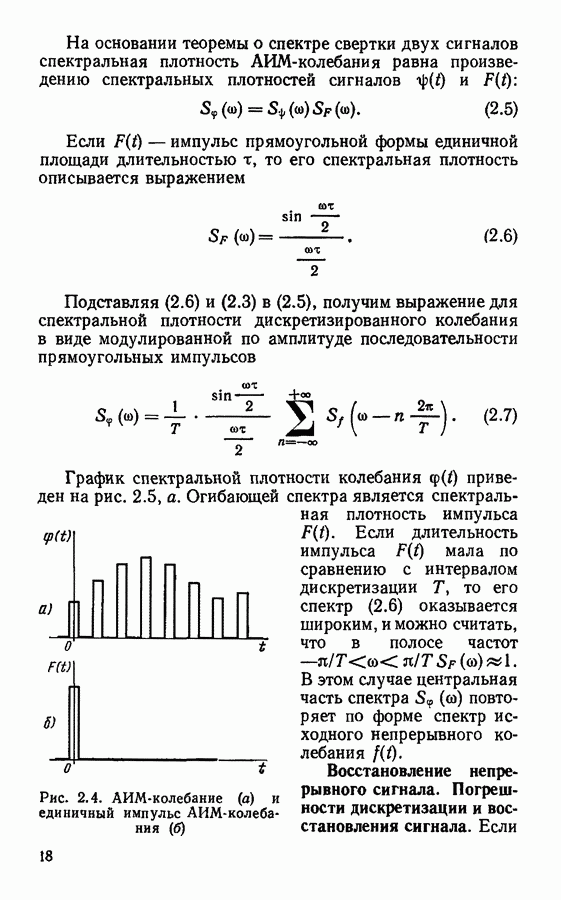
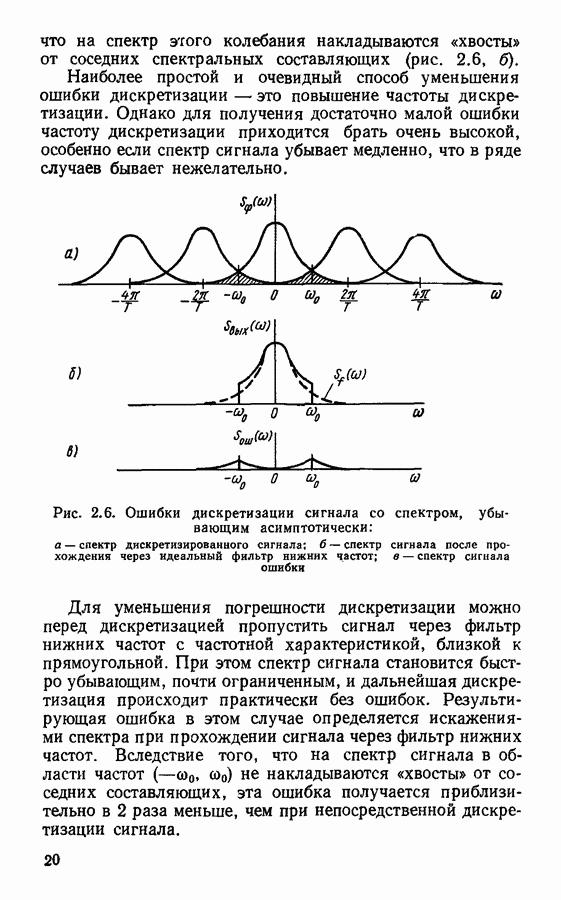
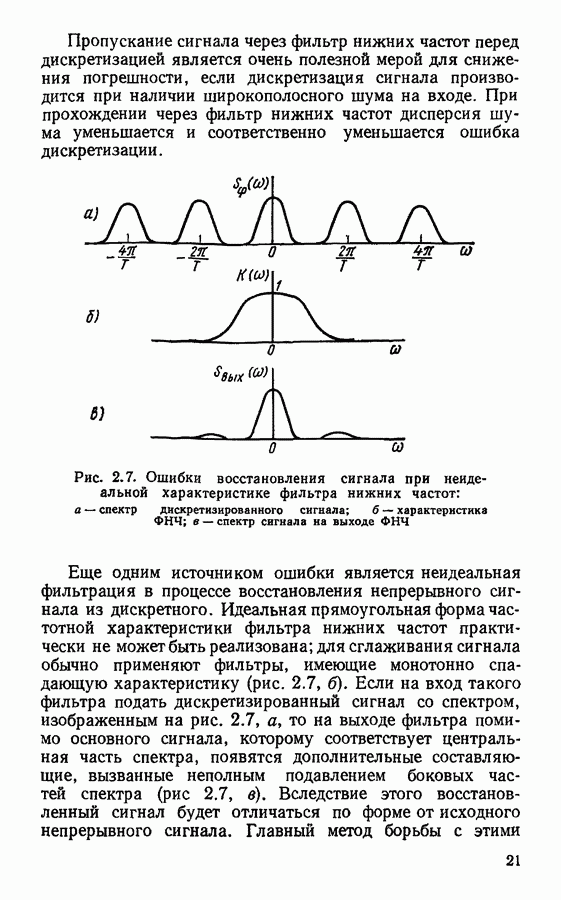
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
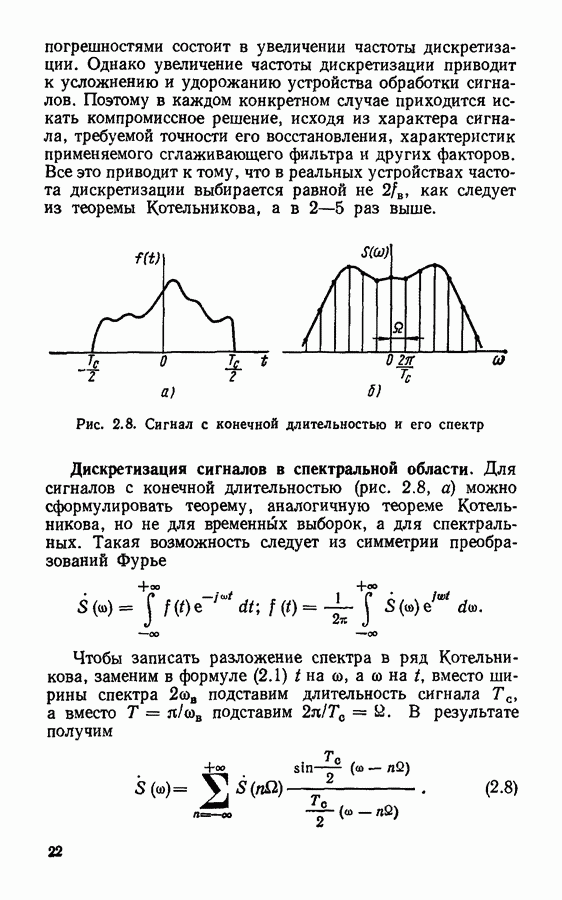
- Дискретизация сигналов в спектральной области.
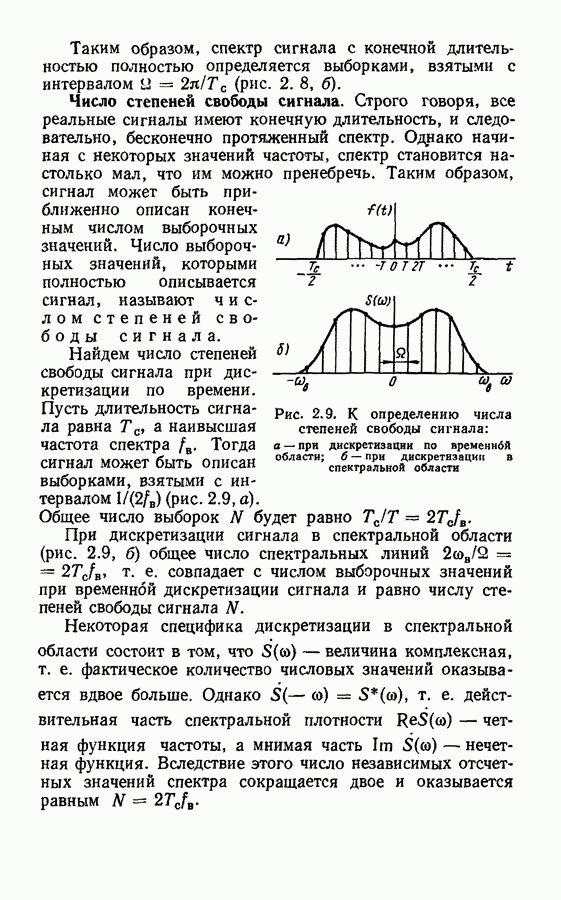
- Число степеней свободы сигнала.
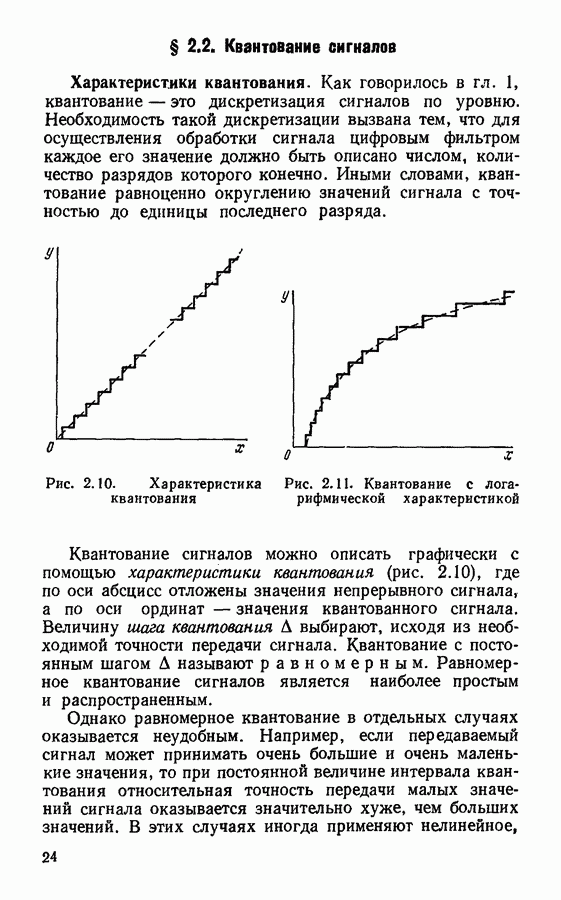
- § 2.2. Квантование сигналов
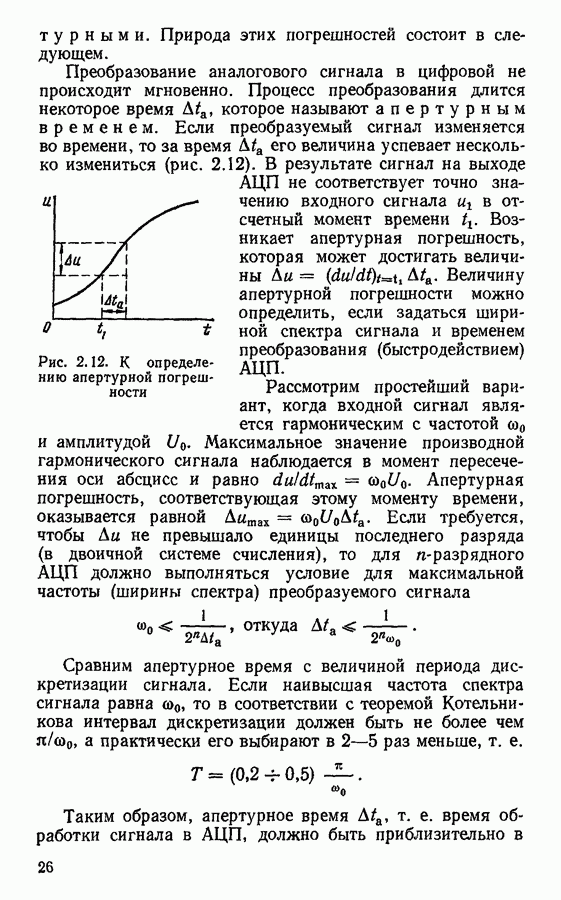
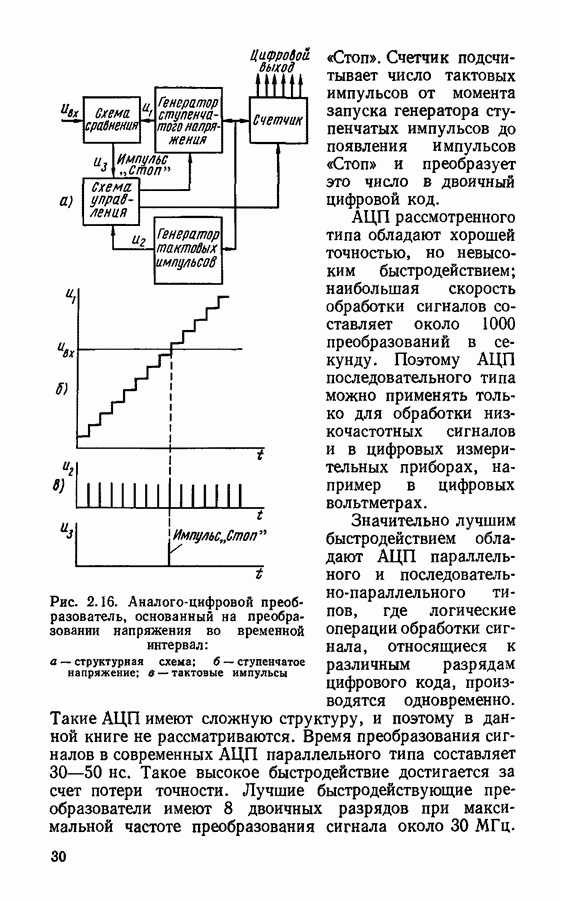
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
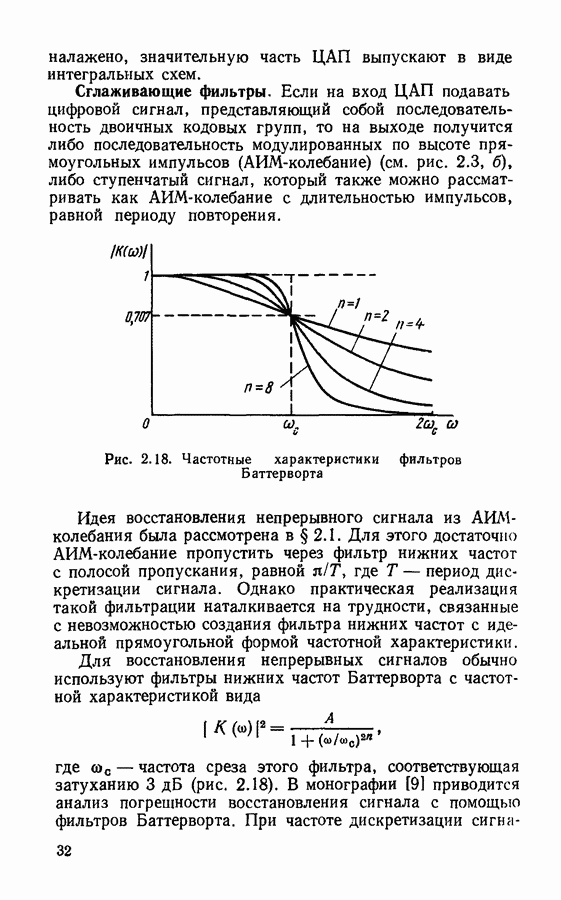
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
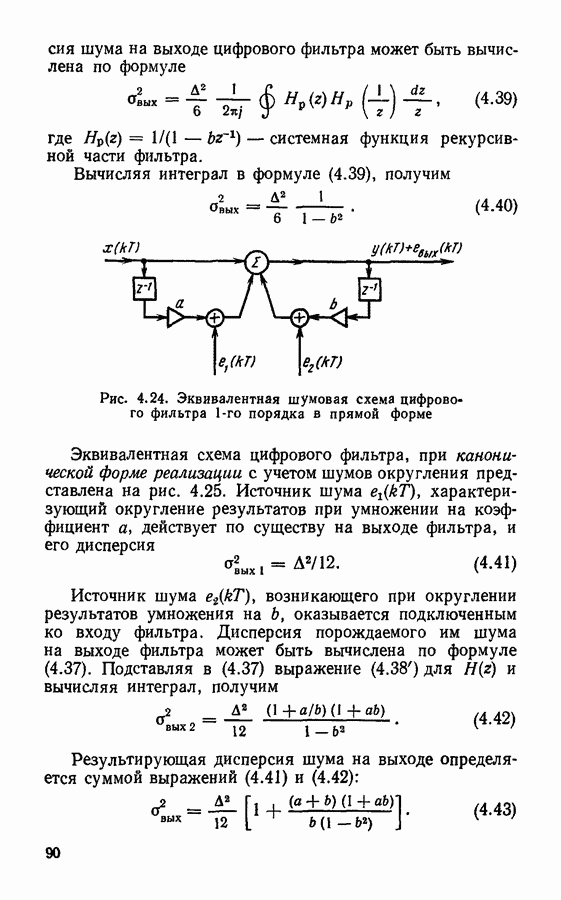
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
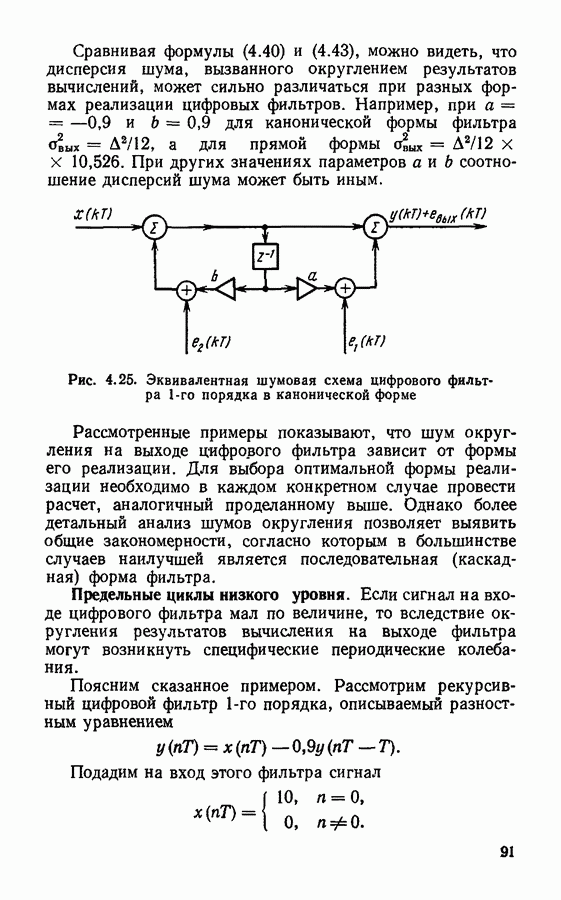
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА