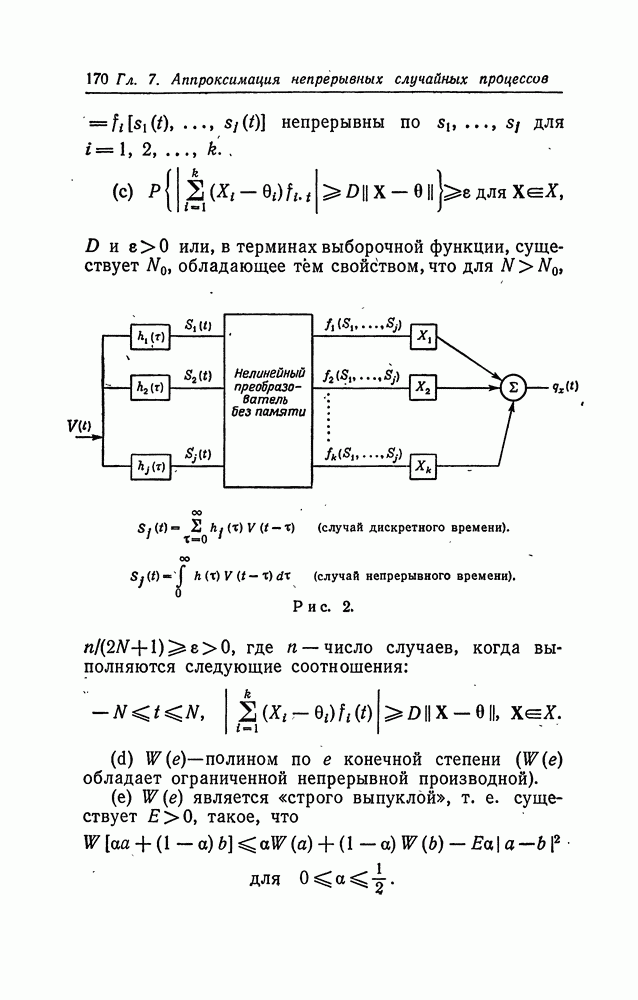
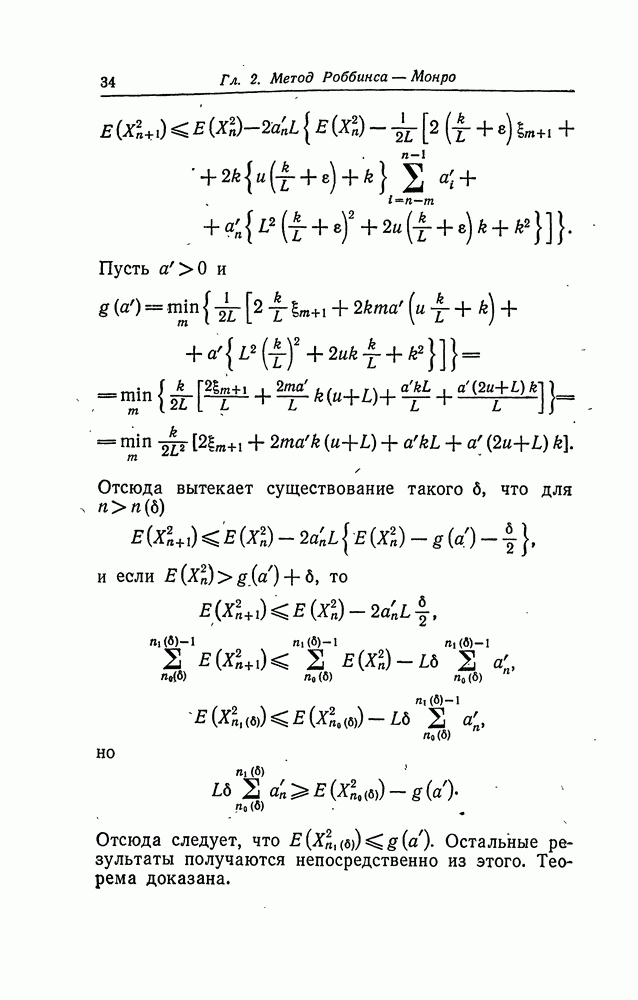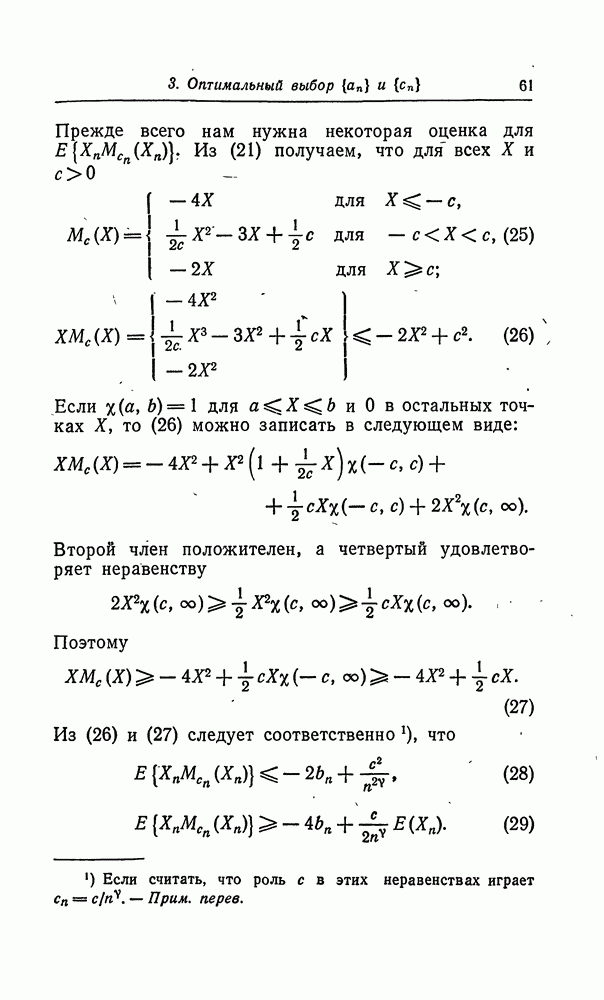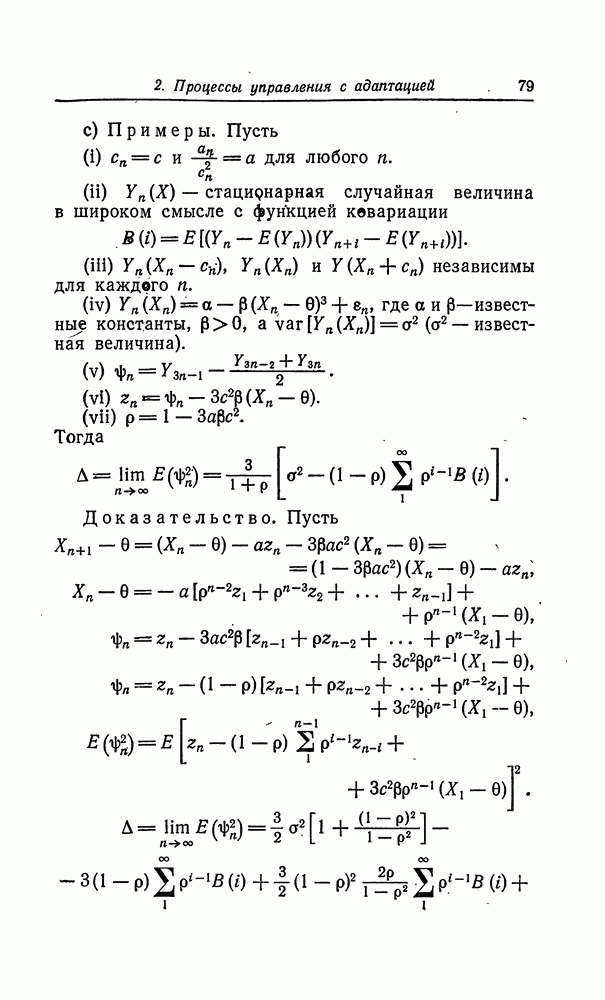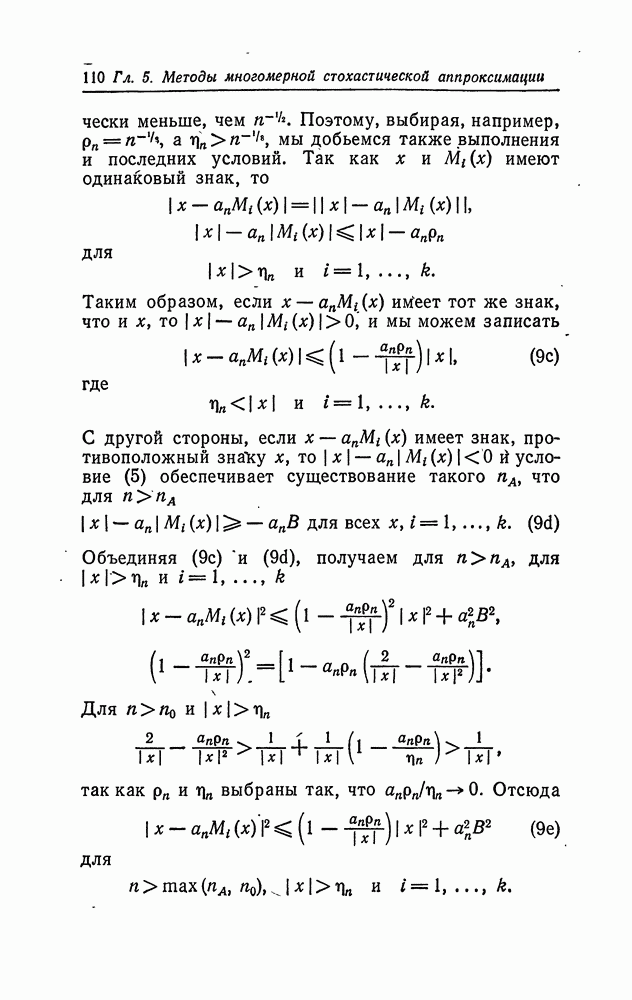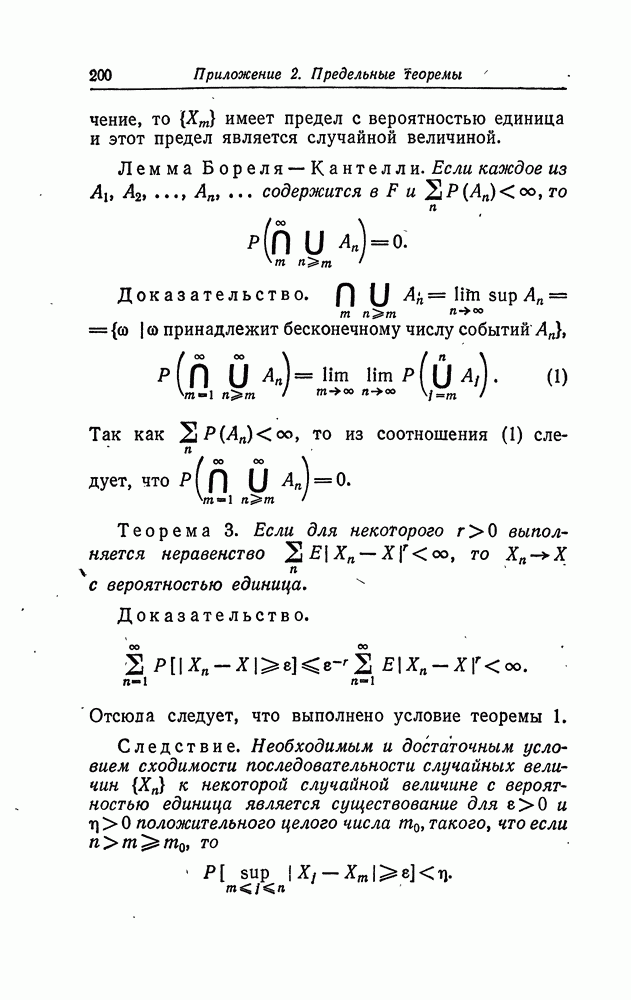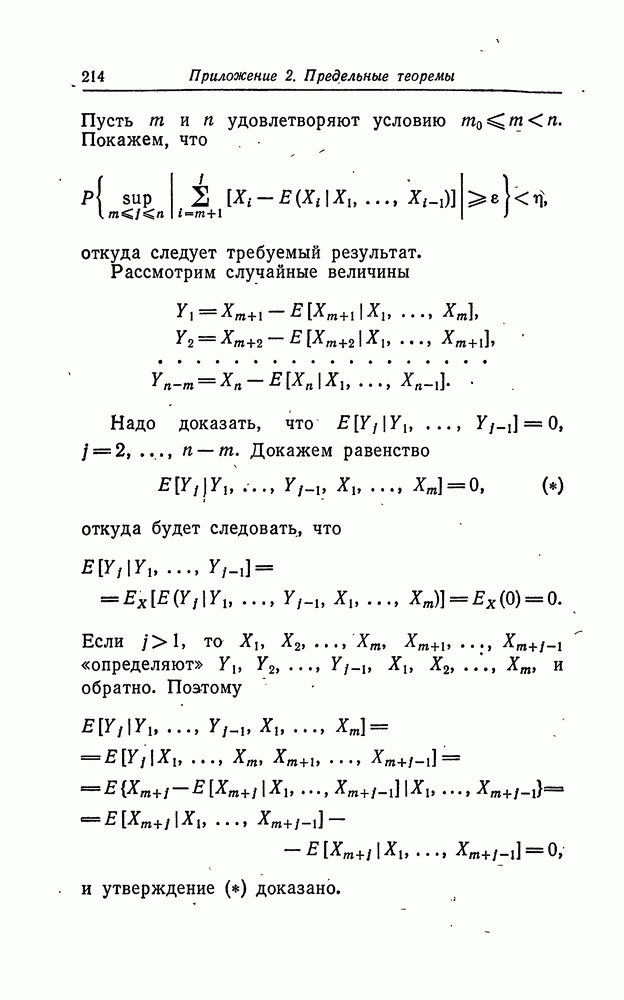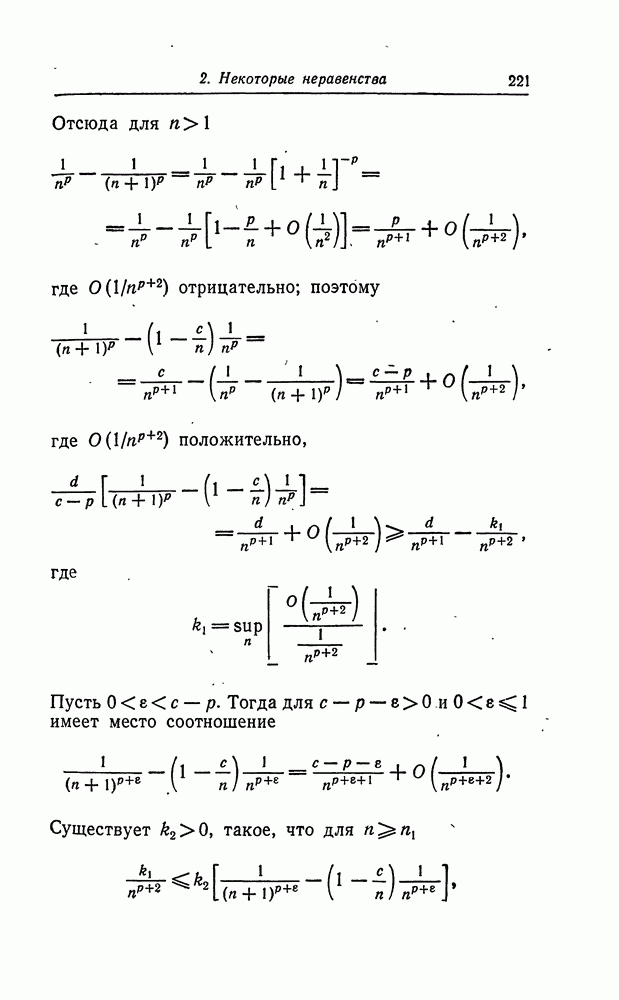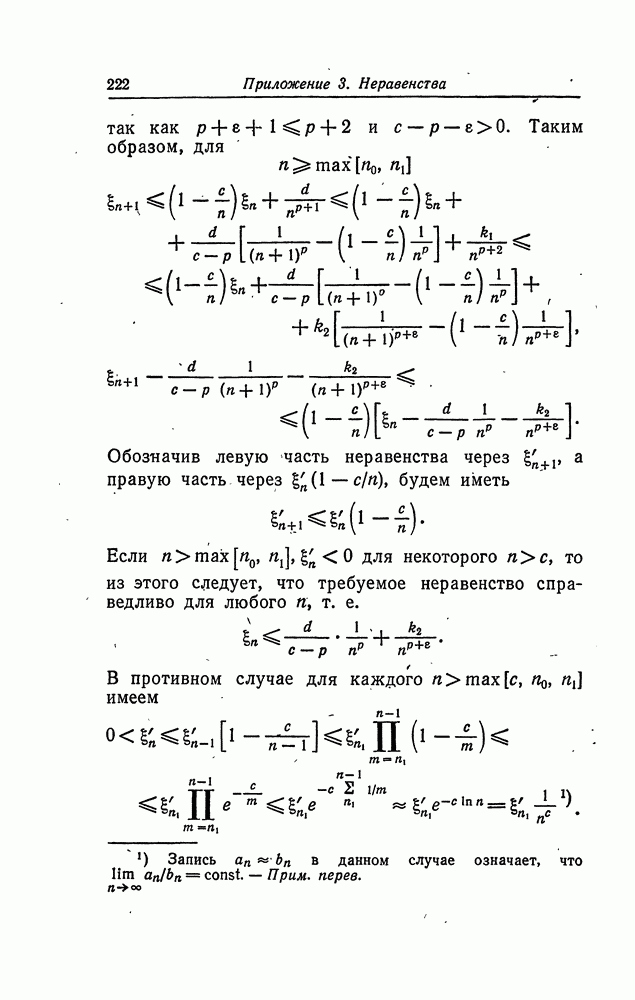| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Метод характеристических функций
Сакс [1] использовал метод характеристических функций и - доказал асимптотическую нормальность.
Теорема 2 (Сакс). Пусть  последовательность положительных чисел, такая, что
последовательность положительных чисел, такая, что

Пусть  фиксированное число или произвольная случайная величина с
фиксированное число или произвольная случайная величина с

и  последовательность, определенная рекуррентным соотношением
последовательность, определенная рекуррентным соотношением

где  случайная величина, условное распределение которой при данных
случайная величина, условное распределение которой при данных  совпадает с распределением
совпадает с распределением  Пусть
Пусть  где
где  предположим, что
предположим, что  а имеет единственное решение для каждого действительного а. Таким образом, соотношение (2) превращается в
а имеет единственное решение для каждого действительного а. Таким образом, соотношение (2) превращается в

 для всех х, и условное распределение
для всех х, и условное распределение  при данных
при данных  совпадает с распределением
совпадает с распределением  Заметим, что следствием этого является
Заметим, что следствием этого является

с вероятностью единица. Сделаем следующие предположения.
(i) М является функцией, измеримой по Борелк  и
и

(ii) Для некоторых положительных констант  и для всех х
и для всех х

(iii) Для всех х

где  при
при  и где
и где 

Пусть  для
для  где А таково, что
где А таково, что  Тогда
Тогда  является асимптотически нормально распределенной величиной со средним нуль и дисперсией
является асимптотически нормально распределенной величиной со средним нуль и дисперсией 
Доказательство. Без ограничения общности положим  и для сокращения обозначений вместо
и для сокращения обозначений вместо  будем использовать символы
будем использовать символы  соответственно. Применяя условия (iii) и (3), получаем
соответственно. Применяя условия (iii) и (3), получаем

Пусть  для
для  для
для  где
где  Итерируя (5), приходим к равенству
Итерируя (5), приходим к равенству

Пусть

В силу леммы 15 приложения 3

Поэтому доказательство того, что  асимптотически нормальна со средним нуль и дисперсией
асимптотически нормальна со средним нуль и дисперсией  эквивалентно доказательству асимптотической нормальности
эквивалентно доказательству асимптотической нормальности  со средним нуль и дисперсией
со средним нуль и дисперсией  Мы должны показать, что
Мы должны показать, что

Пусть в лемме 12 приложения  для всех
для всех  Тогда из этой леммы вытекает, что (7) имеет место. Для доказательства соотношения (9) обратимся к теореме 6 приложения 2 при
Тогда из этой леммы вытекает, что (7) имеет место. Для доказательства соотношения (9) обратимся к теореме 6 приложения 2 при 
Чтобы убедиться в том, что мы имеем право так сделать, заметим, что в силу (4)

Пусть  если и
если и  в противном случае. Для проверки выполнения условия теоремы 6 приложения 2 мы должны доказать, что
в противном случае. Для проверки выполнения условия теоремы 6 приложения 2 мы должны доказать, что

а это равносильно тому, что

В силу леммы 12 приложения 3 и задачи 1 приложения 3 из  следует, что для некоторого
следует, что для некоторого 

Применяя предположение  можно получить следующее:
можно получить следующее:

где

Так как  то применяя лемму 13 приложения 3 с
то применяя лемму 13 приложения 3 с  для всех
для всех  и используя (11), устанавливаем, что справедливо (10). Проверка условия (1) теоремы 6 приложения 2 эквивалентна доказательству того, что
и используя (11), устанавливаем, что справедливо (10). Проверка условия (1) теоремы 6 приложения 2 эквивалентна доказательству того, что

где  означает условное математическое ожидание при условии, которое обозначается в теореме 6 приложения 2 через
означает условное математическое ожидание при условии, которое обозначается в теореме 6 приложения 2 через  Используя снова лемму 13
Используя снова лемму 13
приложения 3, получаем, что достаточно доказать соотношение

справедливость которого вытекает из следующих соображений. Выражение под знаком абсолютной величины равномерно ограничено в силу условия  так что применима теорема Лебега. Кроме того, согласно условию
так что применима теорема Лебега. Кроме того, согласно условию  и в силу сходимости
и в силу сходимости  к 0 с вероятностью единица, имеем
к 0 с вероятностью единица, имеем

Результат (14) и лемма 13 приложения 3 показывают также, что выполняется условие (2) теоремы 6 приложения 2 с

где

Тем самым завершается проверка применимости теоремы 6 приложения 2 и устанавливается справедливость утверждения (9). Чтобы доказать (8), возведем обе части соотношения (3) в квадрат и используем, условие  Мы получим, что
Мы получим, что

Тогда в силу  для достаточно малого
для достаточно малого  такого, что
такого, что  и для достаточно большого
и для достаточно большого  скажем
скажем 

Пусть  и пусть определено, как и выше, с
и пусть определено, как и выше, с  Выберем
Выберем  достаточно большим, чтобы
достаточно большим, чтобы  (это гарантирует выполнение неравенства
(это гарантирует выполнение неравенства
 для
для  так
так  может иметь место). Итерирование (17) дает
может иметь место). Итерирование (17) дает

а это является требуемой оценкой.
Пусть  Так как
Так как  то для этих значений
то для этих значений  можно найти
можно найти  такое, что
такое, что

Как отмечалось выше,  с вероятностью единица, и потому можно выбрать
с вероятностью единица, и потому можно выбрать  так, чтобы
так, чтобы

Пусть  и таково, что а
и таково, что а  Тогда, обозначая
Тогда, обозначая  через
через  через
через  и используя соотношения (20), (19), (18), неравенство Ляпунова и задачу 1 приложения 3, имеем для
и используя соотношения (20), (19), (18), неравенство Ляпунова и задачу 1 приложения 3, имеем для 

где  подходящие константы.
подходящие константы.
Оценка (21) вместе с тем фактом, что  при
при  для любого фиксированного
для любого фиксированного  устанавливает справедливость утверждения (8) и завершает доказательство теоремы.
устанавливает справедливость утверждения (8) и завершает доказательство теоремы.
Теорема 3 (Сакс). Предположим, что выполняются условия теоремы 2 и предположения (i), (iii), (iv) и (v). Заменим (ii) следующим предположением:
(И) для всех х и некоторой положительной константы 

и для любых  таких, что
таких, что 

Пусть  где А таково, что
где А таково, что  Тогда величина
Тогда величина  распределена асимптотически нормально со средним нуль и дисперсией
распределена асимптотически нормально со средним нуль и дисперсией 
Доказательство. Без ограничения общности положим  Пусть
Пусть  таково, что
таково, что  и пусть
и пусть  Тогда можно найти
Тогда можно найти  такое, что для
такое, что для 

Положим

Так как из  следует, что
следует, что  с вероятностью единица, то можно найти
с вероятностью единица, то можно найти  такое, что для
такое, что для 

Пусть  Определим
Определим  с помощью рекуррентного соотношения
с помощью рекуррентного соотношения

Очевидно, что предположения теоремы 2 вместе с условием (1) показывают, что теорема 6 приложения 2 применима к  Поэтому для всех у
Поэтому для всех у

где  функция нормального распределения со средним нуль и дисперсией
функция нормального распределения со средним нуль и дисперсией  Из соотношений (2) и (4) следует результат теоремы.
Из соотношений (2) и (4) следует результат теоремы.
Теперь обсудим результат Фабиана.
Предварительные замечания. В последующем  будет обозначать вероятностное пространство; соотношения между случайными величинами, векторами и матрицами и их сходимость, если не оговорено противное, мы будем понимать с вероятностью единица.
будет обозначать вероятностное пространство; соотношения между случайными величинами, векторами и матрицами и их сходимость, если не оговорено противное, мы будем понимать с вероятностью единица.
Будем писать  если
если  асимптотически
асимптотически  -распределено, и
-распределено, и  для двух последовательностей случайных векторов, если
для двух последовательностей случайных векторов, если  для любого 2 тогда и только тогда, когда
для любого 2 тогда и только тогда, когда 
Индикатор (характеристическая функция) функции на множестве А будет обозначаться через  математическое ожидание и условное математическое ожидание — через
математическое ожидание и условное математическое ожидание — через  Пространство
Пространство  есть
есть  -мерное евклидово пространство, элементы которого рассматриваются как вектор-столбцы,
-мерное евклидово пространство, элементы которого рассматриваются как вектор-столбцы,  есть пространство всех действительных
есть пространство всех действительных  -матриц. Символами.
-матриц. Символами.  обозначаются множества всех измеримых, преобразований из
обозначаются множества всех измеримых, преобразований из  соответственно. Единичная матрица в
соответственно. Единичная матрица в  обозначается через
обозначается через  — это евклидова норма. Для последовательности чисел
— это евклидова норма. Для последовательности чисел  символы о
символы о  обозначают последовательности
обозначают последовательности  элементов одного из множеств
элементов одного из множеств  такие, что
такие, что  для
для  и всех
и всех  равномерно на множестве вероятности единица,
равномерно на множестве вероятности единица,  для
для  и всех
и всех  . В особых случаях
. В особых случаях  может быть константой на
может быть константой на  и рассматриваться как последовательность элементов из
и рассматриваться как последовательность элементов из  или
или  Аналогичные определения можно дать и в других случаях
Аналогичные определения можно дать и в других случаях
Теорема 4 (Фабиан). Предположим, что к — целое положительное число,  неубывающая
неубывающая
последовательностьч  -полей,
-полей,  Пусть
Пусть

матрица  положительно определена;
положительно определена;  ортогональна, а
ортогональна, а  диагональна. Предположим, что
диагональна. Предположим, что  являются
являются  -измеримыми,
-измеримыми, 

а для каждого 

либо

Предположим также, что для  если
если  если
если  ,
,

и

Тогда асимптотическое распределение вектора  является нормальным со средним
является нормальным со средним  и матрицей ковариации РМР где
и матрицей ковариации РМР где

Доказательство. Пусть  нормально распределенный вектор со средним
нормально распределенный вектор со средним  и матрицей ковариации
и матрицей ковариации 
Сначала покажем, что можно без ограничения общности предположить следующее:

Если мы положим  то
то  снова будет удовлетворять предположениям теоремы, но
снова будет удовлетворять предположениям теоремы, но  и если теорема окажется справедливой, то для
и если теорема окажется справедливой, то для  мы получим
мы получим

откуда следует, что

Поэтому можно положить  Заметим теперь, что
Заметим теперь, что  и мы должны доказать, что
и мы должны доказать, что  но
но  удовлетворяет соотношению (6) с
удовлетворяет соотношению (6) с  а
а  удовлетворяет соотношению
удовлетворяет соотношению

затем легко проверить, что  и теорема будет справедлива, если она окажется верной для
и теорема будет справедлива, если она окажется верной для  Теперь для любого
Теперь для любого  в силу теоремы Егорова можно изменить
в силу теоремы Егорова можно изменить  на множестве вероятности не более
на множестве вероятности не более  и получить
и получить  сходящиеся равномерно на
сходящиеся равномерно на  к своим пределам
к своим пределам  (последнее верно, если только
(последнее верно, если только  Можно сделать это так, чтобы
Можно сделать это так, чтобы  оставались
оставались  -измеримыми, и определить тогда
-измеримыми, и определить тогда  равенством (6) с
равенством (6) с  подставленными вместо
подставленными вместо  Если теперь теорема имеет место при равномерной сходимости
Если теперь теорема имеет место при равномерной сходимости  то мы получим
то мы получим  так как
так как  было выбрано произвольно, а
было выбрано произвольно, а

Итак, можно предполагать, что  равномерно и
равномерно и  Если
Если  равномерно, то можно заменить
равномерно, то можно заменить  на
на  на I без изменения
на I без изменения  без нарушения соотношений (2), (3), (4) и
без нарушения соотношений (2), (3), (4) и  -измеримости
-измеримости  Далее, допустим, что
Далее, допустим, что 
определяется равенством (6), в правую часть которого вместо  подставляется
подставляется  кроме того, вычитается
кроме того, вычитается  Если теперь
Если теперь  мы получаем
мы получаем

Если  то из задачи 5 приложения 3 следует, что
то из задачи 5 приложения 3 следует, что  таким образом, можно положить
таким образом, можно положить  Далее положим
Далее положим  ; мы можем взять в (9) математические ожидания и, так как
; мы можем взять в (9) математические ожидания и, так как  получим
получим  можно предполагать, что
можно предполагать, что  Теперь, полагая
Теперь, полагая  мы получим из (9), что
мы получим из (9), что  а из соотношения, предшествующего (9), что
а из соотношения, предшествующего (9), что  Последний член есть
Последний член есть  и покоординатное применение результата задачи 5 приложения 3 дает
и покоординатное применение результата задачи 5 приложения 3 дает  Поэтому
Поэтому  тогда и только тогда, когда
тогда и только тогда, когда  удовлетворяет всем условиям теоремы при
удовлетворяет всем условиям теоремы при  Поэтому мы можем считать соотношения (8) выполненными.
Поэтому мы можем считать соотношения (8) выполненными.
Мы имеем, теперь  и в силу
и в силу  Отсюда
Отсюда

и из задачи 5 приложения 3 следует, что  Полагая затем
Полагая затем  мы получим неравенство (9) для
мы получим неравенство (9) для  а также соотношения
а также соотношения  Кроме того, можно считать
Кроме того, можно считать  тогда
тогда

Отсюда в силу условия (2) получаем 

и покоординатное применение результата задачи 5 приложения 3 дает

На следующем этапе нам потребуется следующее стандартное, соотношение (см., например, Феллер [2], доказательство теоремы 1 гл. XV, § 6). Если  то
то  Ясно, что мы можем выбрать последовательность
Ясно, что мы можем выбрать последовательность  так, чтобы выполнялись соотношения (3) и (4), если вместо
так, чтобы выполнялись соотношения (3) и (4), если вместо  подставить
подставить  Для
Для  получаем
получаем

Отсюда, ограничиваясь рассмотрением фиксированного шара

и замечая, что из (2) следует соотношение  получаем 4
получаем 4

где

так что либо  либо
либо  и
и

Теперь положим  Тогда перегруппировка членов в (11) и
Тогда перегруппировка членов в (11) и  -измеримость
-измеримость  дают
дают

Соотношение  имеет место при
имеет место при  для
для  Если оно выполняется для
Если оно выполняется для  то в силу неравенства
то в силу неравенства

оно имеет место также при  и для
и для  Для достаточно больших
Для достаточно больших  имеем
имеем  можно положить тогда равным
можно положить тогда равным  Из результатов задач 4 и 5 приложения 3 теперь следует, что
Из результатов задач 4 и 5 приложения 3 теперь следует, что  Так как
Так как  было произвольным, то
было произвольным, то

Доказательство будет полностью закончено, если  покажем, что
покажем, что  сходится к характеристической функции
сходится к характеристической функции  соответствующей
соответствующей  Предположим, что
Предположим, что  независимы и
независимы и  -распределены. Тогда
-распределены. Тогда  является нормальным для любого
является нормальным для любого  в силу уже доказанного, и, таким образом,
в силу уже доказанного, и, таким образом, 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- Глава 1. ВВЕДЕНИЕ
- 3. Стохастическая аппроксимация
- 4. Метод «вверх и вниз»
- 5. Метод Ньютона — Рафсона
- 6. Применения
- 7. Резюме
- Глава 2. МЕТОД РОББИНСА—МОНРО
- 3. Одномерная стохастическая аппроксимация
- 4. Аппроксимация для асимптотически регулярного процесса
- 5. Теория малых выборок
- 6. Различные модификации метода Роббинса — Монро
- Глава 3. МЕТОД КИФЕРА—ВОЛЬФОВИЦА
- 3. Оптимальный выбор {аn} и {сn}
- 4. Класс процессов стохастической аппроксимации
- 5. Иллюстративный пример
- Глава 4. ПРИМЕНЕНИЯ
- 3. Две функции регрессии для кинетической модели
- 4. Применение стохастической аппроксимации к задаче надежности
- 5. Оценка интенсивности реакции
- Глава 5. МЕТОДЫ МНОГОМЕРНОЙ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ
- 2. Многомерный метод Роббинса — Монро
- 3. Применение к одной задаче из фармакологии
- 4. Многомерный метод Кифера — Вольфовица
- Глава 6. АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ
- 2. Метод моментов
- 3. Метод характеристических функций
- 4. Применения
- Глава 7. АППРОКСИМАЦИЯ ДЛЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 3. Процедура Кифера — Вольфовица для непрерывных случайных процессов
- 4. Применение к задаче фильтрации
- Глава 8. МЕТОД «ВВЕРХ И ВНИЗ»
- 3. Применение к преобразованию эмпирической кривой эффекта
- 4. Метод «вверх и вниз» для малых выборок (Браунли, Ходж и Розенблатт [1]).
- 5. Непараметрический метод «вверх и вниз» (Дерман [2]).
- 6. Иллюстративный пример
- Приложение 1. ИТЕРАЦИОННЫЕ МЕТОДЫ ЧИСЛЕННОГО АНАЛИЗА
- 3. Метод Ньютона — Рафсона
- 4. Задача о неподвижной, точке
- Приложение 2. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
- 2. Сходимость последовательности случайных величин
- 3. Многомерные характеристические функции
- 4. Некоторые теоремы об условном математическом ожидании
- Приложение 3. НЕРАВЕНСТВА
- 2. Неравенства, используемые в стохастической аппроксимации
- 3. Другие неравенства
- Дополнение. ОБЗОР НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТОВ В СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ
- 2. Многомерная стохастическая аппроксимация
- 3. Стохастическая аппроксимация для задач на условный экстремум
- 4. Об оптимизации процесса стохастической аппроксимации
- 5. Стохастическая аппроксимация в задачах оптимизации сложных функций
- 6. Многоэкстремальная стохастическая аппроксимация
- 7. Бесконечномерная стохастическая аппроксимация
- 8. Интуитивные основы стохастической аппроксимации
- 9. Приложения метода стохастической аппроксимации
- БИБЛИОГРАФИЯ