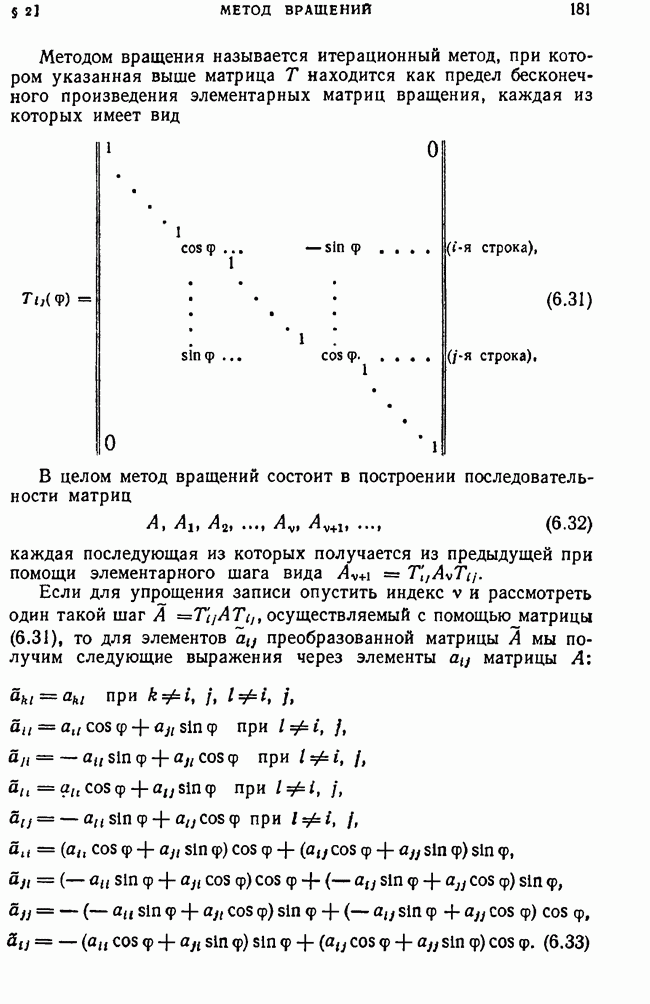
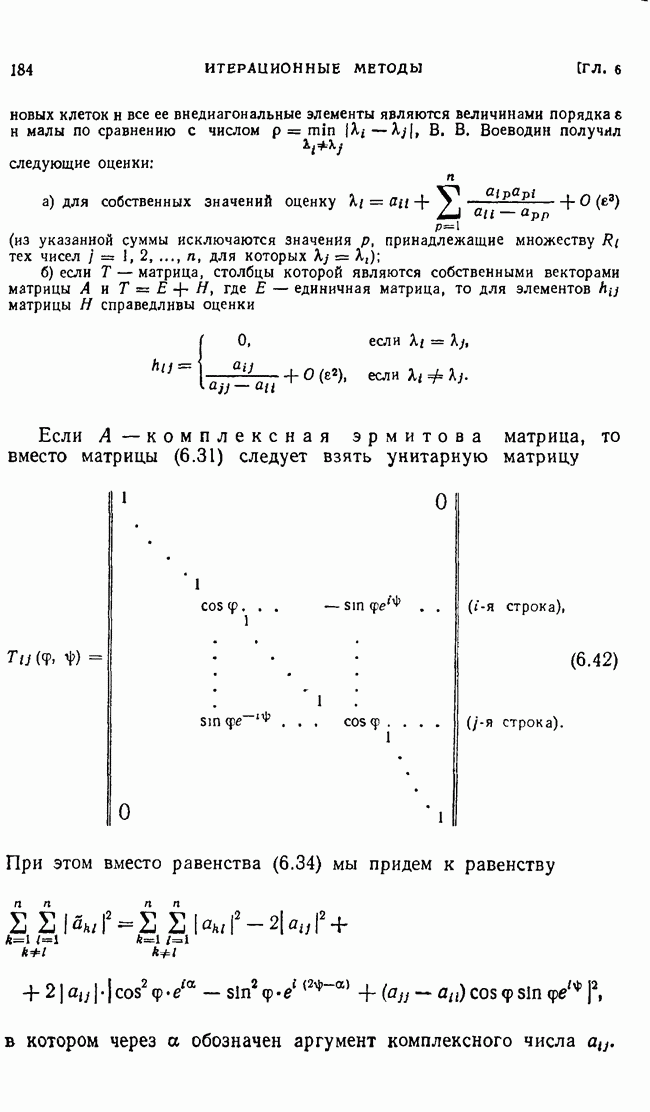
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Простейшие свойства произвольного евклидова пространства.
Устанавливаемые в этом пункте свойства справедливы для совершенно произвольного евклидова пространства как конечной, так и бесконечной размерности.
Теорема 4.1. Для любых двух элементов х и у произвольного евклидова пространства справедливо неравенство

называемое неравенством Коши-Буняковского.
Доказательство. Для любого вещественного, числа X, в силу аксиомы 4° скалярного произведения, справедливо неравенство  . В силу аксиом
. В силу аксиом  последнее неравенство можно переписать в виде
последнее неравенство можно переписать в виде

Необходимым и достаточным условием неотрицательности последнего квадратного трехчлена является неположительность его дискриминанта, т. е. неравенство

Из (4.7) сразу же вытекает неравенство (4.6). Теорема доказана.
Наша очередная задача — ввести в произвольном евклидовом пространстве понятие нормы (или длины) каждого элемента. Для этого введем понятие линейного нормированного пространства.
Определение. Линейное пространство  называется нормированным, если выполнены следующие два требования:
называется нормированным, если выполнены следующие два требования:
I. Имеется правило, посредством которого каждому элементу х пространства  ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое символом
ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое символом 
II. Указанное правило подчинено следующим трем аксиомам:
 если х — ненулевой элемент,
если х — ненулевой элемент,  если х — нулевой элемент.
если х — нулевой элемент.
 для любого элемента х и любого вещественного числа
для любого элемента х и любого вещественного числа 
3°. Для любых двух элементов х и у справедливо следующее неравенство:

называемое неравенством треугольника (или неравенством Минковского).
Теорема 4.2. Всякое евклидово пространство является нормированным, если в нем норму любого элемента х определить равенством

Доказательство. Достаточно доказать, что для нормы, определенной соотношением (4.9), справедливы аксиомы 1 —3° из определения нормированного пространства.
Справедливость для нормы аксиомы 1° сразу вытекает из аксиомы 4° скалярного произведения. Справедливость для нормы аксиомы 2° почти непосредственно вытекает из аксиом 1° и 3° скалярного произведения.
Остается убедиться в справедливости для нормы аксиомы 3°, т. е. неравенства (4.8). Будем опираться на неравенство Коши—Буняковского (4.6), которое перепишем в виде

С помощью последнего неравенства, аксиом 1°-4° скалярного произведения и определения нормы получим

Теорема доказана.
Следствие. Во всяком евклидовом пространстве с нормой элементов, определяемой соотношением (4.9), для любых двух элементов х и у справедливо неравенство треугольника (4.8).
Заметим далее, что в любом вещественном евклидовом пространстве можно ввести понятие угла между двумя произвольными элементами х и у этого пространства. В полной аналогии с векторной алгеброй, мы назовем  между элементами
между элементами  тот (изменяющийся в пределах от 0 до
тот (изменяющийся в пределах от 0 до  ) угол, косинус которого определяется соотношением
) угол, косинус которого определяется соотношением 

Данное нами определение угла корректно, ибо в силу неравенства Коши—Буняковского (4.7) дробь, стоящая в правой части последнего равенства, по модулю не превосходит единицы.
Далее договоримся называть два произвольных элемента х и у евклидова пространства Е ортогональными, если скалярное произведение этих элементов  равно нулю (в этом случае косинус угла
равно нулю (в этом случае косинус угла  между элементами х и у будет равен нулю).
между элементами х и у будет равен нулю).
Снова апеллируя к векторной алгебре, назовем сумму  двух ортогональных элементов х и у гипотенузой прямоугольного треугольника, построенного на элементах х и у.
двух ортогональных элементов х и у гипотенузой прямоугольного треугольника, построенного на элементах х и у.
Заметим, что во всяком евклидовом пространстве справедлива теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В самом деле, поскольку х и у ортогональны и  то в силу аксиом и определения нормы
то в силу аксиом и определения нормы

Этот результат обобщается и на  попарно ортогональных элементов
попарно ортогональных элементов  если
если  то
то

В заключение запишем норму, неравенство Коши—Буняковского и неравенство треугольника в каждом из конкретных евклидовых пространств, рассмотренных в предыдущем пункте.
В евклидовом пространстве всех свободных векторов с обычным определением скалярного произведения норма вектора а совпадает с его длиной  неравенство Коши—Буняковского приводится к виду
неравенство Коши—Буняковского приводится к виду  , а неравенство треугольника — к виду
, а неравенство треугольника — к виду 
В евклидовом пространстве  всех непрерывных на сегменте
всех непрерывных на сегменте  функций
функций  со скалярным произведением (4.1) норма элемента
со скалярным произведением (4.1) норма элемента  равна
равна  а неравенства Коши—Буняковского и треугольника имеют вид
а неравенства Коши—Буняковского и треугольника имеют вид

Оба эти неравенства играют важную роль в различных разделах математического анализа.
В евклидовом пространстве  упорядоченных совокупностей
упорядоченных совокупностей  вещественных чисел со скалярным произведением (4.2) норма любого элемента
вещественных чисел со скалярным произведением (4.2) норма любого элемента  равна
равна

а неравенства Коши—Буняковского и треугольника имеют вид

Наконец, в евклидовом пространстве упорядоченных совокупностей  вещественных чисел со скалярным произведением (4.5) норма любого элемента
вещественных чисел со скалярным произведением (4.5) норма любого элемента  равна
равна

а неравенства Коши—Буняковского и треугольника имеют вид

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- 1. Понятие матрицы.
- 2. Основные операции над матрицами и их свойства.
- 3. Блочные матрицы.
- § 2. Определители
- 2. Выражение определителя непосредственно через его элементы.
- 3. Теорема Лапласа.
- 4. Свойства определителей.
- 5. Примеры вычисления определителей.
- 6. Определитель суммы и произведения матриц.
- 7. Понятие обратной матрицы.
- § 3. Теорема о базисном миноре матрицы
- 1. Понятие линейной зависимости строк.
- 2. Теорема о базисном мнноре.
- 3. Необходимое и достаточное условие равенства нулю определителя.
- ГЛАВА 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- § 1. Понятие линейного пространства
- 2. Некоторые свойства произвольных линейных пространств.
- § 2. Базис и размерность линейного пространства
- 1. Понятие линейной зависимости элементов линейного пространства.
- 2. Базис и координаты.
- 3. Размерность линейного пространства.
- 4. Понятие изоморфизма линейных пространств.
- § 3. Подпространства линейных пространств
- 1. Понятие подпространства и линейной оболочки.
- 2. Новое определение ранга матрицы.
- 3. Сумма и пересечение подпространств.
- 4. Разложение линейного пространства в прямую сумму подпространств.
- § 4. Преобразование координат при преобразовании базиса n-мерного линейного пространства
- 2. Связь между преобразованием базисов и преобразованием соответствующих координат.
- ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Условие совместности линейной системы
- 2. Нетривиальная совместность однородной системы.
- 3. Условие совместности общей линейной системы.
- § 2. Отыскание решений линейной системы
- 2. Отыскание всех решений общей линейной системы.
- 3. Свойства совокупности решений однородной системы.
- 4. Заключительные замечания о решении линейных систем.
- ГЛАВА 4. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- § 1. Вещественное евклидово пространство и его простейшие свойства
- 2. Простейшие свойства произвольного евклидова пространства.
- § 2. Ортонормированный базис конечномерного евклидова пространства
- 2. Свойства ортонормированного базиса.
- 3. Разложение n-мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения.
- 4. Изоморфизм n-мерных евклидовых пространств.
- § 3. Комплексное евклидово пространство
- 2. Неравенство Коши — Буняковского. Понятие нормы.
- 3. Ортонормированный базис и его свойства.
- § 4. Метод регуляризации для отыскания нормального решения линейной системы
- ГЛАВА 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. Понятие линейного оператора. Основные свойства
- 2. Действия над линейными операторами. Пространство линейных операторов.
- 3. Свойства множества L(V, V) линейных операторов.
- § 2. Матричная запись линейных операторов
- 2. Преобразование матрицы линейного оператора при переходе к новому базису.
- 3. Характеристический многочлен линейного оператора.
- § 3. Собственные значения и собственные векторы линейных операторов
- § 4. Линейные и полуторалинейные формы в евклидовом пространстве
- 2. Полуторалинейные формы в евклидовом пространстве. Специальное представление таких форм.
- § 5. Линейные самосопряженные операторы в евклидовом пространстве
- 2. Самосопряженные операторы. Основные свойства.
- 3. Норма линейного оператора.
- 4. Дальнейшие свойства самосопряженных операторов.
- 5. Спектральное разложение самосопряженных операторов. Теорема Гамильтона—Кэли.
- 6. Положительные операторы. Корни m-й степени из оператора.
- § 6. Приведение квадратичной формы к сумме квадратов
- § 7. Унитарные и нормальные операторы
- § 8. Канонический вид линейных операторов
- § 9. Линейные операторы в вещественном евклидовом пространстве
- 2. Ортогональные операторы.
- ГЛАВА 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ И ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
- § 1. Итерационные методы решения линейных систем
- 2. Общий неявный метод простой итерации.
- 3. Модифицированный метод простой итерации.
- 4. Метод Зейделя.
- 5. Метод верхней релаксации.
- 6. Случай несимметричной матрицы А.
- 7. Итерационный метод П. Л. Чебышева.
- § 2. Решение полной проблемы собственных значений методом вращений
- ГЛАВА 7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейные формы
- 2. Представление билинейной формы в конечномерном линейном пространстве.
- 3. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы.
- § 2. Квадратичные формы
- § 3. Приведение квадратичной формы к сумме квадратов
- 2. Метод Якоби.
- § 4. Закон инерции квадратичных форм. Классификация квадратичных форм
- 2. Классификация квадратичных форм.
- 3. Критерий Сильвестра знакоопределенности квадратичной формы.
- § 5. Полилинейные формы
- § 6. Билинейные и квадратичные формы в евклидовом пространстве
- 2. Приведение квадратичной формы к сумме квадратов в ортогональном базисе.
- 3. Одновременное приведение двух квадратичных форм к сумме квадратов в линейном пространстве.
- 4. Экстремальные свойства квадратичной формы.
- § 7. Гиперповерхности второго порядка
- 2. Параллельные переносы в евклидовом пространстве. Преобразования ортонормированных базисов в ортонормированные.
- 3. Преобразование общего уравнения гиперповерхности второго порядка при параллельном переносе.
- 4. Преобразование общего уравнения гиперповерхности второго порядка при переходе от ортонормированного базиса к ортонормированиому.
- 5. Инварианты общего уравнения гиперповерхности второго порядка.
- 6. Центр гиперповерхности второго порядка.
- 7. Стандартное упрощение любого уравнения гиперповерхности второго порядка путем преобразования ортонормированного базиса.
- 8. Упрощение уравнения центральной гиперповерхности второго порядка. Классификация центральных гиперповерхностей.
- 9. Упрощение уравнения нецентральной гиперповерхности второго порядка. Классификация нецентральных гиперповерхностей.
- ГЛАВА 8. ТЕНЗОРЫ
- § 1. Преобразование базисов и координат
- 2. Взаимные базисы. Ковариантные и контравариантные координаты векторов.
- 3. Преобразования базиса и координат.
- § 2. Понятие тензора. Основные операции над тензорами
- 2. Примеры тензоров.
- 3. Основные операции над тензорами.
- § 3. Метрический тензор. Основные операции векторной алгебры в тензорных обозначениях
- 2. Операция поднятия и опускания индексов с помощью метрического тензора.
- 3. Ортонормированные базисы в E^n.
- 4. Дискриминантный тензор.
- 5. Ориентированный объем.
- 6. Векторное произведение.
- 7. Двойное векторное произведение.
- § 4. Метрический тензор псевдоевклидова пространства
- 2. Галилеевы координаты. Преобразования Лоренца.
- 3. Преобразования Лоренца пространства
- § 5. Тензор момента инерции
- ГЛАВА 9. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- § 1. Понятие группы. Основные свойства групп
- 2. Понятие группы. Некоторые свойства групп.
- 3. Изоморфизм групп. Подгруппы.
- 4. Смежные классы. Нормальные делители.
- 5. Гомоморфизмы. Фактор-группы.
- § 2. Группы преобразований
- 2. Группа линейных преобразований.
- 3. Сходимость элементов в группе GL(n). Подгруппы группы GL(n).
- 4. Группа ортогональных преобразований.
- 5. Некоторые дискретные и конечные подгруппы ортогональной группы.
- 6. Группа Лоренца.
- 7. Унитарные группы.
- § 3. Представления групп
- 2. Матрицы линейных представлений. Эквивалентные представления.
- 3. Приводимые и неприводимые представления.
- 4. Характеры.
- 5. Примеры представлений групп.