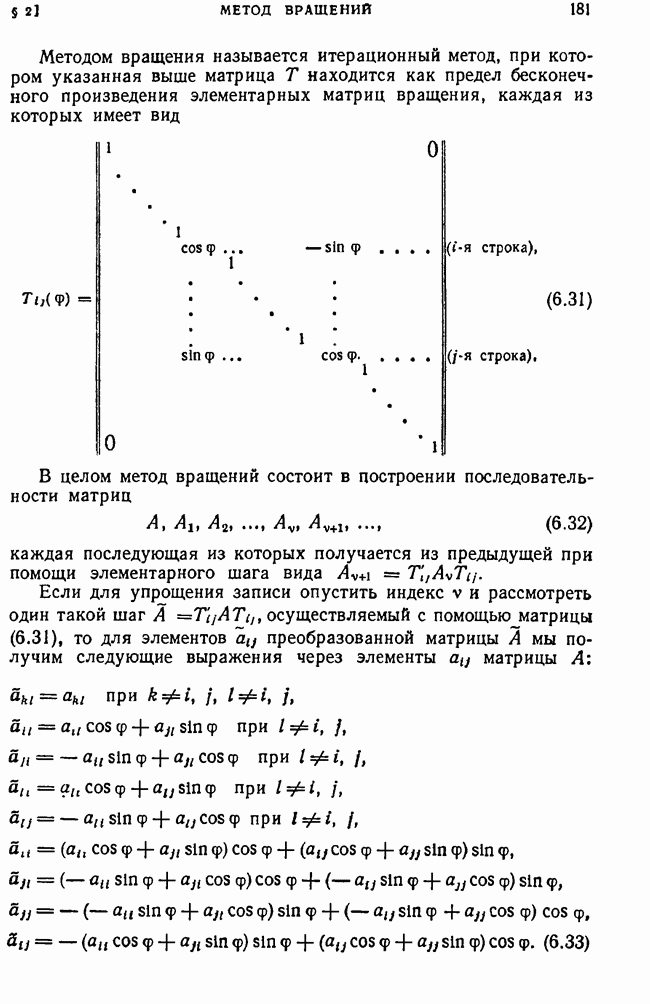
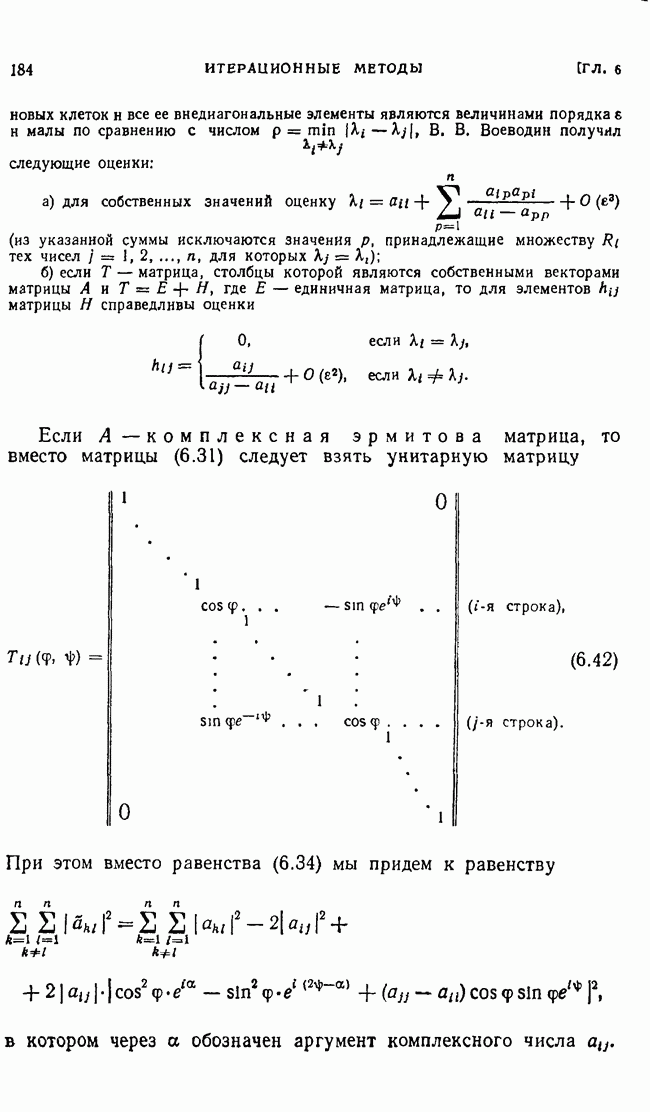
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Метод регуляризации для отыскания нормального решения линейной системы
Снова возвратимся к рассмотрению общей линейной системы  уравнений с
уравнений с  неизвестными вида (3.1). Эту систему кратко запишем в матричной форме
неизвестными вида (3.1). Эту систему кратко запишем в матричной форме

Напомним, что в этой записи символ А обозначает матрицу  , а символы X и В обозначают столбцы (или векторы) вида
, а символы X и В обозначают столбцы (или векторы) вида

первый из которых подлежит определению, а второй — задан.
Будем рассматривать случай, когда значения элементов матрицы А и столбца свободных членов В заданы нам лишь приближенно. Тогда естественно говорить лишь о приближенных
значениях искомого столбца X. Изложенные в предыдущей главе и основанные на формулах Крамера алгоритмы вычисления столбца решений X в этом случае могут приводить к большим погрешностям и теряют практический смысл
В этом параграфе мы изложим принадлежащий А. Н. Тихонову алгоритм, позволяющий находить так называемое нормальное (т. е. наиболее близкое к началу координат) решение X с точностью, соответствующей точности задания элементов матрицы А и столбца В.
Введем в рассмотрение так называемые сферические нормы столбцов В и X и матрицы А, положив их равными

Заметим, что нормы столбцов В и X определяются как обычные нормы векторов — элементов пространств  и соответственно
и соответственно  Норма матрицы А согласована с нормой n-мерного столбца X в том смысле, что норма
Норма матрицы А согласована с нормой n-мерного столбца X в том смысле, что норма  -мерного столбца
-мерного столбца  равного произведению матрицы А на столбец X, удовлетворяет условию
равного произведению матрицы А на столбец X, удовлетворяет условию

Будем считать, что вместо точных значений элементов матрицы  и столбца правых частей
и столбца правых частей  нам заданы приближенные значения
нам заданы приближенные значения  .
.
Матрицу А (столбец В) будем называть  риближением матрицы А (столбца В), если справедливо неравенство
риближением матрицы А (столбца В), если справедливо неравенство

Назовем нормальным решением совместной системы (4.26) то ее решение  норма
норма  которого является наименьшей среди норм
которого является наименьшей среди норм  всех решений X этой системы. Заметим, что у всякой совместной системы (4.26) (в том числе и у неопределенной) существует единственное нормальное решение. Введем в рассмотрение следующую функцию
всех решений X этой системы. Заметим, что у всякой совместной системы (4.26) (в том числе и у неопределенной) существует единственное нормальное решение. Введем в рассмотрение следующую функцию  переменных
переменных  или одного столбца
или одного столбца 

зависящую как от параметров от элементов матрицы А и столбца В, а также зависящую от некоторого числового параметра а. В подробной записи эта функция выглядит так:

Фактически  является функцией от элементов X евклидова пространства n-мерных столбцов
является функцией от элементов X евклидова пространства n-мерных столбцов  Такого рода функцию, аргументом которой служат элементы некоторого линейного пространства, принято называть функционало
Такого рода функцию, аргументом которой служат элементы некоторого линейного пространства, принято называть функционало 
Легко убедиться в том, что при любом фиксированном  неотрицательный функционал (4.30) достигает своего минимального (во всем пространстве
неотрицательный функционал (4.30) достигает своего минимального (во всем пространстве  значения в единственной точке
значения в единственной точке  пространства
пространства 
В самом деле, дважды дифференцируя функцию (4.30), получим  где
где  о при
о при 
Следовательно, второй дифференциал функции  имеет вид
имеет вид

Из этого равенства вытекает оценка  означающая, что функция
означающая, что функция  является с
является с  о выпуклой вниз. Кроме того,
о выпуклой вниз. Кроме того,  Отсюда очевидным образом следует, что
Отсюда очевидным образом следует, что  имеет и притом единственную точку минимума
имеет и притом единственную точку минимума 
Методы отыскания минимальных значений функционалов вида (4.30) хорошо разработаны.
Докажем следующую фундаментальную теорему, сводящую вопрос о приближенном отыскании нормального решения системы 4.26) к отысканию того элемента  на котором достигает своего минимального значения функционал (4.30).
на котором достигает своего минимального значения функционал (4.30).
Теорема А. Н. Тихонова. Пусть матрица А и столбец В удовлетворяют условиям, обеспечивающим совместность системы (4.26),  — нормальное решение этой системы, А —
— нормальное решение этой системы, А —  -приближение матрицы
-приближение матрицы  -приближение столбца
-приближение столбца  — какие-либо возрастающие функции
— какие-либо возрастающие функции  стремящиеся к нулю при
стремящиеся к нулю при  и такие, что
и такие, что  Тогда для любого
Тогда для любого  найдется положительное число
найдется положительное число  такое, что при любом
такое, что при любом  и при любом а, удовлетворяющем условию
и при любом а, удовлетворяющем условию

элемент  доставляющий минимум функционалу (4.30), удовлетворяет неравенству
доставляющий минимум функционалу (4.30), удовлетворяет неравенству

Доказательство. Рассмотрим в линейном пространстве  подмножество
подмножество  всех элементов
всех элементов  представимых в виде
представимых в виде  где
где  — произвольный элемент
— произвольный элемент
пространства  Совершенно очевидно, что подмножество
Совершенно очевидно, что подмножество  представляет собой линейное пространство и поэтому является подпространством Ет. Обозначим через
представляет собой линейное пространство и поэтому является подпространством Ет. Обозначим через  ортогональное дополнение
ортогональное дополнение  всего
всего  и разложим
и разложим  в прямую сумму подпространств
в прямую сумму подпространств  . Пусть В а обозначает проекцию столбца В на подпространство
. Пусть В а обозначает проекцию столбца В на подпространство  так что
так что  где
где  — элемент
— элемент  Тогда, поскольку для любого элемента X пространства
Тогда, поскольку для любого элемента X пространства  столбец
столбец  является элементом
является элементом  мы получим следующее разложение:
мы получим следующее разложение:

в котором элементы  и
и  ортогональны друг другу и принадлежат соответственно и
ортогональны друг другу и принадлежат соответственно и 
Пользуясь теоремой Пифагора (см. п. 2 § 1), мы получим (для любого элемента X пространства 

Из (4.33) следует, в частности, неравенство

также справедливое для любого элемента X пространства  Из (4.33) и (4.30) мы получим, что для любого X из
Из (4.33) и (4.30) мы получим, что для любого X из 

т. е. функционалы, стоящие в левой и в правой частях (4.35), имеют общий элемент  доставляющий им минимум.
доставляющий им минимум.
Установим теперь для любого а, удовлетворяющего условиям (4.31), следующее неравенство

в котором через С обозначена величина  — нормальное решение системы (4.26).
— нормальное решение системы (4.26).
Так как столбец  доставляет минимум функционалу, стоящему в правой части (4.35), то
доставляет минимум функционалу, стоящему в правой части (4.35), то

Пользуясь соотношением  и неравенством треугольника, получим
и неравенством треугольника, получим  . В правой части последнего неравенства воспользуемся соотношениями (4.28) и (4.29), а также неравенством (4.34), взятым при
. В правой части последнего неравенства воспользуемся соотношениями (4.28) и (4.29), а также неравенством (4.34), взятым при  Получим
Получим

Еще раз учитывая, что  и снова пользуясь неравенством треугольника и соотношениями (4.28) и (4.29), получим, что
и снова пользуясь неравенством треугольника и соотношениями (4.28) и (4.29), получим, что

Из (4.38) и (4.39) следует, что

где 
Для завершения доказательства оценки (4.36) остается подставить (4.40) в (4.37) и воспользоваться неравенством (4.31).
Поскольку из определения функционала  сразу вытекает, что
сразу вытекает, что  , Вто из доказанного нами неравенства (4.36) вытекает также следующее неравенство:
, Вто из доказанного нами неравенства (4.36) вытекает также следующее неравенство:

в котором  при
при  . Из (4.41) вытекает, что при всех достаточно малых
. Из (4.41) вытекает, что при всех достаточно малых  множество
множество  точек
точек  пространства
пространства  является ограниченным.
является ограниченным.
Теперь уже нетрудно доказать теорему от противного. Предположим, что для некоторого  существует последовательность
существует последовательность  и отвечающая ей последовательность
и отвечающая ей последовательность  чисел
чисел  удовлетворяющих условию
удовлетворяющих условию

такая, что для всех номеров 

Так как множество  ограничено, то в силу теоремы Больцано—Вейерштрасса из последовательности
ограничено, то в силу теоремы Больцано—Вейерштрасса из последовательности  можно выделить сходящуюся подпоследовательность. Чтобы не менять обозначений, будем считать, что вся последовательность
можно выделить сходящуюся подпоследовательность. Чтобы не менять обозначений, будем считать, что вся последовательность  сходится к некоторому столбцу
сходится к некоторому столбцу  то есть
то есть  при
при 
Убедимся в том, что

В самом деле, пользуясь неравенством треугольника, оценками (4.28), (4.29), (4.36) и (4.40) и соотношением (4.31, получим

Из неравенства (4.43) вытекает, что  т. е. предельный элемент
т. е. предельный элемент  является решением системы (4.26), удовлетворяющим в силу соотношения (4.41) неравенству
является решением системы (4.26), удовлетворяющим в силу соотношения (4.41) неравенству  Так как по определению для нормального решения
Так как по определению для нормального решения  справедливо обратное неравенство
справедливо обратное неравенство  а это противоречит неравенству (4.42), справедливому для любого номера
а это противоречит неравенству (4.42), справедливому для любого номера 
Полученное противоречие завершает доказательство теоремы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- 1. Понятие матрицы.
- 2. Основные операции над матрицами и их свойства.
- 3. Блочные матрицы.
- § 2. Определители
- 2. Выражение определителя непосредственно через его элементы.
- 3. Теорема Лапласа.
- 4. Свойства определителей.
- 5. Примеры вычисления определителей.
- 6. Определитель суммы и произведения матриц.
- 7. Понятие обратной матрицы.
- § 3. Теорема о базисном миноре матрицы
- 1. Понятие линейной зависимости строк.
- 2. Теорема о базисном мнноре.
- 3. Необходимое и достаточное условие равенства нулю определителя.
- ГЛАВА 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- § 1. Понятие линейного пространства
- 2. Некоторые свойства произвольных линейных пространств.
- § 2. Базис и размерность линейного пространства
- 1. Понятие линейной зависимости элементов линейного пространства.
- 2. Базис и координаты.
- 3. Размерность линейного пространства.
- 4. Понятие изоморфизма линейных пространств.
- § 3. Подпространства линейных пространств
- 1. Понятие подпространства и линейной оболочки.
- 2. Новое определение ранга матрицы.
- 3. Сумма и пересечение подпространств.
- 4. Разложение линейного пространства в прямую сумму подпространств.
- § 4. Преобразование координат при преобразовании базиса n-мерного линейного пространства
- 2. Связь между преобразованием базисов и преобразованием соответствующих координат.
- ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Условие совместности линейной системы
- 2. Нетривиальная совместность однородной системы.
- 3. Условие совместности общей линейной системы.
- § 2. Отыскание решений линейной системы
- 2. Отыскание всех решений общей линейной системы.
- 3. Свойства совокупности решений однородной системы.
- 4. Заключительные замечания о решении линейных систем.
- ГЛАВА 4. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- § 1. Вещественное евклидово пространство и его простейшие свойства
- 2. Простейшие свойства произвольного евклидова пространства.
- § 2. Ортонормированный базис конечномерного евклидова пространства
- 2. Свойства ортонормированного базиса.
- 3. Разложение n-мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения.
- 4. Изоморфизм n-мерных евклидовых пространств.
- § 3. Комплексное евклидово пространство
- 2. Неравенство Коши — Буняковского. Понятие нормы.
- 3. Ортонормированный базис и его свойства.
- § 4. Метод регуляризации для отыскания нормального решения линейной системы
- ГЛАВА 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. Понятие линейного оператора. Основные свойства
- 2. Действия над линейными операторами. Пространство линейных операторов.
- 3. Свойства множества L(V, V) линейных операторов.
- § 2. Матричная запись линейных операторов
- 2. Преобразование матрицы линейного оператора при переходе к новому базису.
- 3. Характеристический многочлен линейного оператора.
- § 3. Собственные значения и собственные векторы линейных операторов
- § 4. Линейные и полуторалинейные формы в евклидовом пространстве
- 2. Полуторалинейные формы в евклидовом пространстве. Специальное представление таких форм.
- § 5. Линейные самосопряженные операторы в евклидовом пространстве
- 2. Самосопряженные операторы. Основные свойства.
- 3. Норма линейного оператора.
- 4. Дальнейшие свойства самосопряженных операторов.
- 5. Спектральное разложение самосопряженных операторов. Теорема Гамильтона—Кэли.
- 6. Положительные операторы. Корни m-й степени из оператора.
- § 6. Приведение квадратичной формы к сумме квадратов
- § 7. Унитарные и нормальные операторы
- § 8. Канонический вид линейных операторов
- § 9. Линейные операторы в вещественном евклидовом пространстве
- 2. Ортогональные операторы.
- ГЛАВА 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ И ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
- § 1. Итерационные методы решения линейных систем
- 2. Общий неявный метод простой итерации.
- 3. Модифицированный метод простой итерации.
- 4. Метод Зейделя.
- 5. Метод верхней релаксации.
- 6. Случай несимметричной матрицы А.
- 7. Итерационный метод П. Л. Чебышева.
- § 2. Решение полной проблемы собственных значений методом вращений
- ГЛАВА 7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейные формы
- 2. Представление билинейной формы в конечномерном линейном пространстве.
- 3. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы.
- § 2. Квадратичные формы
- § 3. Приведение квадратичной формы к сумме квадратов
- 2. Метод Якоби.
- § 4. Закон инерции квадратичных форм. Классификация квадратичных форм
- 2. Классификация квадратичных форм.
- 3. Критерий Сильвестра знакоопределенности квадратичной формы.
- § 5. Полилинейные формы
- § 6. Билинейные и квадратичные формы в евклидовом пространстве
- 2. Приведение квадратичной формы к сумме квадратов в ортогональном базисе.
- 3. Одновременное приведение двух квадратичных форм к сумме квадратов в линейном пространстве.
- 4. Экстремальные свойства квадратичной формы.
- § 7. Гиперповерхности второго порядка
- 2. Параллельные переносы в евклидовом пространстве. Преобразования ортонормированных базисов в ортонормированные.
- 3. Преобразование общего уравнения гиперповерхности второго порядка при параллельном переносе.
- 4. Преобразование общего уравнения гиперповерхности второго порядка при переходе от ортонормированного базиса к ортонормированиому.
- 5. Инварианты общего уравнения гиперповерхности второго порядка.
- 6. Центр гиперповерхности второго порядка.
- 7. Стандартное упрощение любого уравнения гиперповерхности второго порядка путем преобразования ортонормированного базиса.
- 8. Упрощение уравнения центральной гиперповерхности второго порядка. Классификация центральных гиперповерхностей.
- 9. Упрощение уравнения нецентральной гиперповерхности второго порядка. Классификация нецентральных гиперповерхностей.
- ГЛАВА 8. ТЕНЗОРЫ
- § 1. Преобразование базисов и координат
- 2. Взаимные базисы. Ковариантные и контравариантные координаты векторов.
- 3. Преобразования базиса и координат.
- § 2. Понятие тензора. Основные операции над тензорами
- 2. Примеры тензоров.
- 3. Основные операции над тензорами.
- § 3. Метрический тензор. Основные операции векторной алгебры в тензорных обозначениях
- 2. Операция поднятия и опускания индексов с помощью метрического тензора.
- 3. Ортонормированные базисы в E^n.
- 4. Дискриминантный тензор.
- 5. Ориентированный объем.
- 6. Векторное произведение.
- 7. Двойное векторное произведение.
- § 4. Метрический тензор псевдоевклидова пространства
- 2. Галилеевы координаты. Преобразования Лоренца.
- 3. Преобразования Лоренца пространства
- § 5. Тензор момента инерции
- ГЛАВА 9. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- § 1. Понятие группы. Основные свойства групп
- 2. Понятие группы. Некоторые свойства групп.
- 3. Изоморфизм групп. Подгруппы.
- 4. Смежные классы. Нормальные делители.
- 5. Гомоморфизмы. Фактор-группы.
- § 2. Группы преобразований
- 2. Группа линейных преобразований.
- 3. Сходимость элементов в группе GL(n). Подгруппы группы GL(n).
- 4. Группа ортогональных преобразований.
- 5. Некоторые дискретные и конечные подгруппы ортогональной группы.
- 6. Группа Лоренца.
- 7. Унитарные группы.
- § 3. Представления групп
- 2. Матрицы линейных представлений. Эквивалентные представления.
- 3. Приводимые и неприводимые представления.
- 4. Характеры.
- 5. Примеры представлений групп.