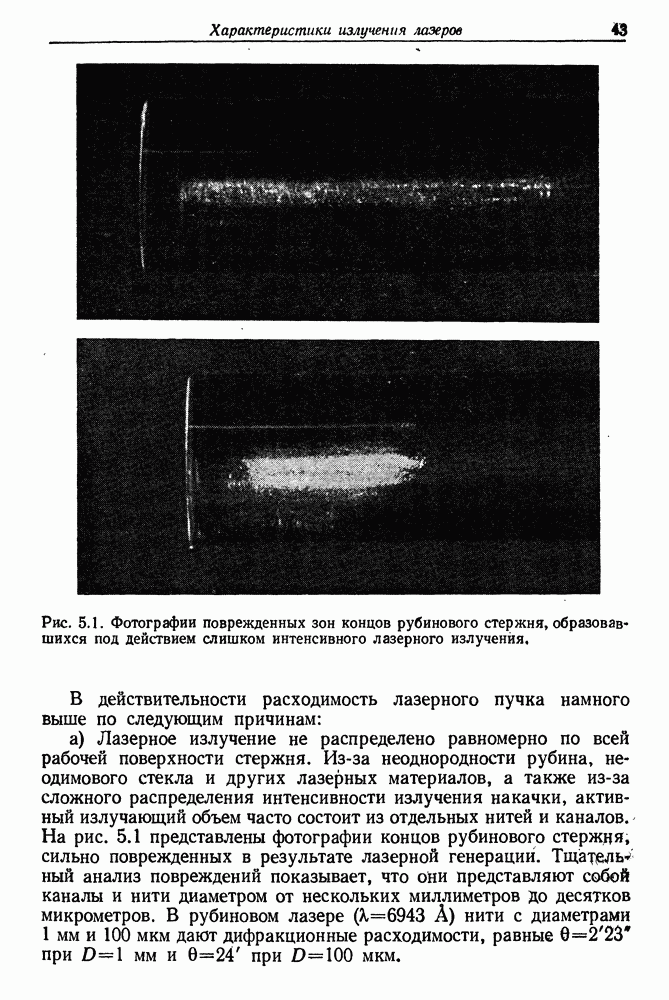
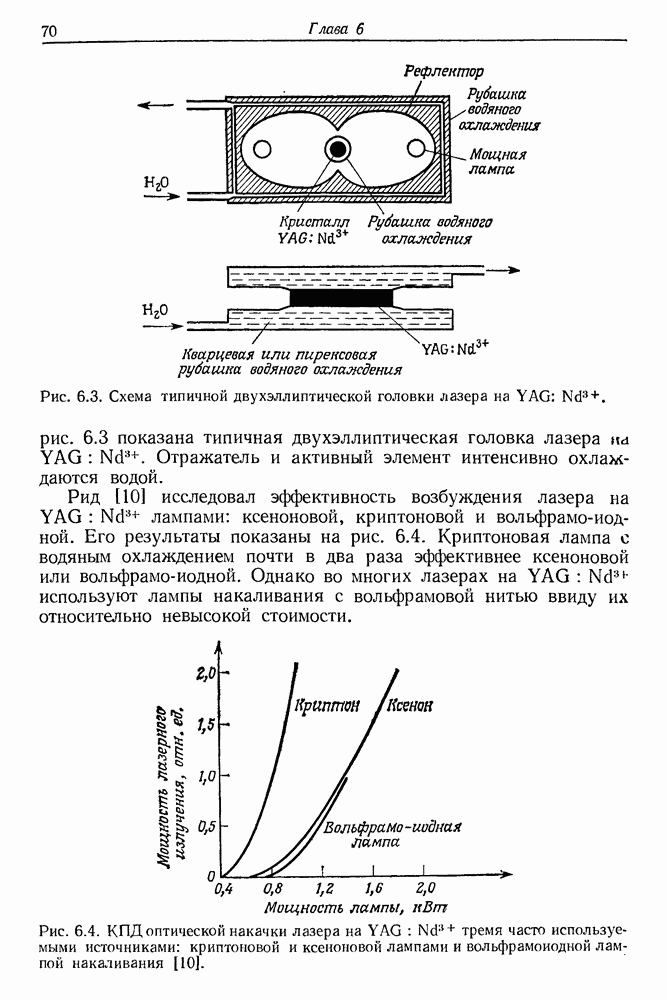
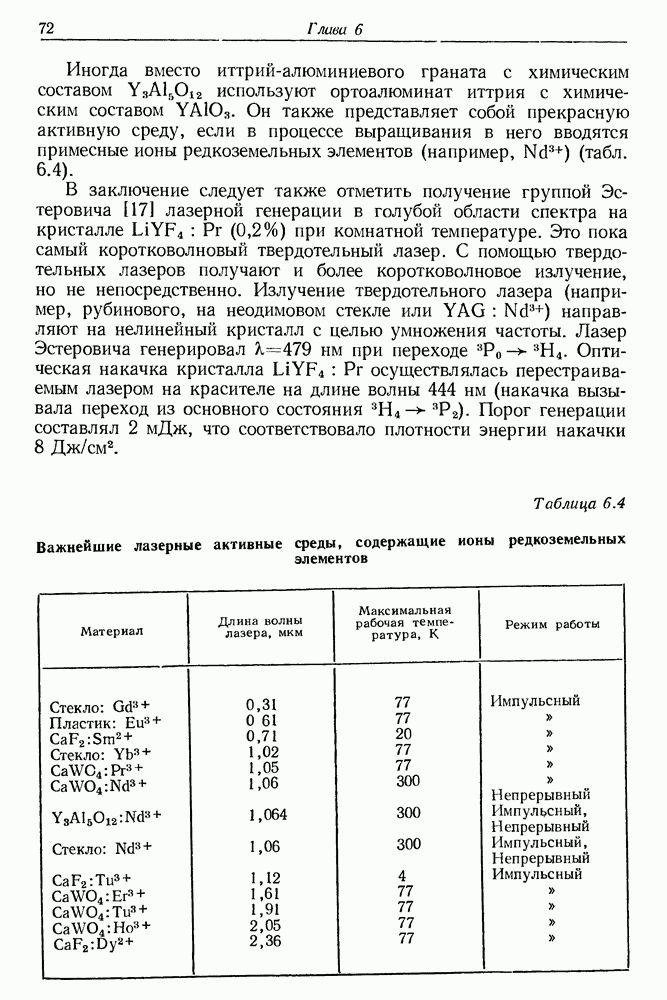
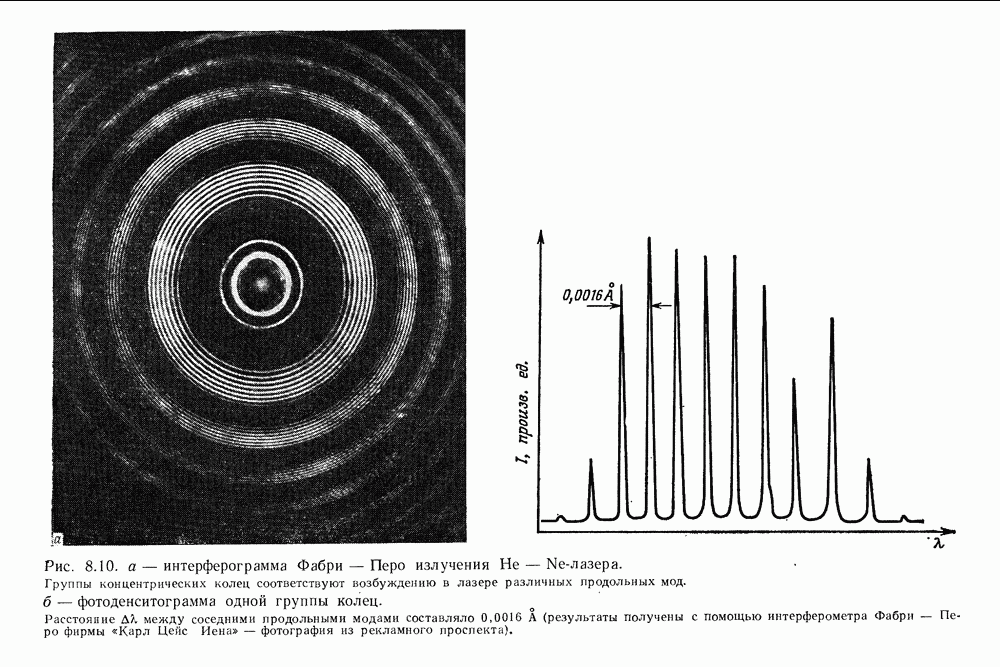
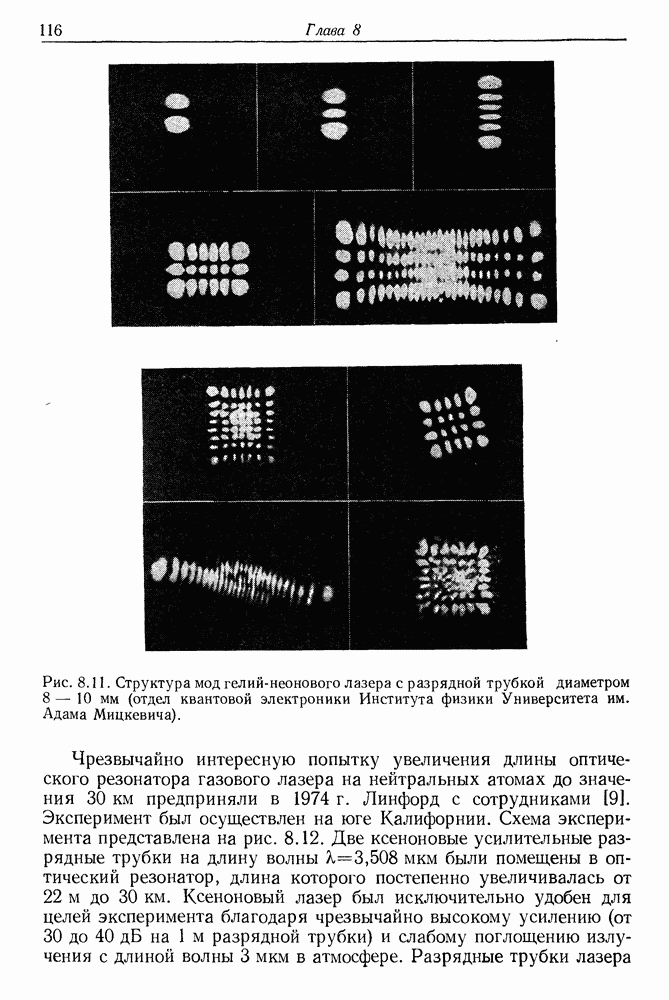
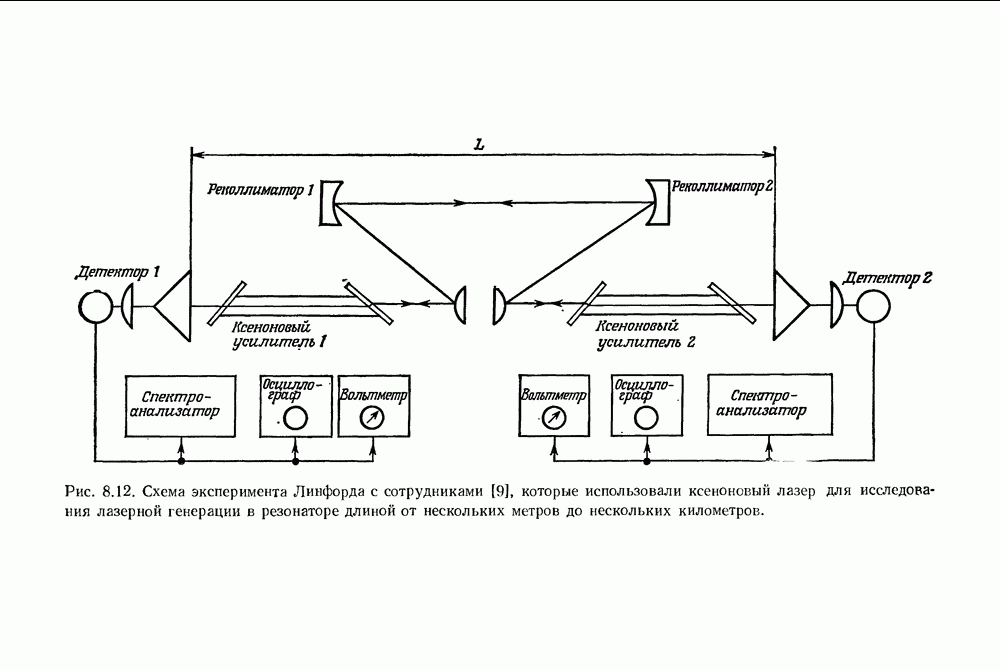
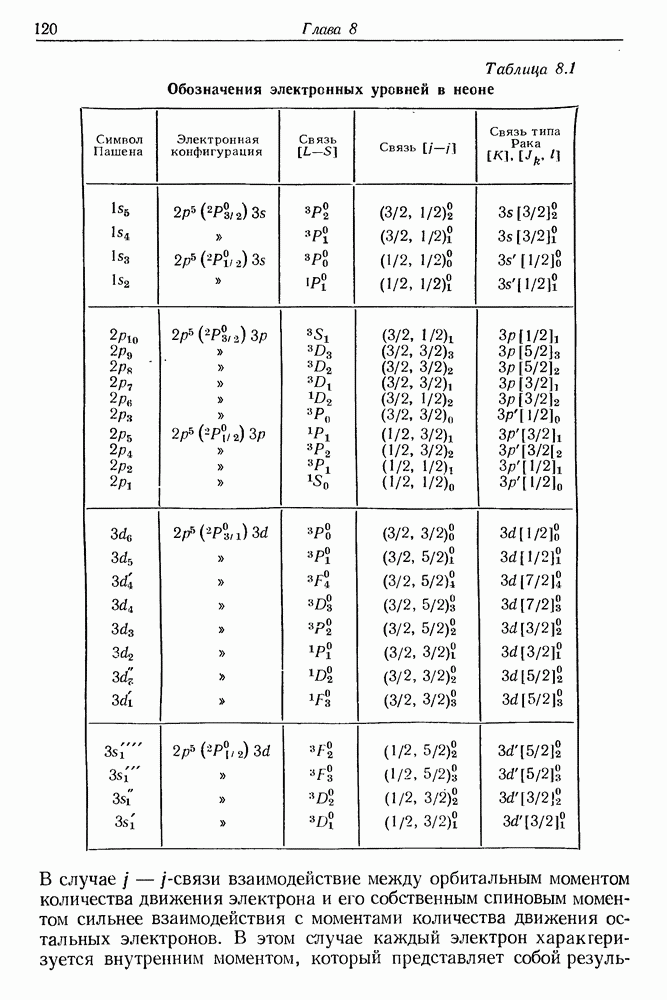
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
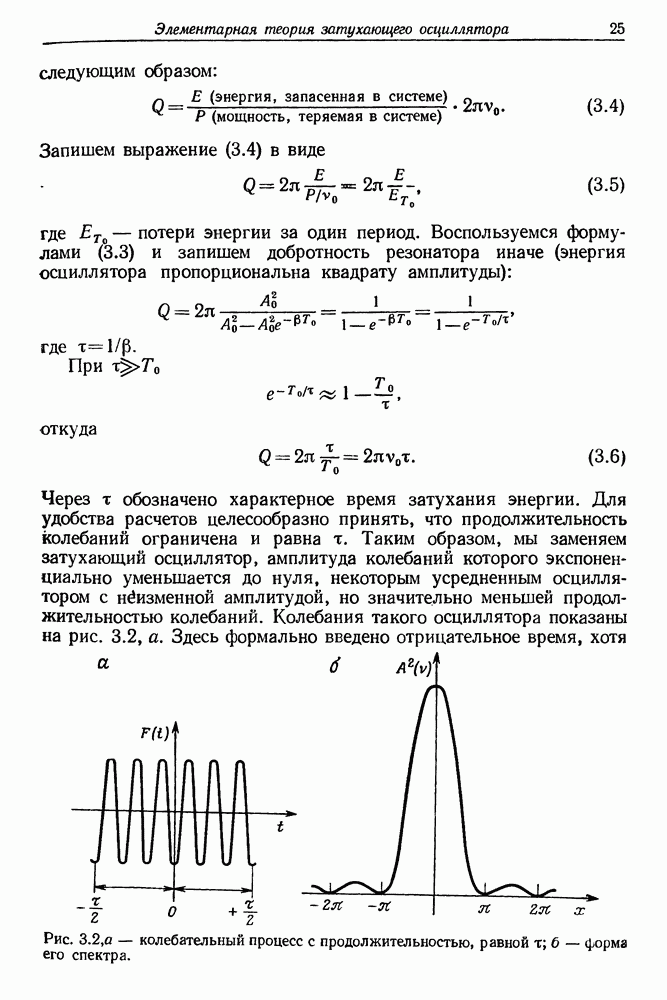
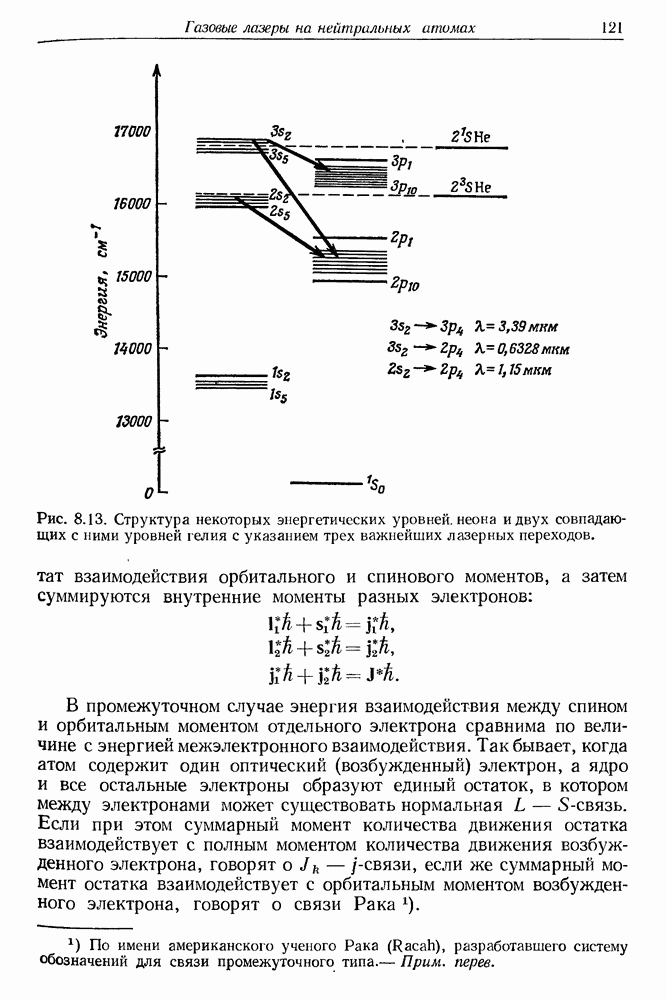
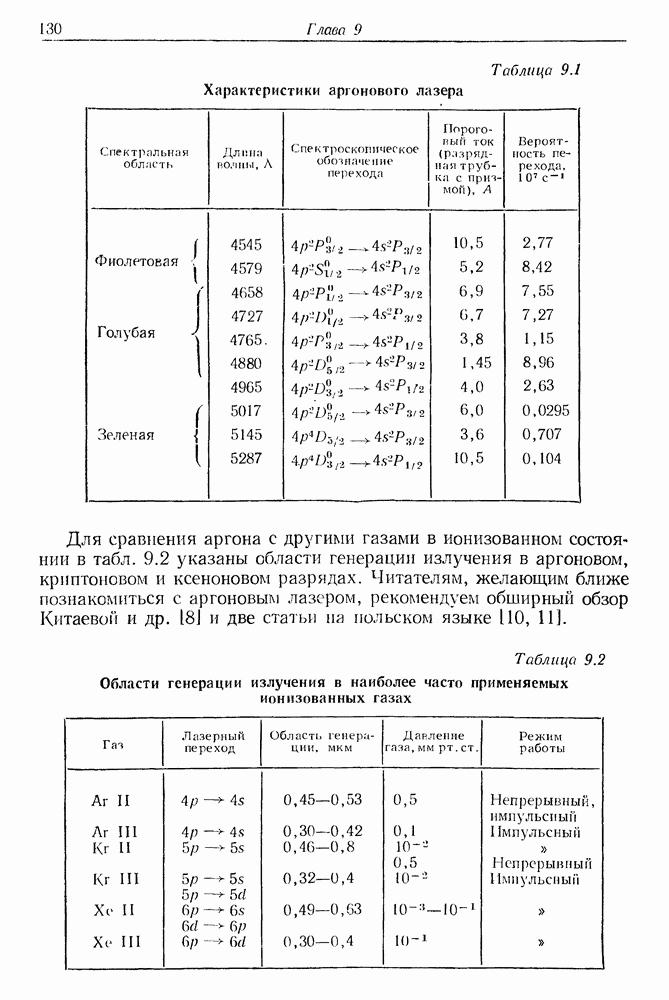
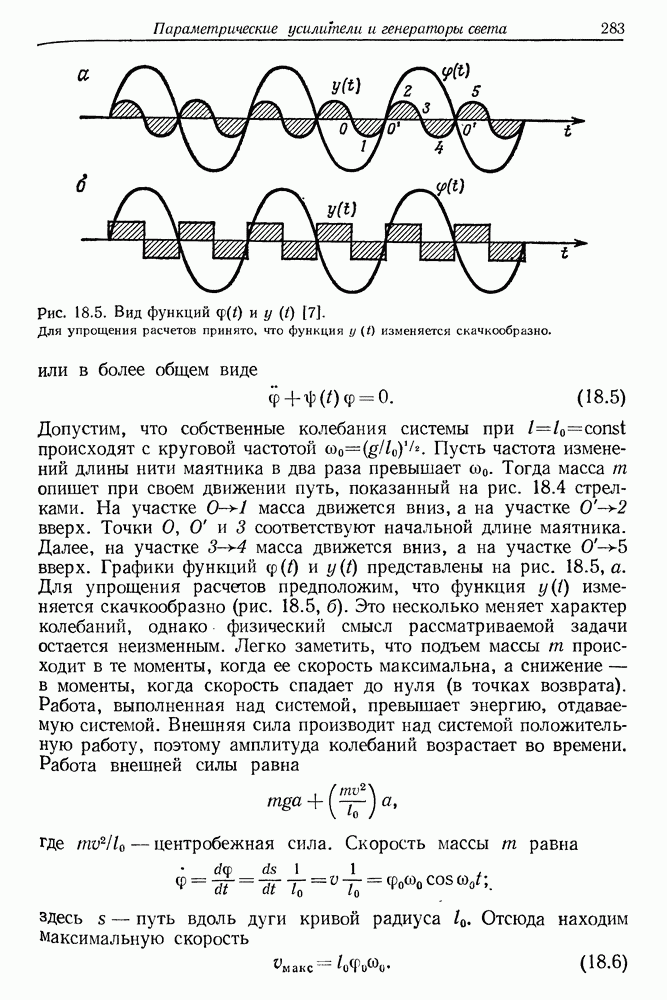
§ 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
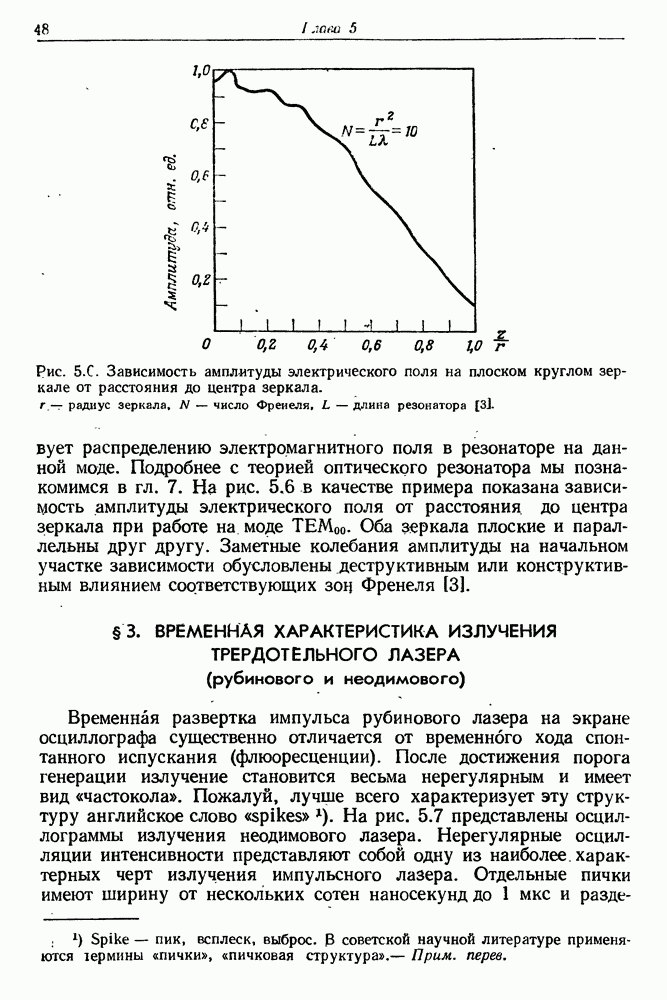
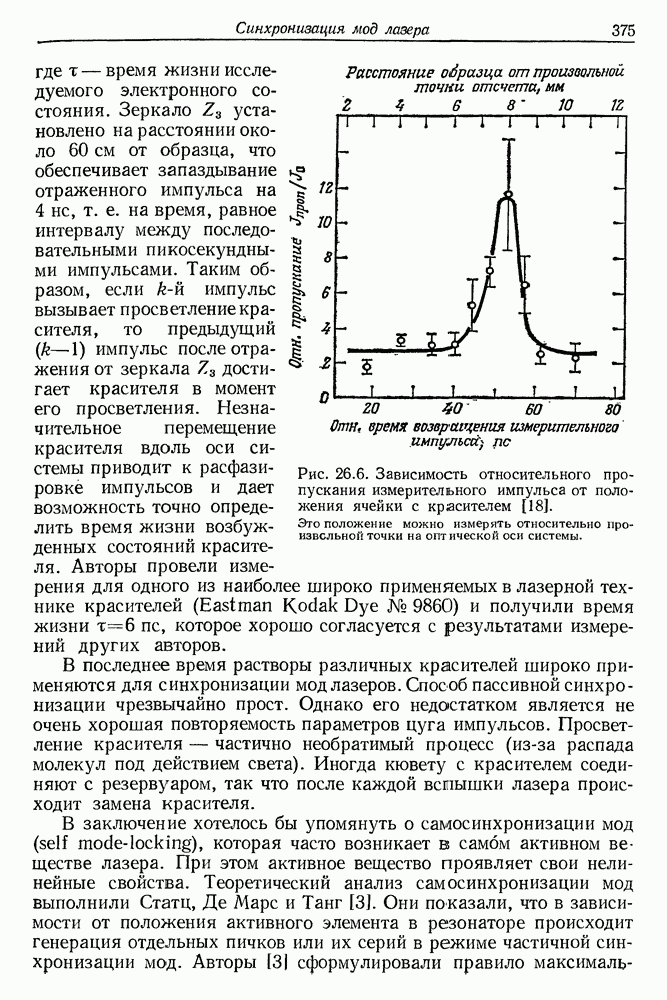
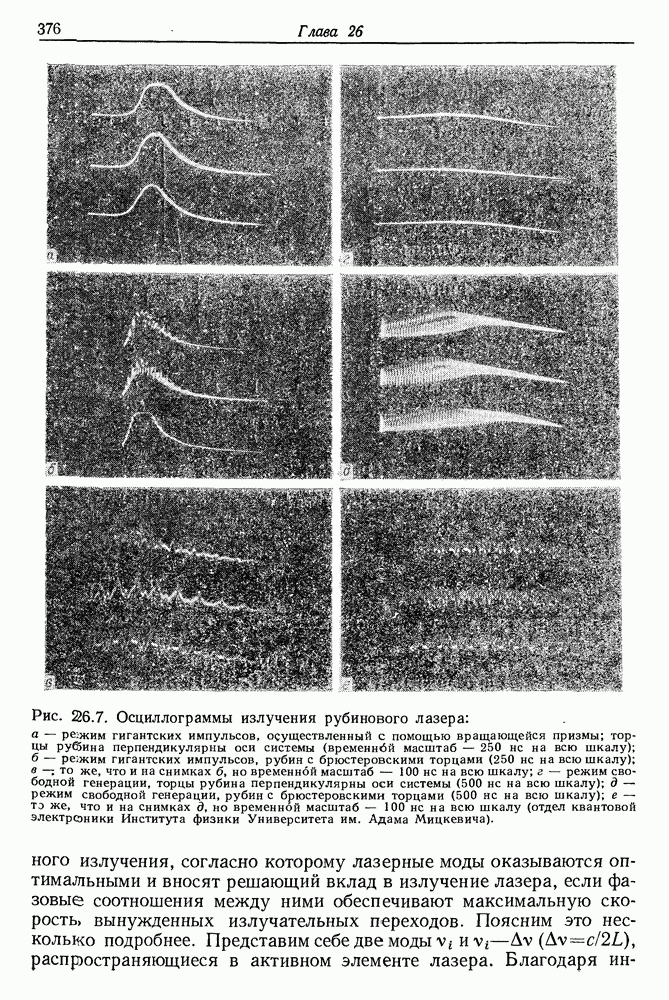
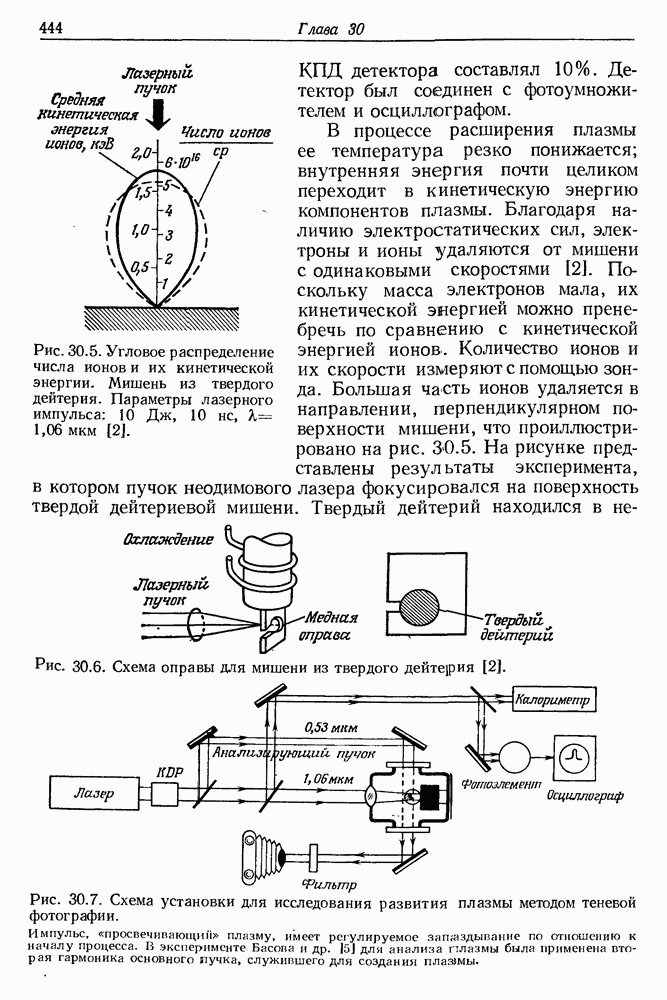
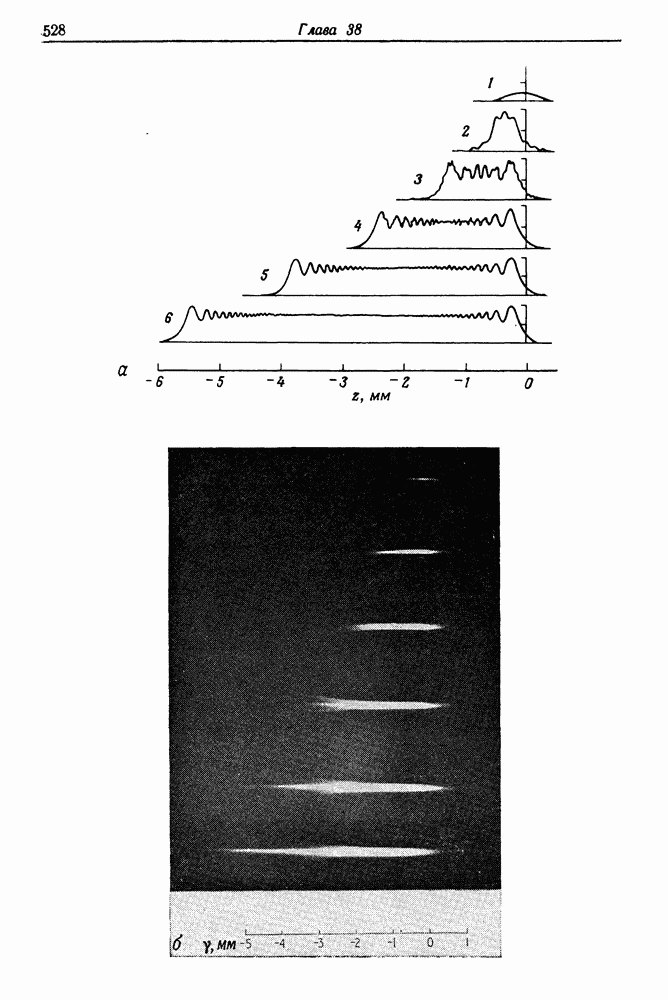
Временная развертка импульса рубинового лазера на экране осциллографа существенно отличается от временного хода спонтанного испускания (флюоресценции). После достижения порога генерации излучение становится весьма нерегулярным и имеет вид «частокола». Пожалуй, лучше всего характеризует эту структуру английское слово «spikes». На рис. 5.7 представлены осциллограммы излучения неодимового лазера. Нерегулярные осцилляции интенсивности представляют собой одну из наиболее, характерных черт излучения импульсного лазера. Отдельные пички имеют ширину от нескольких сотен наносекунд до  и
и
Рис. 5.7. (см. скан) Излучение импульсного лазера, работающего в условиях свободной генерации. На снимках  скорость временнбй развертки осциллографа составляла 50 мкс/см. Резонатор лазера состоял из двух плоских зеркал. Вследствие отрицательной полярности диода детектора излучения пички интенсивности направлены вниз. Значения энергии накачки;
скорость временнбй развертки осциллографа составляла 50 мкс/см. Резонатор лазера состоял из двух плоских зеркал. Вследствие отрицательной полярности диода детектора излучения пички интенсивности направлены вниз. Значения энергии накачки;  (пороговое значение). На снимке
(пороговое значение). На снимке  показан небольшой фрагмент лазерного импульса при скорости развертки 1 мкс/см.
показан небольшой фрагмент лазерного импульса при скорости развертки 1 мкс/см.
разделены временными интервалами порядка нескольких микросекунд. Общая продолжительность всех осцилляций считается длительностью лазерной генерации. В типичном лазере она составляет от 100 до 1000 мкс. Длительность лазерной генерации зависит прежде всего от параметров импульсной лампы, которая служит для возбуждения активной среды. В специальных системах питания, где используется линейная импульсная лампа высокой мощности, смонтированная непосредственно на электродах высоковольтного конденсатора, длительность вспышки уменьшается до 
Однако обычно используют не столь быстродействующие схемы питания; батарея конденсаторов емкостью в несколько сотен микрофарад заряжается до напряжения около  а затем разряжается через линейную или спиральную импульсную лампу. Для предохранения лампы последовательно с ней обычно включают катушку без сердечника с индуктивностью порядка нескольких сотен микрогенри. Длительность вспышки лампы составляет несколько сотен микросекунд для линейной лампы и может возрастать до нескольких миллисекунд в случае использования спиральной лампы. Таким образом, длительность лазерного импульса можно изменять в широких пределах в зависимости от длительности и интенсивности вспышки лампы накачки.
а затем разряжается через линейную или спиральную импульсную лампу. Для предохранения лампы последовательно с ней обычно включают катушку без сердечника с индуктивностью порядка нескольких сотен микрогенри. Длительность вспышки лампы составляет несколько сотен микросекунд для линейной лампы и может возрастать до нескольких миллисекунд в случае использования спиральной лампы. Таким образом, длительность лазерного импульса можно изменять в широких пределах в зависимости от длительности и интенсивности вспышки лампы накачки.
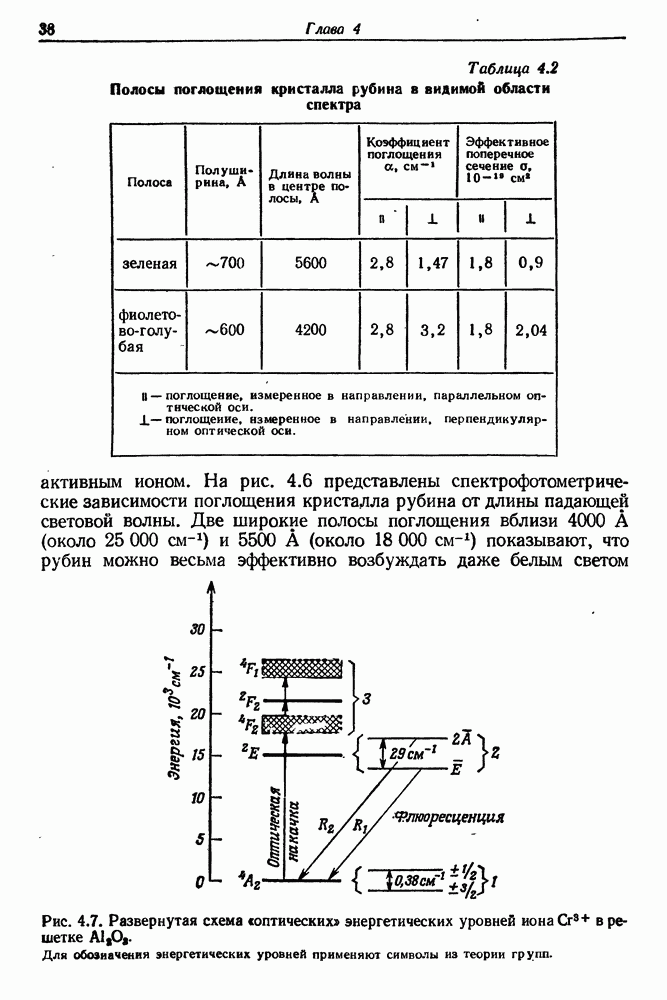
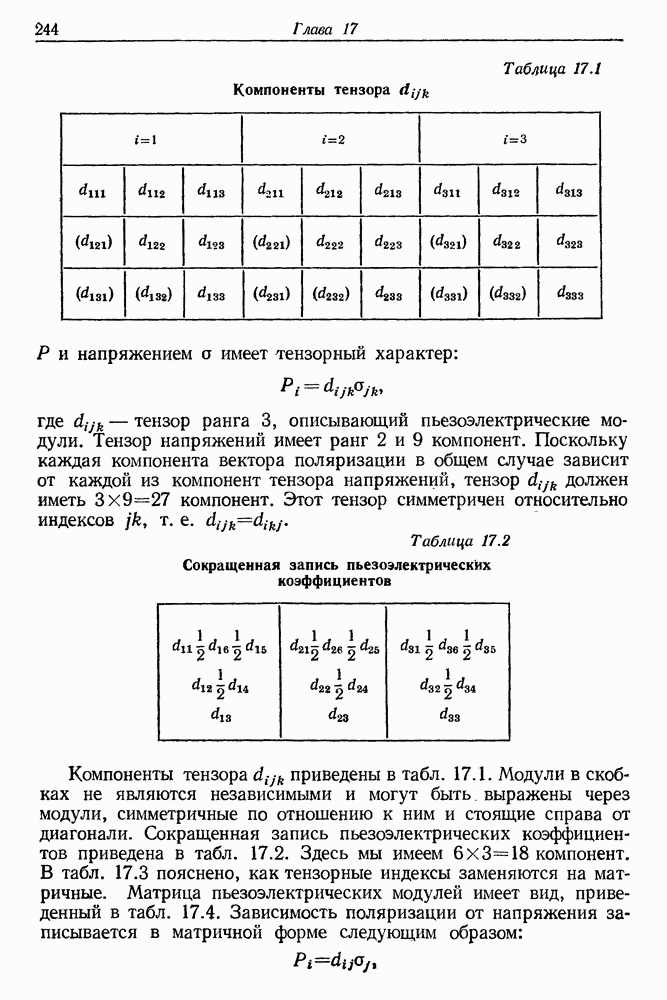
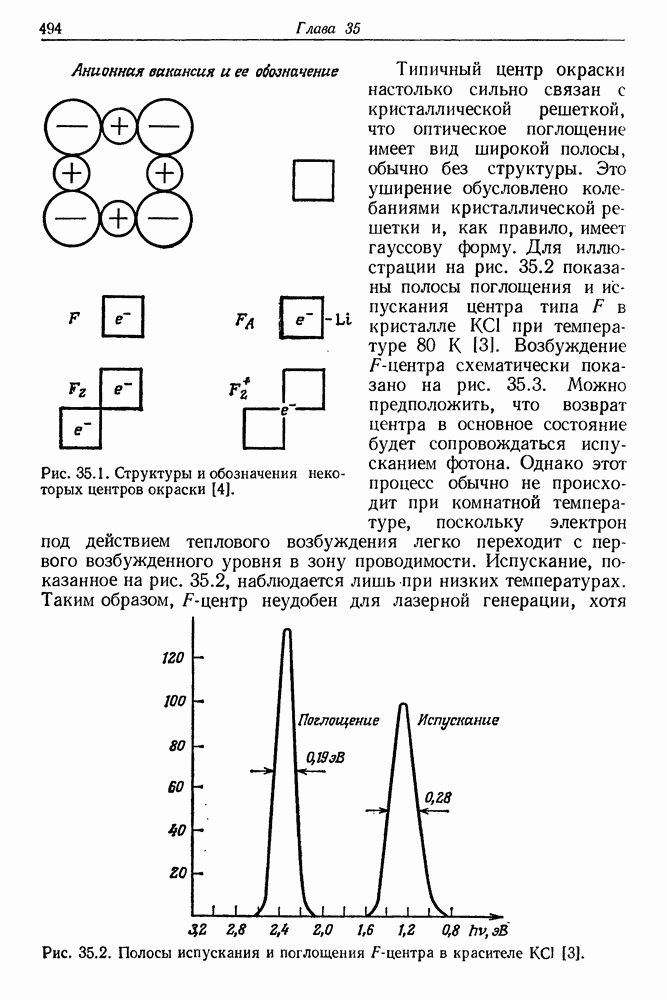
На рис. 4.2 показана схема энергетических уровней, используемых при оптической накачке рубина. Переход типа  является безызлучательным; разница энергий
является безызлучательным; разница энергий  передается кристаллической решетке и приводит к разогреву всей активной среды. Кроме того, тепло выделяется в кристалле также в результате поглощения энергии лампы накачки в ультрафиолетовой и инфракрасной областях спектра. Это приводит к повышению температуры кристалла, а следовательно, и к изменениям его плотности и показателя преломления. Указанные изменения являются источником модовой нестабильности. Предположим, что в определенных условиях произошло возбуждение моды к, для которой выполняется соотношение
передается кристаллической решетке и приводит к разогреву всей активной среды. Кроме того, тепло выделяется в кристалле также в результате поглощения энергии лампы накачки в ультрафиолетовой и инфракрасной областях спектра. Это приводит к повышению температуры кристалла, а следовательно, и к изменениям его плотности и показателя преломления. Указанные изменения являются источником модовой нестабильности. Предположим, что в определенных условиях произошло возбуждение моды к, для которой выполняется соотношение

где — длина световой волны в вакууме,  — показатель преломления. Для соседней моды
— показатель преломления. Для соседней моды  получаем
получаем

Оказывается, что в типичных условиях оптической накачки в кристалле выделяется достаточно тепла для того, чтобы в течение  длина кристалла увеличилась на
длина кристалла увеличилась на  Это приводит к непрерывному переходу моды к в моду
Это приводит к непрерывному переходу моды к в моду 
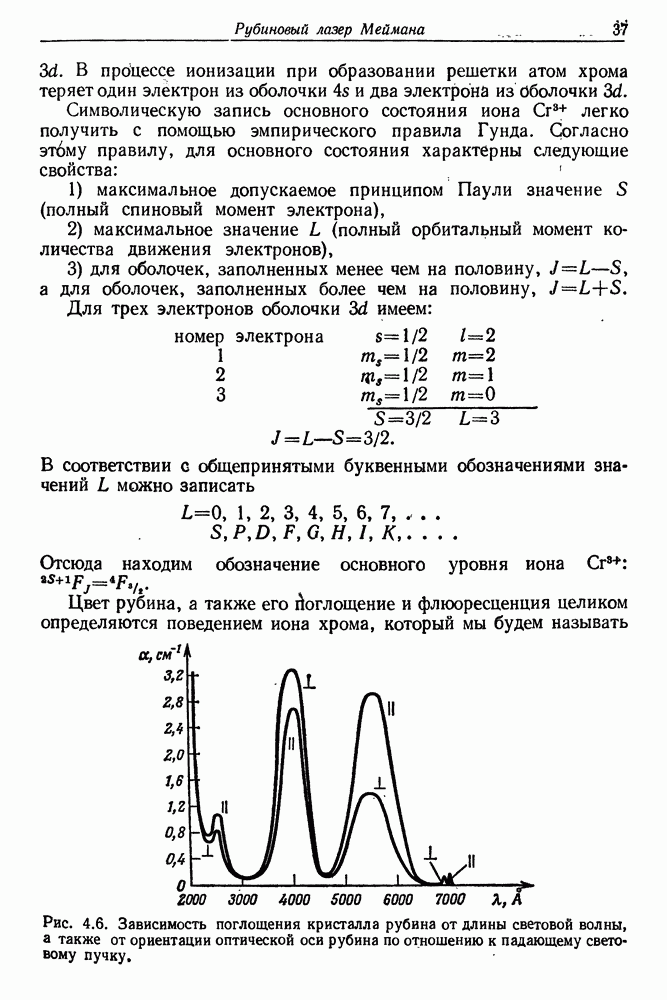
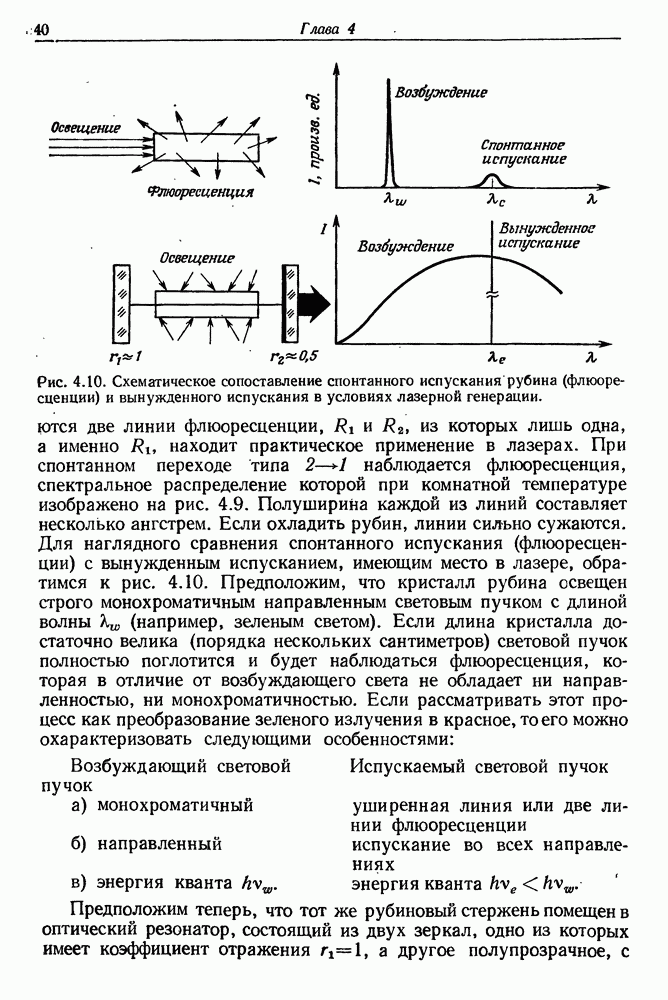
Другим источником нестабильной работы лазера является относительно сильная зависимость ширины и положения линий флюоресценции рубина от температуры. Например, линия  (см. рис. 4.9), максимум которой располагается на длине волны
(см. рис. 4.9), максимум которой располагается на длине волны  , а полуширина равна
, а полуширина равна  (при комнатной температуре), при охлаждении рубина до 77 К смещается в более коротковолновую область (максимум при
(при комнатной температуре), при охлаждении рубина до 77 К смещается в более коротковолновую область (максимум при  и сужается до
и сужается до  При комнатной температуре смещение максимума линии
При комнатной температуре смещение максимума линии  составляет 0,05 А на
составляет 0,05 А на  Этот «дрейф» линии флюоресценции приводит в типичных условиях оптической накачки к изменению номера
Этот «дрейф» линии флюоресценции приводит в типичных условиях оптической накачки к изменению номера

Рис. 5.8. Проф. Кончи Шимода из Токийского университета вставляет рубиновый стержень в головку лазера для исследования затухающих и незатухающих осцилляций излучения в зависимости от условий оптической накачки и типа оптического резонатора.
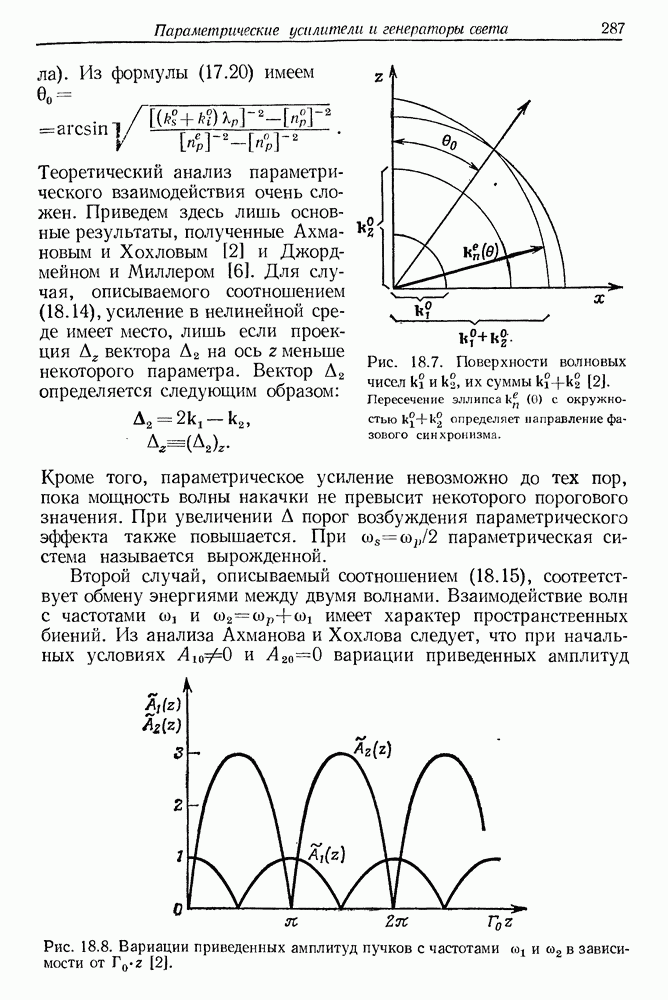
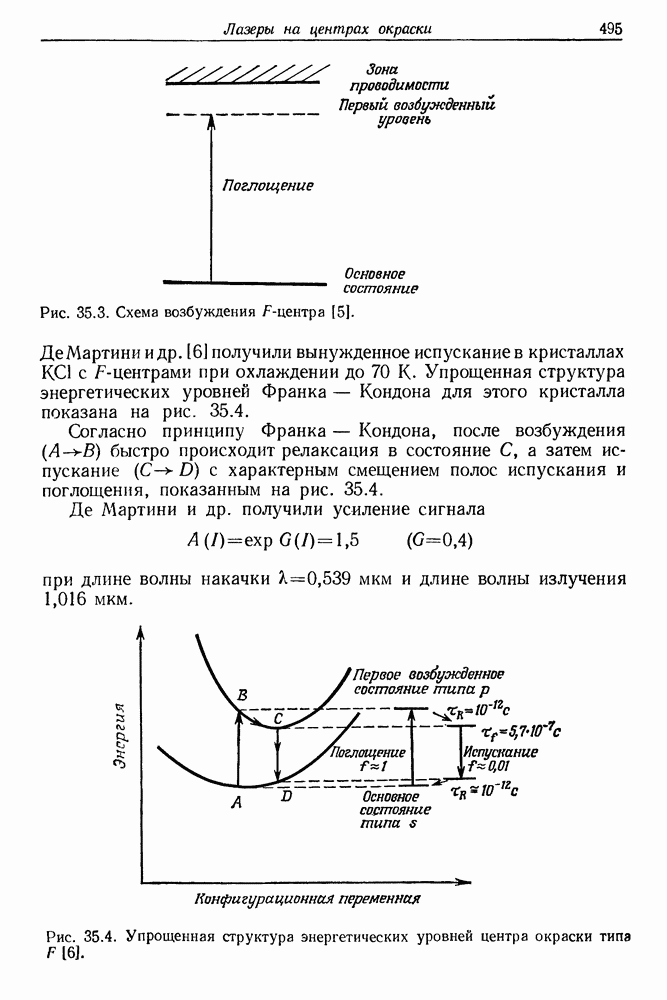
продольной моды на единицу за время около 10 мкс. Наружное водяное охлаждение, даже очень интенсивное, не может предотвратить этих явлений, поскольку тепло выделяется во всем объеме рубина. Термические эффекты могут быть источником модовой нестабильности, а значит, приводить к осцилляциям интенсивности излучения лазера. Однако эксперименты, по-видимому, не подтверждают тепловой природы осцилляций. Оказалось, что в некоторых условиях оптической накачки, и прежде всего в зависимости от типа оптического резонатора, осцилляции излучения становятся весьма регулярными и медленно затухают по мере увеличения длительности излучения. Явление осцилляций лазерного излучения исследовалось во множестве работ как экспериментальных, так и теоретических. Удивительно, что до сих пор мы не имеем ясного представления о причинах этого сложного явления. Следует упомянуть здесь о некоторых экспериментальных факторах. В 1962 г. Шимода (рис. 5.8) исследовал лазерную генерацию в рубиновых стержнях с плоскими или выпуклыми торцами. Выпуклые торцы образуют конфокальный резонатор. Лазерная генерация в рубине с конфокальными торцами в отличие от генерации в рубине с плоскими торцами была весьма регулярной и обнаруживала характерный спад в течение нескольких миллисекунд. Эти результаты были затем подтверждены многими авторами. Установлено, что регулярные осцилляции легче всего получить, если уровень возбуждения лишь немного превышает пороговый
В гл. 7 дан краткий очерк теории лазерных резонаторов. Из нее следует, что в конфокальном резонаторе возникает сильное вырождение мод. Считают, что оно является причиной регулярных осцилляций излучения лазера, работающего с таким резонатором. Осцилляции интенсивности вынужденного испускания обусловлены также характером процессов, происходящих в трех- или четырехуровневой квантовой системе. В процессе оптической накачки происходят вынужденные переходы типа 1-3 (см. рис. 4.2). Среднее время жизни ионов хрома в состоянии 3 очень мало. В результате спонтанных безызлучательных переходов типа 3-2 происходит временное накопление ионов в метастабильном состоянии 2. Лазерная генерация возникает после достижения инверсии населенностей уровней 1 и 2. Генерация сопровождается сильным опустошением уровня  число вынужденных переходов в любой момент времени пропорционально плотности потока квантов с энергией
число вынужденных переходов в любой момент времени пропорционально плотности потока квантов с энергией  Интенсивность излучения нарастает лавино-. образно, а оптическая накачка приблизительно постоянна во времени. Это приводит к уменьшению инверсии населенностей, а значит, и к спаду интенсивности излучения лазера. Затем в результате оптической накачки уровень возбуждения повышается и процесс повторяется сначала.
Интенсивность излучения нарастает лавино-. образно, а оптическая накачка приблизительно постоянна во времени. Это приводит к уменьшению инверсии населенностей, а значит, и к спаду интенсивности излучения лазера. Затем в результате оптической накачки уровень возбуждения повышается и процесс повторяется сначала.
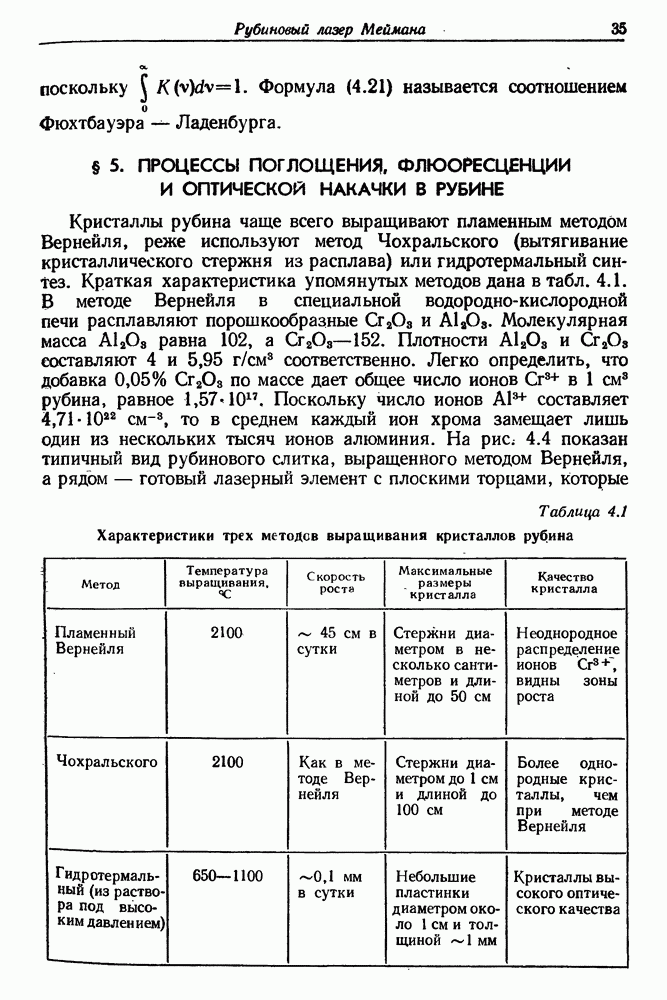
Относительно простой анализ этого процесса дали Ищенко и Климков [4]. Достаточно общая теория релаксационно-осцилляционных процессов разработана в 1960 г. Статцем и де Марсом [5]. Мы проведем упрощенный анализ трехуровневой системы, основанный на работе 14]. Обозначим вероятность перехода типа  за 1 с через
за 1 с через  Уровень 2 заселяется также в результате вынужденных переходов типа
Уровень 2 заселяется также в результате вынужденных переходов типа  , связанных с поглощением света «лазерной» частоты. Вероятность этого процесса за 1 с равна
, связанных с поглощением света «лазерной» частоты. Вероятность этого процесса за 1 с равна  Условие равновесия для уровня 2 приобретает вид
Условие равновесия для уровня 2 приобретает вид

а для уровня 1—

В последнем уравнении мы пренебрегли приростом населенности уровня  обусловленным переходами типа
обусловленным переходами типа  вероятность которых мала. Опустошение уровня 1 в результате оптической накачки выражено членом
вероятность которых мала. Опустошение уровня 1 в результате оптической накачки выражено членом  и — плотность лучистой энергии на частоте, соответствующей переходу
и — плотность лучистой энергии на частоте, соответствующей переходу  Вычитая второе уравнение из первого, получаем
Вычитая второе уравнение из первого, получаем

Обозначим

тогда

В этом выражении величина и непостоянна, поскольку значение энергии в системе заметно изменяется во времени. Прирост энергии в результате вынужденного испускания равен  а ее уменьшение за счет поглощения —
а ее уменьшение за счет поглощения —  Очевидно,
Очевидно,  Обозначим через
Обозначим через  потери энергии в единицу времени на единицу объема активной среды, находящейся в оптическом резонаторе. Тогда
потери энергии в единицу времени на единицу объема активной среды, находящейся в оптическом резонаторе. Тогда

Решение уравнений (5.3), (5.4) в аналитическом виде невозможно. Обычно приводят приближенное решение, которое представляет собой суперпозицию постоянной составляющей и значительно меньшей по величине переменной составляющей. Пусть

Учитывая только постоянные составляющие решений уравнений (5.3) и (5.4), получаем

откуда

Теперь учтем переменные составляющие:

Пренебрегая членом высшего порядка малости  эти уравнения можно переписать в виде
эти уравнения можно переписать в виде

Члены в квадратных скобках обращаются в нуль в соответствии с выражениями (5.5) для  Таким образом,
Таким образом,

Мы получили значительно более простую линейную систему дифференциальных уравнений, которая допускает аналитическое решение. Продифференцируем второе уравнение по времени и подставим полученное выражение для  в первое уравнение. Одновременно выделим из второго уравнения величину
в первое уравнение. Одновременно выделим из второго уравнения величину  и также подставим ее в первое уравнение. Это даст
и также подставим ее в первое уравнение. Это даст

Будем искать решение уравнения (5.7) в виде

Аналогичный вид будет иметь решение для  :
:

Подставляя, например, выражение для бы в уравнение (5.7), получим характеристическое уравнение, корни которого определяют поведение рассматриваемой системы (этот метод известен из теории колебательных систем):

Введем обозначение

Теперь

При  корни комплексные и решение уравнений (5.8), (5.9) имеет осциллирующий характер. С учетом выражений (5.5) получаем
корни комплексные и решение уравнений (5.8), (5.9) имеет осциллирующий характер. С учетом выражений (5.5) получаем

Параметр  описывает потери энергии в системе,
описывает потери энергии в системе,  характеризует скорость оптической накачки. Возрастание потерь в системе, а также уменьшение интенсивности оптической накачки приводит
характеризует скорость оптической накачки. Возрастание потерь в системе, а также уменьшение интенсивности оптической накачки приводит
к возникновению осцилляций лазерного излучения  Этот вывод в общих чертах согласуется с экспериментальными данными. При
Этот вывод в общих чертах согласуется с экспериментальными данными. При  можно пренебречь единицами в формуле (5.10):
можно пренебречь единицами в формуле (5.10):

Положив  получим
получим

Круговая частота осцилляций равна

Характерное время затухания осцилляций при получим, пренебрегая лишь единицей под знаком корня:

Подставляя значения и  в уравнение (5.8), получаем характерное время затухания:
в уравнение (5.8), получаем характерное время затухания:

откуда 

Проведенный анализ, несмотря на существенные упрощения, указывает на осциллирующий характер лазерного излучения. Эта теория, разумеется, не может объяснить нерегулярных пульсаций интенсивности, которые чаще всего наблюдаются в эксперименте. На практике оптическая накачка рубина неоднородна. Неоднородность эта обусловлена не столько характеристиками импульсной лампы, сколько формой активного элемента. Цилиндрический рубиновый (или неодимовый) стержень действует подобно линзе, создавая сложное распределение интенсивности излучения накачки внутри кристалла.
Суммируя все сказанное о временных характеристиках лазерного излучения, можно сказать, что они определяются процессами оптической накачки, вынужденного и спонтанного испускания, а также тепловыми эффектами, которые, с одной стороны, приводят к перестройке мод, а с другой — к смещению и изменению ширины линии флюоресценции.
Следует обратить внимание на еще один важный процесс, который имеет место при взаимодействии стоячей электромагнитной волны в резонаторе лазера с активной средой. Подробное описание
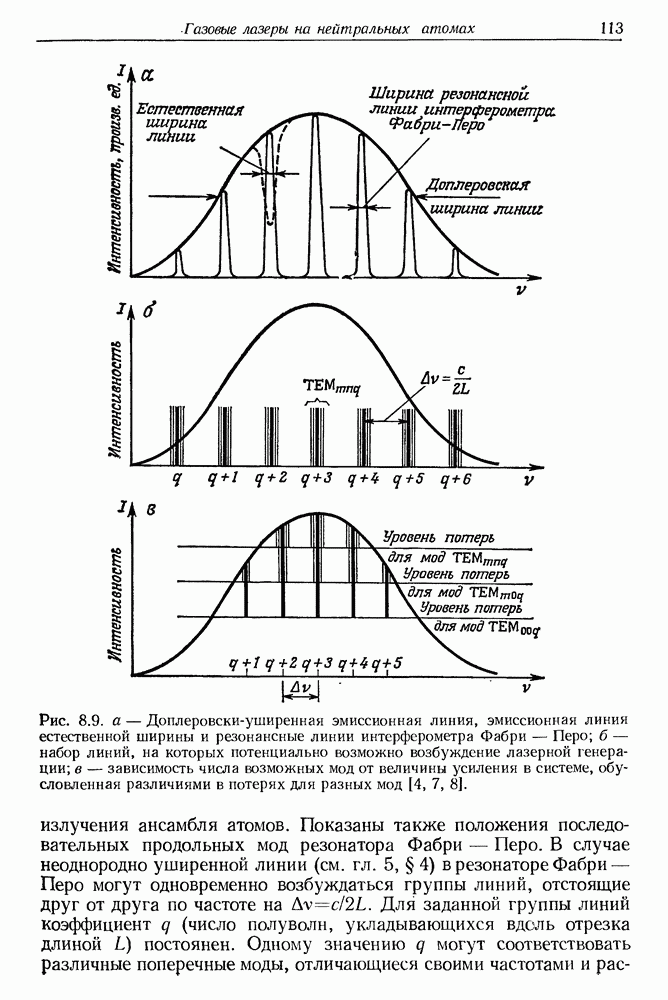
этого процесса дано в работе Лифшица [61. Мы уже упоминали в предыдущих главах, что в пределах ширины линии флюоресценции рубина помещается довольно большое число продольных мод лазера. У неодимового лазера, который имеет широкую линию флюоресценции (десятки ангстрем), это число достигает нескольких тысяч. Если длина резонатора равна  известное условие резонанса для продольных мод дает
известное условие резонанса для продольных мод дает

При  мкм и
мкм и  см
см  Номер моды в оптическом диапазоне очень велик. Предположим для простоты, что в системе возбудилась одна мода с номером
Номер моды в оптическом диапазоне очень велик. Предположим для простоты, что в системе возбудилась одна мода с номером  . В активной среде возникает стоячая волна с неизменным распределением узлов и пучностей. Поскольку вынужденное испускание прямо пропорционально плотности излучения, в пучностях происходит сильное опустошение возбужденного (лазерного) состояния, а в узлах инверсия населенностей сохраняется значительно дольше (уменьшается лишь спонтанное испускание). В активной среде возникает слоистая структура, в которой чередуются области «бедные» и «богатые» с точки зрения инверсии населенностей. Ясно, что такая ситуация не способствует поддержанию генерации моды
. В активной среде возникает стоячая волна с неизменным распределением узлов и пучностей. Поскольку вынужденное испускание прямо пропорционально плотности излучения, в пучностях происходит сильное опустошение возбужденного (лазерного) состояния, а в узлах инверсия населенностей сохраняется значительно дольше (уменьшается лишь спонтанное испускание). В активной среде возникает слоистая структура, в которой чередуются области «бедные» и «богатые» с точки зрения инверсии населенностей. Ясно, что такая ситуация не способствует поддержанию генерации моды  . В этих условиях система поддерживает развитие других мод, пучности которых оказываются вблизи узлов моды
. В этих условиях система поддерживает развитие других мод, пучности которых оказываются вблизи узлов моды  т. е. в местах, где имеет место инверсия, а значит и усиление излучения. В свою очередь возбуждение новых мод приводит к изменению слоистой структуры активной среды. За это время оптическая накачка может привести к увеличению инверсной населенности в тех местах, где она была нарушена. Механизм, предложенный Лифшицем, дает простое объяснение модовому дрейфу и нестабильности излучения твердотельного лазера. Лифшиц построил лазер, в котором активный элемент приводился в движение вдоль оптической оси резонатора. Это сопровождалось перемещением узлов и пучностей по лазерному стержню, т. е. препятствовало расслоению стержня на области с высоким или нулевым уровнем инверсии. Скорость перемещения активной среды должна быть равна [6]
т. е. в местах, где имеет место инверсия, а значит и усиление излучения. В свою очередь возбуждение новых мод приводит к изменению слоистой структуры активной среды. За это время оптическая накачка может привести к увеличению инверсной населенности в тех местах, где она была нарушена. Механизм, предложенный Лифшицем, дает простое объяснение модовому дрейфу и нестабильности излучения твердотельного лазера. Лифшиц построил лазер, в котором активный элемент приводился в движение вдоль оптической оси резонатора. Это сопровождалось перемещением узлов и пучностей по лазерному стержню, т. е. препятствовало расслоению стержня на области с высоким или нулевым уровнем инверсии. Скорость перемещения активной среды должна быть равна [6]

где  означает число фотонов моды
означает число фотонов моды  — среднее время жизни активного иона в возбужденном состоянии в поле одного фотона,
— среднее время жизни активного иона в возбужденном состоянии в поле одного фотона,
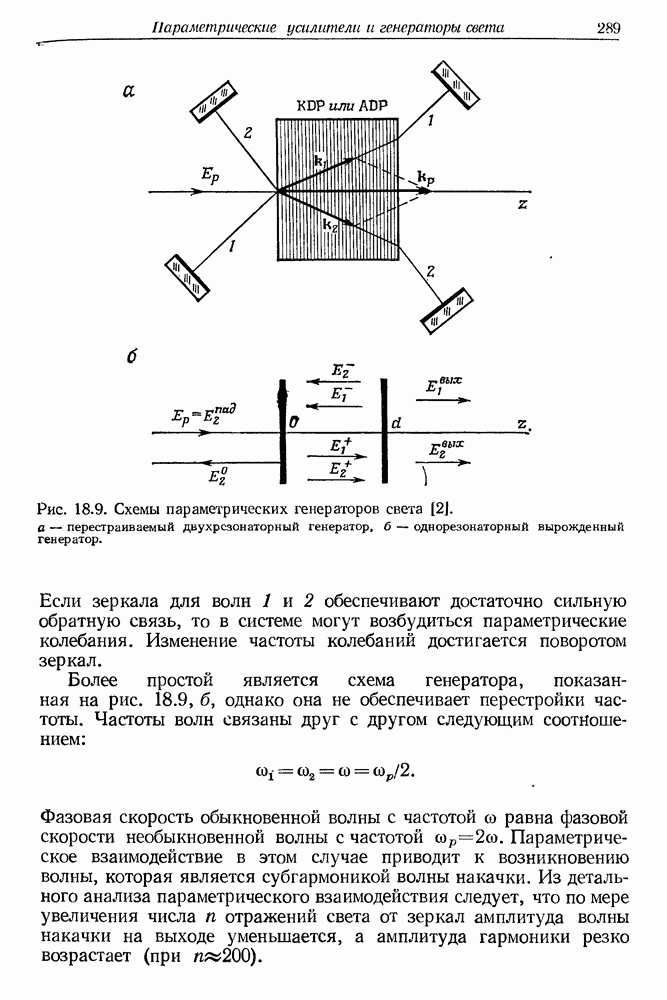
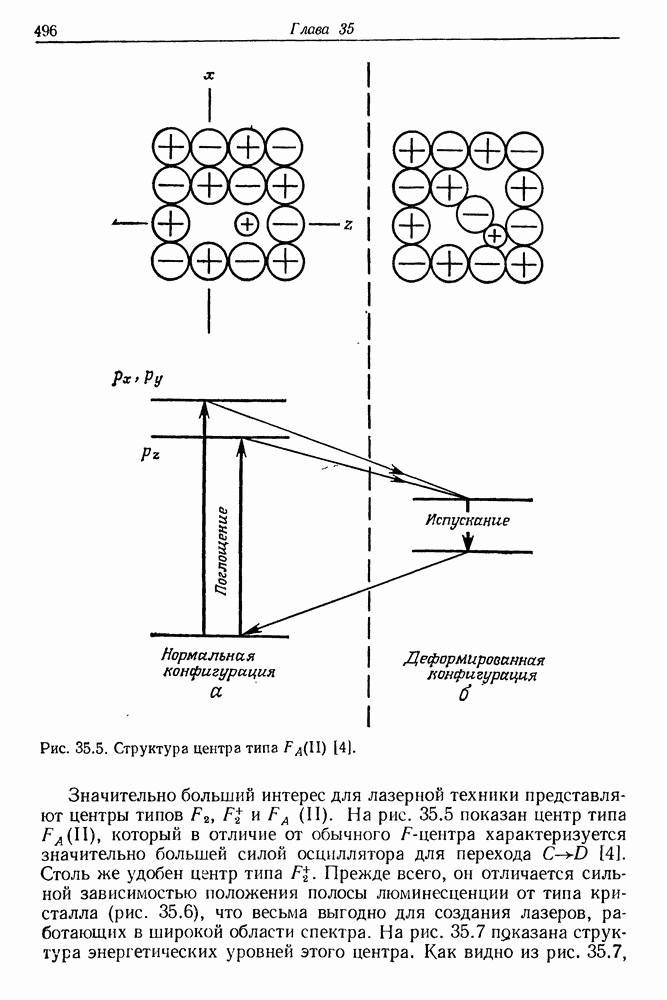
— число возможных продольных мод в пределах полуширины линии флюоресценции активной среды. Чтобы в лазере возбуждалась только одна мода, «перенос» инверсии в среде должен происходить тем быстрее, чем больше расстояние между узлами,

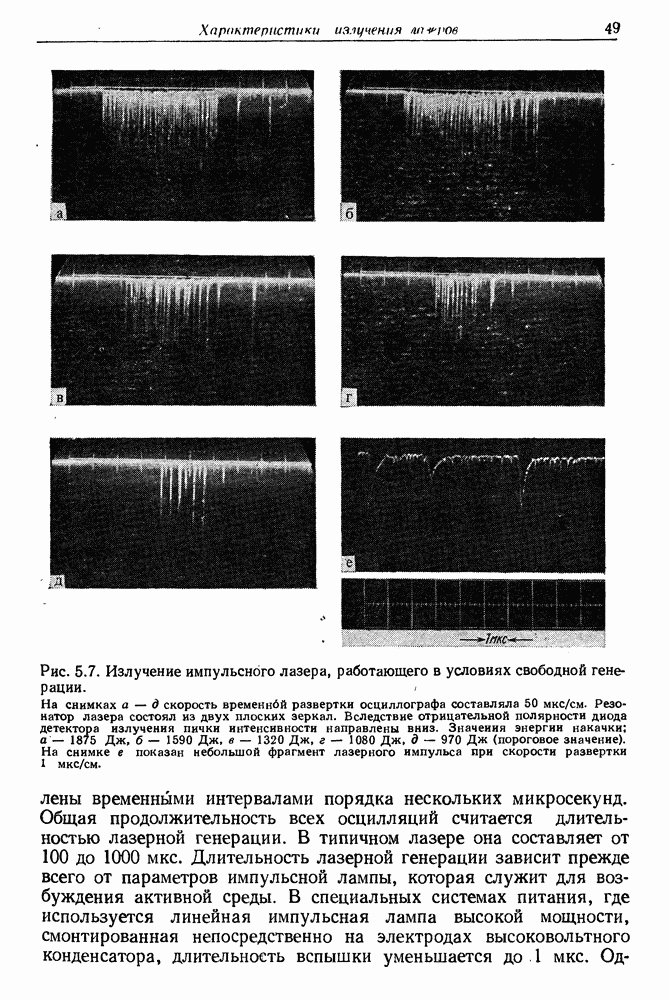
Рис. 5.9. Интерферограммы излучения рубинового лазера с движущимся активным элементом (а) и в статическом режиме (б) [6].
вероятность разрушения состояния инверсии в пучности  и конкуренция между возможными модами. В рубиновом лазере скорость
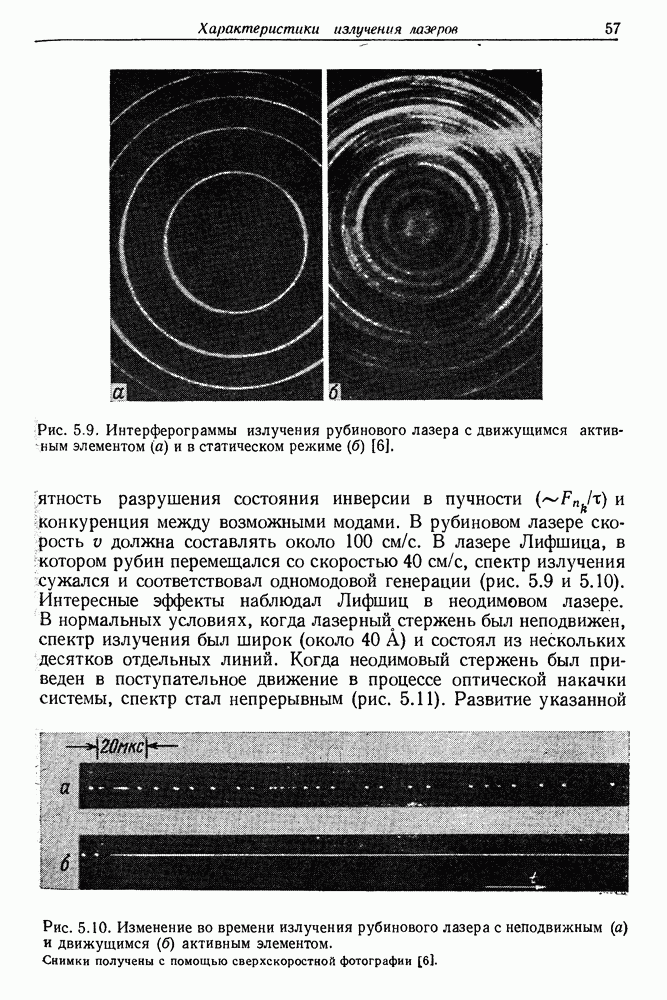
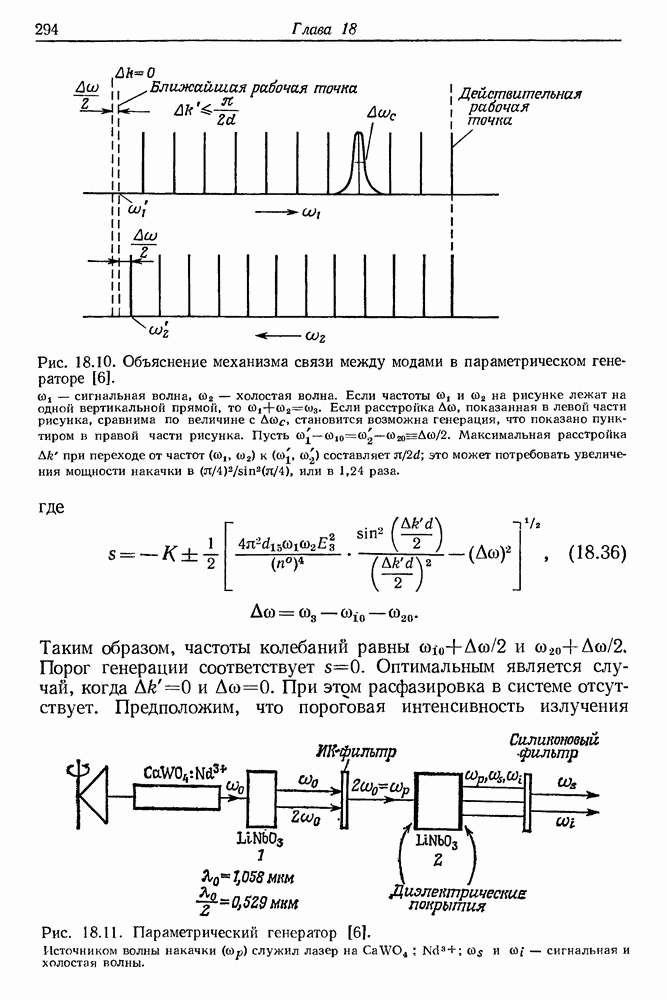
и конкуренция между возможными модами. В рубиновом лазере скорость  должна составлять около 100 см/с. В лазере Лифшица, в котором рубин перемещался со скоростью 40 см/с, спектр излучения сужался и соответствовал одномодовой генерации (рис. 5.9 и 5.10). Интересные эффекты наблюдал Лифшиц в неодимовом лазере. В нормальных условиях, когда лазерный стержень был неподвижен, спектр излучения был широк (около 40 А) и состоял из нескольких десятков отдельных линий. Когда неодимовый стержень был приведен в поступательное движение в процессе оптической накачки системы, спектр стал непрерывным (рис. 5.11). Развитие указанной
должна составлять около 100 см/с. В лазере Лифшица, в котором рубин перемещался со скоростью 40 см/с, спектр излучения сужался и соответствовал одномодовой генерации (рис. 5.9 и 5.10). Интересные эффекты наблюдал Лифшиц в неодимовом лазере. В нормальных условиях, когда лазерный стержень был неподвижен, спектр излучения был широк (около 40 А) и состоял из нескольких десятков отдельных линий. Когда неодимовый стержень был приведен в поступательное движение в процессе оптической накачки системы, спектр стал непрерывным (рис. 5.11). Развитие указанной

Рис. 5.10. Изменение во времени излучения рубинового лазера с неподвижным (а) и движущимся (б) активным элементом. Снимки получены с помощью сверхскоростной фотографии [6].

Рис. 5.11. Спектр излучения лазера на неодимовом стекле с движущимся активным элементом (а) и в статическом режиме (б) [6].
моды в резонаторе лазера зависит от коэффициента усиления, а также от величины потерь энергии. Следовательно, спектр мод лазера определяется зависимостью коэффициента усиления и по терь от частоты. Преобразование хаотического спектра лазерного излучения в непрерывный свидетельствует о том, что движение активной среды усредняет указанные величины в диапазоне усиливаемых частот. Результаты этого эксперимента можно подытожить следующим образом. Если внутрь лазерного резонатора поместить небольшую диафрагму (для рубинового лазера от 0,7 до 1 мм, для неодимового — от 1,0 до 1,1 мм) и в процессе оптической накачки приводить активную среду в поступательное движение со скоростью нескольких десятков сантиметров в секунду, то излучение лазера приобретает весьма регулярный характер, т. е. освобождается от присущих обычной лазерной генерации осцилляций интенсивности (нерегулярных пичков). Движение активной среды усредняет все неоднородности и приводит к упорядочению лазерной генерации.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
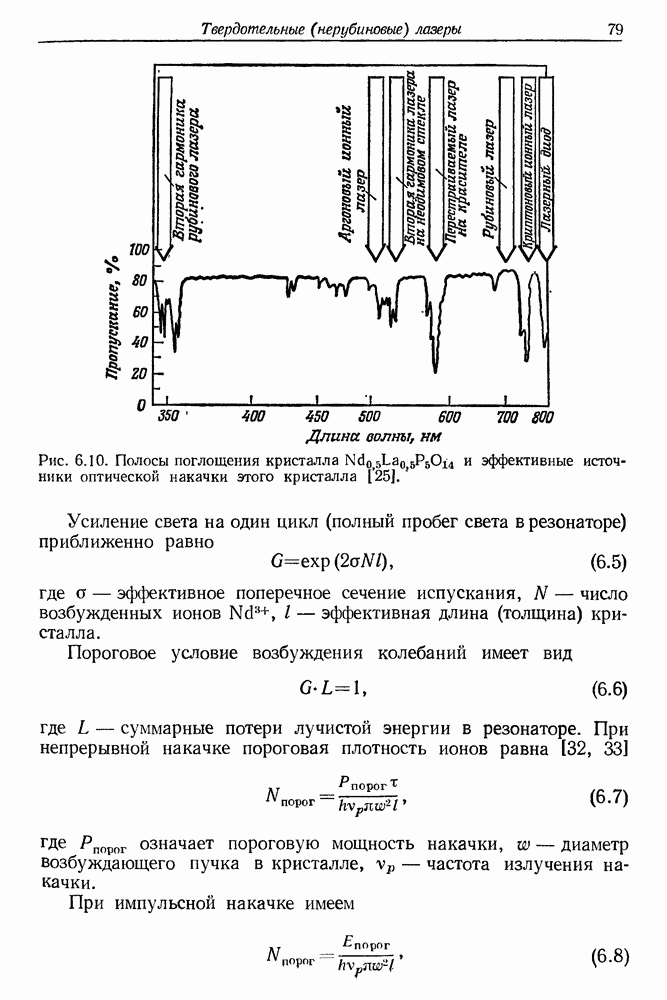
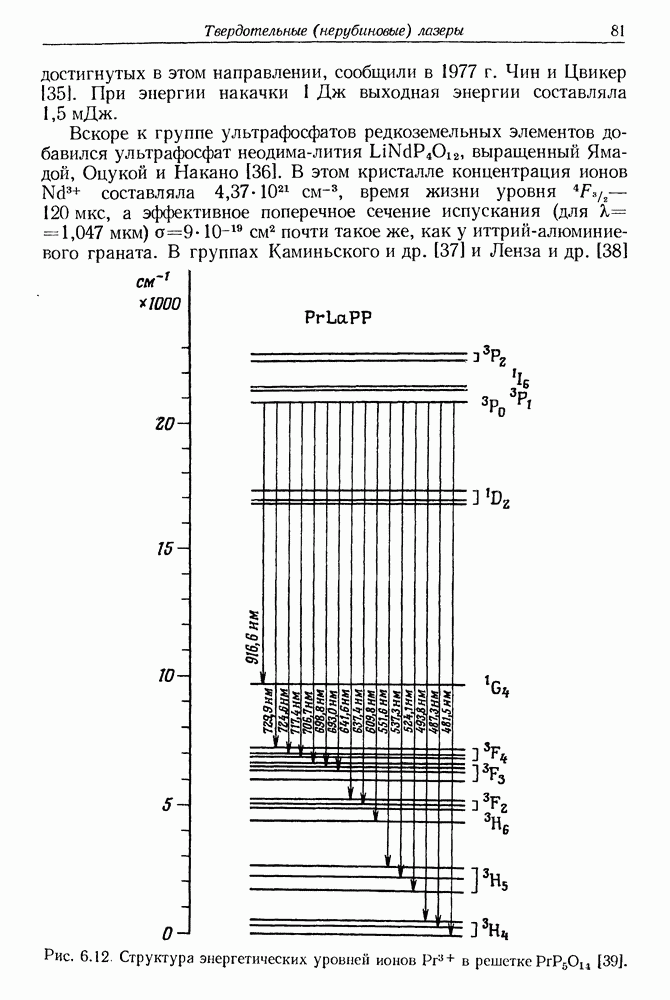
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
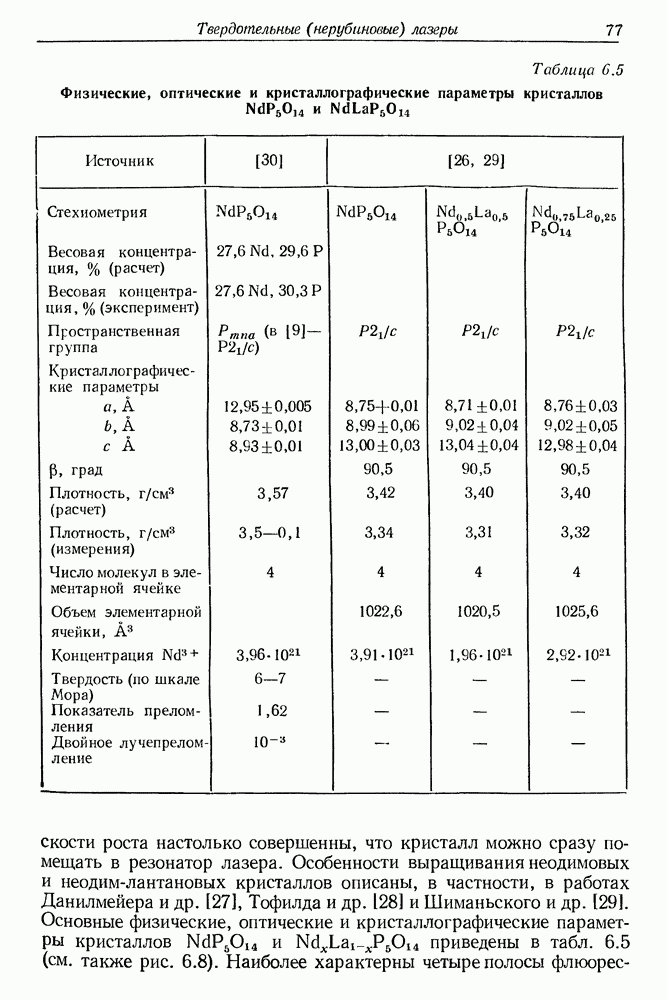
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
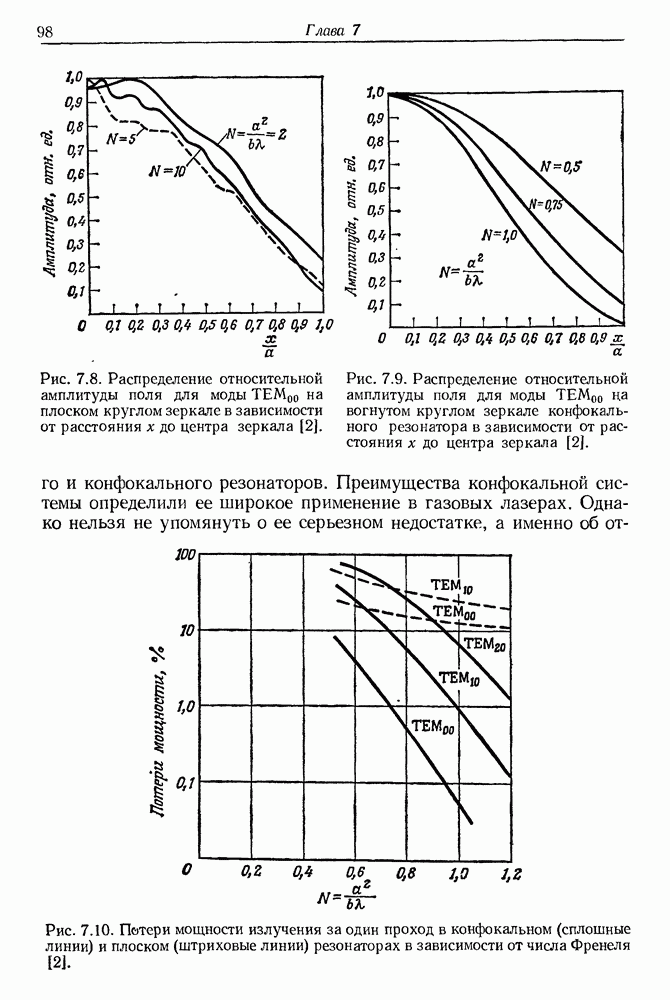
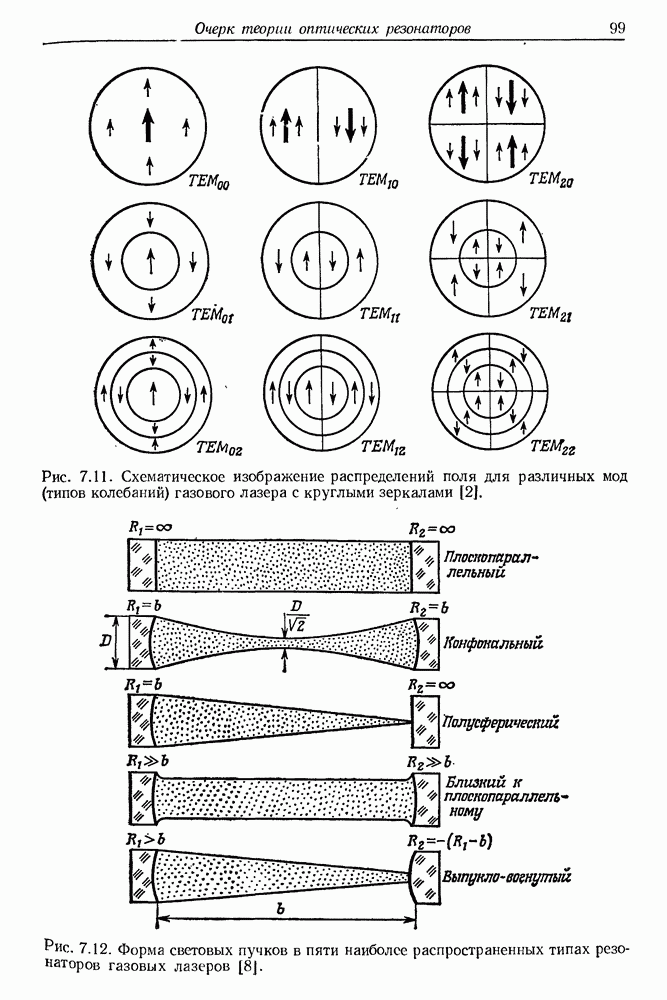
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
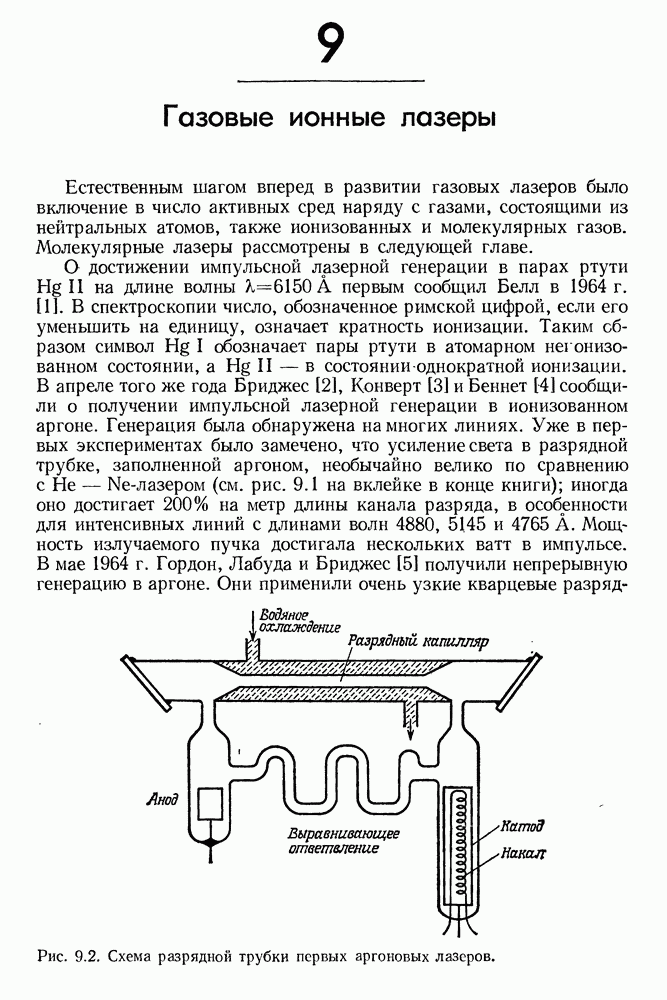
- 9. Газовые ионные лазеры
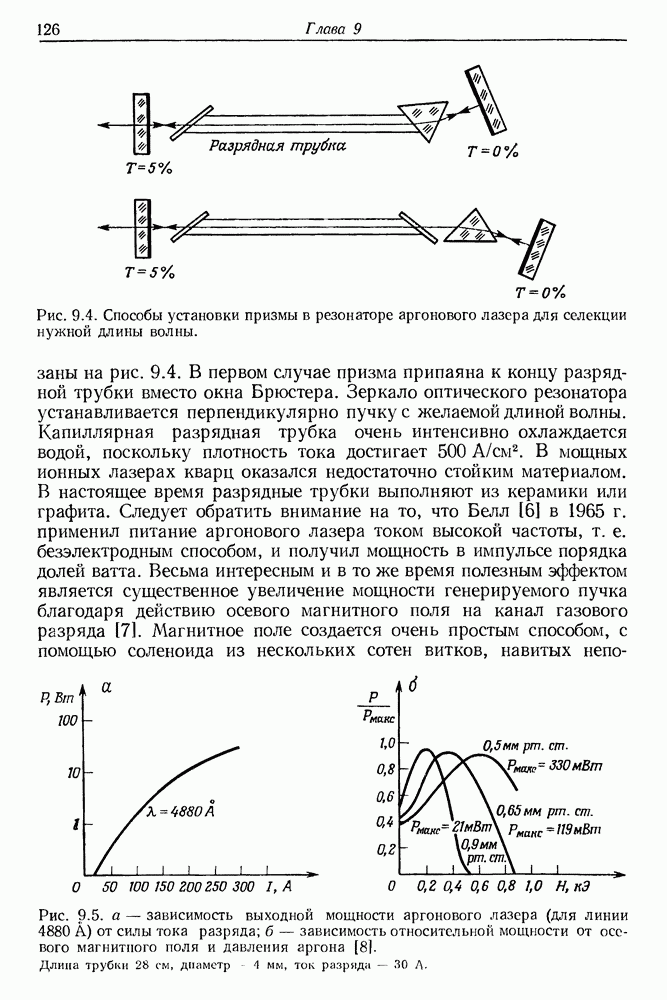
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
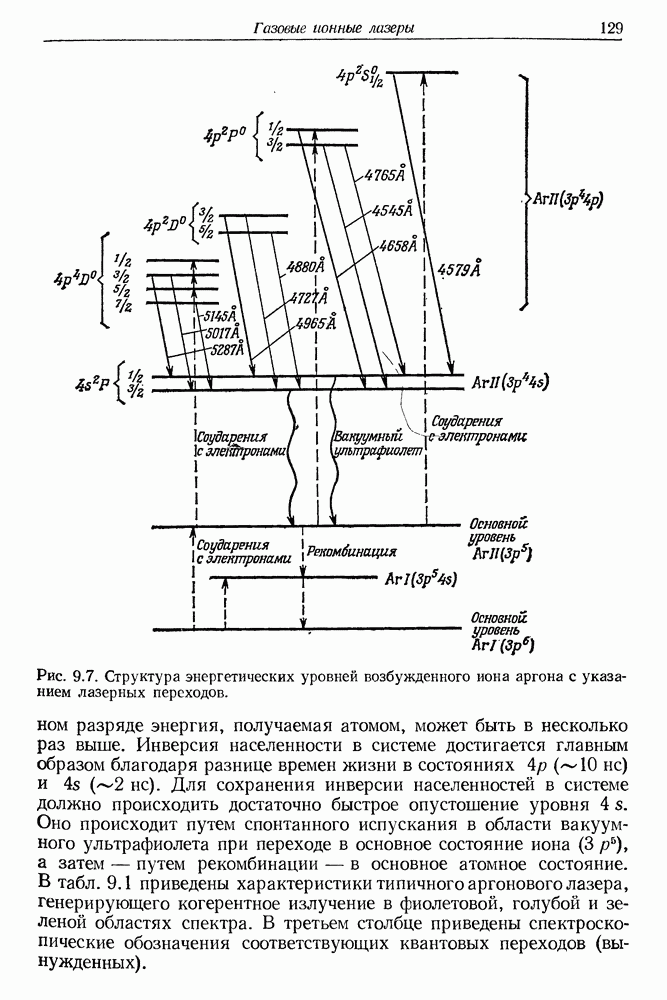
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
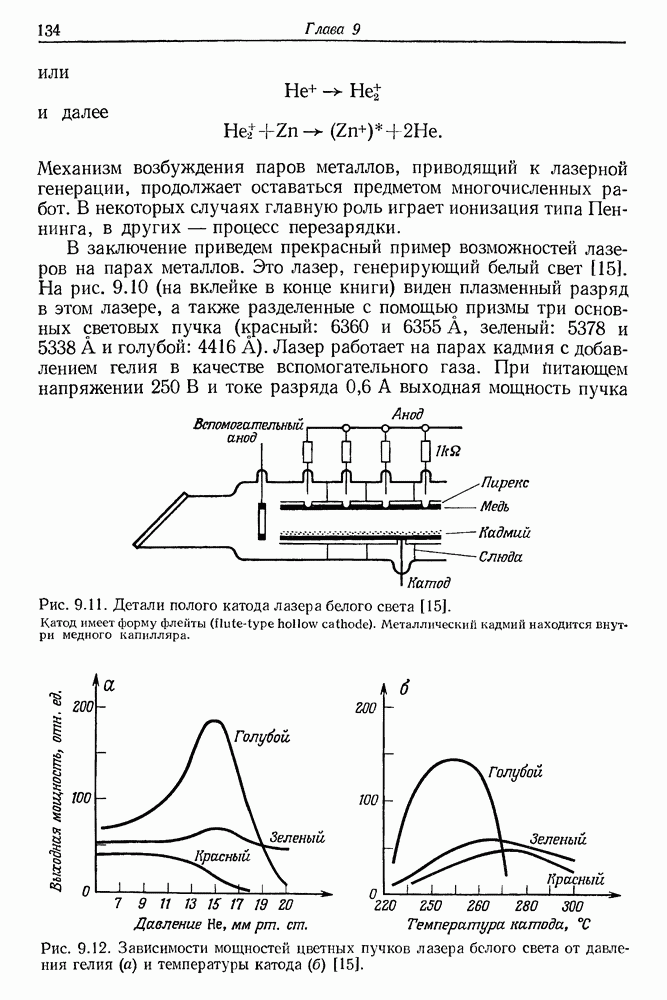
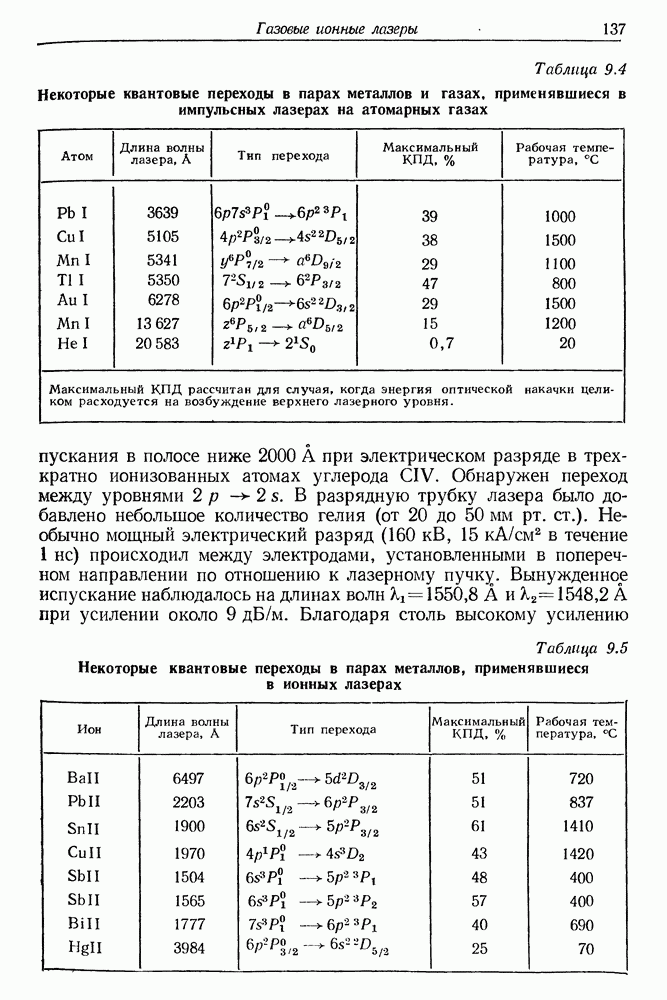
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
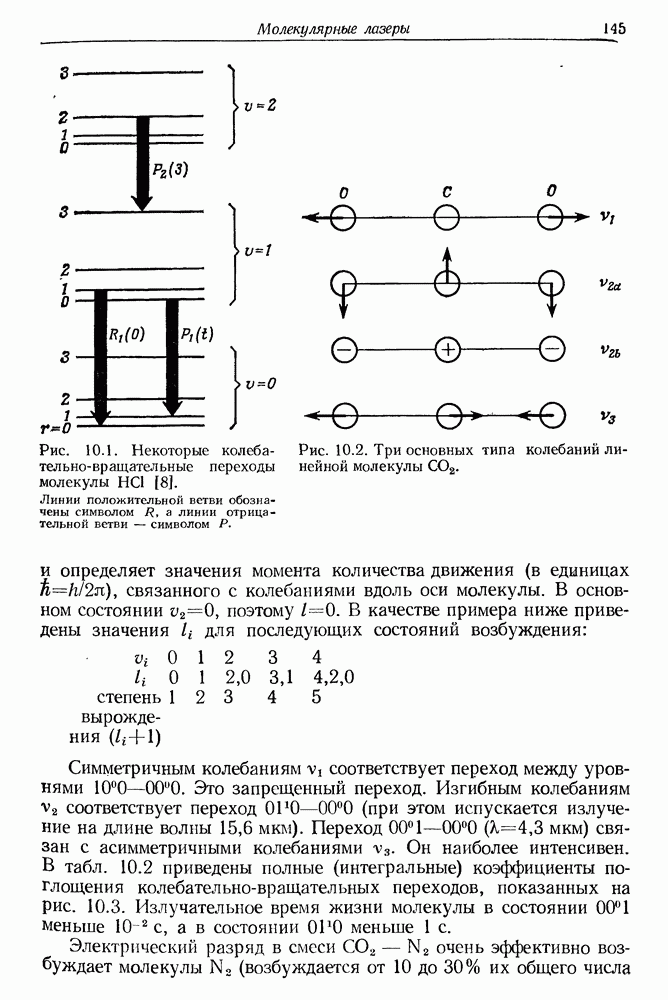
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
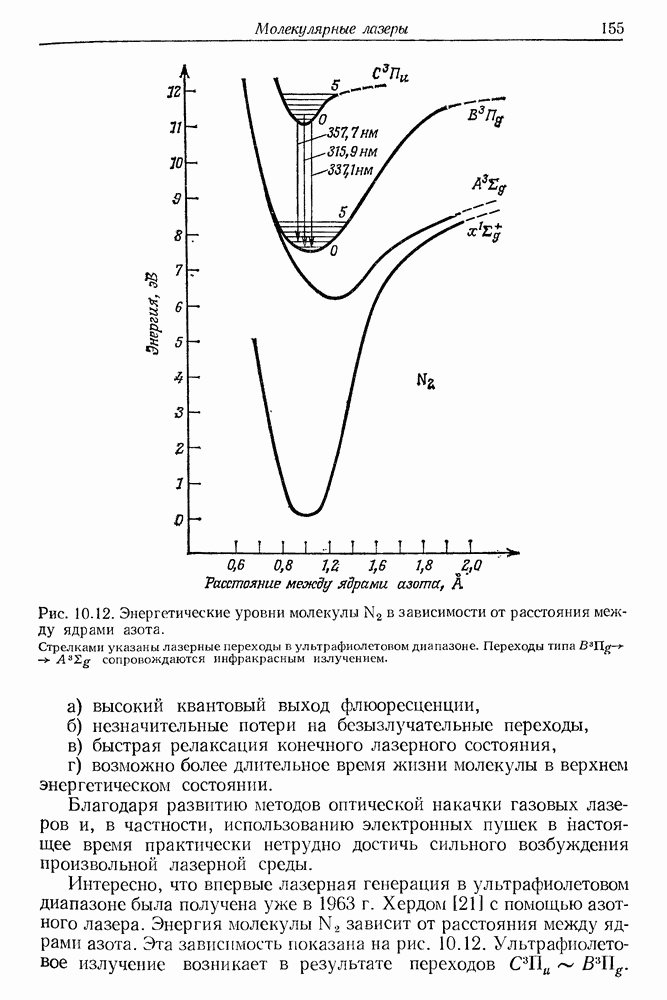
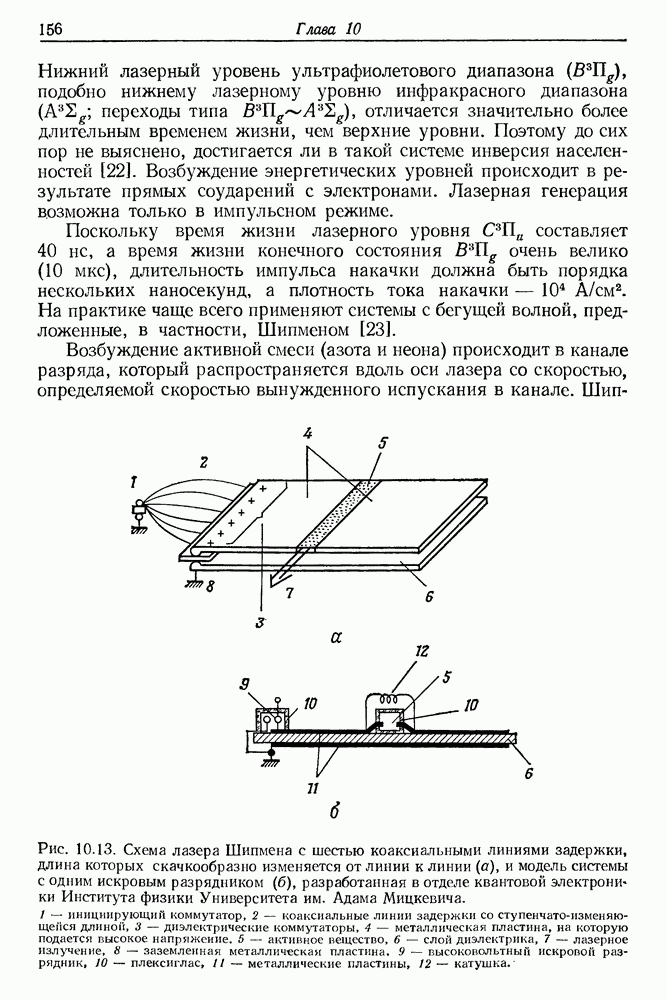
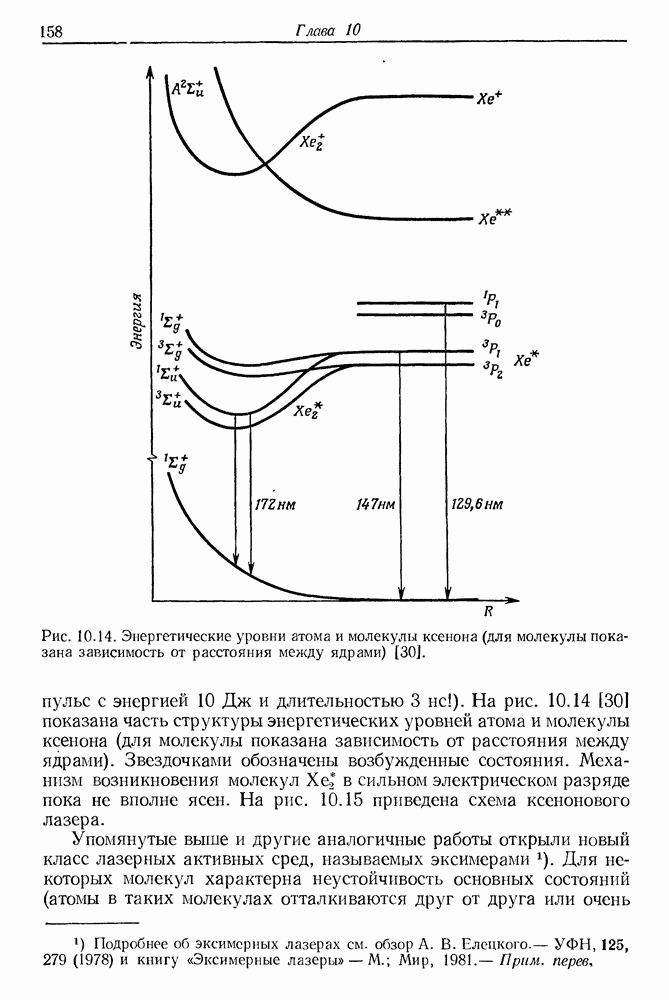
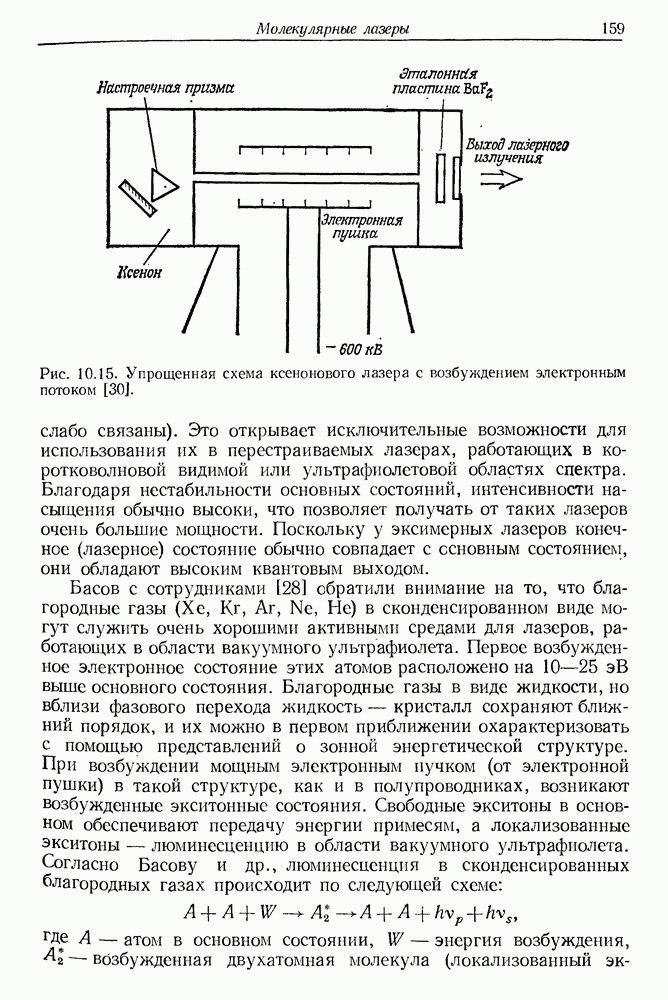
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
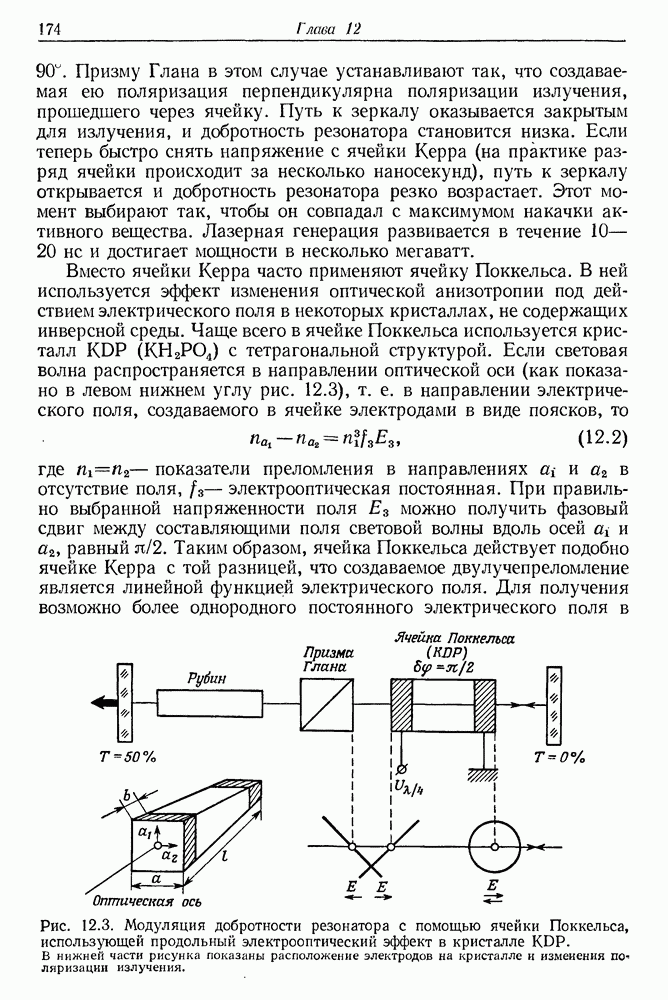
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
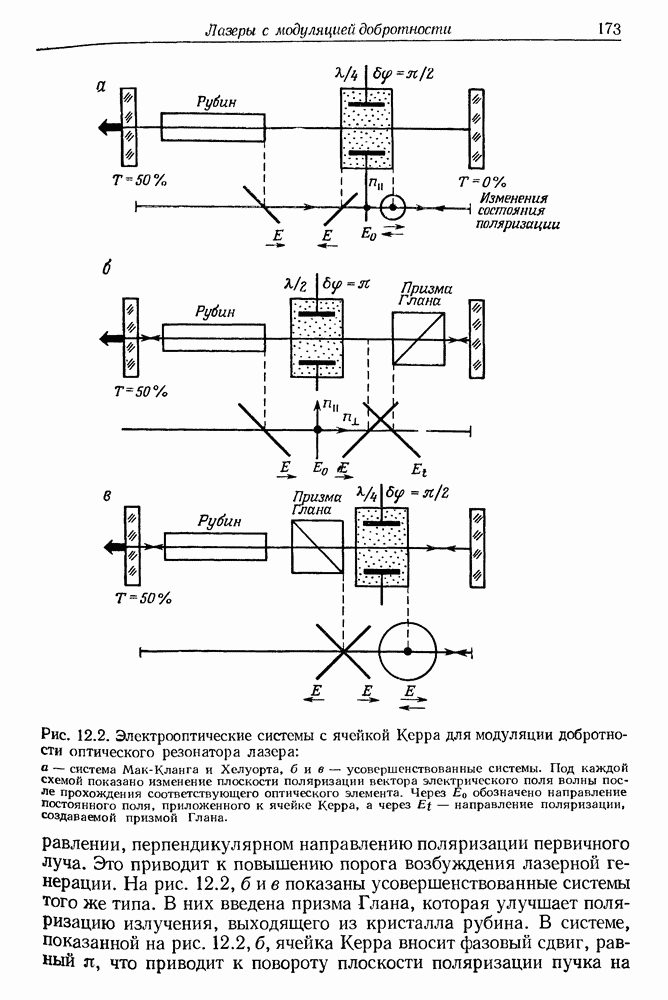
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
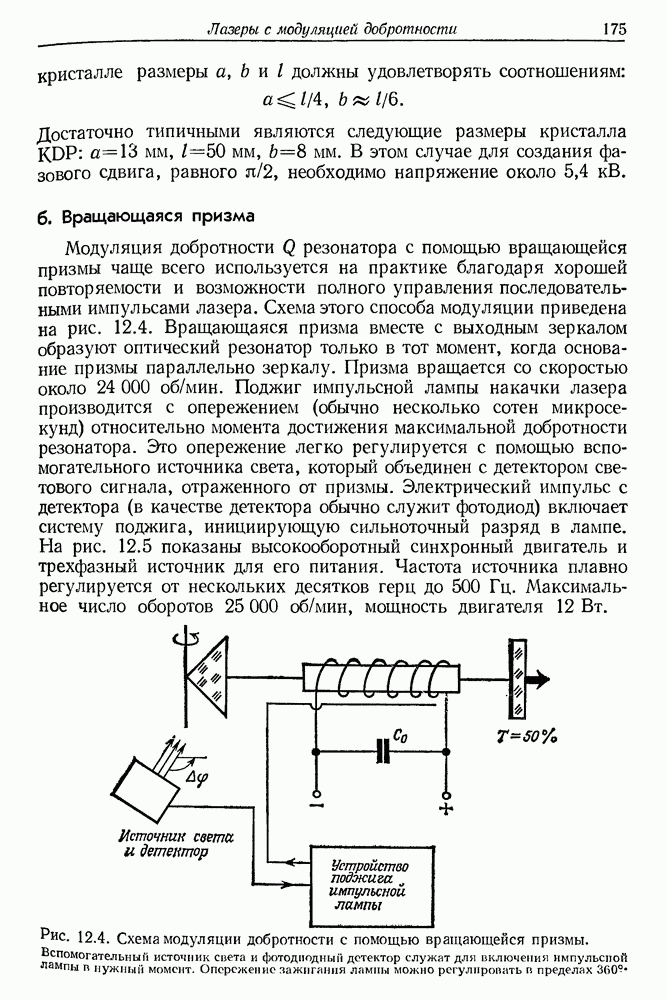
- б. Вращающаяся призма
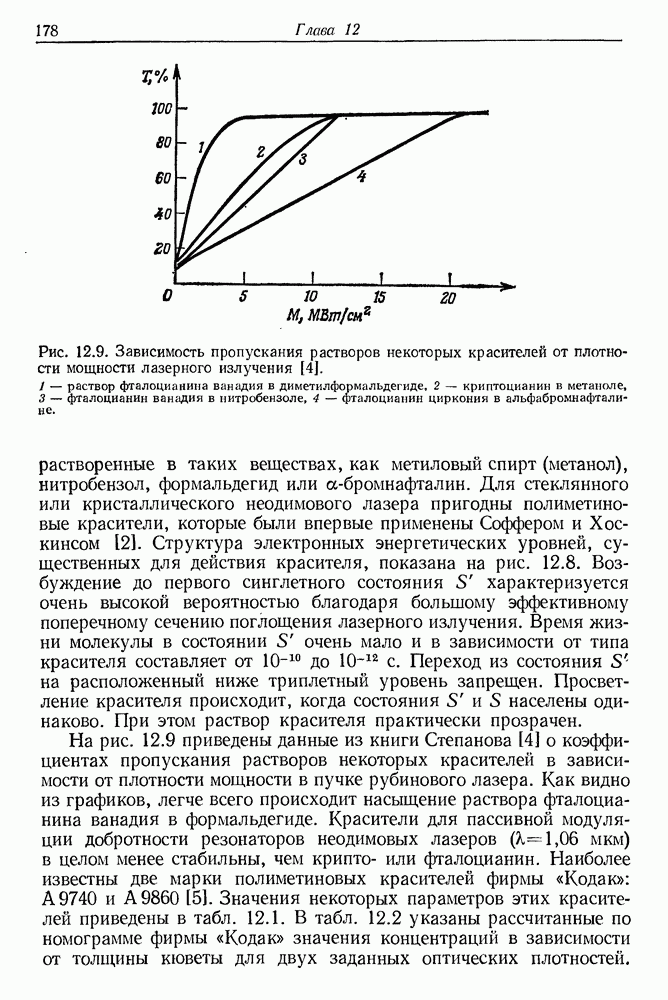
- в. Пассивная модуляция Q с помощью красителей
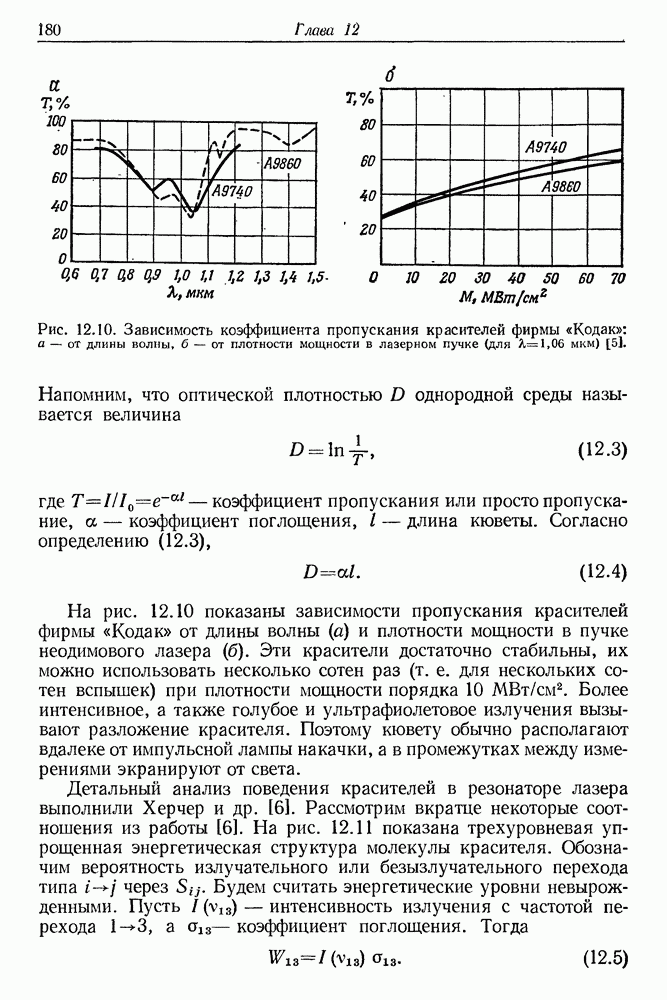
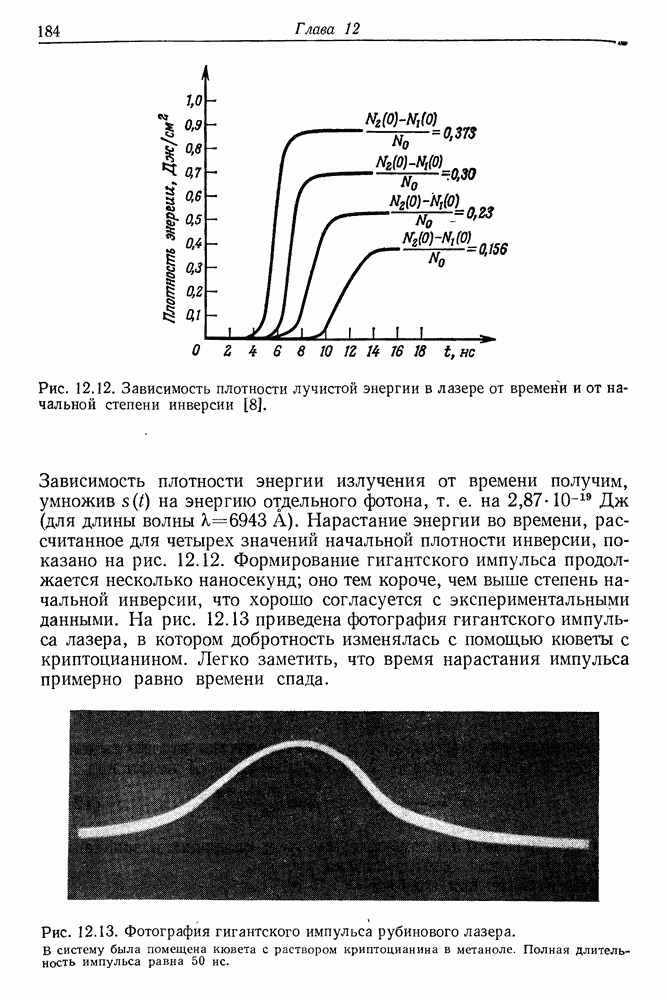
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
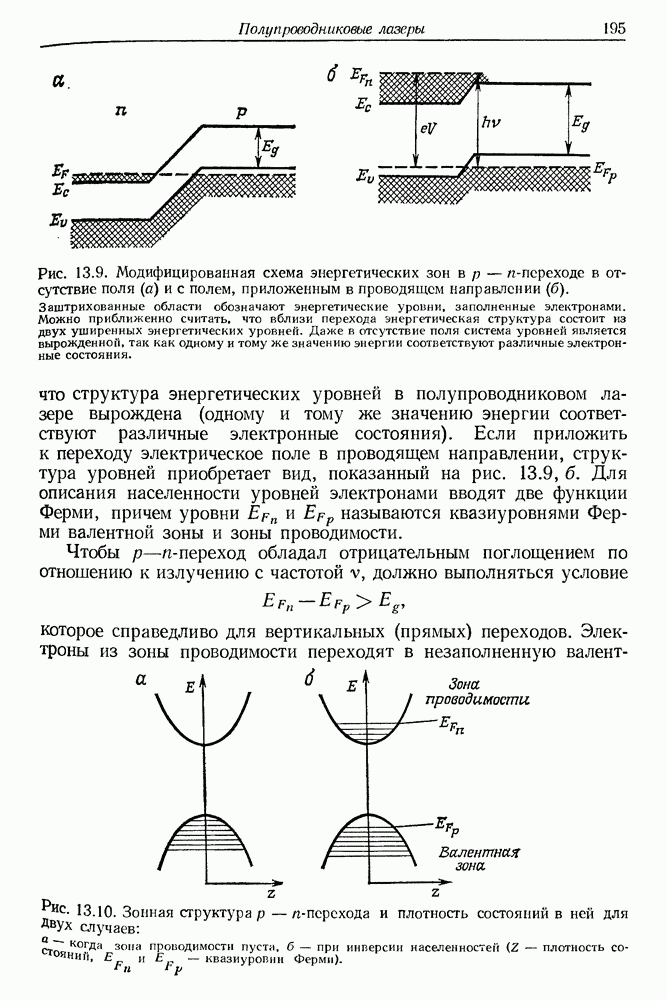
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
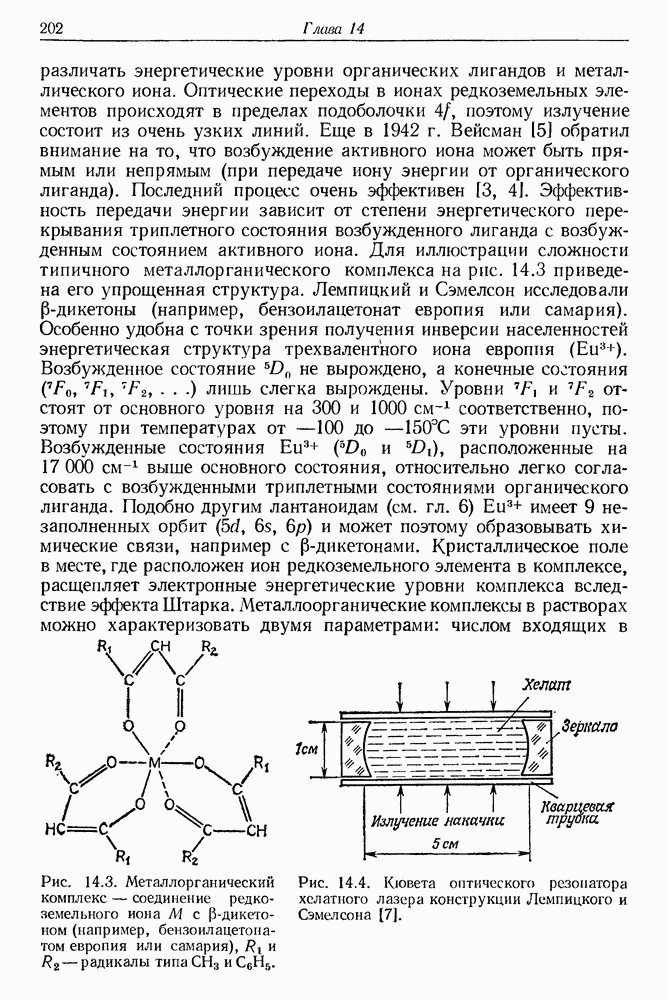
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
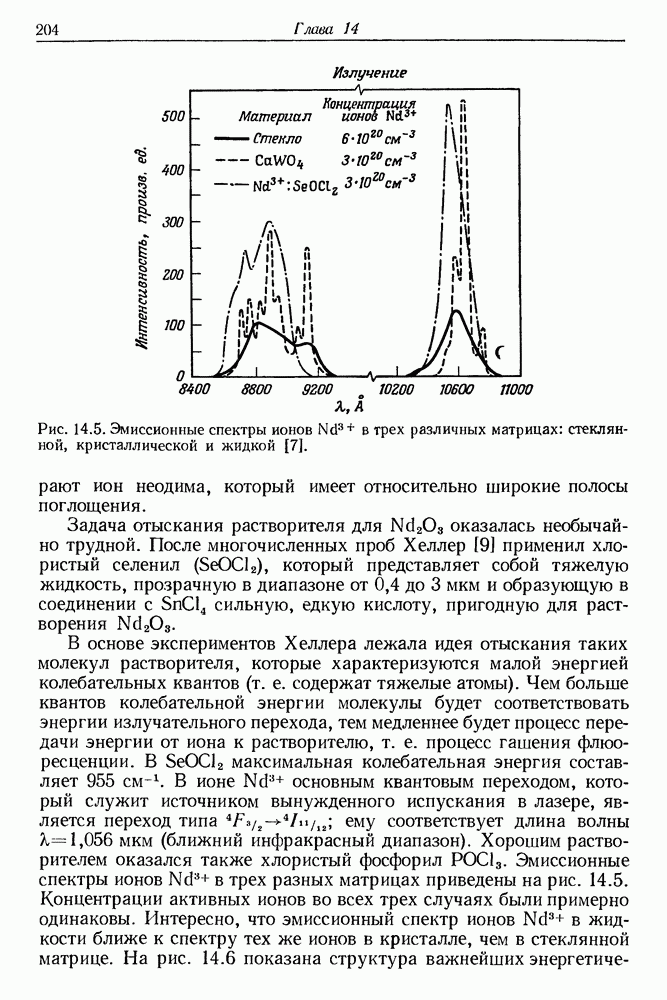
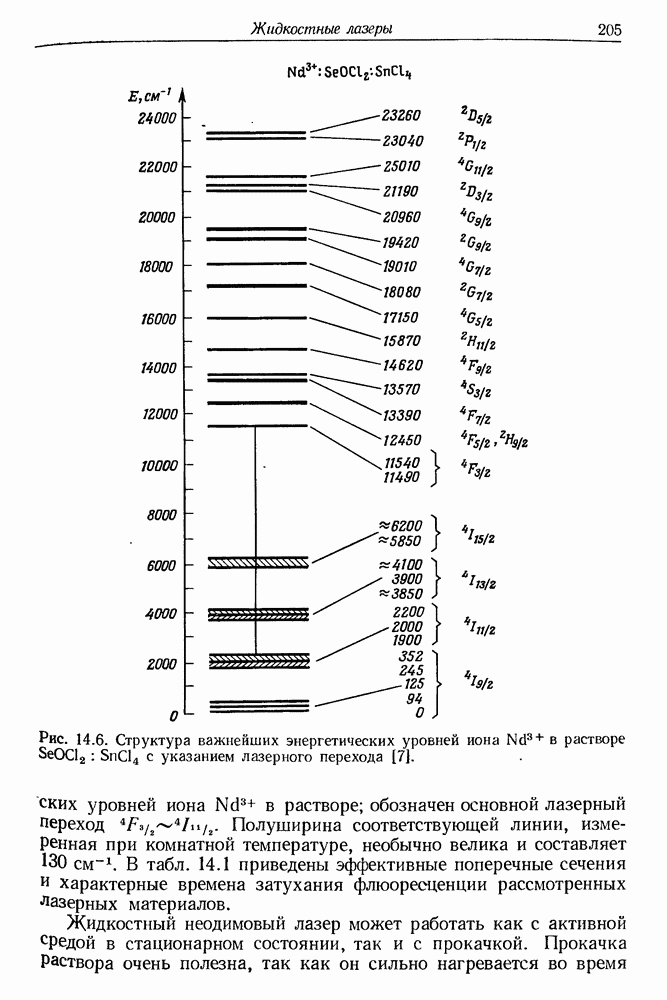
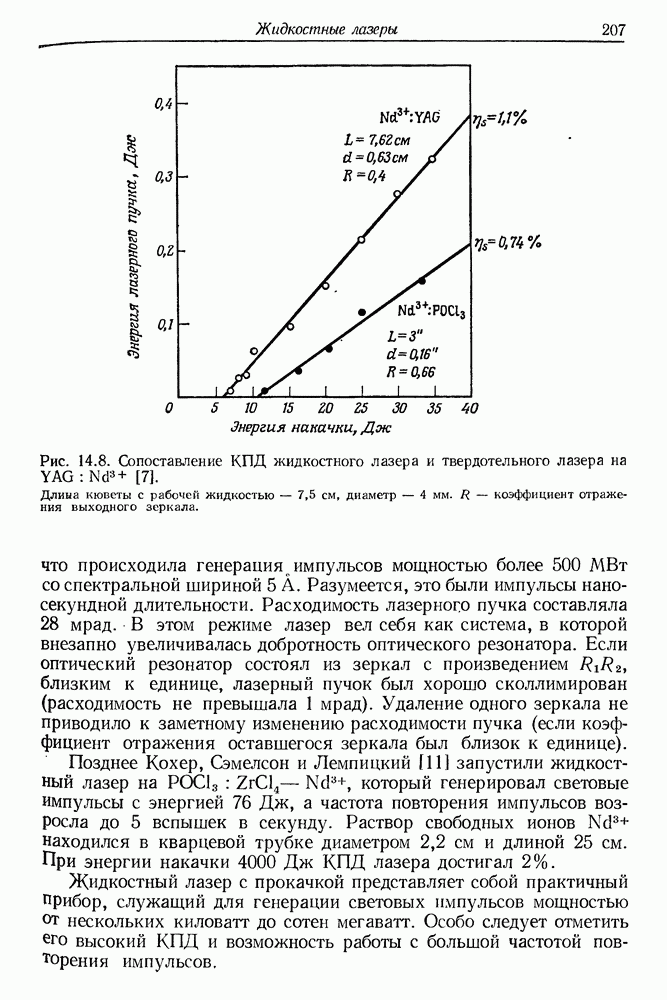
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
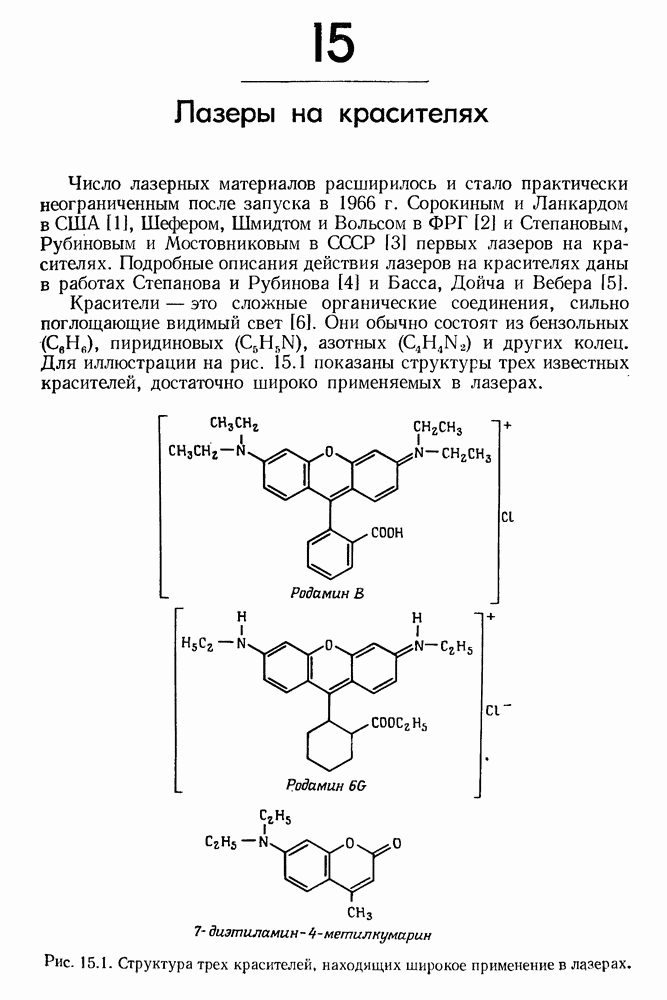
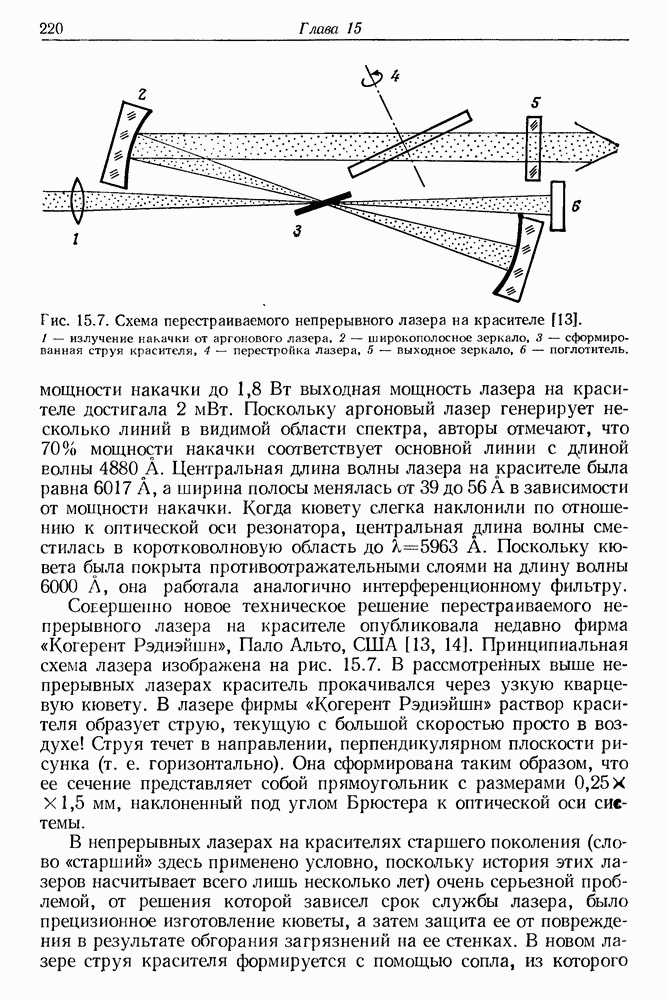
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
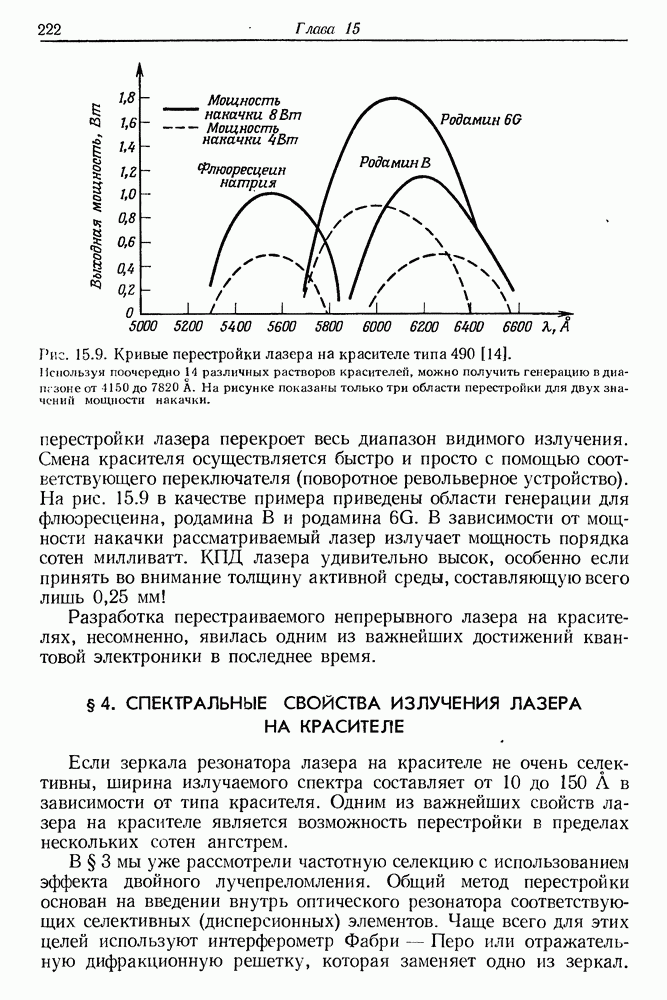
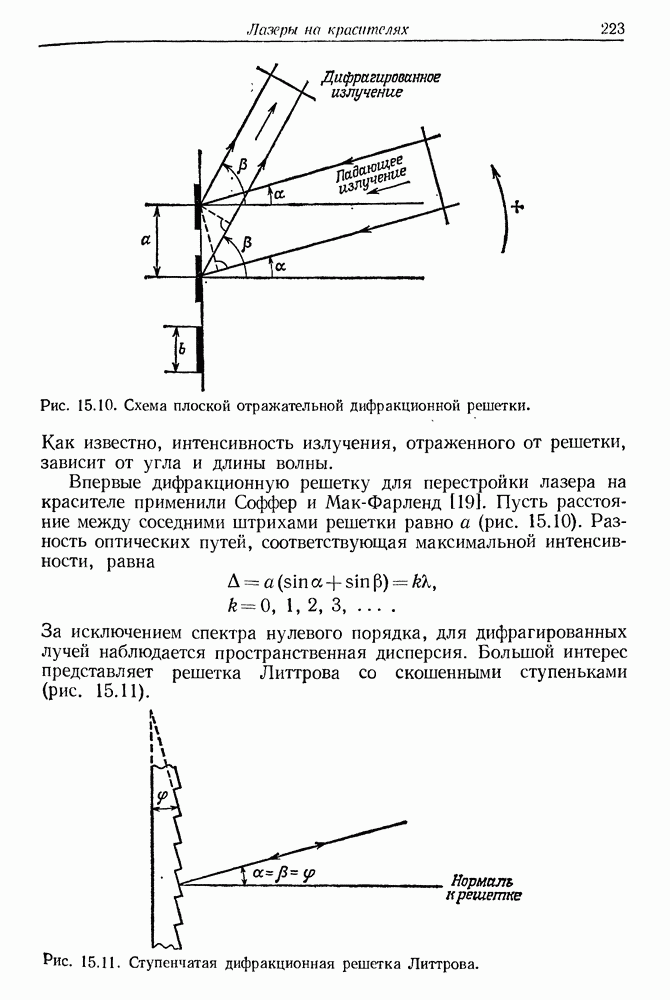
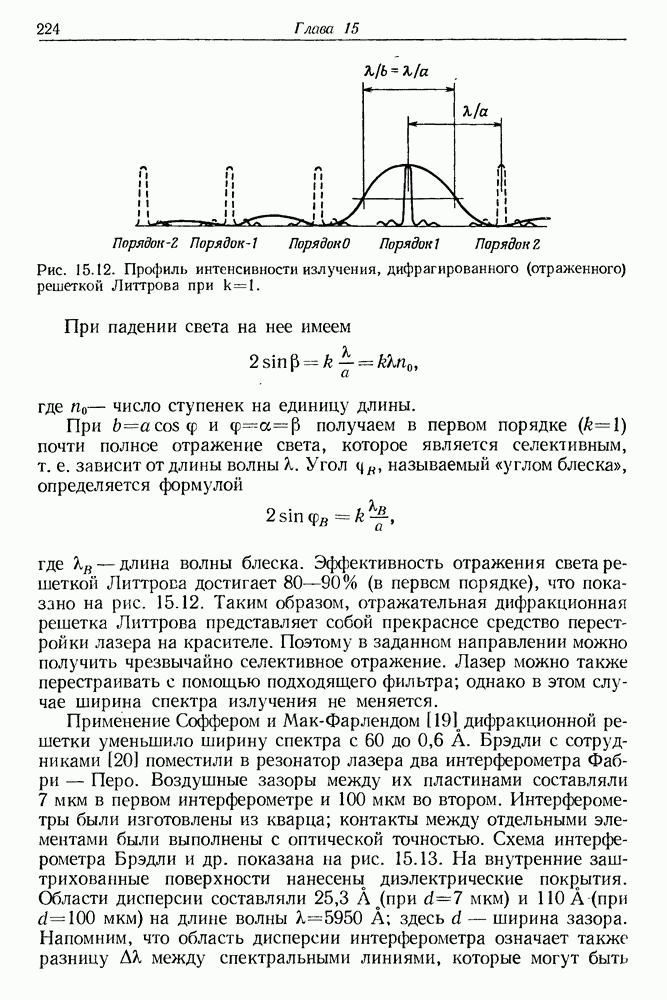
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
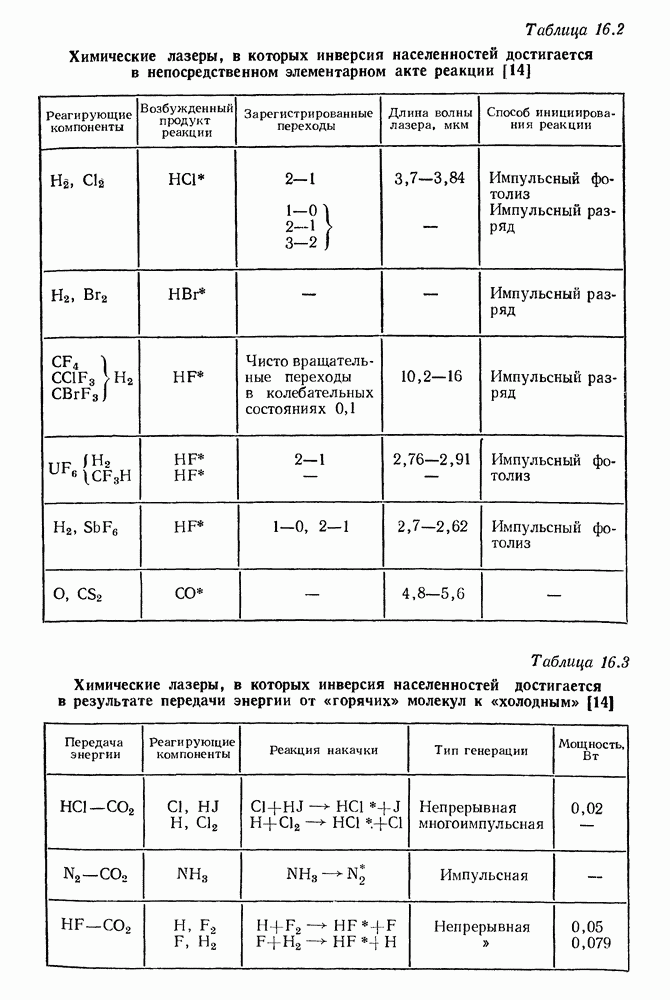
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
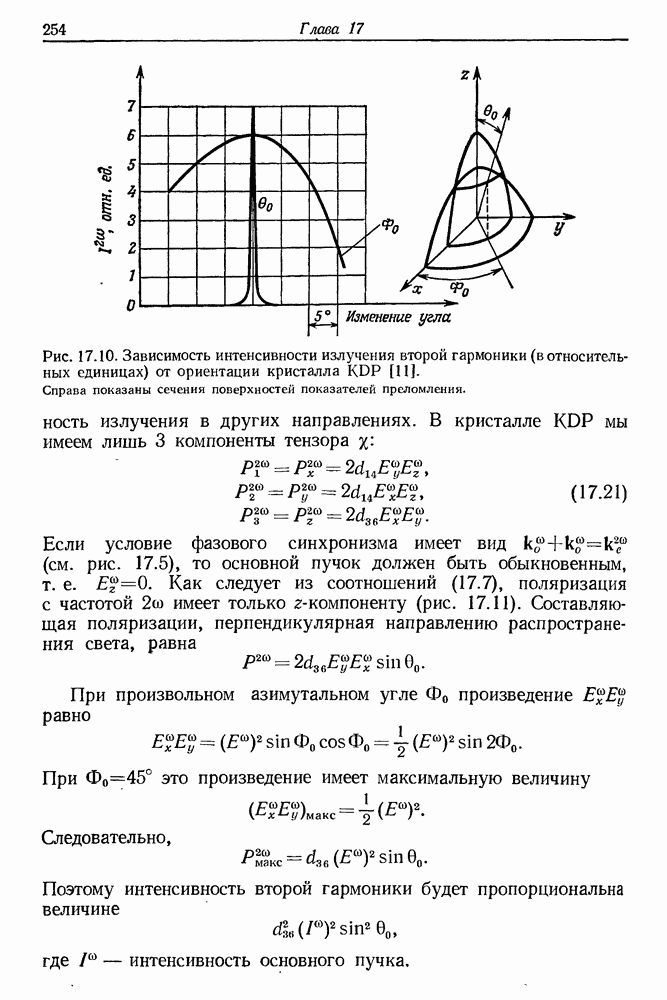
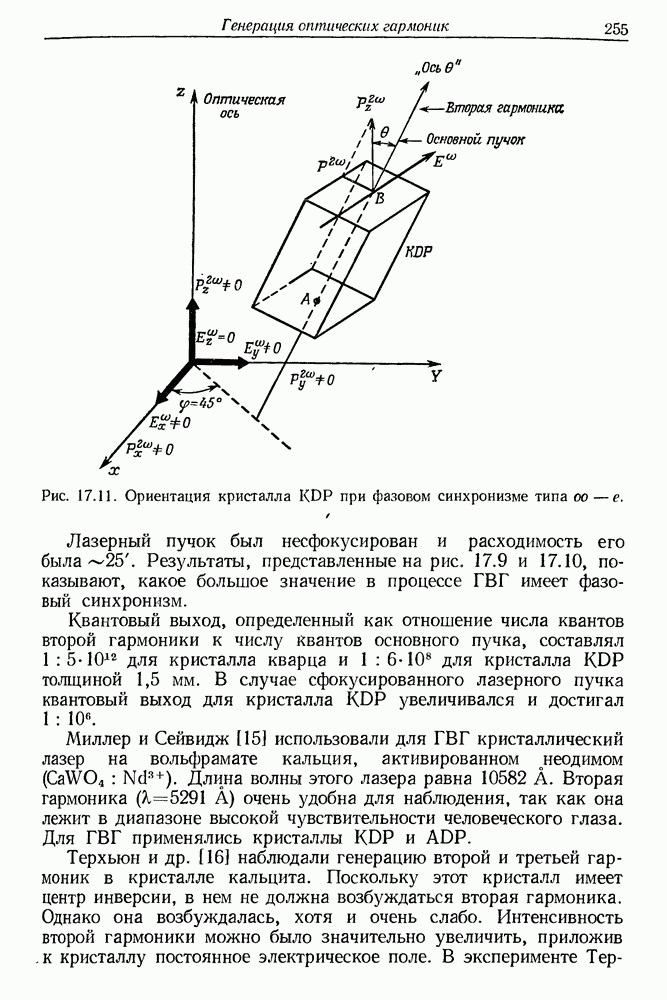
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
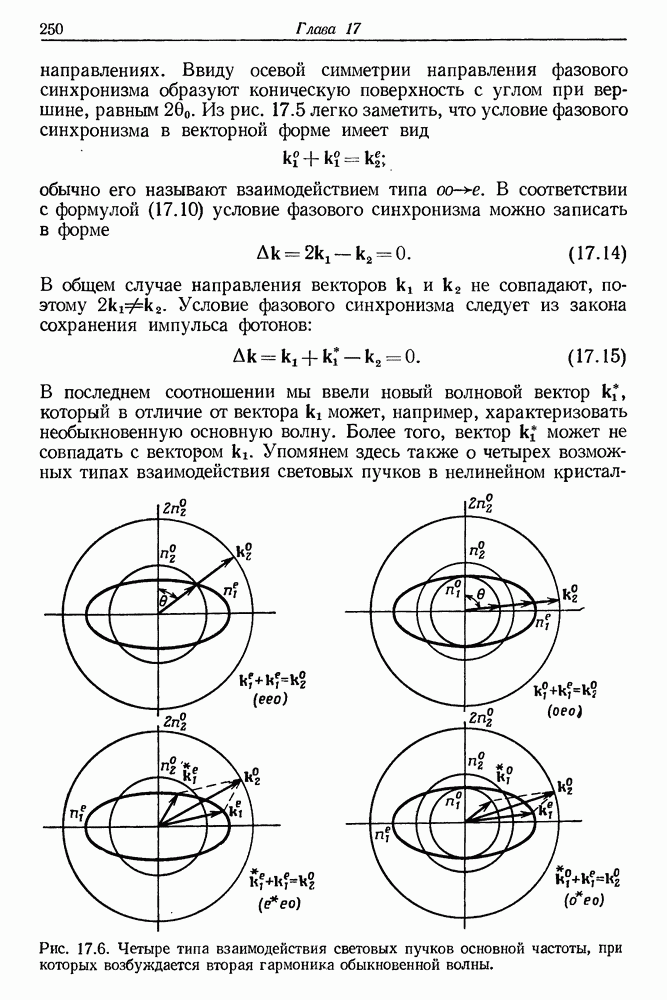
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
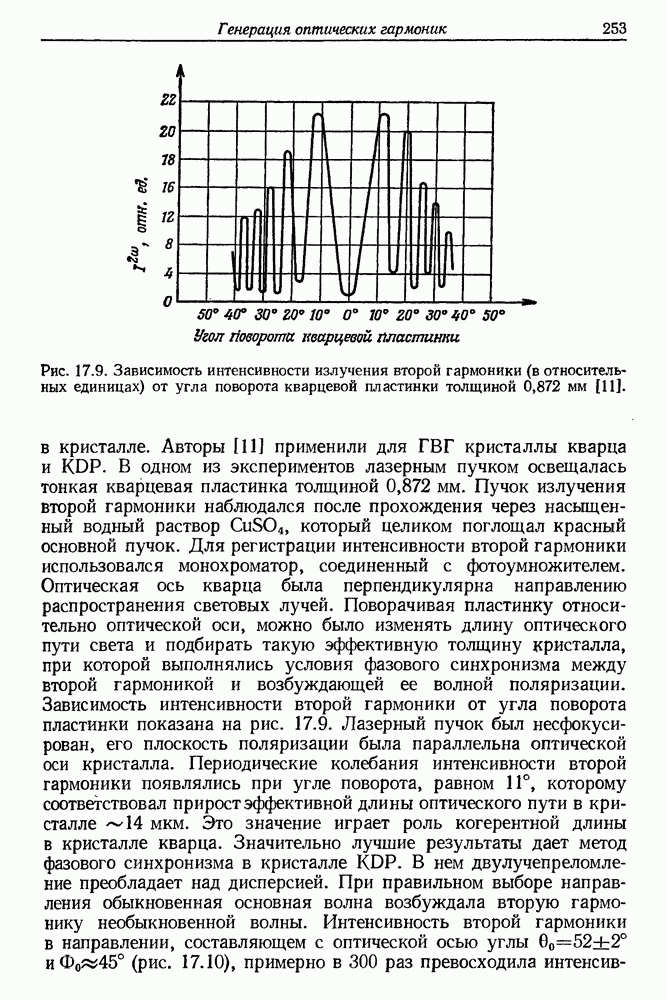
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
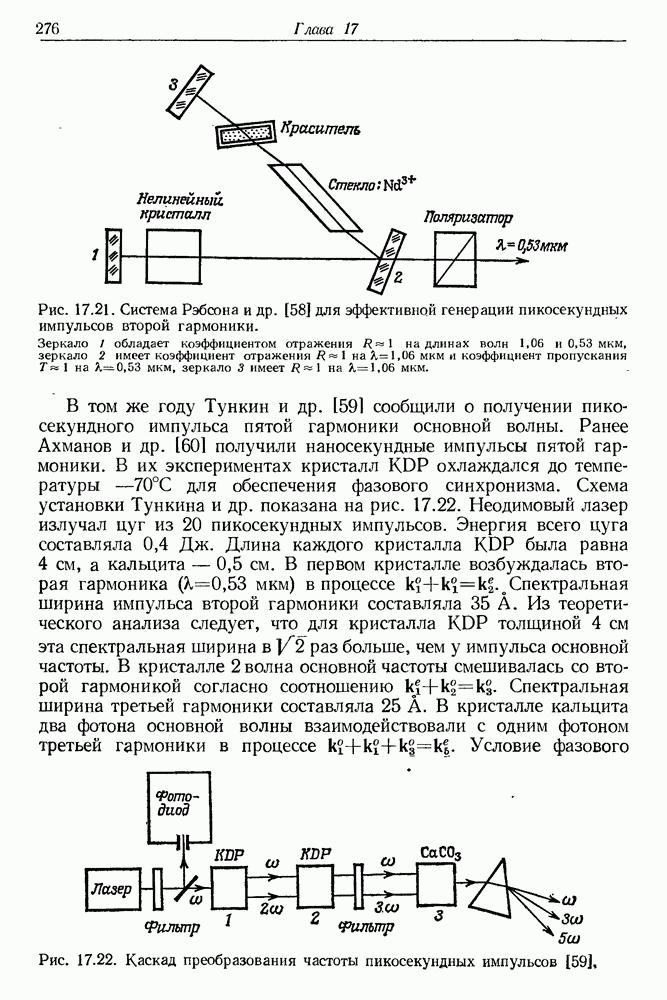
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
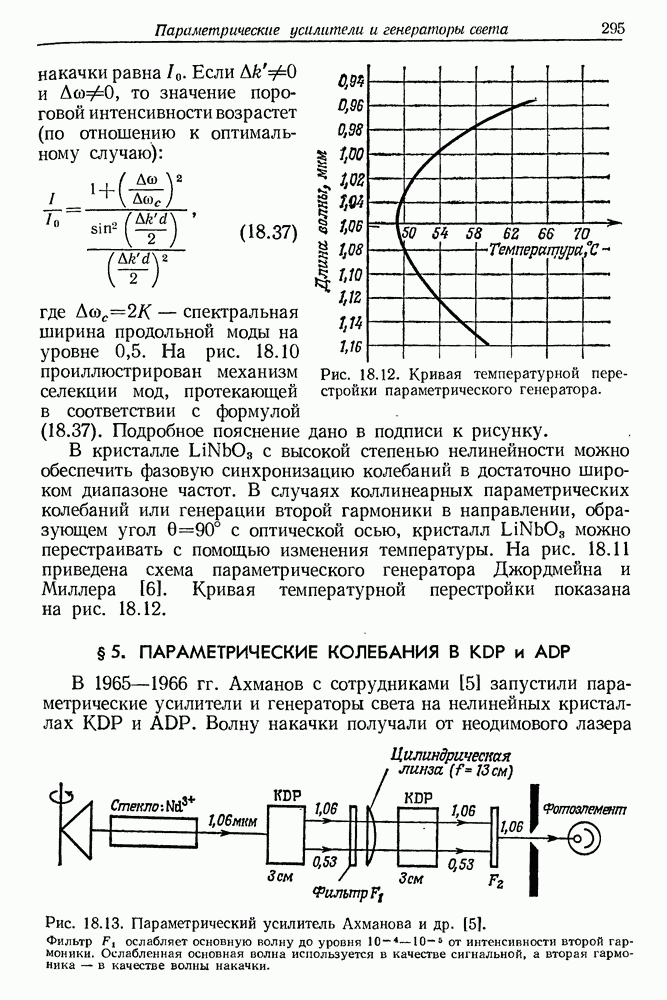
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
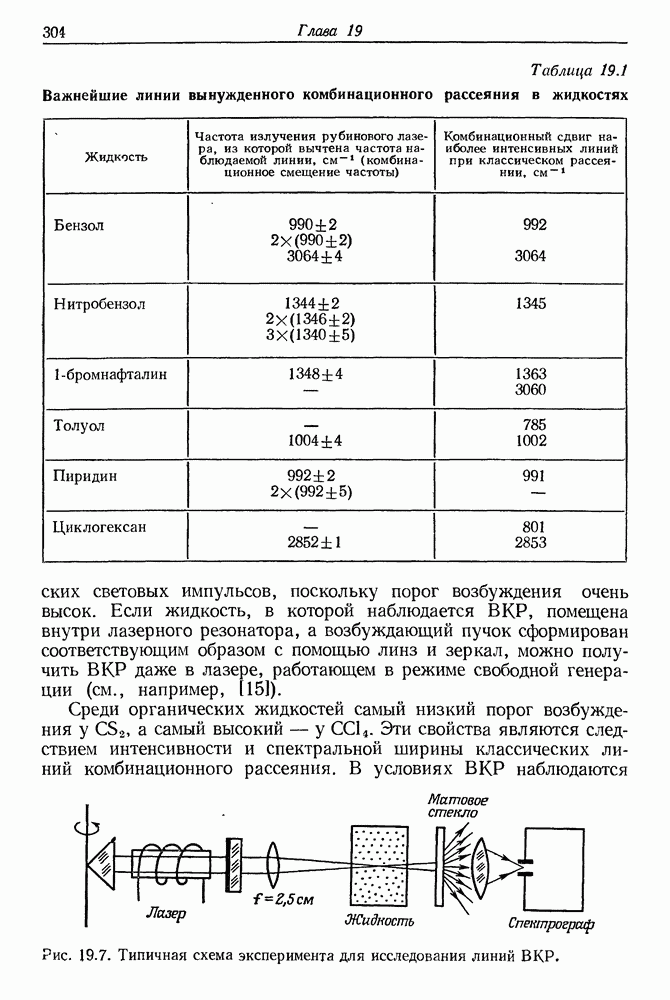
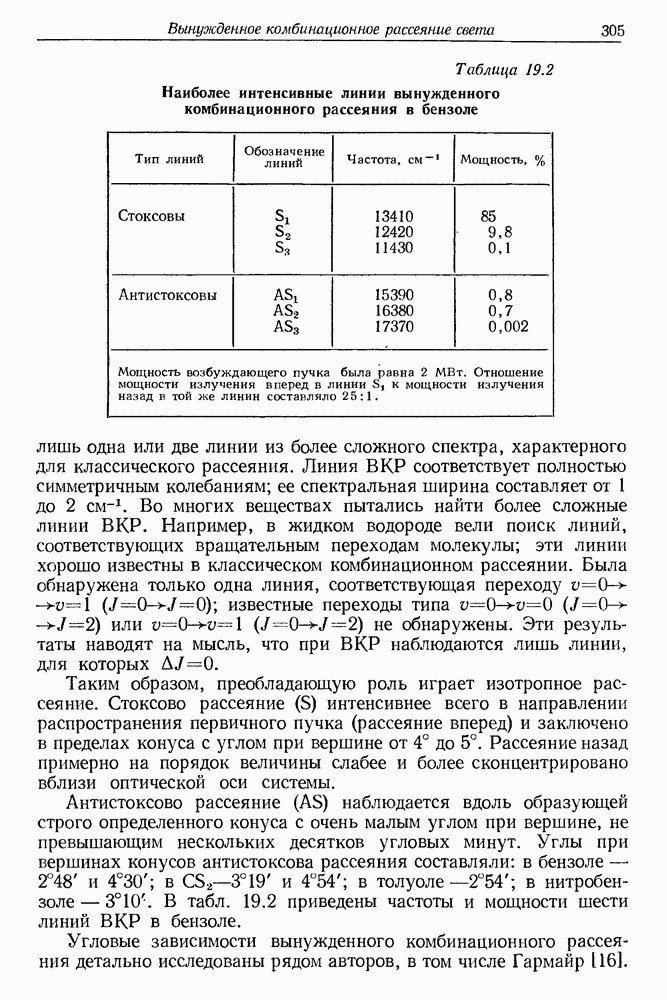
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
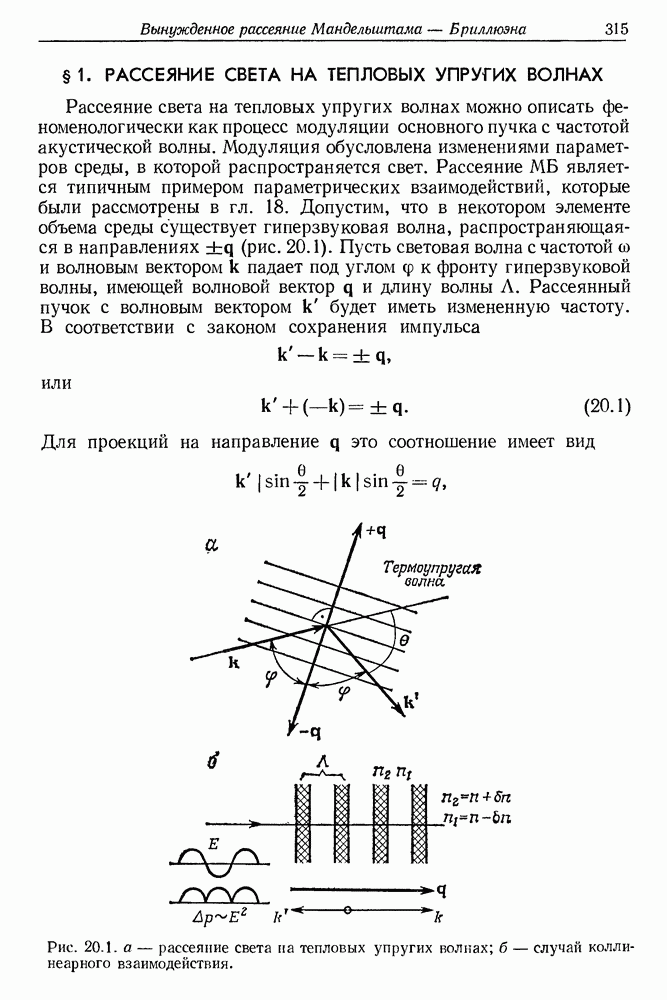
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
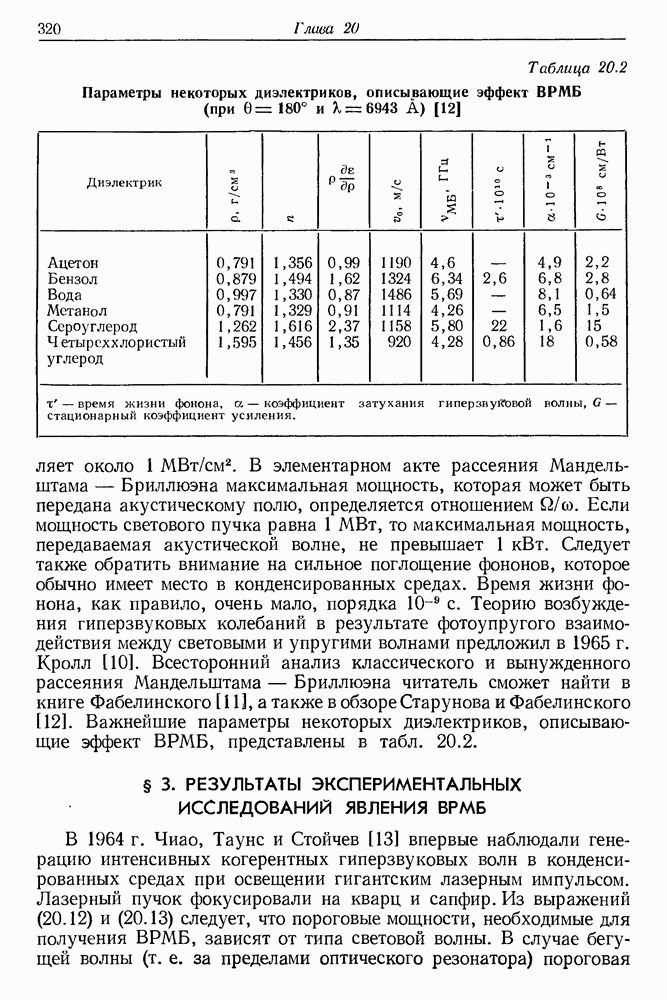
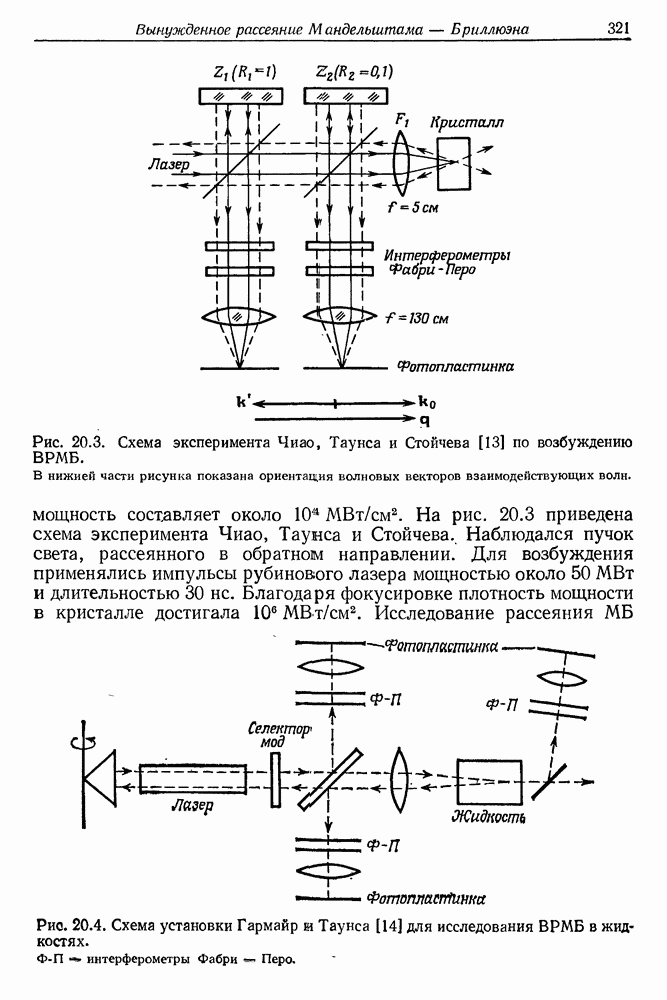
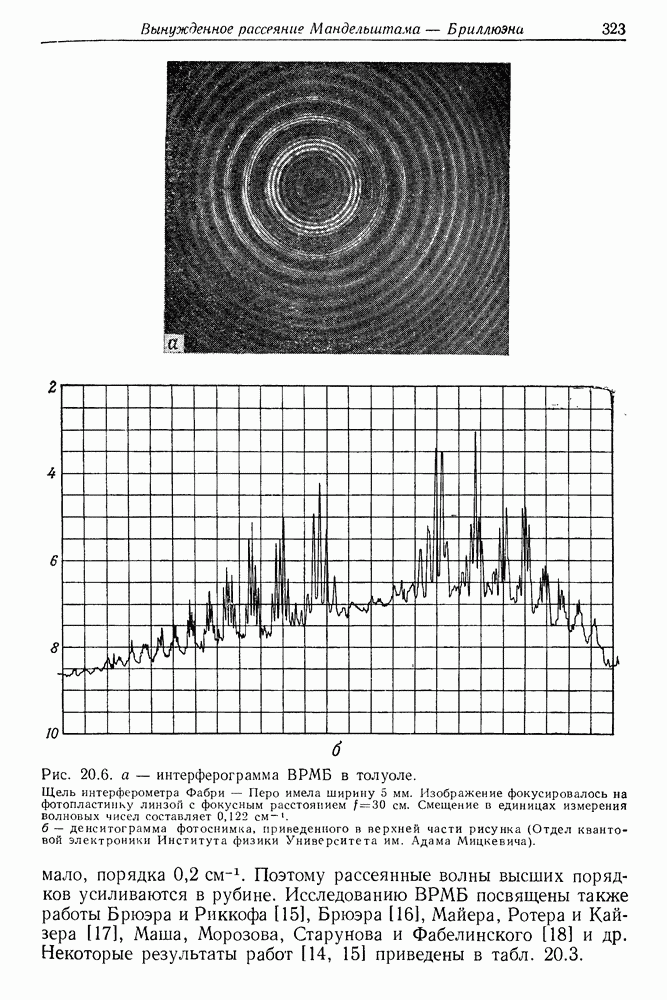
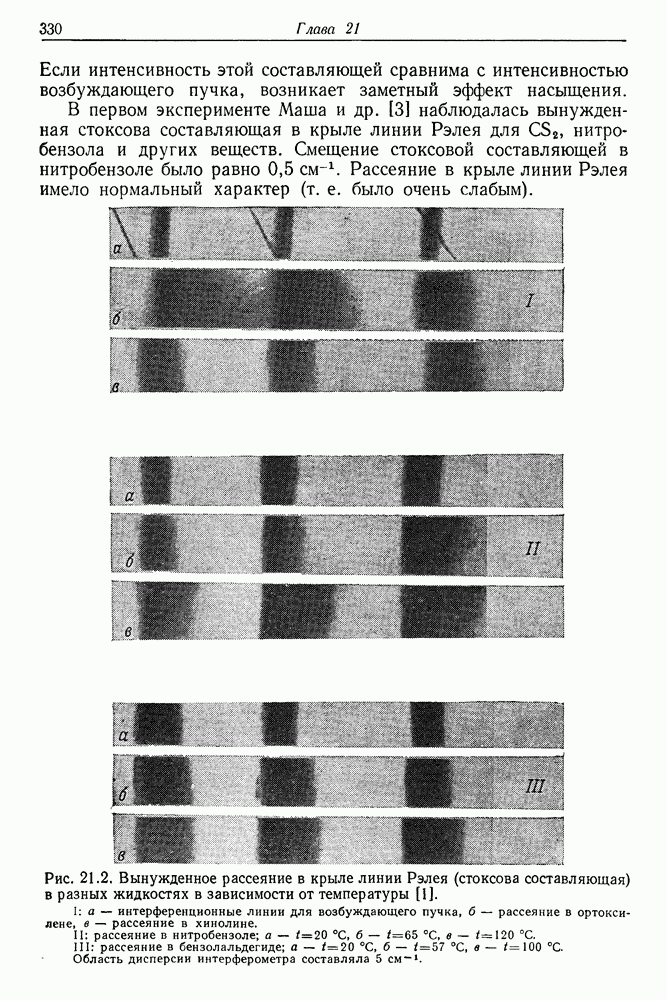
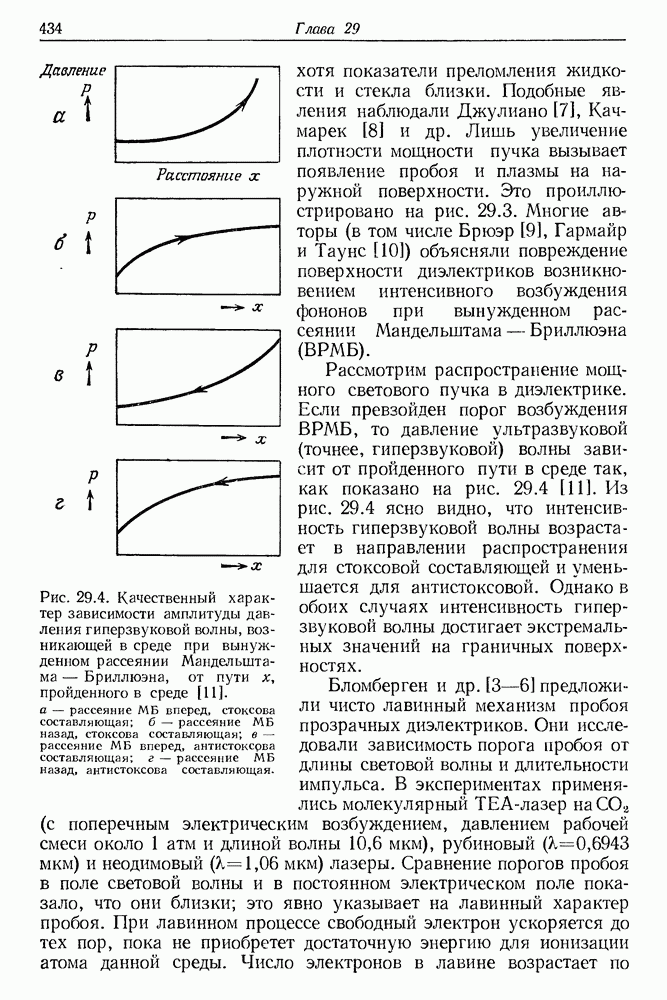
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
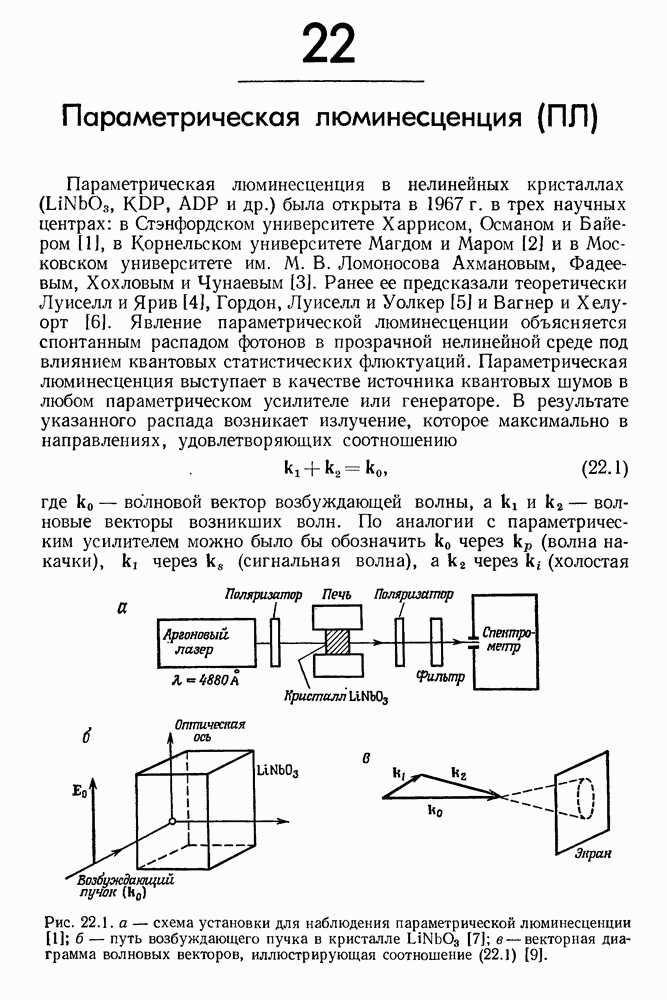
- 22. Параметрическая люминесценция (ПЛ)
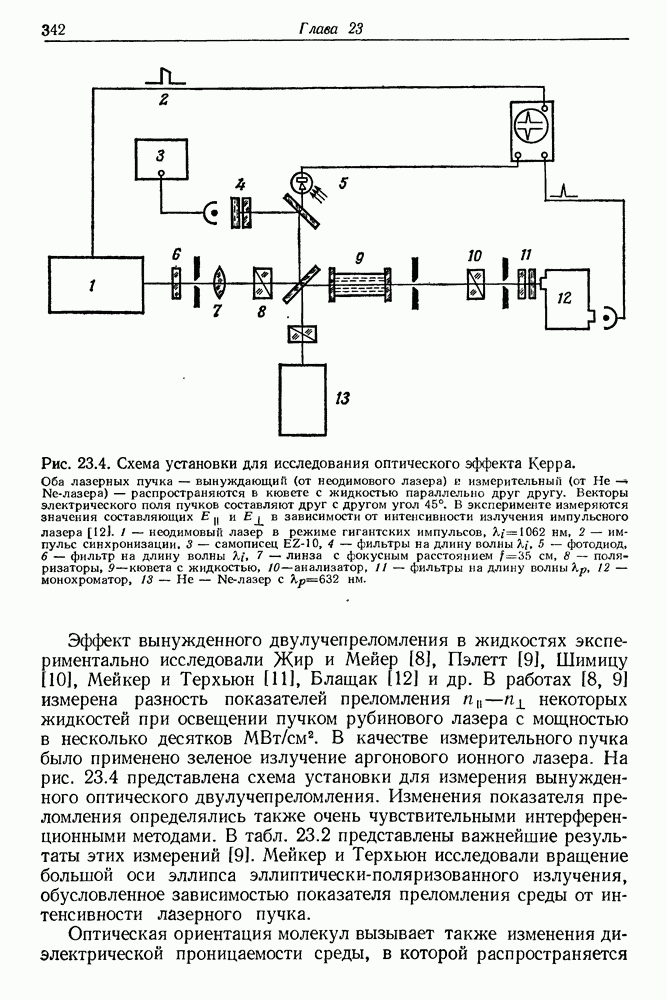
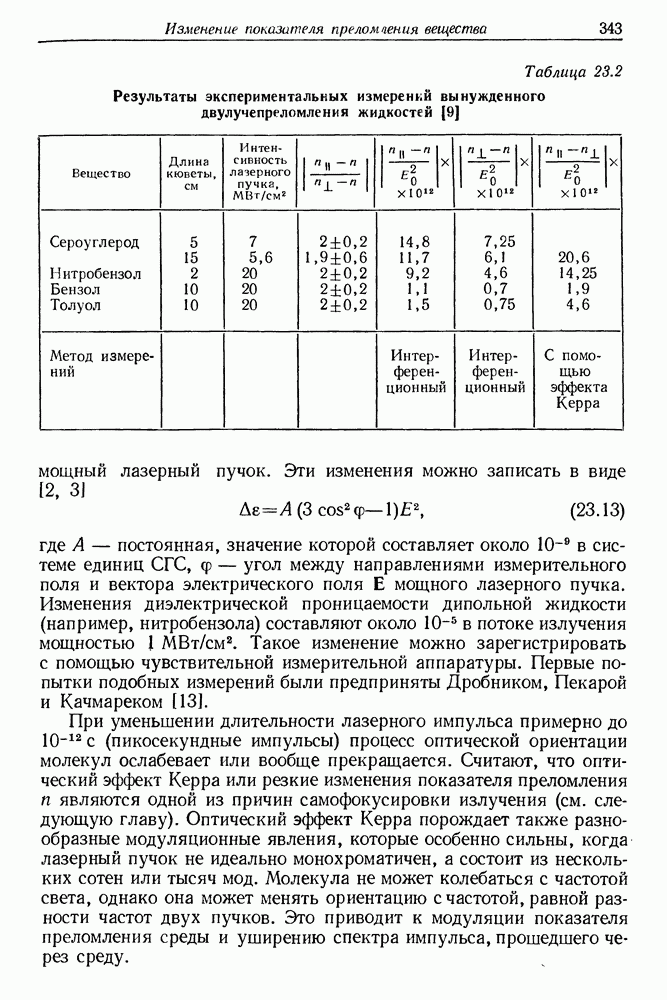
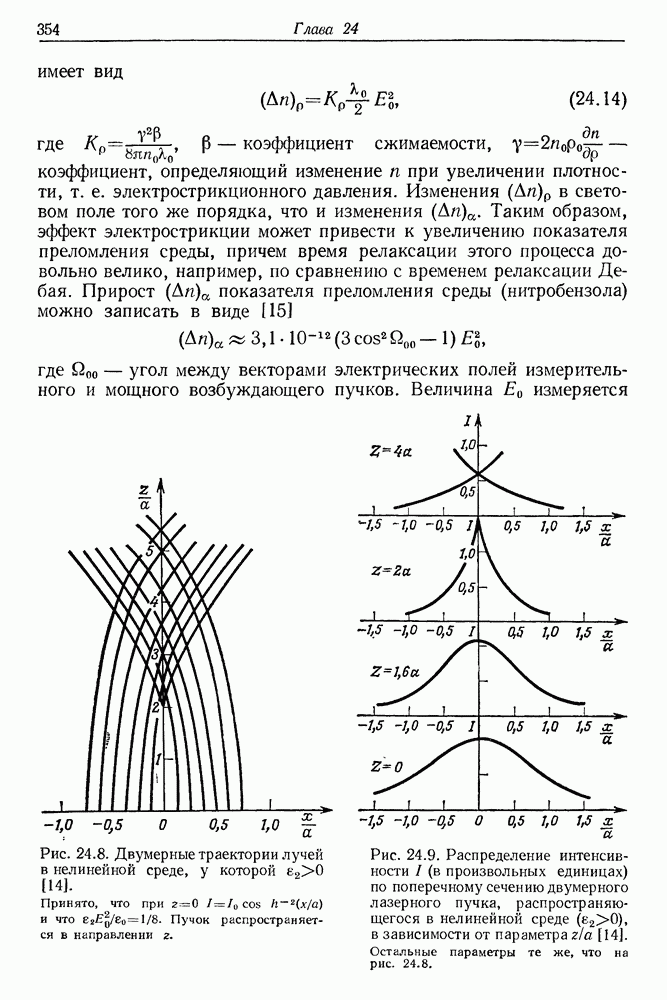
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
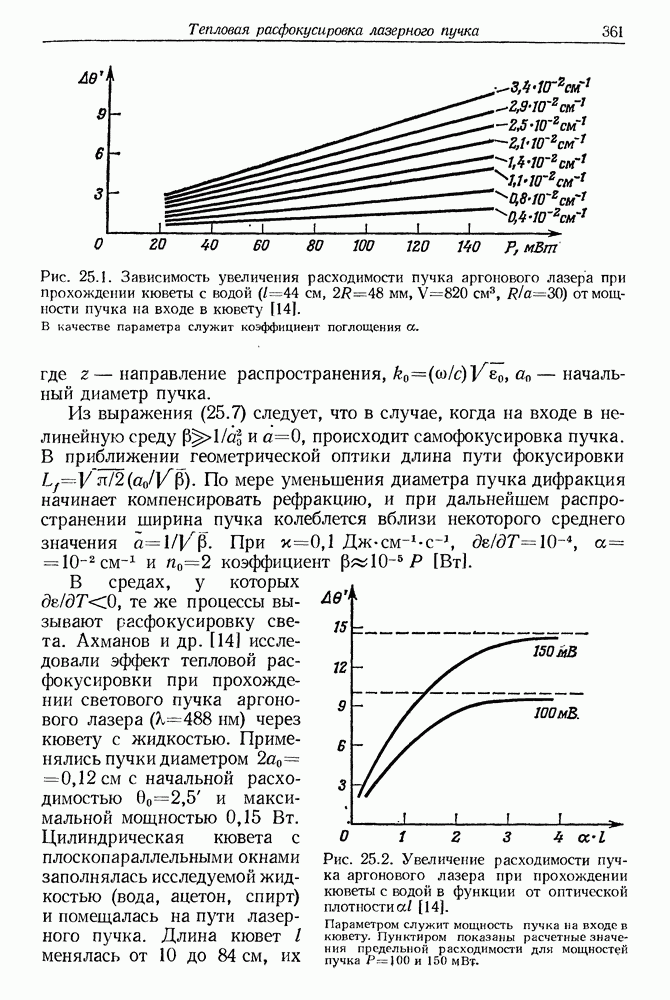
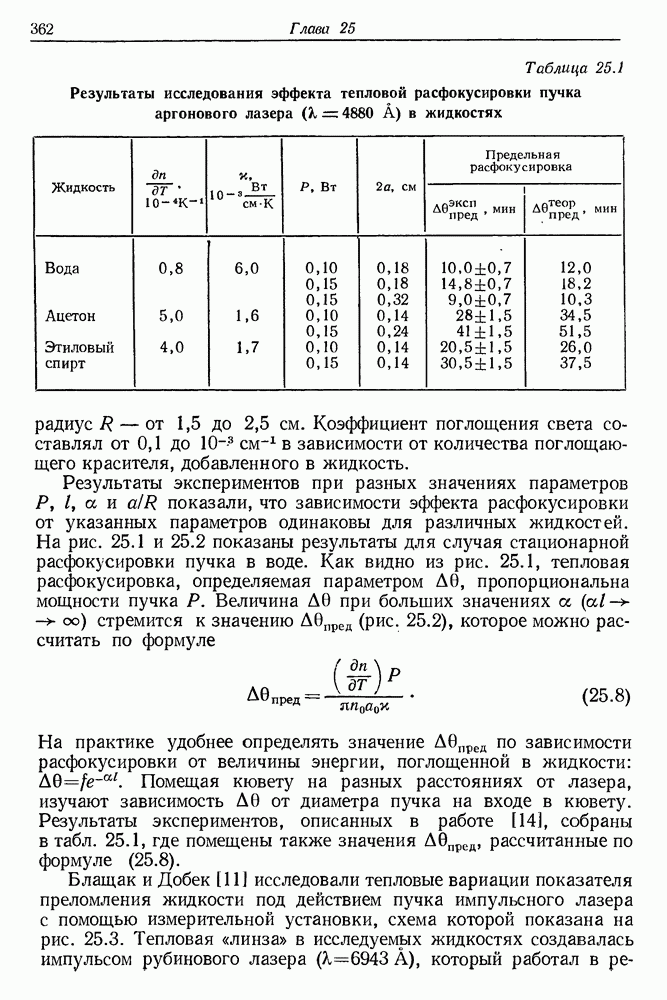
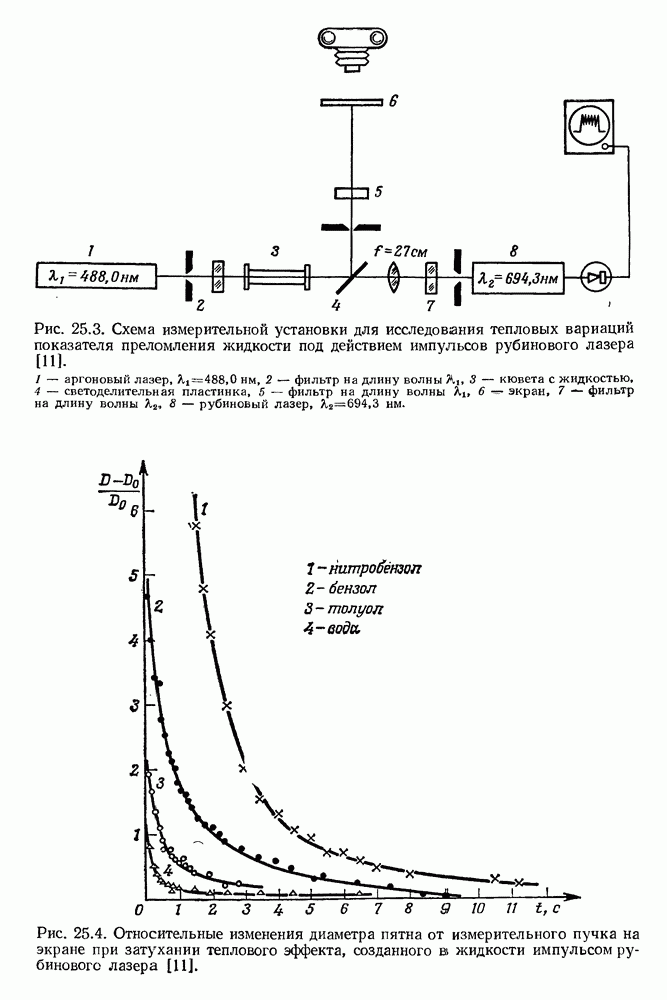
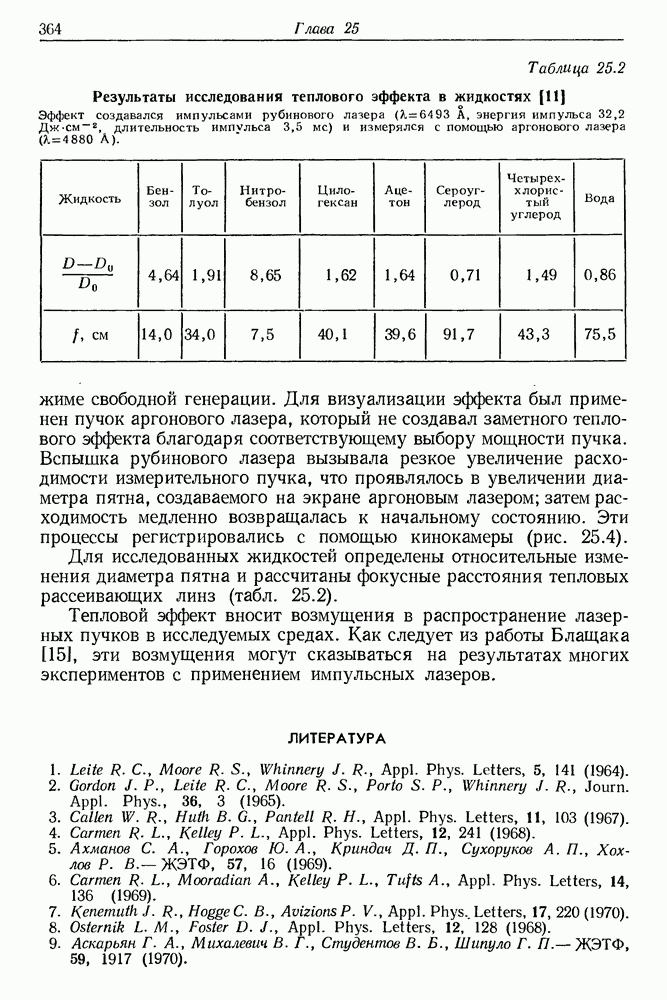
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
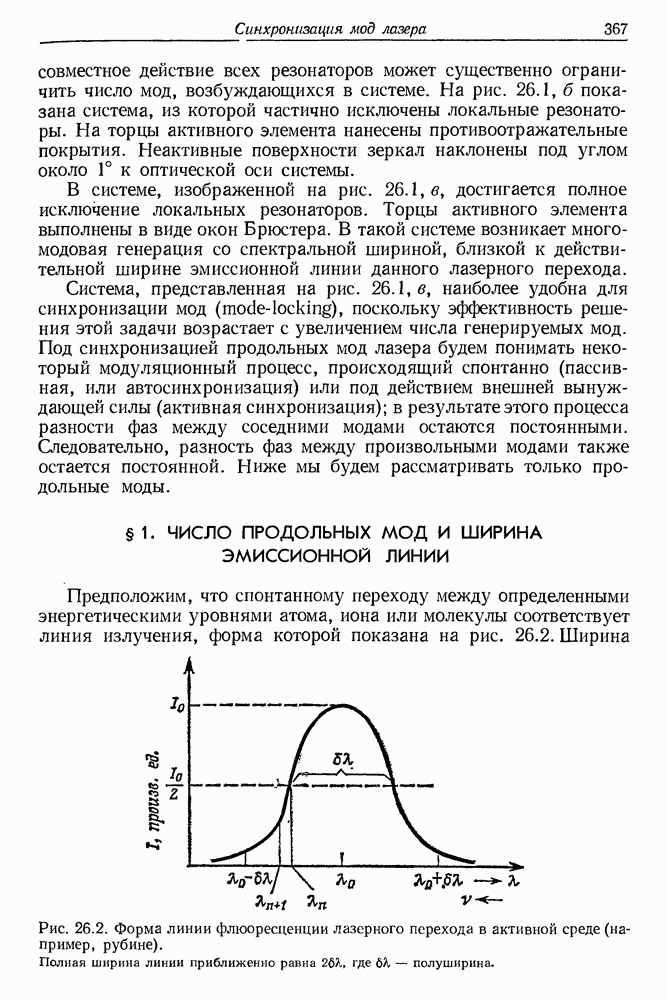
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
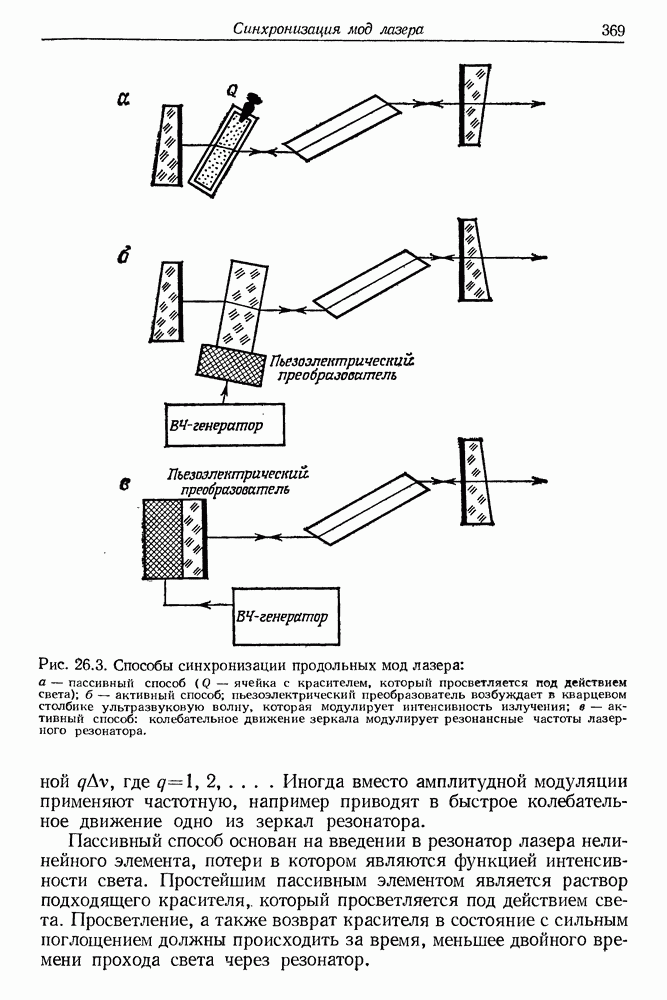
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
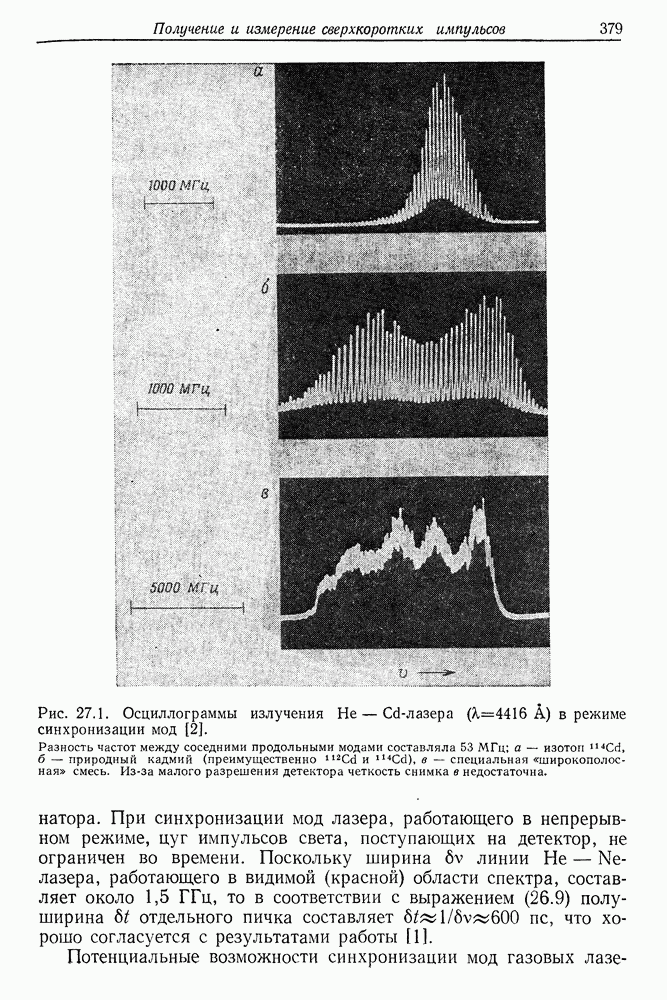
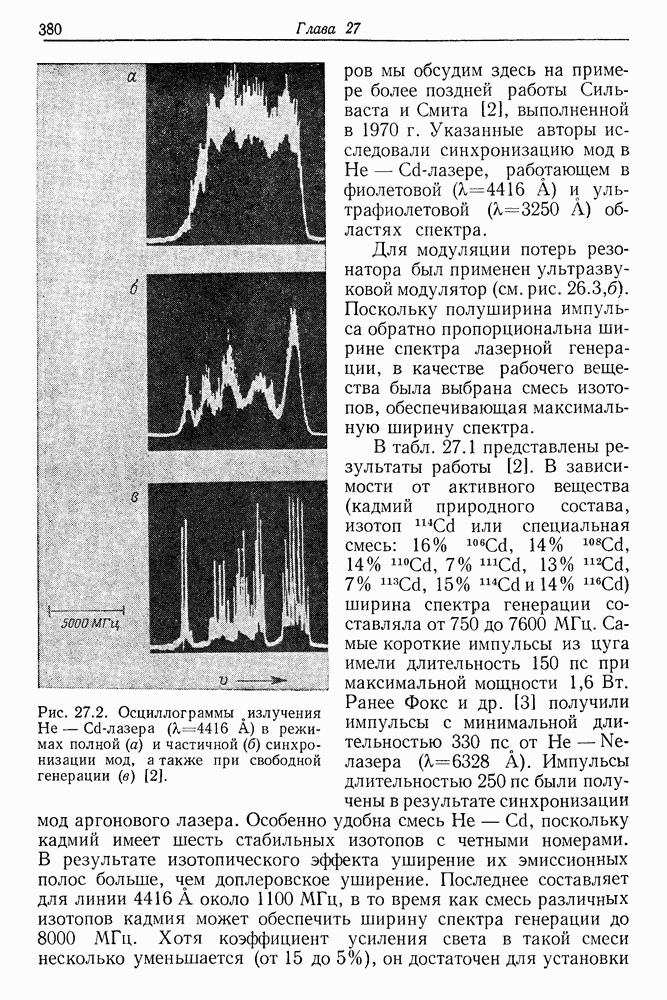
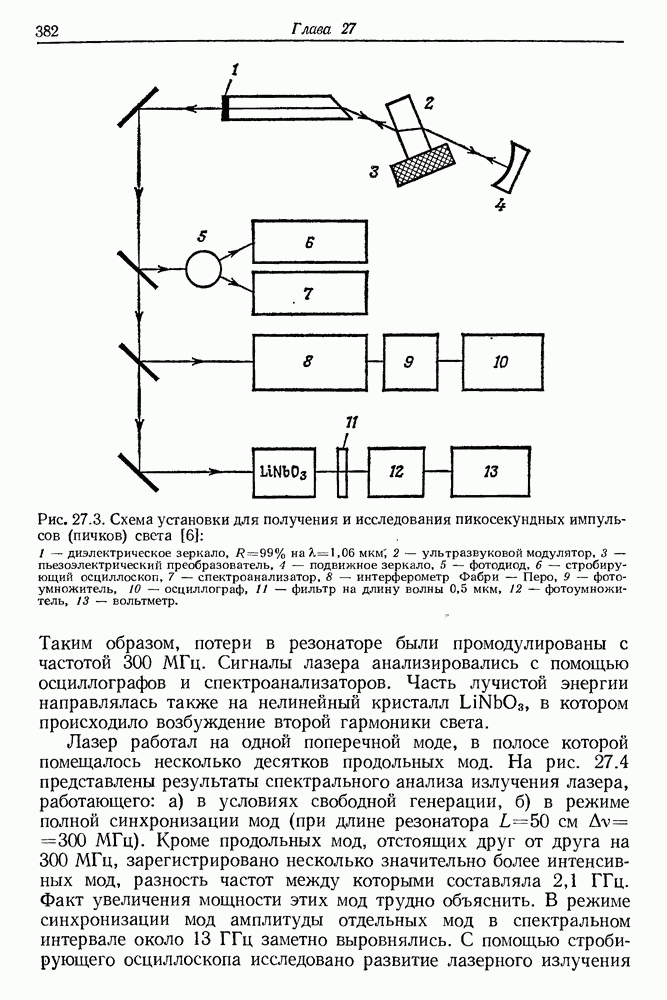
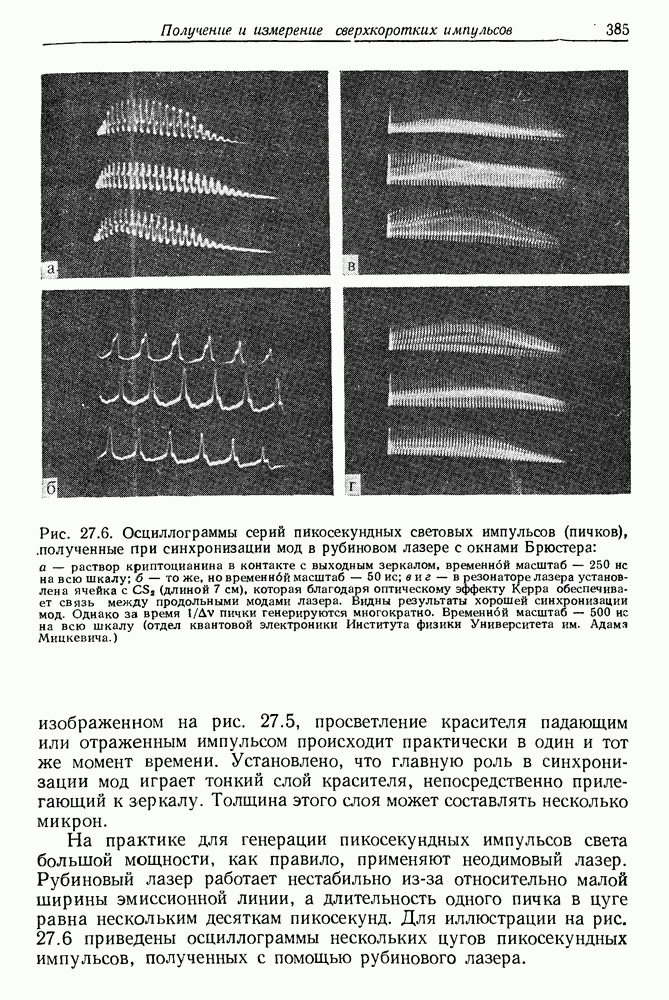
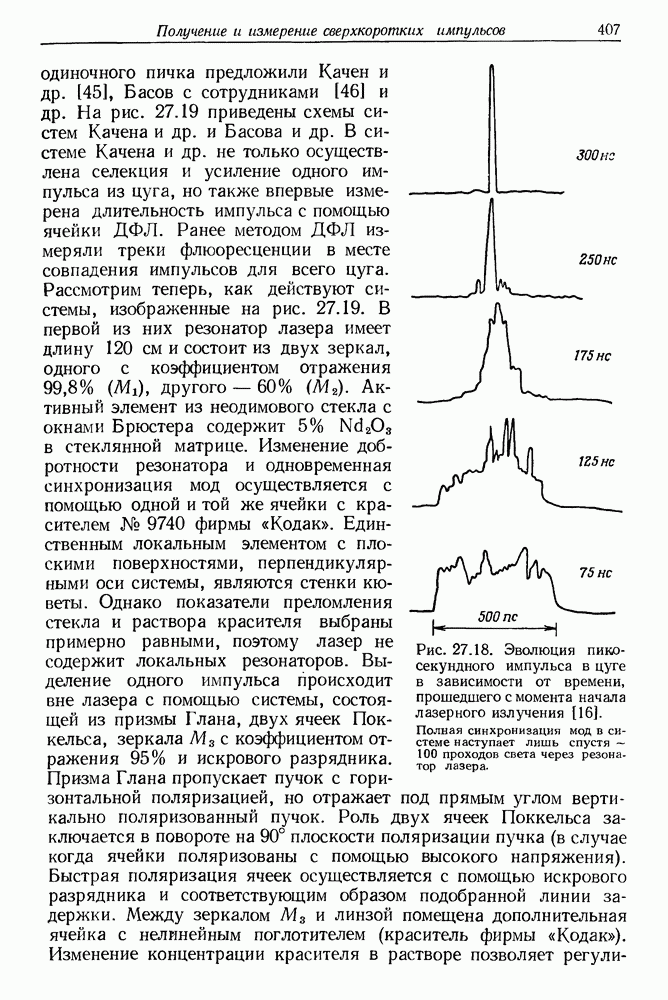
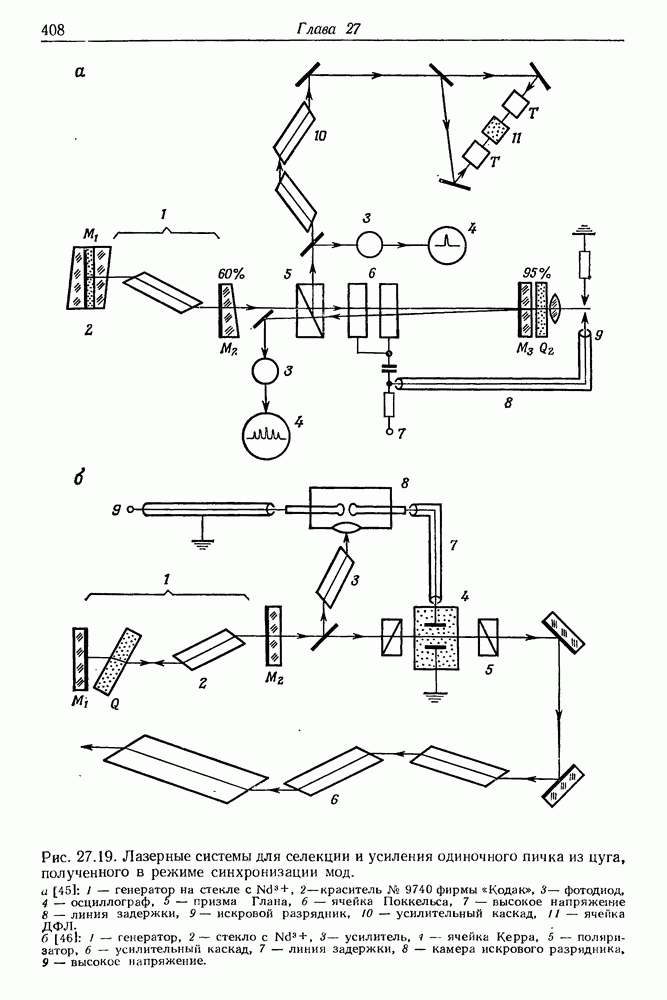
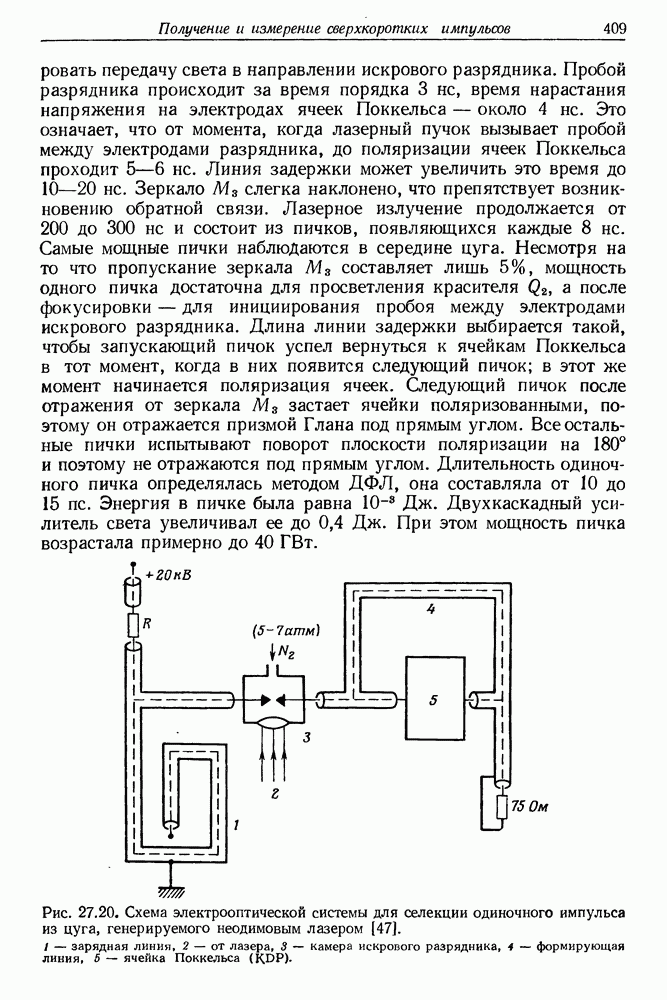
- 27. Получение и измерение сверхкоротких импульсов света
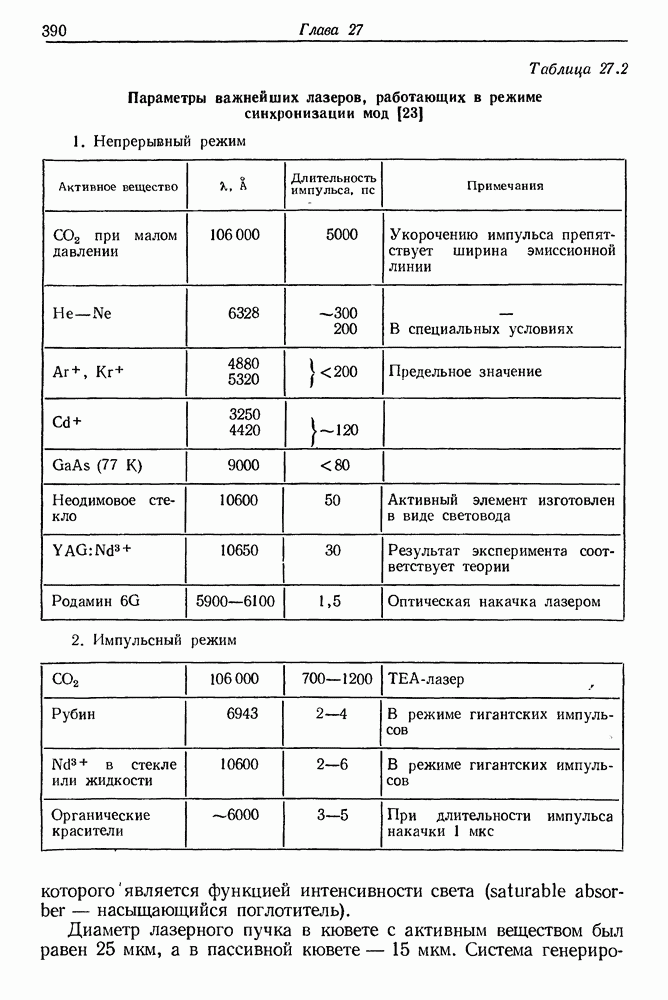
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
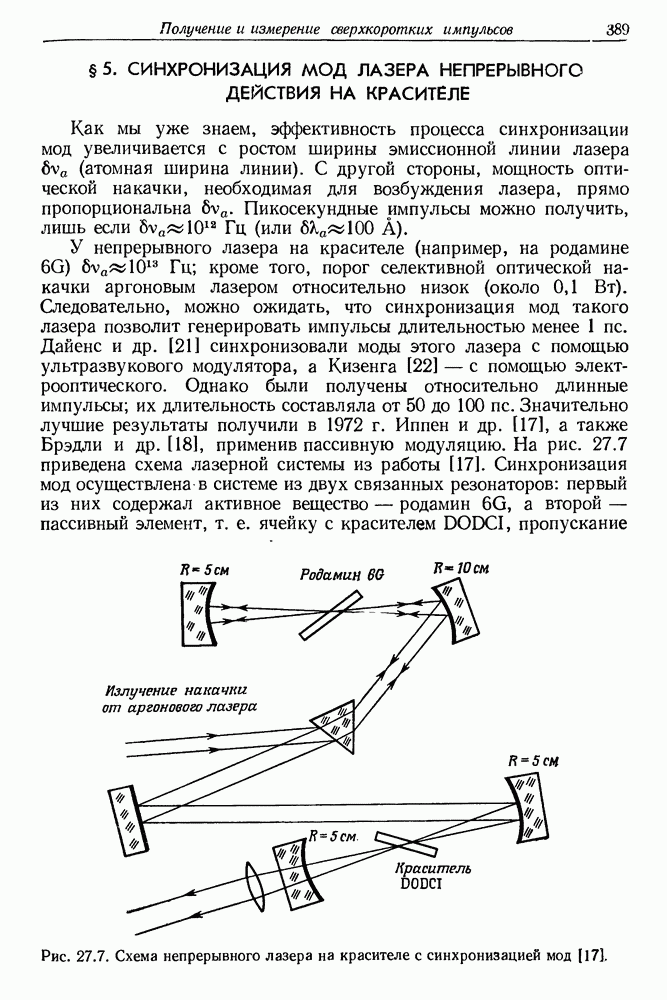
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
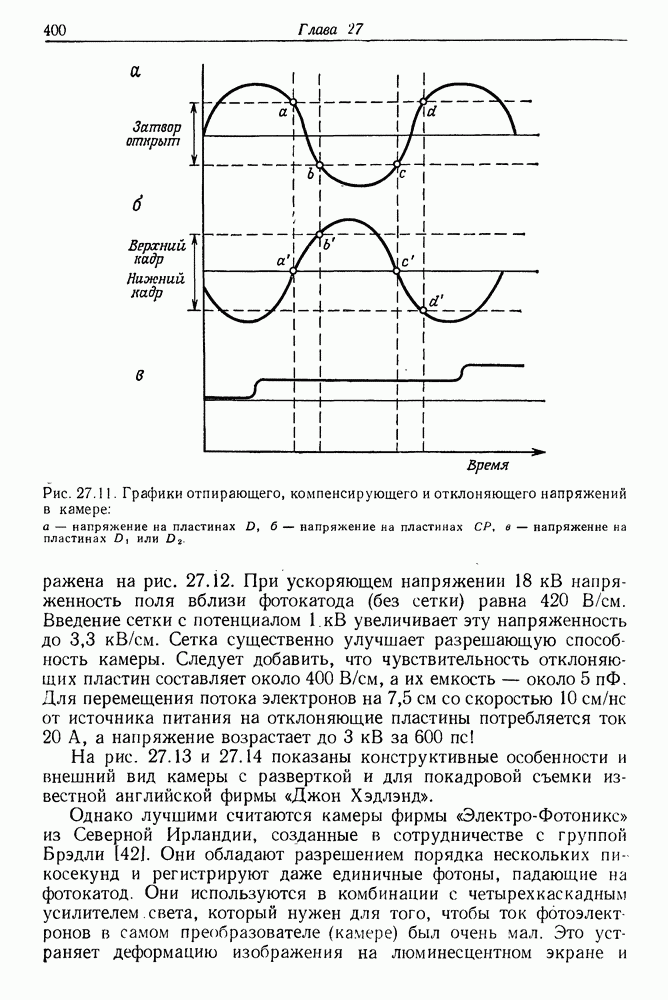
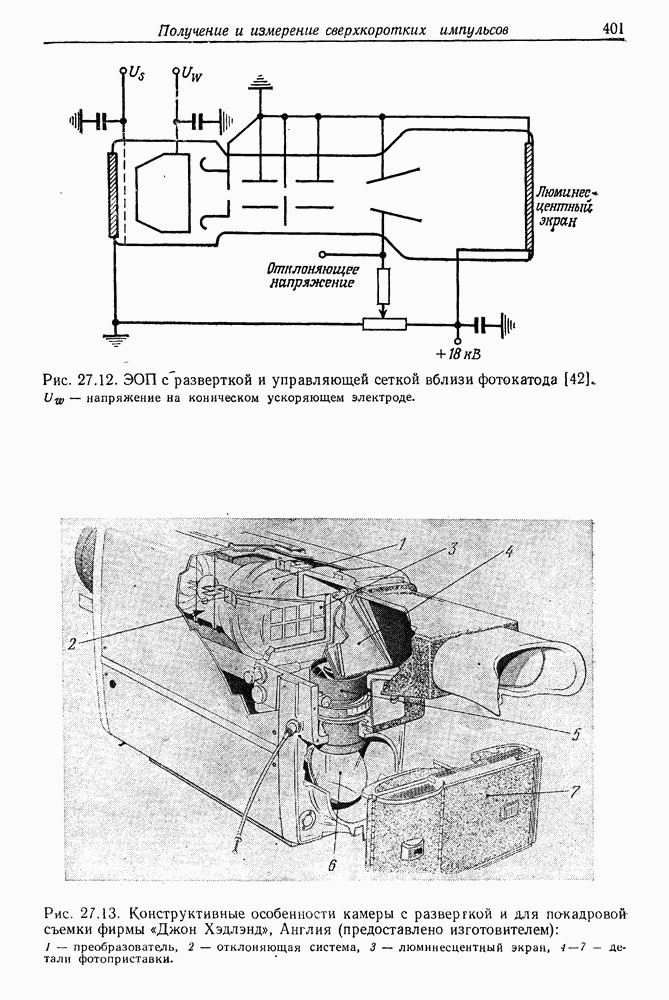
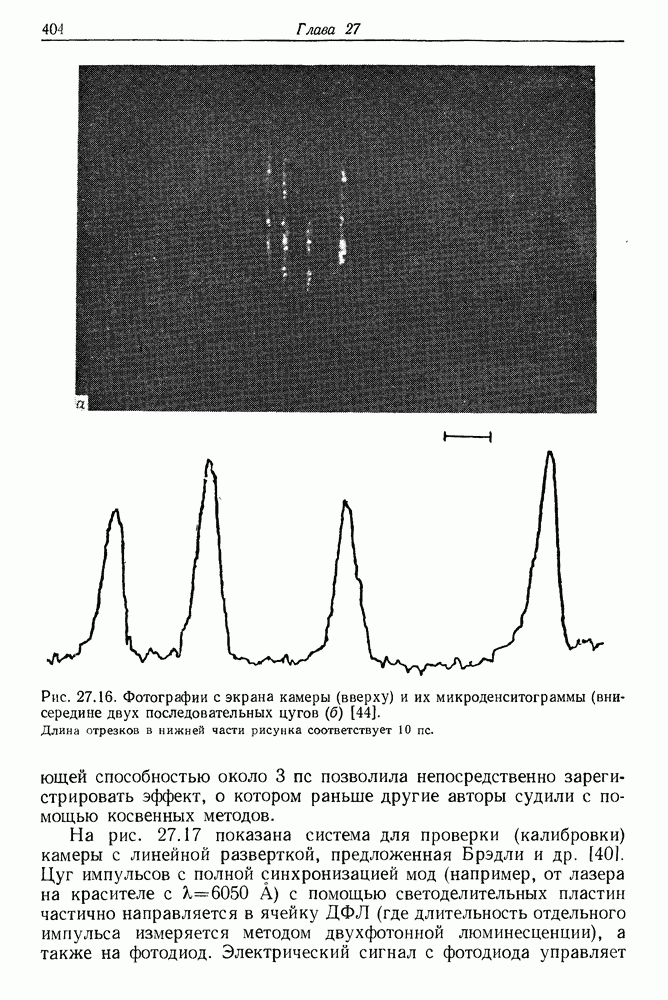
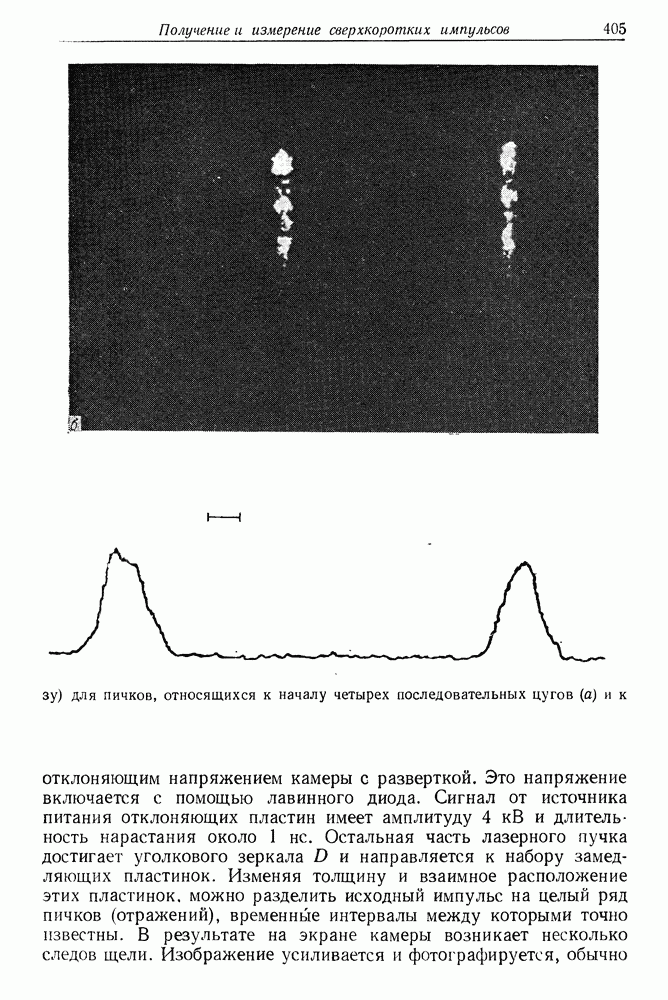
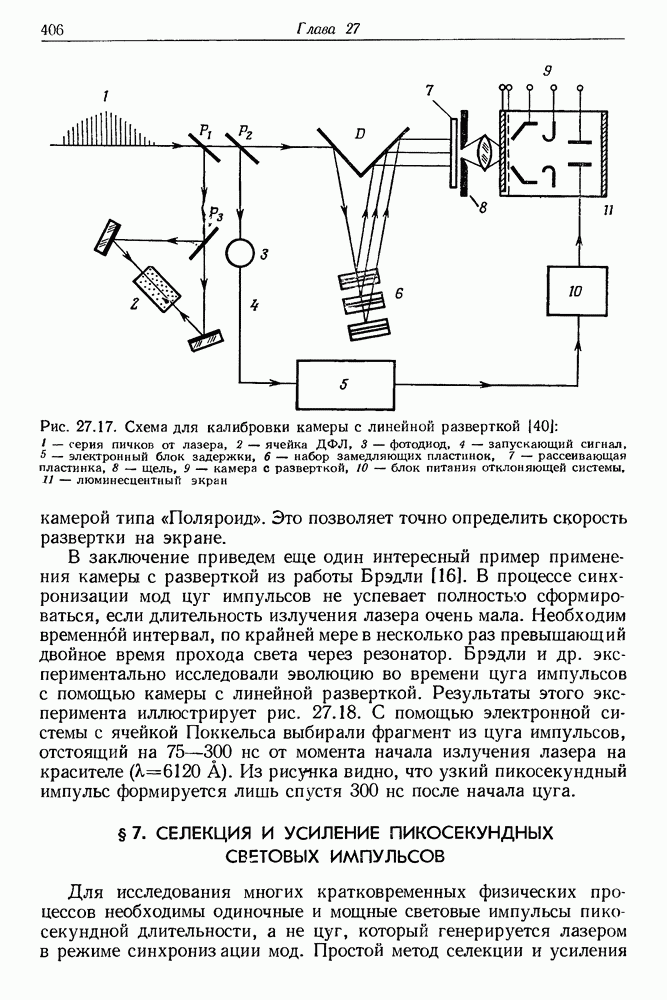
- в. Примеры использования камеры с разверткой
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
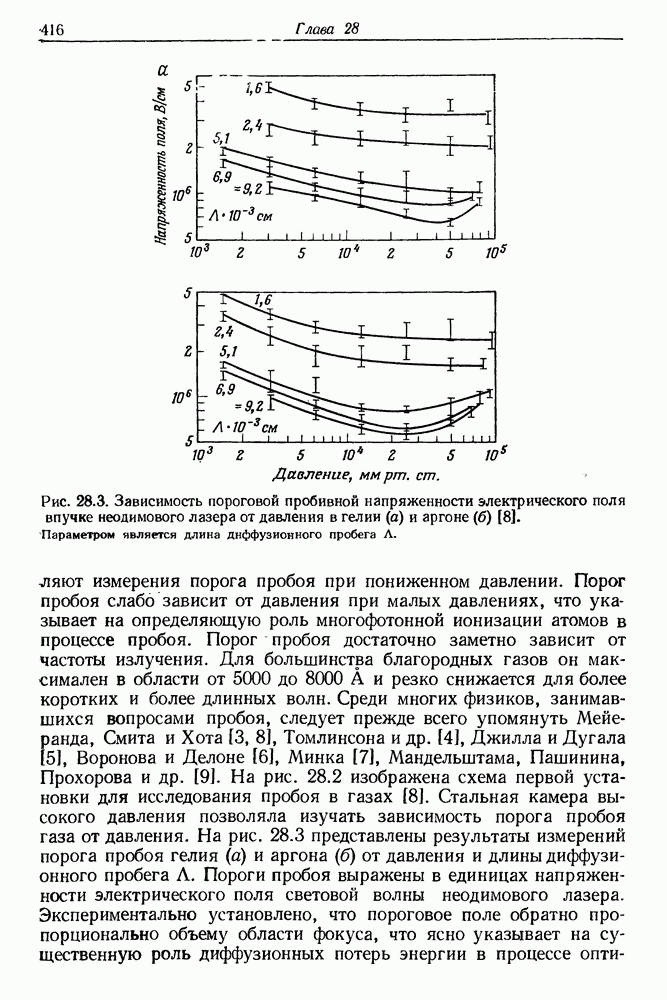
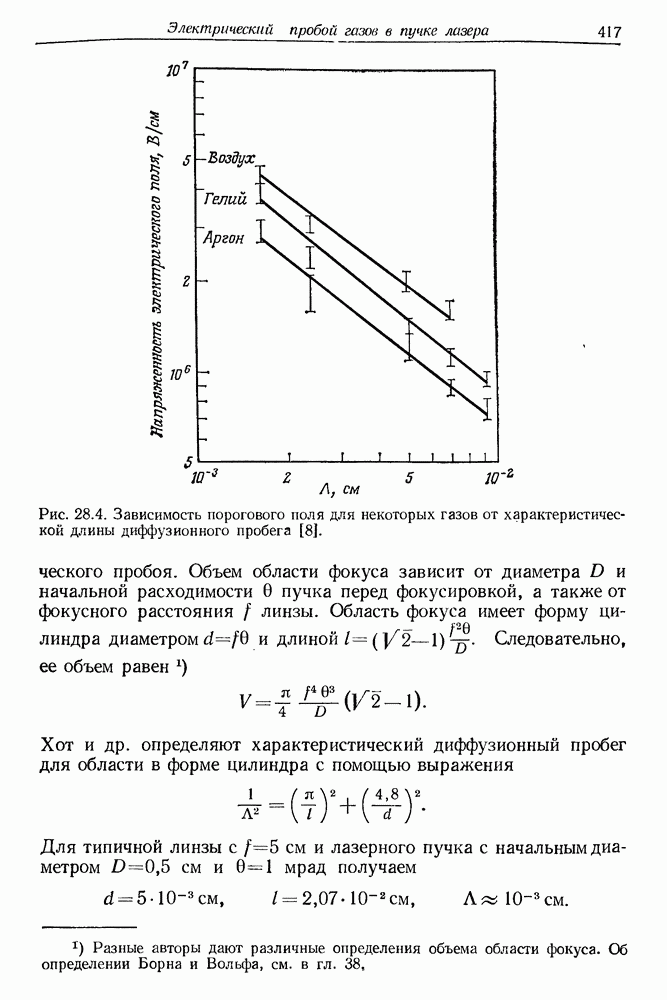
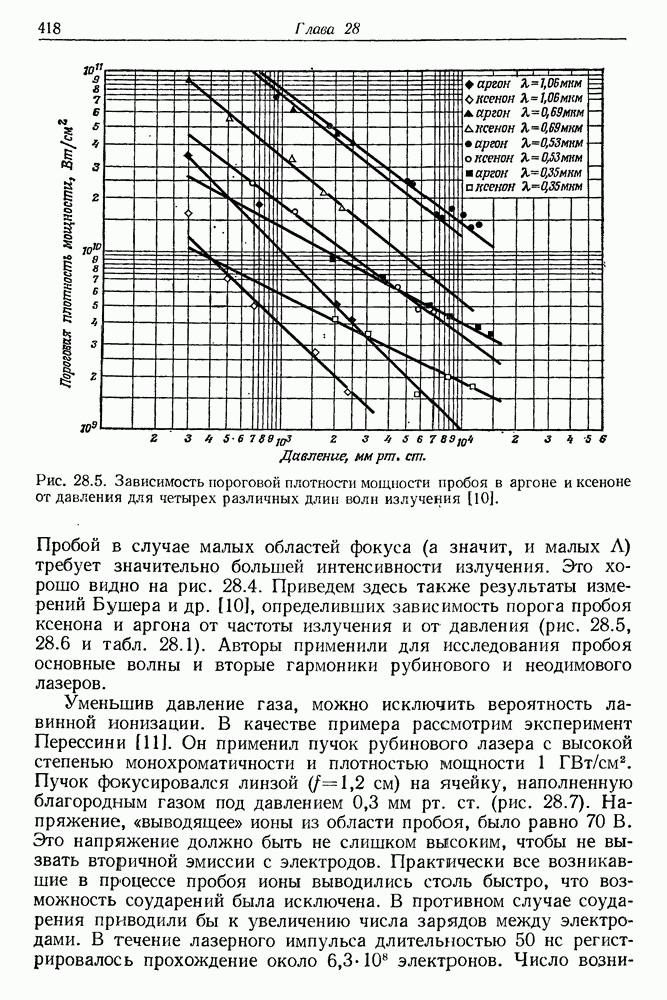
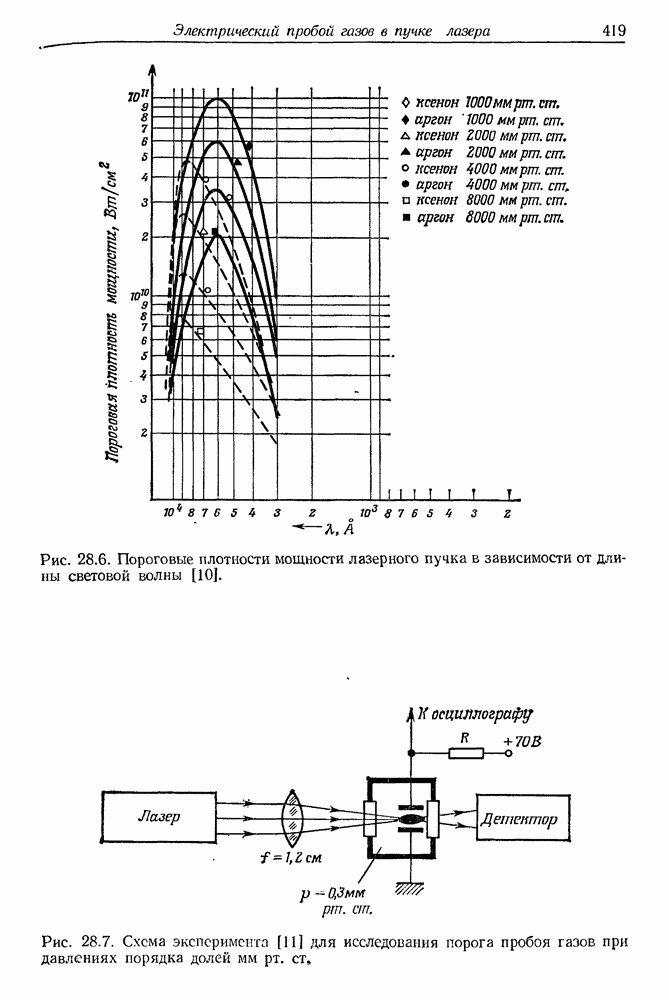
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
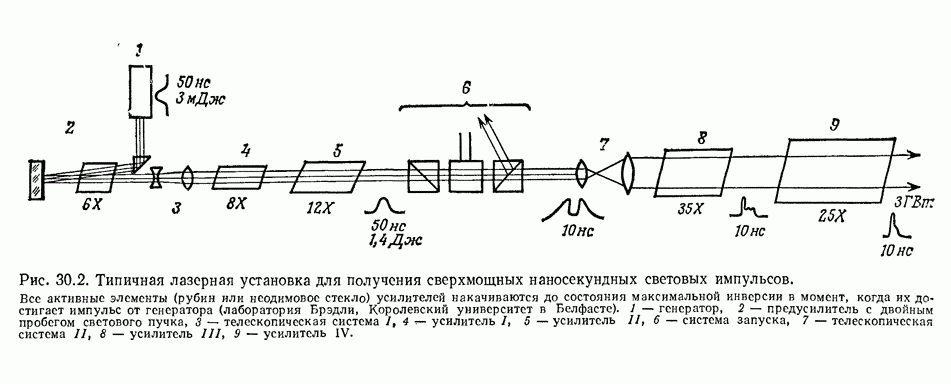
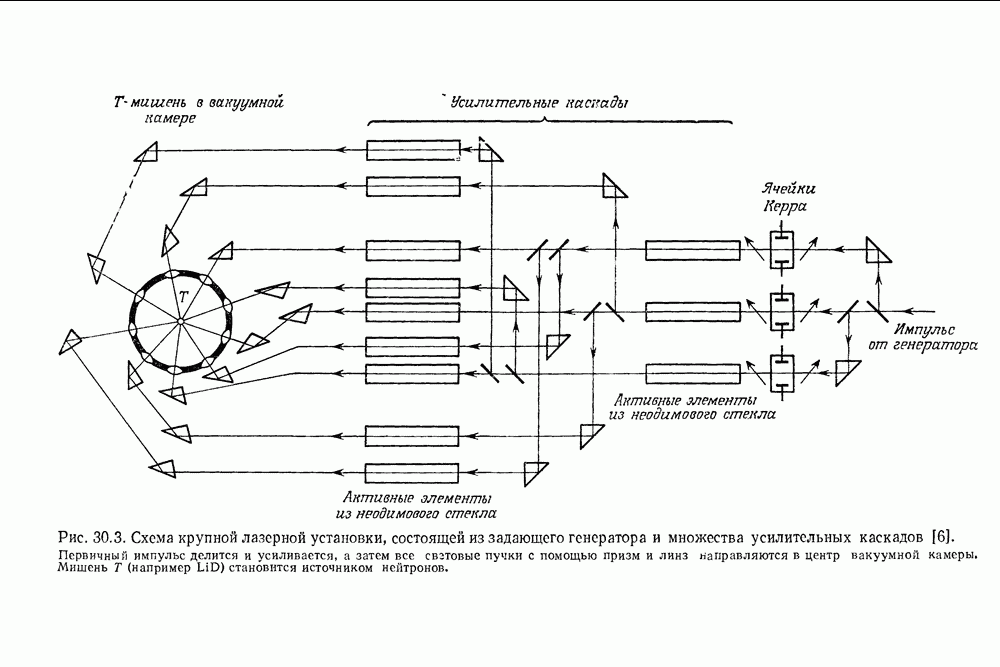
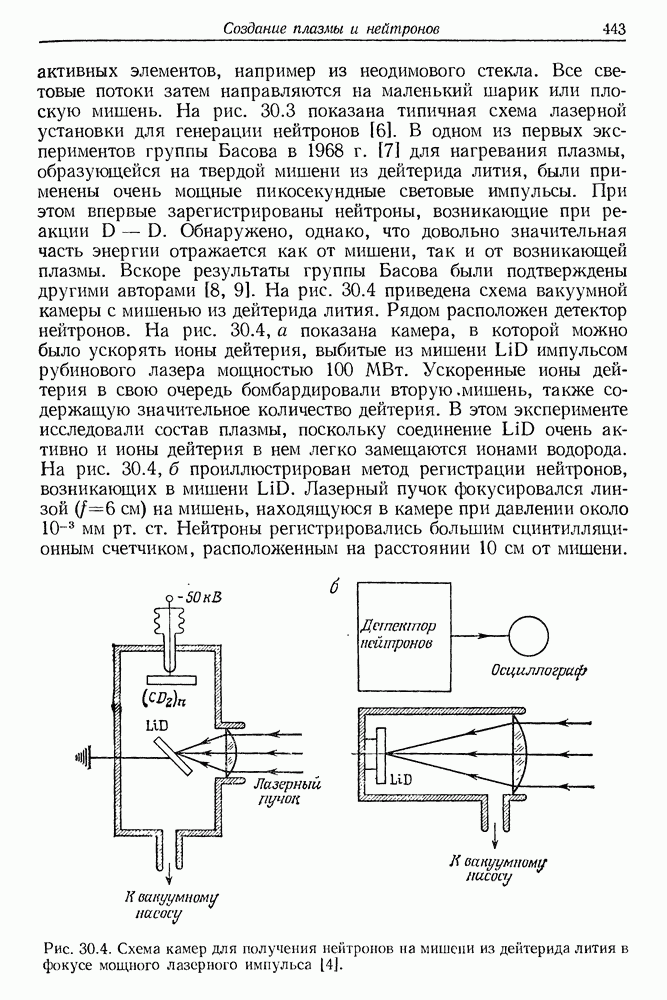
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
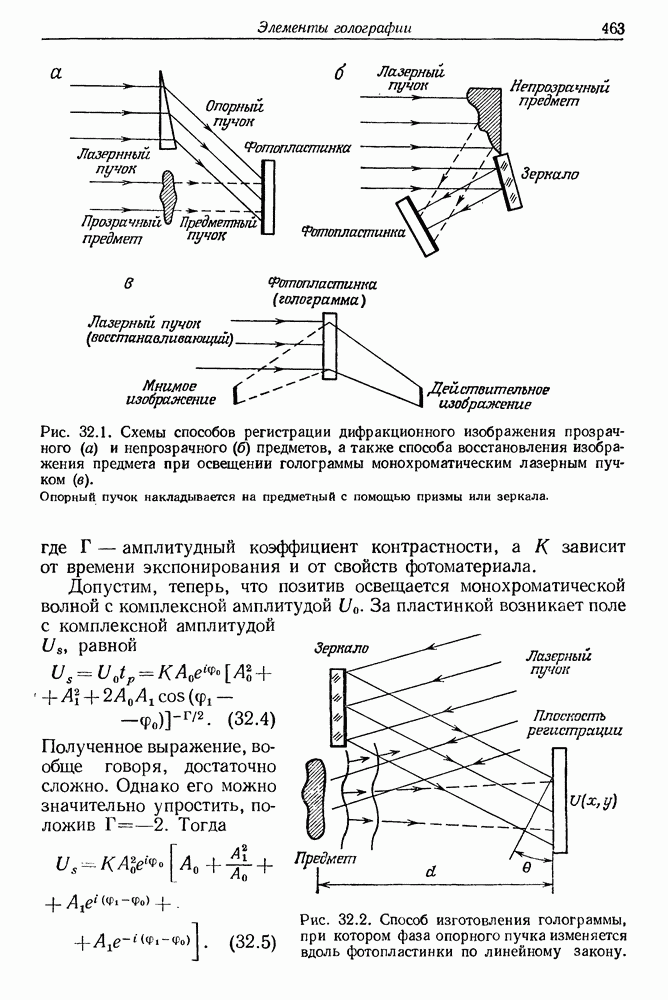
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
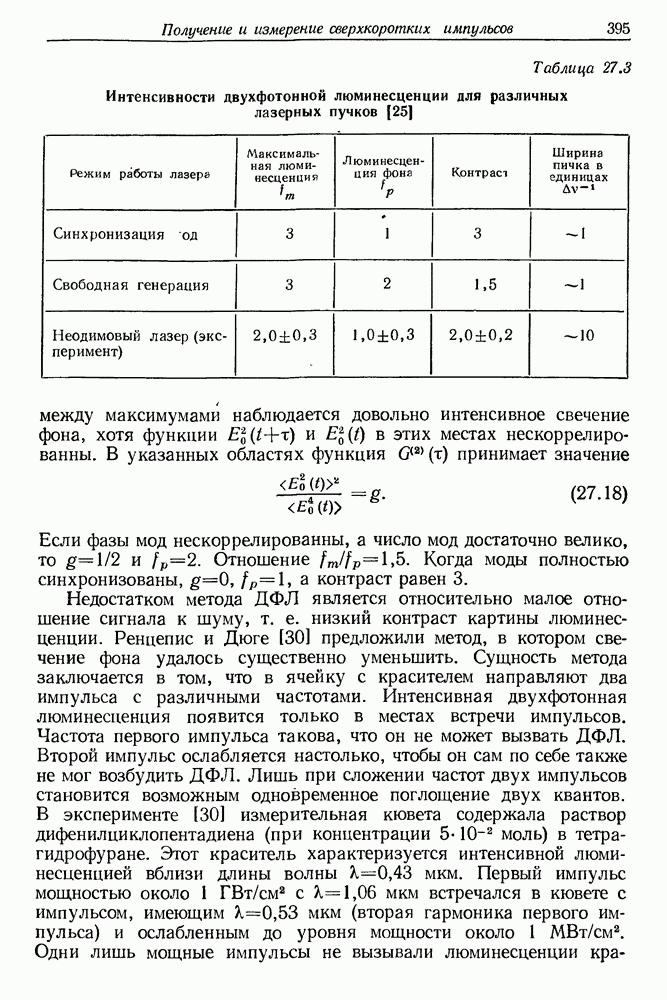
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
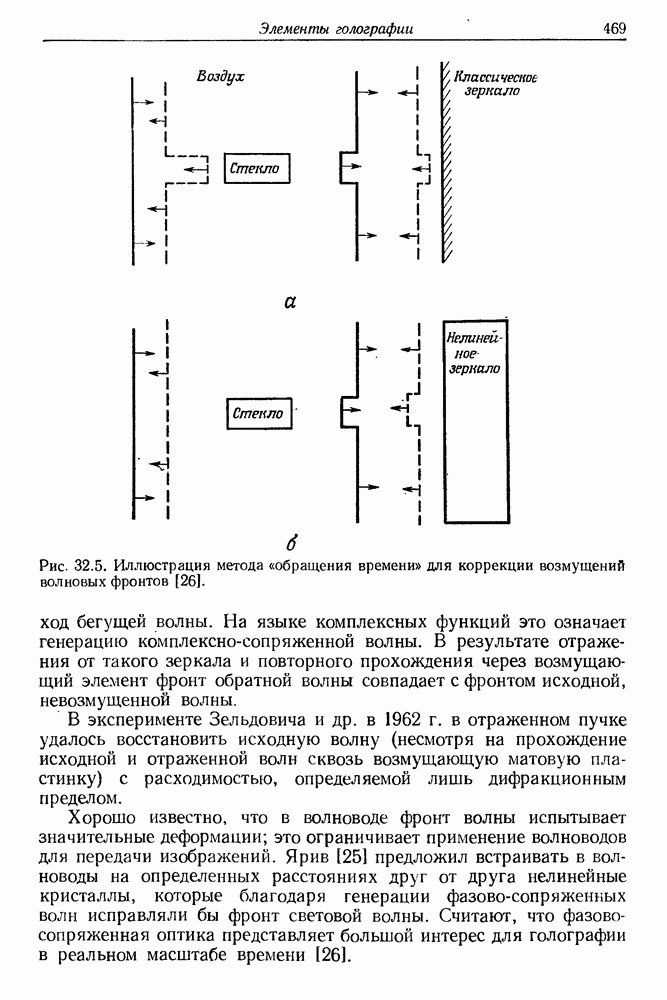
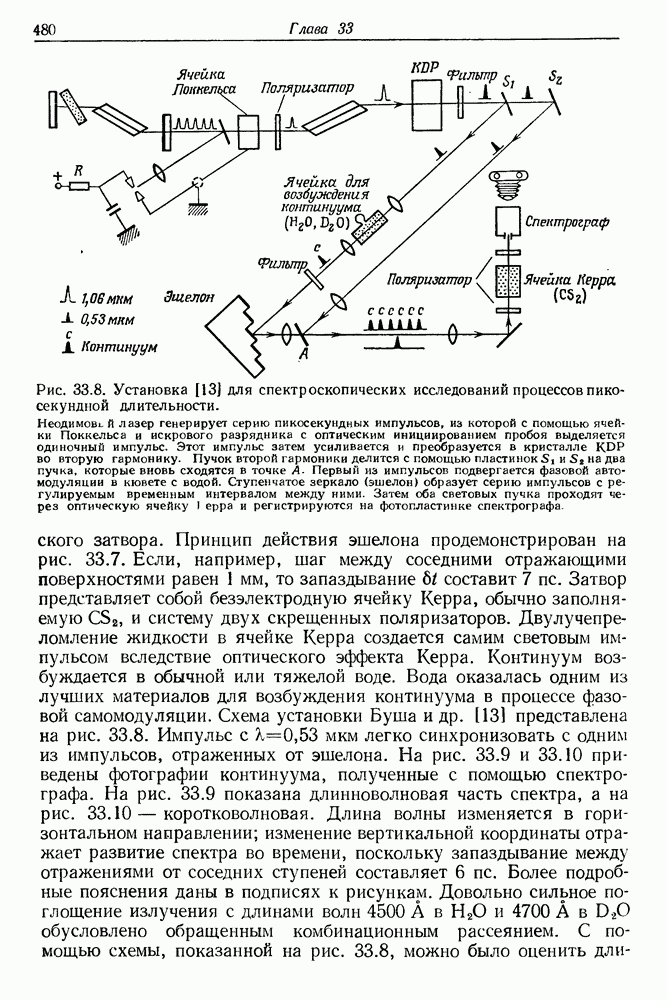
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
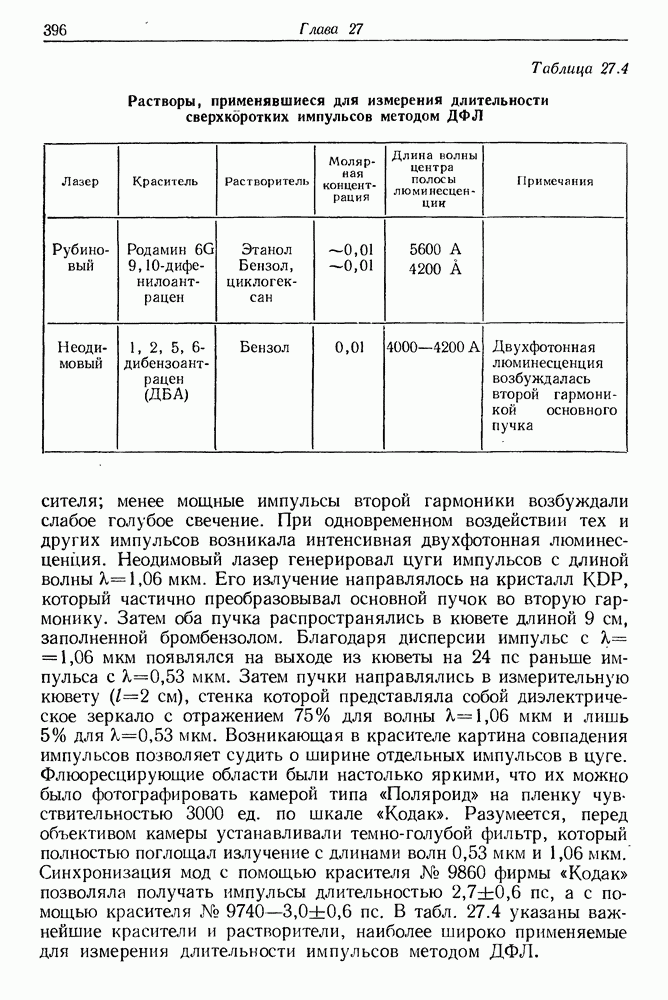
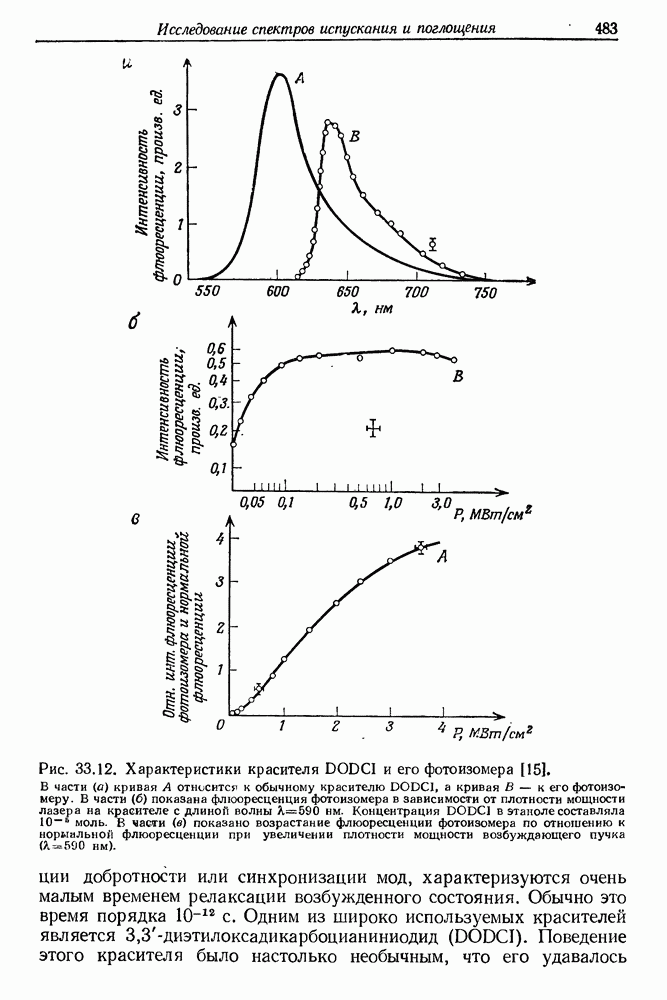
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
- 35. Лазеры на центрах окраски
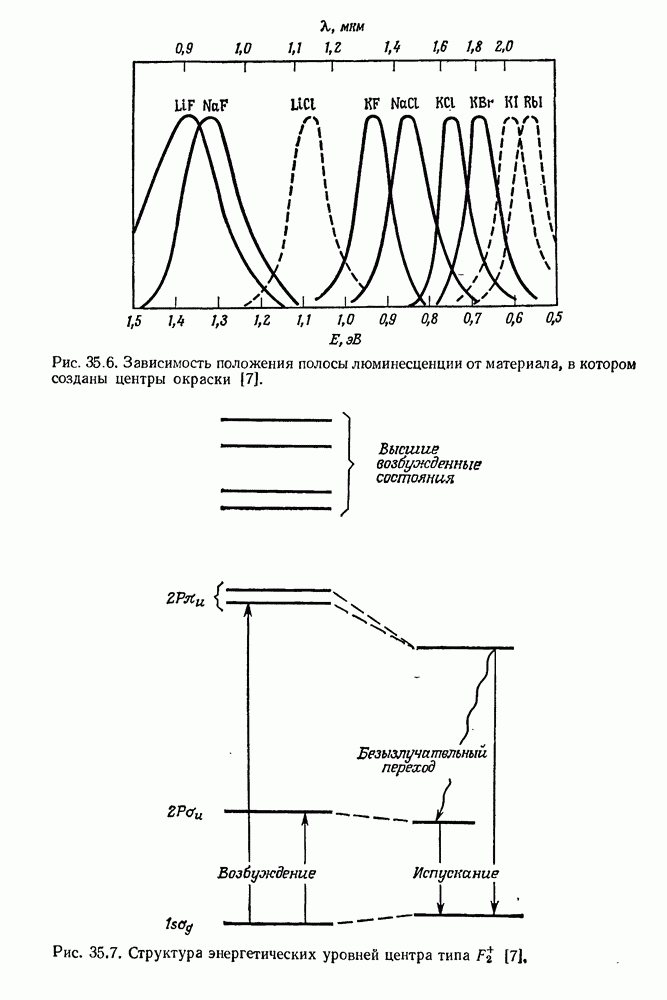
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
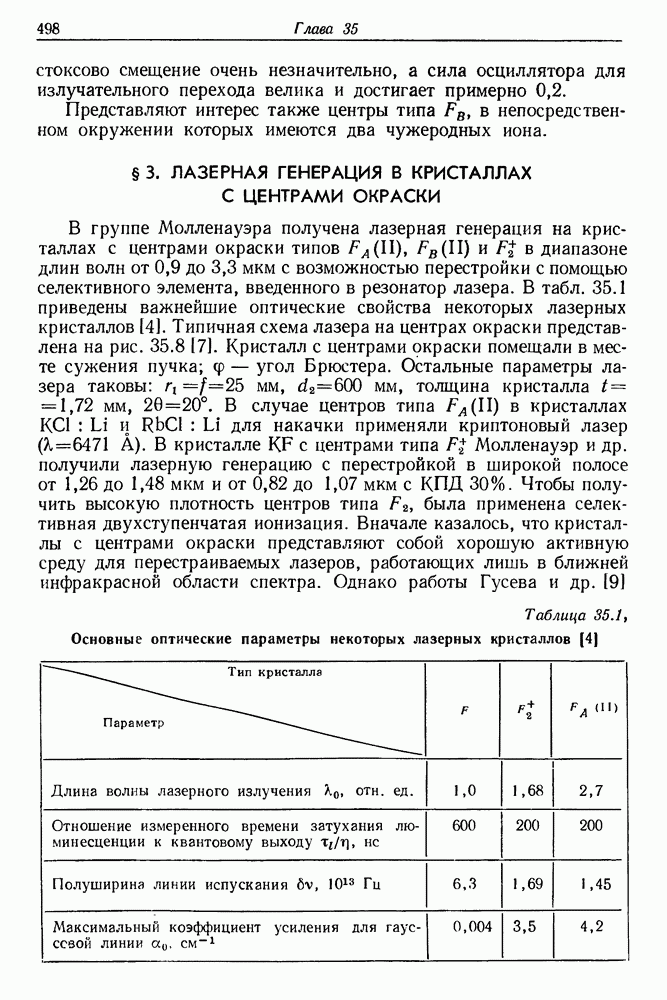
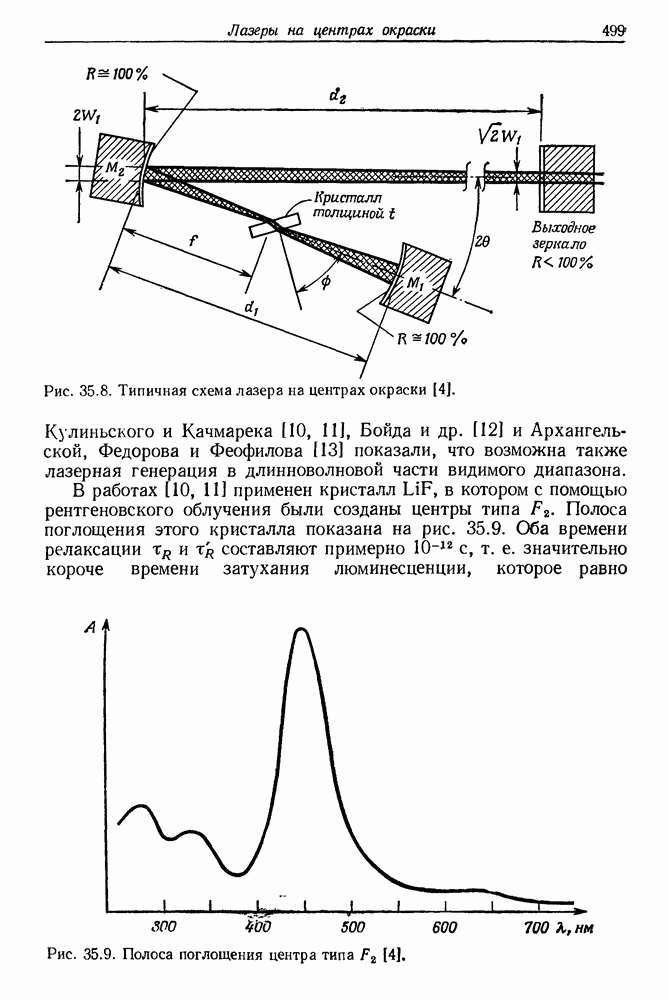
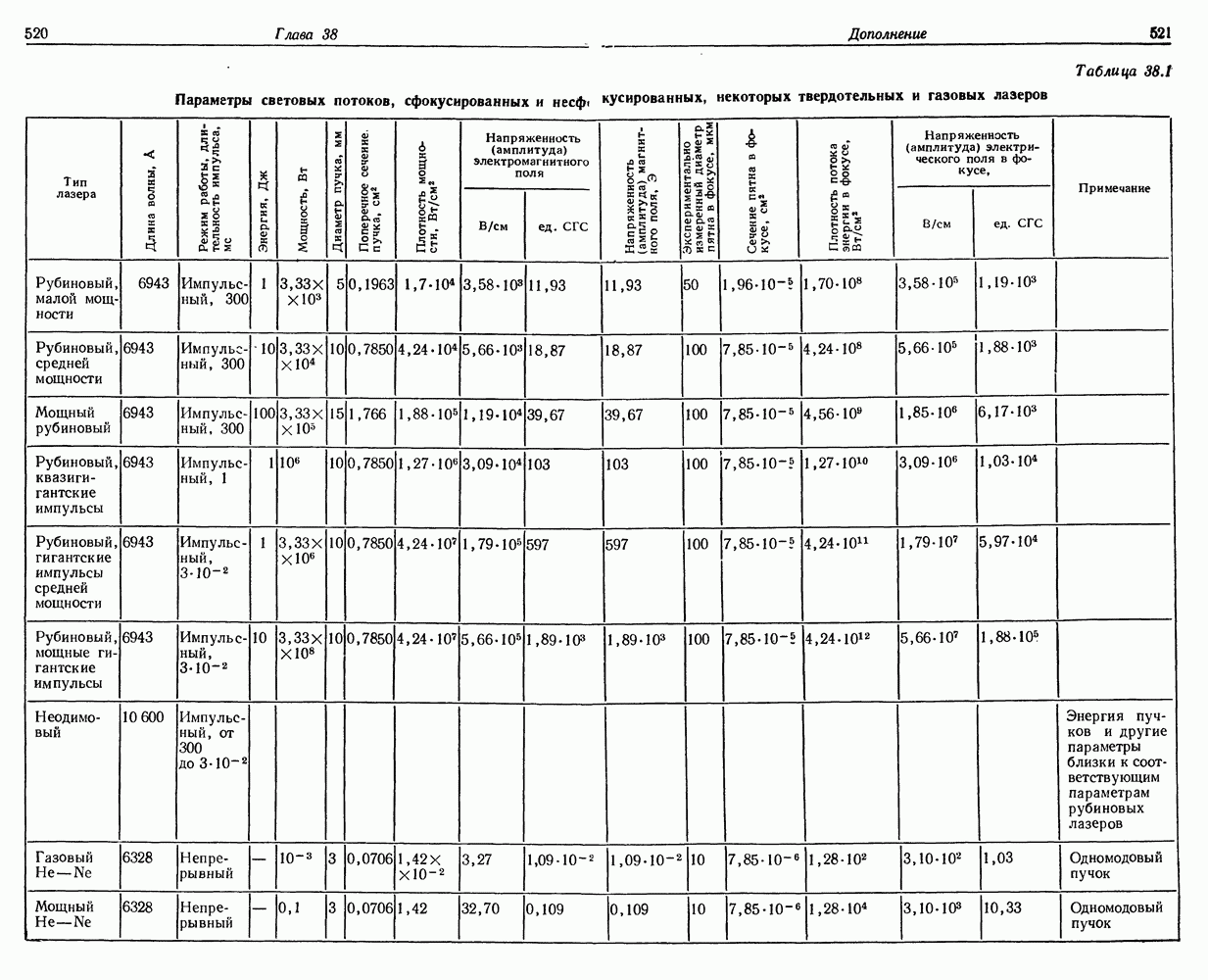
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
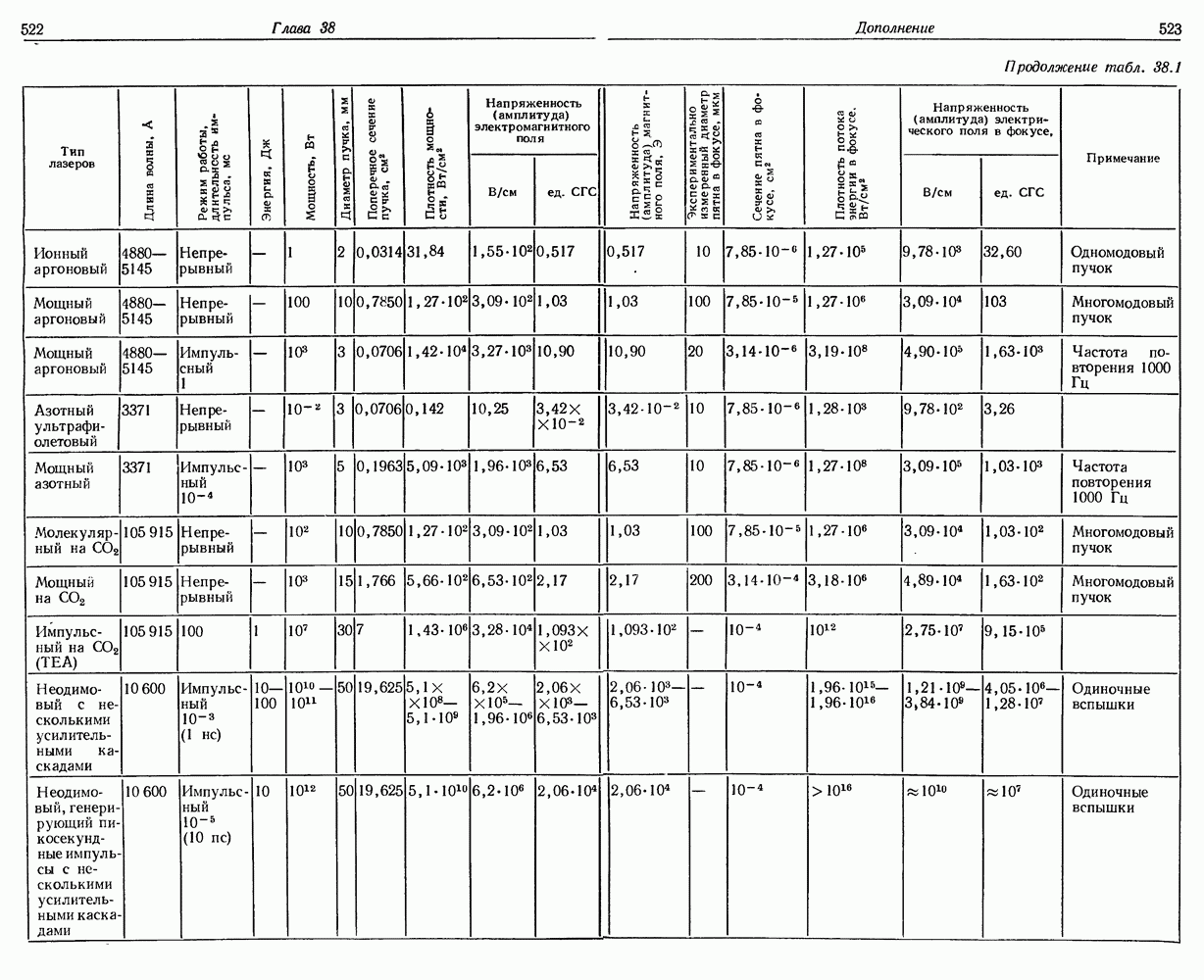
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
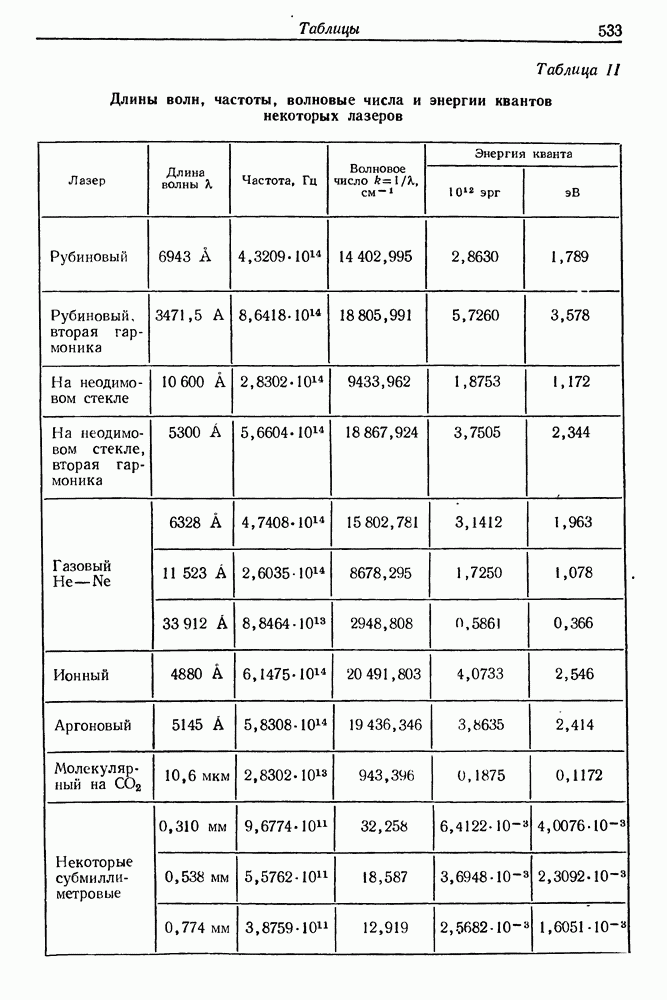
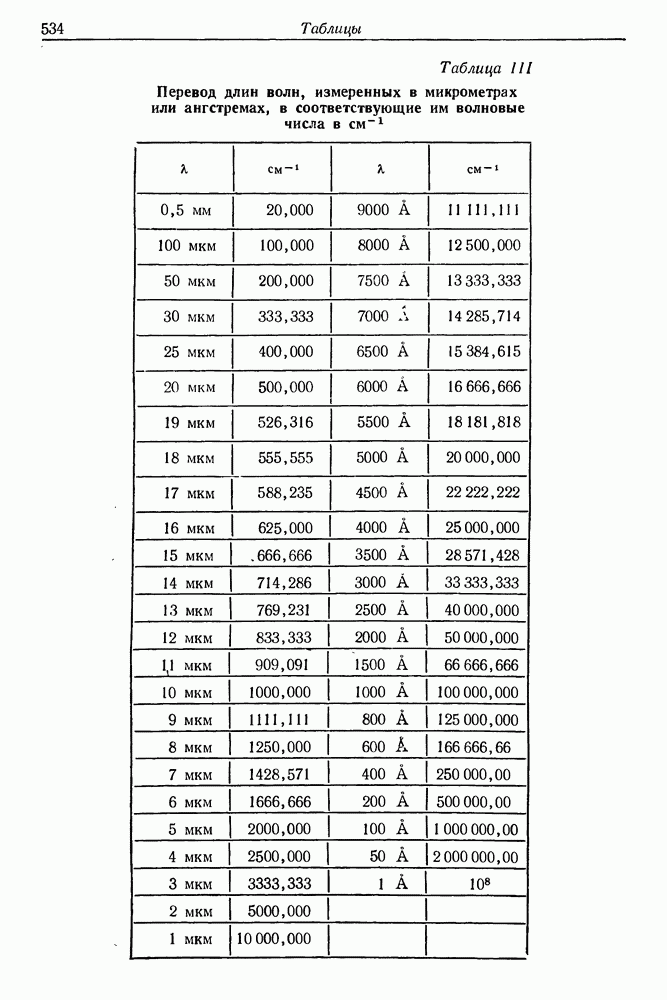
- Таблицы