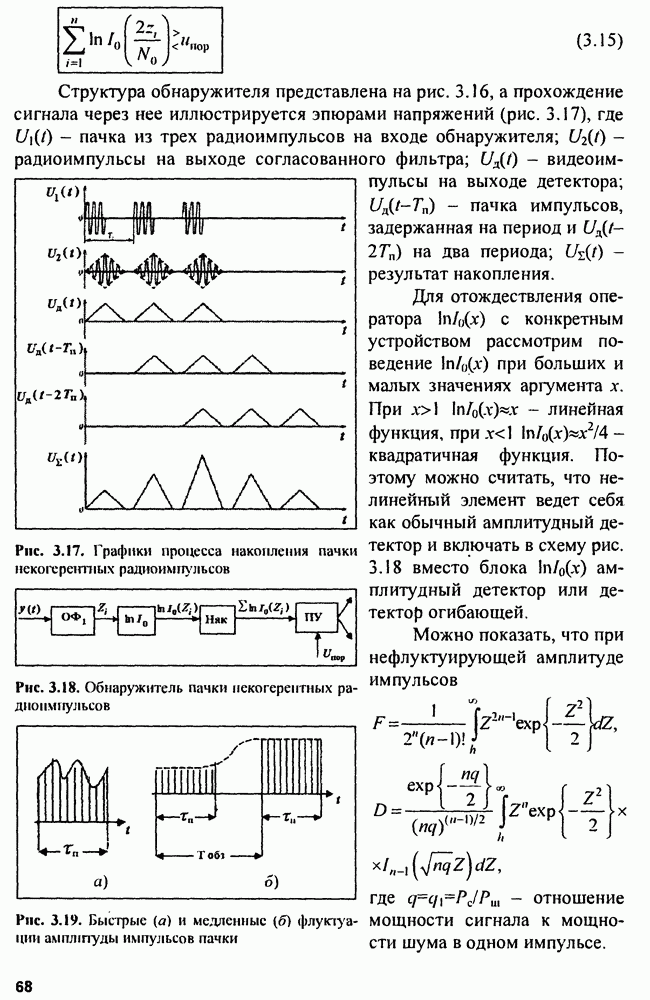
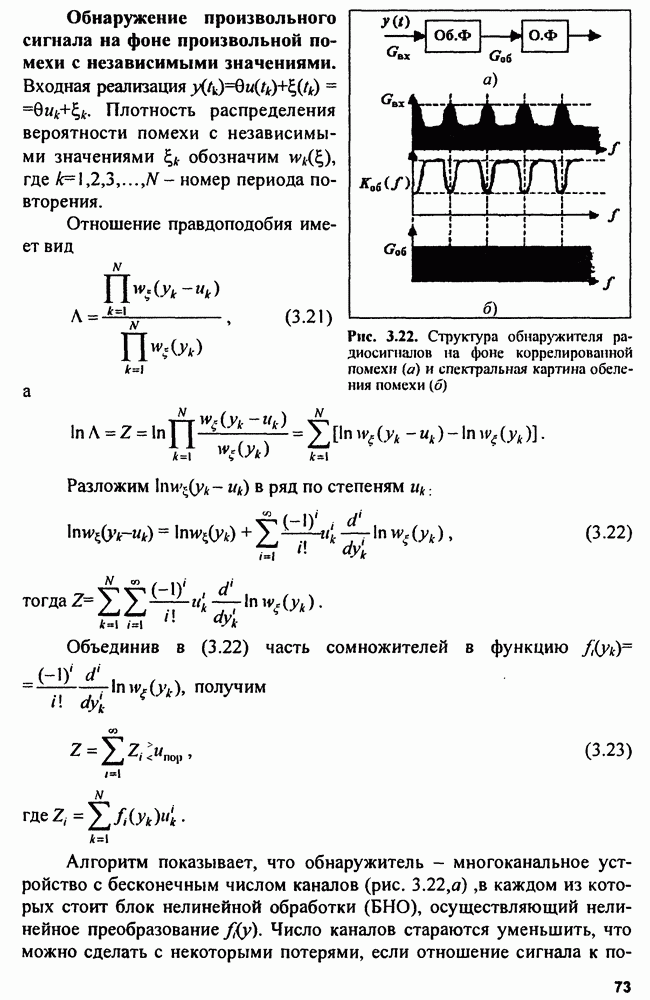
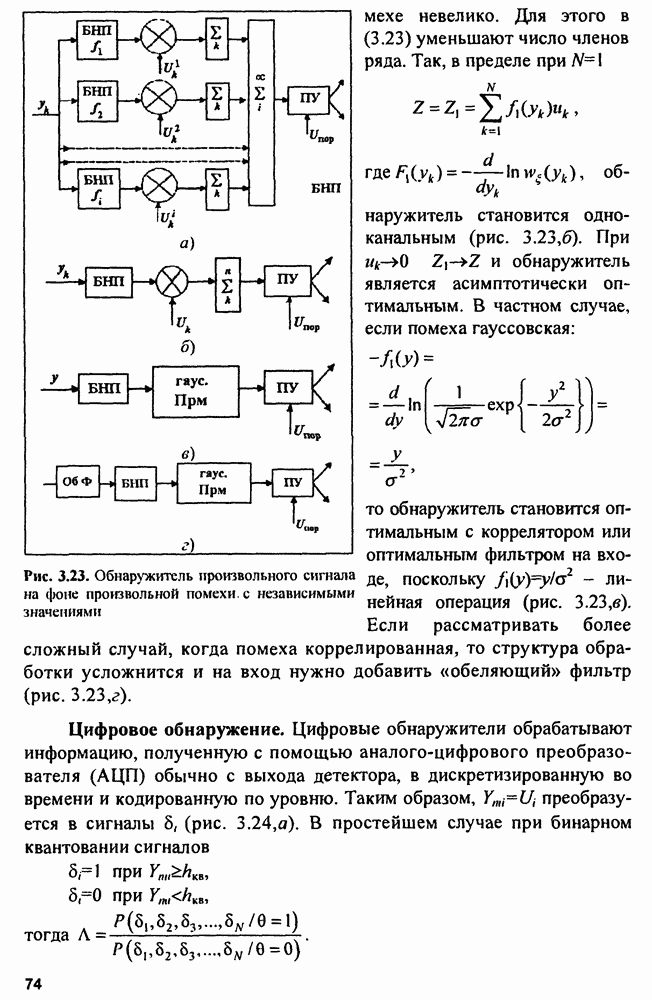
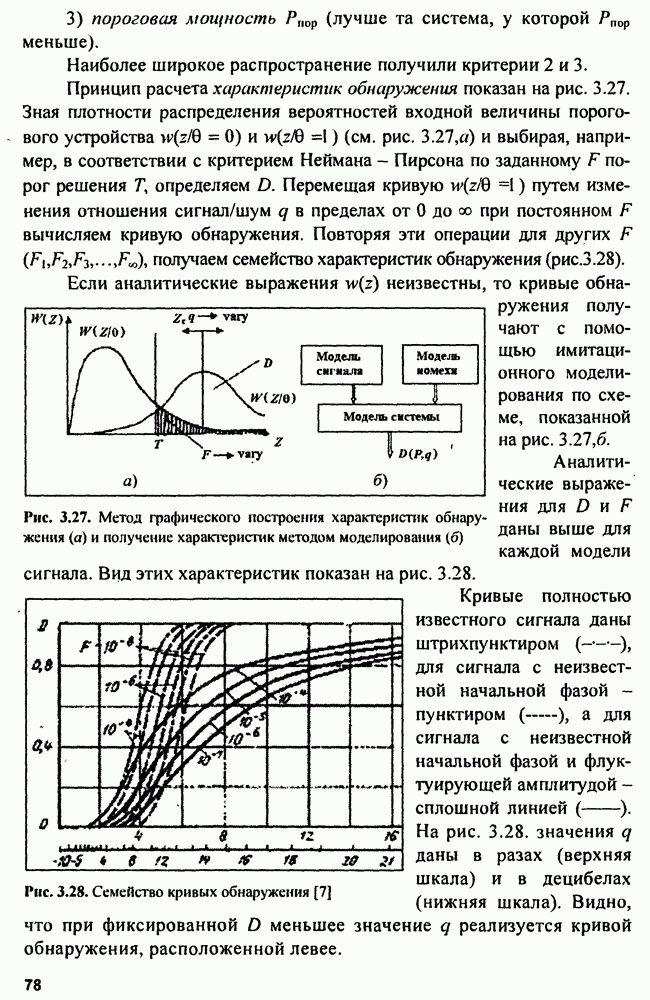
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
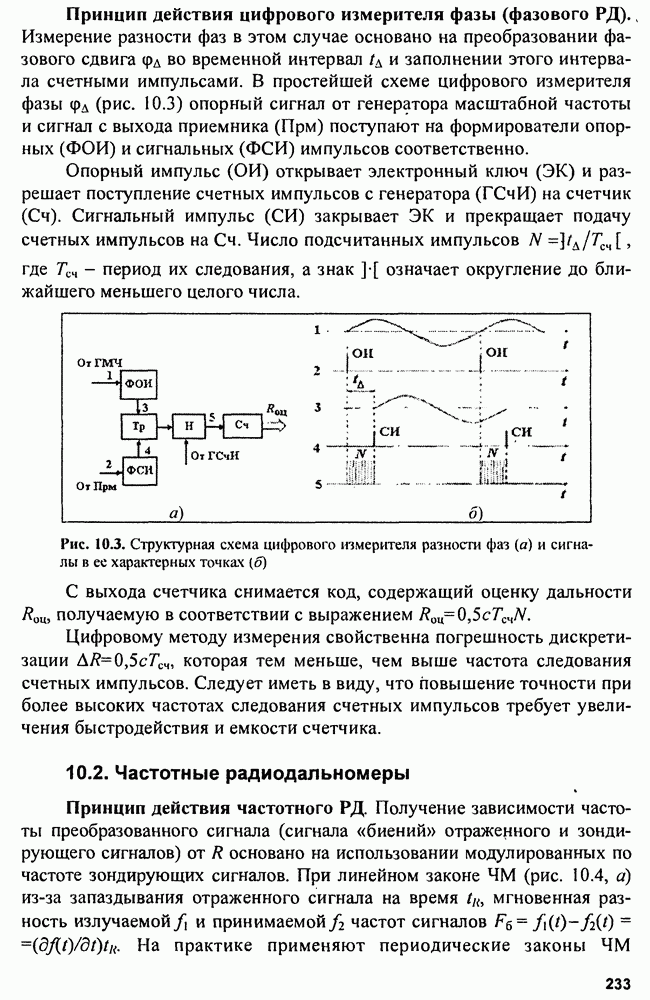
3.2. Критерии оптимального обнаружения
Критерий Байеса. Пусть  соответствует наличию сигнала в
соответствует наличию сигнала в  его отсутствию. Множество решений
его отсутствию. Множество решений  вырождается в два:
вырождается в два: 
При простом бинарном обнаружении  и функция потерь переходит в квадратную матрицу
и функция потерь переходит в квадратную матрицу

Можно положить  (потерь нет), и
(потерь нет), и 
Задача обнаружения эквивалентна проверке гипотезы  о том, что
о том, что  при альтернативной гипотезе
при альтернативной гипотезе  о том, что
о том, что  По результатам наблюдения
По результатам наблюдения  нужно выбрать одно из двух решений:
нужно выбрать одно из двух решений:  или
или 
Класс решений  состоит из правил разбиения области
состоит из правил разбиения области  на две подобласти:
на две подобласти:  Отыскание байесова решения сводится к выбору подобластей таким образом, чтобы средний риск был минимален:
Отыскание байесова решения сводится к выбору подобластей таким образом, чтобы средний риск был минимален:

В случае простого обнаружения  средний риск
средний риск

где  условный риск при
условный риск при  условный риск при
условный риск при  априорная вероятность присутствия сигнала в
априорная вероятность присутствия сигнала в  априорная вероятность отсутствия сигнала в
априорная вероятность отсутствия сигнала в  вероятность правильного обнаружения;
вероятность правильного обнаружения;  вероятность ложной тревоги. Тогда средний риск
вероятность ложной тревоги. Тогда средний риск

Поскольку  постоянная положительная величина, минимум
постоянная положительная величина, минимум  будет получен при
будет получен при

или

Величина  называется отношением правдоподобия, а
называется отношением правдоподобия, а  является порогом решения.
является порогом решения.
Таким образом, алгоритм обнаружения состоит в следующем: если  то принимается решение
то принимается решение  справедлива гипотеза
справедлива гипотеза  принадлежит области
принадлежит области  а если
а если  то принимается решение
то принимается решение  справедлива гипотеза
справедлива гипотеза  принадлежит области
принадлежит области  как это показано на рис. 3.3, при этом область
как это показано на рис. 3.3, при этом область  разделена границей
разделена границей  на две области
на две области 

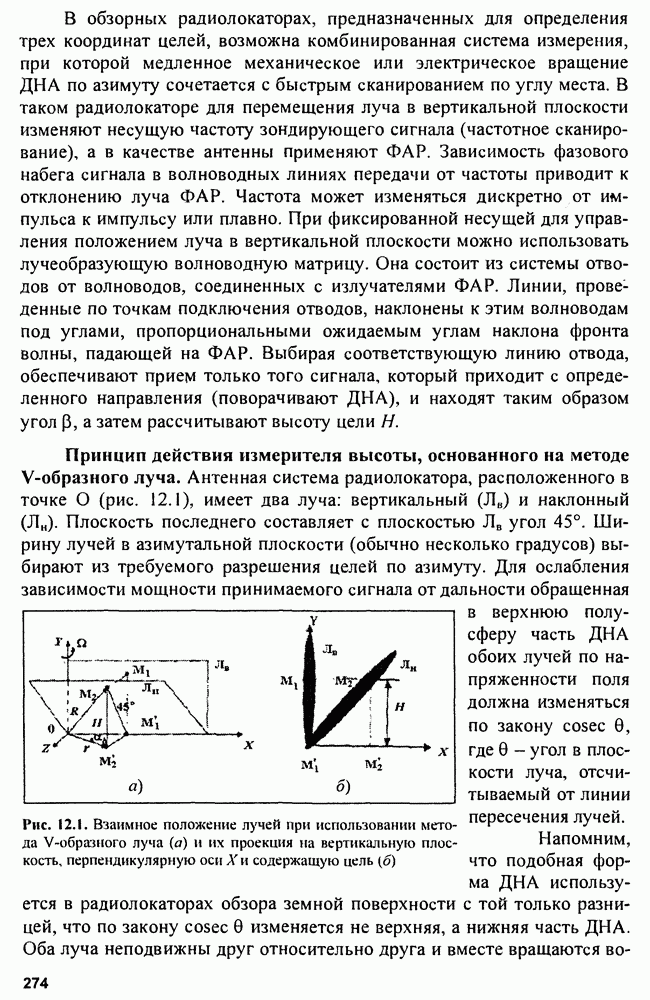
Рис. 3.3. Области гипотез
Недостаток этого критерия - необходимость знать априорные сведения о величинах  Один из выходов при неизвестных
Один из выходов при неизвестных  принятие гипотезы их равенства:
принятие гипотезы их равенства:  тогда
тогда

и алгоритм обнаружения имеет вид

Критерий максимума апостериорной вероятности и максимума правдоподобия. Известно, что согласно теореме Байеса формулы условных плотностей распределения вероятностей состояний  имеют вид
имеют вид

Очевидно, что та ситуация правдоподобней, вероятность которой больше. Если  то правдоподобней
то правдоподобней  и нужно принять решение
и нужно принять решение  Если
Если  то правдоподобней
то правдоподобней  и таким образом, если
и таким образом, если

то принимается решение  справедлива гипотеза
справедлива гипотеза  принадлежит области
принадлежит области 

то принимается решение  справедлива гипотеза Но, у принадлежит области
справедлива гипотеза Но, у принадлежит области  т.е., как и в критерии Байеса,
т.е., как и в критерии Байеса,

Это соответствует случаю, когда  причем средний риск
причем средний риск  а алгоритм обнаружения остается прежним:
а алгоритм обнаружения остается прежним:

Если априорные сведения  отсутствуют, то их считают равновероятными
отсутствуют, то их считают равновероятными  и тогда
и тогда  Это так называемый критерий правдоподобия, или критерий идеального наблюдателя (Зигерта).
Это так называемый критерий правдоподобия, или критерий идеального наблюдателя (Зигерта).
Критерий Неймана - Пирсона. При критерии Неймана - Пирсона фиксируется вероятность ложной тревоги  время обнаружения
время обнаружения  и максимизируется вероятность правильного обнаружения
и максимизируется вероятность правильного обнаружения  т.е. ищется такое правило решений
т.е. ищется такое правило решений  которое обеспечивает при заданном
которое обеспечивает при заданном  среди всех прочих решений максимальное
среди всех прочих решений максимальное  Порог решения выбирается из соотношения
Порог решения выбирается из соотношения

Доказывается, что для максимизации  необходимо использовать правило принятия решений
необходимо использовать правило принятия решений

Ввиду того, что критерий Неймана - Пирсона не требует знания априорных вероятностей ситуаций  в радиолокации он является основным.
в радиолокации он является основным.
Минимаксный критерий. Если априорное распределение  неизвестно, то байесово решение использовать нельзя, так как не удается найти 7. При минимаксном критерии в классе решающих правил 8 ищут максимальные значения условных рисков
неизвестно, то байесово решение использовать нельзя, так как не удается найти 7. При минимаксном критерии в классе решающих правил 8 ищут максимальные значения условных рисков  при вариации
при вариации  , т.е. находят
, т.е. находят  Затем выбирают правило решений 8, обеспечивающее наименьшее значение риска среди полученных максимальных:
Затем выбирают правило решений 8, обеспечивающее наименьшее значение риска среди полученных максимальных:

Здесь  минимальный риск, причем
минимальный риск, причем 
Вальдом получена связь между минимаксным и байесовым решениями: минимаксное решение является байесовым относительно наименее благоприятного априорного распределения параметров  максимизирующих байесов риск:
максимизирующих байесов риск:

Функция  не зависит от значений
не зависит от значений  . Таким образом, если байесов риск
. Таким образом, если байесов риск  для некоторого
для некоторого  не зависит от 9, то наиболее
не зависит от 9, то наиболее
неблагоприятно распределение  а байесово решение 5 - минимаксное. Это позволяет облегчить отыскание минимаксных значений и наименее благоприятных априорных распределений, которые часто оказываются равномерными.
а байесово решение 5 - минимаксное. Это позволяет облегчить отыскание минимаксных значений и наименее благоприятных априорных распределений, которые часто оказываются равномерными.
Критерий последовательной проверки гипотез Вальда. В рассмотренных критериях ограничивалось (фиксировалось) время принятия решений Тнабл или объем выборки  Однако можно заранее объем выборки не фиксировать. При критерии Вальда область
Однако можно заранее объем выборки не фиксировать. При критерии Вальда область  делится на три подобласти
делится на три подобласти  нижним
нижним  и верхним
и верхним  порогами, как показано на рис. 3.3,6:
порогами, как показано на рис. 3.3,6:
 если
если  в этом случае справедлива гипотеза
в этом случае справедлива гипотеза  принадлежит области Г0;
принадлежит области Г0;
 - в этом случае справедлива гипотеза
- в этом случае справедлива гипотеза  принадлежит области Г| ;
принадлежит области Г| ;
 если
если  в этом случае принимается решение продолжить наблюдение.
в этом случае принимается решение продолжить наблюдение.
Здесь 
Таким образом критерий Вальда двухпороговый:

Пороги определяются вероятностями 
Длительность наблюдений - величина случайная. Критерий Вальда является оптимальным в смысле минимизации среднего времени наблюдения (обнаружения) по большему ансамблю экспериментов.
Сведение сложной гипотезы к простой. Если кроме параметров  имеются другие:
имеются другие:  в пространстве
в пространстве  для случая
для случая  в пространстве
в пространстве  Для случая
Для случая  с распределениями
с распределениями  при известных
при известных  то можно сформировать отношение правдоподобия, не зависящее от параметров
то можно сформировать отношение правдоподобия, не зависящее от параметров 

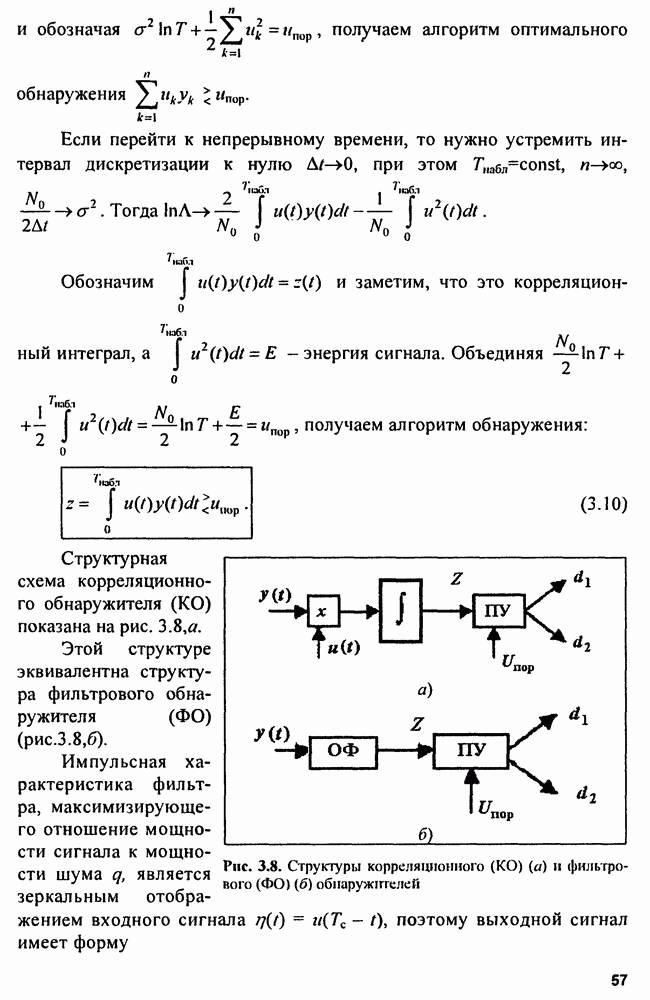
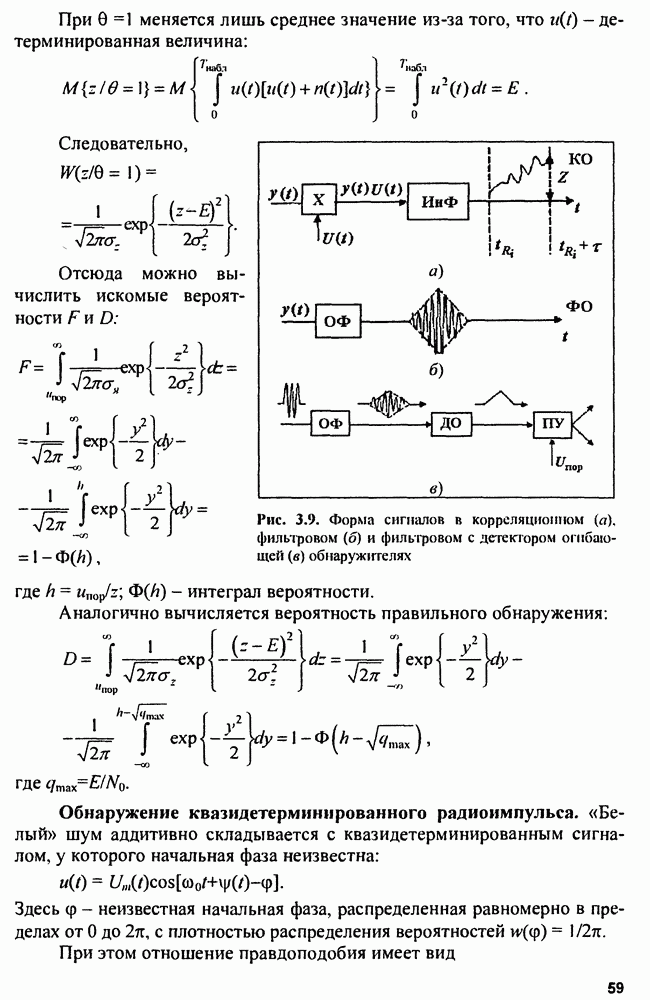
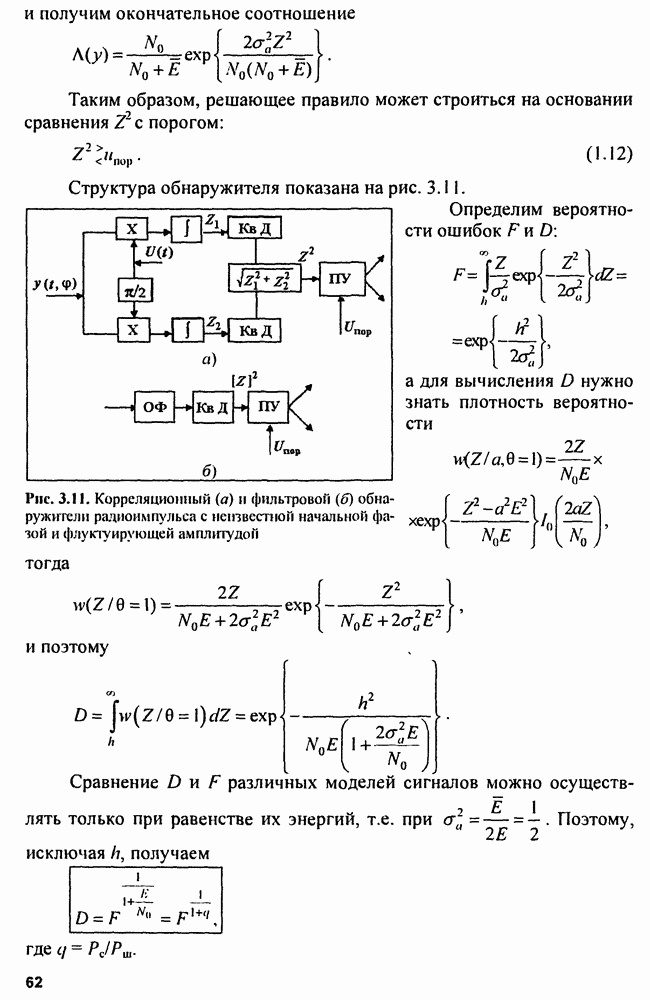
Структура обнаружителя. В соответствии с полученными алгоритмами обнаружения можно представить их структуру при различных критериях оптимальности:
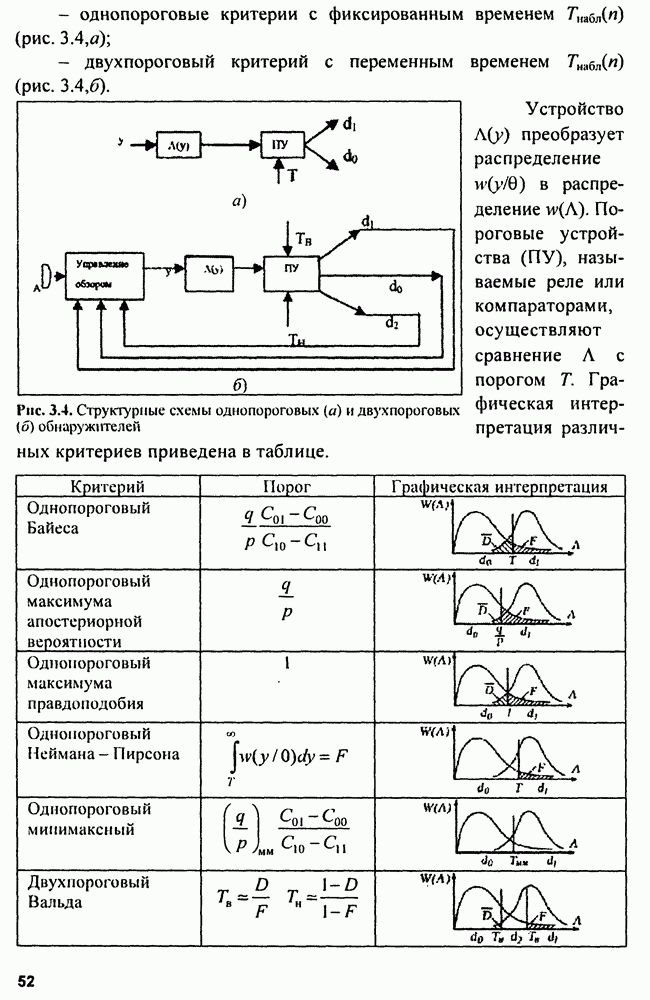
- однопороговые критерии с фиксированным временем 
- двухпороговый критерий с переменным временем  (рис.
(рис. 

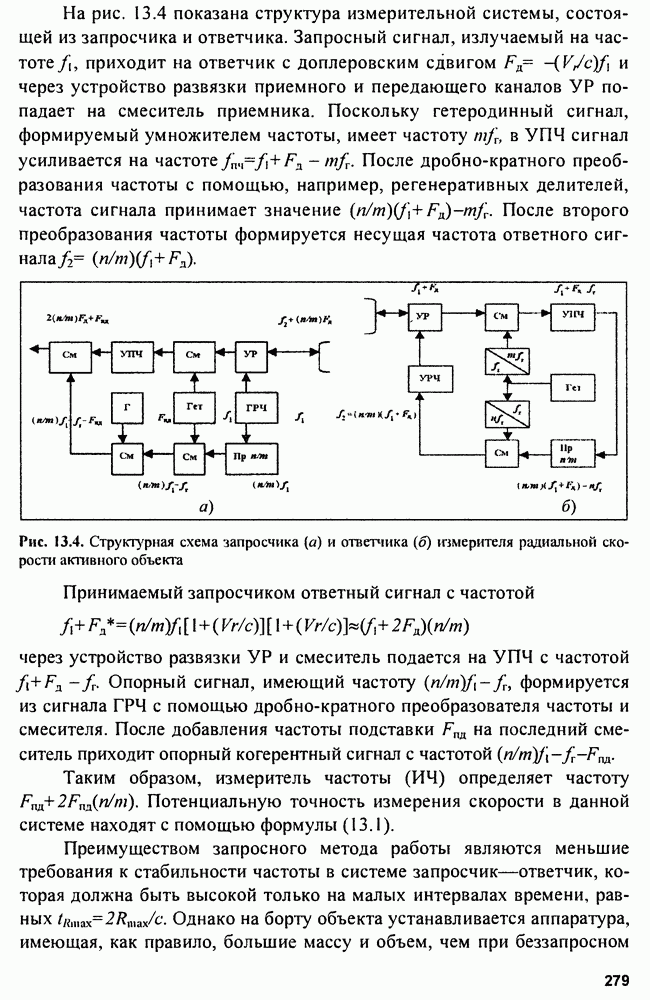
Рис. 3.4. Структурные схемы однопороговых (а) и двухпороговых (б) обнаружителей
Устройство  преобразует распределение
преобразует распределение  в распределение
в распределение  Пороговые устройства
Пороговые устройства  называемые реле или компараторами, осуществляют сравнение
называемые реле или компараторами, осуществляют сравнение  с порогом
с порогом  Графическая интерпретация различных критериев приведена в таблице.
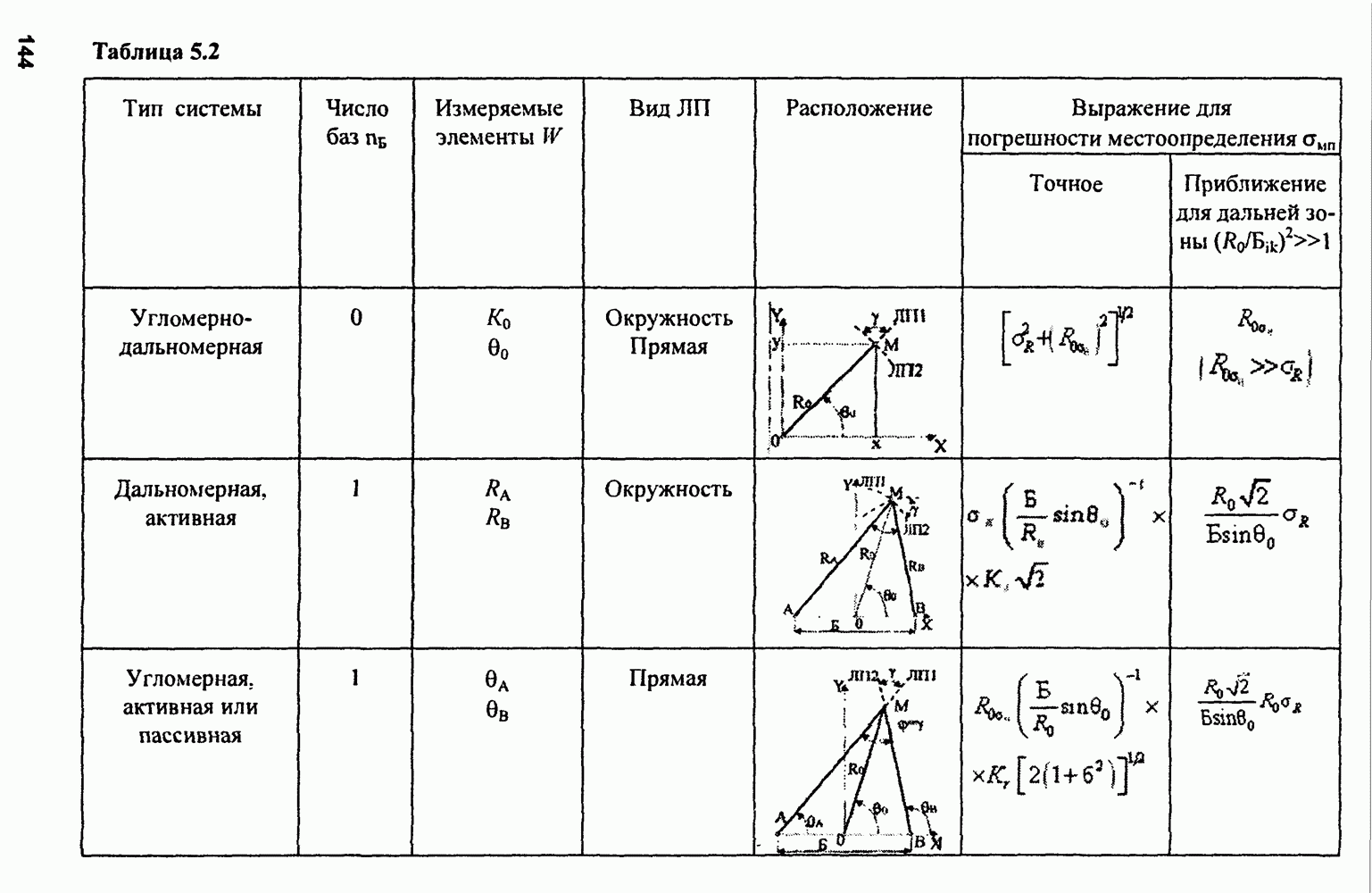
Графическая интерпретация различных критериев приведена в таблице.
(см. скан)
Задача обнаружения решается в каждом элементе разрешения. Способ просмотра элементов разрешения определяется выбранным методом обзора пространства. Количество элементов разрешения зависит от величины области обзора или пространства обнаружения. Вероятность ложной тревоги  и вероятность пропуска цели
и вероятность пропуска цели  обычно задаются на все пространство обнаружения. Вероятность правильного необнаружения во всем пространстве
обычно задаются на все пространство обнаружения. Вероятность правильного необнаружения во всем пространстве  равна произведению вероятностей правильного необнаружения во всех
равна произведению вероятностей правильного необнаружения во всех  элементах:
элементах:

Если  то
то 

При  можно считать
можно считать  или
или  Таким образом, если задано
Таким образом, если задано  то
то 
Пример. Задано  число элементов разрешения по дальности
число элементов разрешения по дальности  число элементов разрешения по азимуту
число элементов разрешения по азимуту  число элементов разрешения по углу места
число элементов разрешения по углу места  Общее число элементов разрешения
Общее число элементов разрешения 
Что касается  то вероятность правильного обнаружения равна
то вероятность правильного обнаружения равна  а эта последняя равна произведению вероятности пропуска цели в одном элементе на вероятность правильного необнаружения во всех остальных
а эта последняя равна произведению вероятности пропуска цели в одном элементе на вероятность правильного необнаружения во всех остальных  элементах:
элементах:

т. е.

Таким образом, 
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
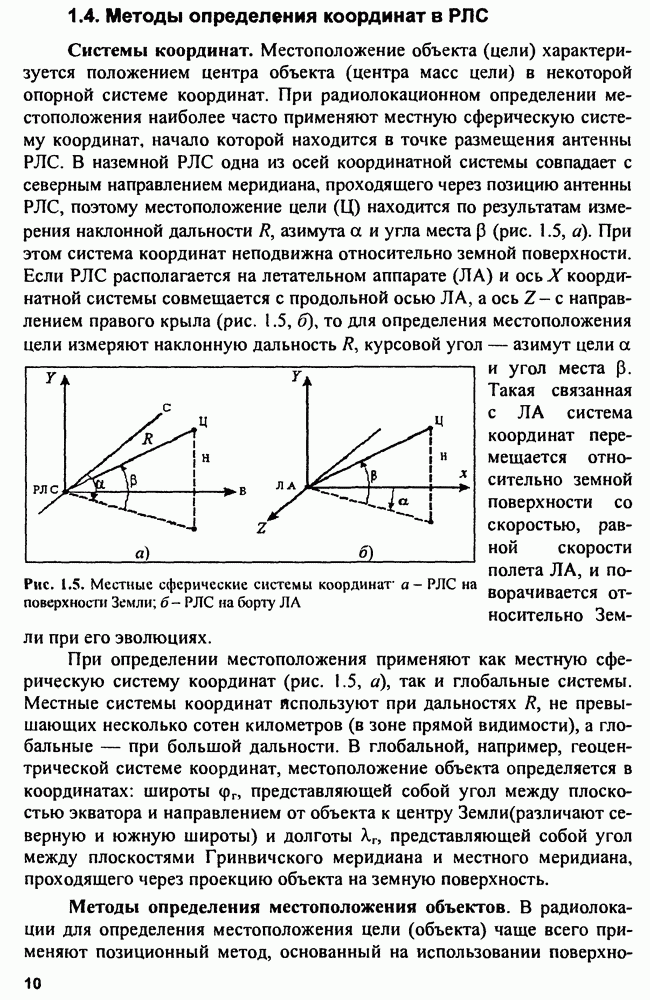
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
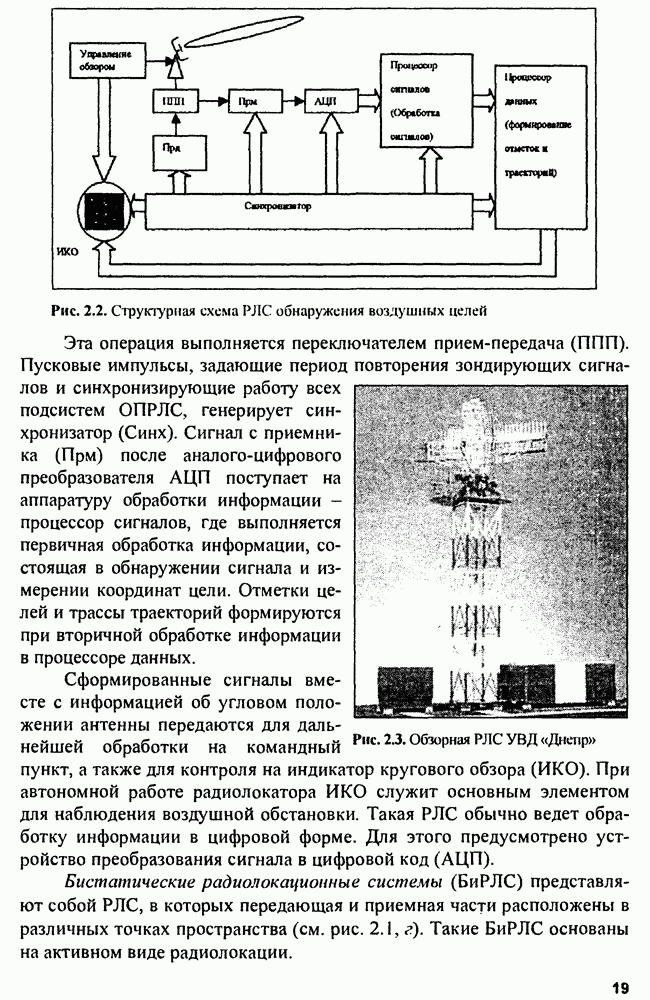
- Глава 2. Радиолокационные системы
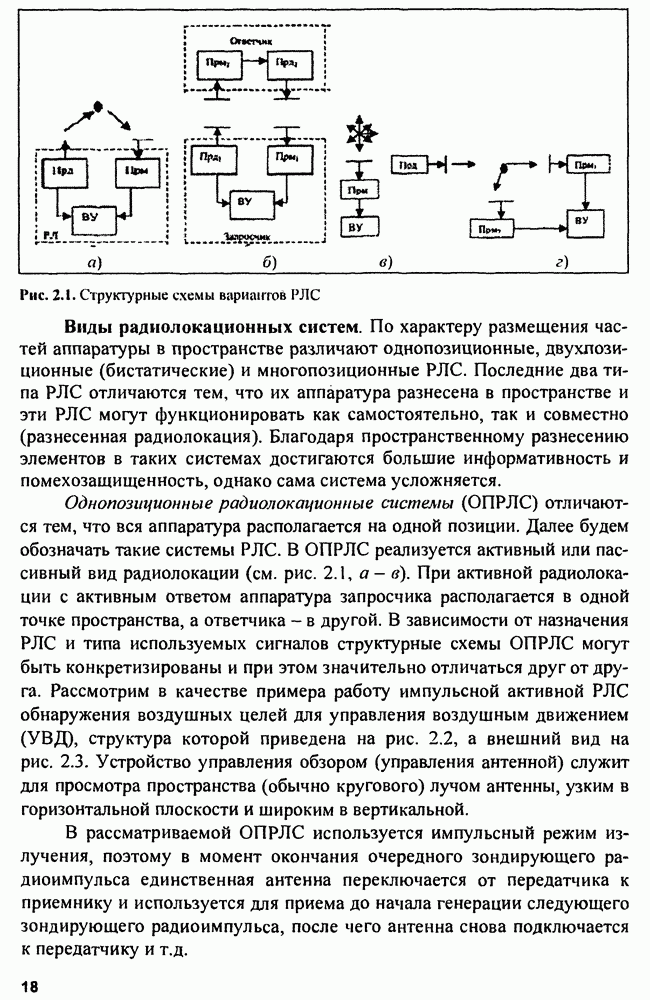
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
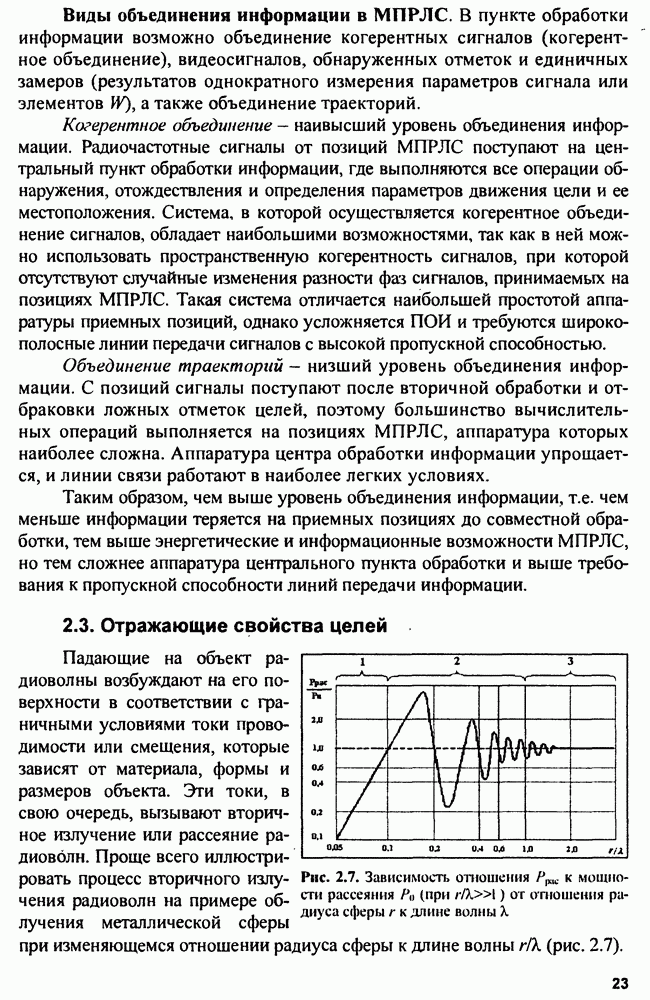
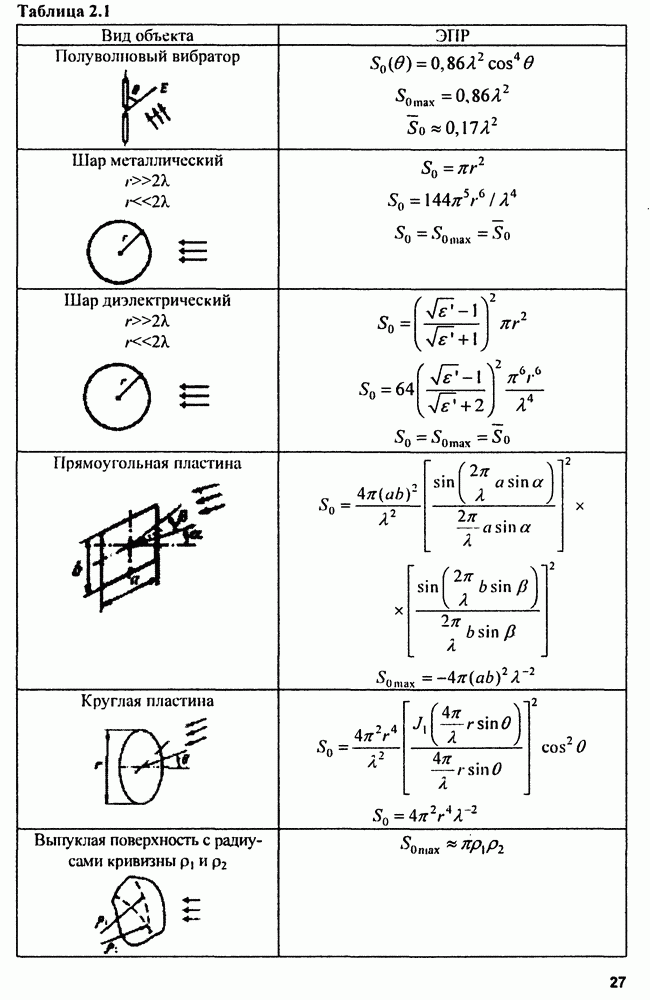
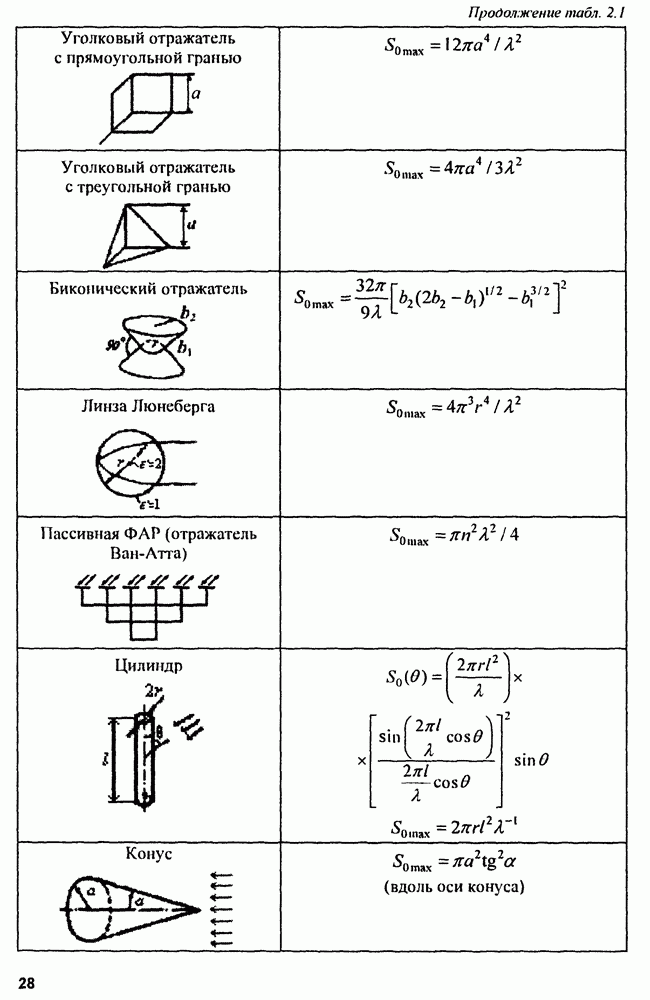
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
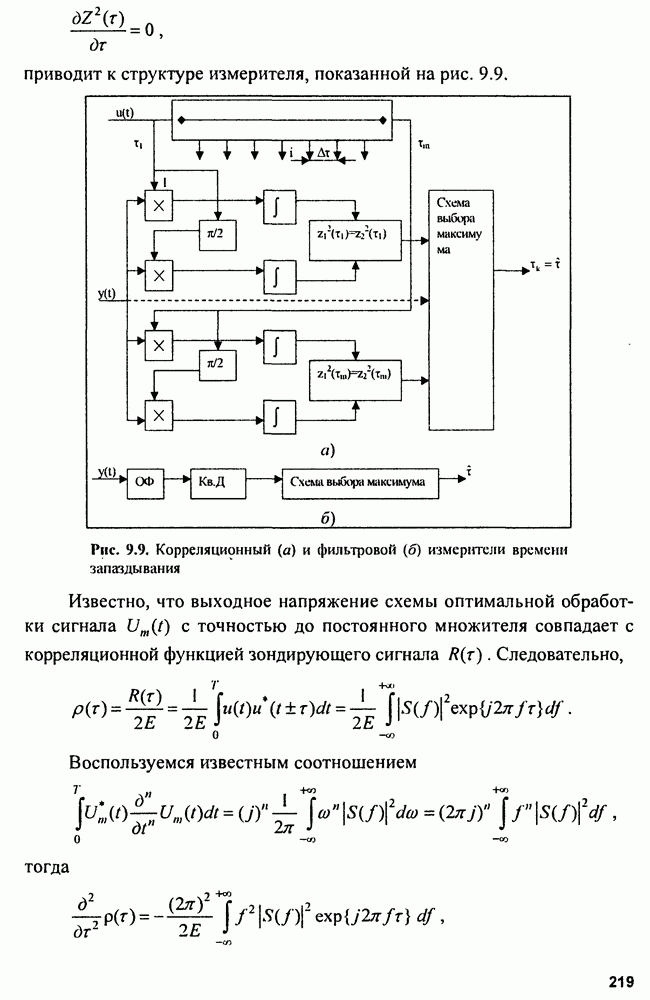
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
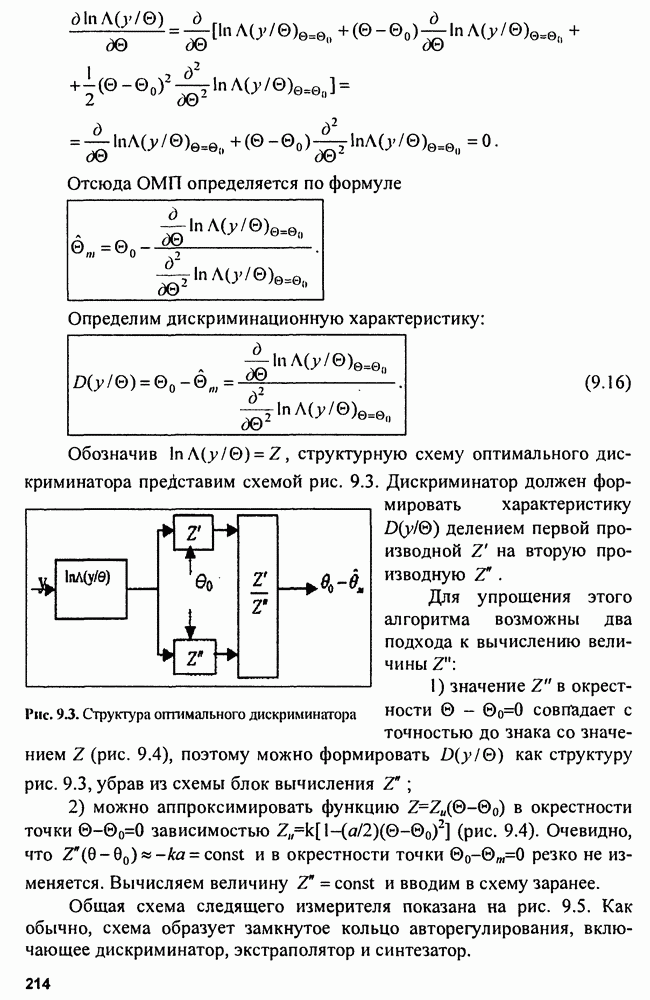
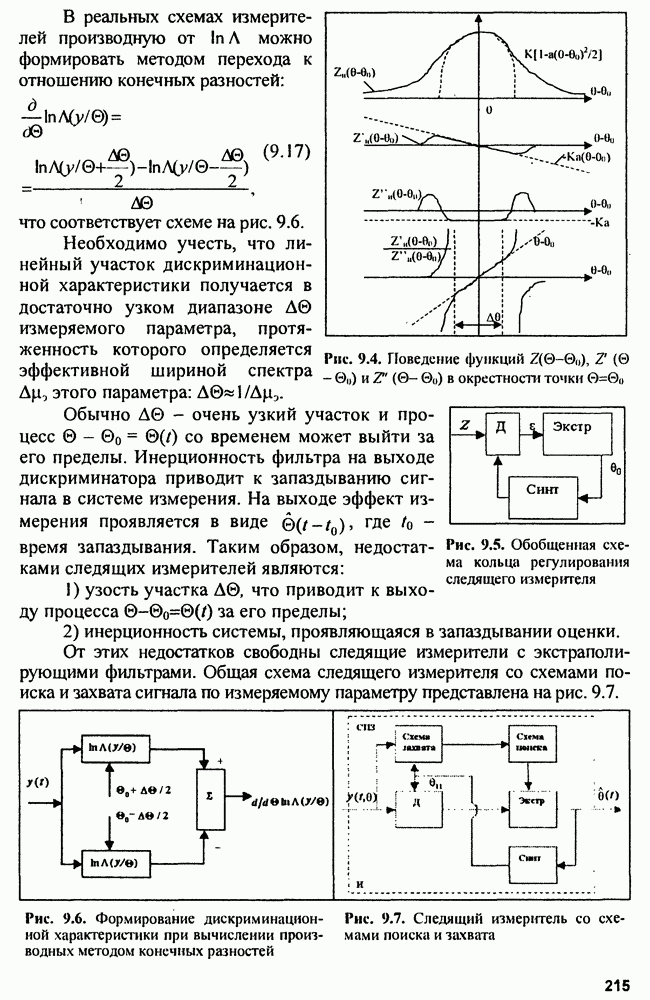
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
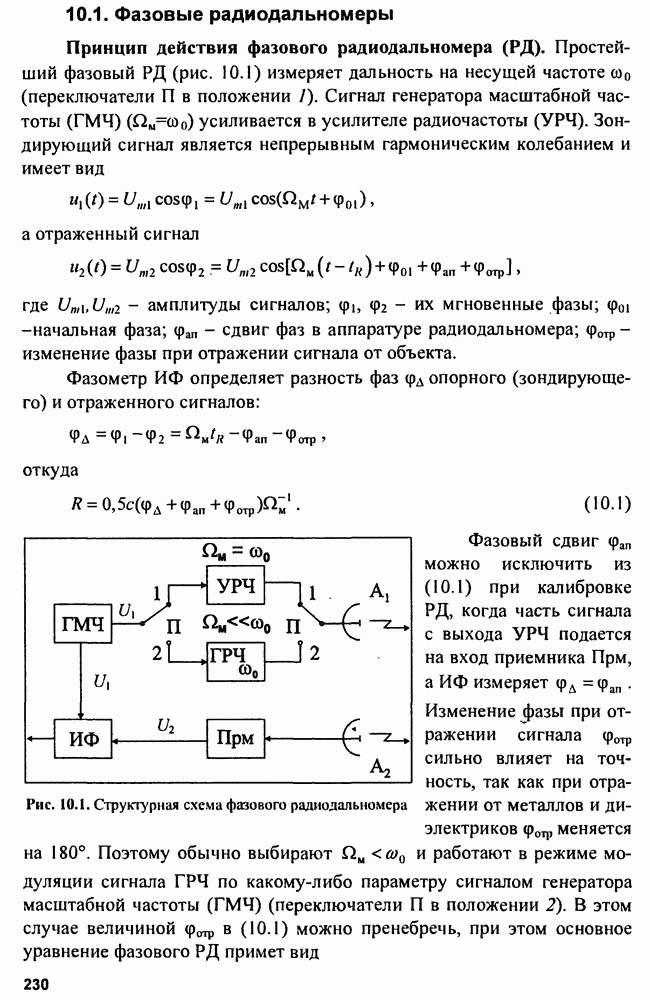
- 10.1. Фазовые радиодальномеры
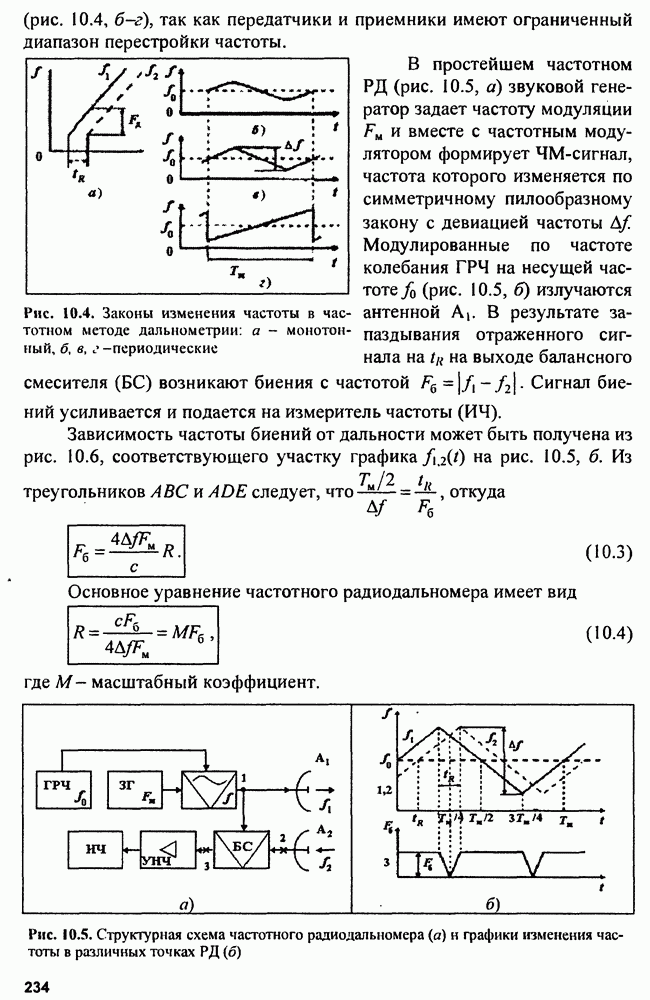
- 10.2. Частотные радиодальномеры
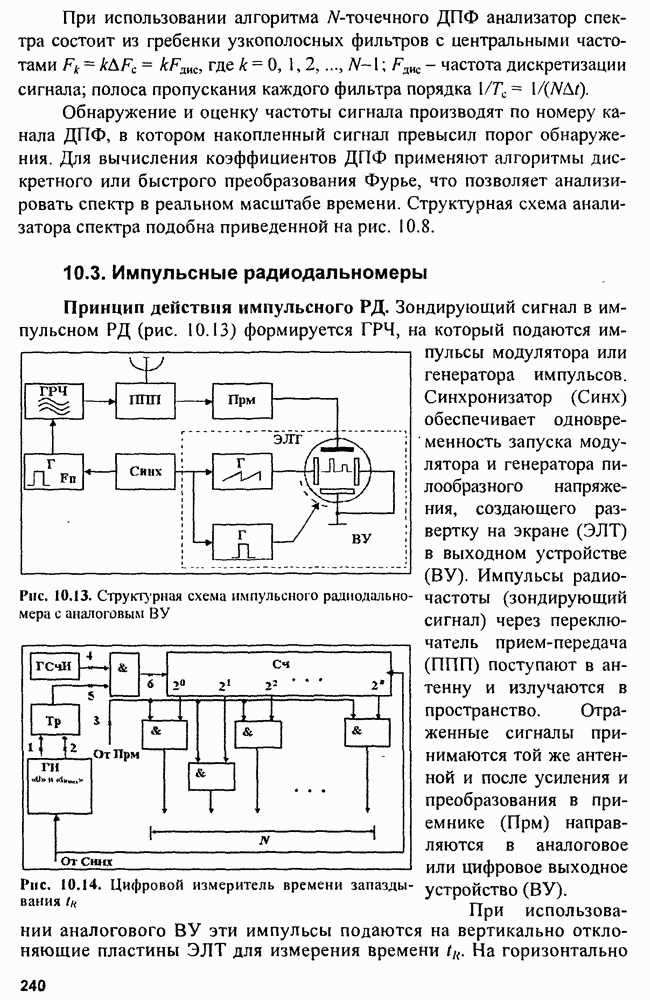
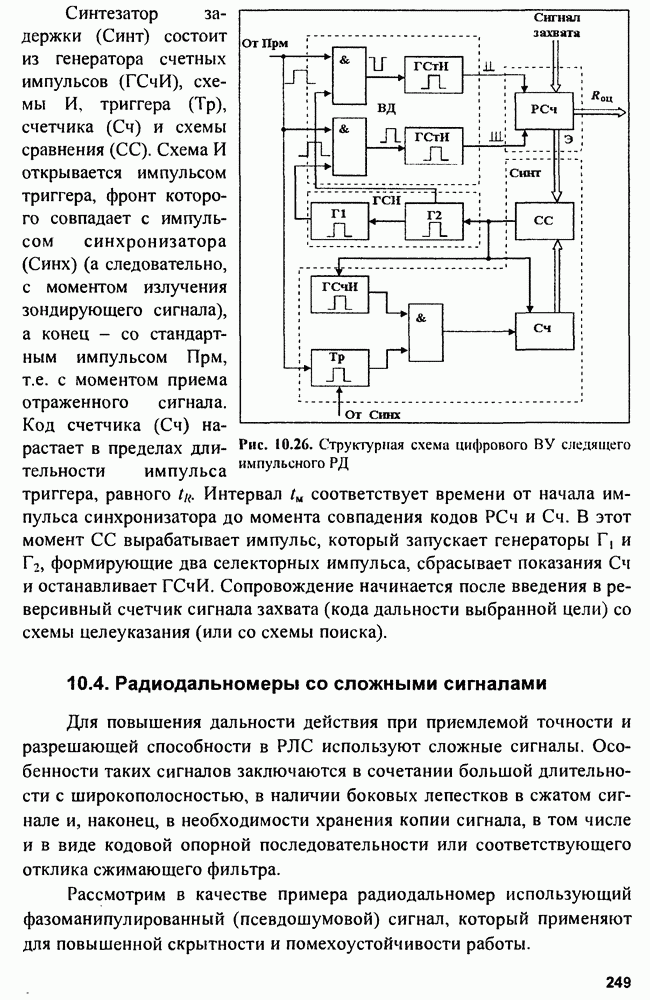
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
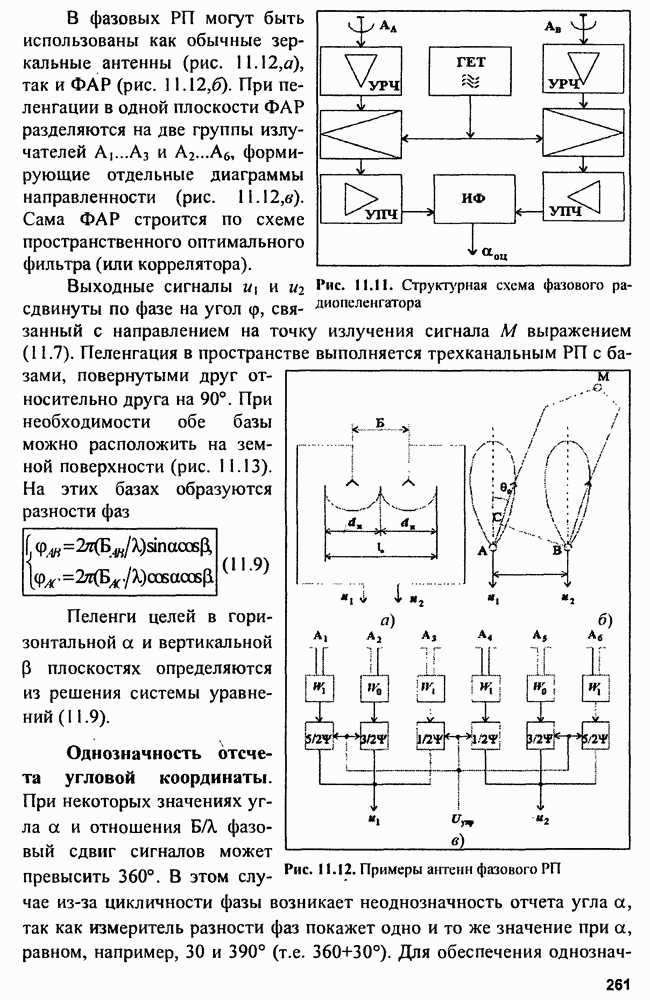
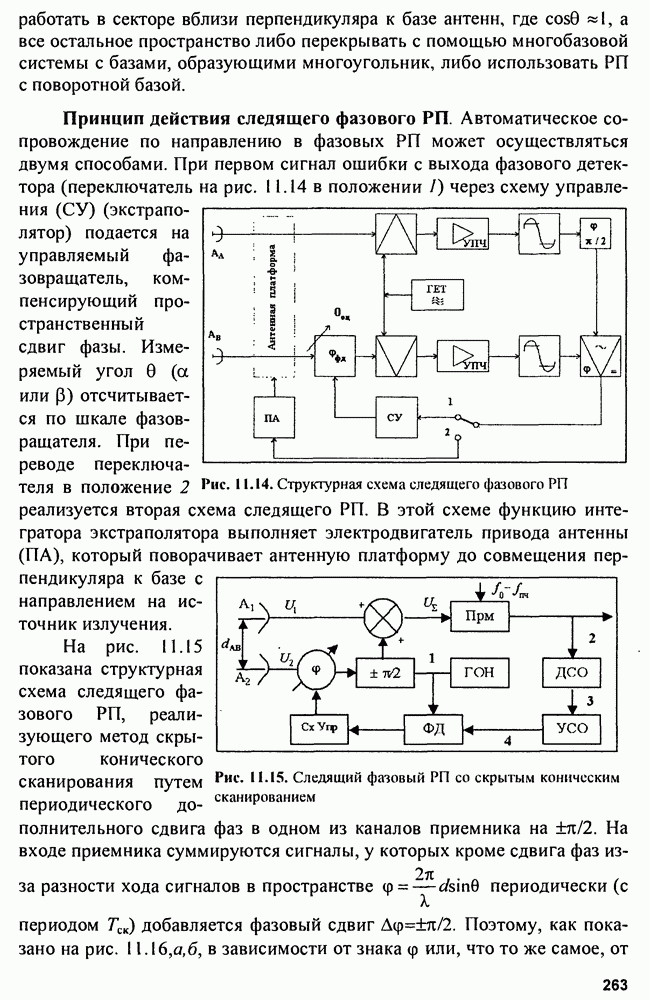
- 11.2. Фазовые радиопеленгаторы
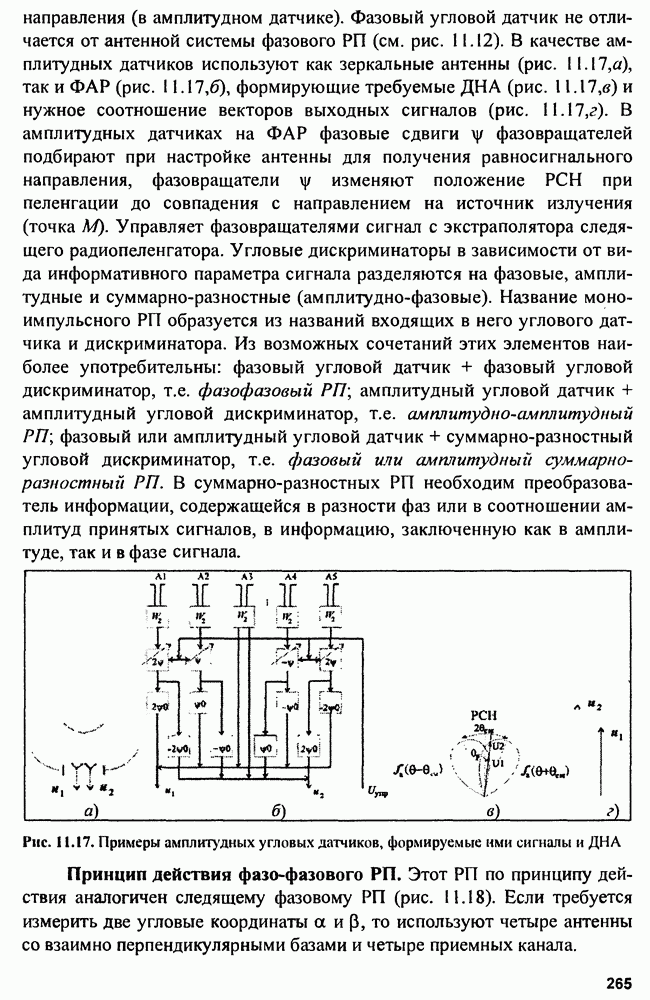
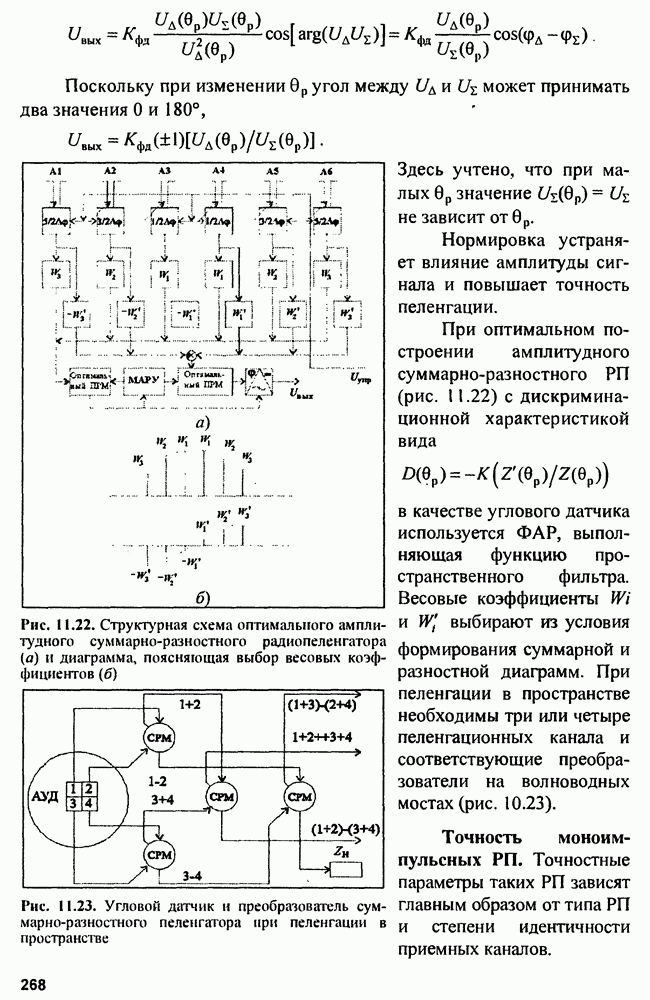
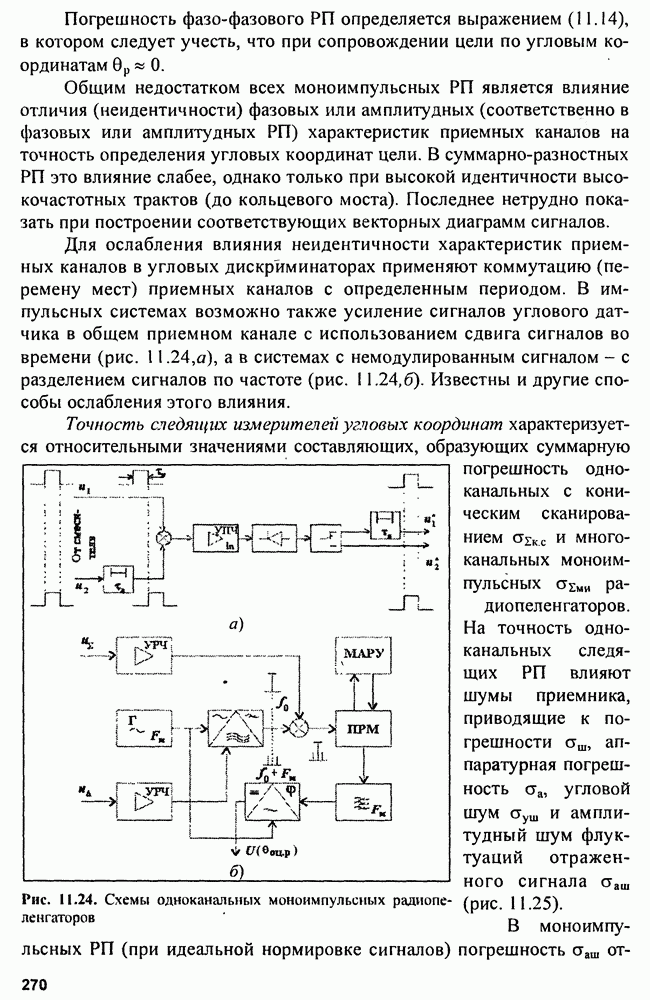
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение