| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
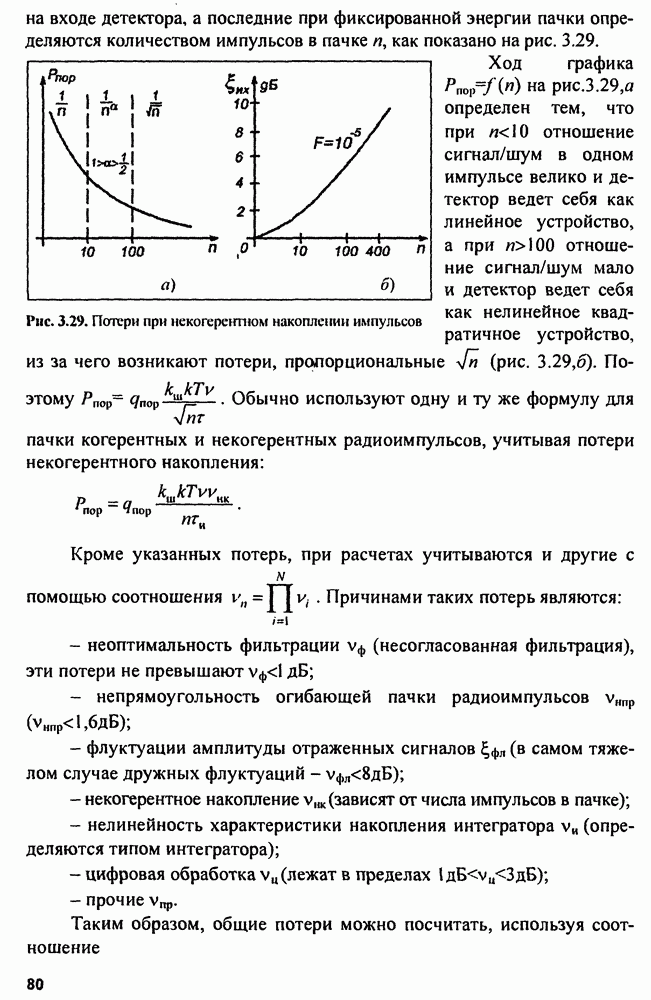
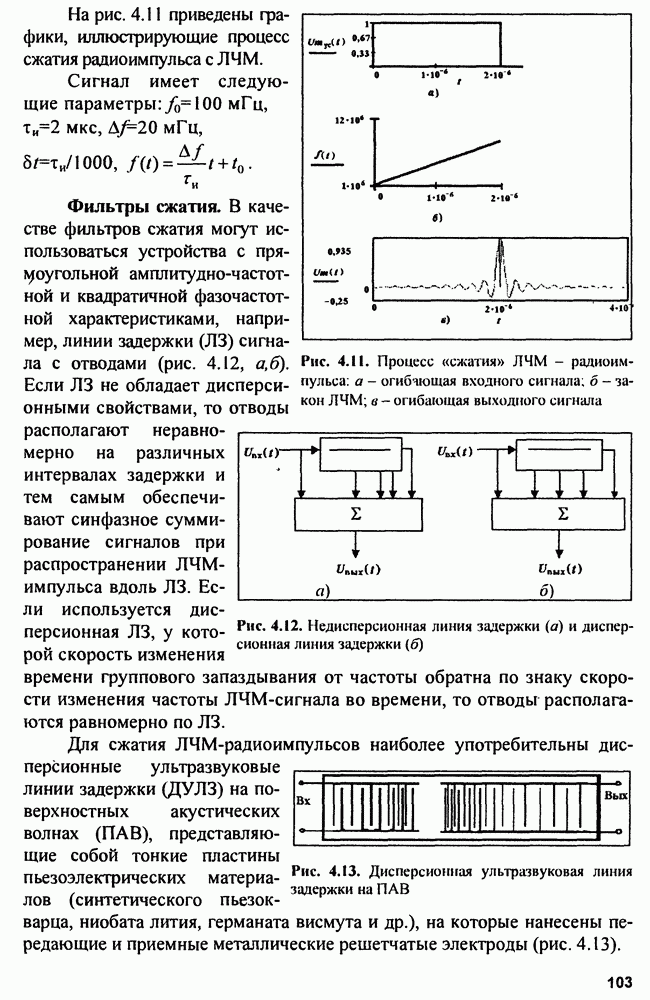
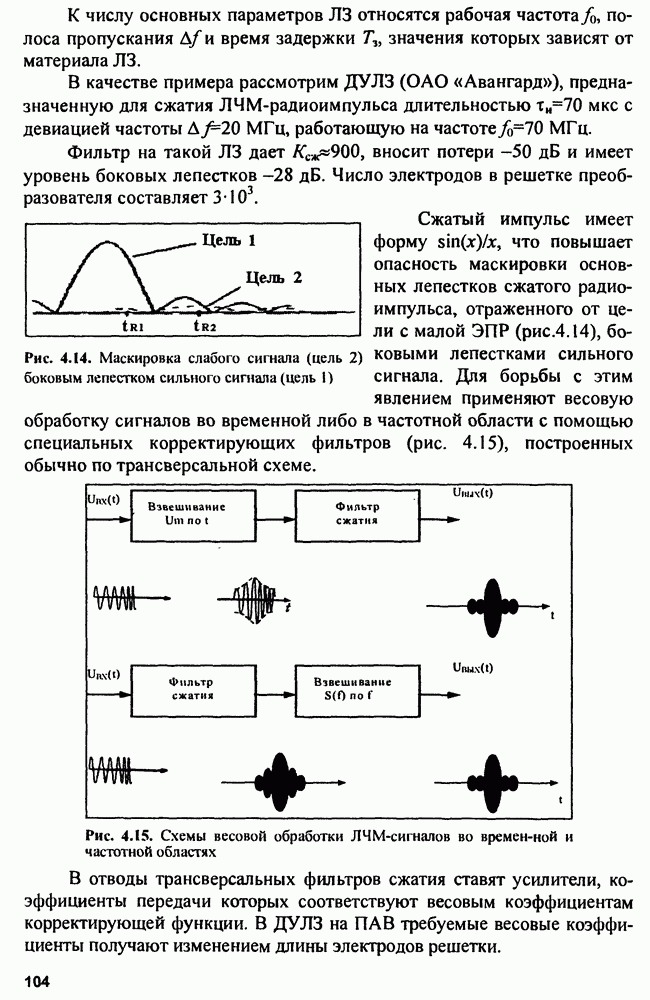
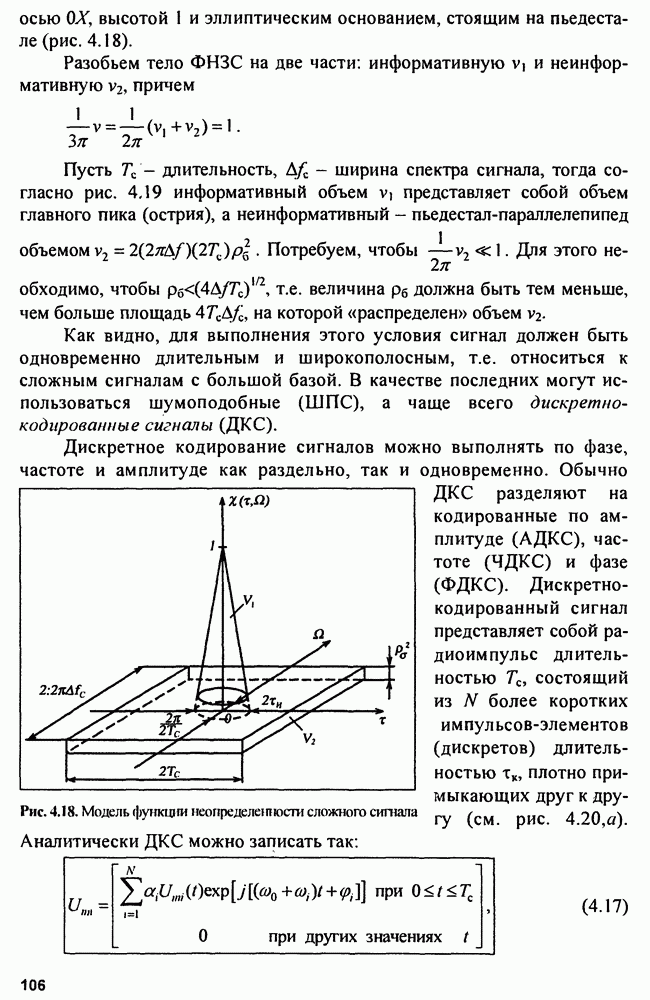
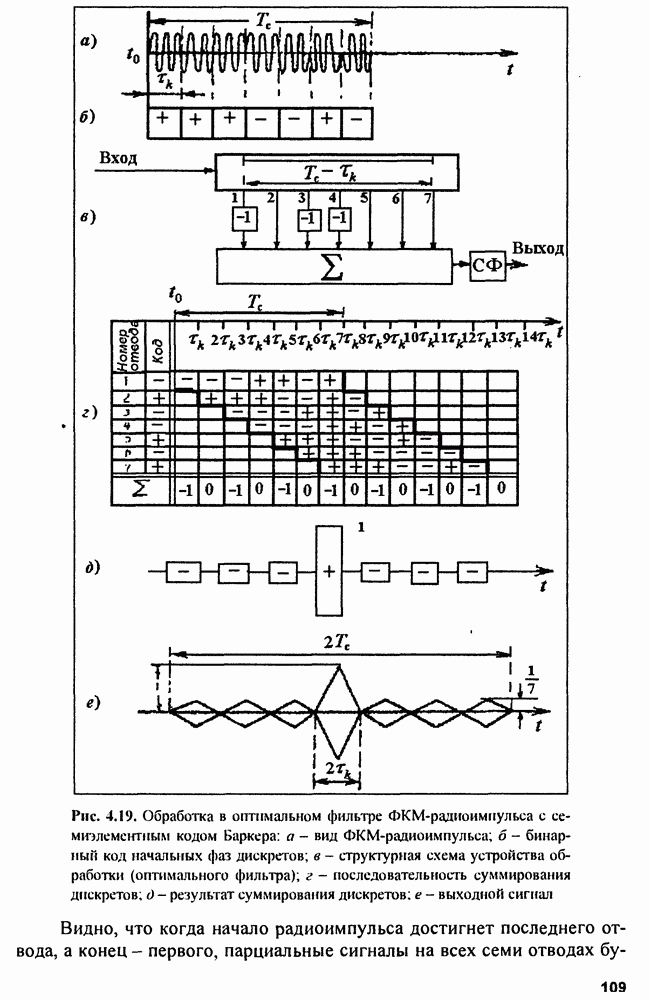
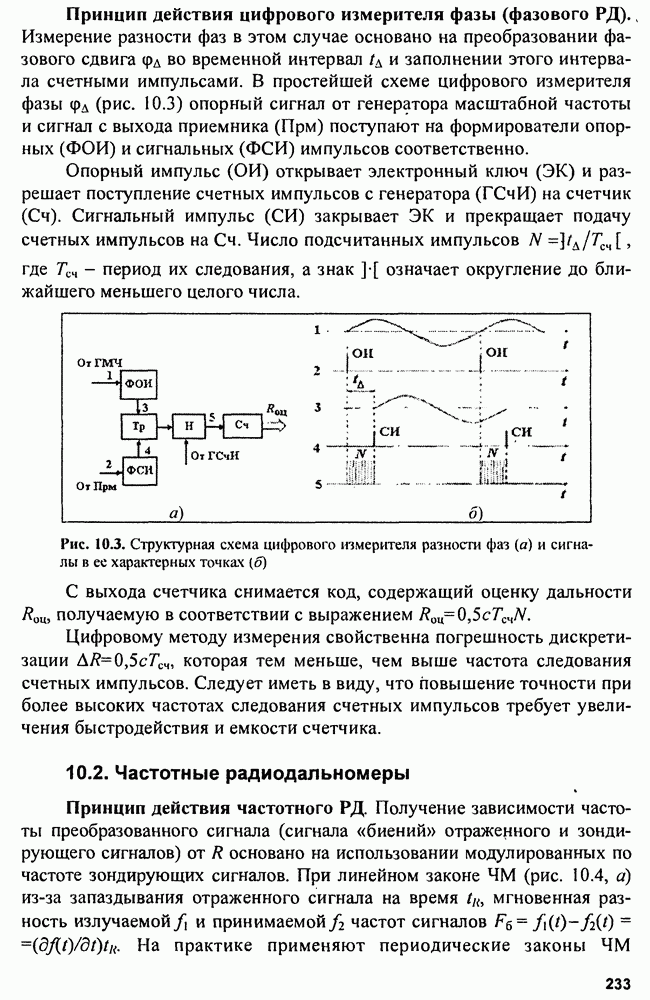
5.2.4. Погрешность местоположения определения
Определим связь СКП местоположения  устройств, входящих в данную систему. Погрешности
устройств, входящих в данную систему. Погрешности  как показано на рис. 5.19, приводят к погрешности
как показано на рис. 5.19, приводят к погрешности  определения места объекта или цели
определения места объекта или цели 

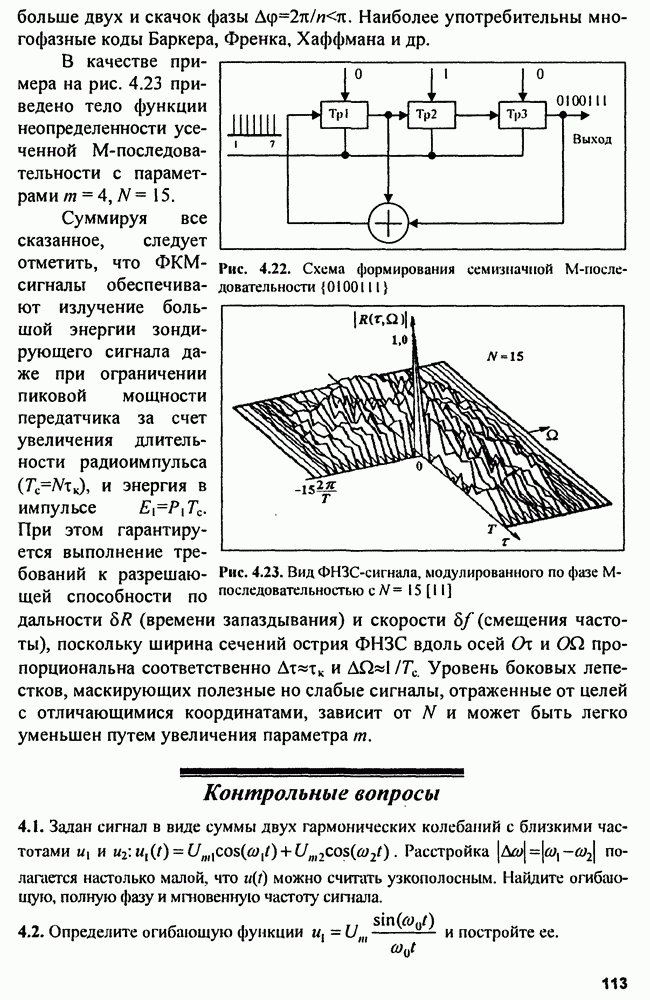
Рис. 5.19. Погрешность определения местоположения объекта на плоскости
Если у - угол пересечения линий положения ЛП в точке  то при одинаковых знаках
то при одинаковых знаках  из треугольника
из треугольника  следует, что
следует, что  Если
Если  имеют разные знаки, то последний член формулы будет положительным. Выразим стороны треугольника через погрешности линий положения, где знак "плюс" будет при разных знаках
имеют разные знаки, то последний член формулы будет положительным. Выразим стороны треугольника через погрешности линий положения, где знак "плюс" будет при разных знаках 

Пусть линии положения пересекаются под углом у (рис. 5.19), а случайные ошибки их  подчиняются нормальным законам распределения. Из теории вероятностей известно, что в этом случае двумерная плотность распределения вероятностей ошибок
подчиняются нормальным законам распределения. Из теории вероятностей известно, что в этом случае двумерная плотность распределения вероятностей ошибок  и V:
и V:

где  средние квадратичные ошибки линий положения;
средние квадратичные ошибки линий положения;  коэффициент корреляции ошибок.
коэффициент корреляции ошибок.
Коэффициент корреляции характеризует степень вероятностной связи между случайными ошибками  и V:
и V:

Если случайные ошибки  независимы, то
независимы, то  Приравняв показатель степени к некоторой постоянной величине, получим уравнение линии равной плотности распределения вероятностей:
Приравняв показатель степени к некоторой постоянной величине, получим уравнение линии равной плотности распределения вероятностей:

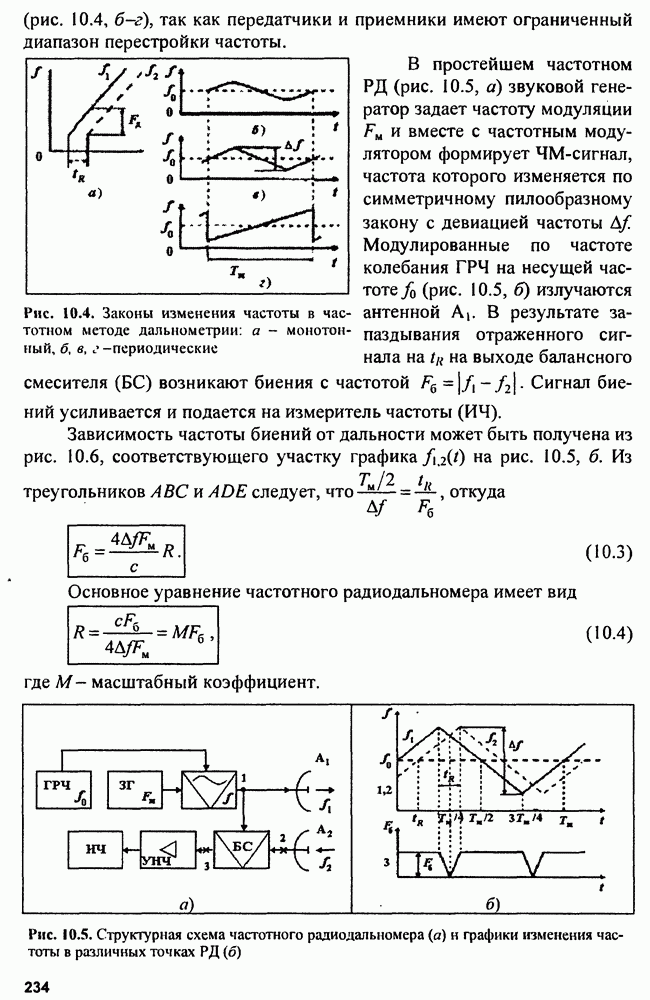
Значение ошибки линий положения в реальных условиях таково, что в пределах возможных положений точки  линии положения практически можно считать параллельными. В этих условиях кривая равной плотности распределения представляет собой эллипс (рис. 5.20).
линии положения практически можно считать параллельными. В этих условиях кривая равной плотности распределения представляет собой эллипс (рис. 5.20).

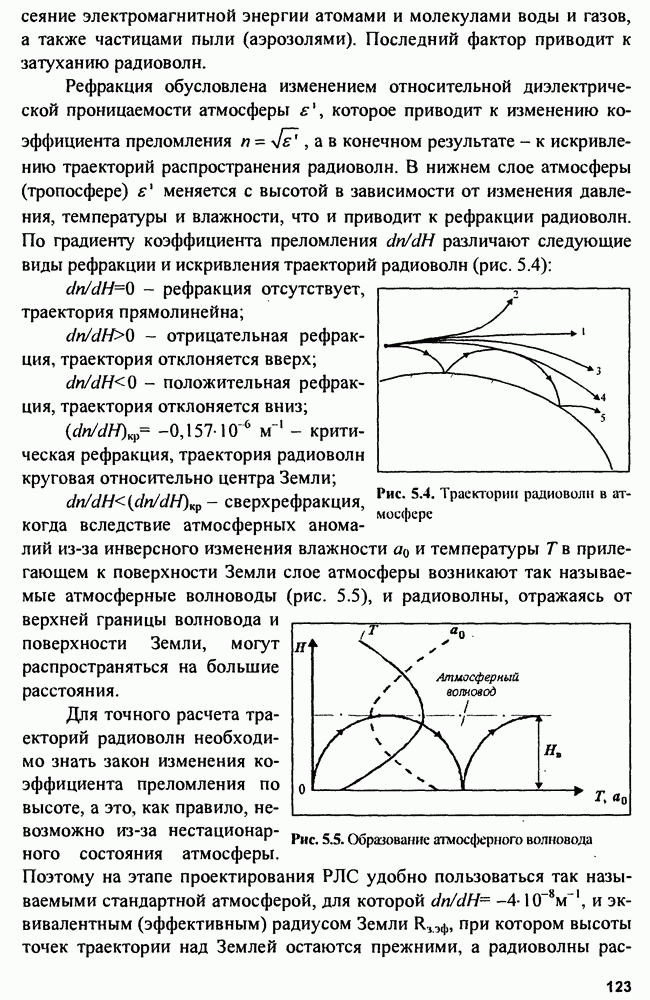
Рис. 5.20. Эллипс ошибок
Различным значениям X соответствует семейство софокусных эллипсов ошибок. Размеры полуосей эллипса ошибок заданной вероятности зависят от величины X, погрешностей а  а у, корреляции погрешностей
а у, корреляции погрешностей  и угла пересечения ЛП у. Положение эллипса ошибок определяется углом
и угла пересечения ЛП у. Положение эллипса ошибок определяется углом  между большой осью эллипса и биссектрисой угла между линиями положения у.
между большой осью эллипса и биссектрисой угла между линиями положения у.
Обычно корреляционная зависимость между ошибками линий положения в РЛС выражена слабо и можно принять  Анализ положений эллипса ошибок при различных значениях
Анализ положений эллипса ошибок при различных значениях  показывает, что большая ось эллипса ошибок всегда лежит между биссектрисой острого угла у пересечения линий положения и той из ЛП, точность определения которой выше.
показывает, что большая ось эллипса ошибок всегда лежит между биссектрисой острого угла у пересечения линий положения и той из ЛП, точность определения которой выше.
Когда точности определения линий положения равны между собой, большая ось эллипса совпадет с биссектрисой острого угла пересечения ЛП. В ОПРЛС, использующих дальномерно-пеленгационный метод определения местоположения, когда угол пересечения прямой  (ошибки
(ошибки  являются взаимно независимыми), оси эллипса ошибок совпадают с линиями положения. В этом случае полуоси эллипса
являются взаимно независимыми), оси эллипса ошибок совпадают с линиями положения. В этом случае полуоси эллипса

где  среднеквадратические ошибки двух взаимно перпендикулярных линий положения.
среднеквадратические ошибки двух взаимно перпендикулярных линий положения.
Если при этом  то рассеяние превращается в круговое, а эллипсы ошибок превращаются в окружности. Вероятность того, что искомое место находится в пределах эллипса ошибок,
то рассеяние превращается в круговое, а эллипсы ошибок превращаются в окружности. Вероятность того, что искомое место находится в пределах эллипса ошибок,

Выполнив интегрирование, получим  откуда
откуда

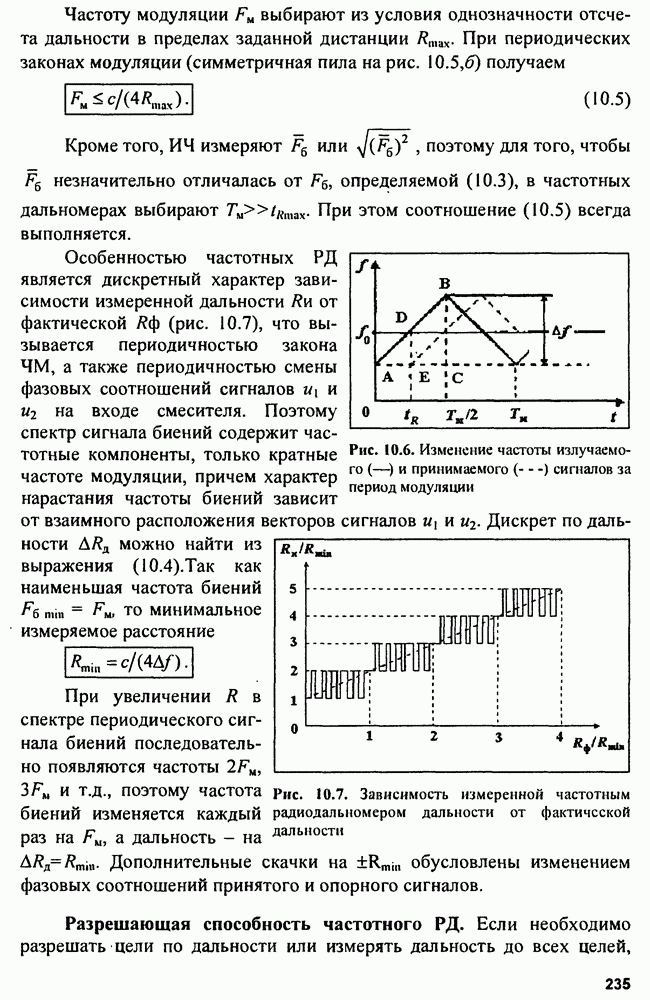
Для эллипса ошибок, обладающего тем свойством, что вероятность нахождения в нем искомого местоположения равна 0,5, значение параметра  Представление о зависимости точности местоопределения от взаимного расположения РЛС и цели дает поле ошибок, представляющее собой ряд эллипсов ошибок заданной вероятности. Для иллюстрации на рис 5.21 представлено поле ошибок при дальномерно-пеленгационном методе определения местоположения.
Представление о зависимости точности местоопределения от взаимного расположения РЛС и цели дает поле ошибок, представляющее собой ряд эллипсов ошибок заданной вероятности. Для иллюстрации на рис 5.21 представлено поле ошибок при дальномерно-пеленгационном методе определения местоположения.

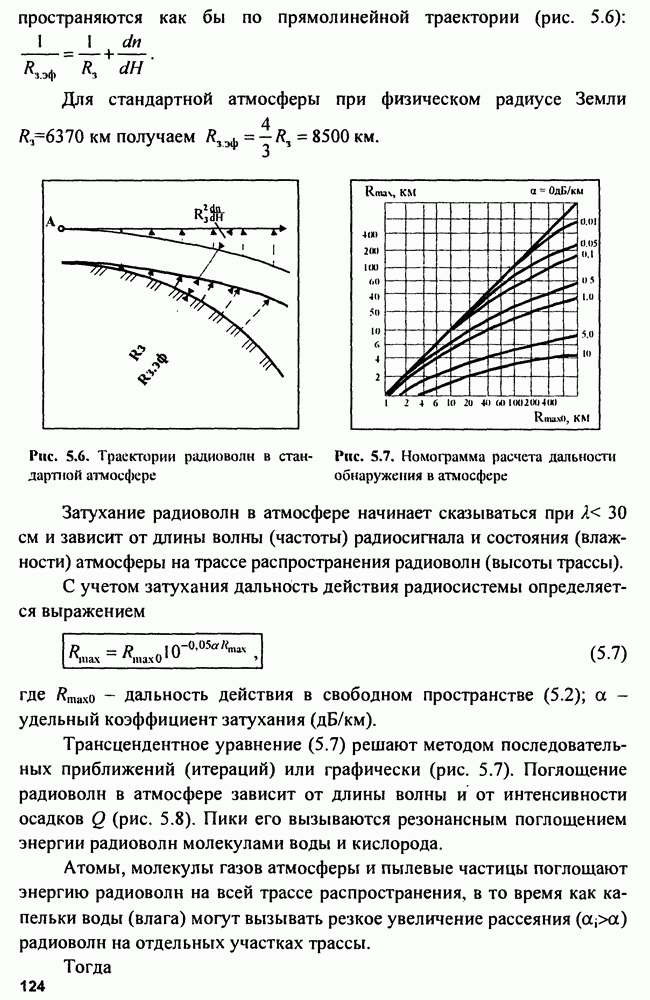
Рис. 5.21. Поле ошибок при дальномерно-пеленгационном методе определения положения цели
Рассмотрим теперь случай определения местоположения объекта в пространстве дальномерно-пеленгационным методом. Если при измерении дальности  азимута
азимута  и угла места
и угла места  возникли ошибки
возникли ошибки  Да и
Да и  то найденное местоположение не будет совпадать с истинным. Ошибка места
то найденное местоположение не будет совпадать с истинным. Ошибка места  в этом случае будет равна расстоянию
в этом случае будет равна расстоянию 
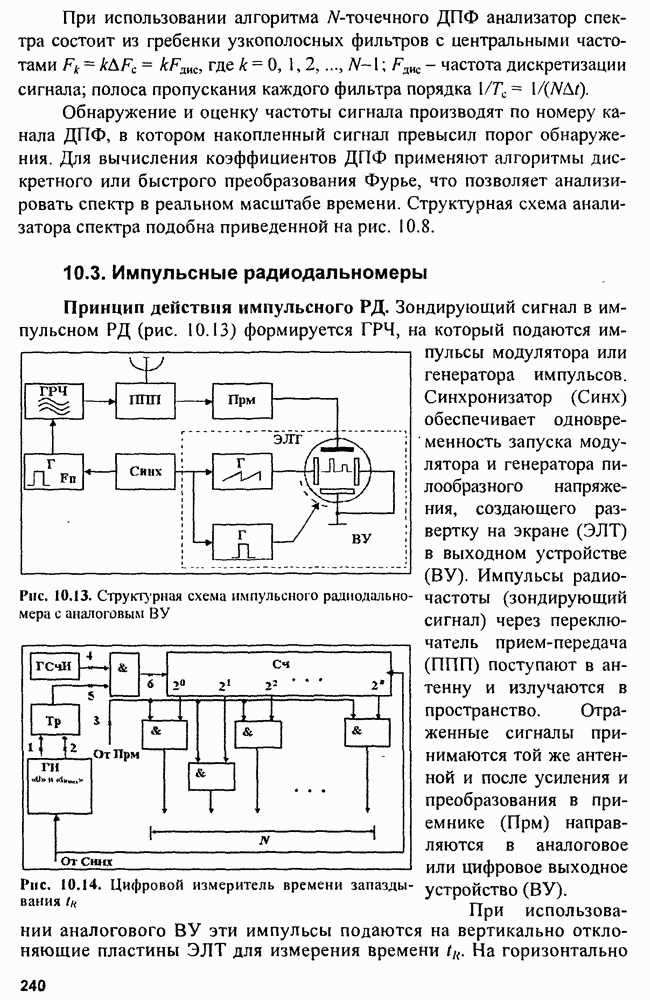
Из рисунка видно, что составляющие ошибки места по трем взаимно перпендикулярным осям 

Если случайные ошибки по трем осям  взаимно независимы и подчиняются нормальным законам распределения, что обычно выполняется в ОПРЛС, то трехмерная плотность распределения вероятности
взаимно независимы и подчиняются нормальным законам распределения, что обычно выполняется в ОПРЛС, то трехмерная плотность распределения вероятности

где 
- среднеквадратичные ошибки по дальности, азимуту и углу места.

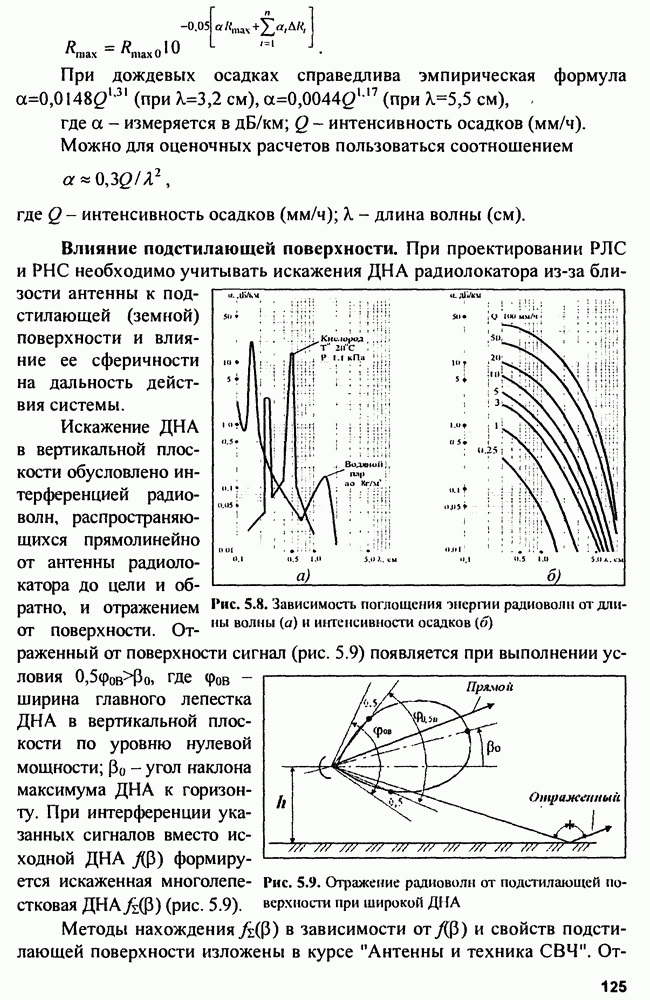
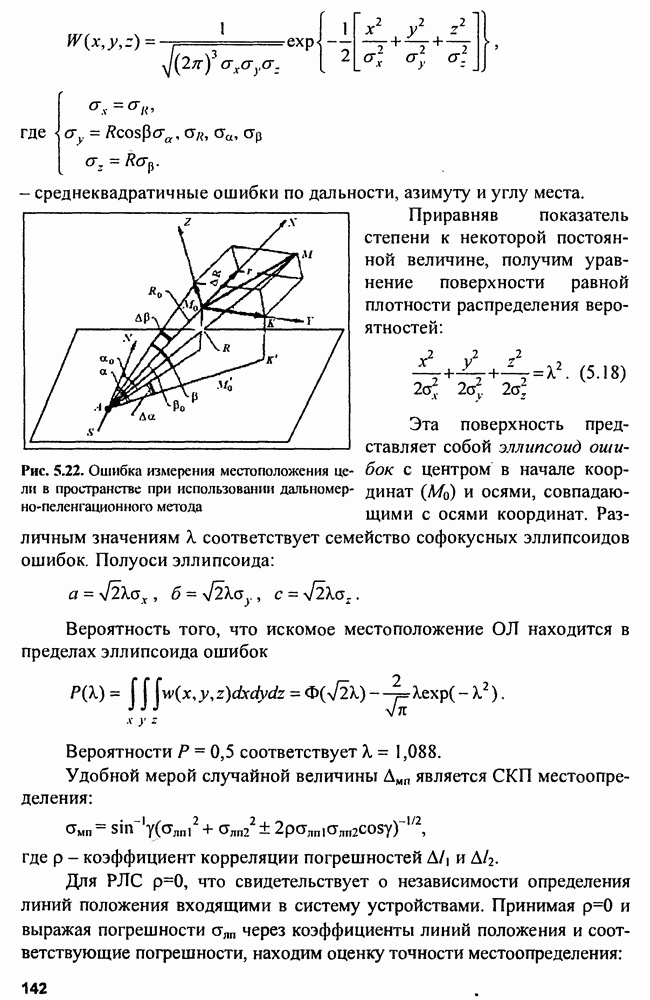
Рис. 5.22. Ошибка измерения местоположения цели в пространстве при использовании дальномерно-пеленгационного метода
Приравняв показатель степени к некоторой постоянной величине, получим уравнение поверхности равной плотности распределения вероятностей:

Эта поверхность представляет собой эллипсоид ошибок с центром в начале координат  и осями, совпадающими с осями координат. Различным значениям X соответствует семейство софокусных эллипсоидов ошибок. Полуоси эллипсоида:
и осями, совпадающими с осями координат. Различным значениям X соответствует семейство софокусных эллипсоидов ошибок. Полуоси эллипсоида:

Вероятность того, что искомое местоположение  находится в пределах эллипсоида ошибок
находится в пределах эллипсоида ошибок

Вероятности  соответствует
соответствует  Удобной мерой случайной величины
Удобной мерой случайной величины  является СКП местоопределения:
является СКП местоопределения:

где  коэффициент корреляции погрешностей
коэффициент корреляции погрешностей 
Для  что свидетельствует о независимости определения линий положения входящими в систему устройствами. Принимая
что свидетельствует о независимости определения линий положения входящими в систему устройствами. Принимая  и выражая погрешности стлп через коэффициенты линий положения и соответствующие погрешности, находим оценку точности местоопределения:
и выражая погрешности стлп через коэффициенты линий положения и соответствующие погрешности, находим оценку точности местоопределения:

Физический смысл формулы (5.19) заключается в следующем. Если построить окружность с центром в точке  где расположен объект или цель, с радиусом, равным допустимому значению
где расположен объект или цель, с радиусом, равным допустимому значению  т.е. ампд, то вероятность того, что при измерениях погрешность
т.е. ампд, то вероятность того, что при измерениях погрешность  окажется внутри этой окружности, т.е. не будет превышать ампд, равна 0,63 - 0,68. Если принять радиус окружности равным
окажется внутри этой окружности, т.е. не будет превышать ампд, равна 0,63 - 0,68. Если принять радиус окружности равным  то эта вероятность лежит в пределах 0,95 - 0,98. Отличия указанных вероятностей от значений 0,68 и 0,95, принятых для соответствующих погрешностей, объясняется тем, что закон распределения
то эта вероятность лежит в пределах 0,95 - 0,98. Отличия указанных вероятностей от значений 0,68 и 0,95, принятых для соответствующих погрешностей, объясняется тем, что закон распределения  не является гауссовским (в простейшем случае при
не является гауссовским (в простейшем случае при  это закон Рэлея). Полученные результаты могут быть использованы для построения рабочих зон позиционных РЛС.
это закон Рэлея). Полученные результаты могут быть использованы для построения рабочих зон позиционных РЛС.
Погрешность определения пространственного положения объекта (цели) при независимости результатов измерений всех координат

где  угол между третьей поверхностью положения и линией положения на плоскости;
угол между третьей поверхностью положения и линией положения на плоскости;  вычисляется по формуле (5.18);
вычисляется по формуле (5.18);  нахождения третьей поверхности положения.
нахождения третьей поверхности положения.
Геометрический фактор. Из (5.18) следует, что погрешность местоопределения зависит не только от точности нахождения элемента  но и от типа позиционной системы, влияющего на значение
но и от типа позиционной системы, влияющего на значение  и от расположения измерителей РЛС и объекта, которое сказывается на значении угла у и на коэффициенте
и от расположения измерителей РЛС и объекта, которое сказывается на значении угла у и на коэффициенте  Для пояснения сказанного рассмотрим системы, состоящие из однотипных устройств (измерителей дальности или углов). В таких системах, к числу которых относятся дальномерные, разностно-дальномерные, угломерные и др., естественно предположить, что точность определения элемента
Для пояснения сказанного рассмотрим системы, состоящие из однотипных устройств (измерителей дальности или углов). В таких системах, к числу которых относятся дальномерные, разностно-дальномерные, угломерные и др., естественно предположить, что точность определения элемента  одинакова, т.е.
одинакова, т.е.  как по условию
как по условию  то
то

где  геометрический фактор (иногда
геометрический фактор (иногда  не включает в
не включает в 
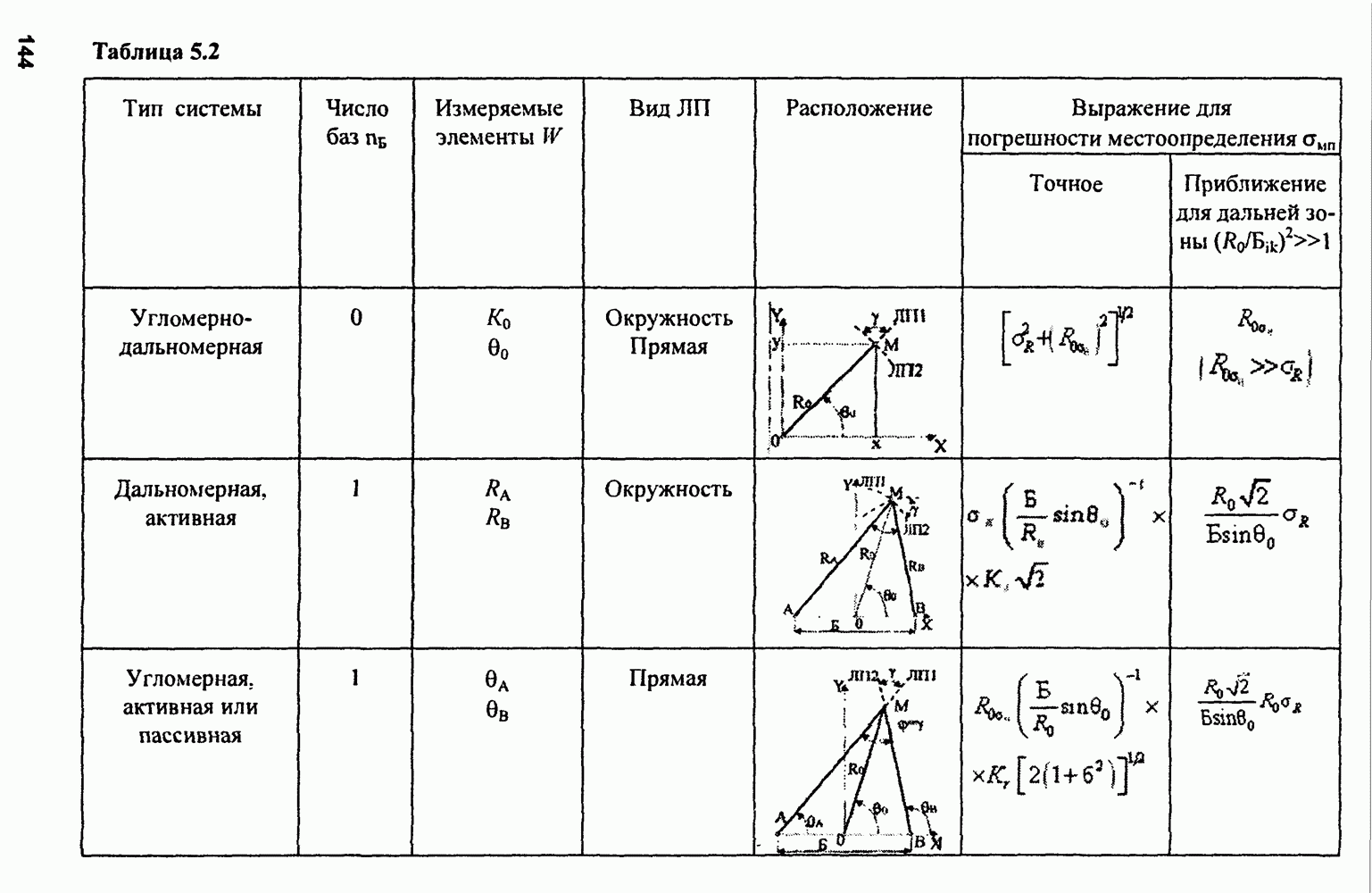
Для нахождения геометрического фактора многопозиционных РЛС можно воспользоваться данными точностных характеристиках этих систем, некоторые из которых приведены в табл. 5.2. Формулы в ней справедливы для расположения станций системы в точках  показанных на приведенных в таблице рисунках. Обозначения в формулах соответствуют обозначениям на этих рисунках, а для упрощения введены следующие сокращения:
показанных на приведенных в таблице рисунках. Обозначения в формулах соответствуют обозначениям на этих рисунках, а для упрощения введены следующие сокращения:  в многобазовых системах
в многобазовых системах 
(см. скан)
В системах, состоящих из однотипных устройств,  Коэффициент корреляции погрешностей
Коэффициент корреляции погрешностей  принят равным нулю. Приближенные выражения справедливы когда
принят равным нулю. Приближенные выражения справедливы когда  Для всех однобазовых систем
Для всех однобазовых систем  точность местоопределения максимальна на перпендикуляре к базе, т.е. при
точность местоопределения максимальна на перпендикуляре к базе, т.е. при 
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
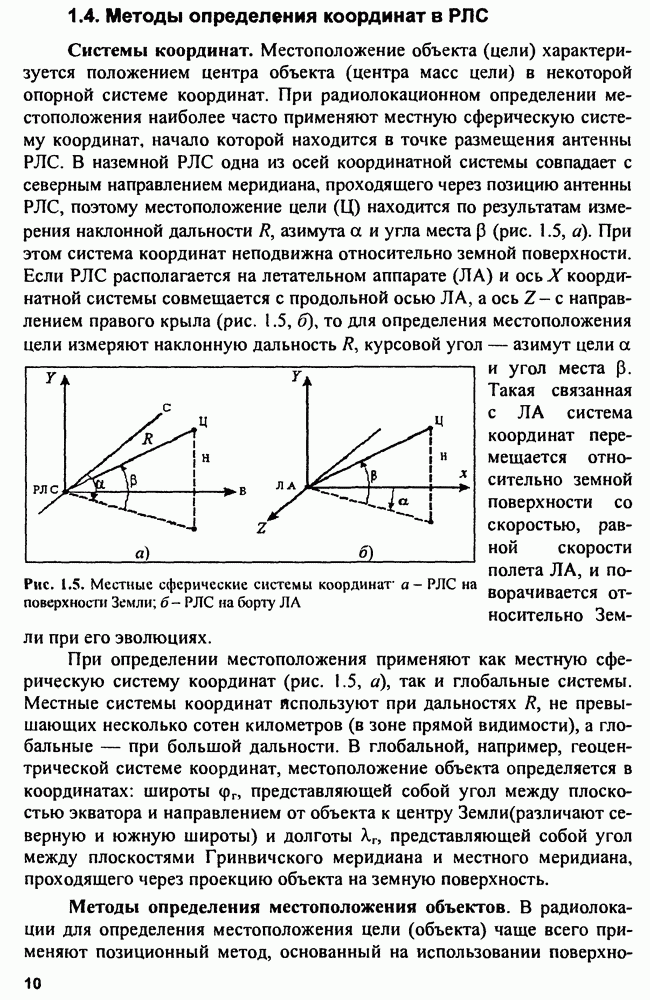
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
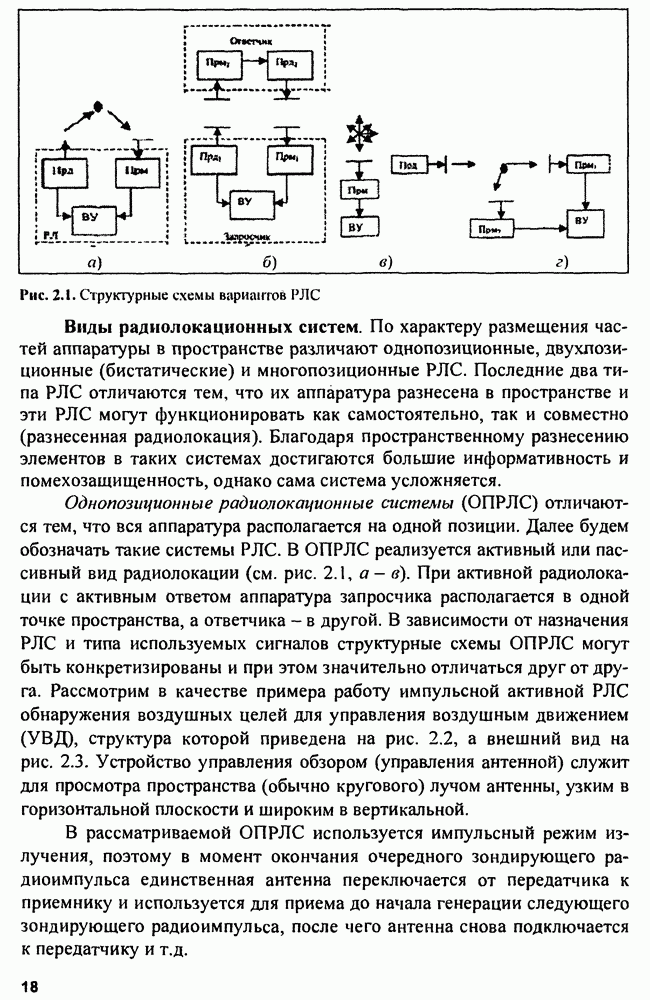
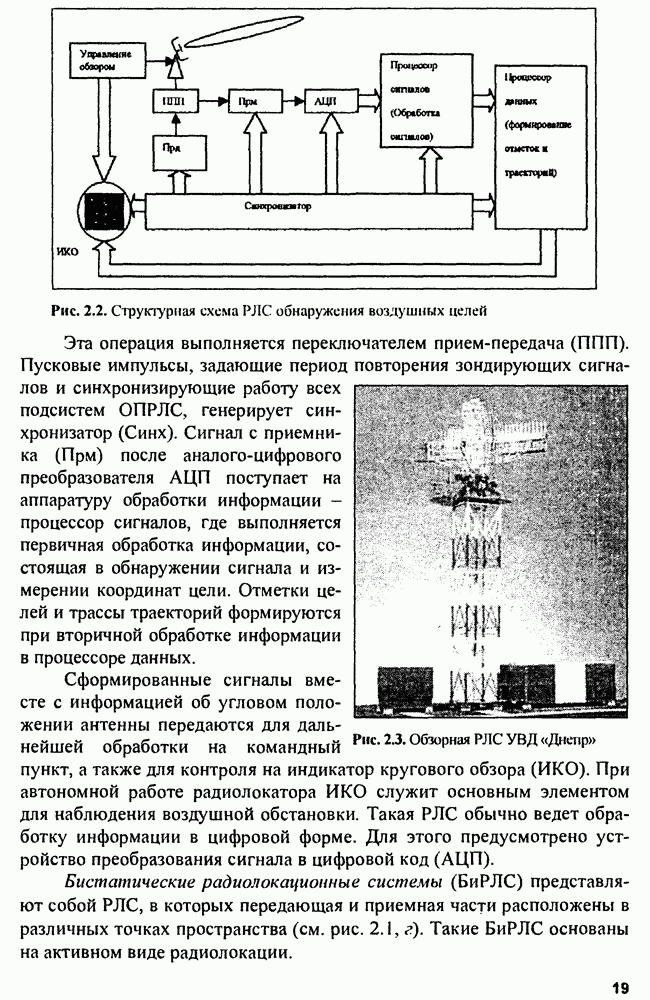
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
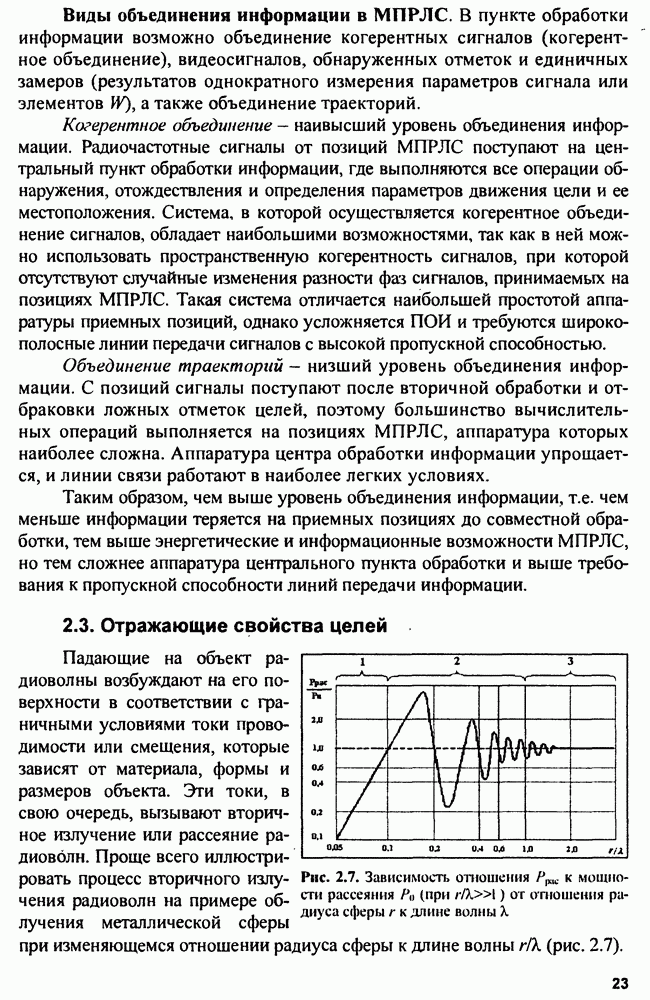
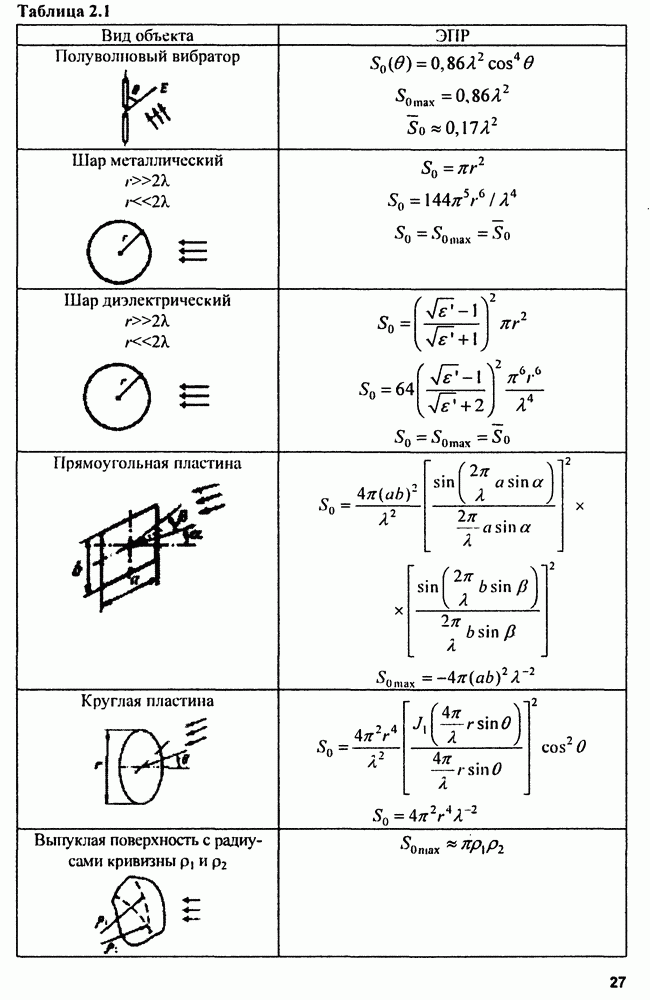
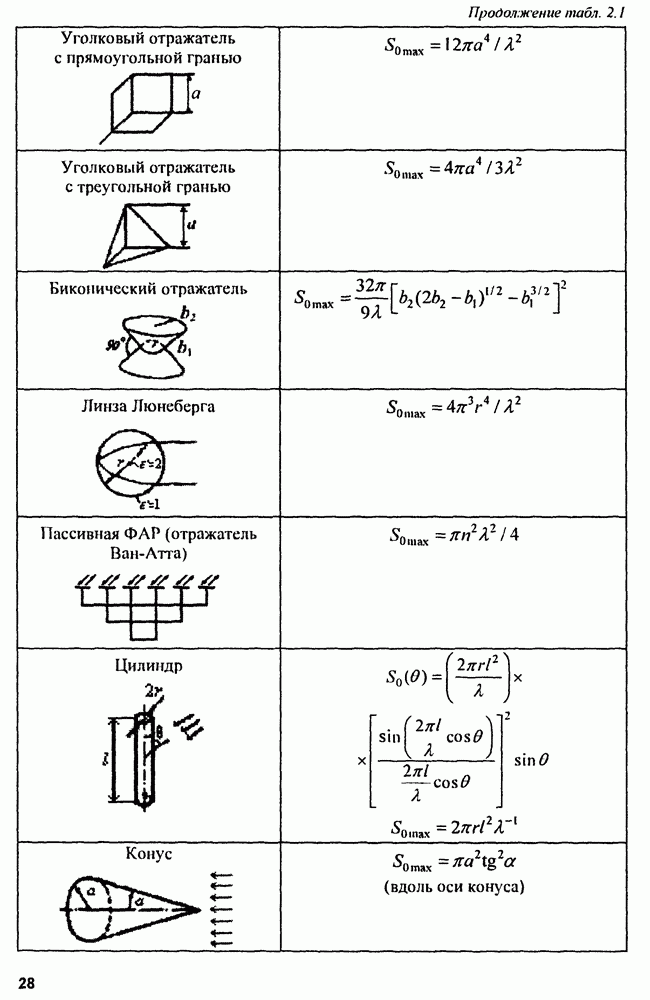
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
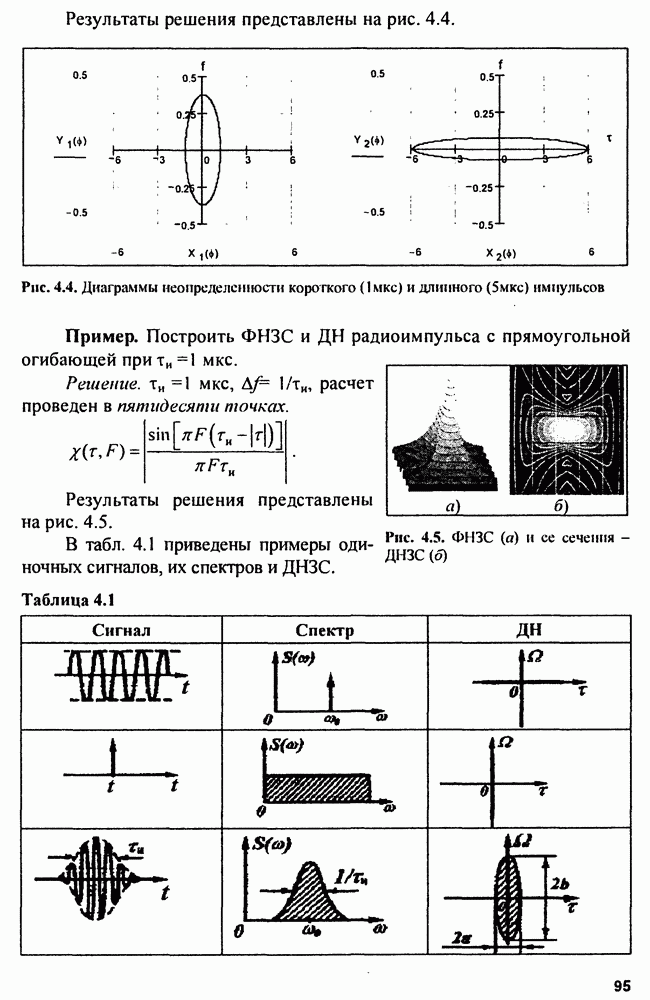
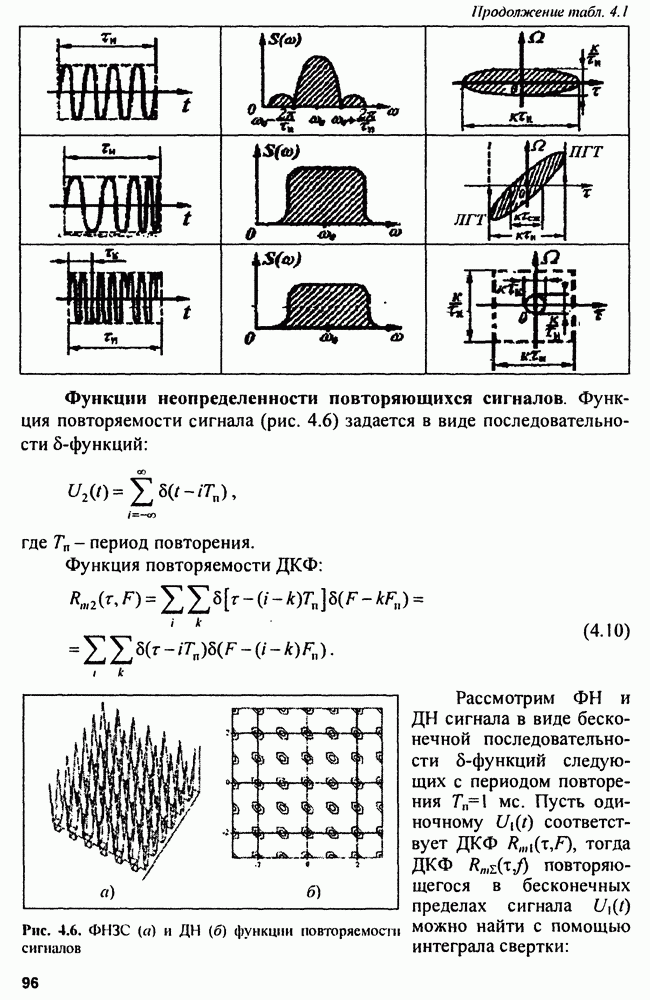
- 4.2. Диаграммы неопределенности
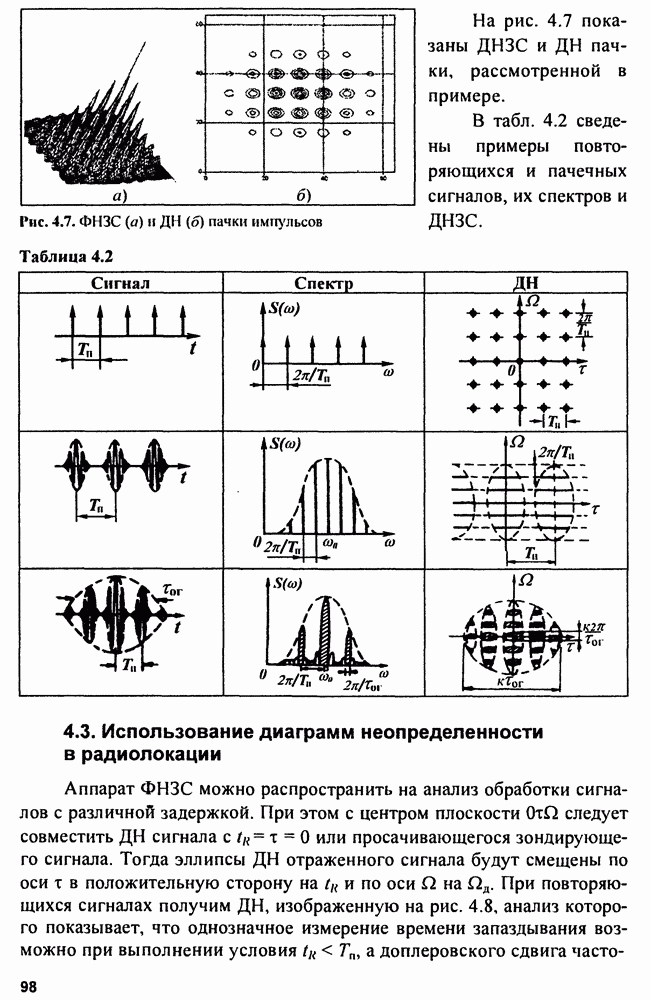
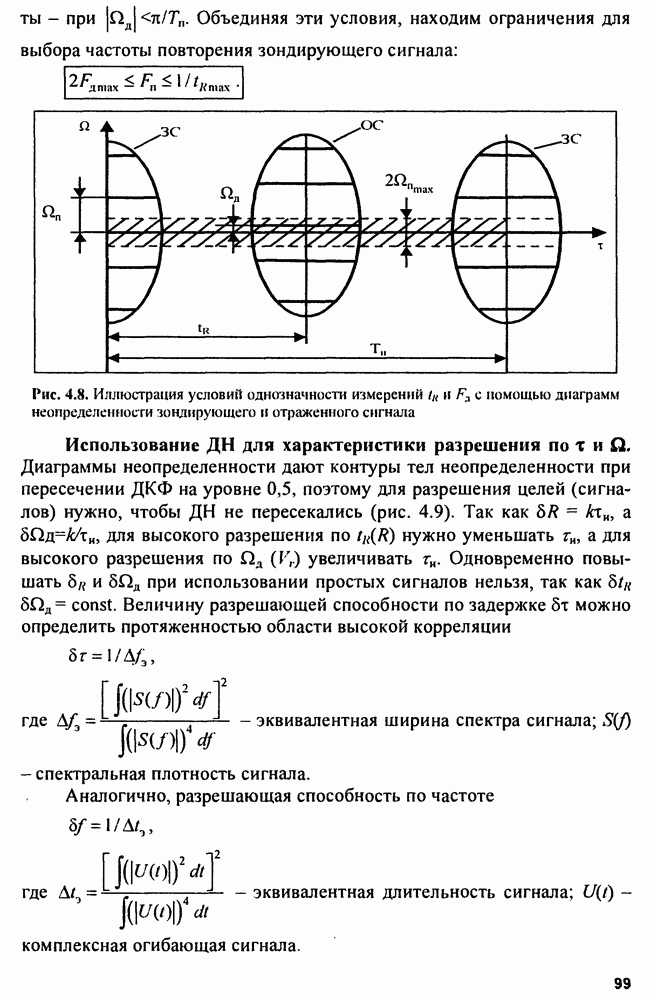
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
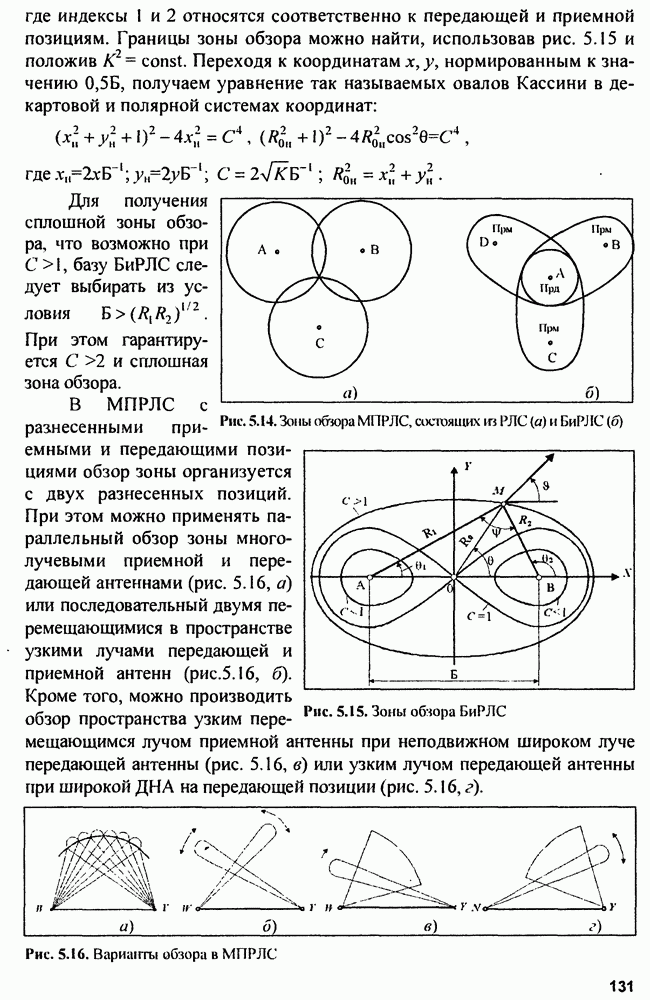
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
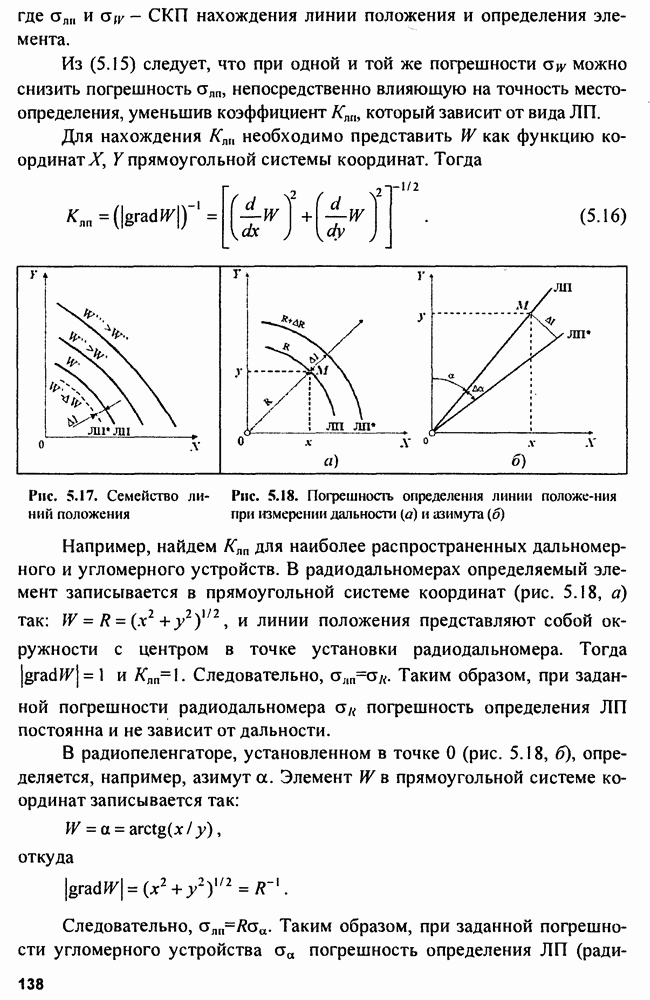
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
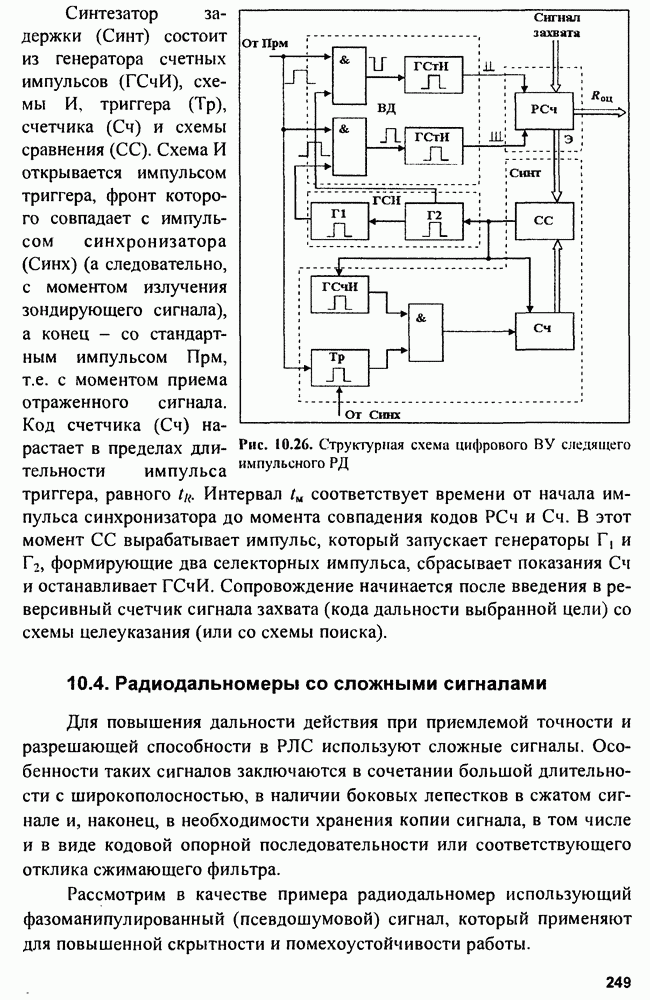
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение