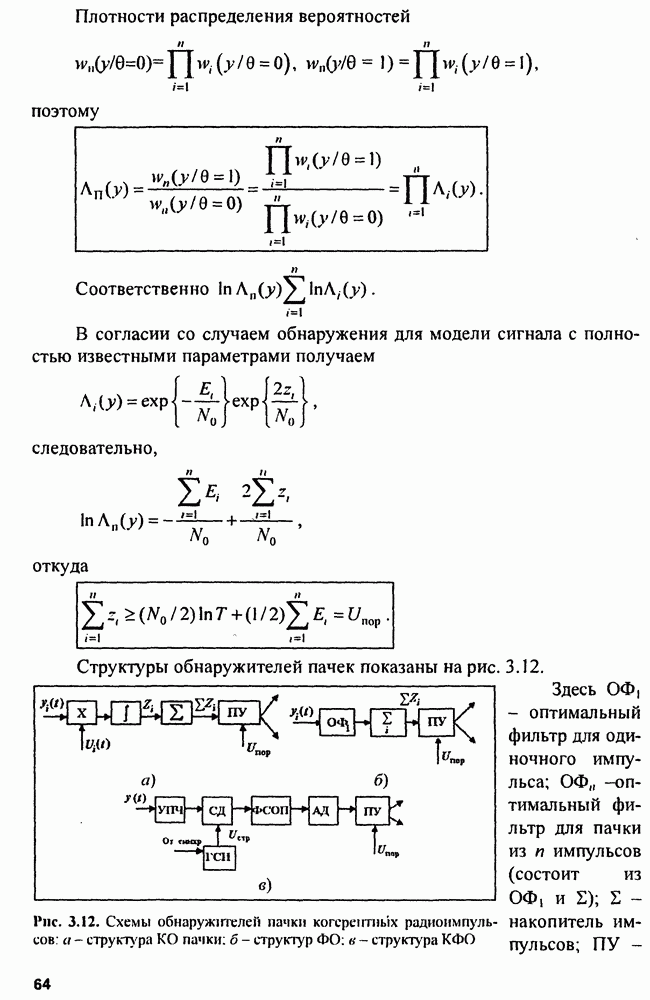
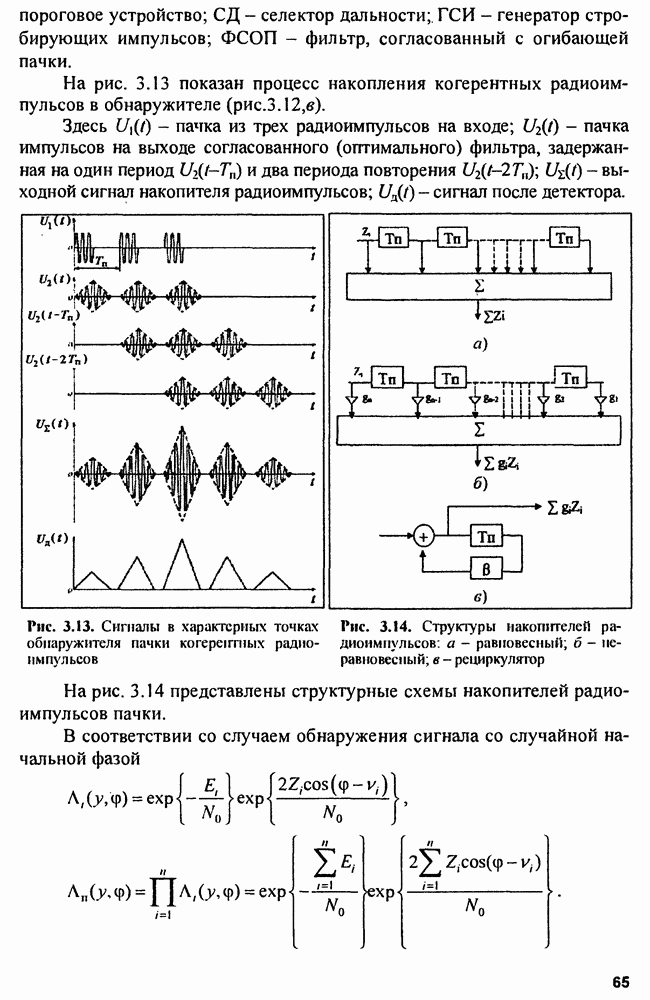
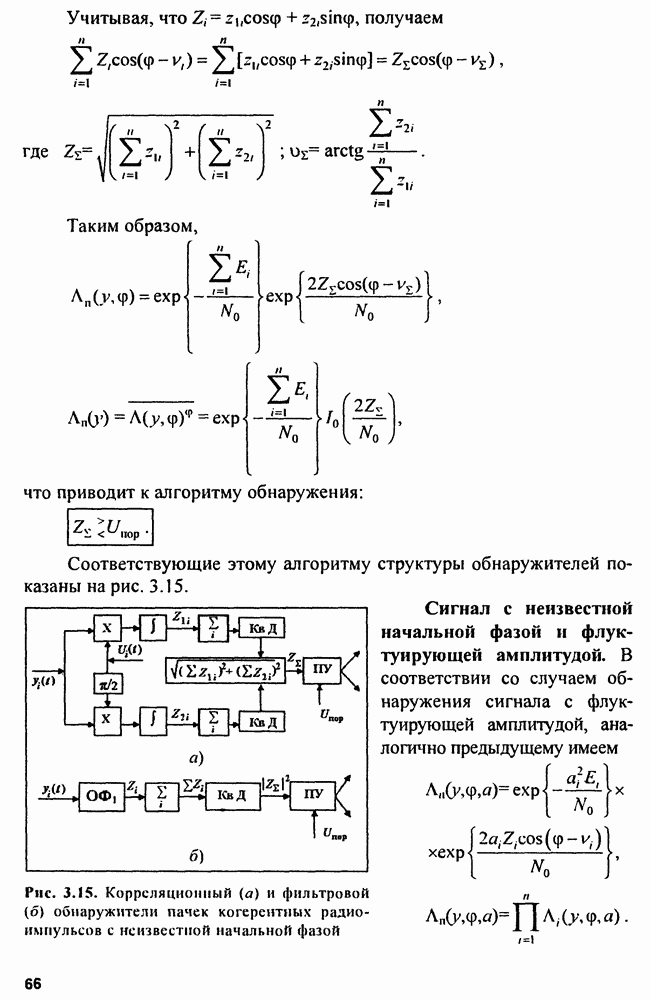
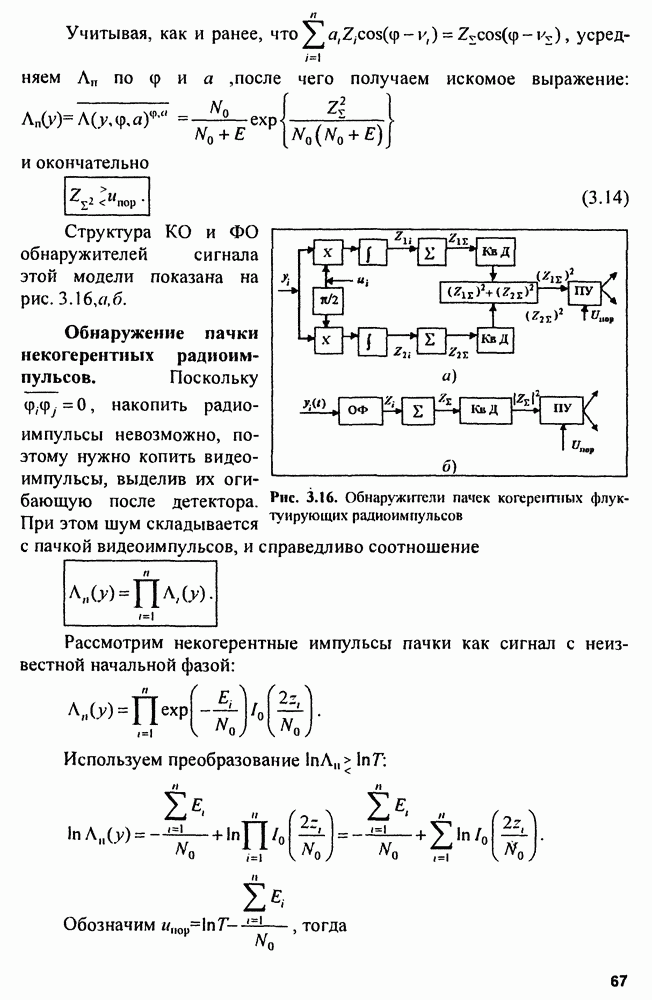
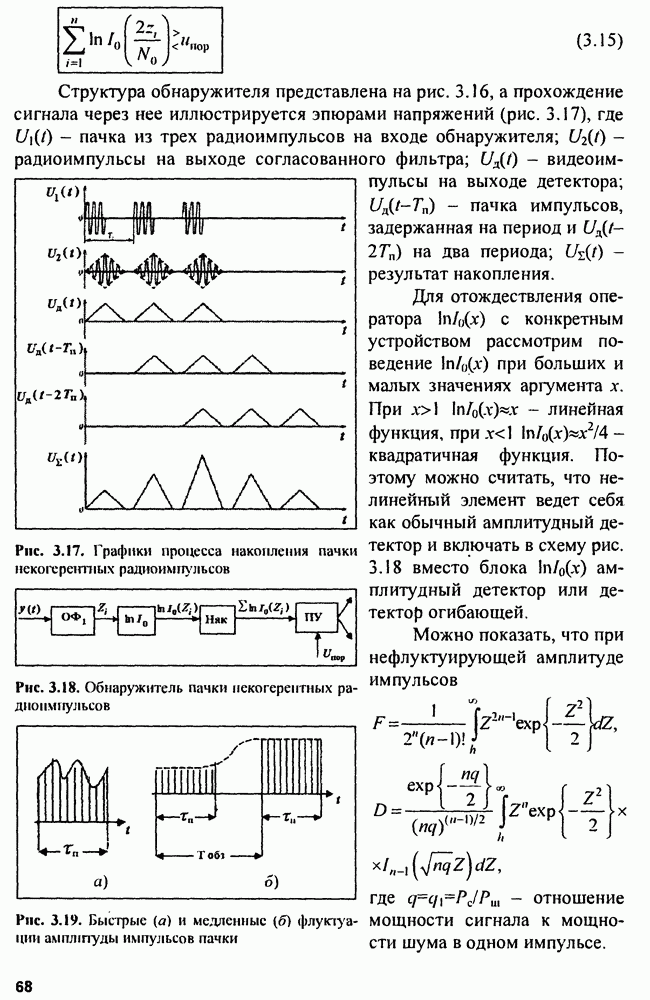
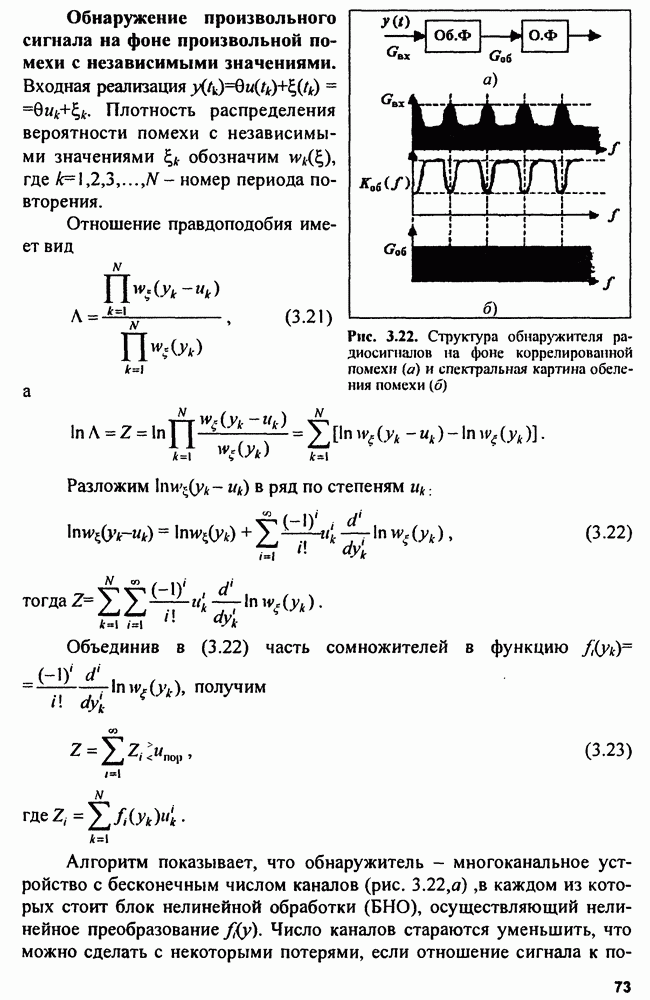
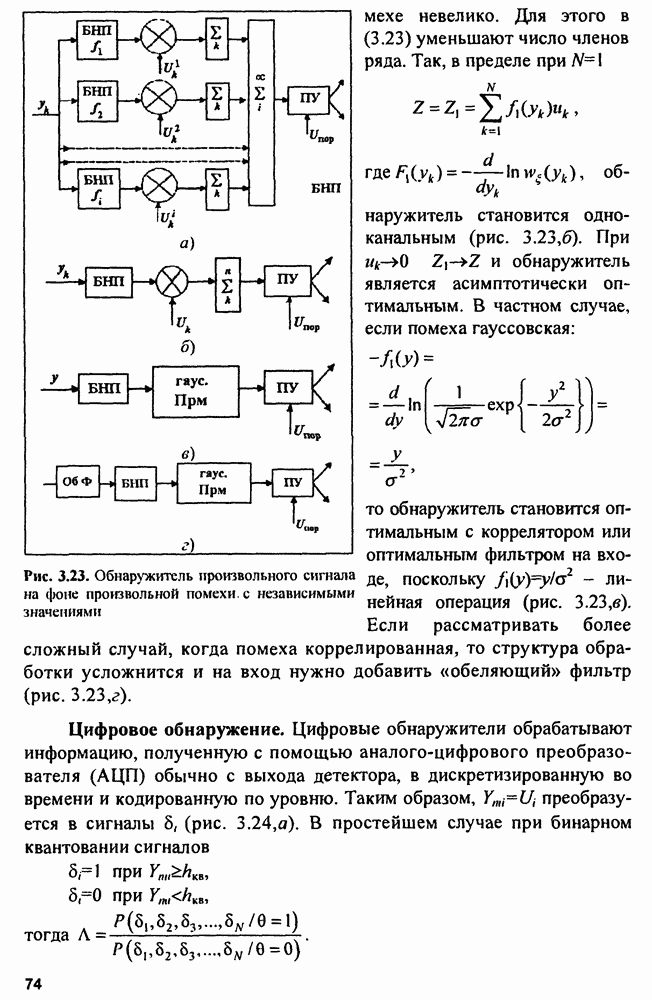
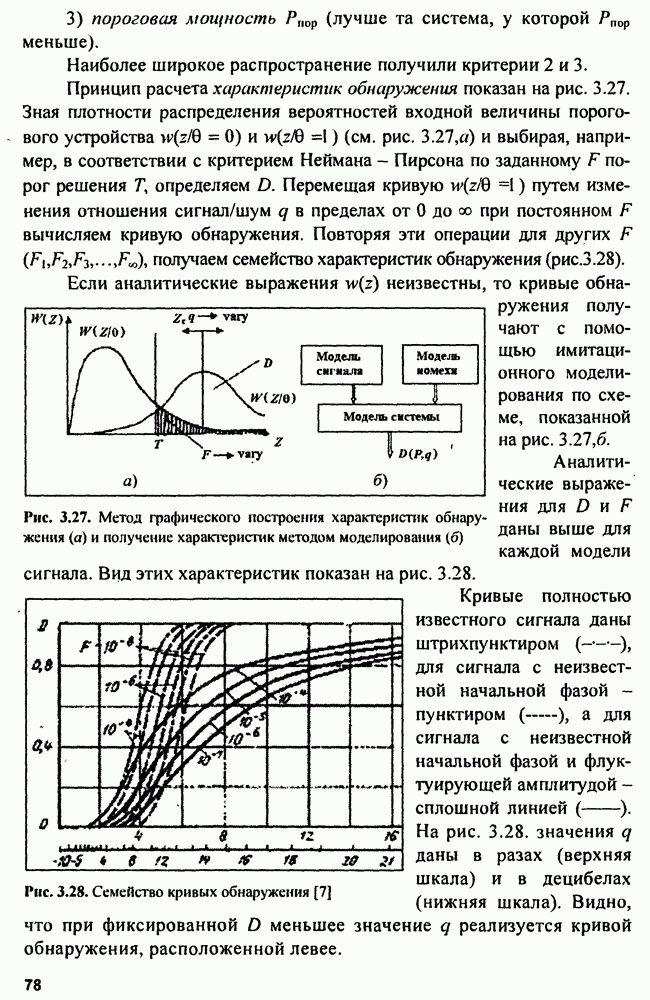
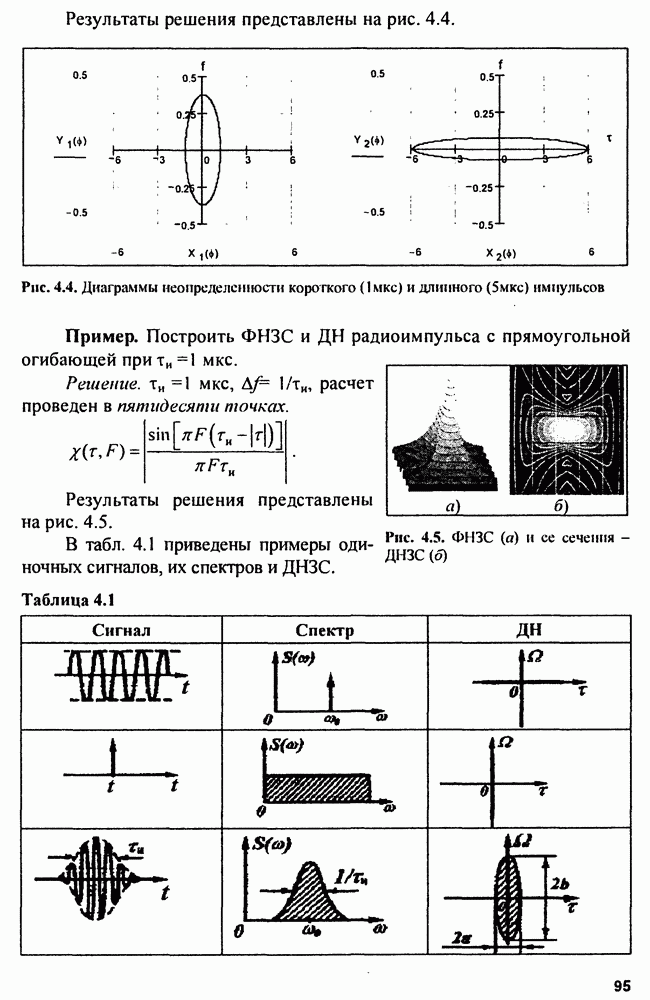
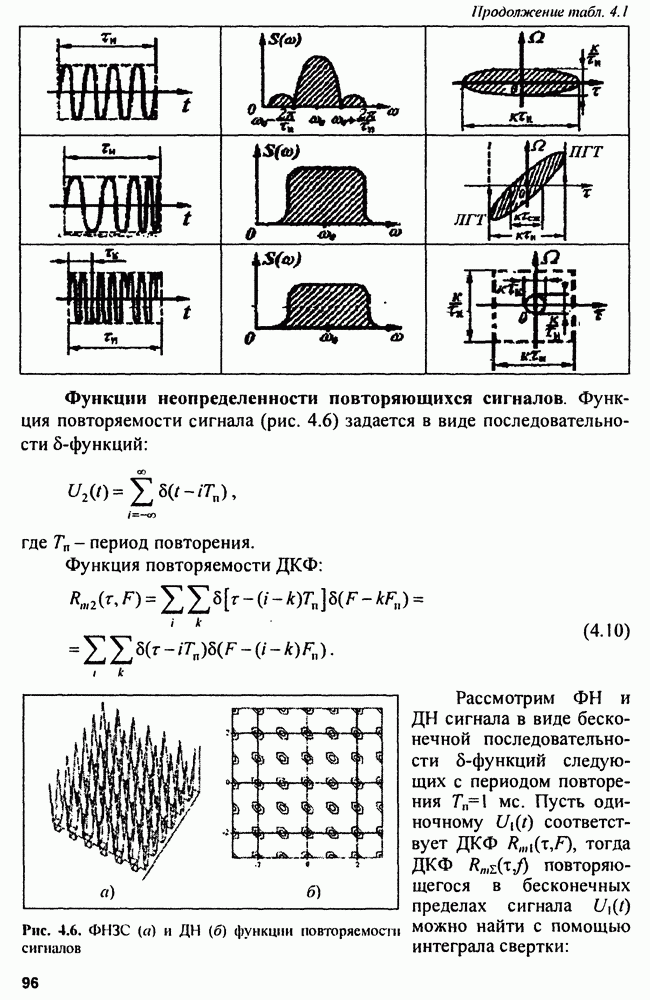
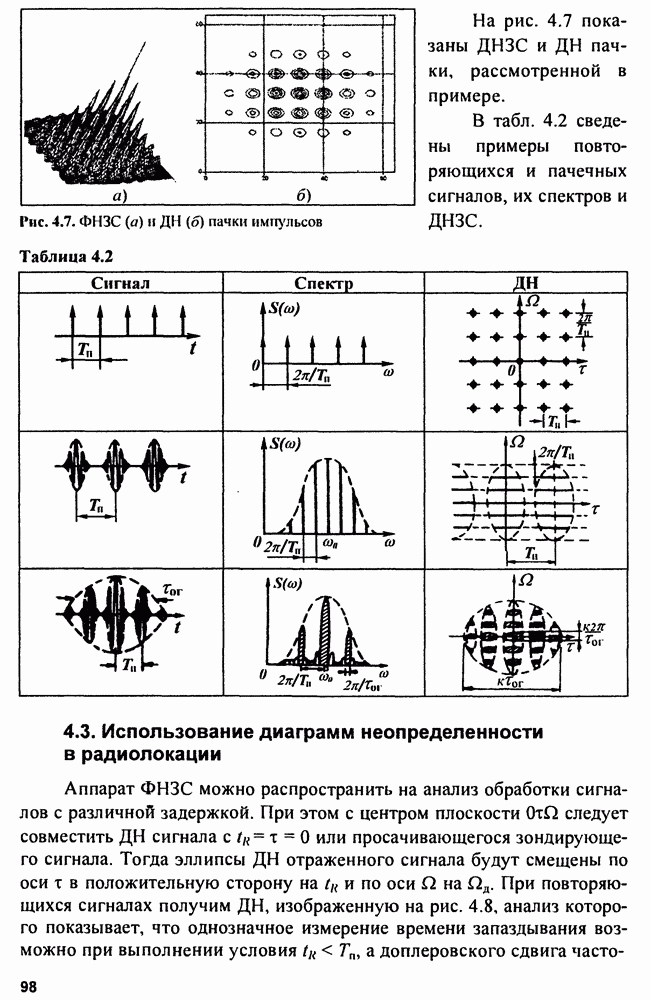
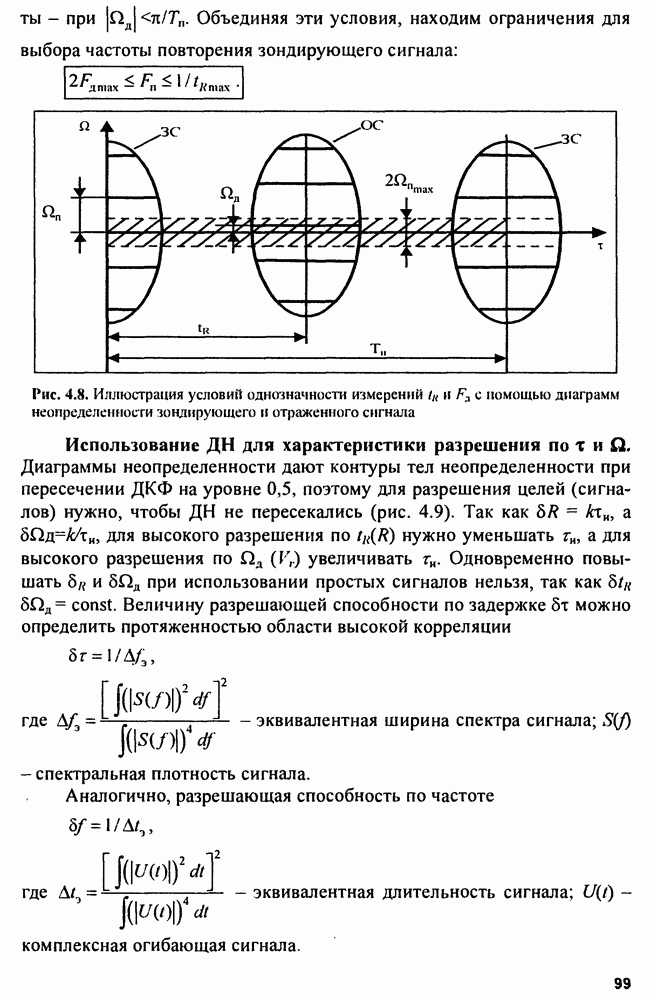
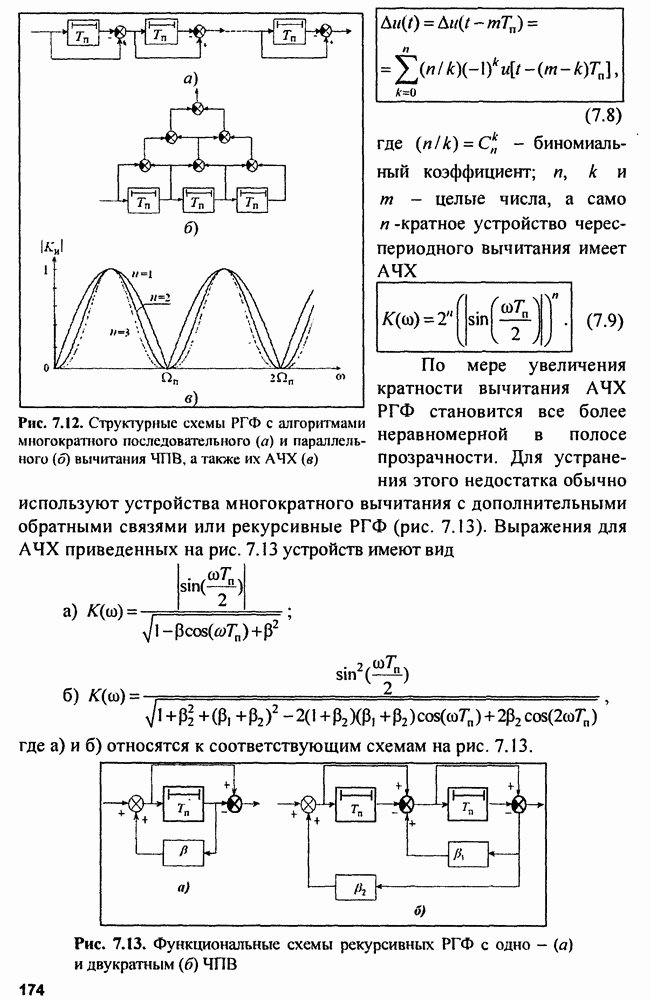
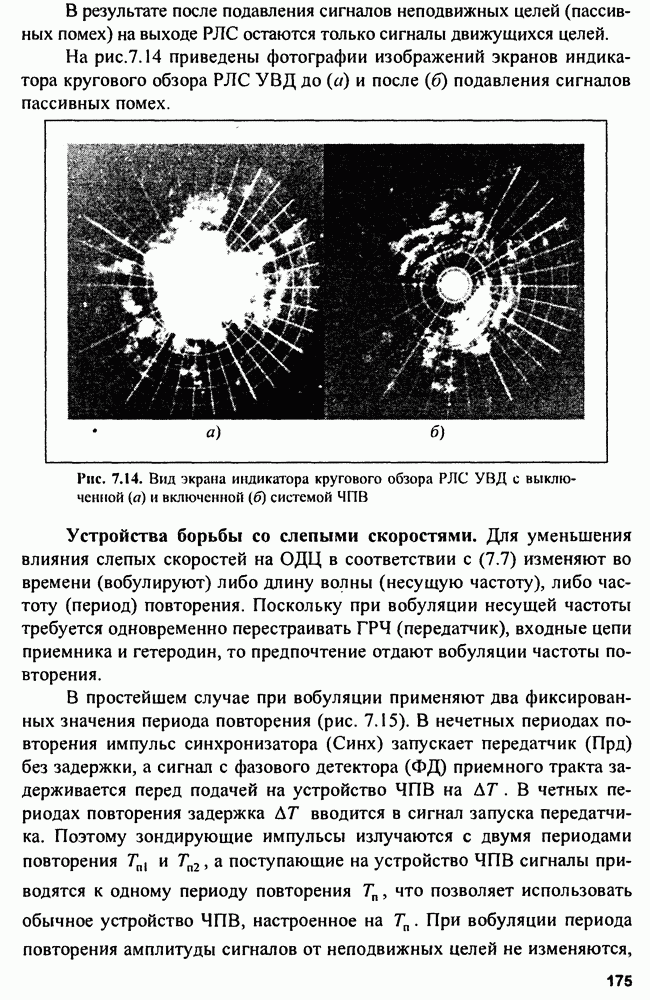
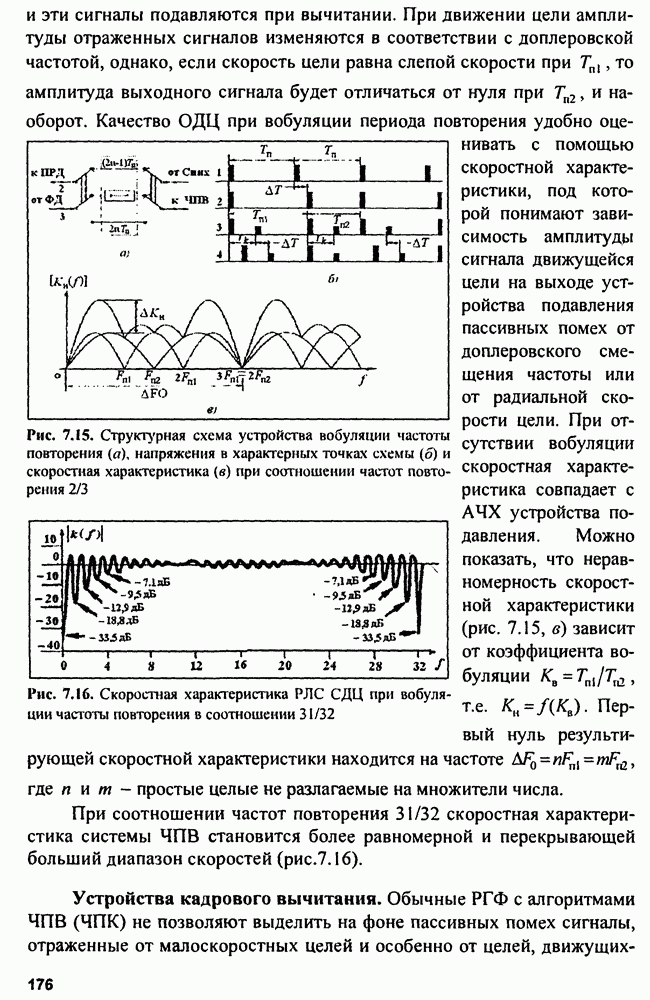
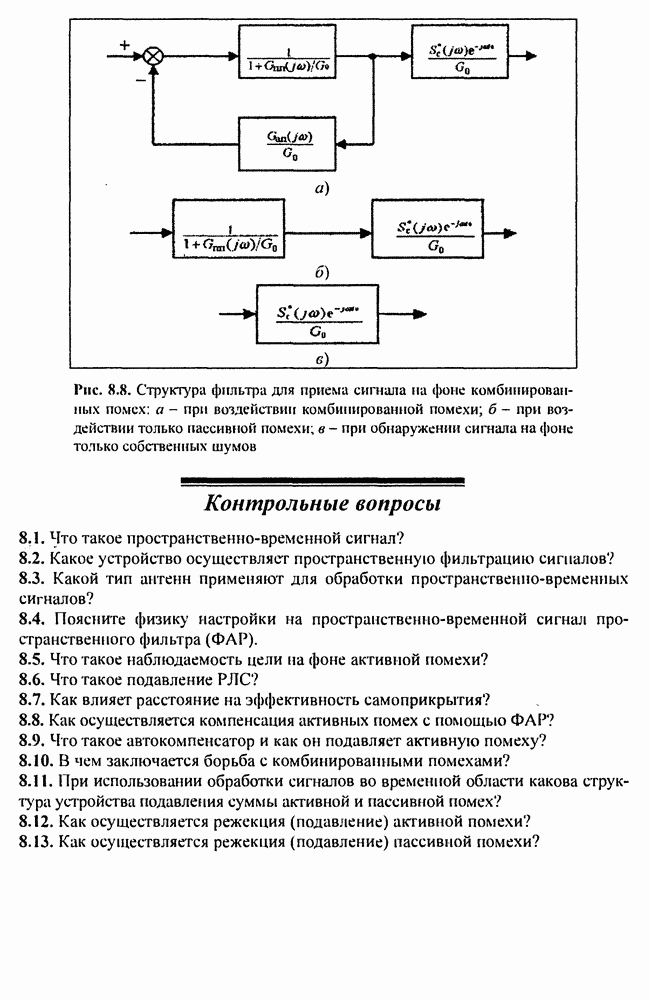
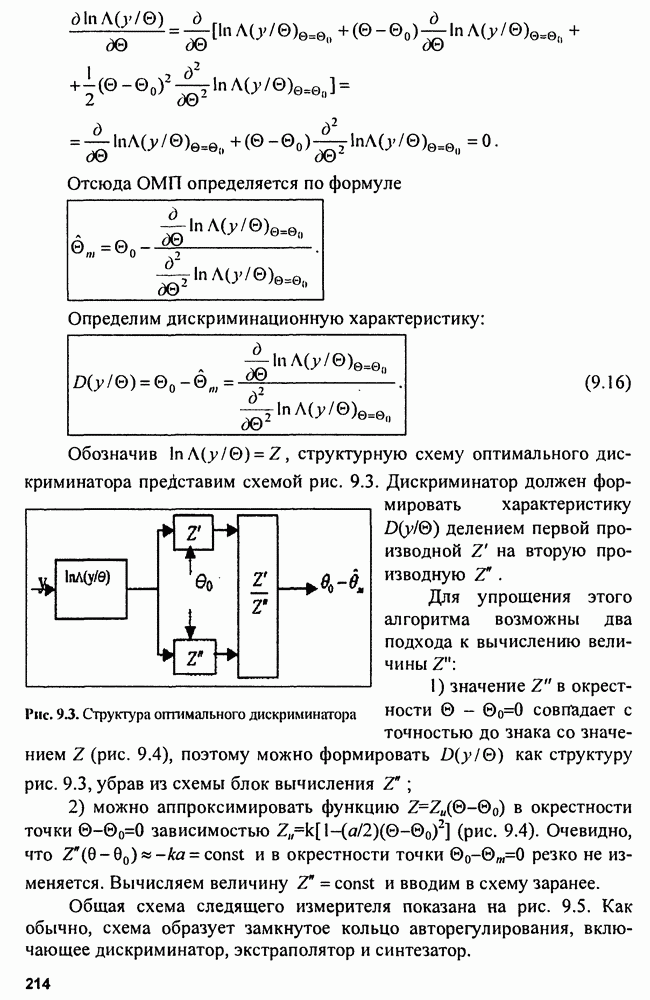
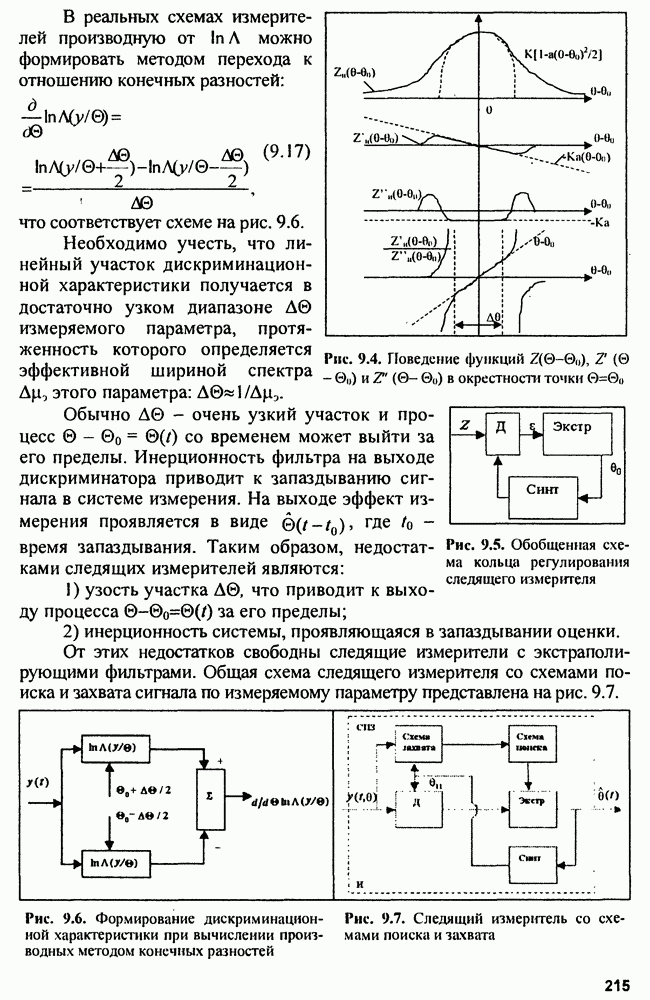
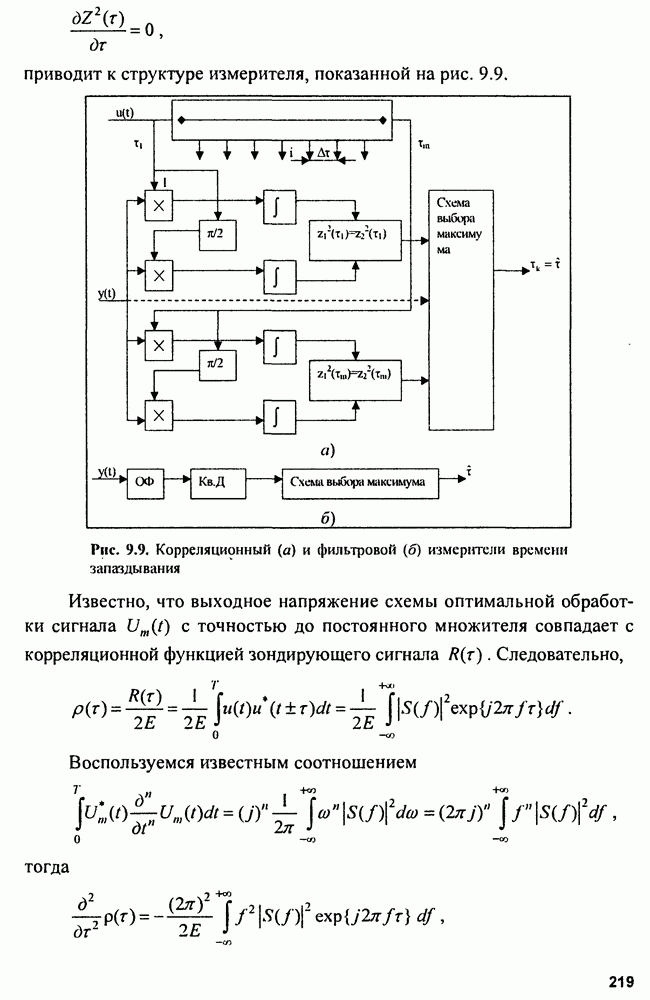
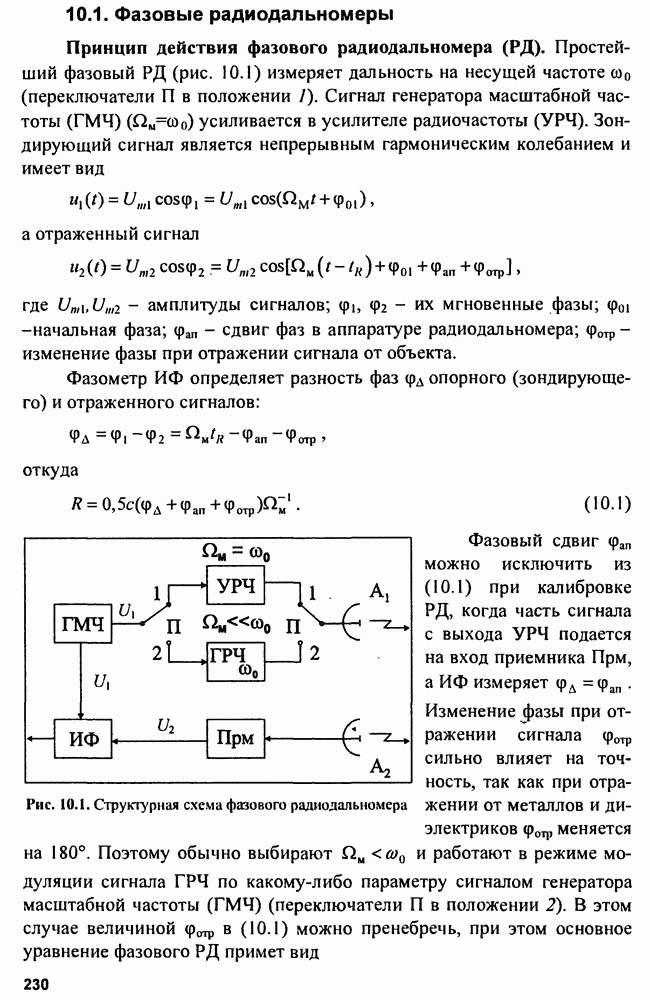
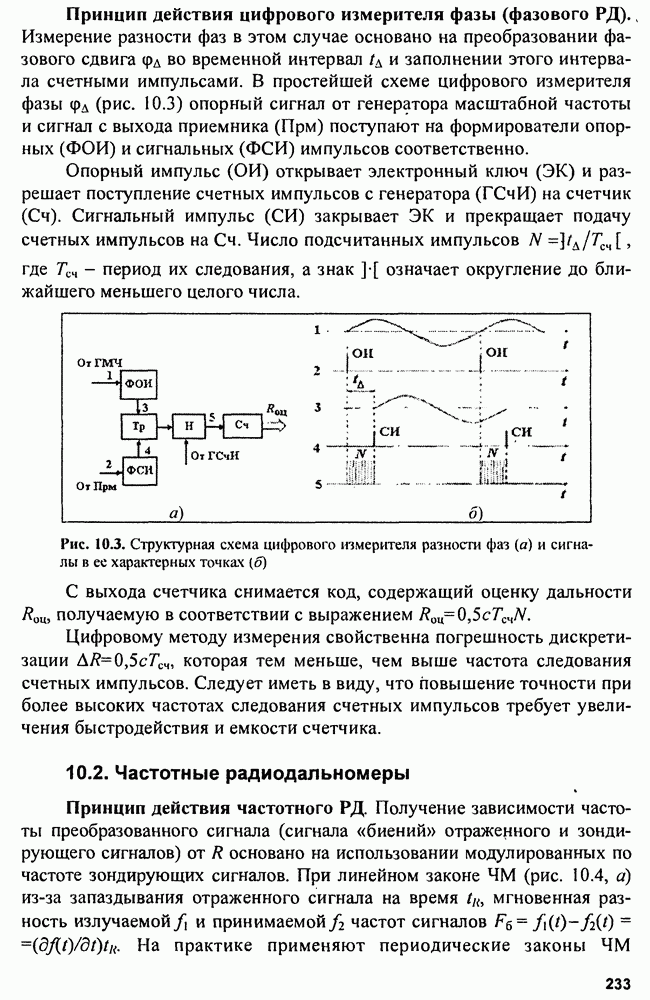
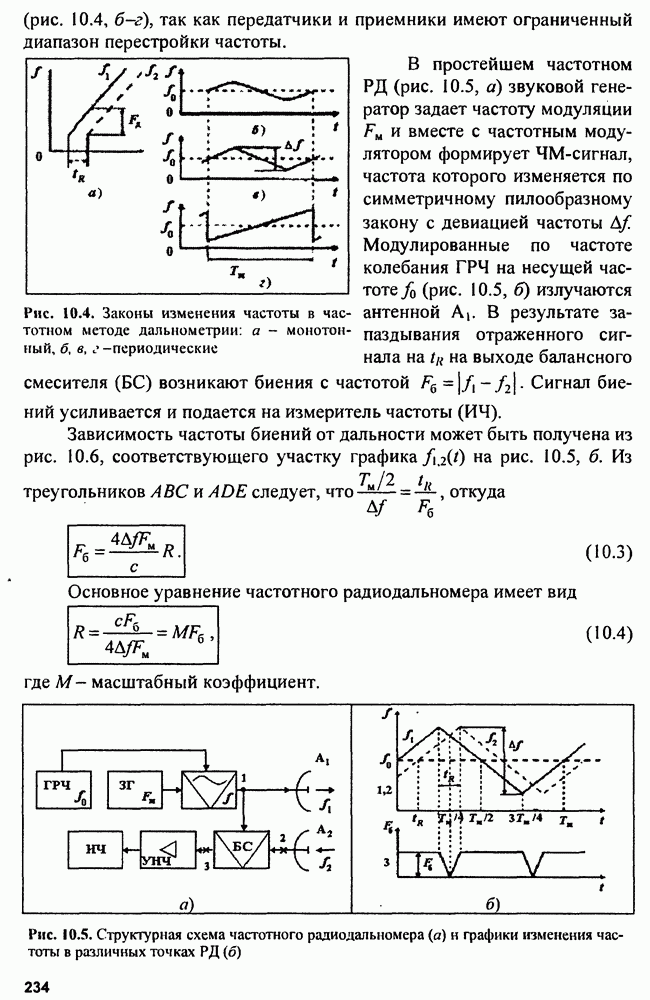
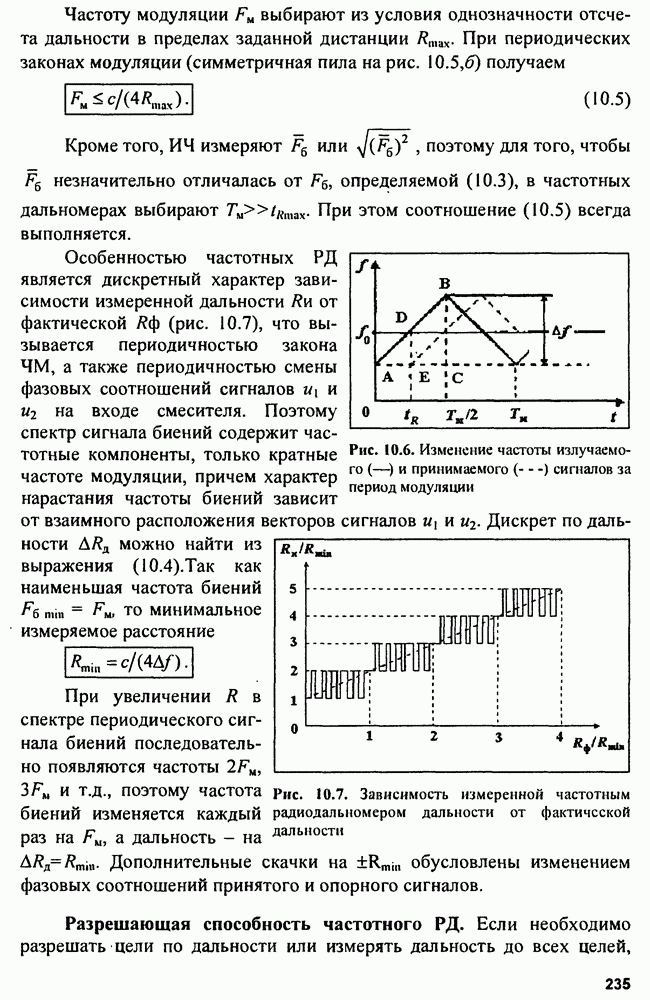
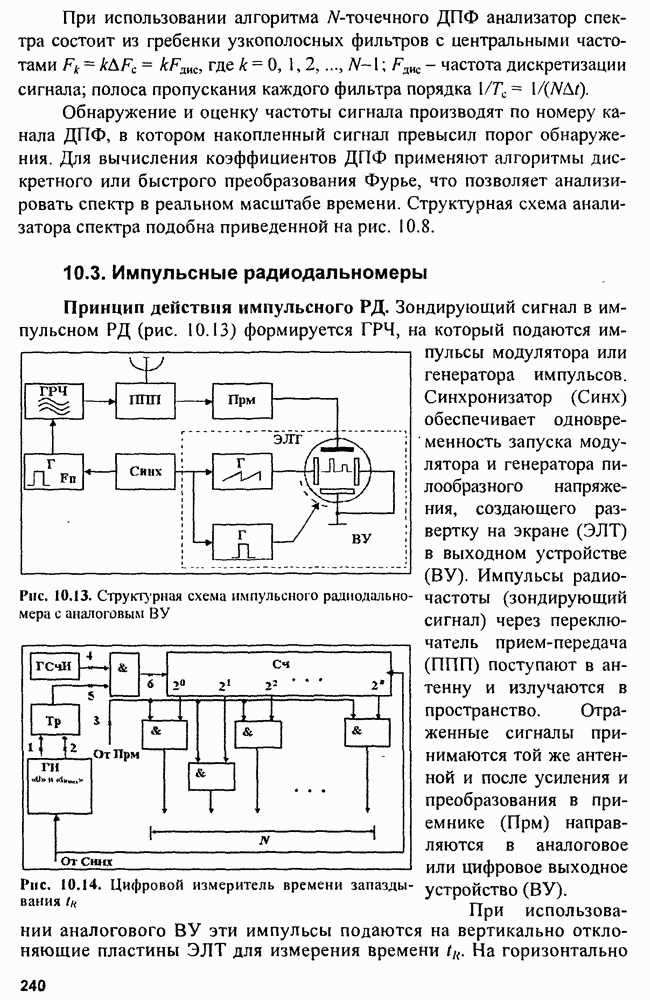
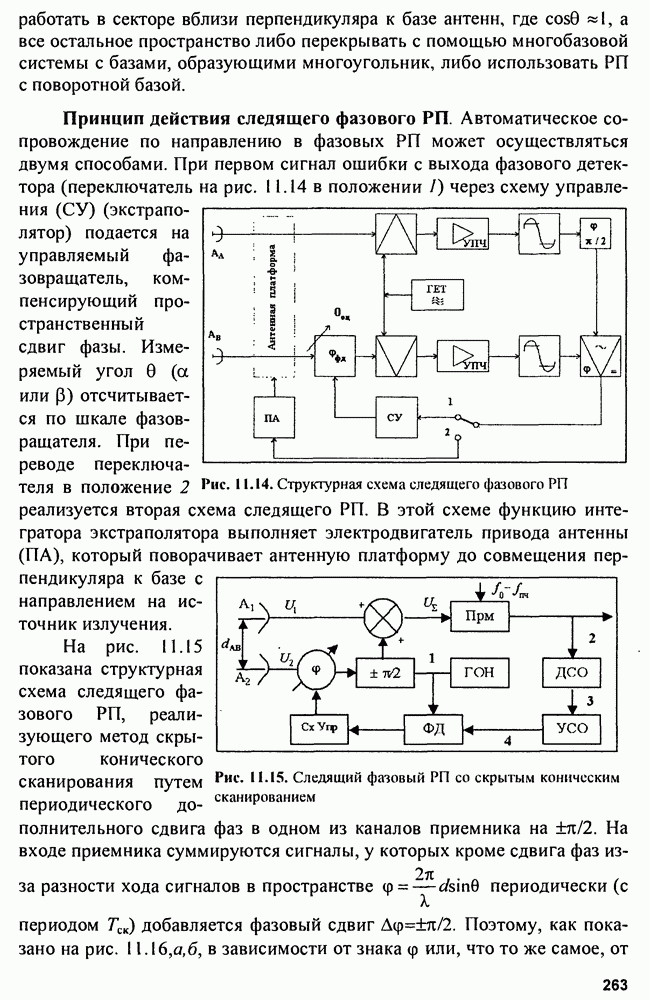
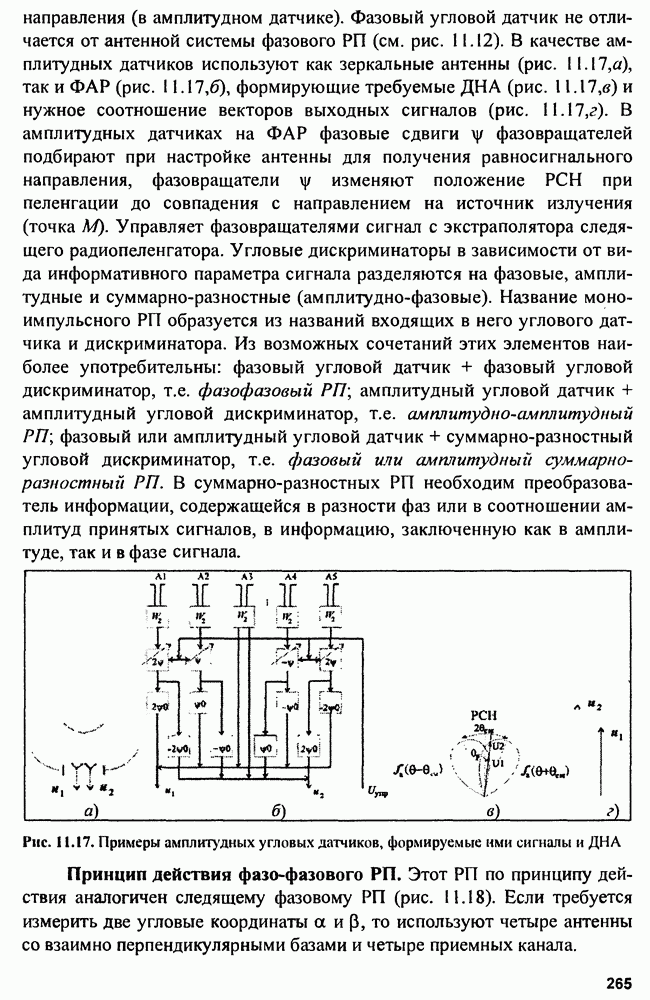
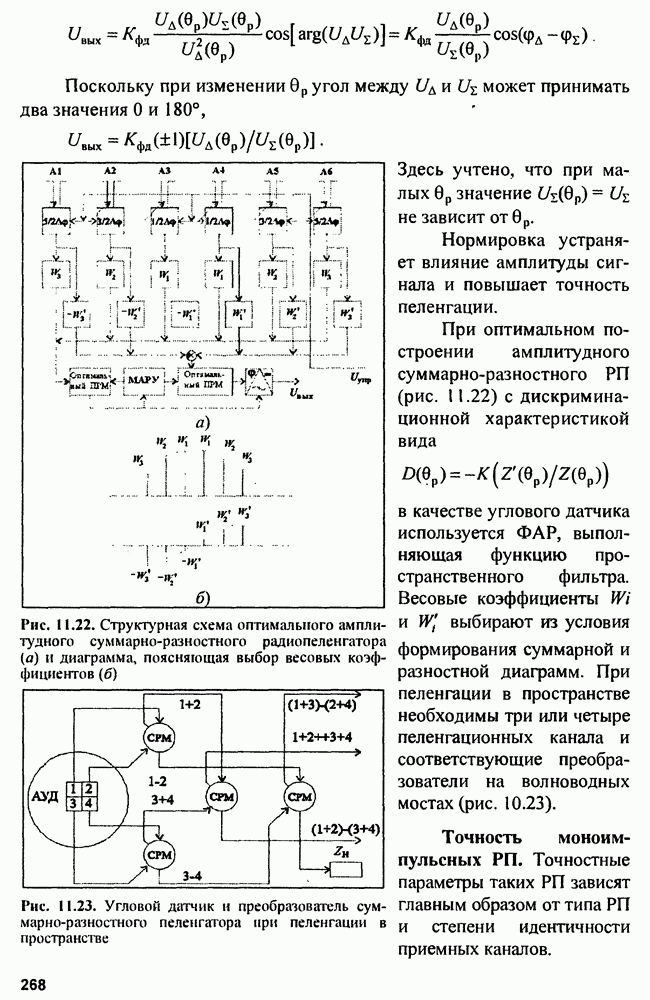
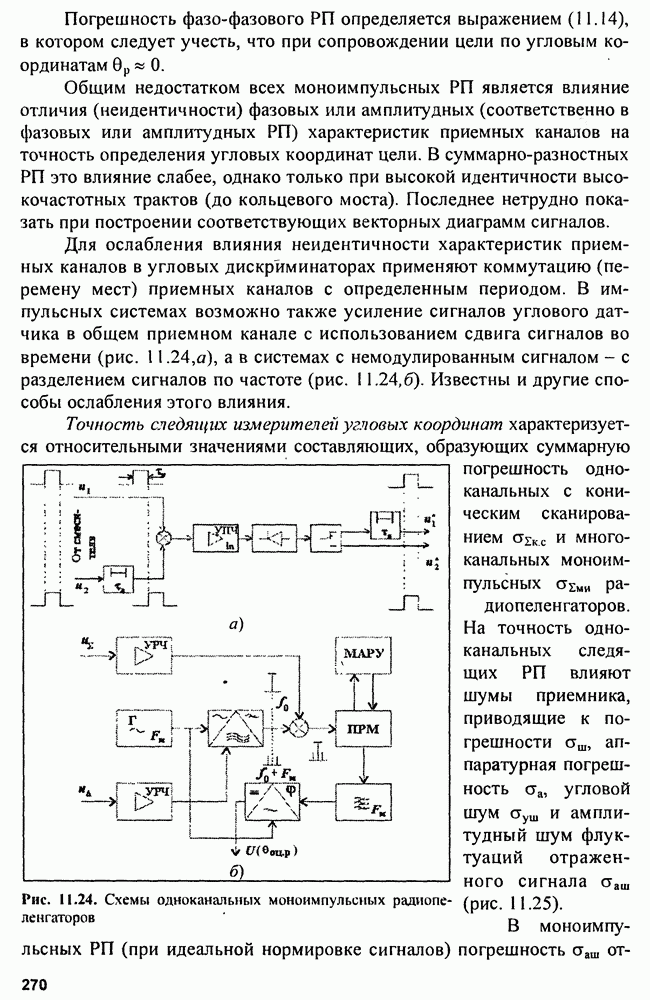
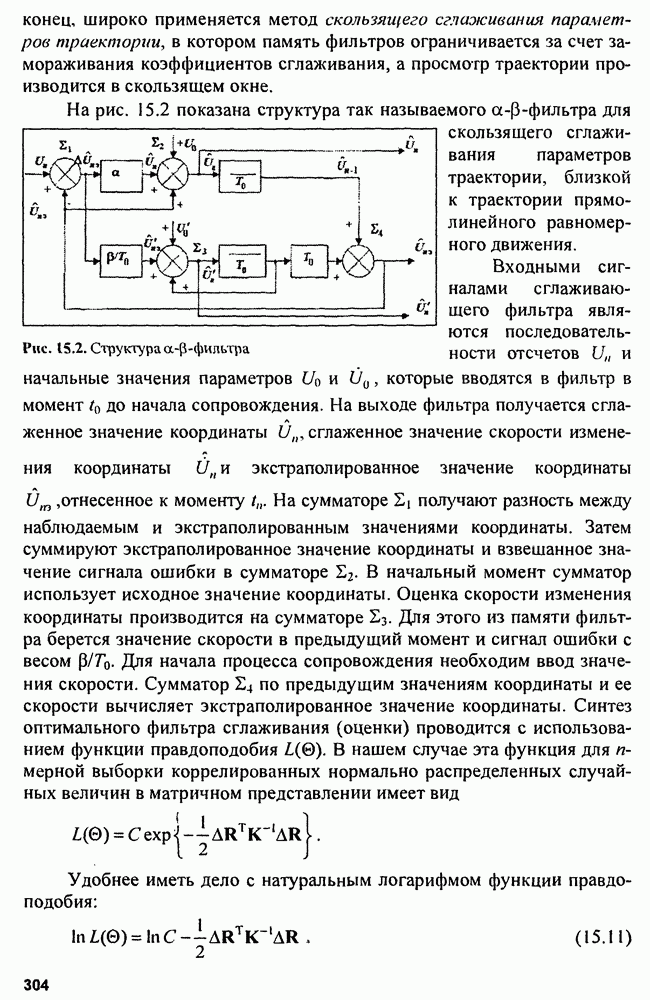
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
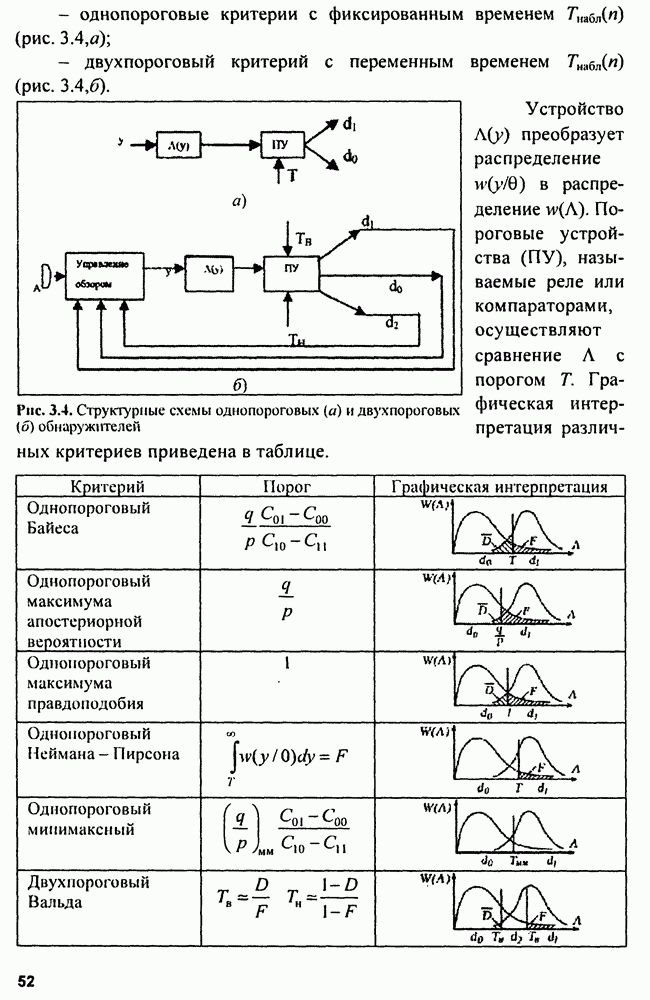
4.4. Сложные сигналы
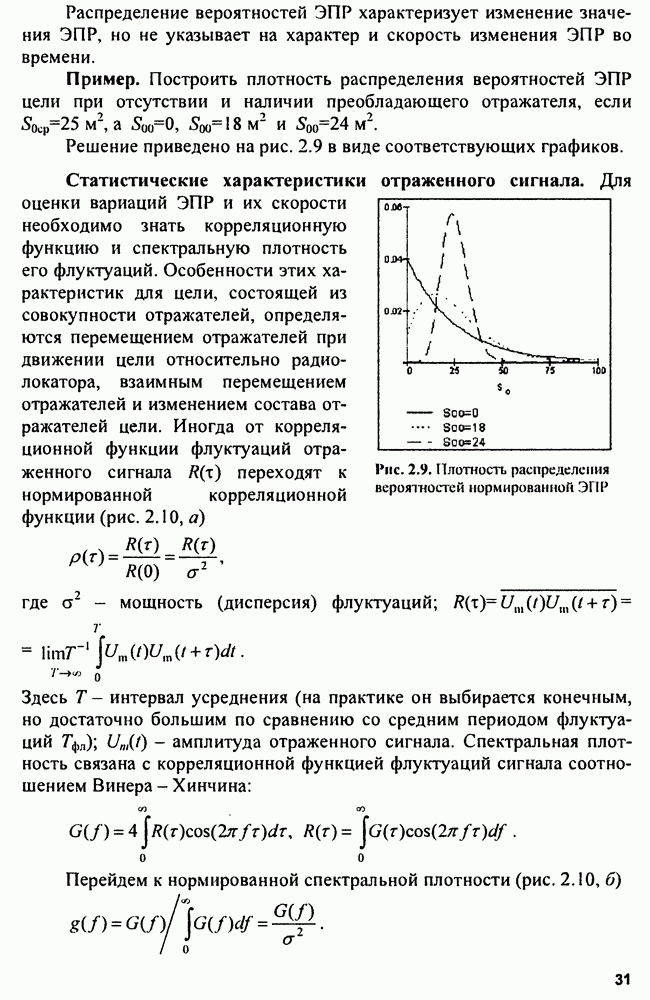
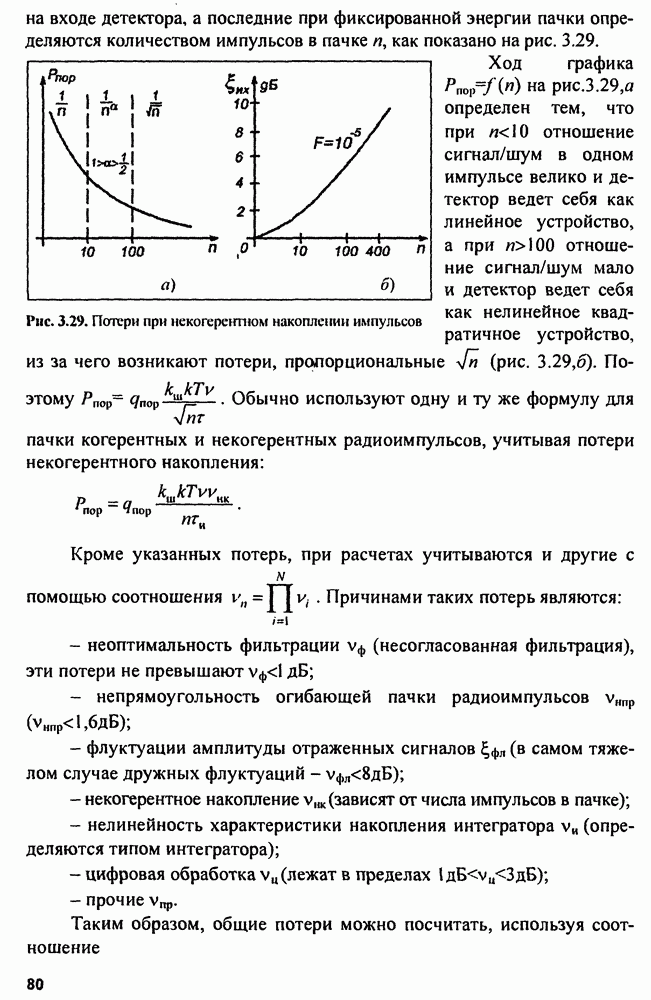
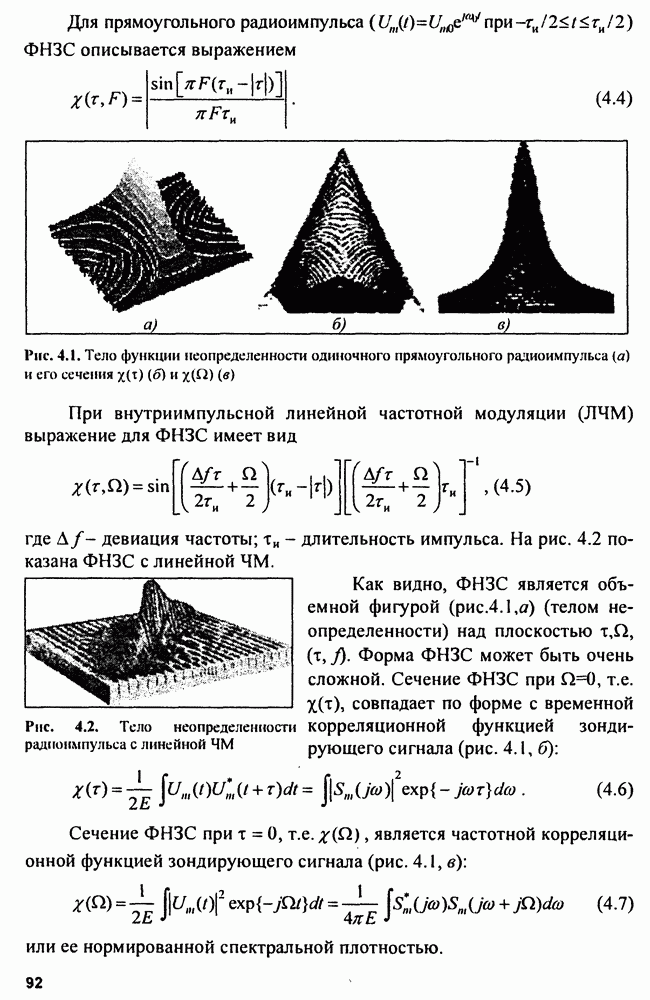
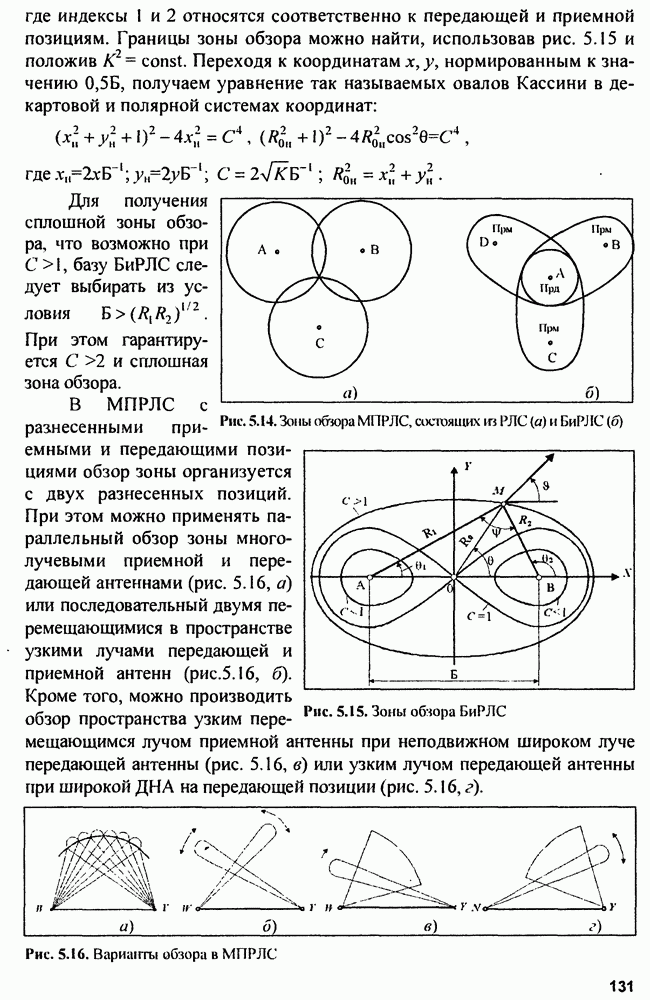
Сложные или энергоемкие сигналы позволяют разрешать противоречивые требования повышения дальности обнаружения и разрешающей способности. Дальность обнаружения повышается при использовании зондирующих сигналов с большой энергией  Увеличение
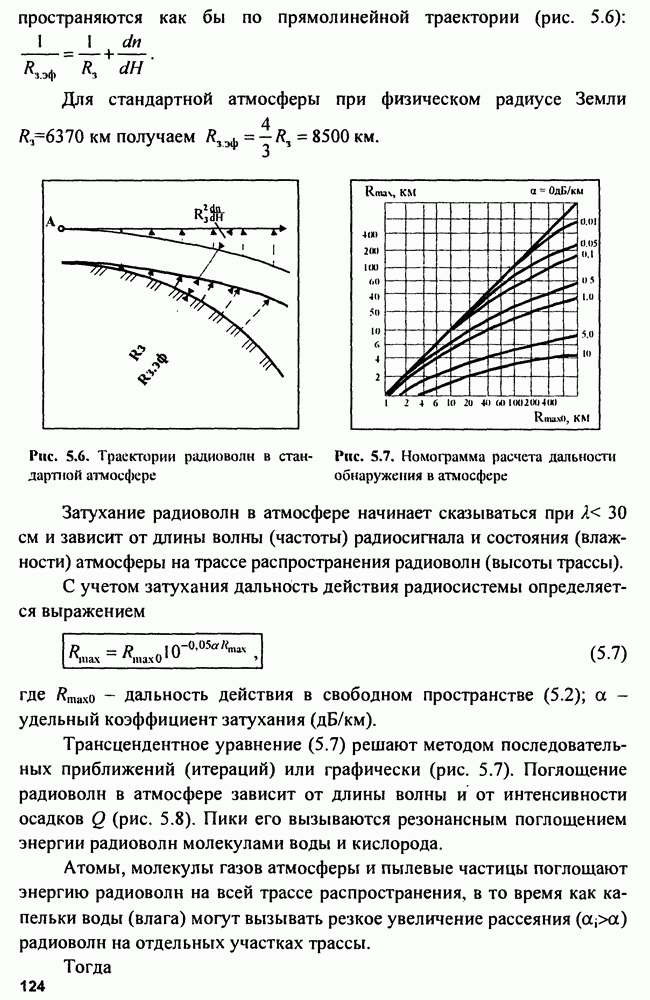
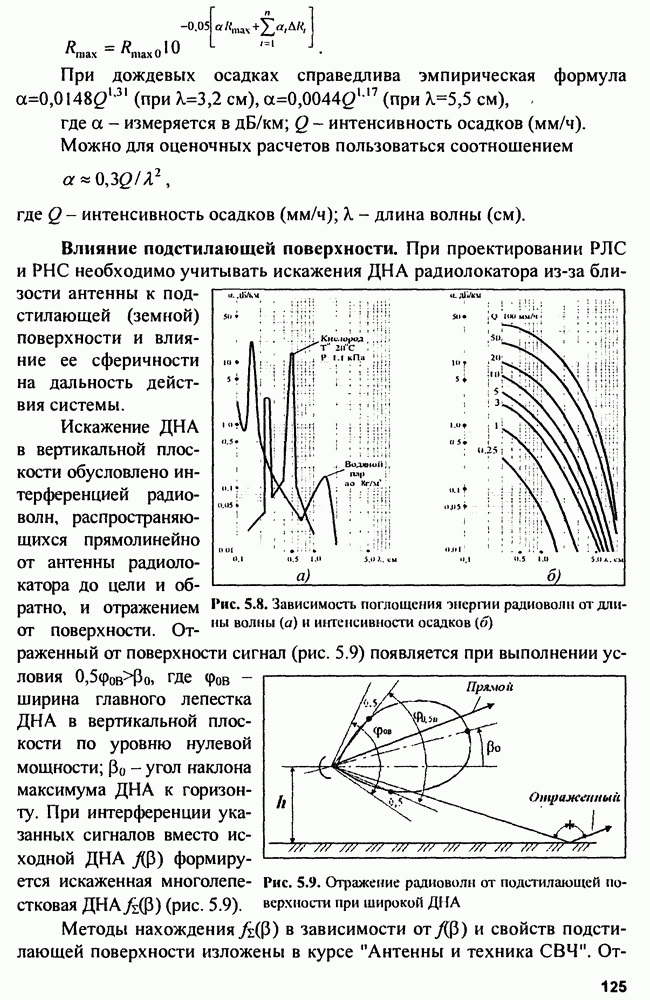
Увеличение  возможно за счет увеличения либо мощности, либо длительности сигнала. Пиковая мощность в РЛС ограничена сверху возможностями генератора радиочастоты и особенно электрической прочностью фидерных линий, соединяющих этот генератор с антенной. При использовании ФАР пиковая мощность ограничена максимальной мощностью модулей ФАР. Следовательно, проще повышать
возможно за счет увеличения либо мощности, либо длительности сигнала. Пиковая мощность в РЛС ограничена сверху возможностями генератора радиочастоты и особенно электрической прочностью фидерных линий, соединяющих этот генератор с антенной. При использовании ФАР пиковая мощность ограничена максимальной мощностью модулей ФАР. Следовательно, проще повышать  путем увеличения длительности сигнала. Однако сигналы большой длительности не обладают хорошим разрешением по дальности. Сложные сигналы с большой базой могут разрешить эти противоречия. В настоящее время широко используются два вида сложных сигналов: линейно-частотно-модулированные (ЛЧМ) и дискретно-кодированные (ДКС).
путем увеличения длительности сигнала. Однако сигналы большой длительности не обладают хорошим разрешением по дальности. Сложные сигналы с большой базой могут разрешить эти противоречия. В настоящее время широко используются два вида сложных сигналов: линейно-частотно-модулированные (ЛЧМ) и дискретно-кодированные (ДКС).
Линейно-частотно-модулированный сигнал. Если в пределах длительности импульса  модулировать несущую частоту по линейному закону с большой девиацией частоты, то база сигнала
модулировать несущую частоту по линейному закону с большой девиацией частоты, то база сигнала  будет большая и огибающая спектральной плотности входного сигнала
будет большая и огибающая спектральной плотности входного сигнала  будет приближаться к прямоугольной, т.е.
будет приближаться к прямоугольной, т.е.  Тогда на выходе оптимального фильтра формируется огибающая сигнала вида
Тогда на выходе оптимального фильтра формируется огибающая сигнала вида

где  спектральная плотность сигнала на выходе оптимального фильтра с коэффициентом передачи
спектральная плотность сигнала на выходе оптимального фильтра с коэффициентом передачи 

Преобразуя по Фурье  в пределах ширины спектра Аеос, находим выходной сигнал:
в пределах ширины спектра Аеос, находим выходной сигнал:

Сделав замену  получим
получим

Видно, что импульс на выходе оптимального фильтра имеет огибающую вида

где  задержка сигнала в фильтре.
задержка сигнала в фильтре.
Длительность выходного импульса  на уровне 0,637 равна
на уровне 0,637 равна  Таким образом, происходит укорочение или сжатие импульса в
Таким образом, происходит укорочение или сжатие импульса в  раз. Коэффициент сжатия
раз. Коэффициент сжатия  равен базе сигнала.
равен базе сигнала.
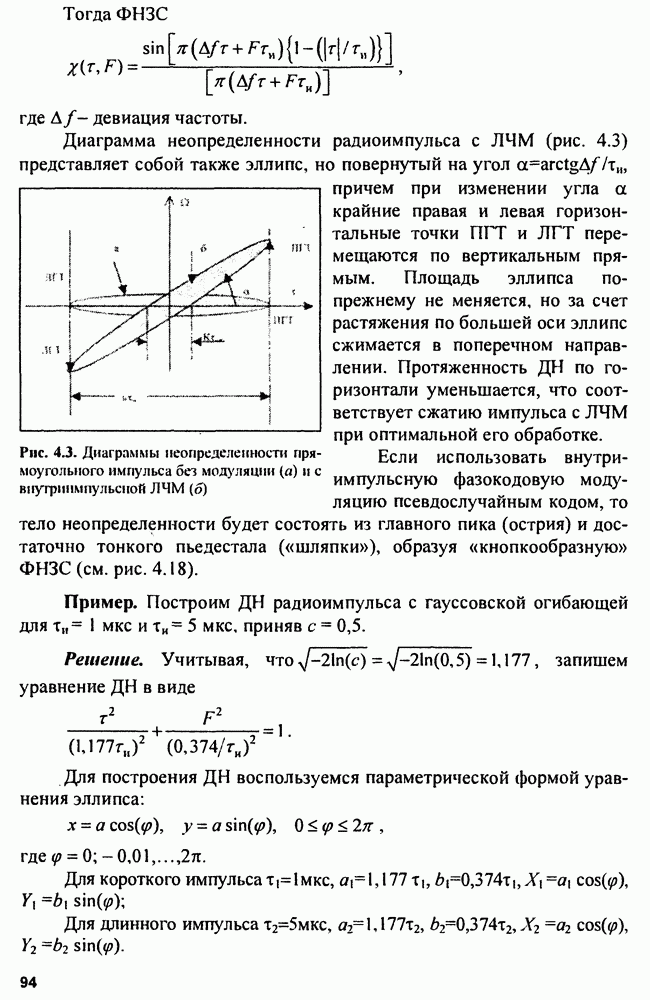
Пример. Построим временную диаграмму прямоугольного радиоимпульса с внутриимпульсной линейной частотной модуляцией. Параметры сигнала: амплитуда  среднее значение частоты
среднее значение частоты  длительность сигнала
длительность сигнала  ширина спектра
ширина спектра 

Рис. 4.10. Вид ЛЧМ-сигнала
Решение. Аналитическое выражение для сигнала (рис. 4.10) имеет вид

где  коэффициент сжатия (база сигнала).
коэффициент сжатия (база сигнала).

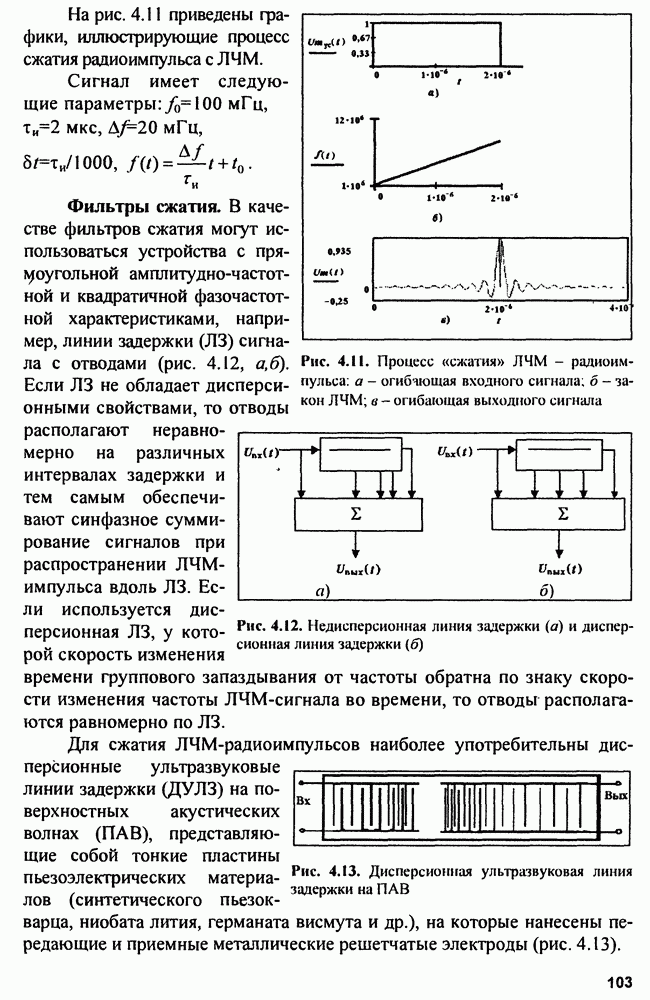
Рис. 4.11. Процесс «сжатия» ЛЧМ - радиоимпульса: а - огибчющая входного сигнала; б - закон ЛЧМ; в - огибающая выходного сигнала
На рис. 4.11 приведены графики, иллюстрирующие процесс сжатия радиоимпульса с ЛЧМ.
Сигнал имеет следующие параметры: 

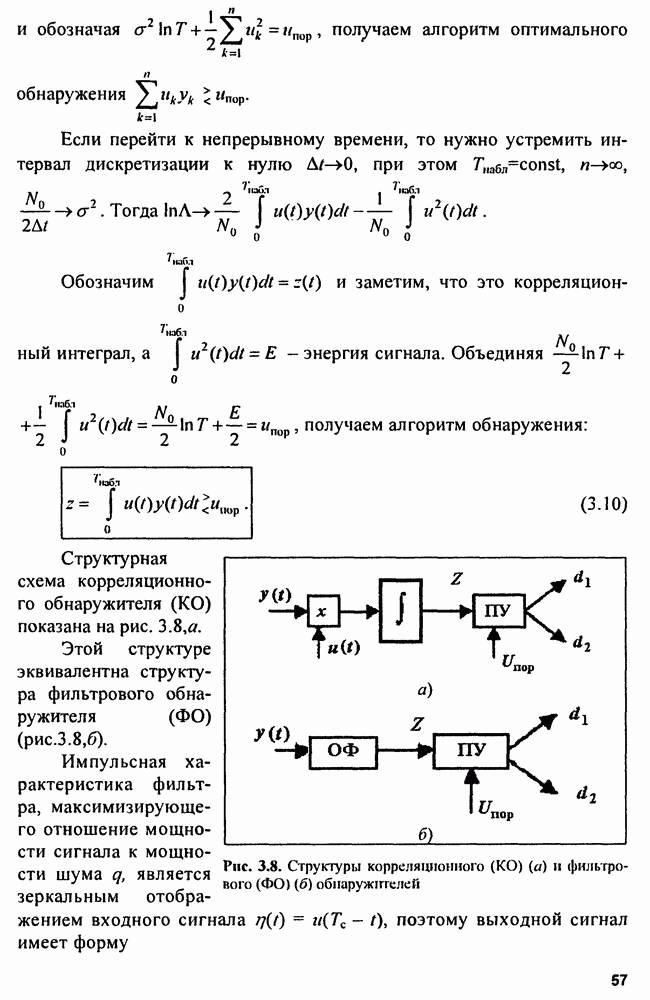
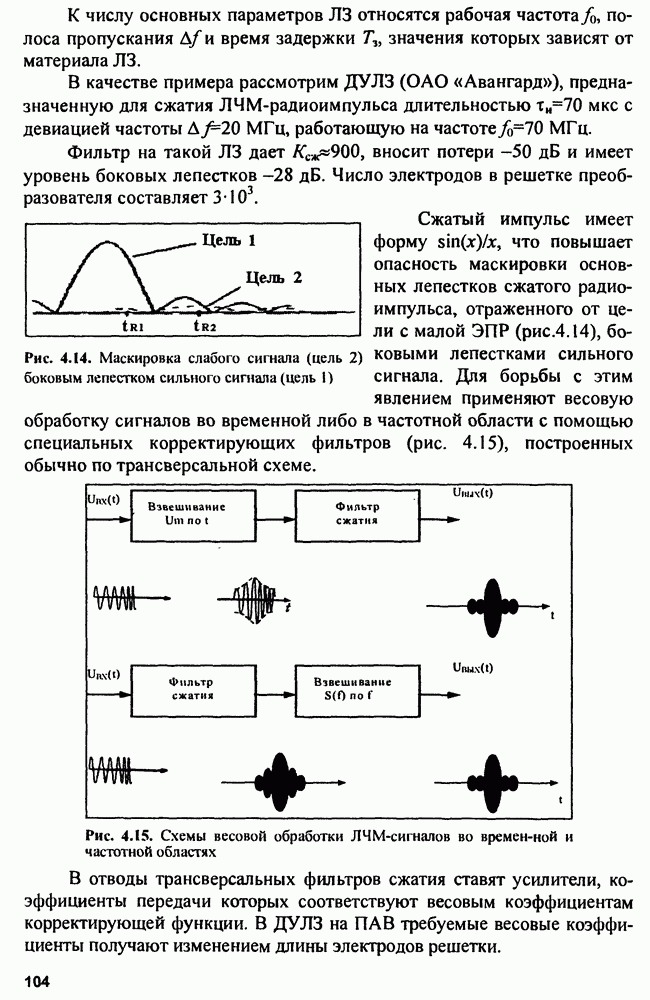
Фильтры сжатия. В качестве фильтров сжатия могут использоваться устройства с прямоугольной амплитудно-частотной и квадратичной фазочастотной характеристиками, например, линии задержки (ЛЗ) сигнала с отводами (рис. 4.12, а,б). Если ЛЗ не обладает дисперсионными свойствами, то отводы располагают неравномерно на различных интервалах задержки и тем самым обеспечивают синфазное суммирование сигналов при распространении ЛЧМ-импульса вдоль ЛЗ. Если используется дисперсионная ЛЗ, у которой скорость изменения времени группового запаздывания от частоты обратна по знаку скорости изменения частоты ЛЧМ-сигнала во времени, то отводы располагаются равномерно по ЛЗ.

Рис. 4.12. Недисперсионная линия задержки (а) и дисперсионная линия задержки (б)

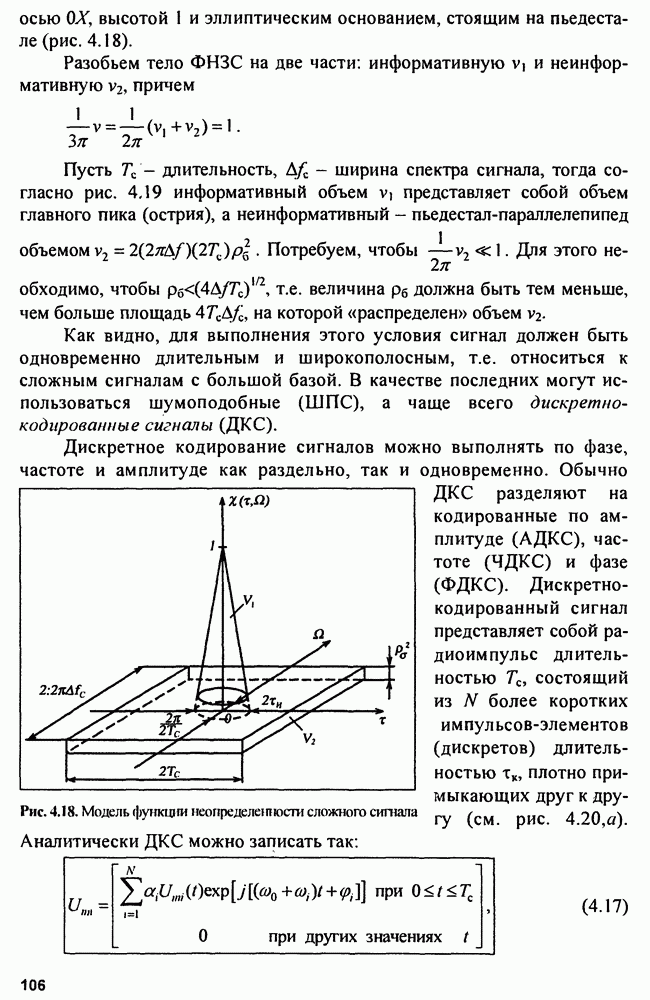
Рис. 4.13. Дисперсионная ультразвуковая линия задержки на ПАВ
Для сжатия ЛЧМ-радиоимпульсов наиболее употребительны дисперсионные ультразвуковые линии задержки (ДУЛЗ) на поверхностных акустических волнах (ПАВ), представляющие собой тонкие пластины пьезоэлектрических материалов (синтетического пьезокварца, ниобата лития, германата висмута и др.), на которые нанесены передающие и приемные металлические решетчатые электроды (рис. 4.13).
К числу основных параметров ЛЗ относятся рабочая частота  полоса пропускания
полоса пропускания  и время задержки
и время задержки  значения которых зависят от материала ЛЗ.
значения которых зависят от материала ЛЗ.
В качестве примера рассмотрим ДУЛЗ (ОАО «Авангард»), предназначенную для сжатия ЛЧМ-радиоимпульса длительностью  с девиацией частоты
с девиацией частоты  работающую на частоте
работающую на частоте 
Фильтр на такой ЛЗ дает  вносит потери
вносит потери  и имеет уровень боковых лепестков
и имеет уровень боковых лепестков  Число электродов в решетке преобразователя составляет
Число электродов в решетке преобразователя составляет  .
.
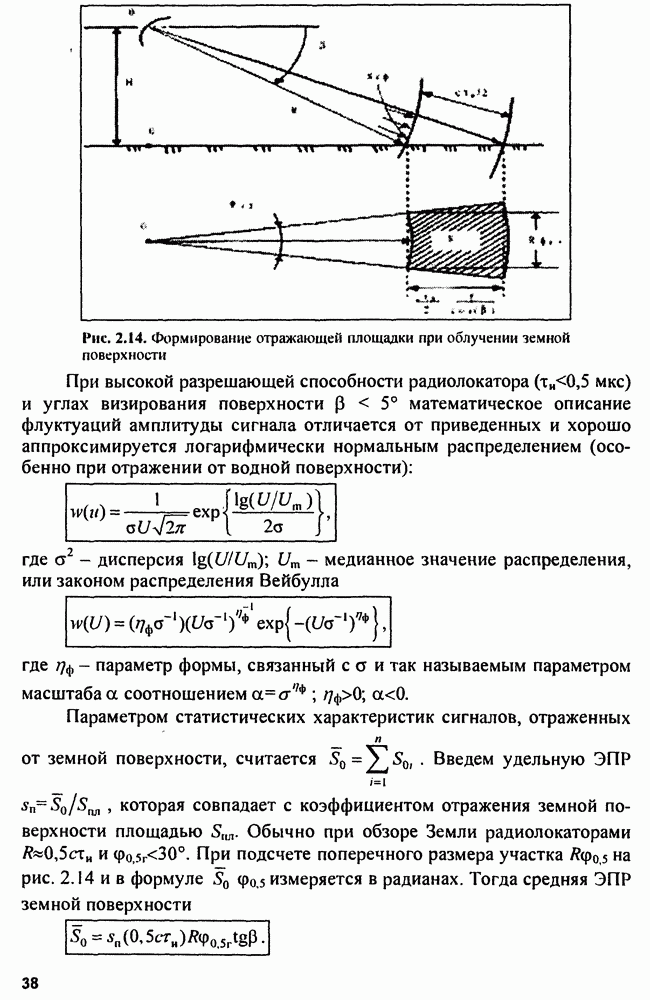
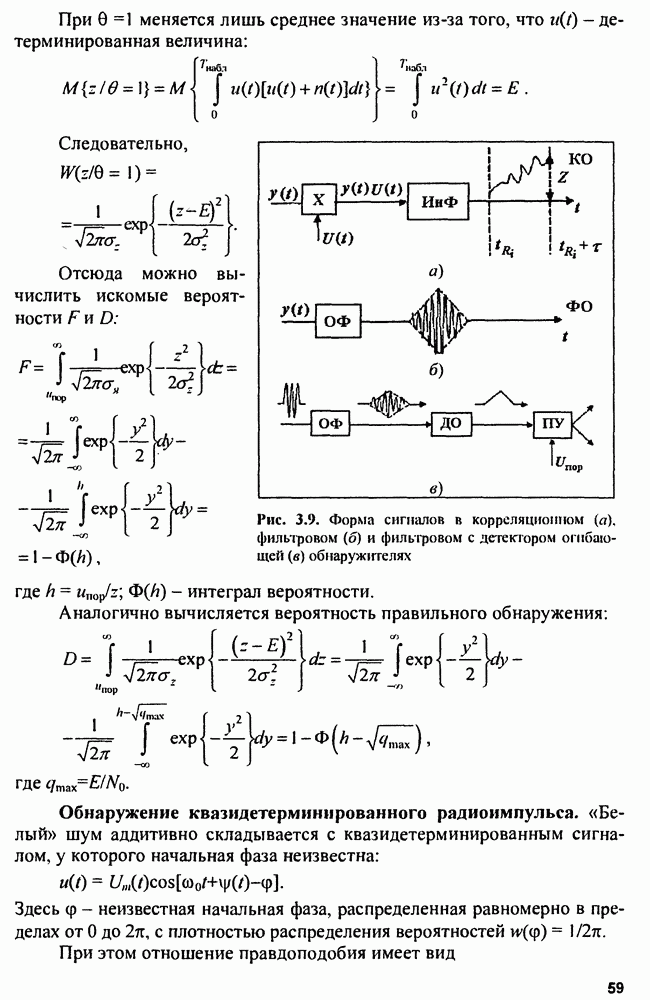
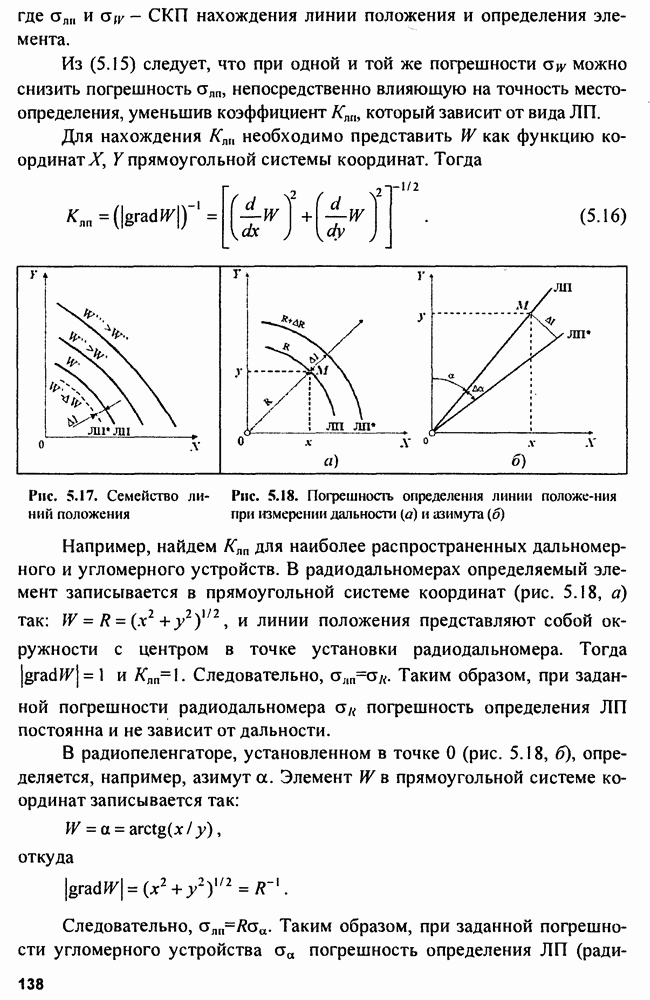
Сжатый импульс имеет форму  что повышает опасность маскировки основных лепестков сжатого радиоимпульса, отраженного от цели с малой ЭПР (рис. 4.14), боковыми лепестками сильного сигнала. Для борьбы с этим явлением применяют весовую обработку сигналов во временной либо в частотной области с помощью специальных корректирующих фильтров (рис. 4.15), построенных обычно по трансверсальной схеме.
что повышает опасность маскировки основных лепестков сжатого радиоимпульса, отраженного от цели с малой ЭПР (рис. 4.14), боковыми лепестками сильного сигнала. Для борьбы с этим явлением применяют весовую обработку сигналов во временной либо в частотной области с помощью специальных корректирующих фильтров (рис. 4.15), построенных обычно по трансверсальной схеме.

Рис. 4.14. Маскировка слабого сигнала (цель 2) боковым лепестком сильного сигнала (цель 

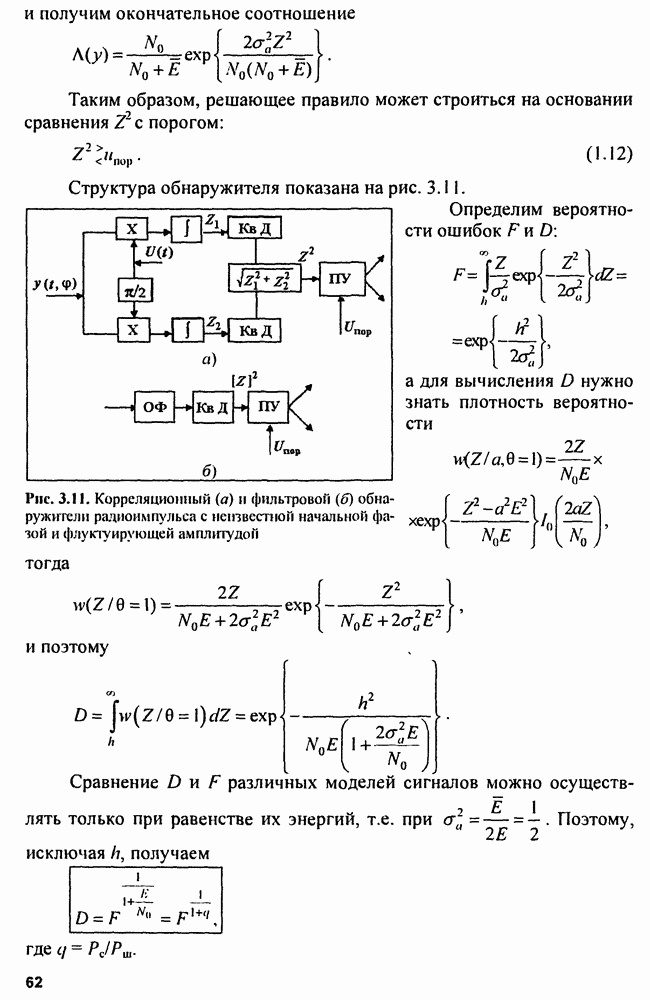
Рис. 4.15. Схемы весовой обработки ЛЧМ-сигналов во временной и частотной областях
В отводы трансверсальных фильтров сжатия ставят усилители, коэффициенты передачи которых соответствуют весовым коэффициентам корректирующей функции. В ДУЛЗ на ПАВ требуемые весовые коэффициенты получают изменением длины электродов решетки.
Весовую обработку можно реализовать, использовав следующие весовые функции корректирующего фильтра:
1) весовая функция Дольфа - Чебышева (рис. 4.16);
2) весовая функция Тейлора;
3) весовая функция общего вида:

Частным случаем весовой функции Тейлора является весовая функция Хэмминга:

Структурная схема фильтра с  показана на рис. 4.17 Фильтр подавления реализуется в виде двух последовательно включенных линий задержки на
показана на рис. 4.17 Фильтр подавления реализуется в виде двух последовательно включенных линий задержки на  трех весовых усилителей и сумматора. При такой обработке уровень боковых лепестков уменьшается до
трех весовых усилителей и сумматора. При такой обработке уровень боковых лепестков уменьшается до  Однако при этом основной лепесток расширяется примерно в 1,47 раза, а отношение сигнал/шум по мощности уменьшается в 1,34 раза по сравнению с отношением сигнап/шум на входе фильтра Хэмминга.
Однако при этом основной лепесток расширяется примерно в 1,47 раза, а отношение сигнал/шум по мощности уменьшается в 1,34 раза по сравнению с отношением сигнап/шум на входе фильтра Хэмминга.
Уровень боковых лепестков уменьшается обратно пропорционально времени при всех видах весовой обработки, кроме весовой функции Дольфа - Чебышева, где он неизменен. При этом несколько расширяется основной лепесток и возрастают энергетические потери по сравнению с оптимальной обработкой (без корректирующего фильтра). Кроме корректирующих фильтров, для борьбы с боковыми лепестками используют изменение формы (предыскажение) зондирующих сигналов и внутриимпульсную нелинейную частотную модуляцию.

Рис. 4.16. Частотная характеристика корректирующего фильтра Дольфа-Чебышева

Рис. 4.17. Структурная схема фильтра Хэмминга
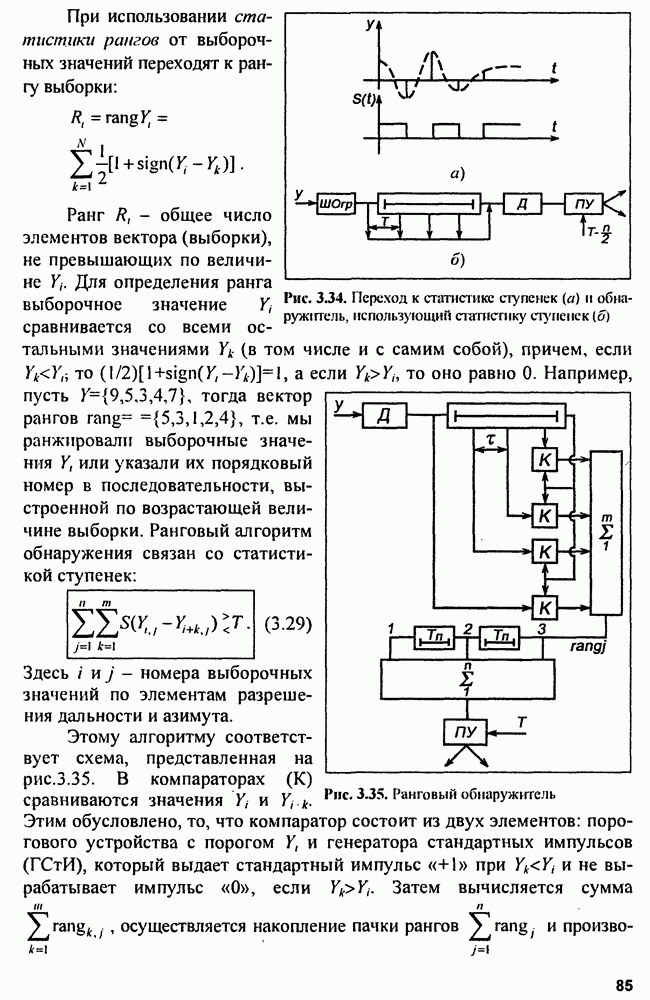
Дискретно кодированные сигналы (ДКС) Представим модель тела неопределенности, удовлетворяющую требованиям к энергоемкому зондирующему сигналу с высокой разрешающей способностью одновременно по времени  и по частоте
и по частоте  (дальности
(дальности  и скорости
и скорости  в виде пьедестала толщиной
в виде пьедестала толщиной  и острого конуса с осью, совпадающей с
и острого конуса с осью, совпадающей с
осью  высотой 1 и эллиптическим основанием, стоящим на пьедестале (рис. 4.18).
высотой 1 и эллиптическим основанием, стоящим на пьедестале (рис. 4.18).
Разобьем тело ФНЗС на две части: информативную  и неинформативную
и неинформативную  причем
причем

Пусть  длительность,
длительность,  ширина спектра сигнала, тогда согласно рис. 4,19 информативный объем
ширина спектра сигнала, тогда согласно рис. 4,19 информативный объем  представляет собой объем главного пика (острия), а неинформативный - пьедестал-параллелепипед объемом
представляет собой объем главного пика (острия), а неинформативный - пьедестал-параллелепипед объемом  Потребуем, чтобы
Потребуем, чтобы  Для этого необходимо, чтобы
Для этого необходимо, чтобы  т.е. величина
т.е. величина  должна быть тем меньше, чем больше площадь
должна быть тем меньше, чем больше площадь  на которой «распределен» объем
на которой «распределен» объем 
Как видно, для выполнения этого условия сигнал должен быть одновременно длительным и широкополосным, т.е. относиться к сложным сигналам с большой базой. В качестве последних могут использоваться шумоподобные (ШПС), а чаще всего дискретно-кодированные сигналы (ДКС).

Рис. 4.18. Модель функции неопределешюсти сложного сигнала
Дискретное кодирование сигналов можно выполнять по фазе, частоте и амплитуде как раздельно, так и одновременно. Обычно ДКС разделяют на кодированные по амплитуде (АДКС), частоте (ЧДКС) и фазе (ФДКС). Дискретно-кодированный сигнал представляет собой радиоимпульс длительностью  состоящий из
состоящий из  более коротких импульсов-элементов (дискретов) длительностью тк, плотно примыкающих друг к другу (см. рис. 4.20, а). Аналитически ДКС можно записать так:
более коротких импульсов-элементов (дискретов) длительностью тк, плотно примыкающих друг к другу (см. рис. 4.20, а). Аналитически ДКС можно записать так:

где  параметры кодовой модуляции последовательности дискретов
параметры кодовой модуляции последовательности дискретов  которая может содержать коды
которая может содержать коды  номер дискрета кодовой последовательности
номер дискрета кодовой последовательности  число дискретов в сигнале;
число дискретов в сигнале;  импульс стандартной амплитуды длительностью тк (длительность элемента кода):
импульс стандартной амплитуды длительностью тк (длительность элемента кода):

При этом длительность сигнала составляет  Поскольку
Поскольку  -энергетический параметр, для сохранения энергии сигнала неизменной при расчетах необходимо нормировать (4.17) с помощью дополнительного делителя
-энергетический параметр, для сохранения энергии сигнала неизменной при расчетах необходимо нормировать (4.17) с помощью дополнительного делителя  Из общего выражения (4.17) следуют формулы, описывающие ДКС с различными видами кодирования. При
Из общего выражения (4.17) следуют формулы, описывающие ДКС с различными видами кодирования. При  имеем амплитудно-кодированный сигнал (АДКС):
имеем амплитудно-кодированный сигнал (АДКС):

О при других значениях 
При  получаем частотно-кодированный сигнал (ЧДКС). Обозначим
получаем частотно-кодированный сигнал (ЧДКС). Обозначим  тогда
тогда

О при других значениях 
Чаще других используются ФДКС или, так называемые фазо-кодо-модулированные (ФКМ) и фазо-манипулированные (ФМ) сигналы. В этом случае  и
и

Число значений  , которые принимают начальные фазы элементов кода, называется основанием кодовой последовательности. При
, которые принимают начальные фазы элементов кода, называется основанием кодовой последовательности. При  имеем бинарную последовательность.
имеем бинарную последовательность.
Бинарная ФКМ-последовательность получается, когда начальная фаза  элемента принимает одно из двух значений
элемента принимает одно из двух значений  или
или  . Тогда код можно задавать в виде последовательности значений фазы
. Тогда код можно задавать в виде последовательности значений фазы 
либо в виде последовательности оператора  либо в виде последовательности символов кода
либо в виде последовательности символов кода 
Иногда в иллюстративном материале вместо символов  используют соответствующие им символы
используют соответствующие им символы 
Таким образом, формирование бинарной кодовой последовательности сводится к заданию дискретных значений 

Логика символов  определяется по правилу:
определяется по правилу:

На рис. 4.19 показан вид бинарного фазоманипулированного (ФМ) сигнала-радиоимпульса (а) и соответствующей кодовой последовательности  В качестве бинарных кодовых последовательностей фазома-нипулированных сигналов чаще других используют бинарные коды Баркера и
В качестве бинарных кодовых последовательностей фазома-нипулированных сигналов чаще других используют бинарные коды Баркера и  -последовательности. Коды Баркера обеспечивают уровень боковых лепестков
-последовательности. Коды Баркера обеспечивают уровень боковых лепестков  равный
равный  т.е.
т.е.

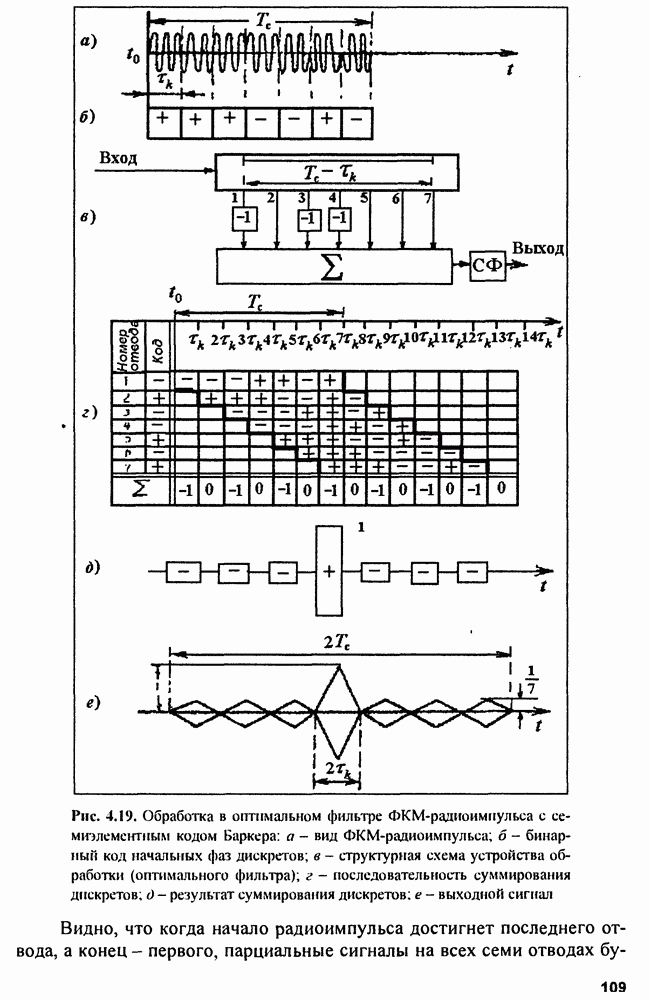
Процесс оптимальной обработки и «сжатия» во времени импульса с внутриимпульсной ФКМ с использованием семизначного кода Баркера показан на рис. 4.19.
Сжатие ФКМ импульса осуществляется с помощью линии задержки (ЛЗ) с отводами и сумматора, сигналы к которому от ЛЗ подаются через отводы либо непосредственно, либо с поворотом фазы на  , т.е. инверсно, для обеспечения последовательности суммирования дискретов, показанной на рис. 4.19,г. Причем процесс суммирования иллюстрирован с использованием кодовой последовательности
, т.е. инверсно, для обеспечения последовательности суммирования дискретов, показанной на рис. 4.19,г. Причем процесс суммирования иллюстрирован с использованием кодовой последовательности  поэтому начальной фазе
поэтому начальной фазе  соответствует
соответствует  а фазе
а фазе  соответствует
соответствует  Закон смены знаков от первого отвода к последнему (от начала ЛЗ к концу) обратен коду С, начальных фаз радиоимпульса (Код на рис. 4.19,г). Этот код является зеркальным отображением модулирующего кода и представляет собой импульсную характеристику оптимального фильтра. Изменение фазы парциальных сигналов на каждом из отводов ЛЗ при прохождении по ней радиосигнала показан на рис. 4.19,г.
Закон смены знаков от первого отвода к последнему (от начала ЛЗ к концу) обратен коду С, начальных фаз радиоимпульса (Код на рис. 4.19,г). Этот код является зеркальным отображением модулирующего кода и представляет собой импульсную характеристику оптимального фильтра. Изменение фазы парциальных сигналов на каждом из отводов ЛЗ при прохождении по ней радиосигнала показан на рис. 4.19,г.
Рис. 4.19. (см. скан) Обработка в оптимальном фильтре ФКМ-радиоимпульса с се-миэлементным кодом Баркера: а - вид ФКМ-радиоимпульса; б - бинарный код начальных фаз дискретов; в - структурная схема устройства обработки (оптимального фильтра); г - последовательность суммирования дискретов; д - результат суммирования дискретов; е - выходной сигнал
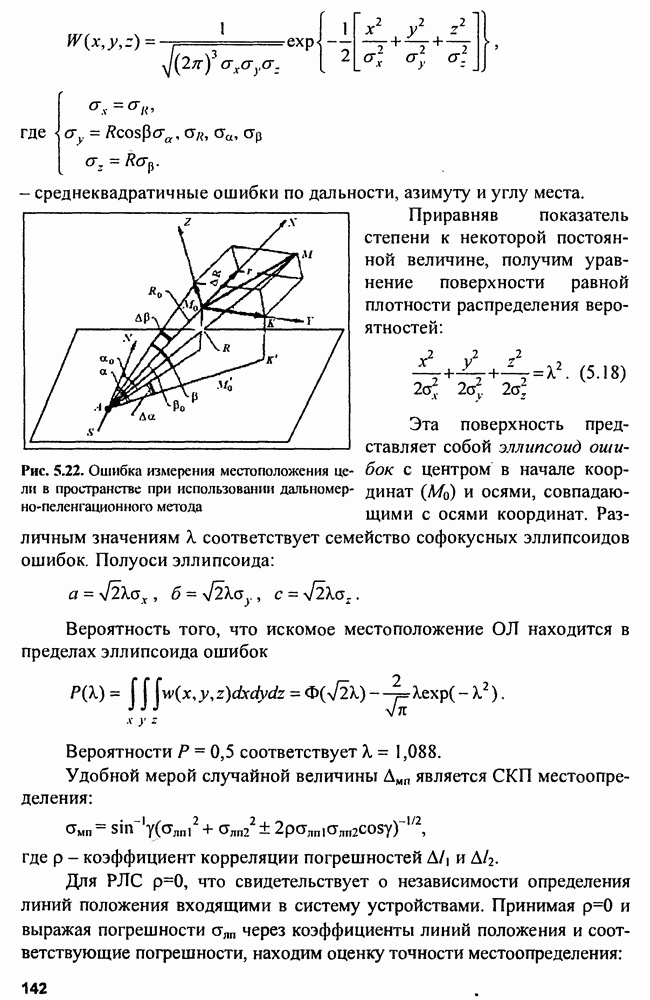
Видно, что когда начало радиоимпульса достигнет последнего отвода, а конец - первого, парциальные сигналы на всех семи отводах
будут иметь одинаковый знак (фазу) и синфазно суммироваться. На выходе получится максимально возможный сигнал - главный пик длительностью  Справа и слева от этого пика располагается по три боковых лепестка с амплитудой
Справа и слева от этого пика располагается по три боковых лепестка с амплитудой  Фильтр согласован с ФКМ-импульсом длительностью
Фильтр согласован с ФКМ-импульсом длительностью  и служит для увеличения
и служит для увеличения  на выходе оптимального фильтра. Однако коды Баркера известны только для
на выходе оптимального фильтра. Однако коды Баркера известны только для 
При тринадцатизначном коде Баркера импульс может быть сжат максимум в 13 раз, а минимальный уровень боковых лепестков ДКФ составит 1/13 от амплитуды главного пика выходного сигнала оптимального фильтра. На рис. 4.20 показана ФНЗС сигнала с фазокодовой манипуляцией кодом Баркера при 

Рис. 4.20. Вид ФНЗС с модуляцией фазы кодом Баркера [11]
Для увеличения коэффициента сжатия  следовательно, для улучшения разрешения целей по дальности и скорости, а также для снижения уровня боковых лепестков применяют линейные рекуррентные кодовые последовательности, практически не имеющие ограничения по длительности кода.
следовательно, для улучшения разрешения целей по дальности и скорости, а также для снижения уровня боковых лепестков применяют линейные рекуррентные кодовые последовательности, практически не имеющие ограничения по длительности кода.
В качестве рекуррентных кодовых последовательностей часто используют  -последо-вательности или коды максимальной длины, которые образуются с помощью рекуррентных соотношений, что позволяет формировать их на регистрах сдвига, охваченных обратными связями. Подразделяют
-последо-вательности или коды максимальной длины, которые образуются с помощью рекуррентных соотношений, что позволяет формировать их на регистрах сдвига, охваченных обратными связями. Подразделяют  -последовательности на периодические, когда период повторения кода
-последовательности на периодические, когда период повторения кода  равен его длительности
равен его длительности  и непериодические (усеченные), когда
и непериодические (усеченные), когда  больше
больше  Наиболее часто
Наиболее часто  -последовательность задают в виде последовательности символов
-последовательность задают в виде последовательности символов 
Для основания 2 значение текущего символа  кодовой последовательности зависит от
кодовой последовательности зависит от  предыдущих символов и рассчитывается по формуле
предыдущих символов и рассчитывается по формуле

где  могут быть равны
могут быть равны  или 1.
или 1.
Величина  называется памятью кодовой последовательности и определяет количество ячеек в регистре сдвига, формирующем код. При
называется памятью кодовой последовательности и определяет количество ячеек в регистре сдвига, формирующем код. При
формировании кодовой последовательности задают произвольный начальный блок или начальную комбинацию символов кода, состоящую из  символов. Вся последовательность получается по рекуррентному соотношению (4.21).
символов. Вся последовательность получается по рекуррентному соотношению (4.21).
Перечислим некоторые основные свойства  -последовательностей:
-последовательностей:
1)  -последовательности содержат
-последовательности содержат  элементов и имеют длительность
элементов и имеют длительность  ;
;
2) сумма двух  -последовательностей по модулю 2 в символах
-последовательностей по модулю 2 в символах  дает снова
дает снова  -последовательность;
-последовательность;
3) уровень боковых лепестков ДКФ для периодической последовательности с периодом  равен
равен  а для одиночной (усеченной) непериодической последовательности длительностью
а для одиночной (усеченной) непериодической последовательности длительностью  он равен
он равен 
4) число различных максимальных линейных рекуррентных последовательностей при одинаковом  определяется алгоритмом
определяется алгоритмом  где
где  функция Эйлера.
функция Эйлера.
Для формирования кодирующей (модулирующей)  -последовательности обычно используют регистры сдвига, охваченные по определенным правилам обратными связями с отводов регистров. Правила осуществления обратных связей в регистрах, формирующих код на основе рекуррентных линейных последовательностей максимальной длины, можно определить, используя так называемые характеристические полиномы кодовых последовательностей:
-последовательности обычно используют регистры сдвига, охваченные по определенным правилам обратными связями с отводов регистров. Правила осуществления обратных связей в регистрах, формирующих код на основе рекуррентных линейных последовательностей максимальной длины, можно определить, используя так называемые характеристические полиномы кодовых последовательностей:

где учтено, что коэффициент  всегда равен 1.
всегда равен 1.
Из теории линейных рекуррентных последовательностей известно, что для формирования  -последовательности размера
-последовательности размера  необходимо использовать неразложимые примитивные полиномы степени
необходимо использовать неразложимые примитивные полиномы степени  с коэффициентами
с коэффициентами  равными
равными  или 1. Неприводимый полином не может быть разложен на множители. Примитивный полином является делителем двучлена
или 1. Неприводимый полином не может быть разложен на множители. Примитивный полином является делителем двучлена  при условии, что
при условии, что 
Рекуррентный алгоритм (4.21) определения символов  кодовой последовательности получают из характеристического полинома (4.22) при замене х на
кодовой последовательности получают из характеристического полинома (4.22) при замене х на 

Полином формирования кода на регистре сдвига условно можно представить в виде многочлена, схожего с характеристическим полиномом, в котором х заменяют на символ задержки во времени тк. Здесь имеется в виду, что  - элемент кода и в то же время элемент (ячейка) задержки регистра сдвига:
- элемент кода и в то же время элемент (ячейка) задержки регистра сдвига:

Этому полиному соответствует каноническая схема устройства формирования кода, показанная на рис. 4.21, в которой коэффициенты а, определяют наличие обратных связей регистра, а «степень» символа тк показывает номер ячейки (триггера) регистра.

Рис. 4.21. Каноническая схема формирования кода  -последовательности
-последовательности
Устройство состоит из регистра сдвига, представленного на рисунке в виде цепочки  элементов задержки тк (ячеек или триггеров),
элементов задержки тк (ячеек или триггеров),  отводов с элементов задержки, ключей (усилителей с коэффициентами усиления
отводов с элементов задержки, ключей (усилителей с коэффициентами усиления  или 1 в отводах и устройств сложения по модулю 2. Количество суммирующихся по модулю 2 слагаемых зависит от вида формирующего полинома, а точнее от того, какие коэффициенты от, равны 0.
или 1 в отводах и устройств сложения по модулю 2. Количество суммирующихся по модулю 2 слагаемых зависит от вида формирующего полинома, а точнее от того, какие коэффициенты от, равны 0.
Правила синтеза схемы формирования  -последовательности на регистре сдвига сводятся к следующему:
-последовательности на регистре сдвига сводятся к следующему:
1) число ячеек регистра  где
где  определяется требуемым уровнем боковых лепестков ДКФ;
определяется требуемым уровнем боковых лепестков ДКФ;
2) количество обратных связей определяется не равными  коэффициентами
коэффициентами 
3) суммирование слагаемых полинома производится по модулю 2;
4) последовательность смены кодовых символов определяется начальным блоком кода, т.е. начальной установкой символов бинарного кода в ячейки регистра.
Рассмотрим частный случай. Пусть  Полином
Полином  для регистра из трех элементов тк, поскольку
для регистра из трех элементов тк, поскольку  представляется следующим образом:
представляется следующим образом:

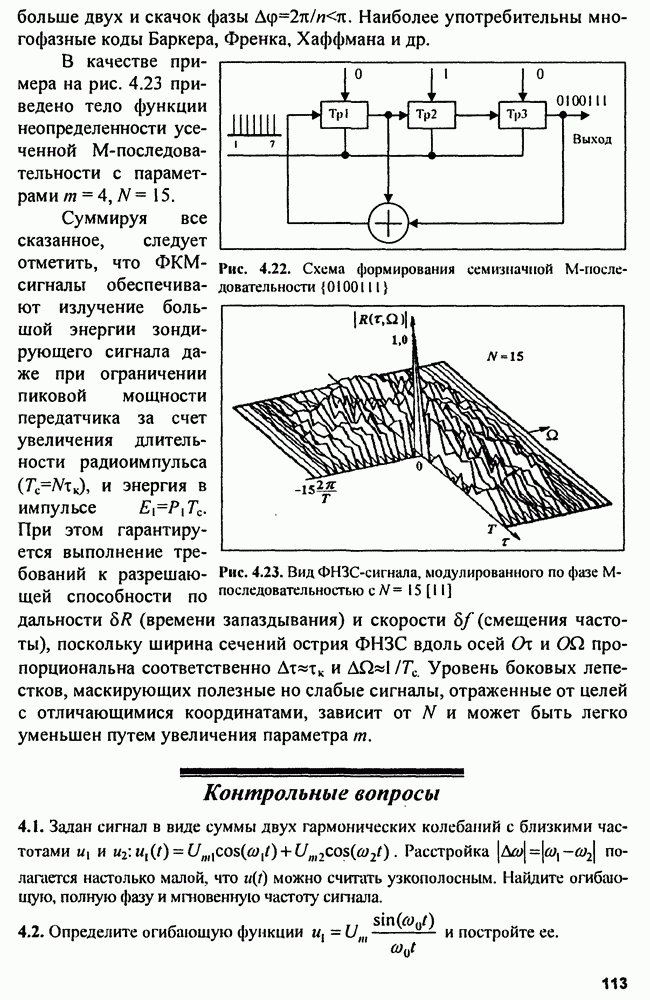
Пусть а, имеют следующие значения:  тогда схема формирования кода
тогда схема формирования кода  конкретизируется в структуру, показанную на рис. 4.22, в которой в качестве элементов задержки тк используются триггеры
конкретизируется в структуру, показанную на рис. 4.22, в которой в качестве элементов задержки тк используются триггеры  Число разрядов регистра при бинарном коде
Число разрядов регистра при бинарном коде  Пусть начальная установка триггеров в рассматриваемом примере следующая:
Пусть начальная установка триггеров в рассматриваемом примере следующая:  находятся в состоянии «0», а
находятся в состоянии «0», а  в состоянии «1». Тактовые импульсы продвигают комбинацию
в состоянии «1». Тактовые импульсы продвигают комбинацию  по регистру. Начальный блок последовательности получился
по регистру. Начальный блок последовательности получился  Кроме бинарных кодовых последовательностей известны так называемые многофазные коды, в которых основание будет
Кроме бинарных кодовых последовательностей известны так называемые многофазные коды, в которых основание будет  тогда число фаз тоже
тогда число фаз тоже
больше двух и скачок фазы  Наиболее употребительны многофазные коды Баркера, Френка, Хаффмана и др.
Наиболее употребительны многофазные коды Баркера, Френка, Хаффмана и др.
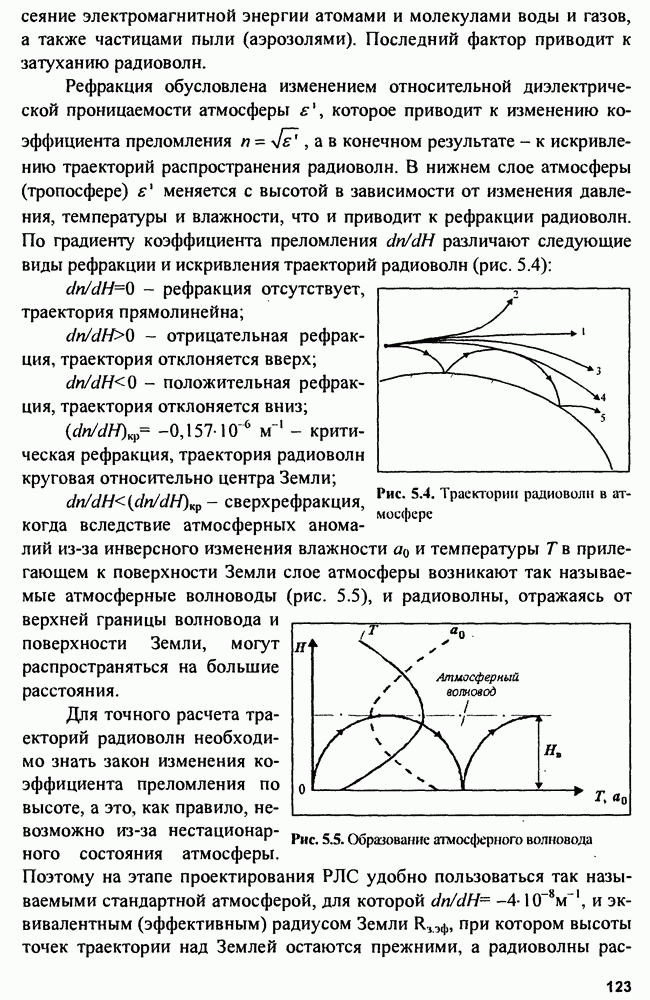
В качестве примера на рис. 4.23 приведено тело функции неопределенности усеченной  -последовательности с параметрами
-последовательности с параметрами 
Суммируя все сказанное, следует отметить, что ФКМ-сигналы обеспечивают излучение большой энергии зондирующего сигнала даже при ограничении пиковой мощности передатчика за счет увеличения длительности радиоимпульса  и энергия в импульсе
и энергия в импульсе  При этом гарантируется выполнение требований к разрешающей способности по дальности
При этом гарантируется выполнение требований к разрешающей способности по дальности  (времени запаздывания) и скорости
(времени запаздывания) и скорости  (смещения частоты), поскольку ширина сечений острия ФНЗС вдоль осей
(смещения частоты), поскольку ширина сечений острия ФНЗС вдоль осей  и
и  пропорциональна соответственно
пропорциональна соответственно  Уровень боковых лепестков, маскирующих полезные но слабые сигналы, отраженные от целей с отличающимися координатами, зависит от
Уровень боковых лепестков, маскирующих полезные но слабые сигналы, отраженные от целей с отличающимися координатами, зависит от  и может быть легко уменьшен путем увеличения параметра
и может быть легко уменьшен путем увеличения параметра 

Рис. 4.22. Схема формирования семизначной М-последовательности 

Рис. 4.23. Вид ФНЗС-сигнала, модулированного по фазе М-последовательностью с 
Контрольные вопросы
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
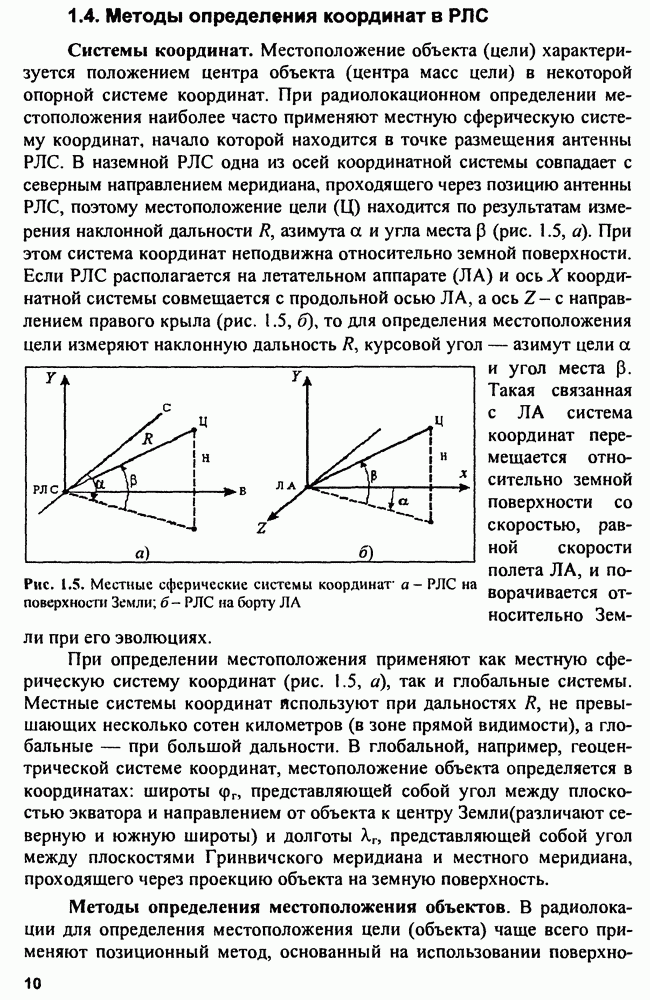
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
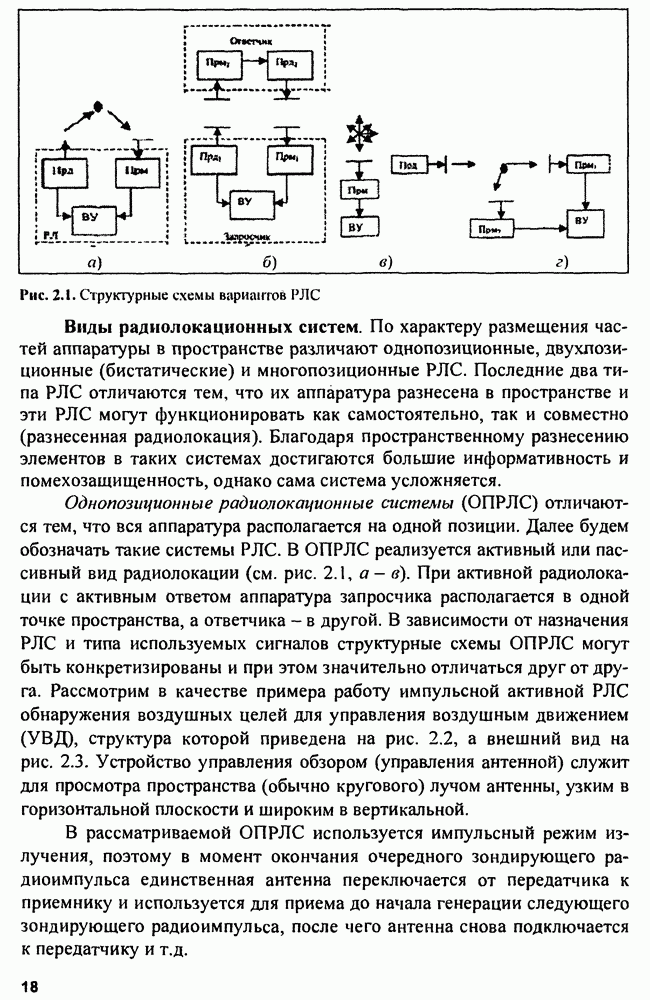
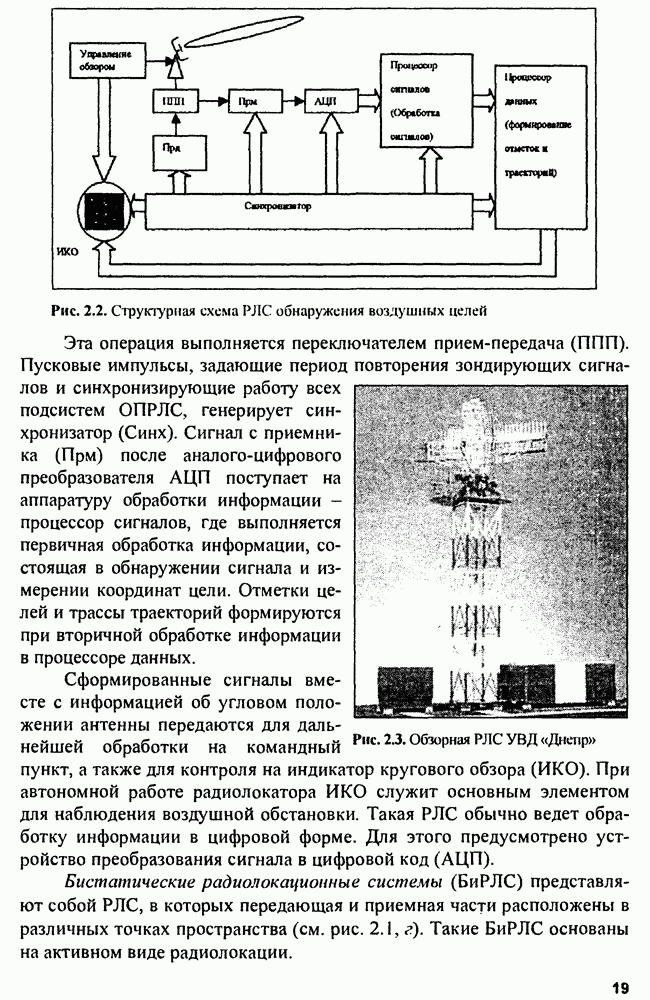
- Глава 2. Радиолокационные системы
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
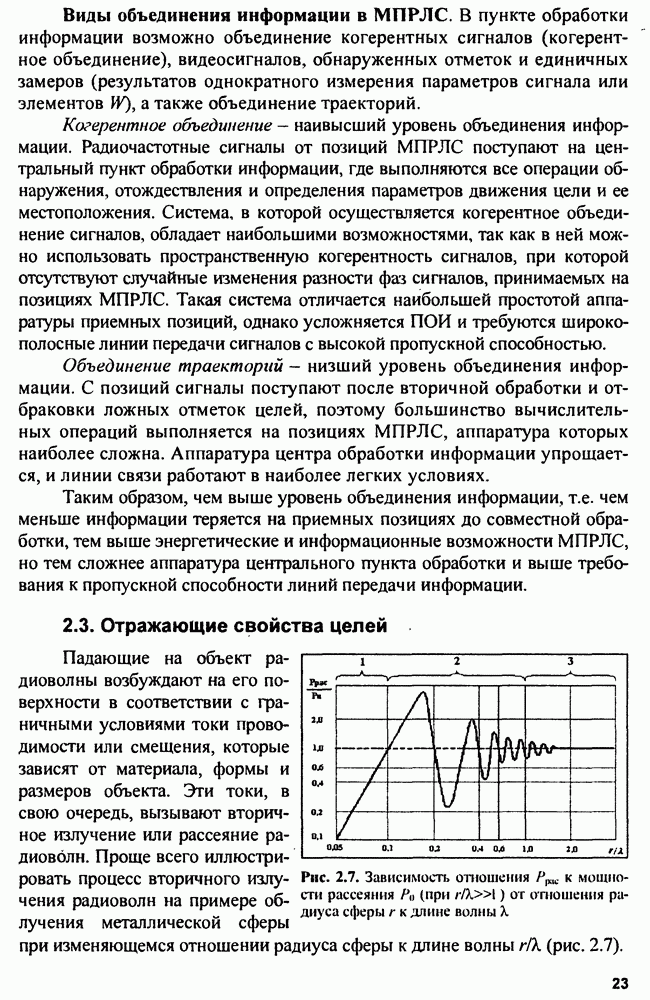
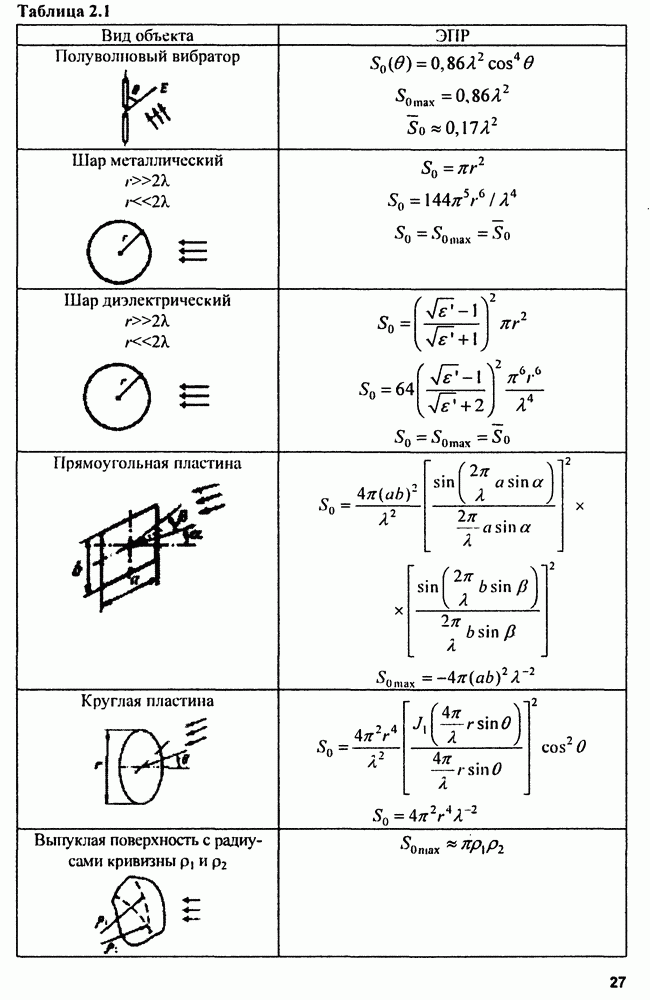
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
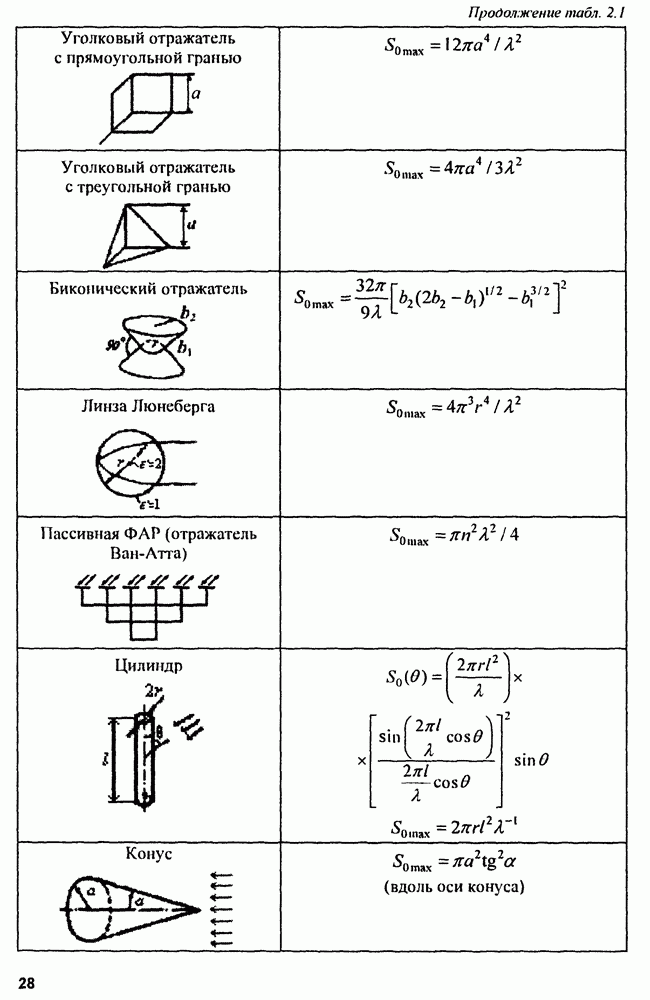
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
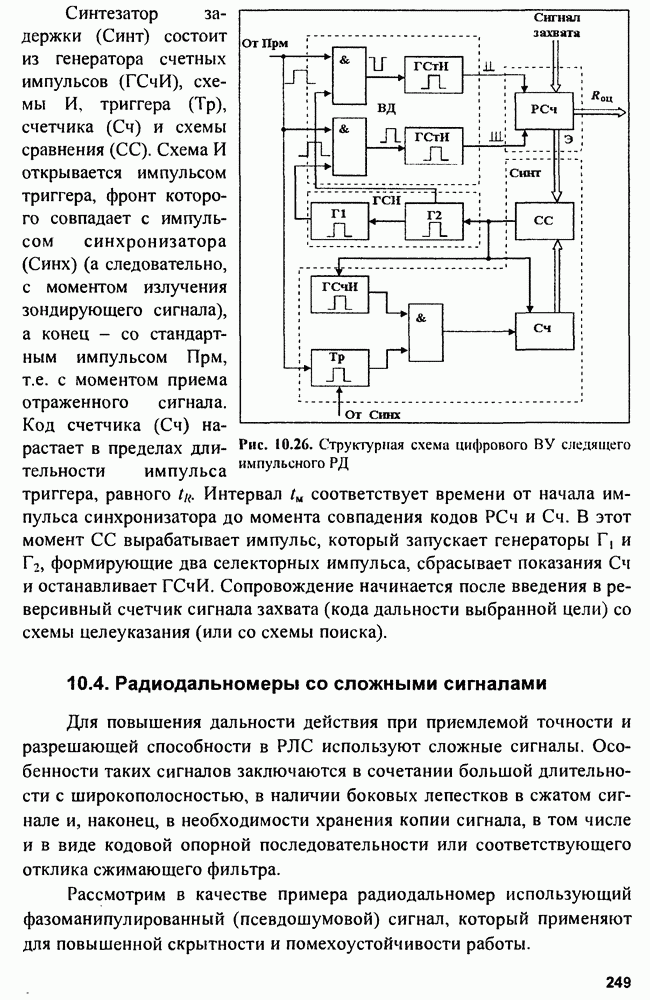
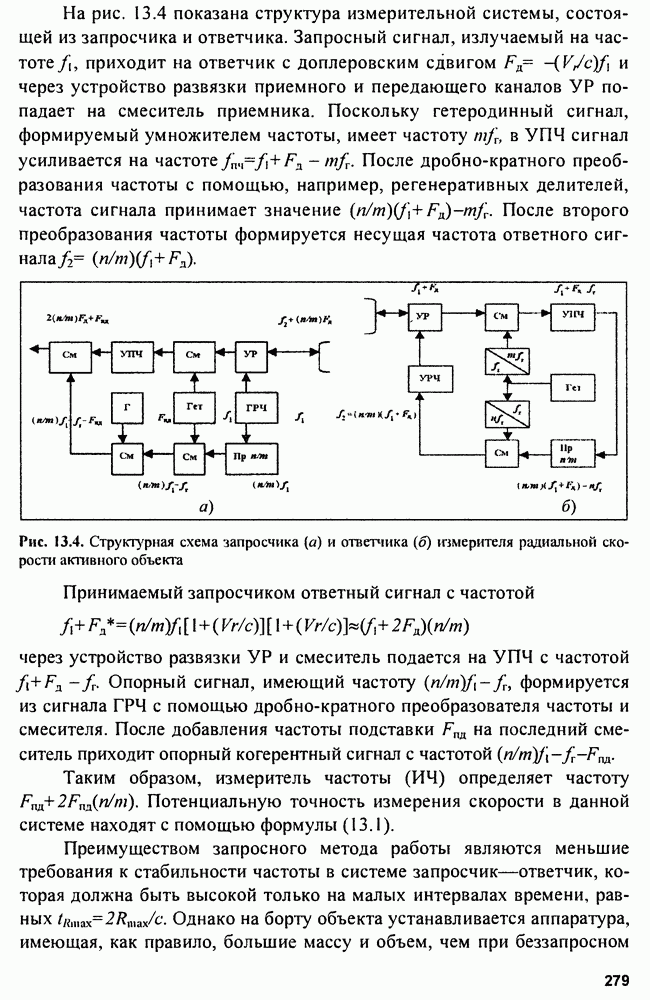
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
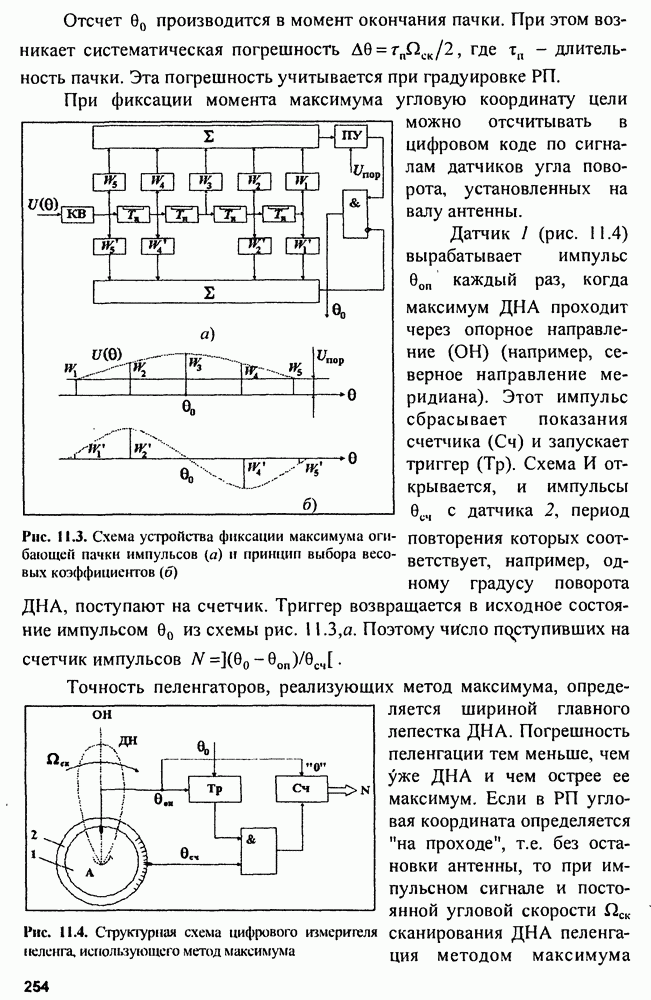
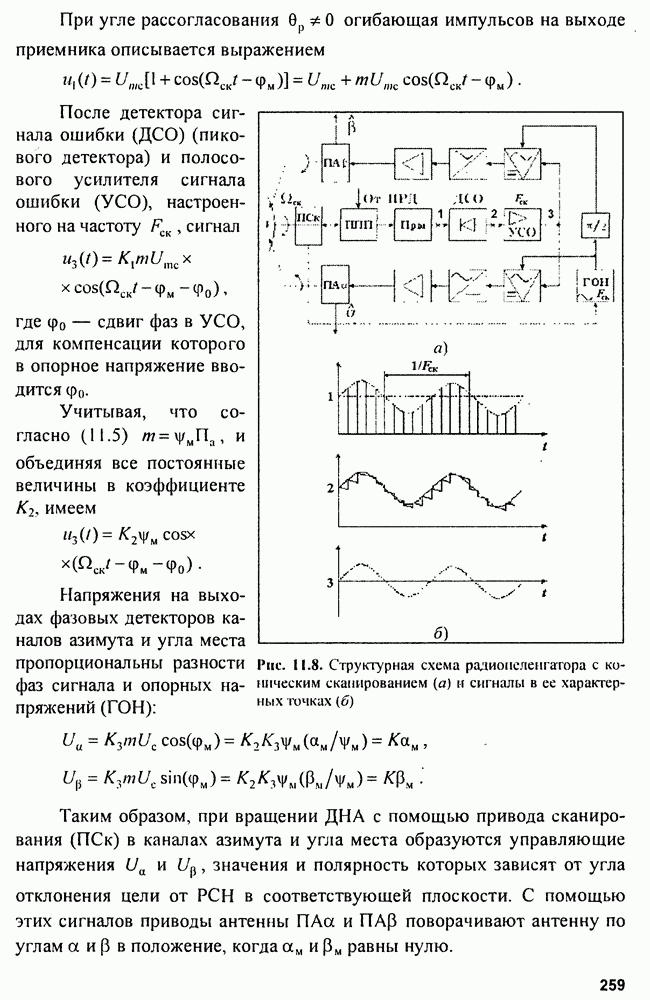
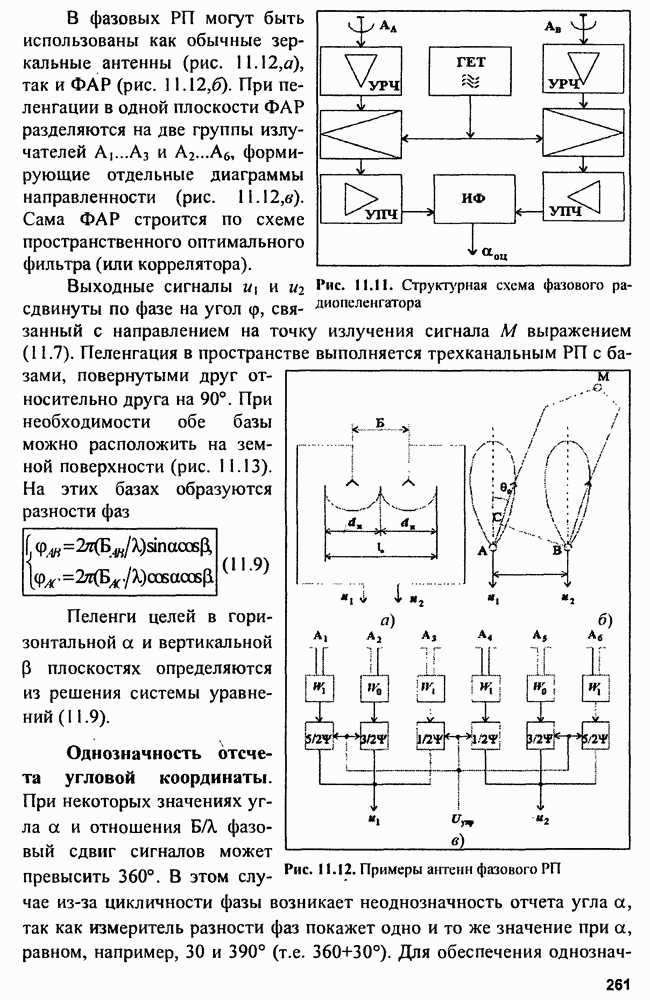
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
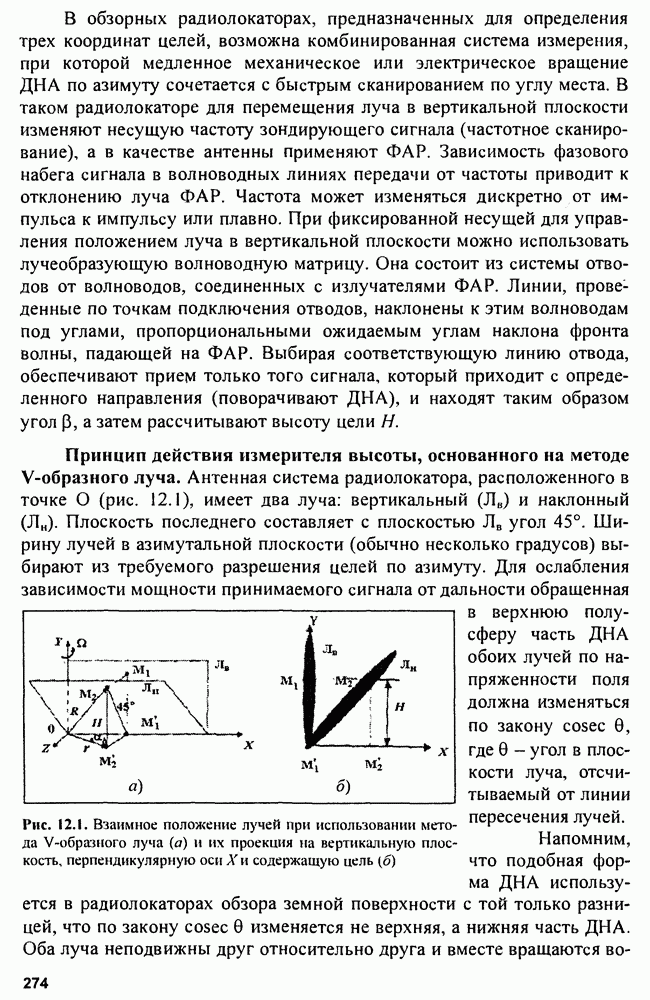
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
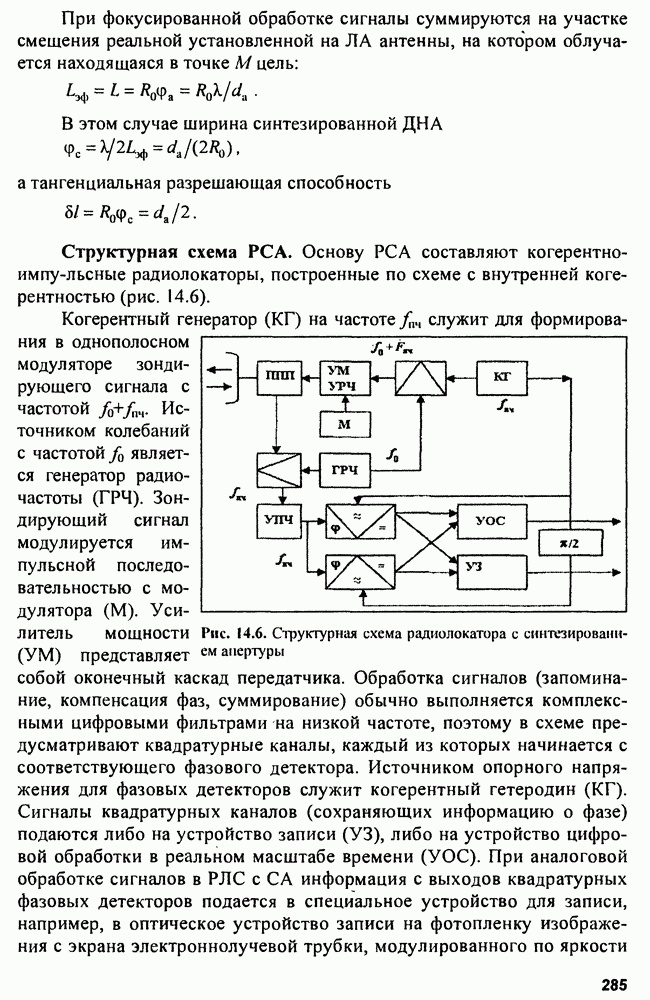
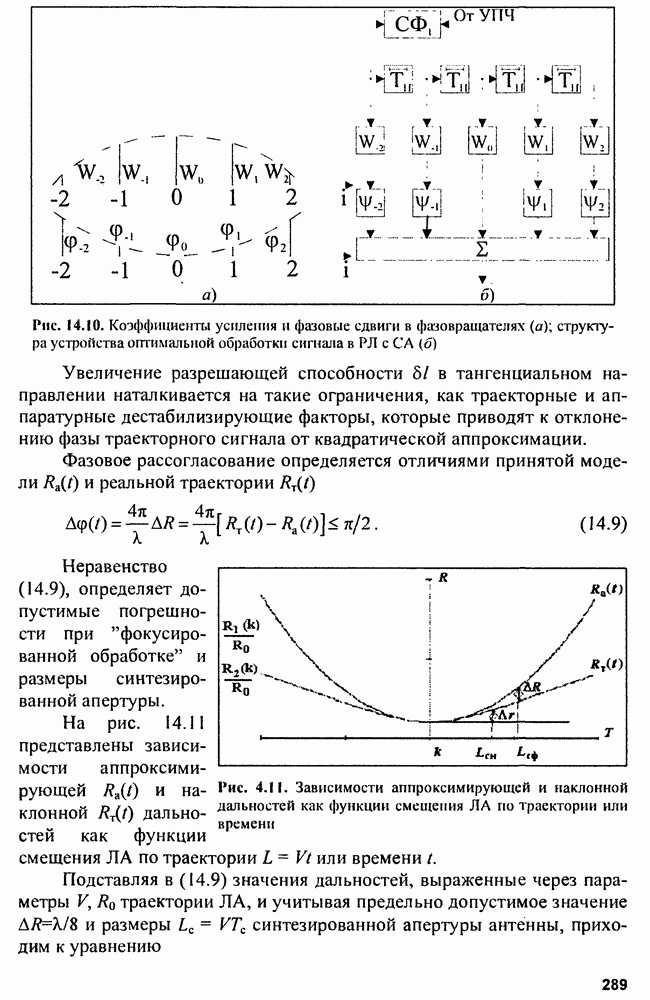
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение