| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2.3. Погрешность определения линии положения
Если местоположение объекта на плоскости находится на пересечении двух линий положения (ЛП), то погрешность местоопределения будет зависеть от погрешности  нахождения каждой из них, за которую обычно принимают минимальное расстояние в точке расположения объекта (цели) между истинной ЛП и ЛП, найденной по результатам определения элемента
нахождения каждой из них, за которую обычно принимают минимальное расстояние в точке расположения объекта (цели) между истинной ЛП и ЛП, найденной по результатам определения элемента  (рис. 5.17). Примем, что погрешность определения
(рис. 5.17). Примем, что погрешность определения  равна
равна  и имеет, как и
и имеет, как и  гауссовский закон распределения с нулевым средним значением. Элементу
гауссовский закон распределения с нулевым средним значением. Элементу  на плоскости соответствует семейство ЛП. Это семейство можно представить как скалярное поле элемента
на плоскости соответствует семейство ЛП. Это семейство можно представить как скалярное поле элемента  причем линии уровня этого поля и есть ЛП. Воспользовавшись теорией скалярного поля, можно найти градиент изменения элемента
причем линии уровня этого поля и есть ЛП. Воспользовавшись теорией скалярного поля, можно найти градиент изменения элемента  который представляет собой вектор, перпендикулярный линиям положения и направленный в сторону возрастания
который представляет собой вектор, перпендикулярный линиям положения и направленный в сторону возрастания  Переходя к конечным приращениям, получаем
Переходя к конечным приращениям, получаем

где  коэффициент погрешности определения ЛП (единицы длины/единицы параметра).
коэффициент погрешности определения ЛП (единицы длины/единицы параметра).
При гауссовском законе распределения погрешностей  погрешности
погрешности  также распределены по гауссовскому закону, как правило, с нулевым средним значением и дисперсией
также распределены по гауссовскому закону, как правило, с нулевым средним значением и дисперсией  . Возводя обе части равенства (5.14) в квадрат, усредняя и извлекая квадратный корень из результата, находим
. Возводя обе части равенства (5.14) в квадрат, усредняя и извлекая квадратный корень из результата, находим

где  нахождения линии положения и определения элемента.
нахождения линии положения и определения элемента.
Из (5.15) следует, что при одной и той же погрешности  можно снизить погрешность
можно снизить погрешность  непосредственно влияющую на точность местоопределения, уменьшив коэффициент
непосредственно влияющую на точность местоопределения, уменьшив коэффициент  который зависит от вида ЛП.
который зависит от вида ЛП.
Для нахождения  необходимо представить
необходимо представить  как функцию координат
как функцию координат  прямоугольной системы координат. Тогда
прямоугольной системы координат. Тогда


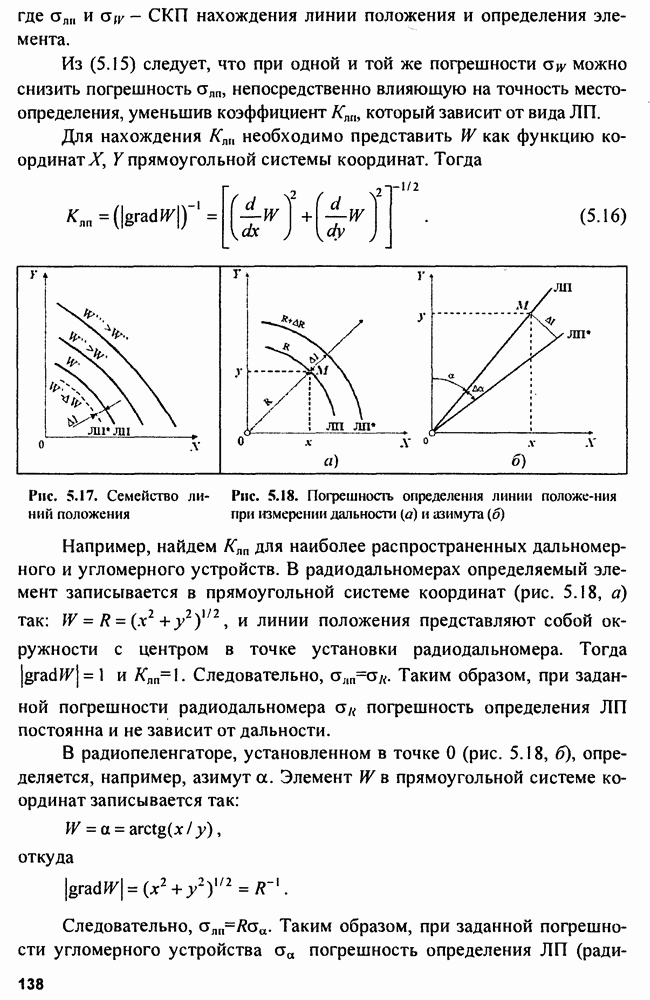
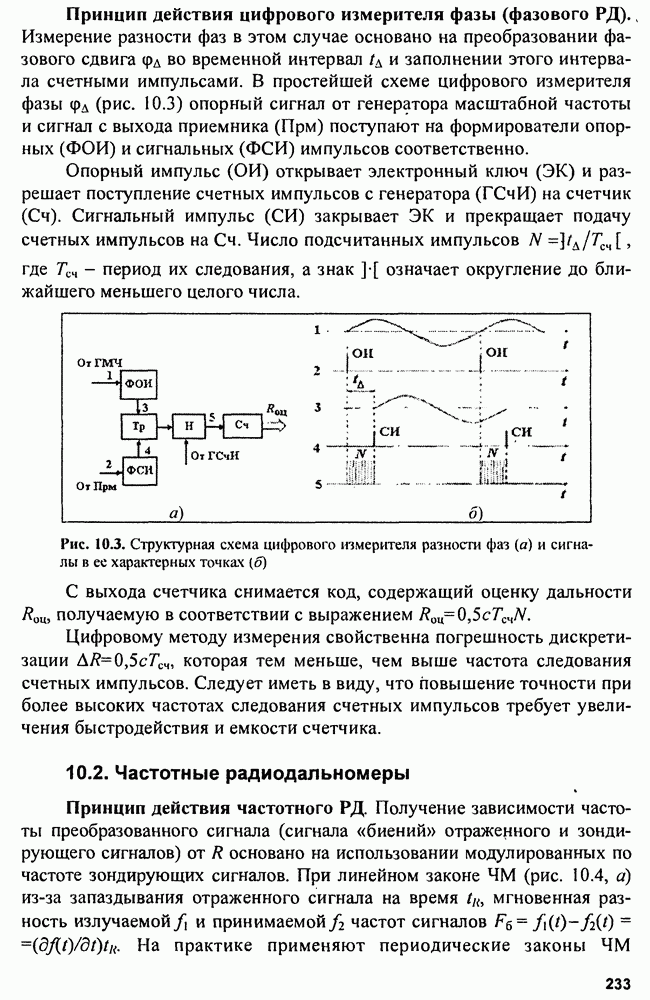
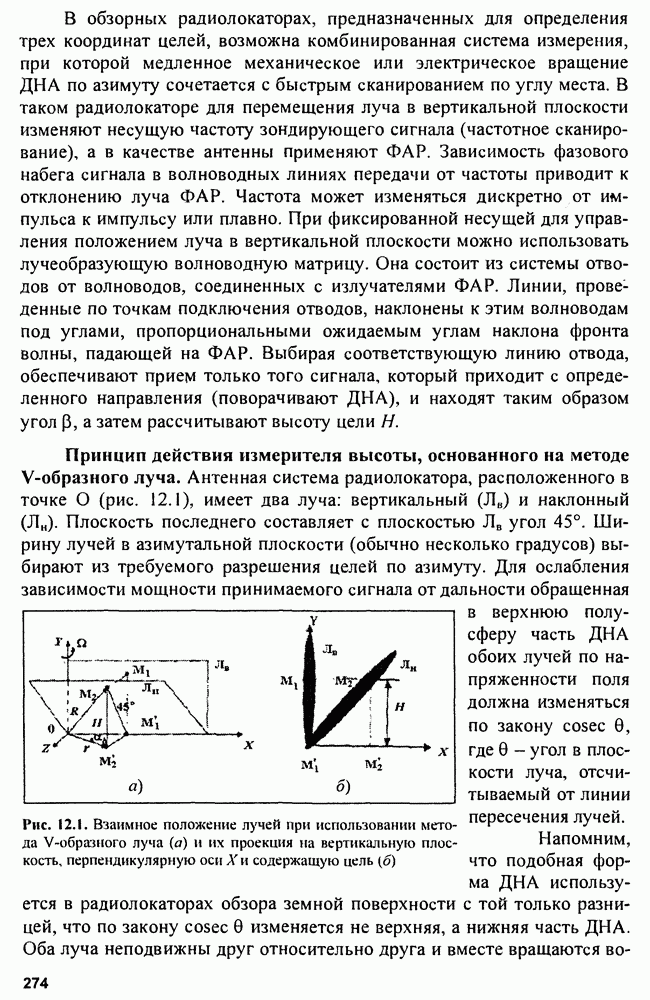
Рис. 5.17. Семейство линий положения

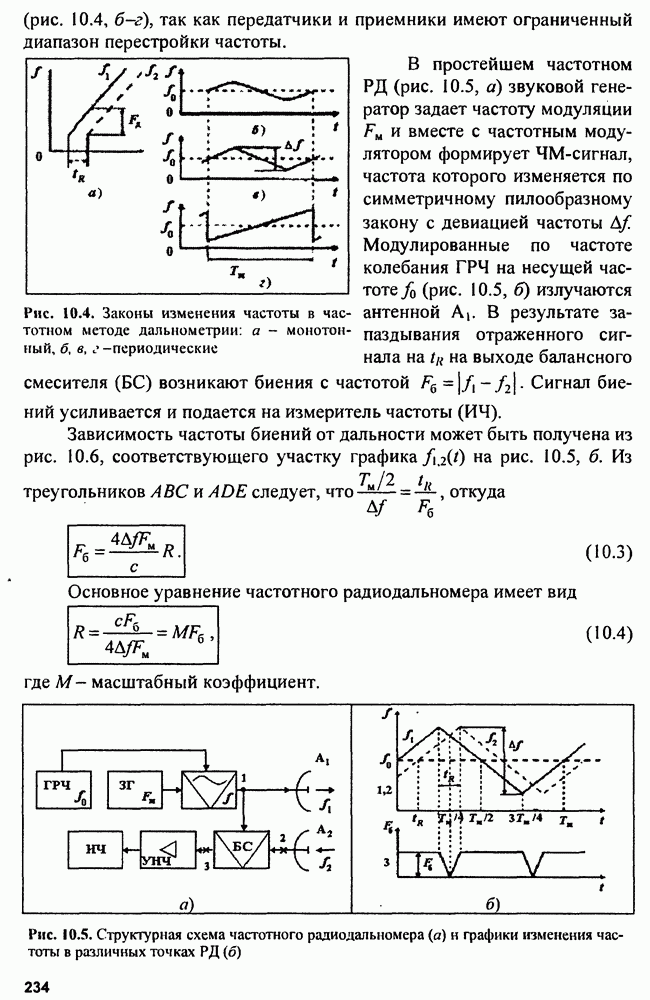
Рис. 5.18. Погрешность определения линии положения при измерении дальности  и азимута (б)
и азимута (б)
Например, найдем  для наиболее распространенных дальномерного и угломерного устройств. В радиодальномерах определяемый элемент записывается в прямоугольной системе координат (рис. 5.18, а) так:
для наиболее распространенных дальномерного и угломерного устройств. В радиодальномерах определяемый элемент записывается в прямоугольной системе координат (рис. 5.18, а) так:  , и линии положения представляют собой окружности с центром в точке установки радиодальномера. Тогда
, и линии положения представляют собой окружности с центром в точке установки радиодальномера. Тогда  Следовательно,
Следовательно,  Таким образом, при заданной погрешности радиодальномера погрешность определения ЛП постоянна и не зависит от дальности.
Таким образом, при заданной погрешности радиодальномера погрешность определения ЛП постоянна и не зависит от дальности.
В радиопеленгаторе, установленном в точке  (рис. 5.18, б), определяется, например, азимут а. Элемент
(рис. 5.18, б), определяется, например, азимут а. Элемент  в прямоугольной системе координат записывается так:
в прямоугольной системе координат записывается так:

откуда

Следовательно,  Таким образом, при заданной погрешности угломерного устройства
Таким образом, при заданной погрешности угломерного устройства  погрешность определения ЛП (радиальные
погрешность определения ЛП (радиальные
прямые) тем больше, чем больше расстояние до объекта (цели). Данное обстоятельство является серьезным недостатком угломерных устройств. Заметим, что подобная зависимость погрешности  от дальности имеет место и в разностно-дальномерных устройствах. На больших дальностях линии положения этих устройств (гиперболы) практически совпадают со своими асимптотами (прямыми), радиально расходящимися из центра базы устройства.
от дальности имеет место и в разностно-дальномерных устройствах. На больших дальностях линии положения этих устройств (гиперболы) практически совпадают со своими асимптотами (прямыми), радиально расходящимися из центра базы устройства.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
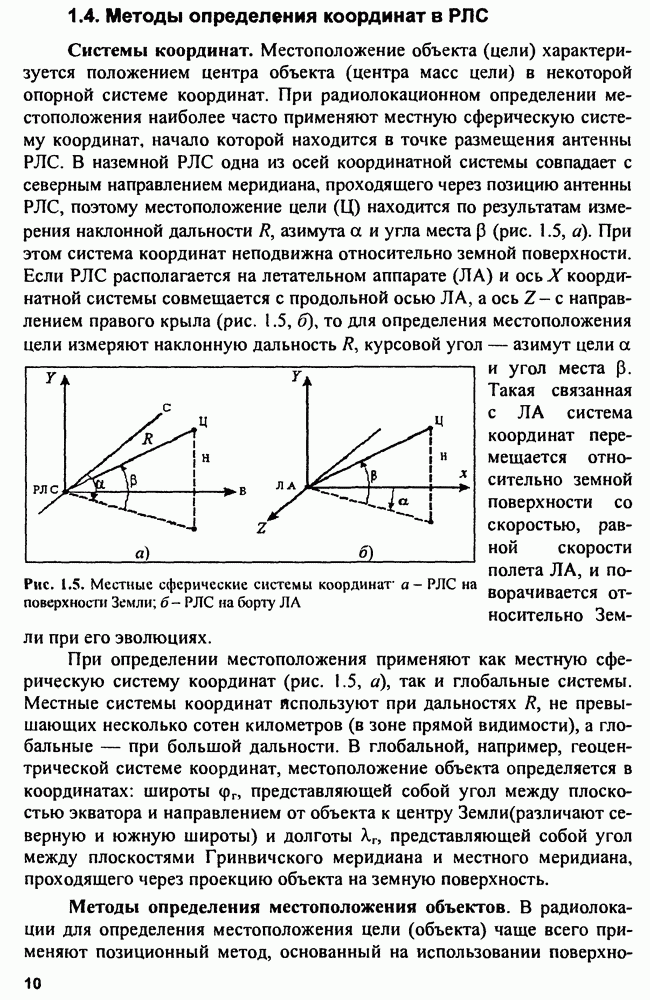
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
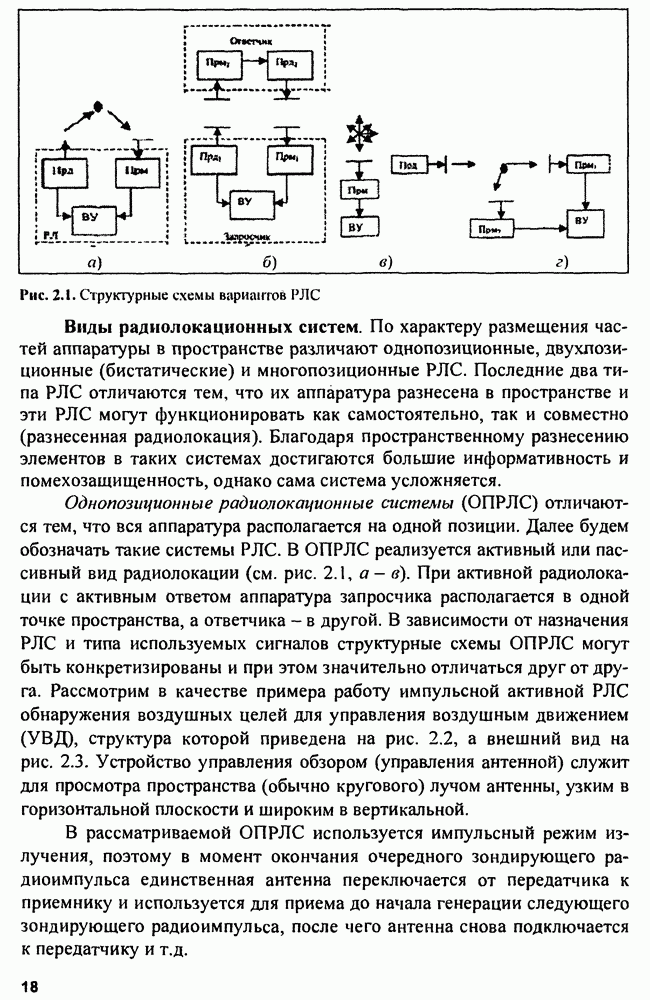
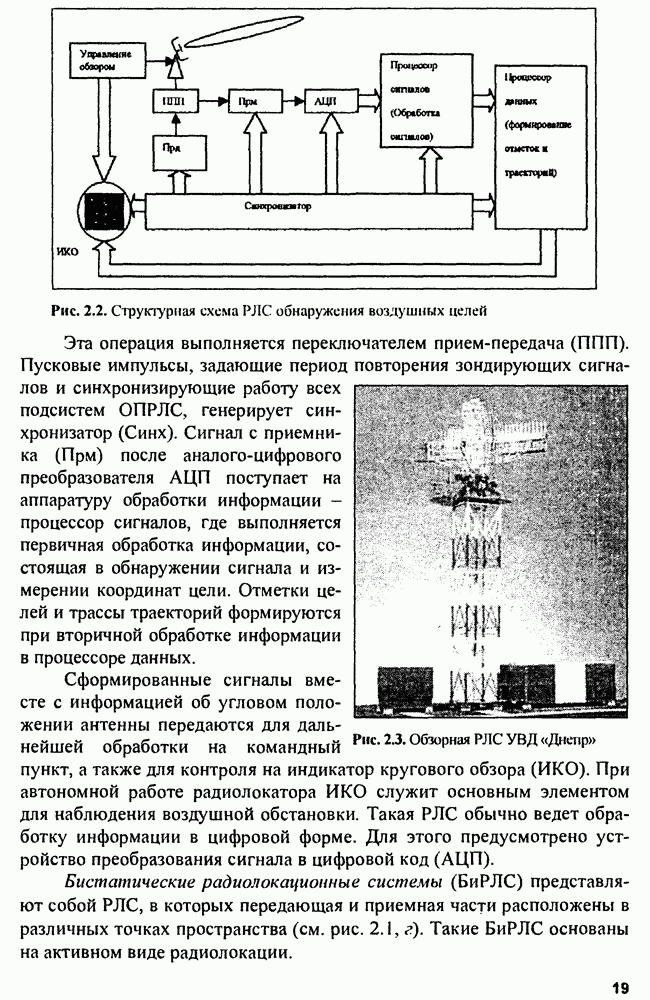
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
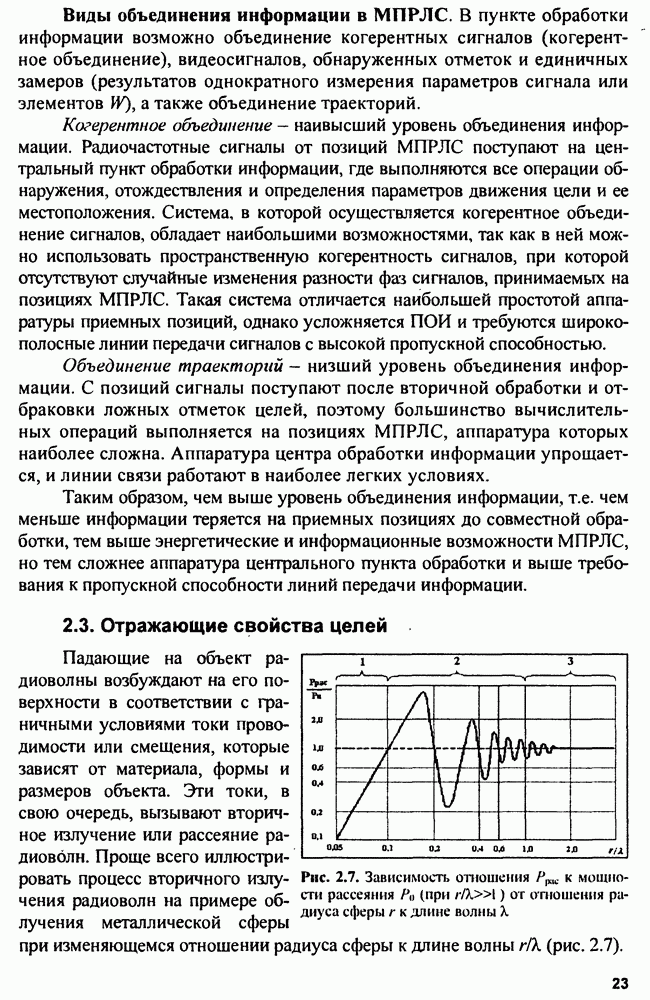
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
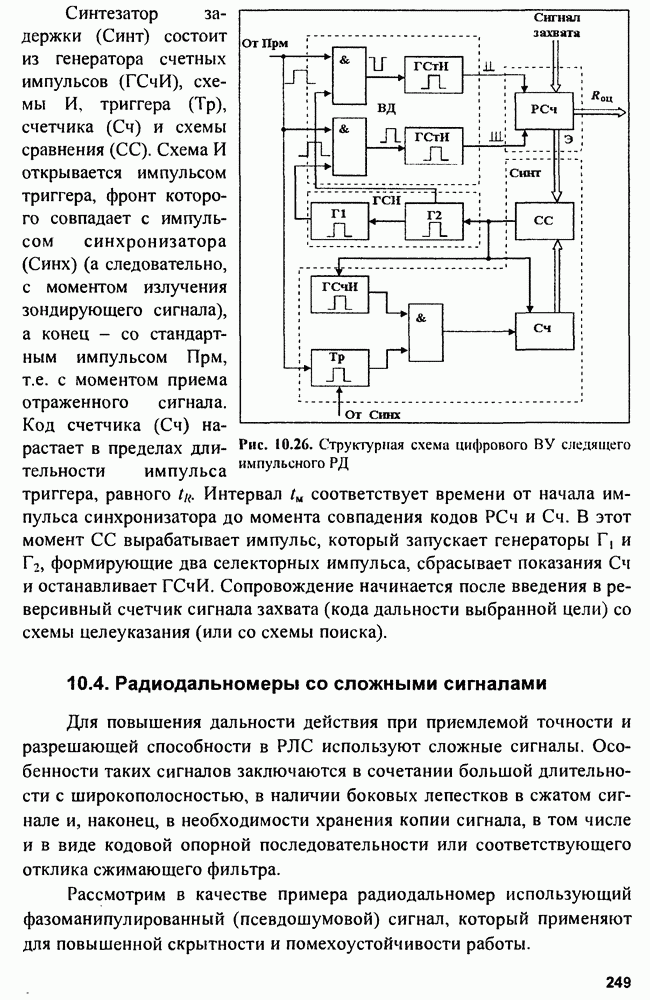
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение