| << Предыдущий параграф | Следующий параграф >> |
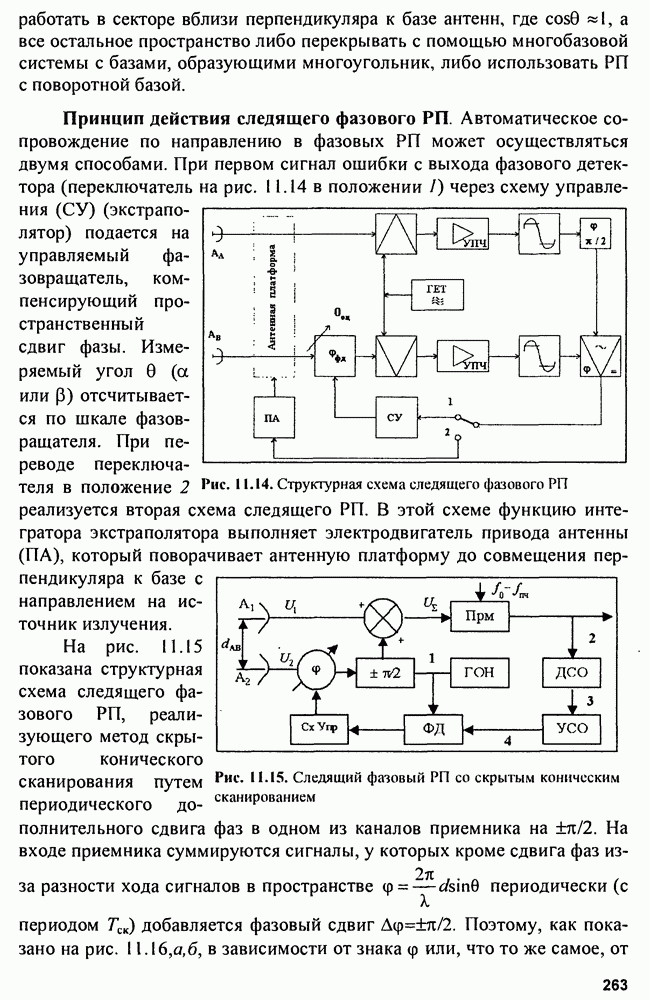
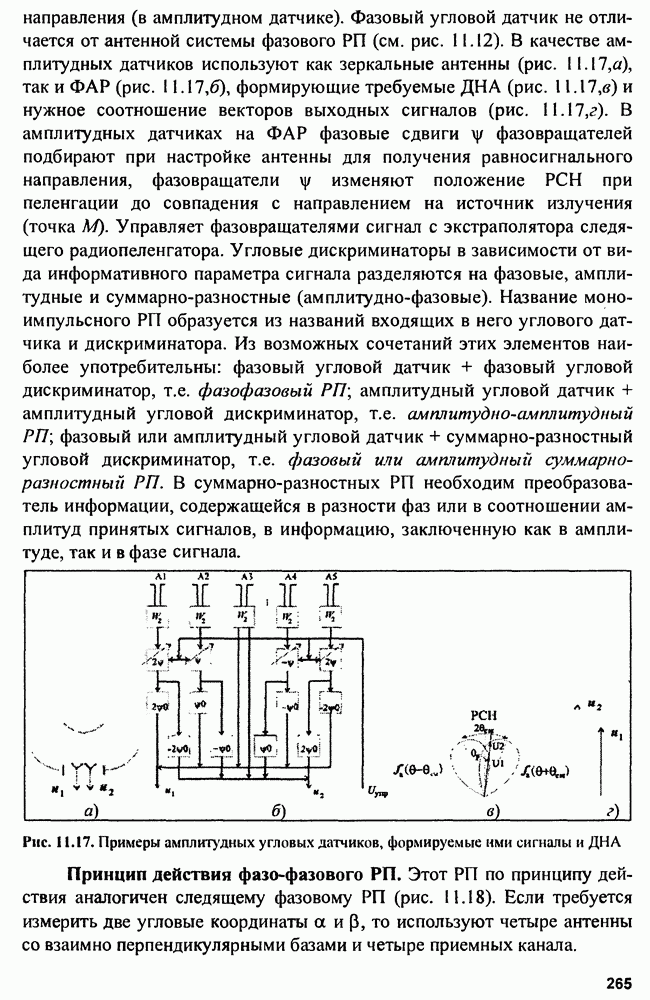
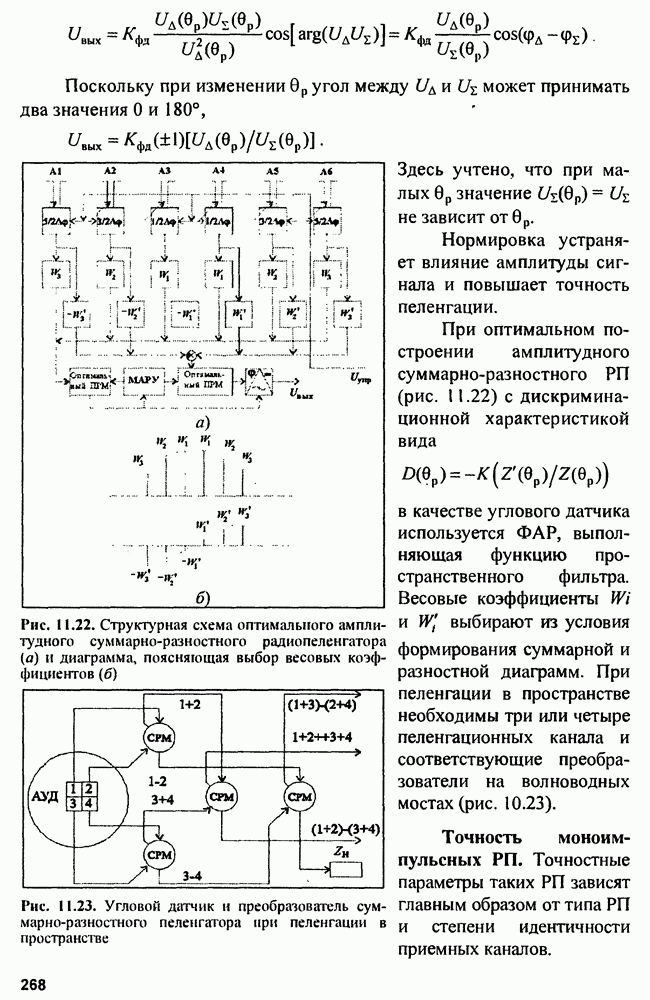
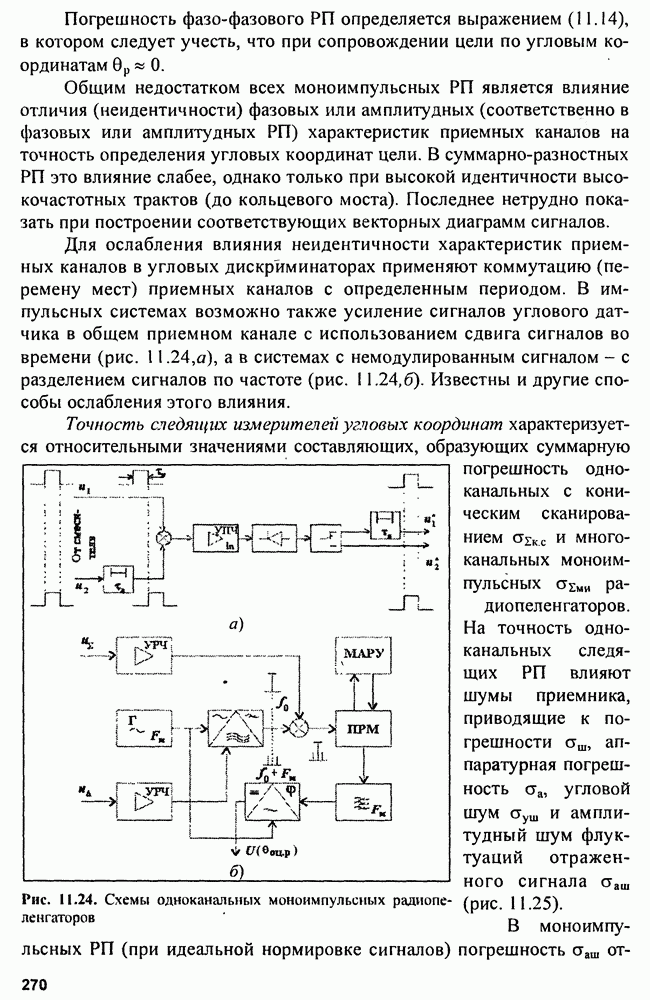
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 4. Выбор зондирующего сигнала в РЛС
4.1. Функция неопределенности
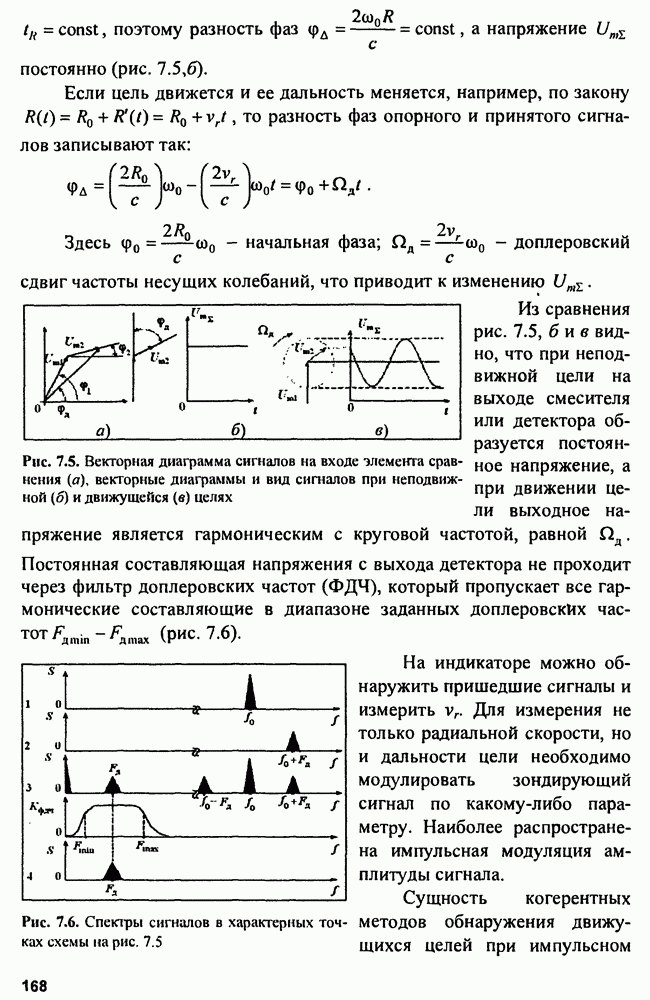
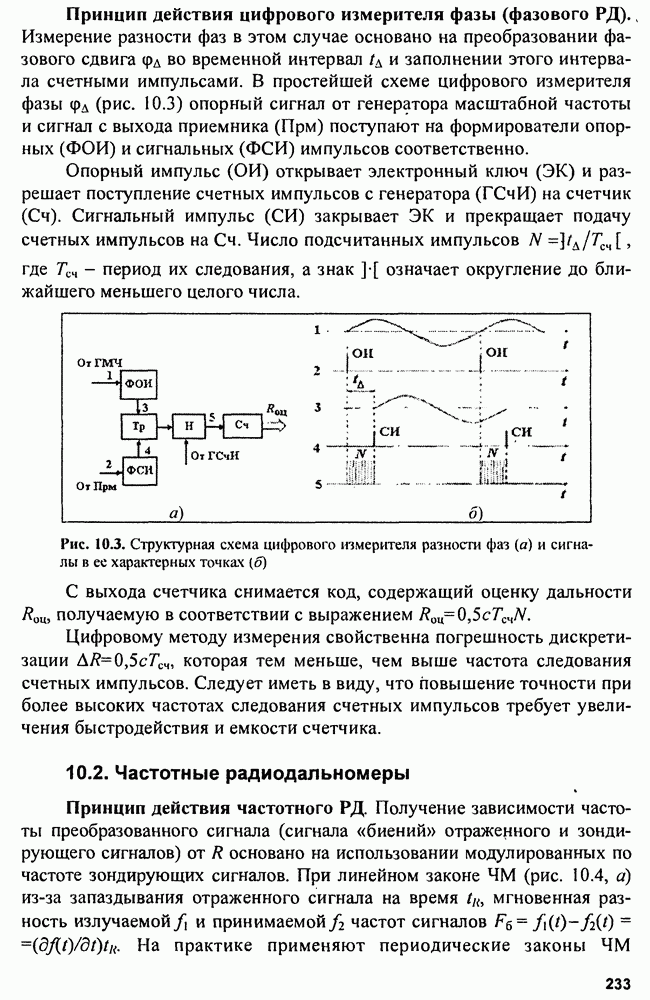
При оптимальном обнаружении сигнала на выходе приемника формируется сигнал, совпадающий по форме с корреляционной функцией зондирующего сигнала. Поэтому особенности разрешения сигнала, оценивания его параметров, распознавания цели и других операций связаны с формой двумерной корреляционной функции (ДКФ) зондирующего сигнала и ее деформацией при расстройке пары «фильтр - сигнал» по частоте  или рассогласовании по времени
или рассогласовании по времени  пары «опорный сигнал - принятый сигнал» при корреляционной обработке.
пары «опорный сигнал - принятый сигнал» при корреляционной обработке.
При описании зондирующего сигнала обычно используют комплексную форму (аналитический сигнал), которая предполагает, что сигнал задан действительной и мнимой частями, связанными преобразованием Гильберта:

где 
Спектральная плотность сигнала

Здесь  спектральная плотность сигнала
спектральная плотность сигнала 
Узкополосные сигналы, обычно используемые в радиолокационных приложениях, можно представить в виде

где  комплексная модулирующая функция, или комплексная огибающая сигнала, которая описывается как
комплексная модулирующая функция, или комплексная огибающая сигнала, которая описывается как 
При узкополосном сигнале  меняется медленно по сравнению с
меняется медленно по сравнению с  В частотной области спектральные плотности составляющих
В частотной области спектральные плотности составляющих  имеют вид
имеют вид

где  спектральная плотность модулирующей функции сигнала
спектральная плотность модулирующей функции сигнала 
Поэтому спектральная плотность комплексного сигнала 

Двумерная корреляционная функция сигнала. Для сигнала  двумерная корреляционная функция
двумерная корреляционная функция  задается корреляционным интегралом
задается корреляционным интегралом

На выходе согласованного фильтра или коррелятора оптимального обнаружителя, как показано в гл. 3, формируются сигналы, описываемые модулем корреляционного интеграла. Поэтому ДКФ является обобщением корреляционного интеграла на случай рассогласования принимаемого и опорного сигналов по времени на интервал  и по частоте на величину расстройки
и по частоте на величину расстройки  При этом
При этом  может физически интерпретироваться как несовпадение времени задержки принимаемого
может физически интерпретироваться как несовпадение времени задержки принимаемого  и опорного
и опорного  сигналов, а
сигналов, а  как расстройка согласованного фильтра относительно несущей частоты принимаемого сигнала, что физически происходит из-за эффекта Доплера при работе с движущимися объектами. Следовательно, сечения тела ДКФ вертикальными плоскостями, параллельными оси
как расстройка согласованного фильтра относительно несущей частоты принимаемого сигнала, что физически происходит из-за эффекта Доплера при работе с движущимися объектами. Следовательно, сечения тела ДКФ вертикальными плоскостями, параллельными оси  и проходящими через различные точки оси
и проходящими через различные точки оси  дают зависимость изменений спектра выходного сигнала от задержки принимаемого сигнала относительно опорного, а сечения ДКФ плоскостями, параллельными оси
дают зависимость изменений спектра выходного сигнала от задержки принимаемого сигнала относительно опорного, а сечения ДКФ плоскостями, параллельными оси  и проходящими через различные точки оси
и проходящими через различные точки оси  дают зависимость изменений огибающей выходного сигнала от расстройки по частоте пары «согласованный фильтр - входной сигнал».
дают зависимость изменений огибающей выходного сигнала от расстройки по частоте пары «согласованный фильтр - входной сигнал».
Двумерная корреляционная функция имеет следующие свойства:
1) максимальное значение ее  достигается в начале координат
достигается в начале координат 

где  энергия сигнала (для реальных сигналов со спектрами в диапазоне частот
энергия сигнала (для реальных сигналов со спектрами в диапазоне частот 
2) она симметрична относительно максимума или начала координат 

Обычно переходят к нормированной ДКФ:

Модуль нормированной ДКФ называется функцией неопределенности зондирующего сигнала (ФНЗС), обозначается  (иногда принимают за
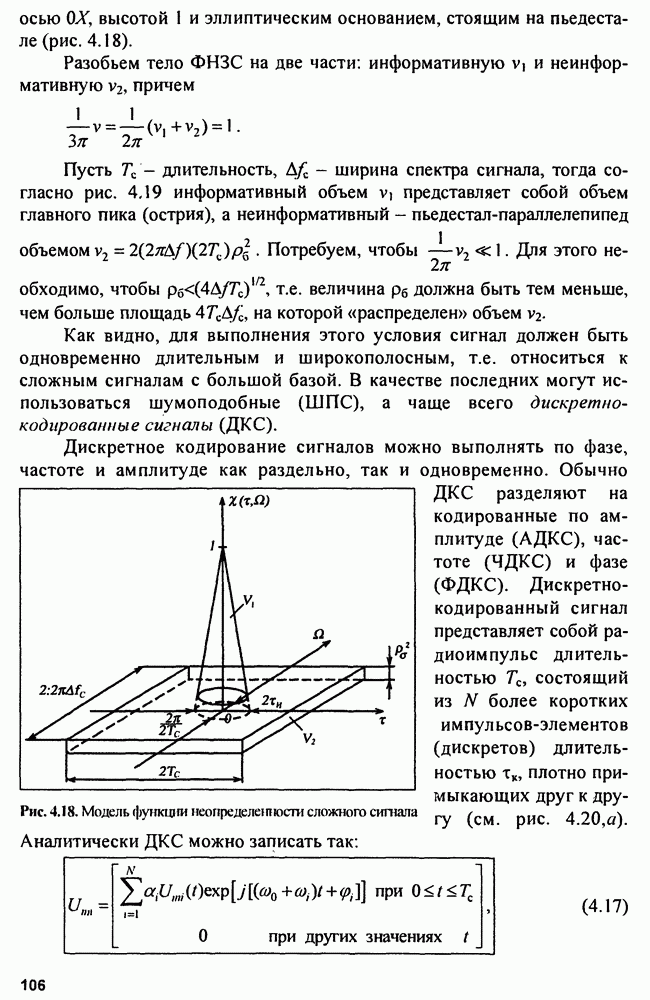
(иногда принимают за  и широко используется для анализа свойств зондирующего сигнала. Функцию неопределенности любого зондирующего сигнала можно представить в виде некоторого тела неопределенности над плоскостью
и широко используется для анализа свойств зондирующего сигнала. Функцию неопределенности любого зондирующего сигнала можно представить в виде некоторого тела неопределенности над плоскостью  причем форма поверхности ФНЗС может быть весьма сложной.
причем форма поверхности ФНЗС может быть весьма сложной.
Основные свойства ФНЗС:
- максимальное значение в начале координат всегда равно единице, т.е.  ;
;
- ФНЗС - фигура центрально-симметричная

- объем тела  постоянен:
постоянен:

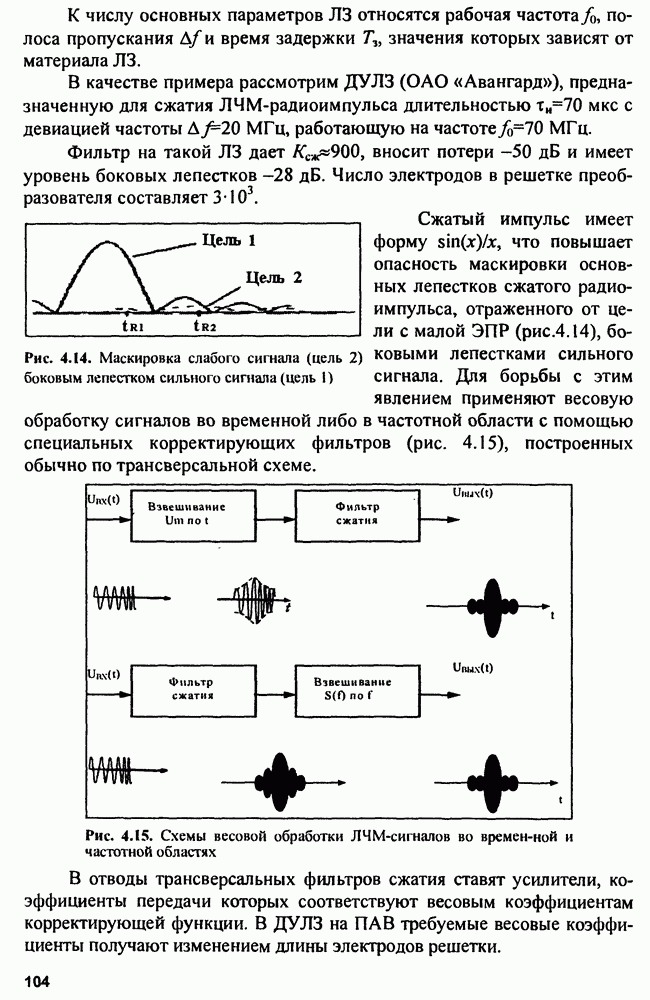
Рельеф ФНЗС позволяет судить о свойствах сигнала при оптимальной его обработке. Например, острота основного максимума свидетельствует о возможности точного измерения дальности  и скорости
и скорости  или о разрешающей способности при наблюдении близко расположенных целей. Наличие дополнительных максимумов рельефа ФНЗС указывает на возможную неоднозначность измерения или маскировку слабого отраженного сигнала «боковыми лепестками» функции неопределенности сильного сигнала. Наконец, постоянство объема ФНЗС при фиксированном максимуме в начале координат говорит о том, что любое изменение вида зондирующего сигнала может только деформировать тело ФНЗС, не меняя его объема.
или о разрешающей способности при наблюдении близко расположенных целей. Наличие дополнительных максимумов рельефа ФНЗС указывает на возможную неоднозначность измерения или маскировку слабого отраженного сигнала «боковыми лепестками» функции неопределенности сильного сигнала. Наконец, постоянство объема ФНЗС при фиксированном максимуме в начале координат говорит о том, что любое изменение вида зондирующего сигнала может только деформировать тело ФНЗС, не меняя его объема.
Найдем ФНЗС с гауссовской огибающей

воспользовавшись формулами (4.1), (4.2) для расчета,

Для прямоугольного радиоимпульса  при
при  описывается выражением
описывается выражением


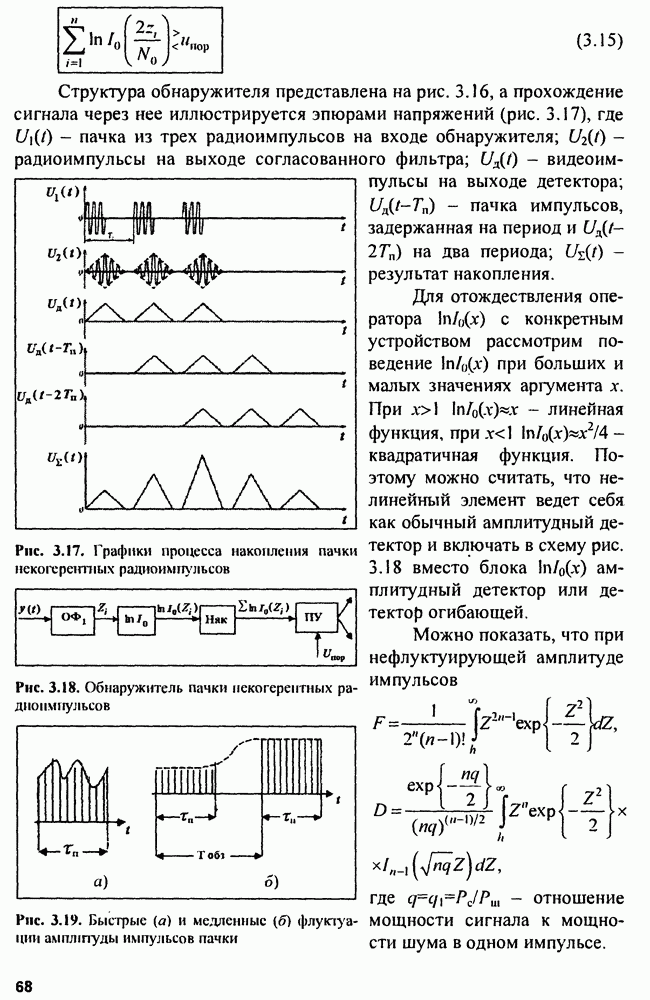
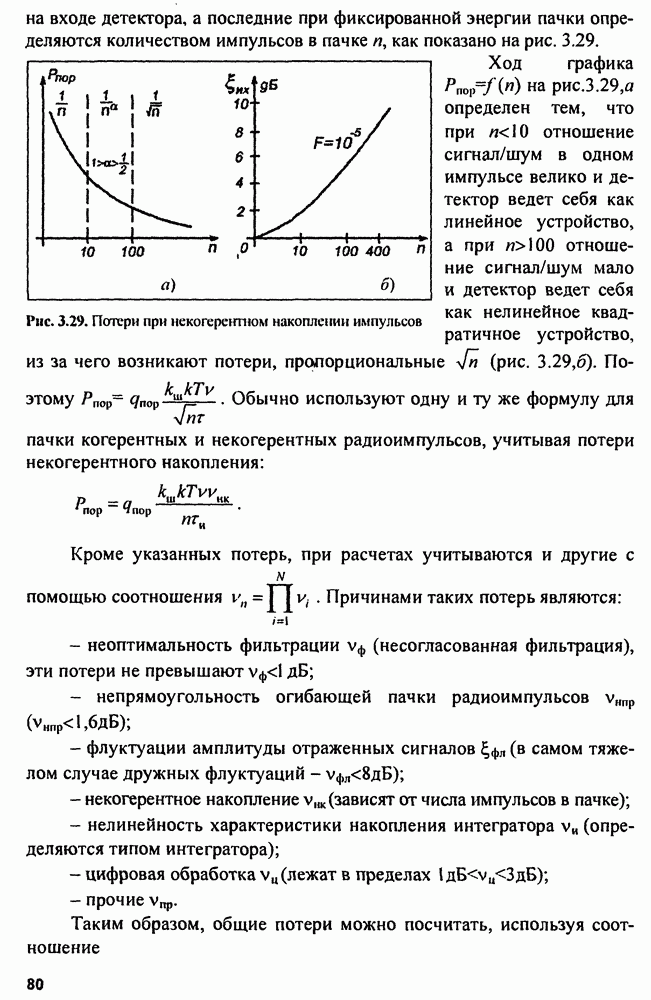
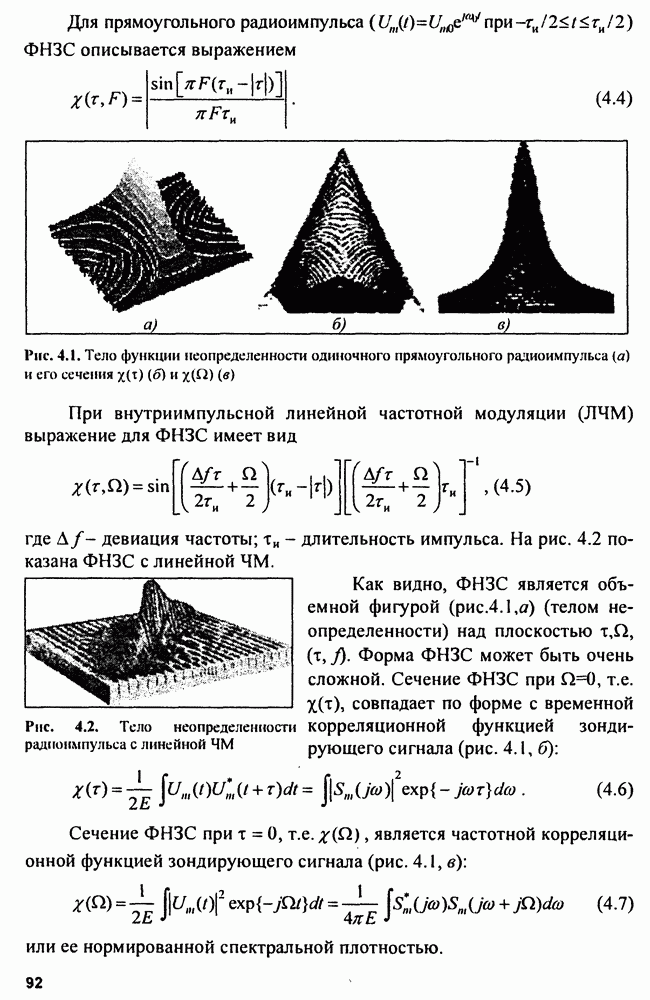
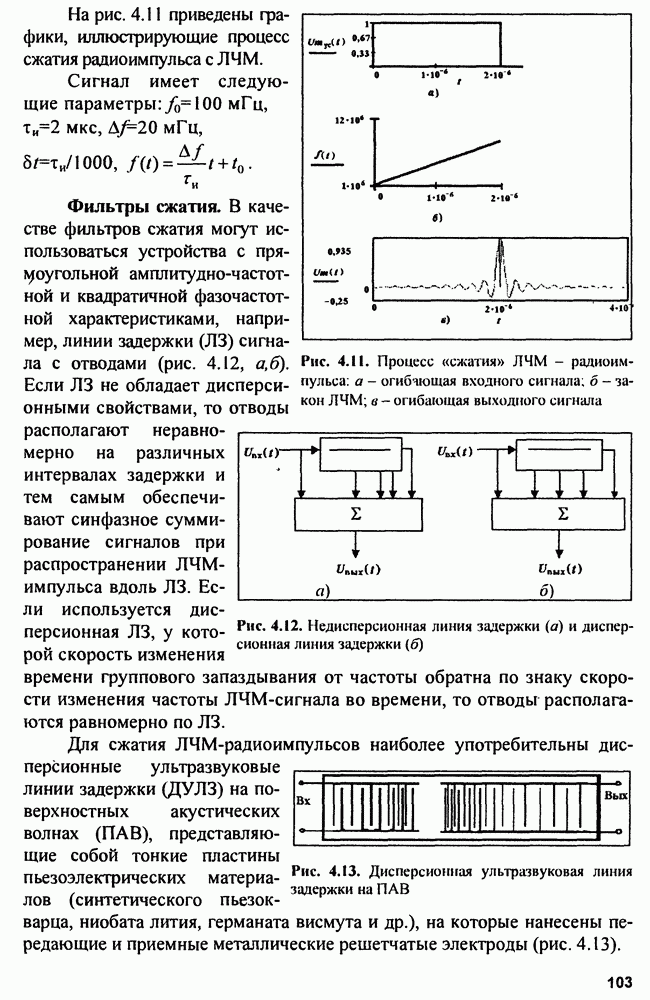
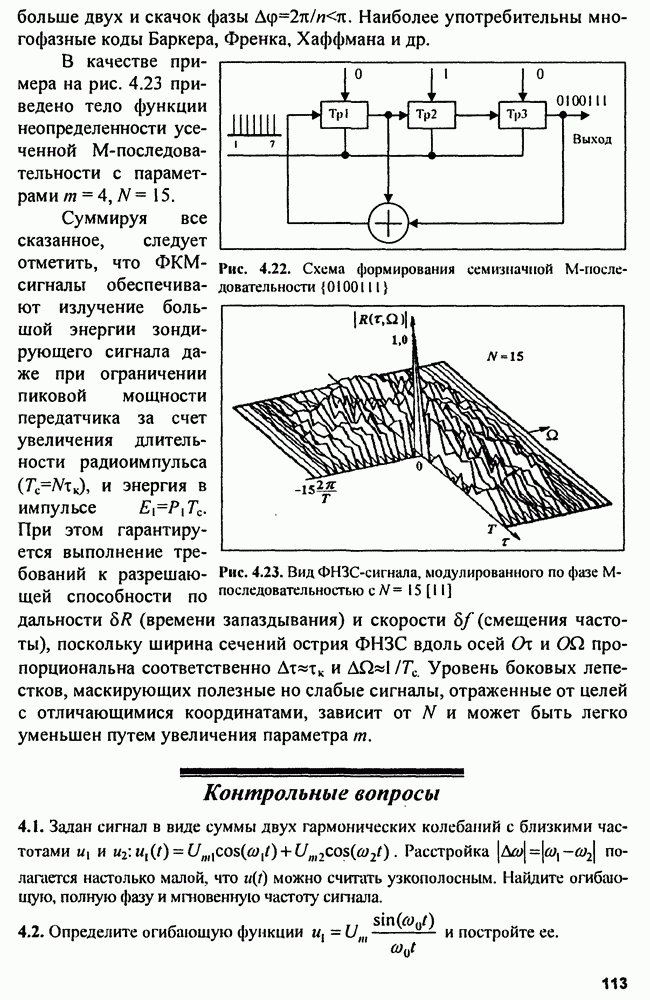
Рис. 4.1. Тело функции неопределенности одиночного прямоугольного радиоимпульса (а) и его сечения 
При внутриимпульсной линейной частотной модуляции (ЛЧМ) выражение для ФНЗС имеет вид

где  девиация частоты;
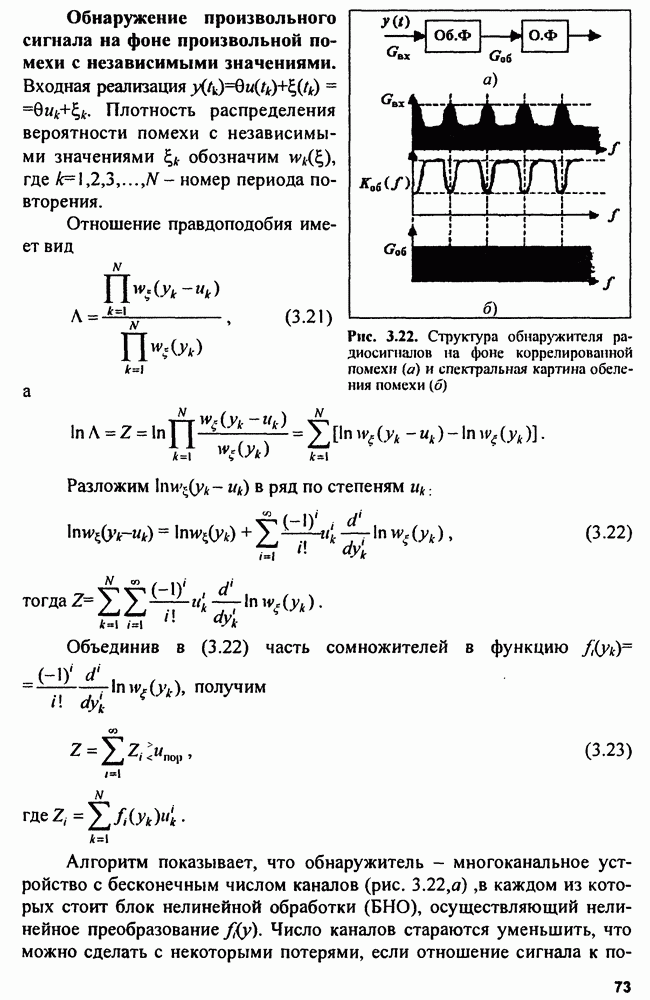
девиация частоты;  длительность импульса. На рис. 4.2 показана ФНЗС с линейной ЧМ.
длительность импульса. На рис. 4.2 показана ФНЗС с линейной ЧМ.

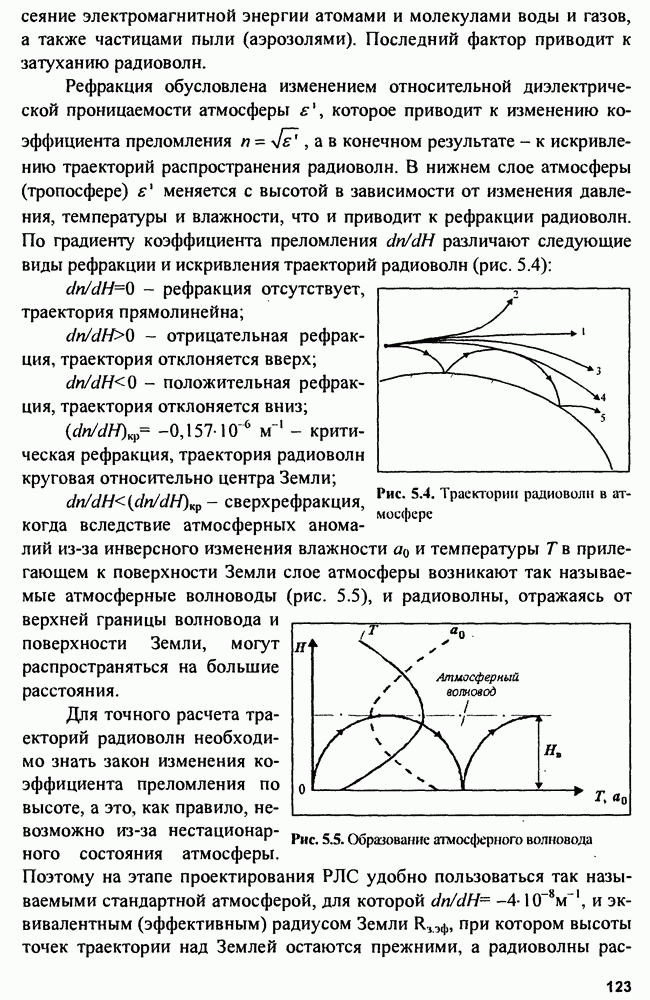
Рис. 4.2. Тело неопределенности радиоимпульса с линейной ЧМ
Как видно, ФНЗС является объемной фигурой  (телом неопределенности) над плоскостью
(телом неопределенности) над плоскостью  Форма ФНЗС может быть очень сложной. Сечение ФНЗС при
Форма ФНЗС может быть очень сложной. Сечение ФНЗС при  т.е.
т.е.  совпадает по форме с временной корреляционной функцией зондирующего сигнала (рис. 4.1, б):
совпадает по форме с временной корреляционной функцией зондирующего сигнала (рис. 4.1, б):

Сечение ФНЗС при  т.е.
т.е.  является частотной корреляционной функцией зондирующего сигнала (рис. 4.1, в):
является частотной корреляционной функцией зондирующего сигнала (рис. 4.1, в):

или ее нормированной спектральной плотностью.
Для радиоимпульса с прямоугольной огибающей сечения  приведены на рис. 4.1,6, в.
приведены на рис. 4.1,6, в.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
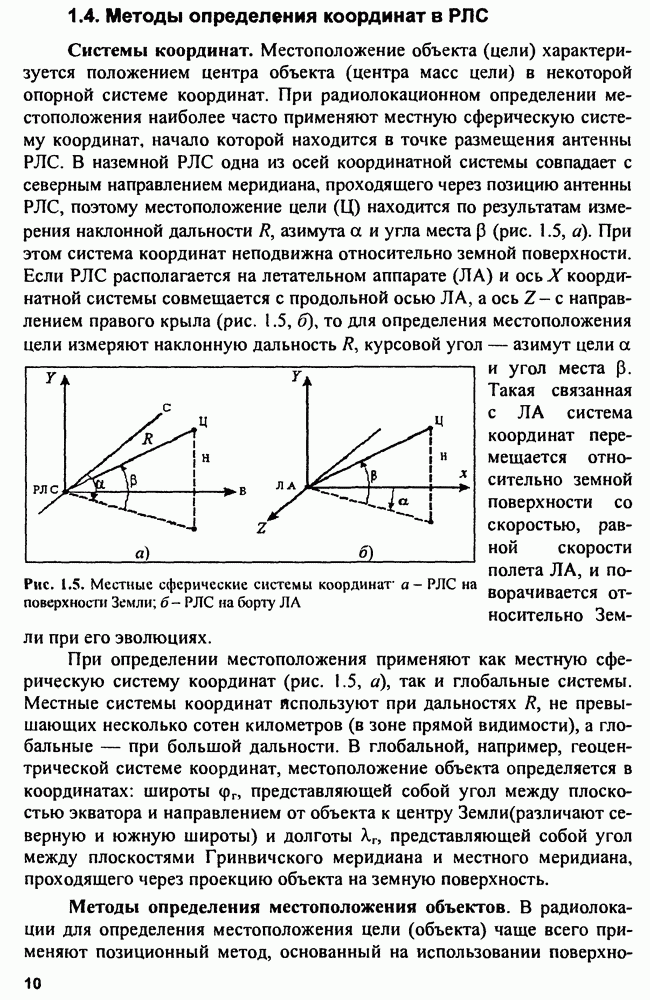
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
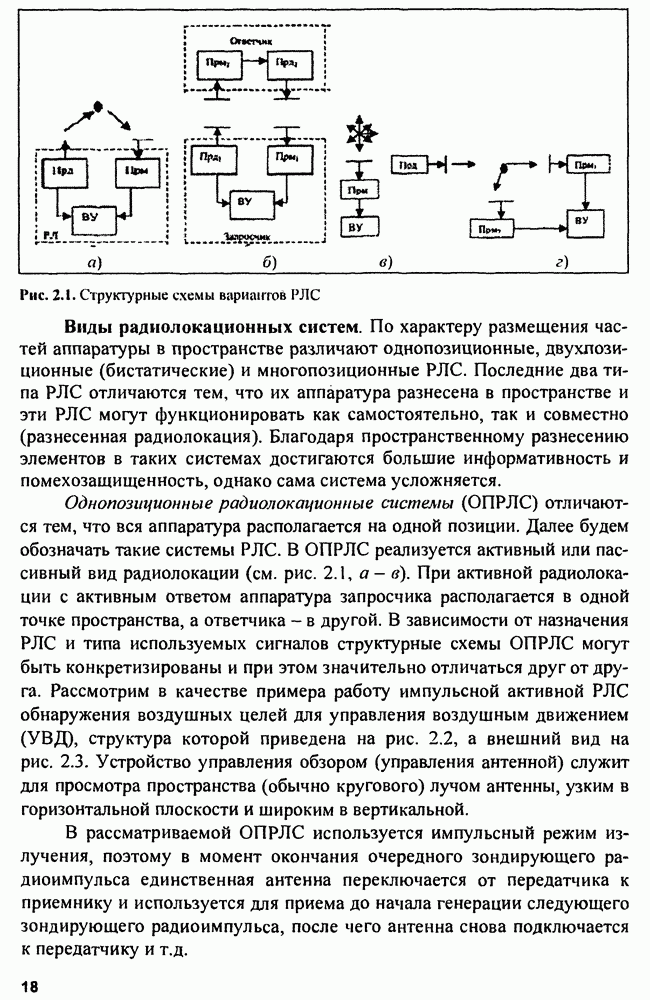
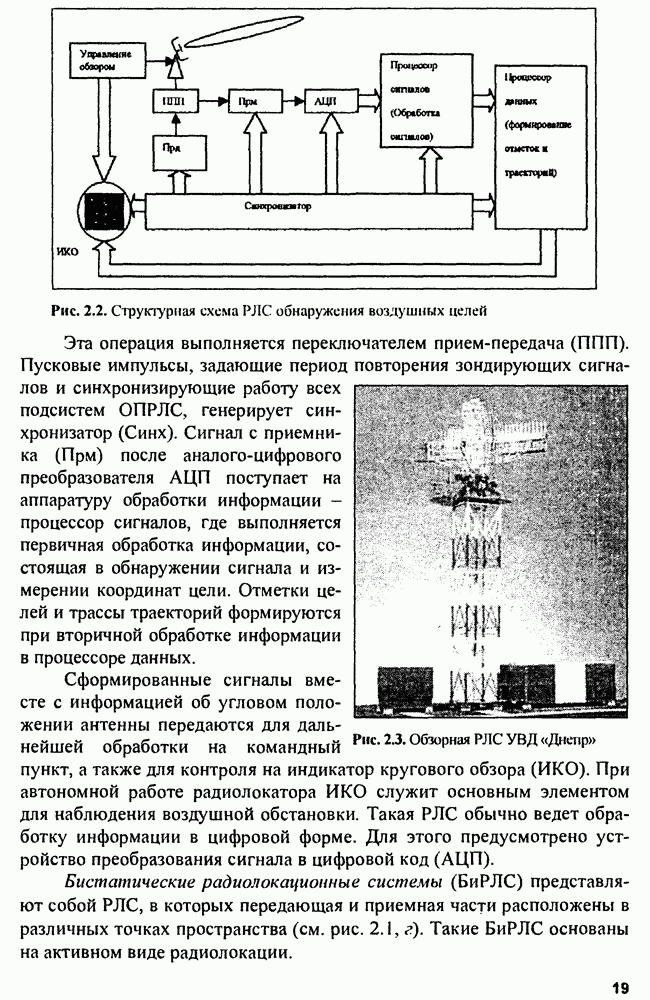
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
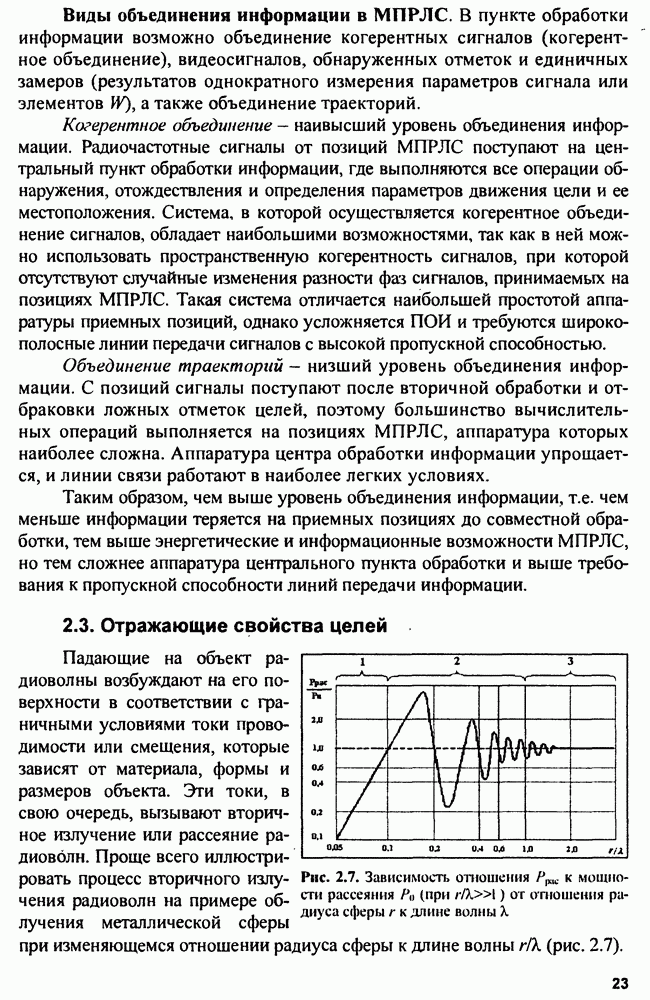
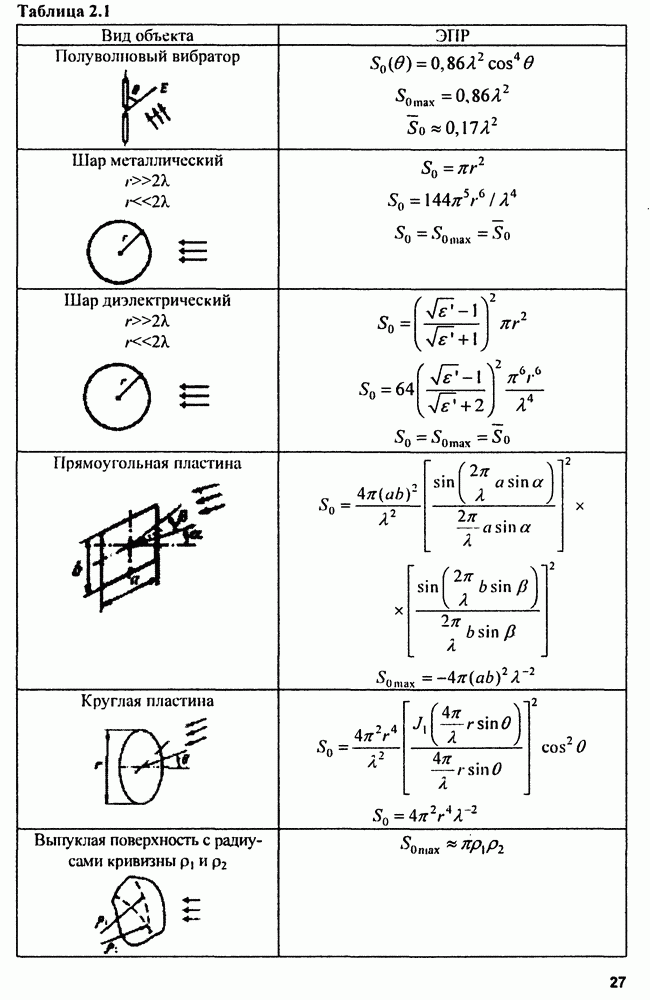
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
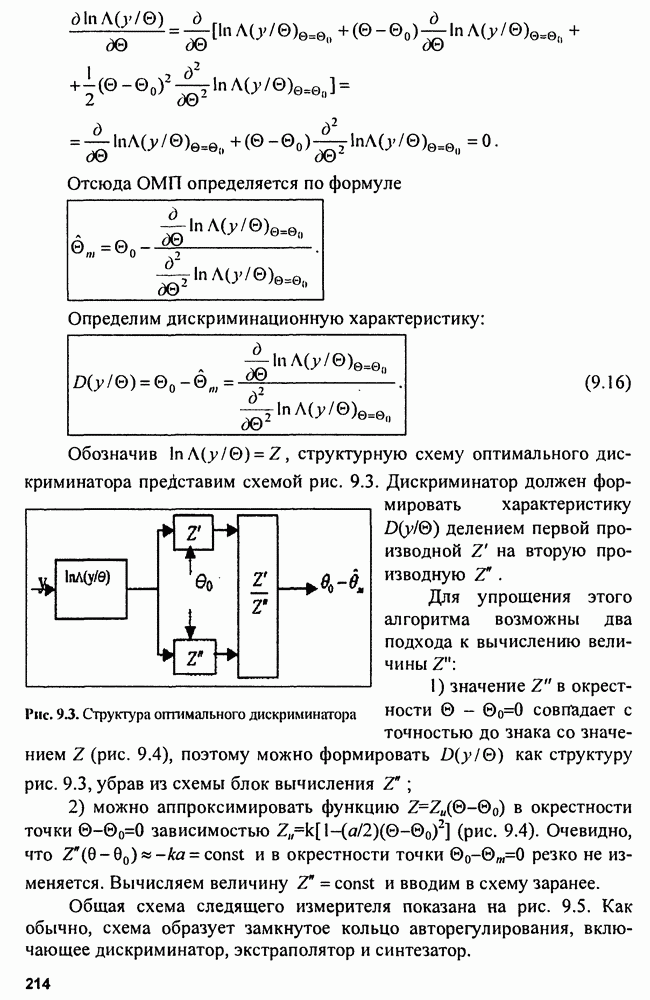
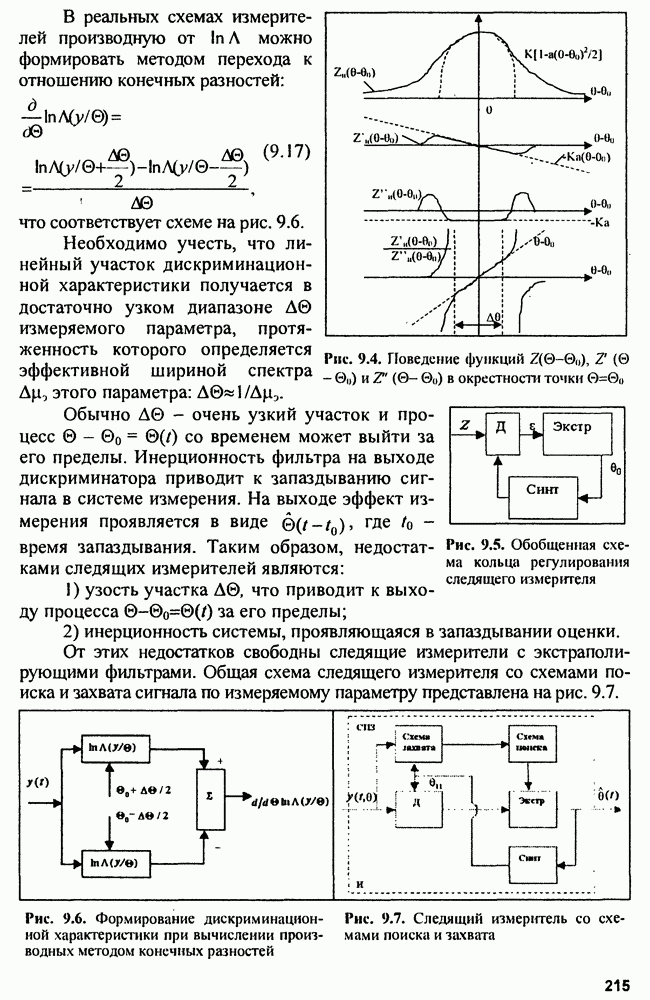
- 9.5. Структура измерителей
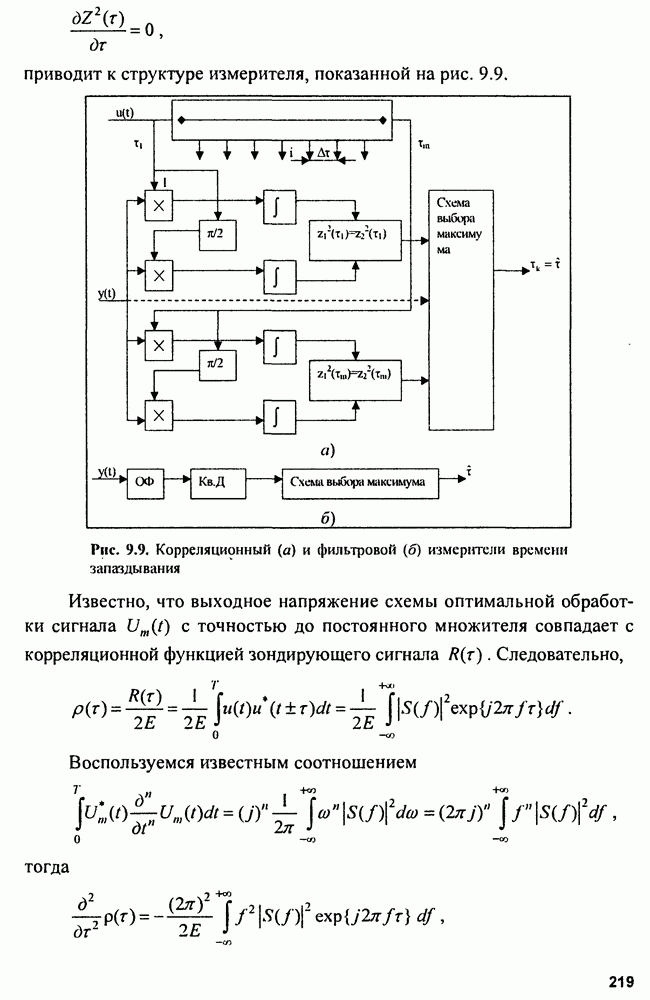
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
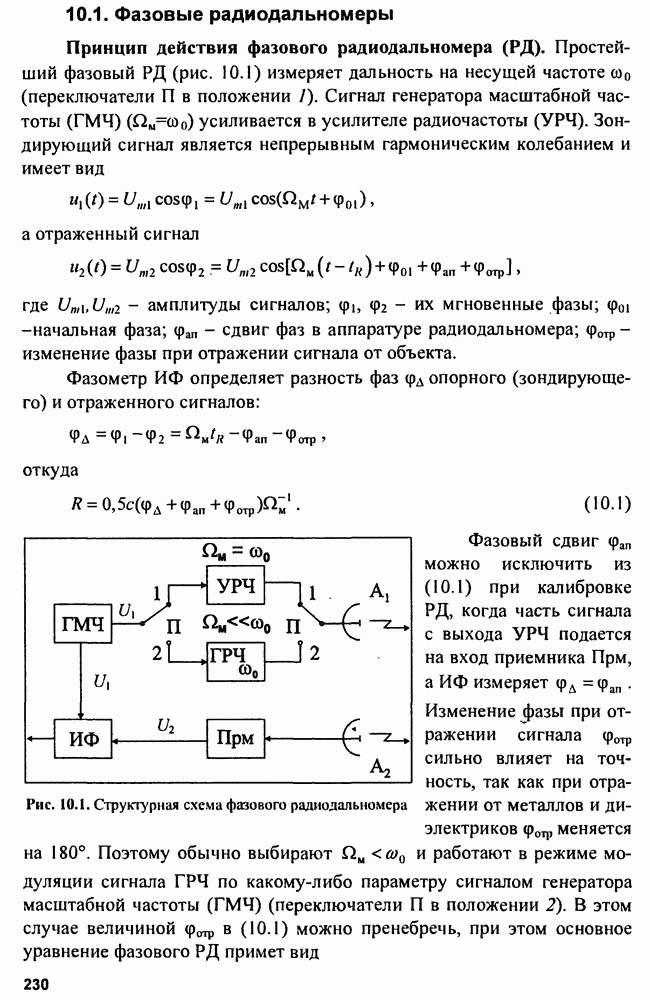
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
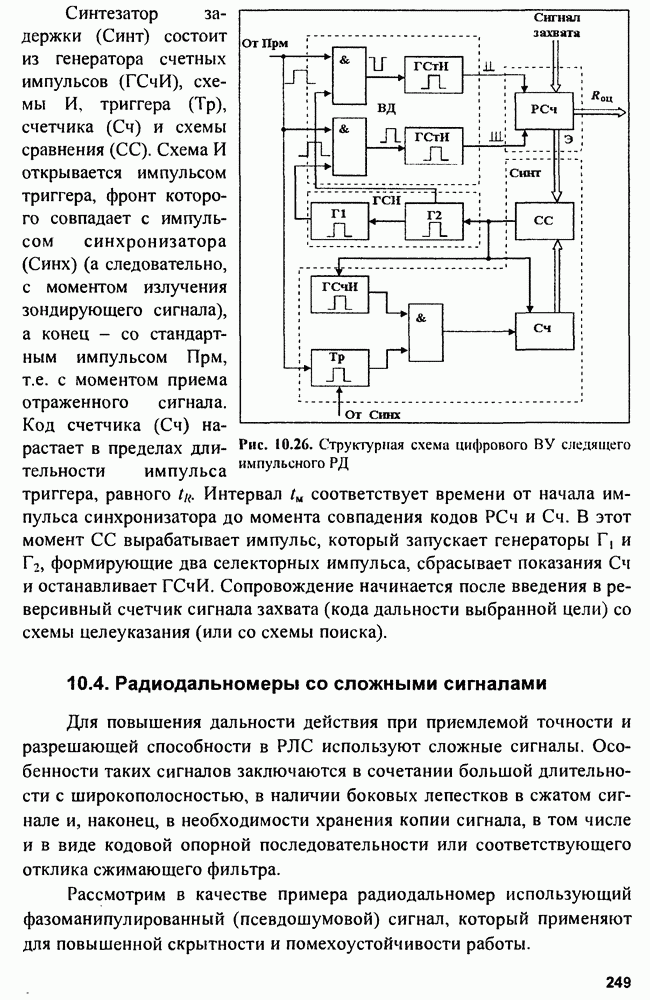
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение