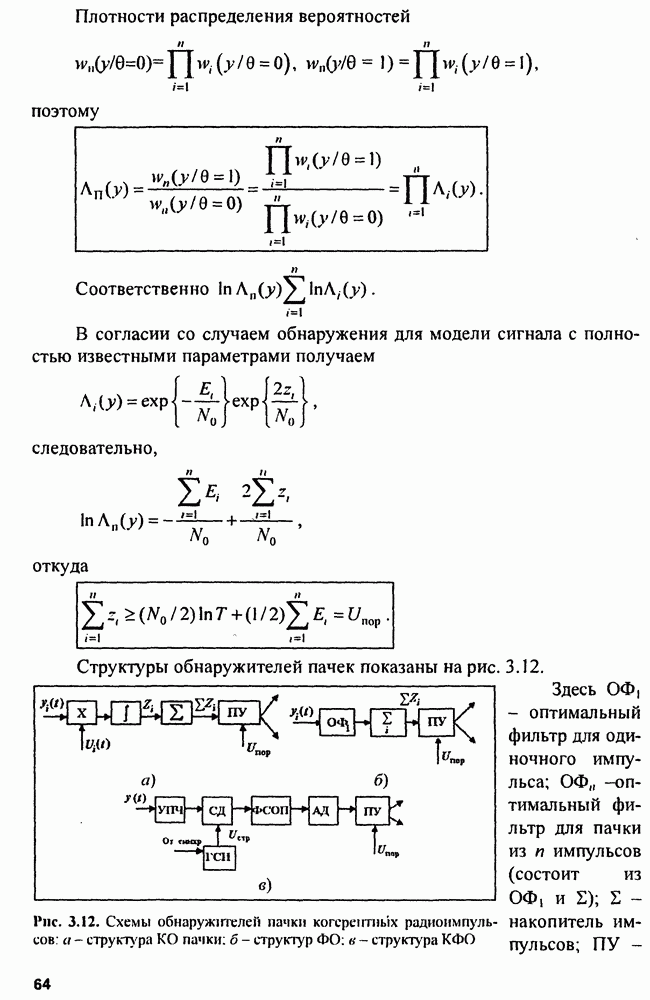
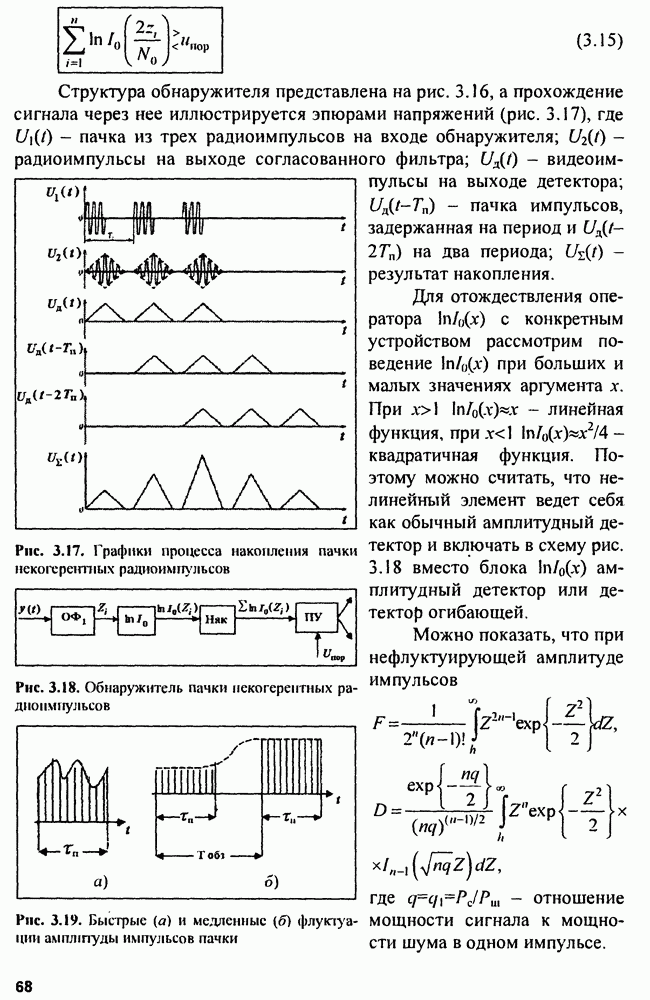
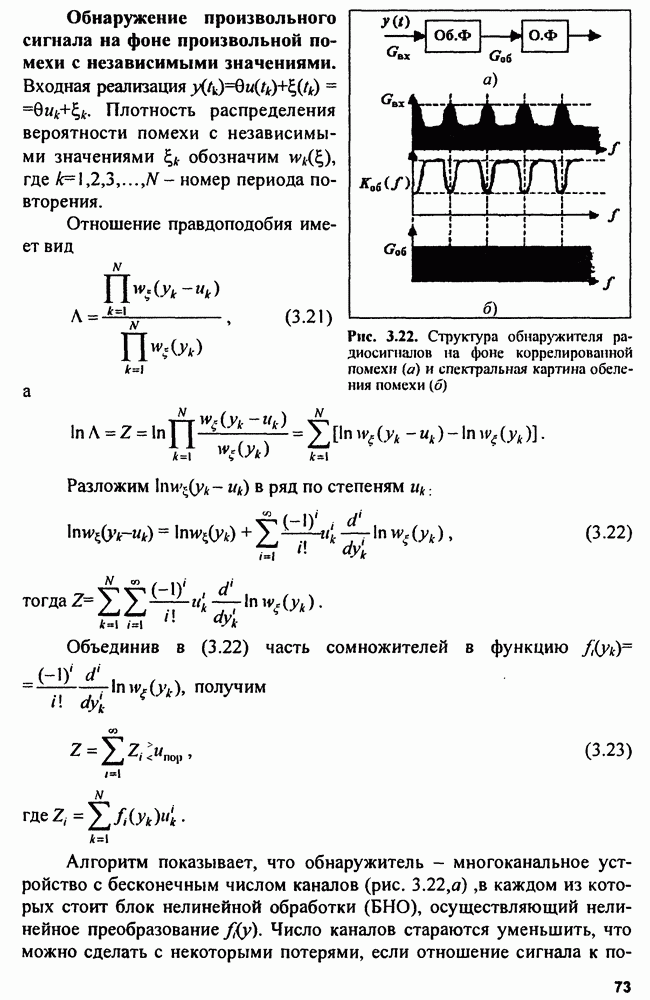
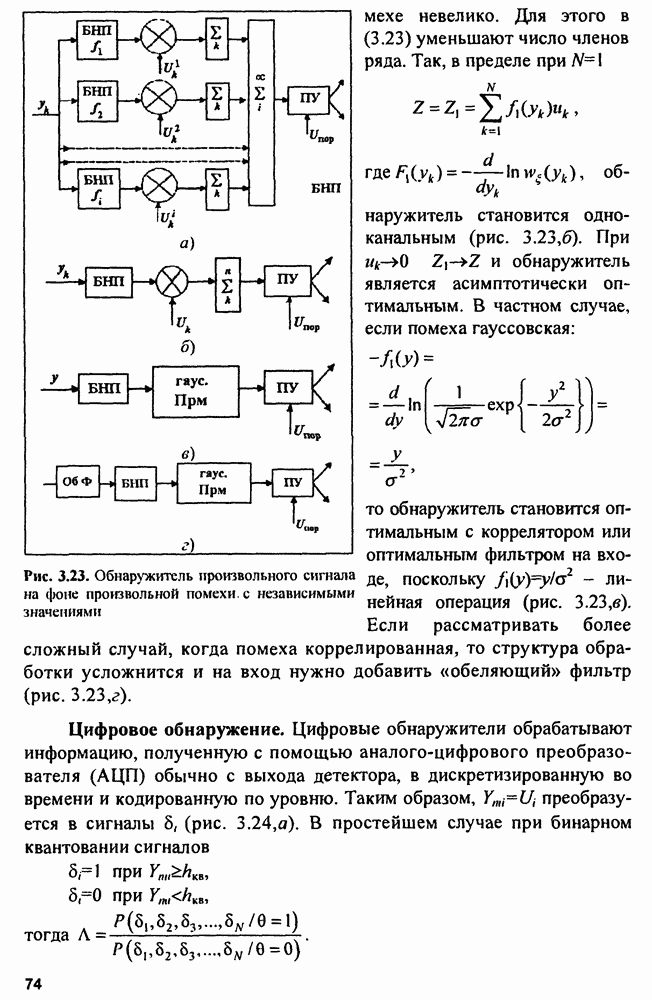
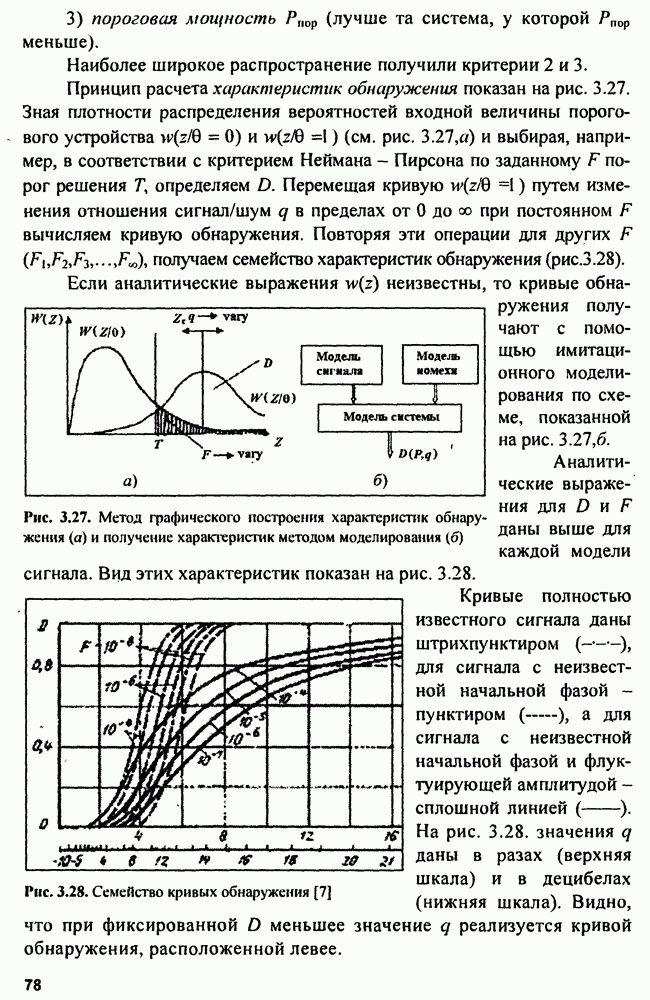
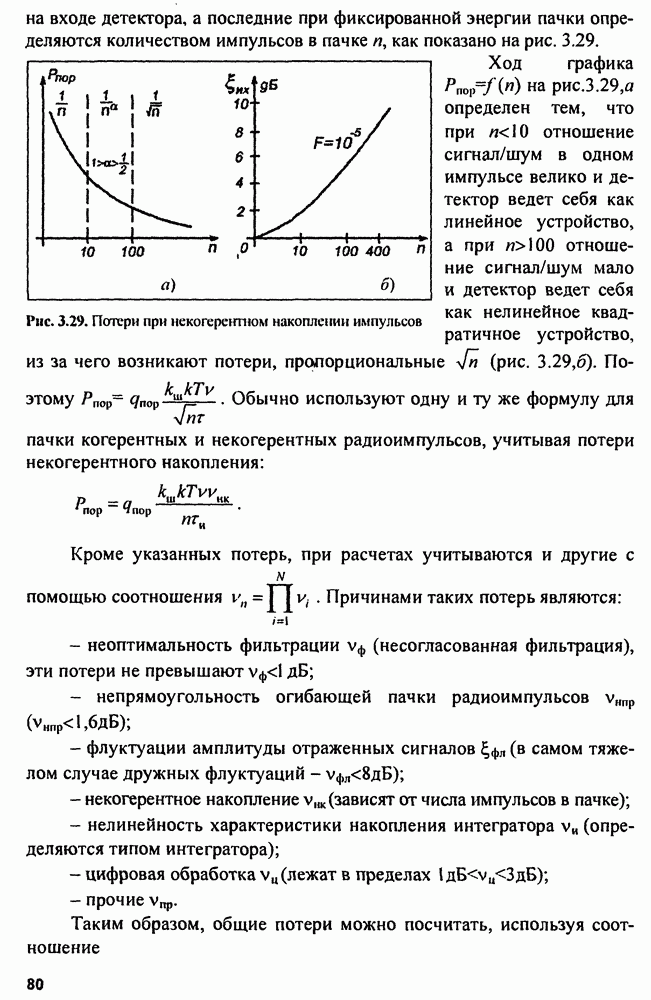
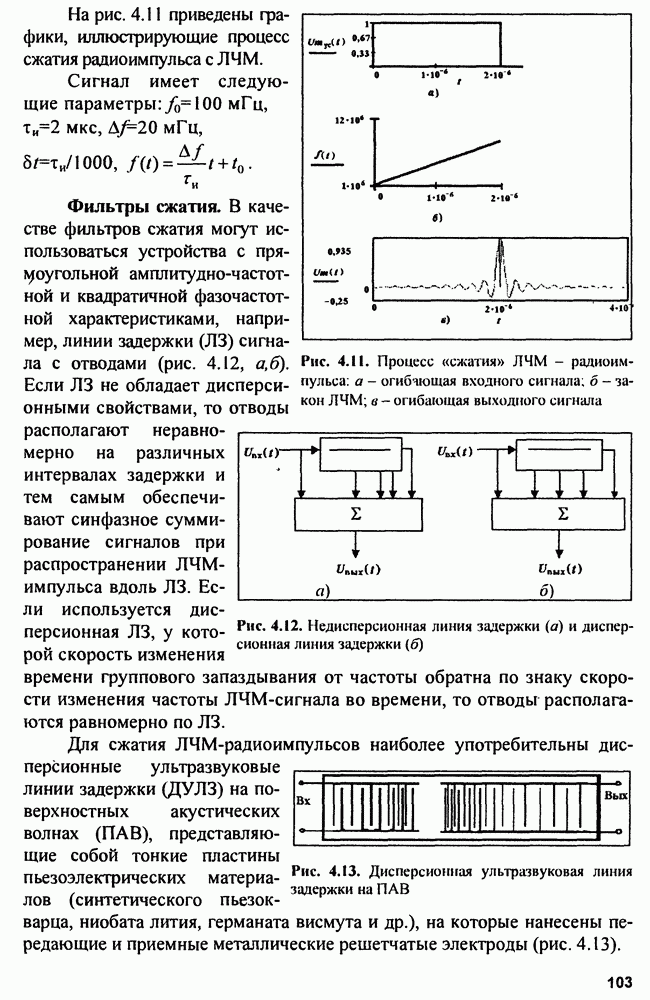
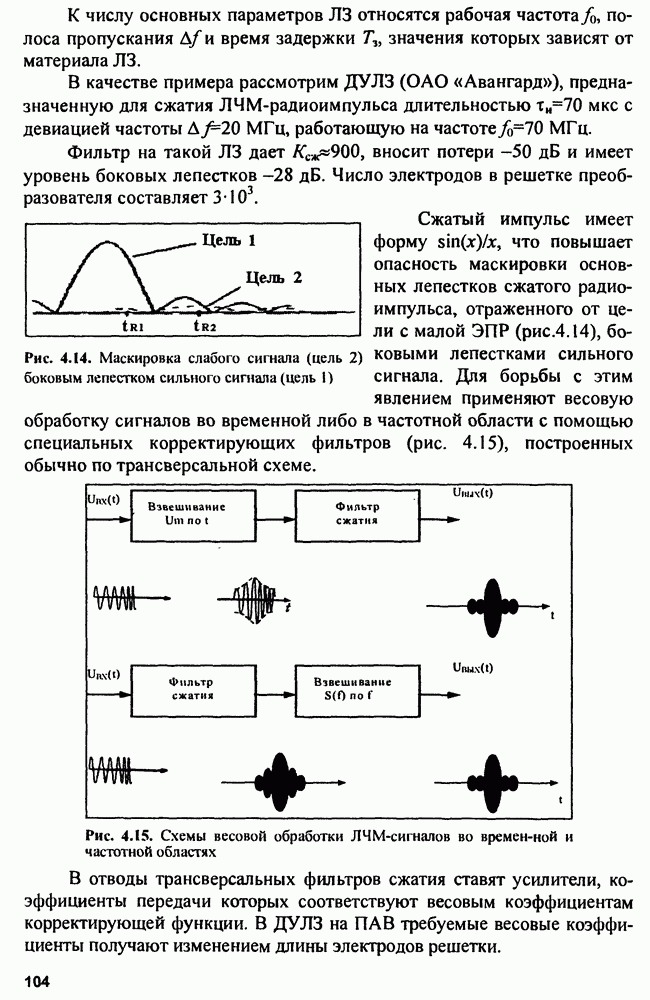
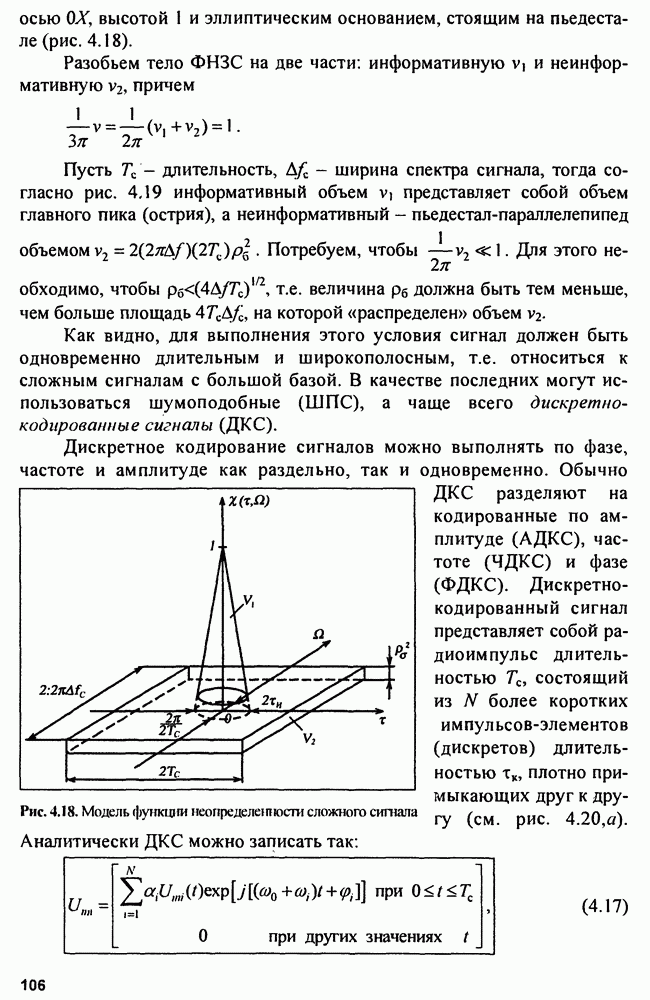
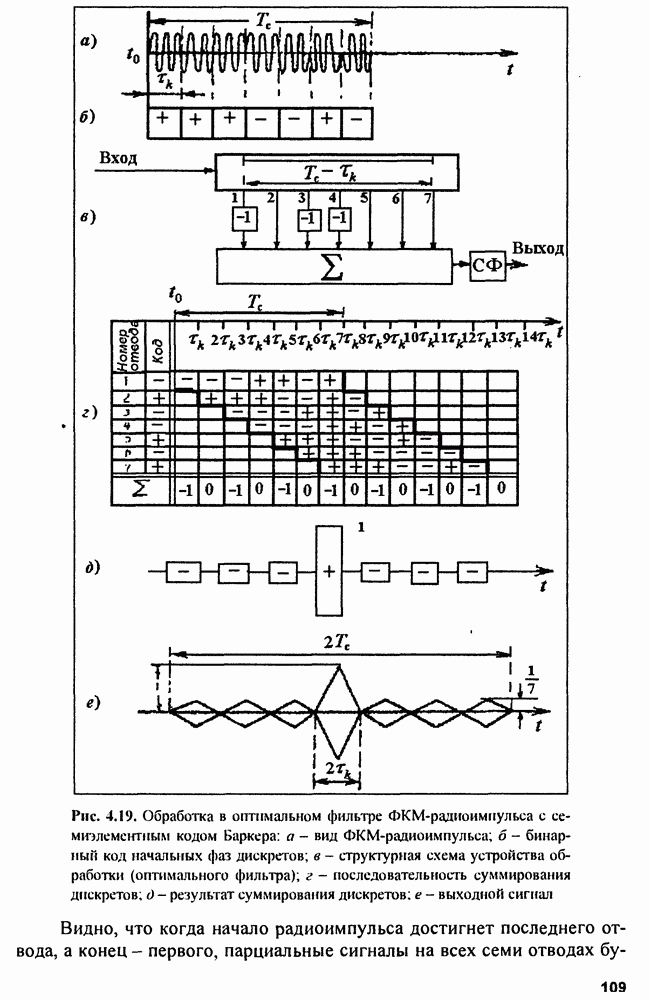
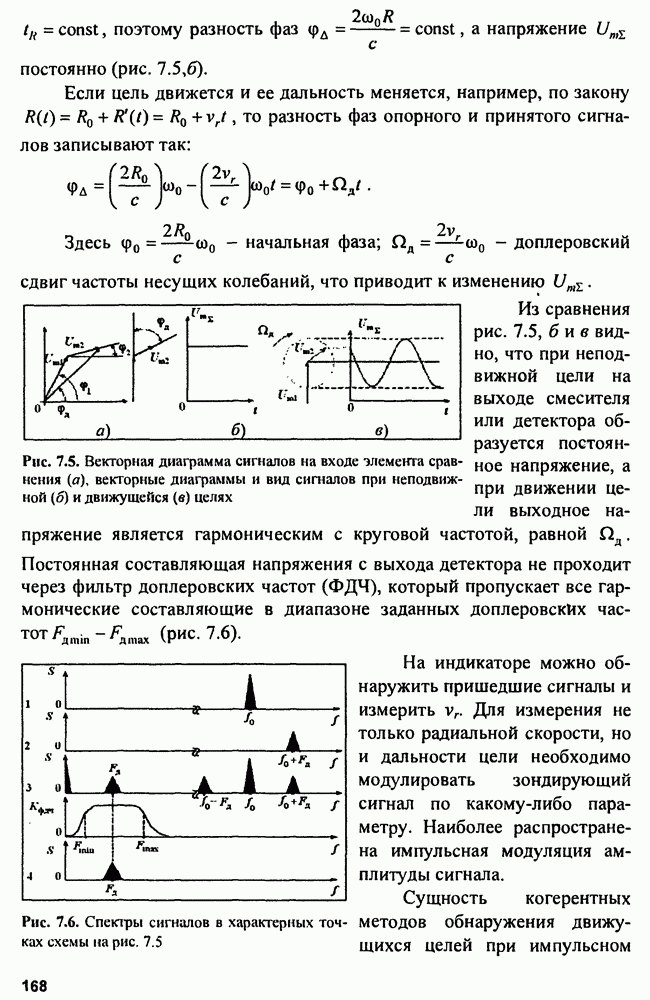
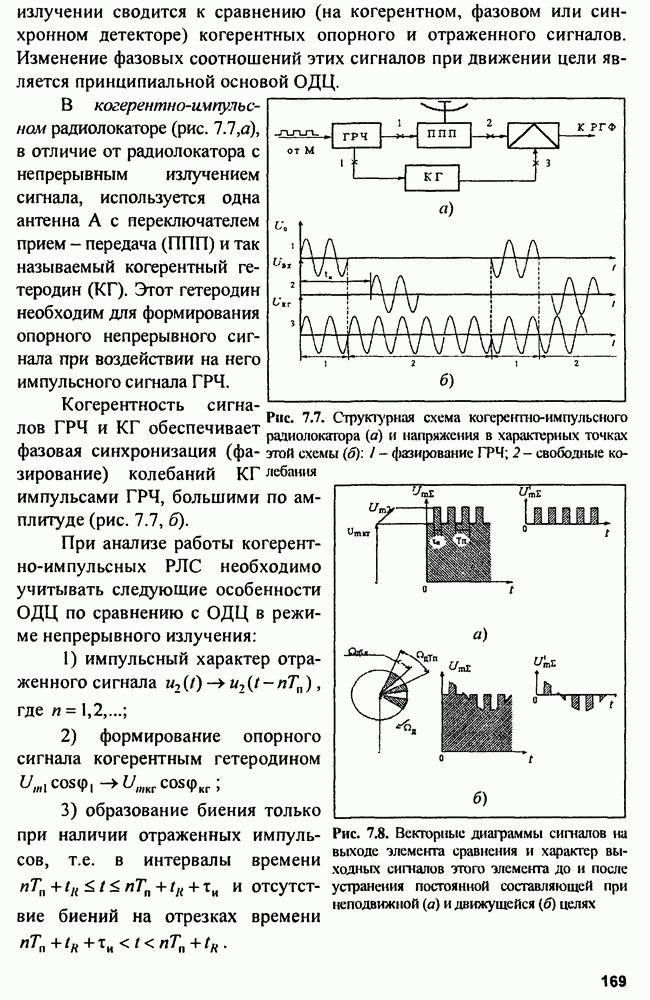
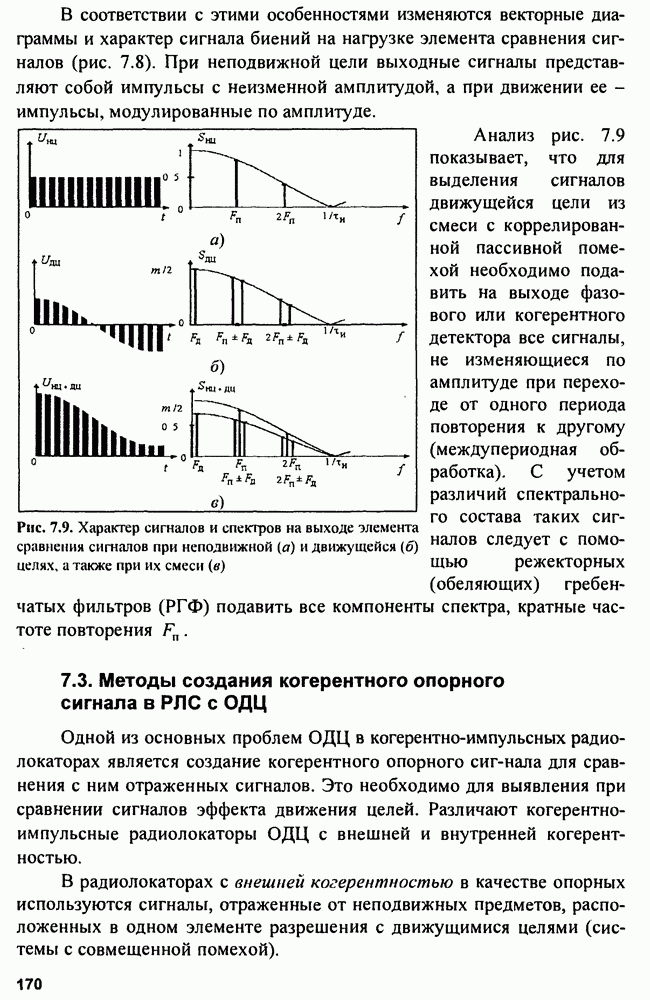
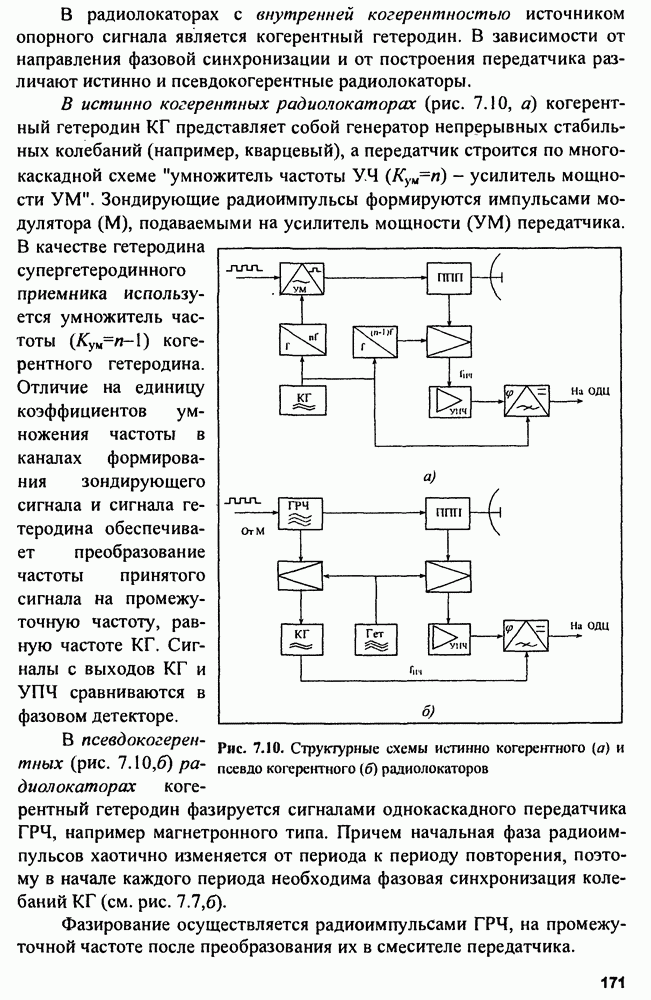
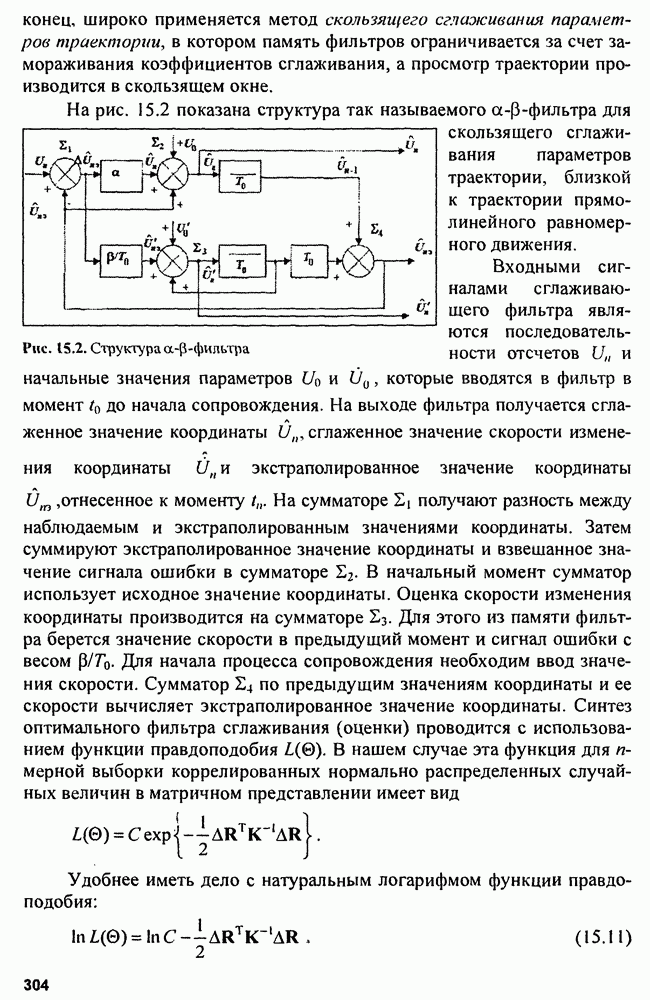
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
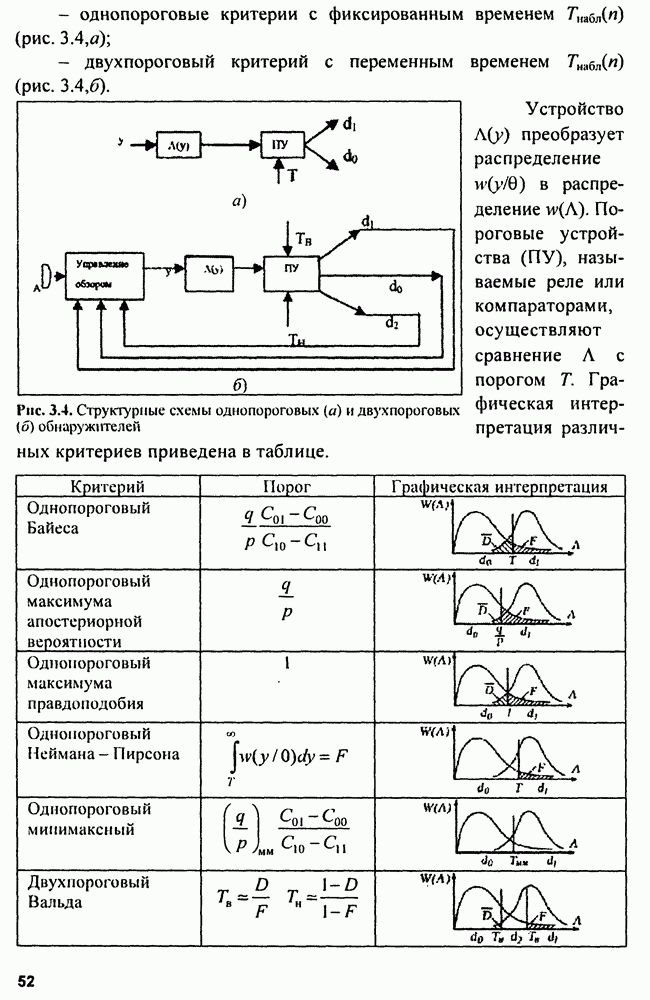
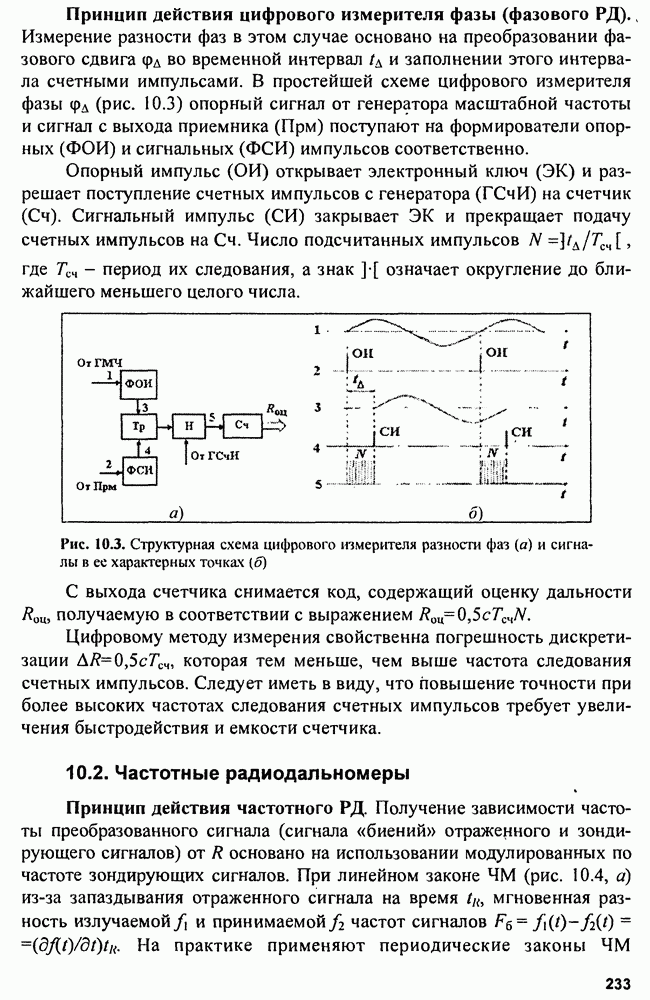
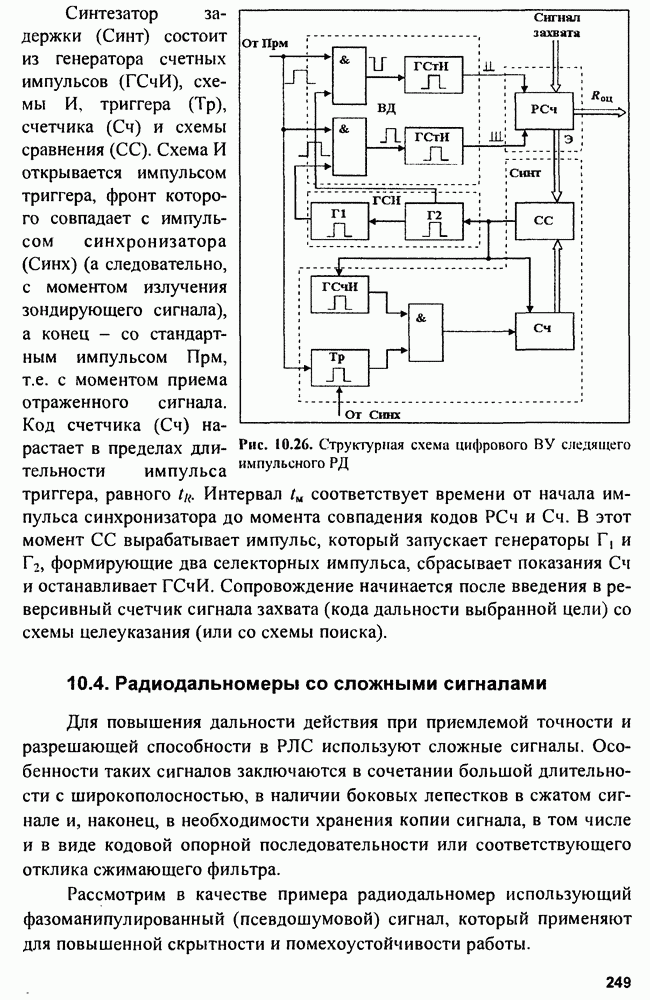
9.5. Структура измерителей
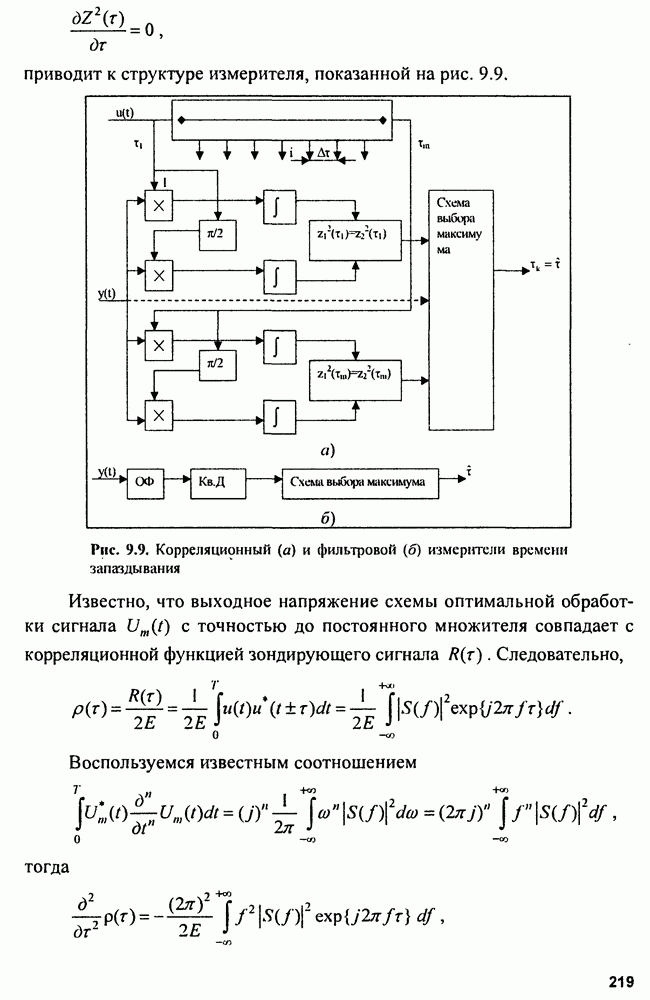
В соответствии с (9.3), (9.4) и (9.6) структуры оптимальных неследящих измерителей параметров сигнала включают устройства формирования функции  функции
функции  или формирователя функции
или формирователя функции  и устройства выбора (фиксации) максимума.
и устройства выбора (фиксации) максимума.
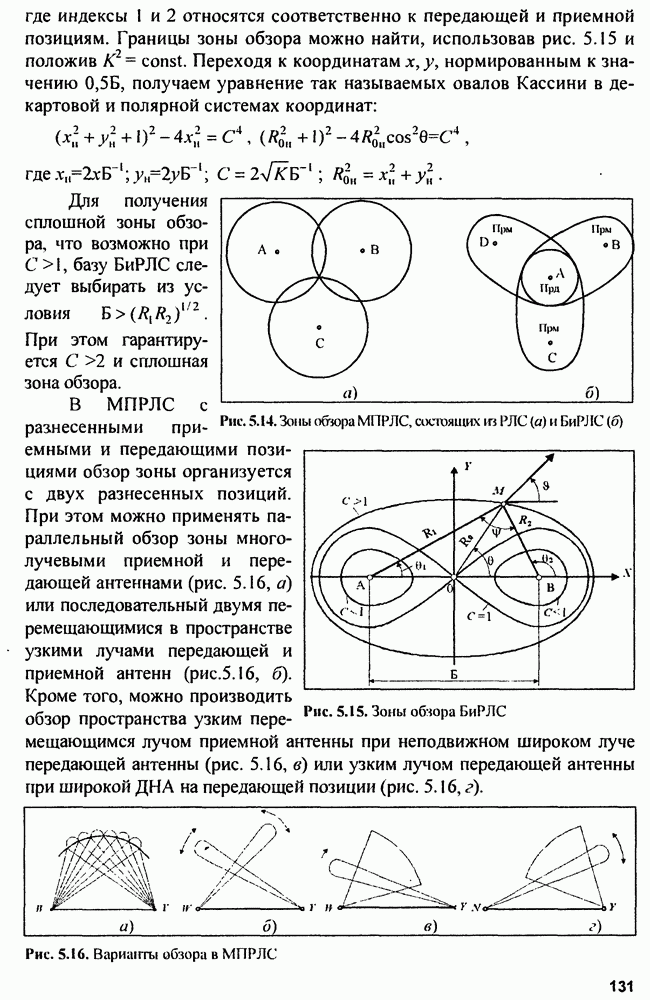
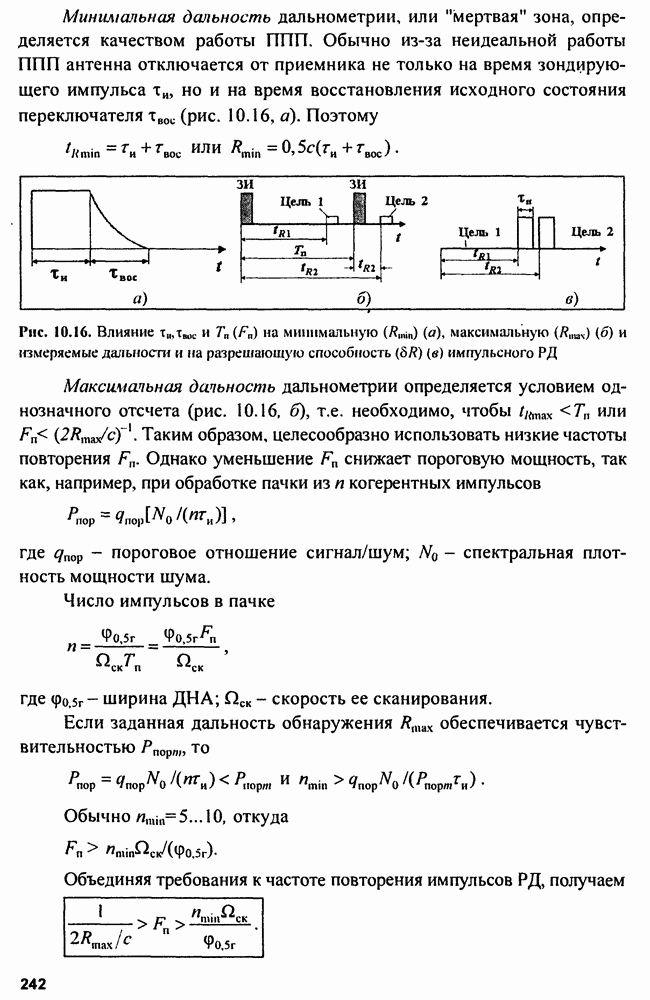
Обычно схема неследящих измерителей реализуется в виде многоканального устройства (рис. 9.1). Для этого диапазон измерения  разбиваем на поддиапазоны
разбиваем на поддиапазоны  где
где  разрешающая способность по параметру
разрешающая способность по параметру 
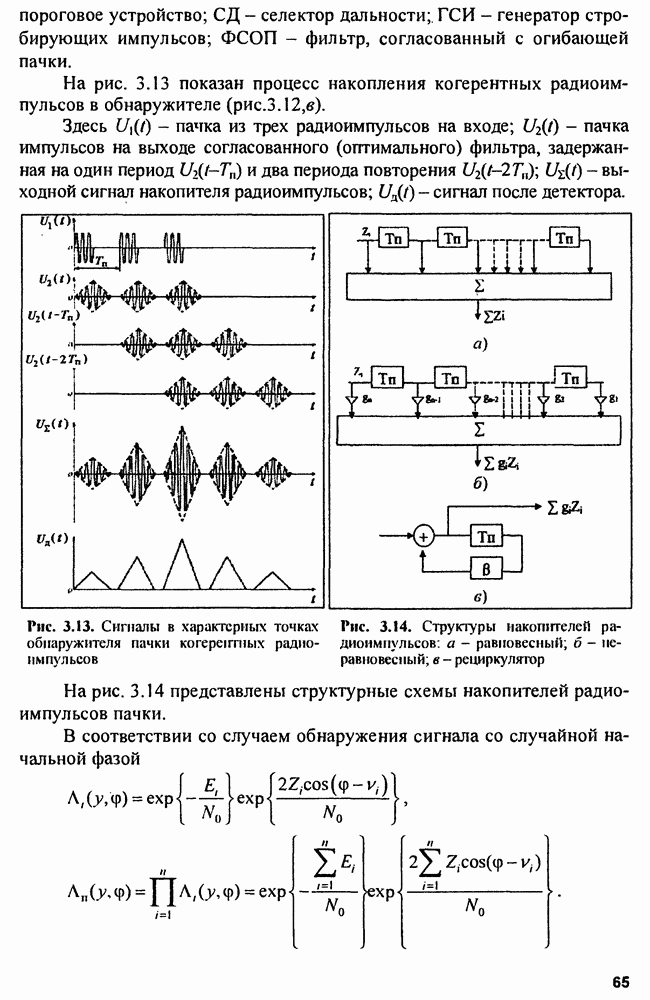
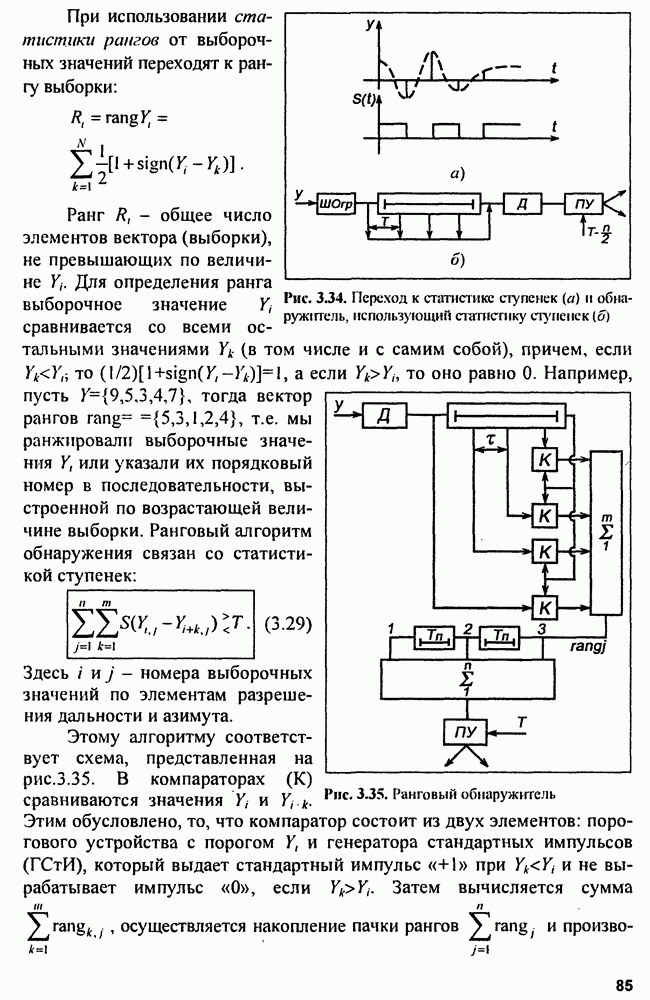
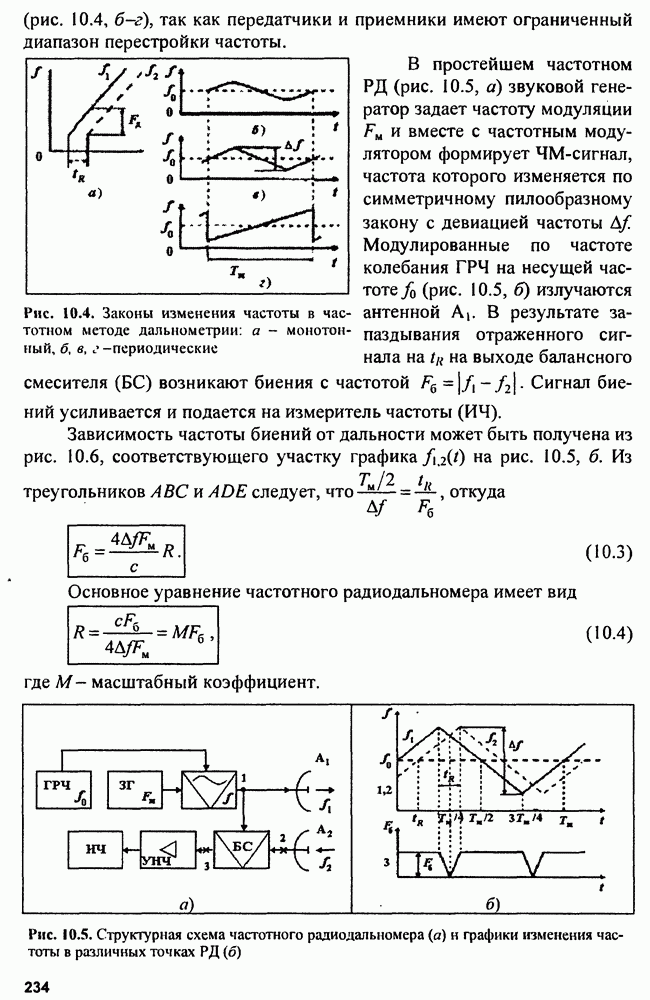
Структуру следящего оптимального измерителя можно представить в виде схемы рис. 9.2, которая содержит оптимальную схему обнаружения, формирующую отношение правдоподобия  дискриминатора и линейного инерционного фильтра, управляющего сигналом ошибки.
дискриминатора и линейного инерционного фильтра, управляющего сигналом ошибки.

Рис. 9.1. Схема оптимального измерителя
При оценке по максимуму вероятности  можно по-прежнему использовать выходной эффект оптимальной системы
можно по-прежнему использовать выходной эффект оптимальной системы  так как в предположении
так как в предположении  получаем
получаем 

Рис. 9.2. Структу  следящего измерителя с дискриминатором
следящего измерителя с дискриминатором
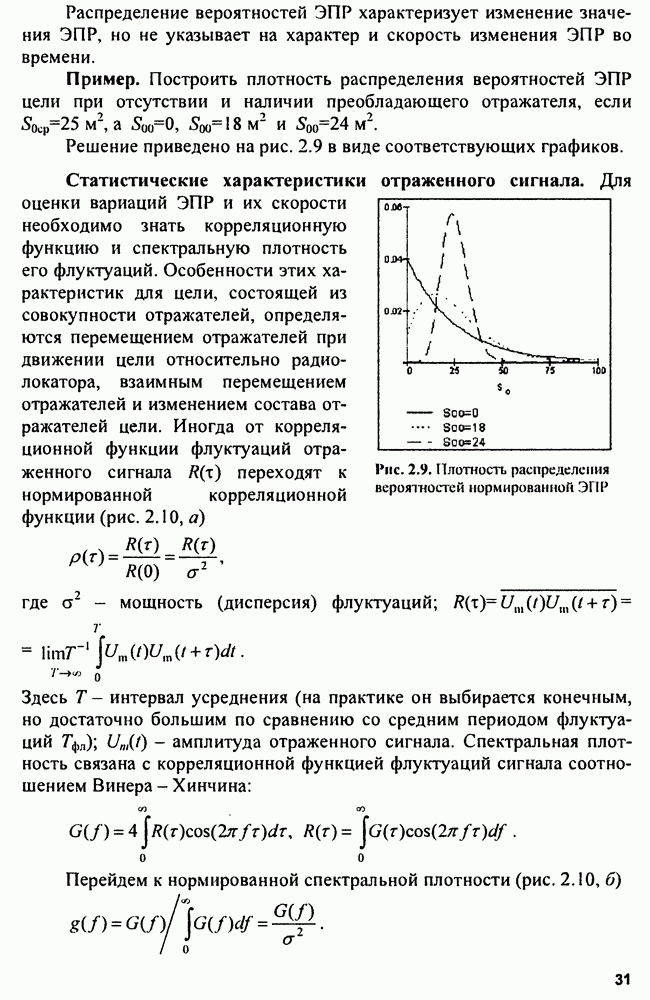
При унимодальности  и его симметричности оценка получается несмещенной, а это обеспечивается лишь при больших отношениях сигнал/шум:
и его симметричности оценка получается несмещенной, а это обеспечивается лишь при больших отношениях сигнал/шум: 
Входное напряжение измерителя является сложной нелинейной функцией оцениваемого параметра  поэтому оптимальный измеритель относится к нелинейным фильтрам. Обычно для упрощения анализа линеаризуют задачу, считая
поэтому оптимальный измеритель относится к нелинейным фильтрам. Обычно для упрощения анализа линеаризуют задачу, считая  обеспечивается при высокоточных намерениях). В случае гауссовых шумов параметры
обеспечивается при высокоточных намерениях). В случае гауссовых шумов параметры  сами становятся гауссовыми процессами со средним значением, равным измеряемому параметру
сами становятся гауссовыми процессами со средним значением, равным измеряемому параметру  Линеаризация состоит в формировании линейной функции малых отклонений измеряемого параметра
Линеаризация состоит в формировании линейной функции малых отклонений измеряемого параметра  опорное значение параметра, близкое к истинному). Устройство, формирующее
опорное значение параметра, близкое к истинному). Устройство, формирующее  называется дискриминатором
называется дискриминатором  (рис. 9.2).
(рис. 9.2).
Линейный фильтр  выдает оценку
выдает оценку  равную математическому ожиданию
равную математическому ожиданию  . Если задано или выбрано опорное значение параметра, близкое к истинному, то разлагая в ряд в окрестности этой точки
. Если задано или выбрано опорное значение параметра, близкое к истинному, то разлагая в ряд в окрестности этой точки  и ограничивая этот ряд тремя первыми членами, получаем
и ограничивая этот ряд тремя первыми членами, получаем

Подставляя это соотношение в уравнение для поиска максимума

находим

Отсюда  определяется по формуле
определяется по формуле

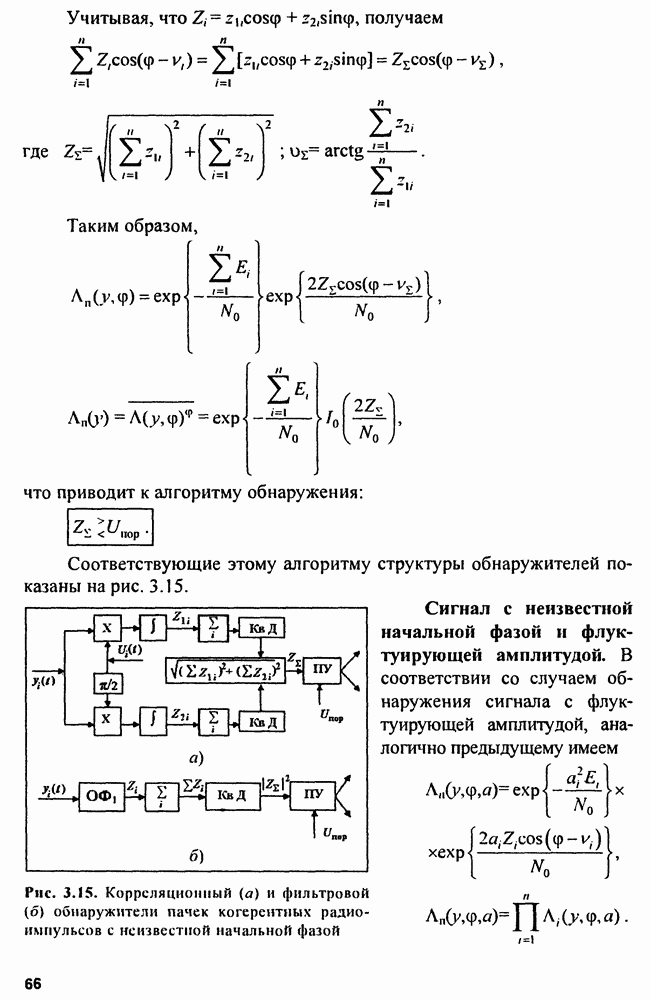
Определим дискриминационную характеристику:

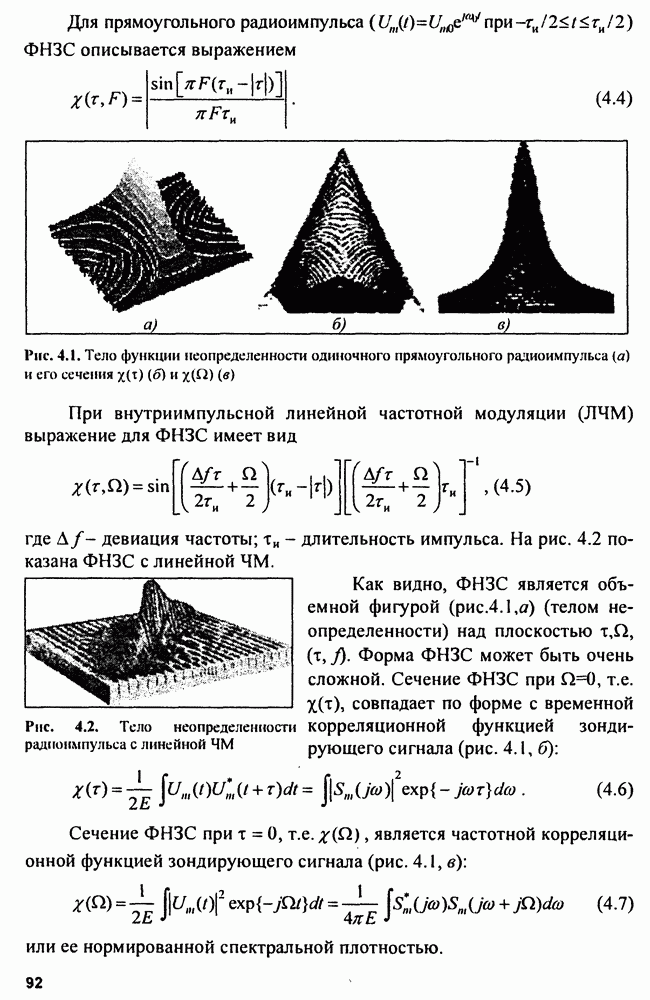
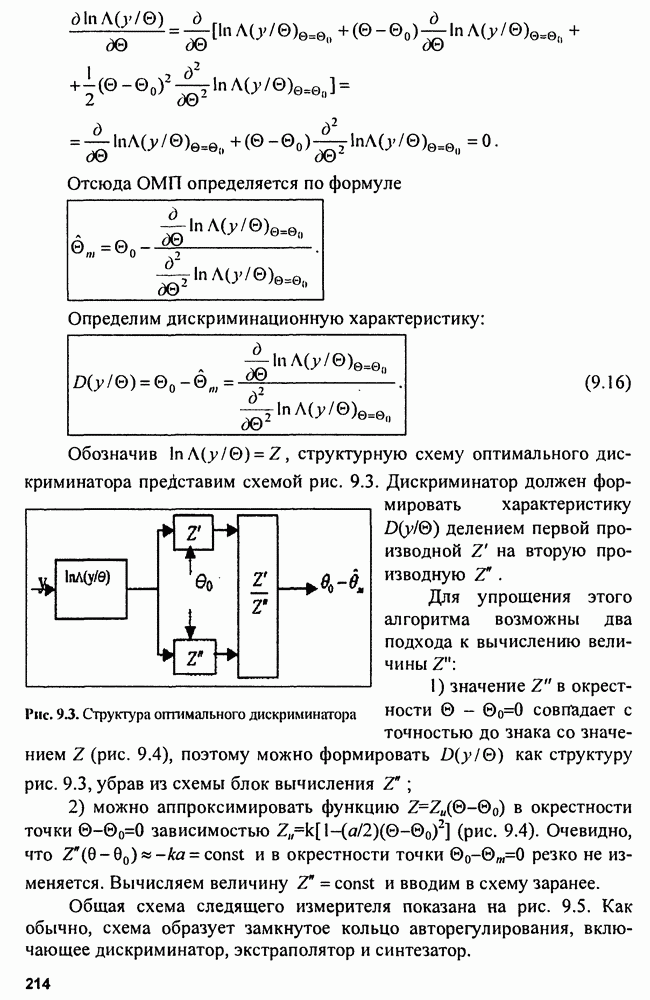
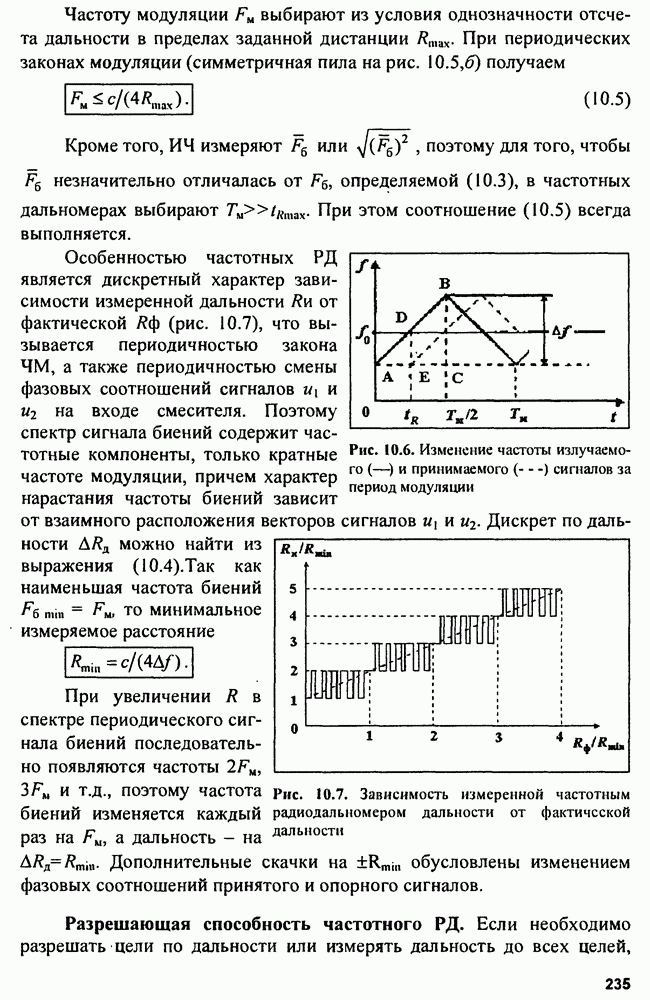
Обозначив  структурную схему оптимального дискриминатора представим схемой рис. 9.3. Дискриминатор должен формировать характеристику
структурную схему оптимального дискриминатора представим схемой рис. 9.3. Дискриминатор должен формировать характеристику  делением первой производной
делением первой производной  на вторую производную
на вторую производную 

Рис. 9.3. Структура оптимального дискриминатора
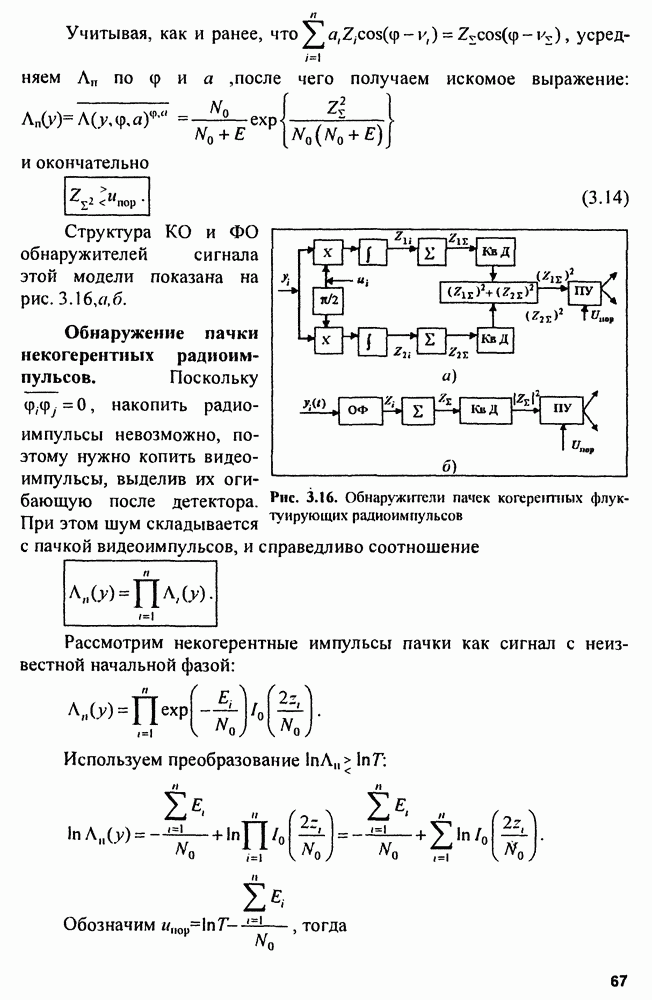
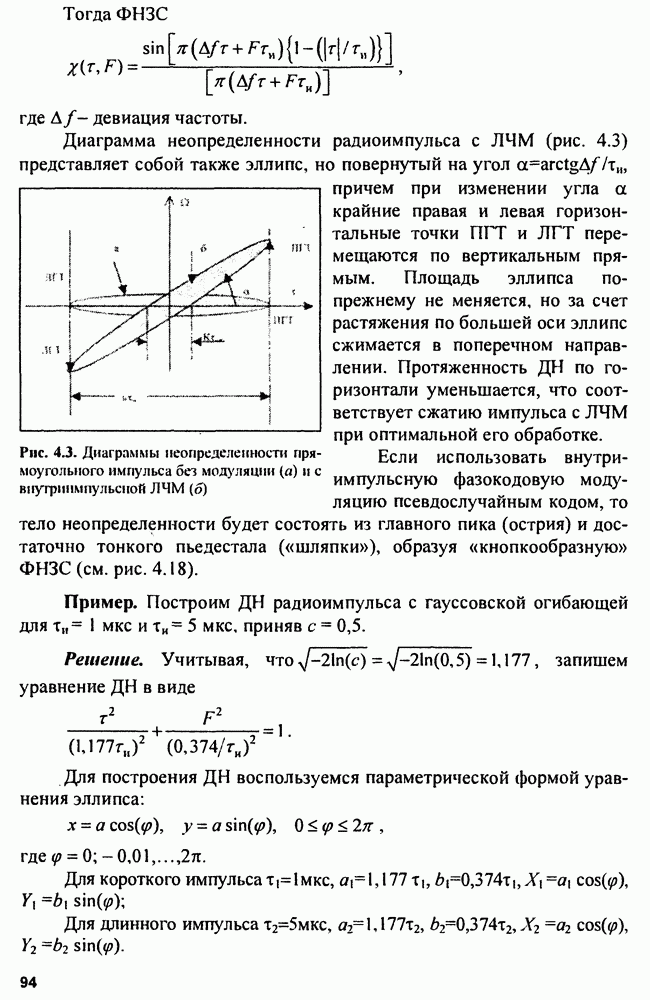
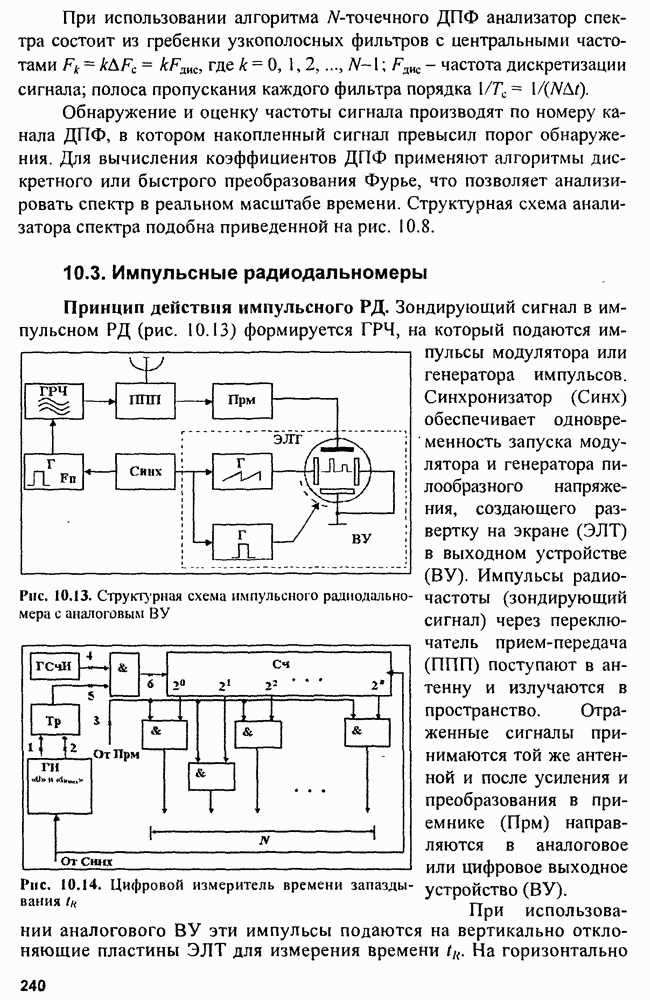
Для упрощения этого алгоритма возможны два подхода к вычислению величины 
1) значение  в окрестности
в окрестности  совпадает с точностью до знака со значением
совпадает с точностью до знака со значением  (рис. 9.4), поэтому можно формировать
(рис. 9.4), поэтому можно формировать  как структуру рис. 9.3, убрав из схемы блок вычисления
как структуру рис. 9.3, убрав из схемы блок вычисления 
2) можно аппроксимировать функцию  в окрестности точки
в окрестности точки  зависимостью
зависимостью  (рис. 9.4). Очевидно, что
(рис. 9.4). Очевидно, что  и в окрестности точки
и в окрестности точки  резко не изменяется. Вычисляем величину
резко не изменяется. Вычисляем величину  и вводим в схему заранее.
и вводим в схему заранее.
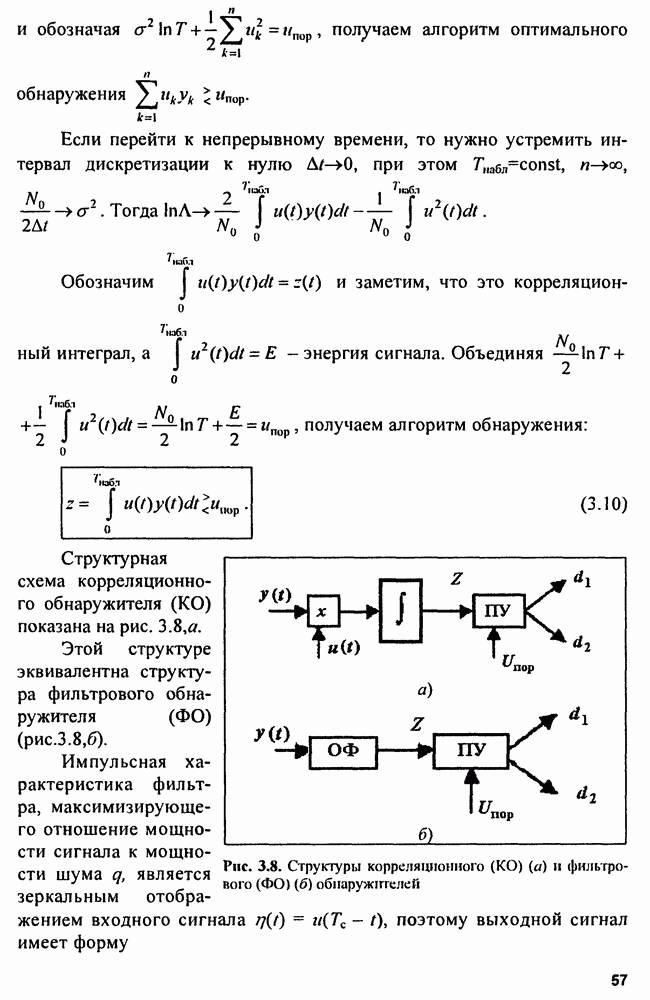
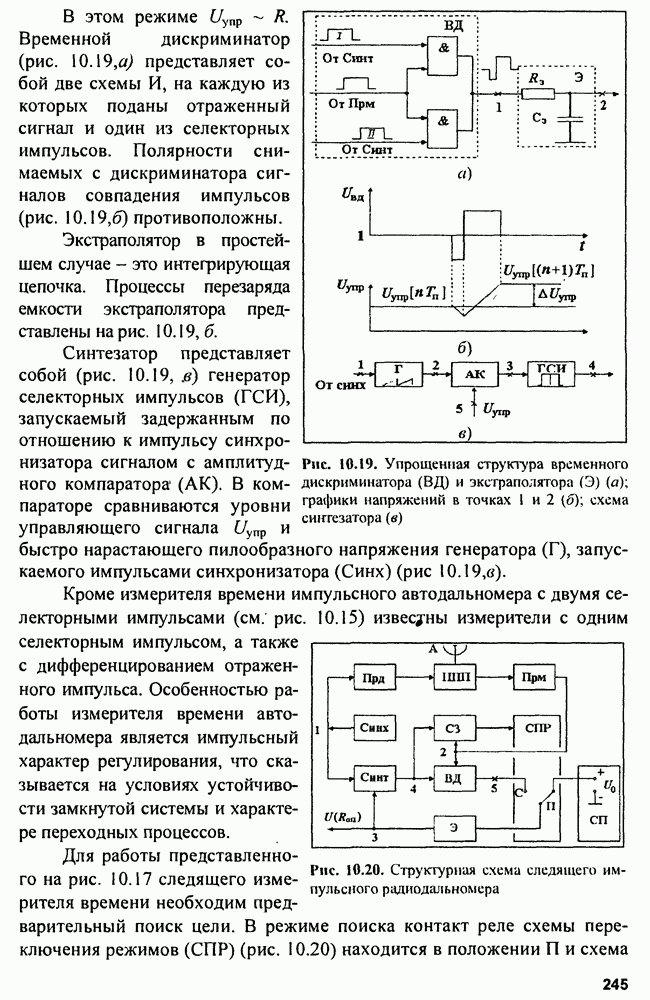
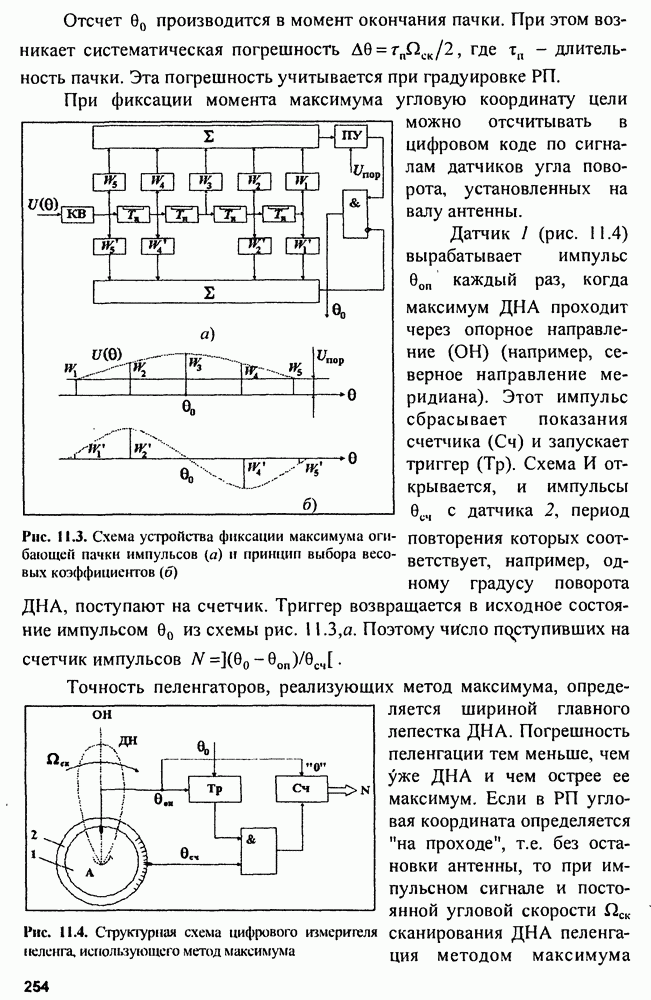
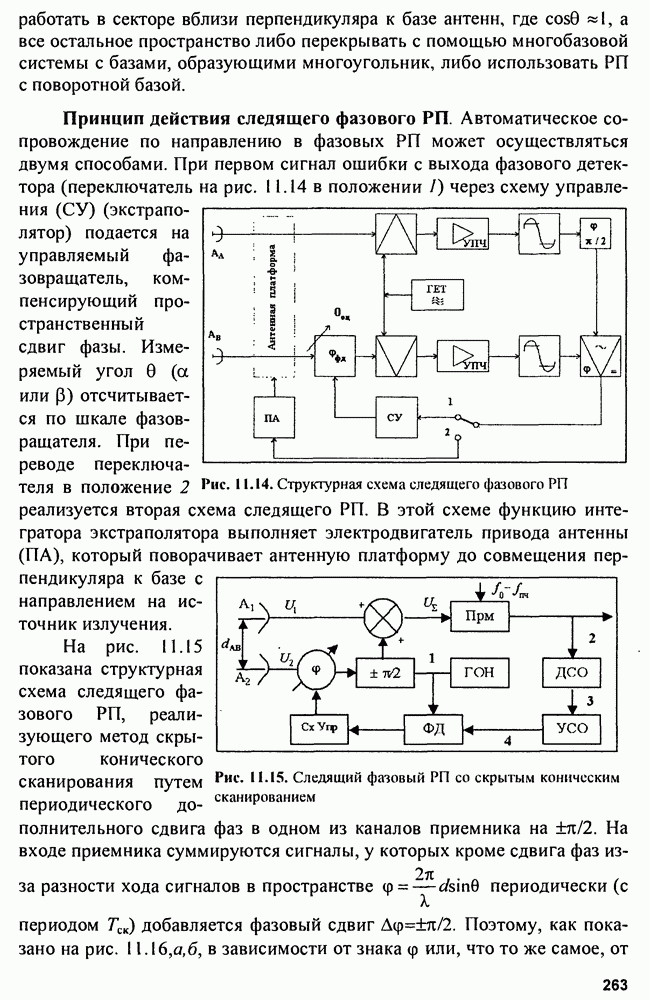
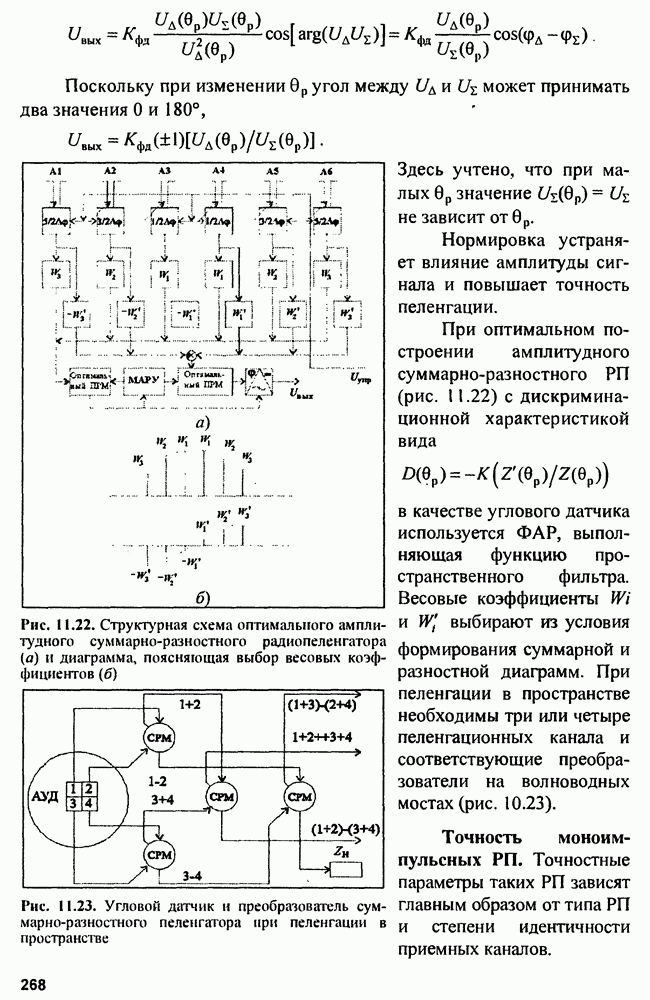
Общая схема следящего измерителя показана на рис. 9.5. Как обычно, схема образует замкнутое кольцо авторегулирования, включающее дискриминатор, экстраполятор и синтезатор.

Рис. 9.4. Поведение функций  в окрестности точки
в окрестности точки 

Рис. 9.5. Обобщенная схема кольца регулирования следящего измерителя
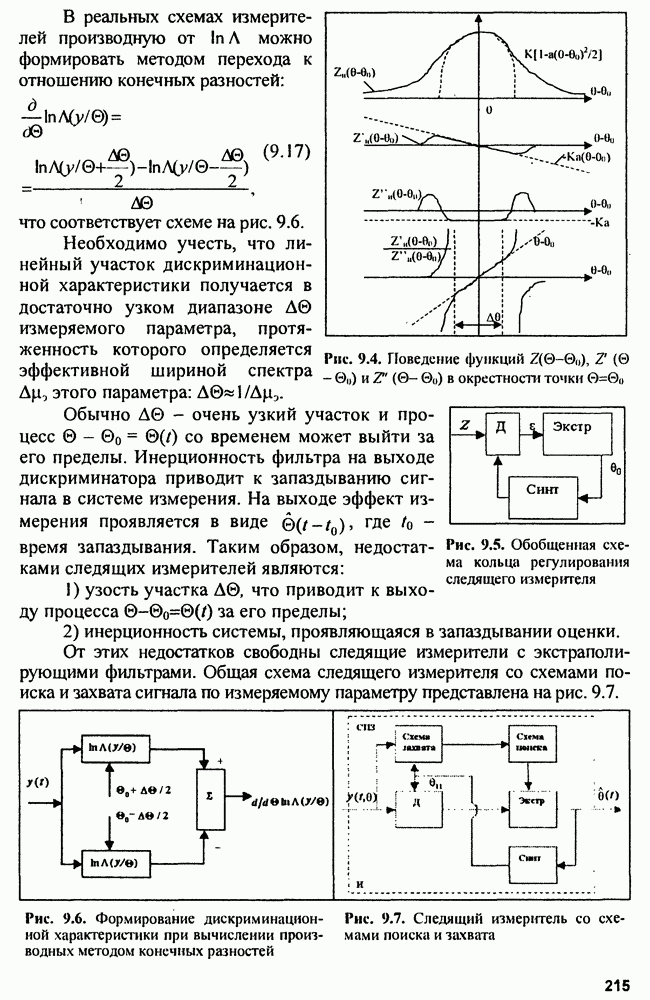
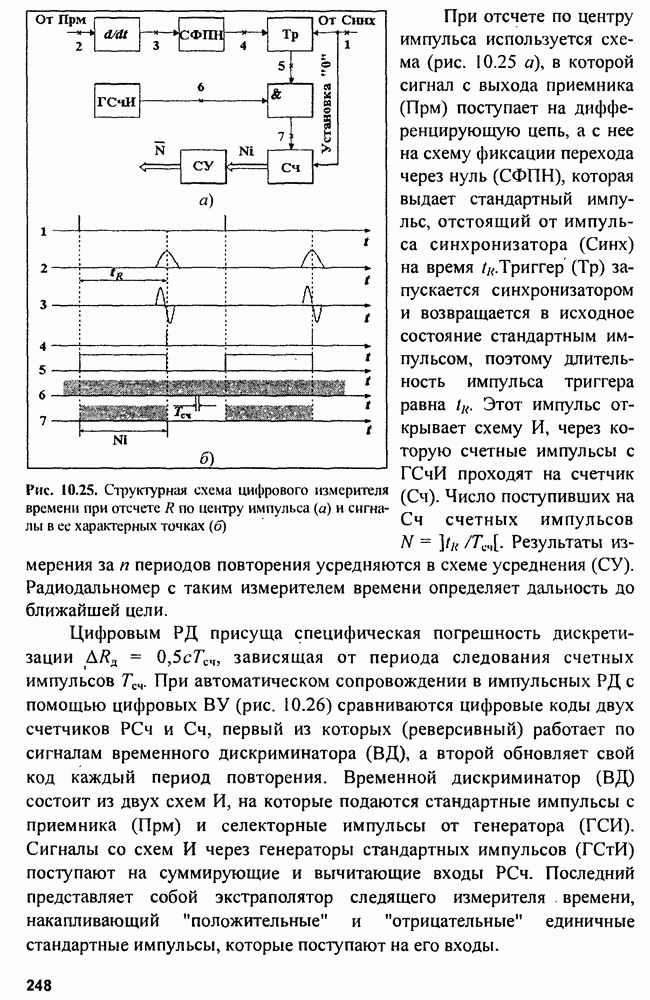
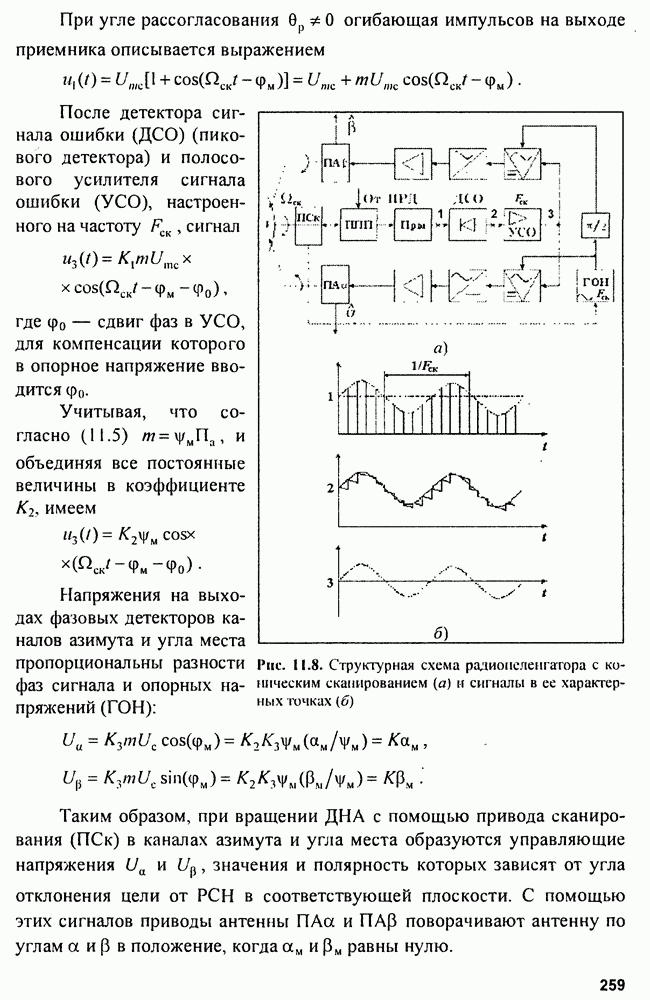
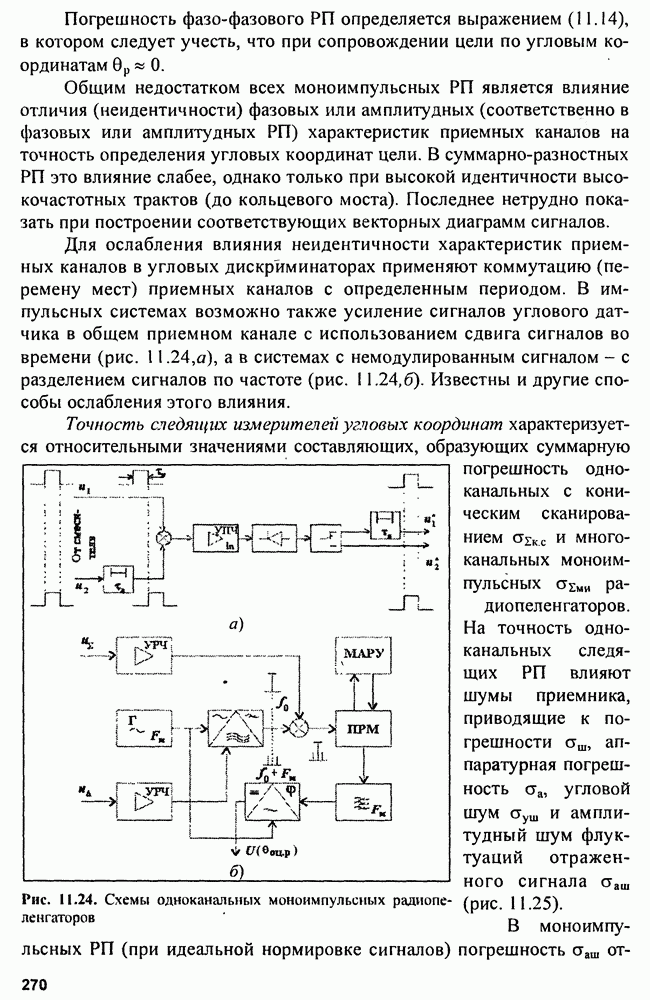
В реальных схемах измерителей производную от  можно формировать методом перехода к отношению конечных разностей:
можно формировать методом перехода к отношению конечных разностей:

что соответствует схеме на рис. 9.6.
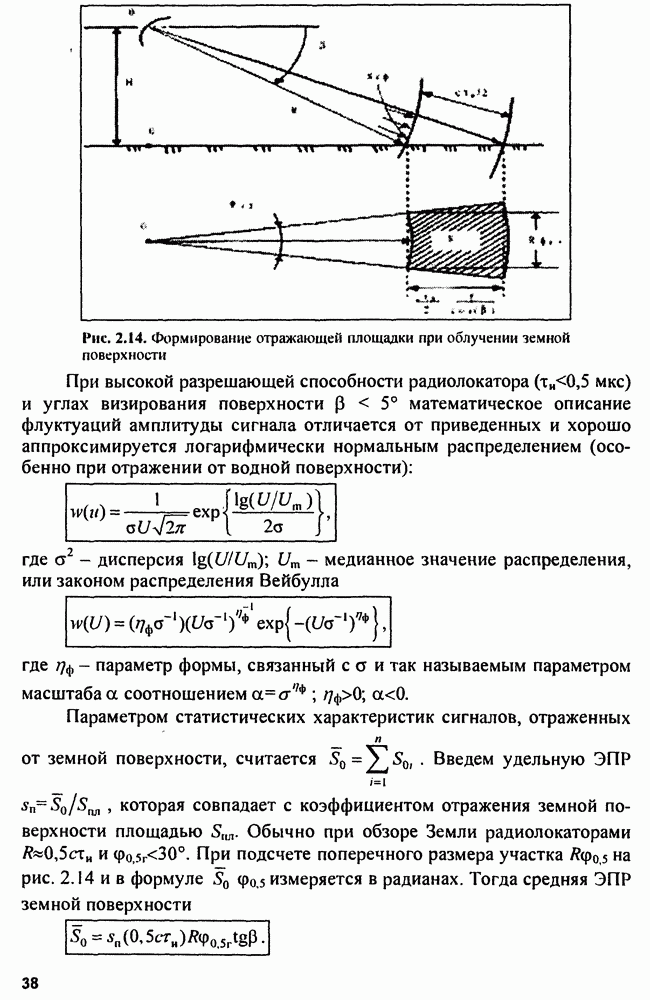
Необходимо учесть, что линейный участок дискриминационной характеристики получается в достаточно узком диапазоне  измеряемого параметра, протяженность которого определяется эффективной шириной спектра
измеряемого параметра, протяженность которого определяется эффективной шириной спектра  этого параметра:
этого параметра: 
Обычно  очень узкий участок и процесс
очень узкий участок и процесс  со временем может выйти за его пределы. Инерционность фильтра на выходе дискриминатора приводит к запаздыванию сигнала в системе измерения. На выходе эффект измерения проявляется в виде где
со временем может выйти за его пределы. Инерционность фильтра на выходе дискриминатора приводит к запаздыванию сигнала в системе измерения. На выходе эффект измерения проявляется в виде где  - время запаздывания. Таким образом, недостатками следящих измерителей являются:
- время запаздывания. Таким образом, недостатками следящих измерителей являются:
1) узость участка  что приводит к выходу процесса
что приводит к выходу процесса  за его пределы;
за его пределы;
2) инерционность системы, проявляющаяся в запаздывании оценки.
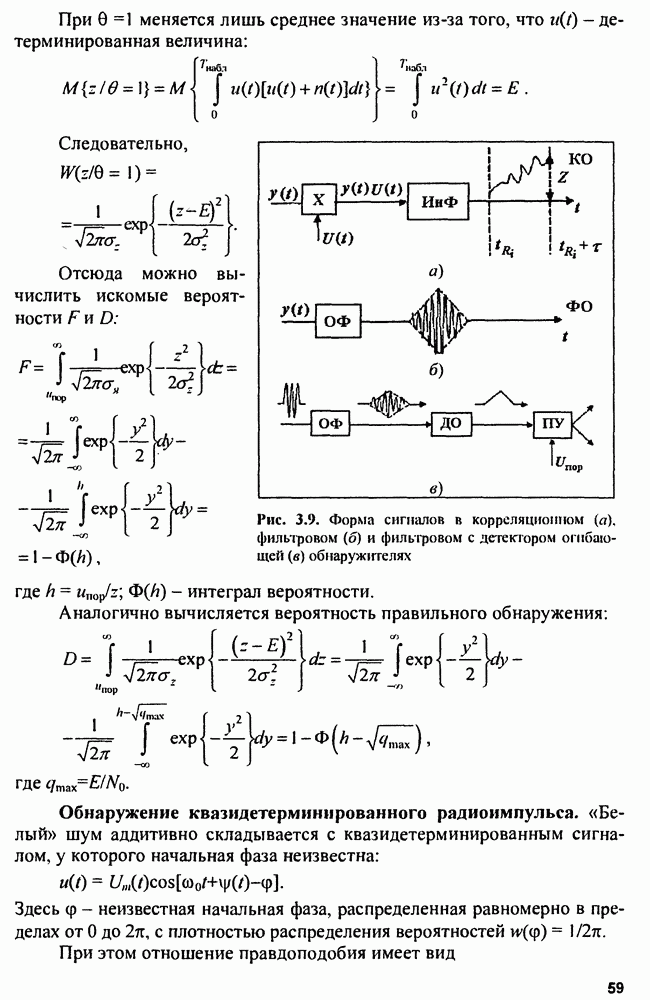
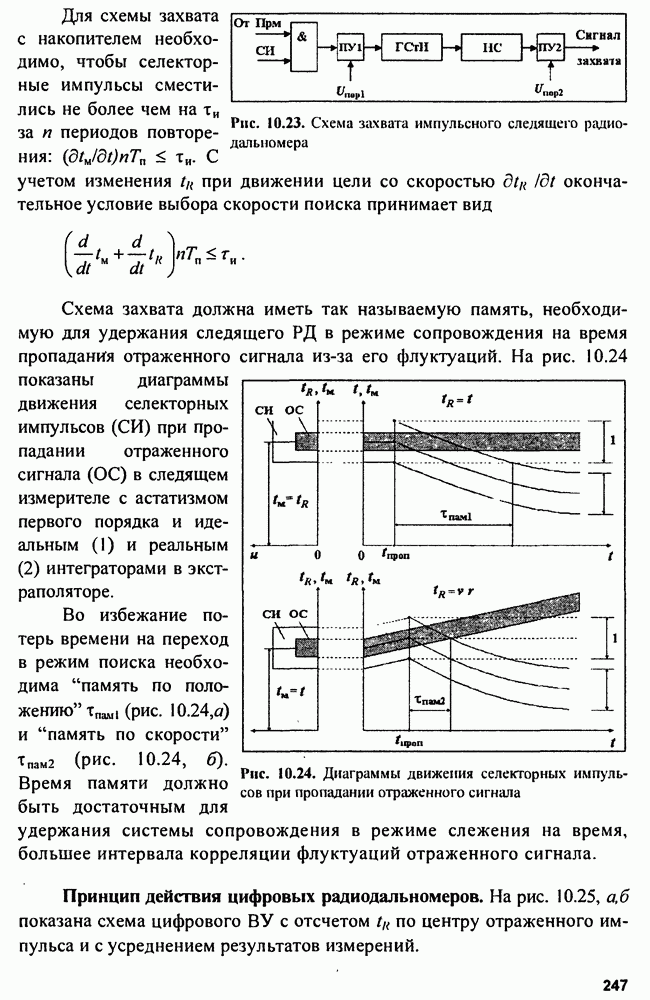
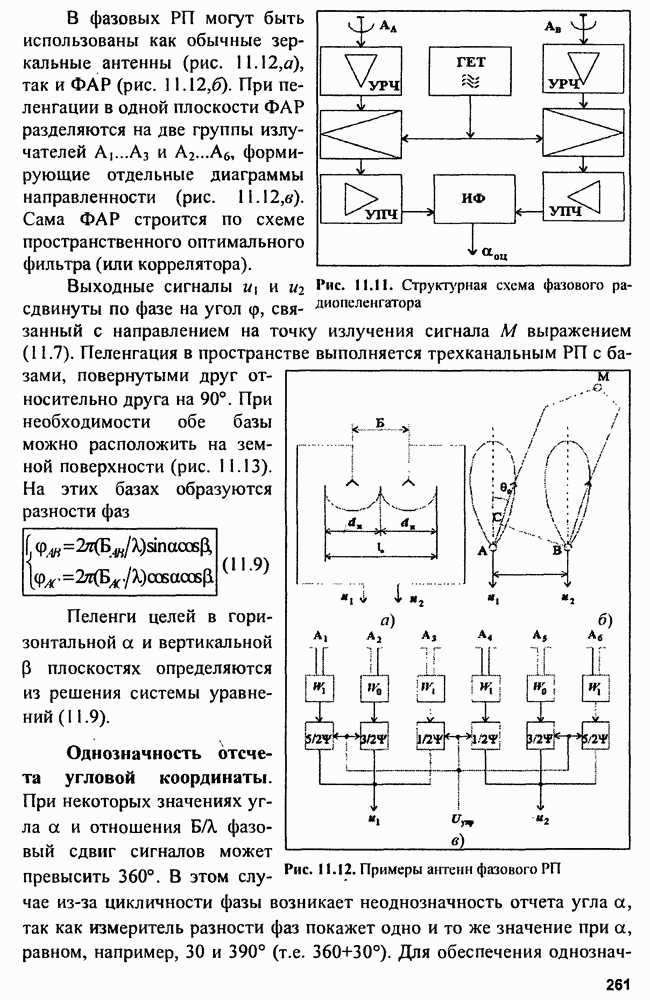
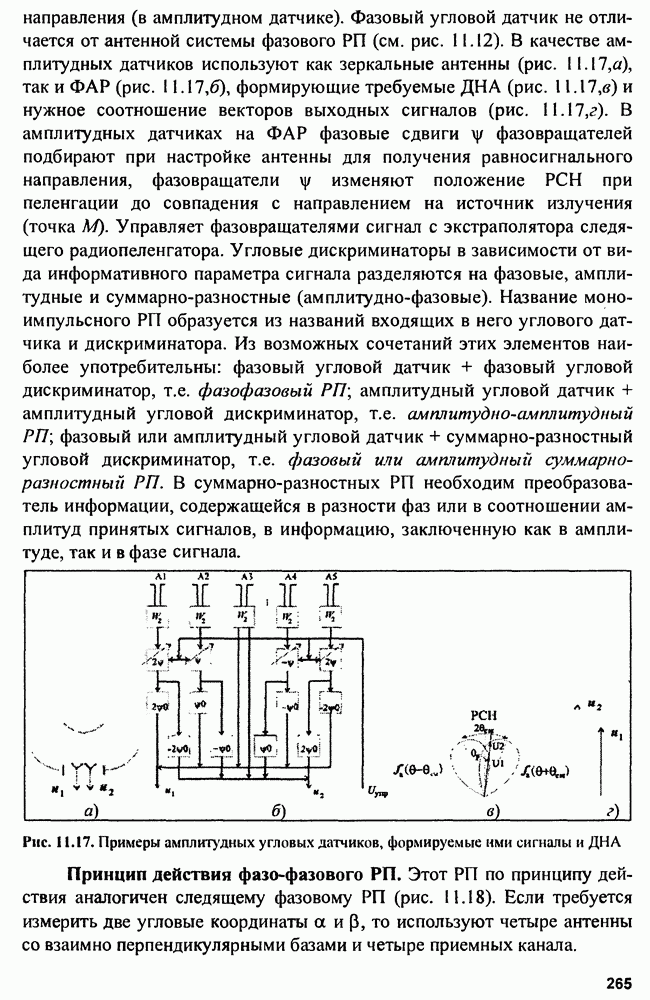
От этих недостатков свободны следящие измерители с экстраполирующими фильтрами. Общая схема следящего измерителя со схемами поиска и захвата сигнала по измеряемому параметру представлена на рис. 9.7.

Рис. 9.6. Формирование дискриминационной характеристики при вычислении производных методом конечных разностей

Рис. 9.7. Следящий измеритель со схемами поиска и захвата
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
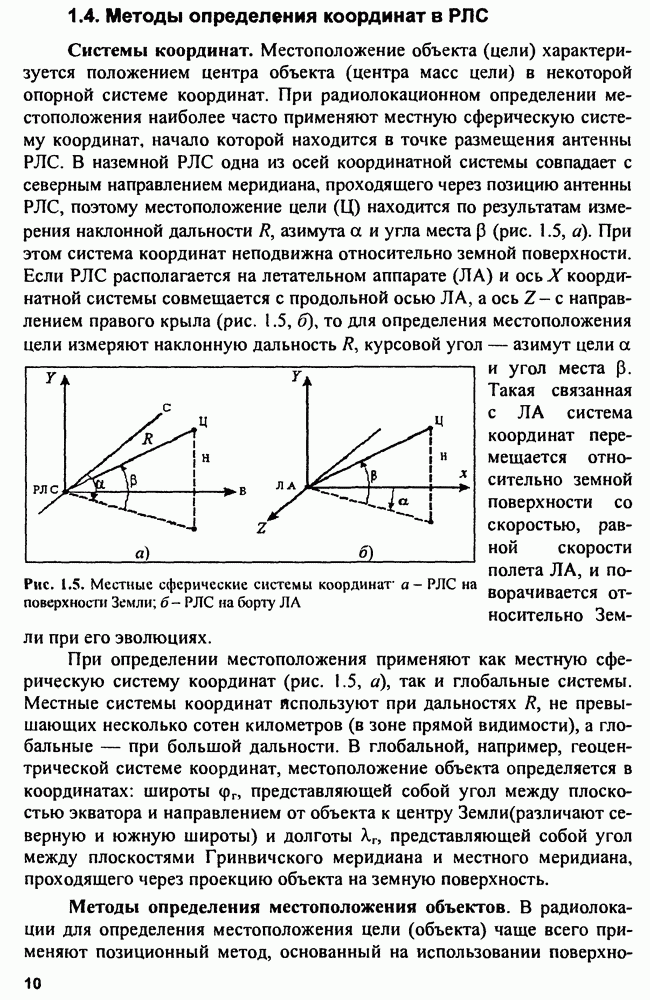
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
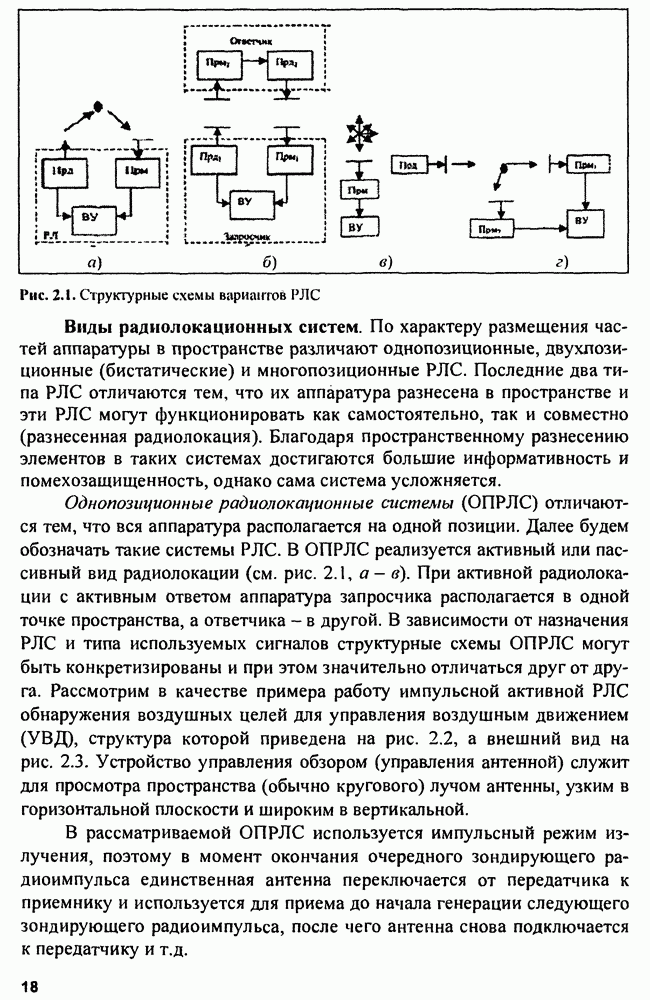
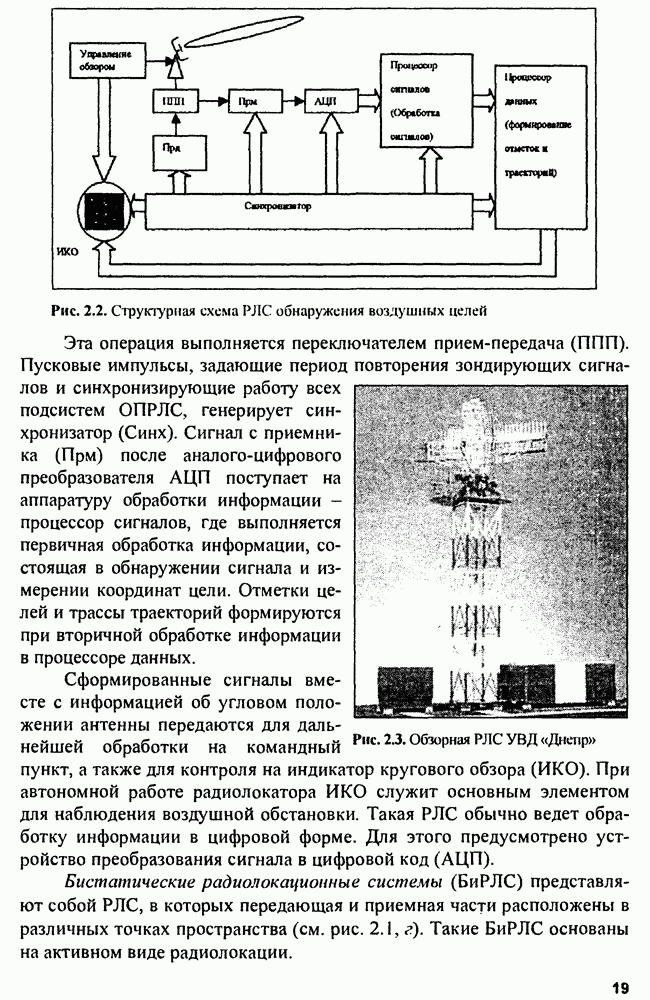
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
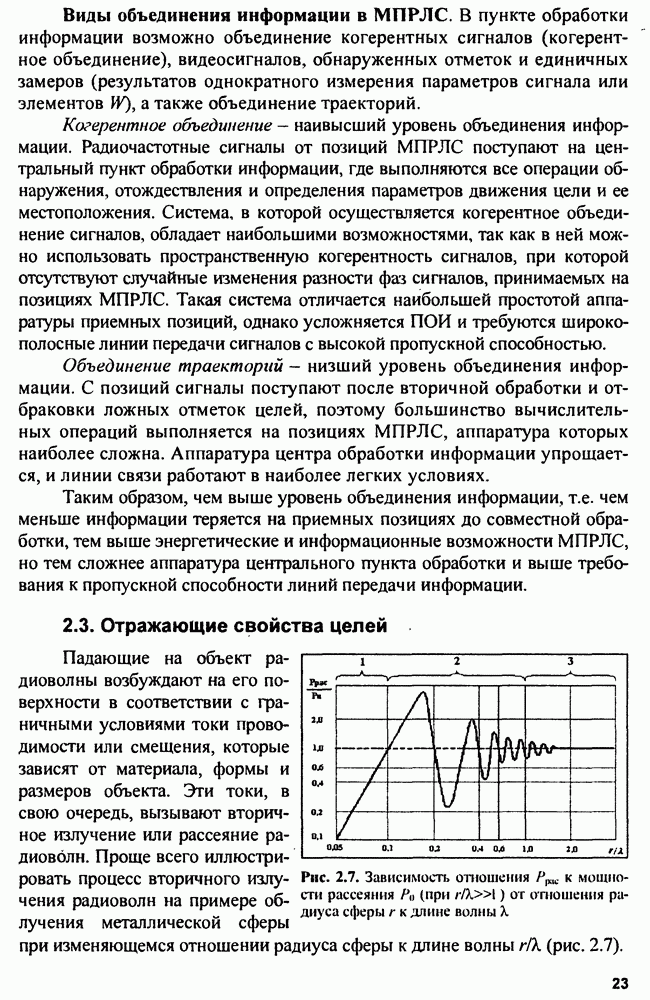
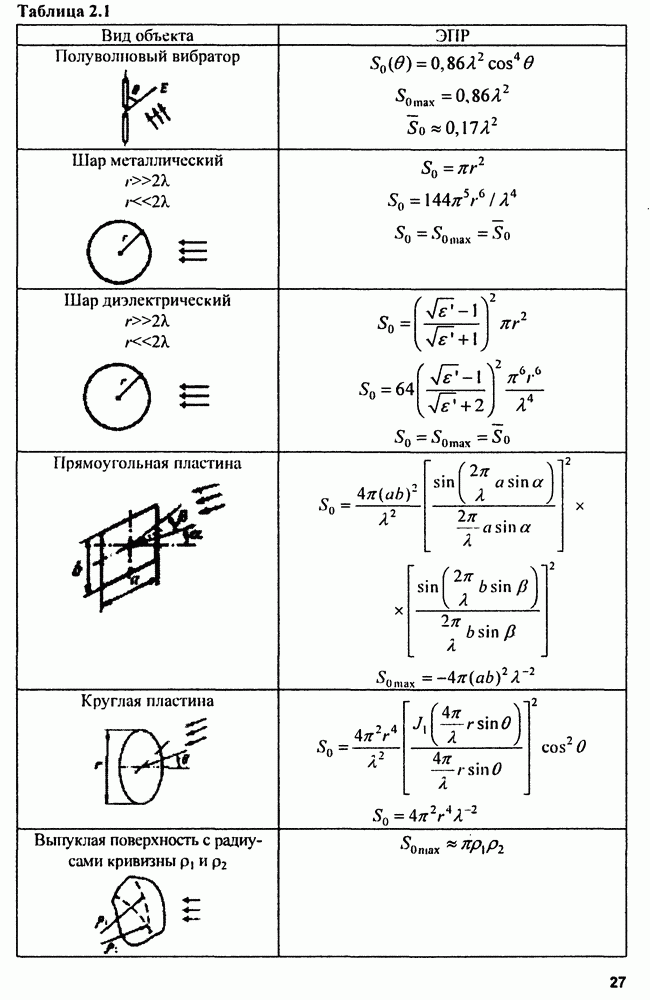
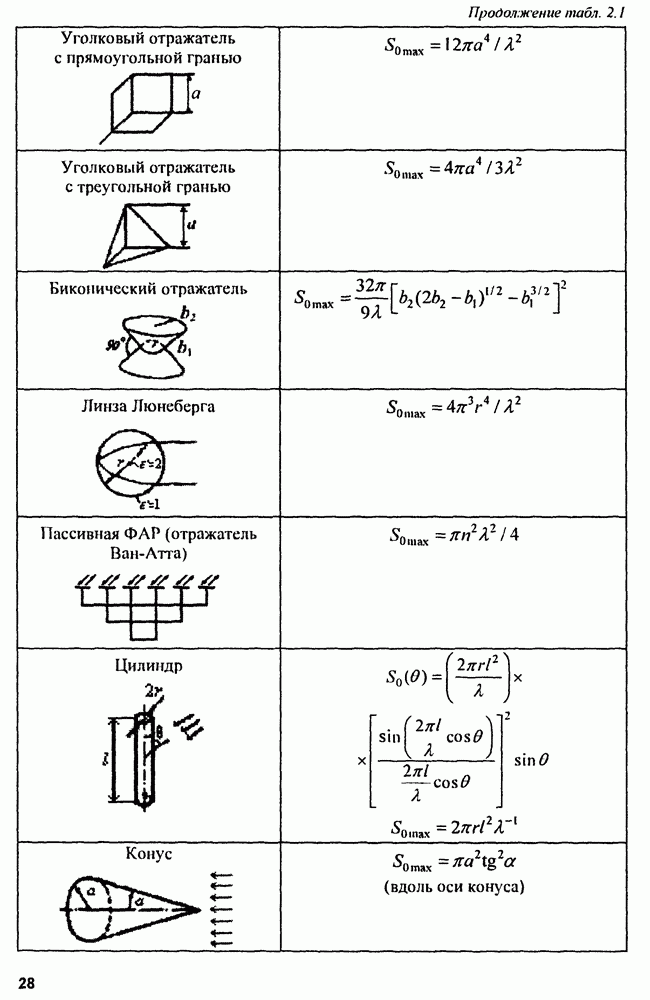
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
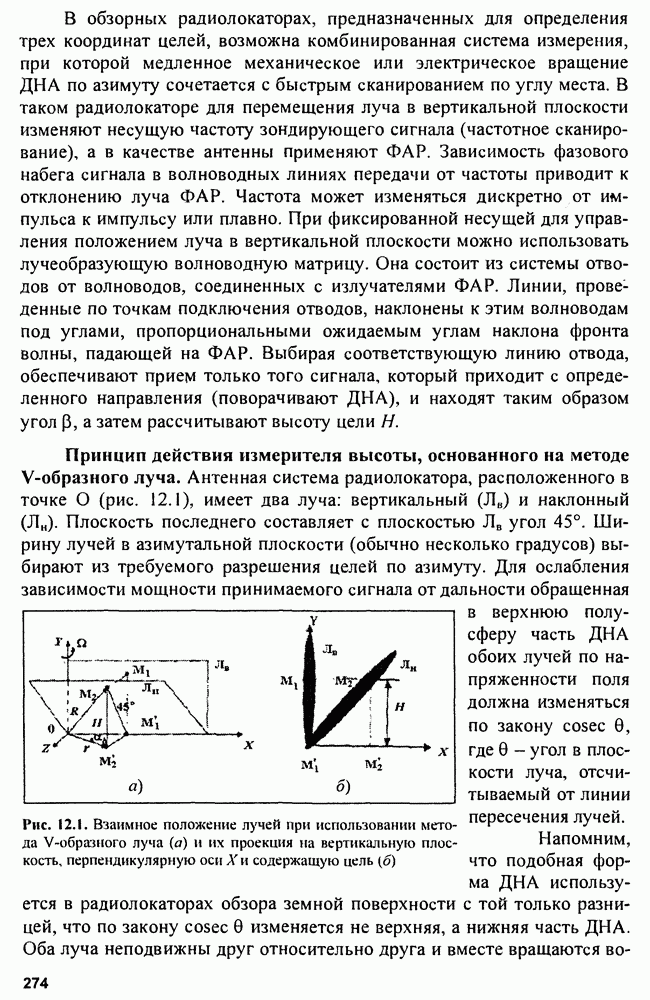
- Глава 12. Измерители высоты
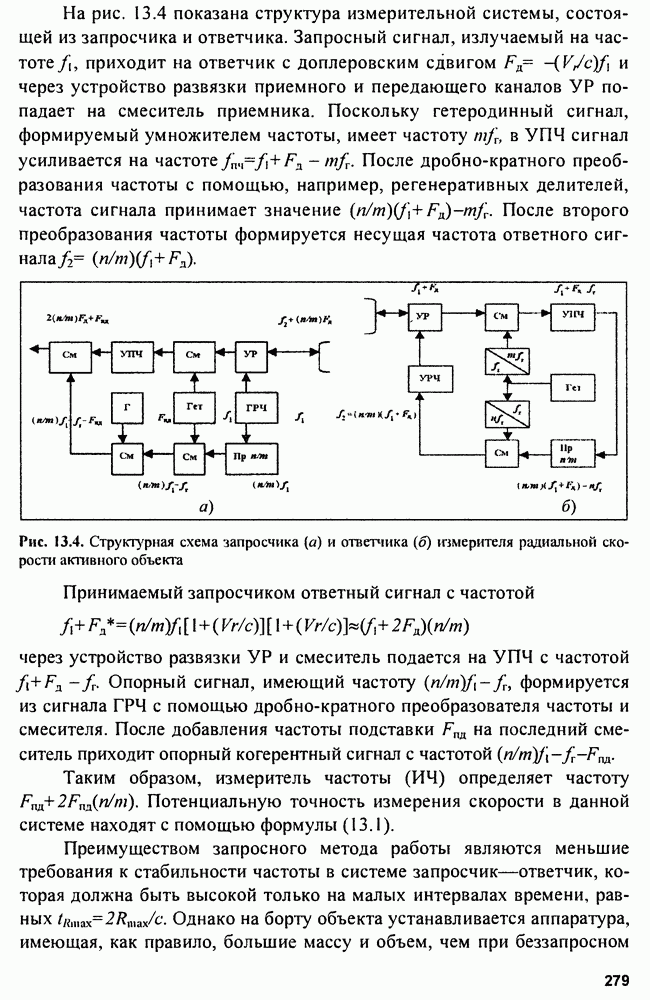
- Глава 13. Измерители скорости цели
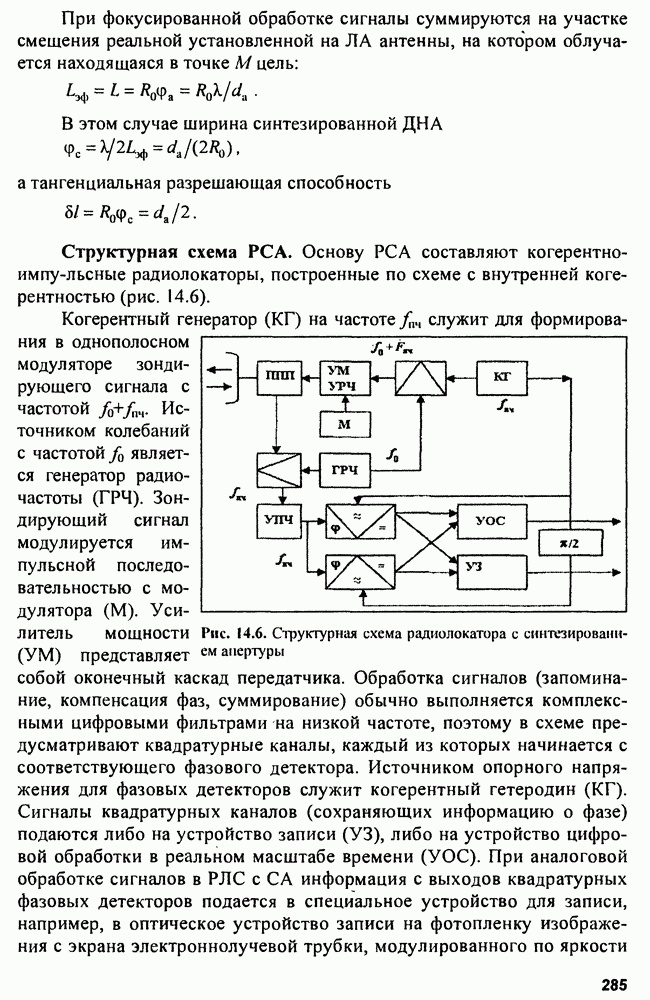
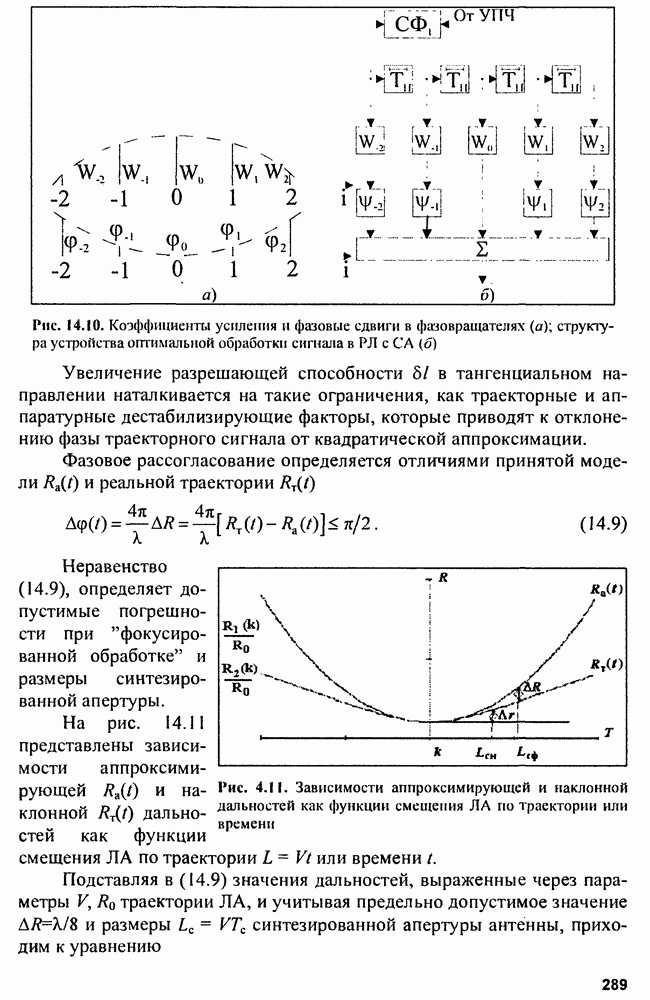
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение