| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
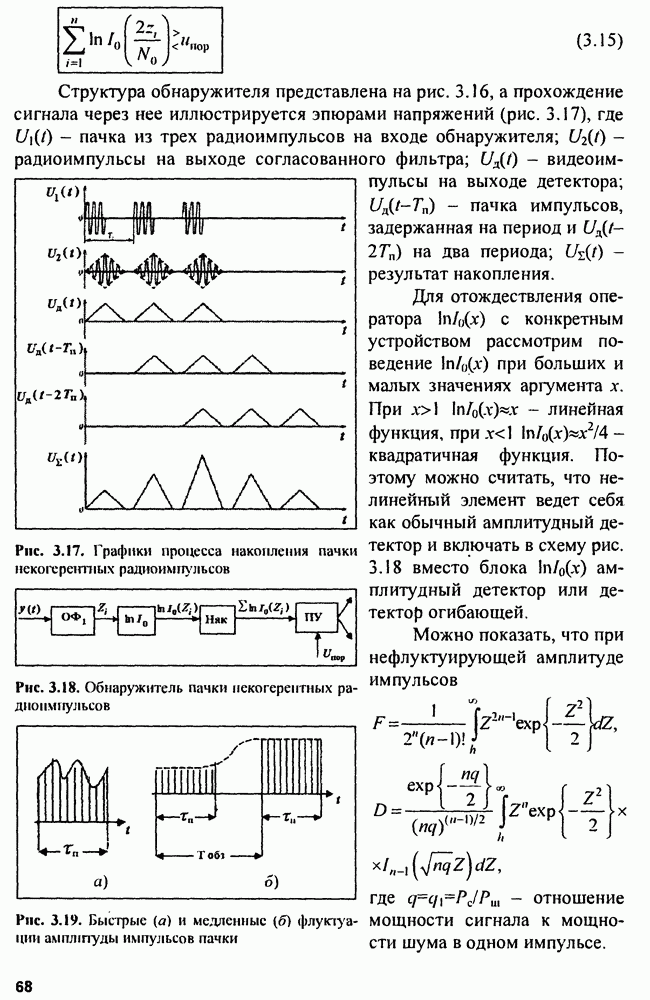
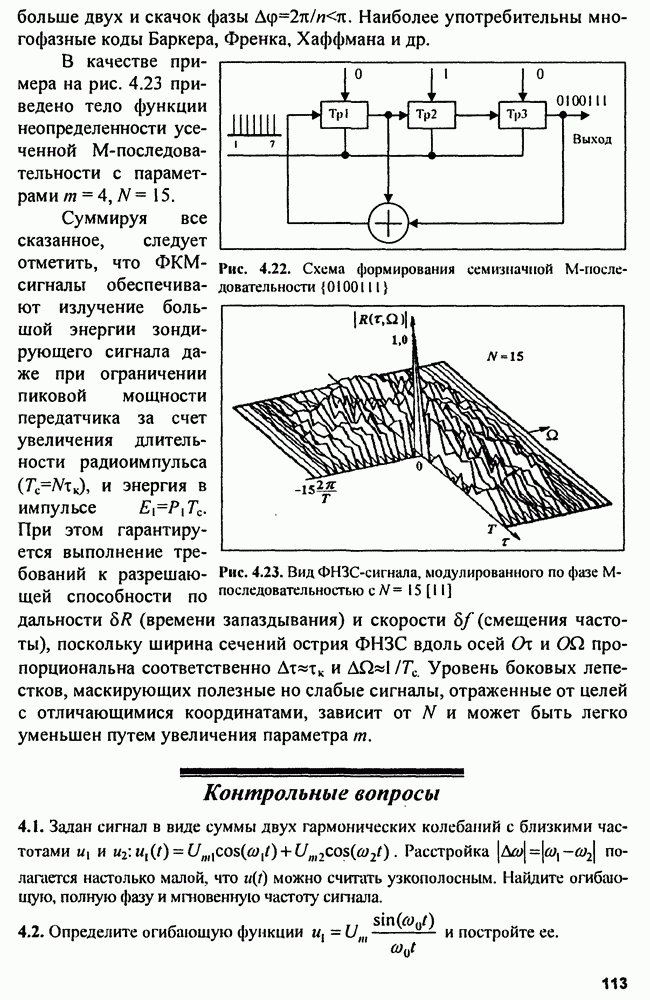
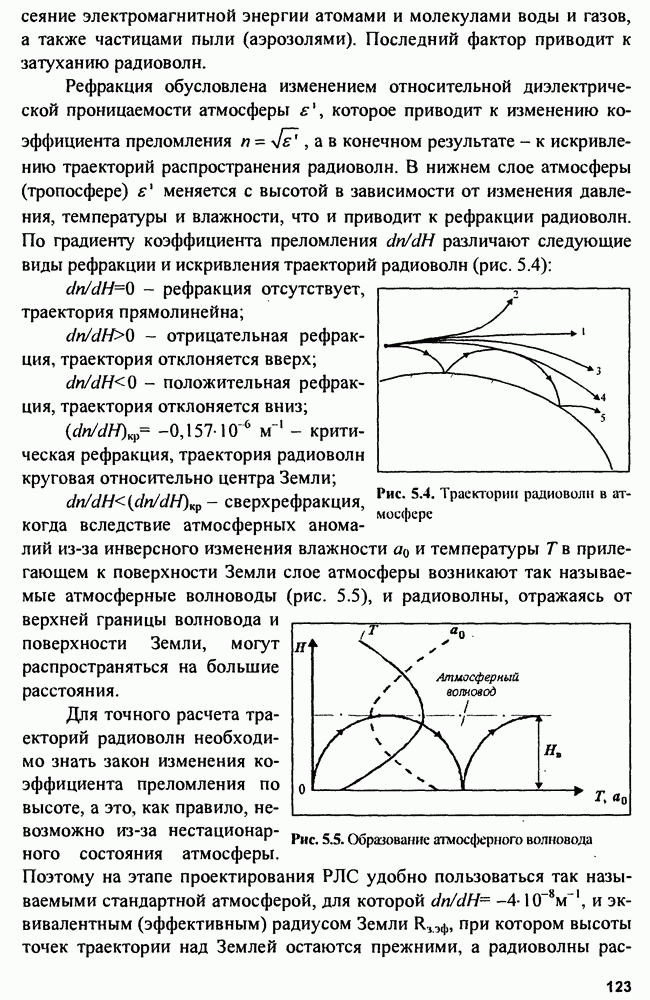
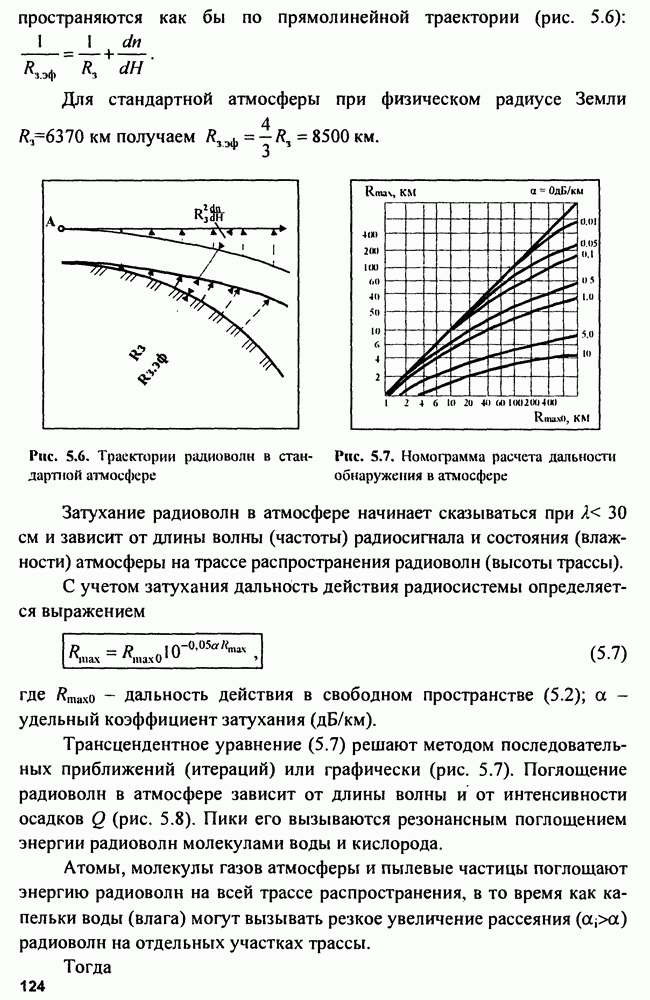
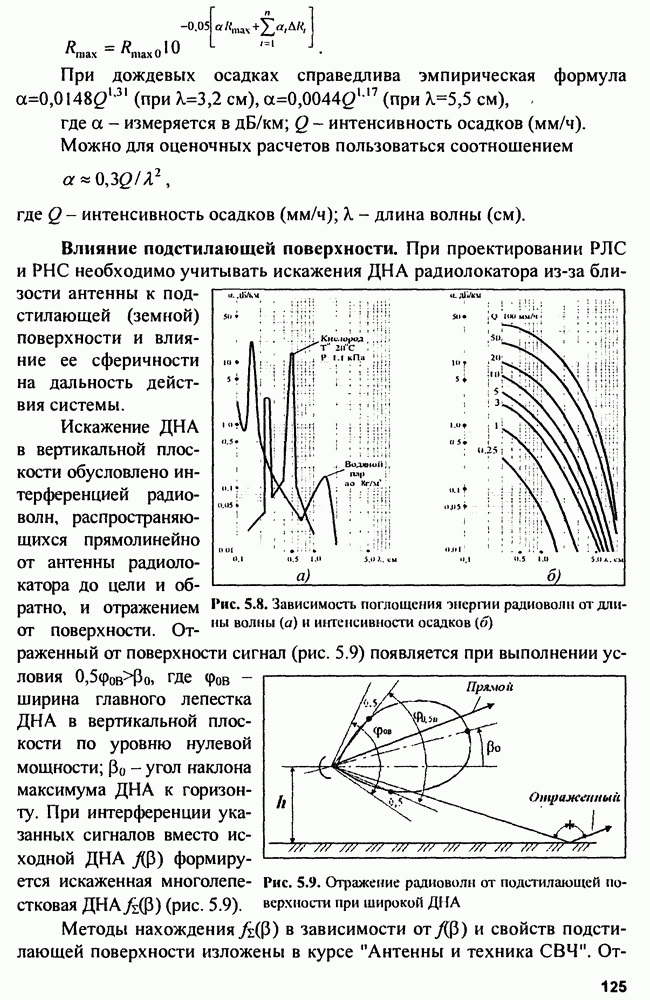
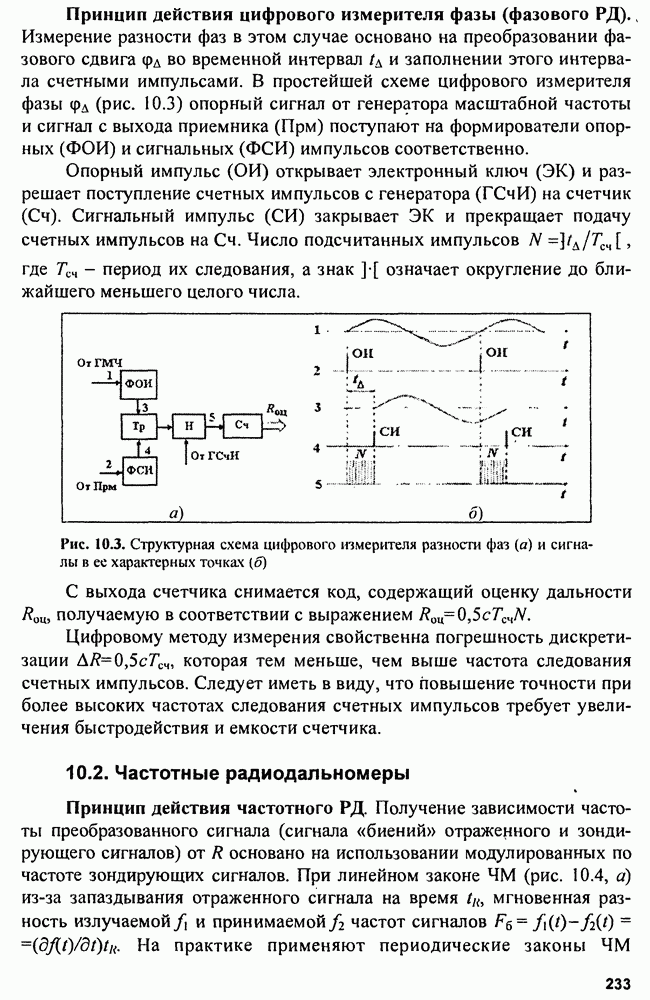
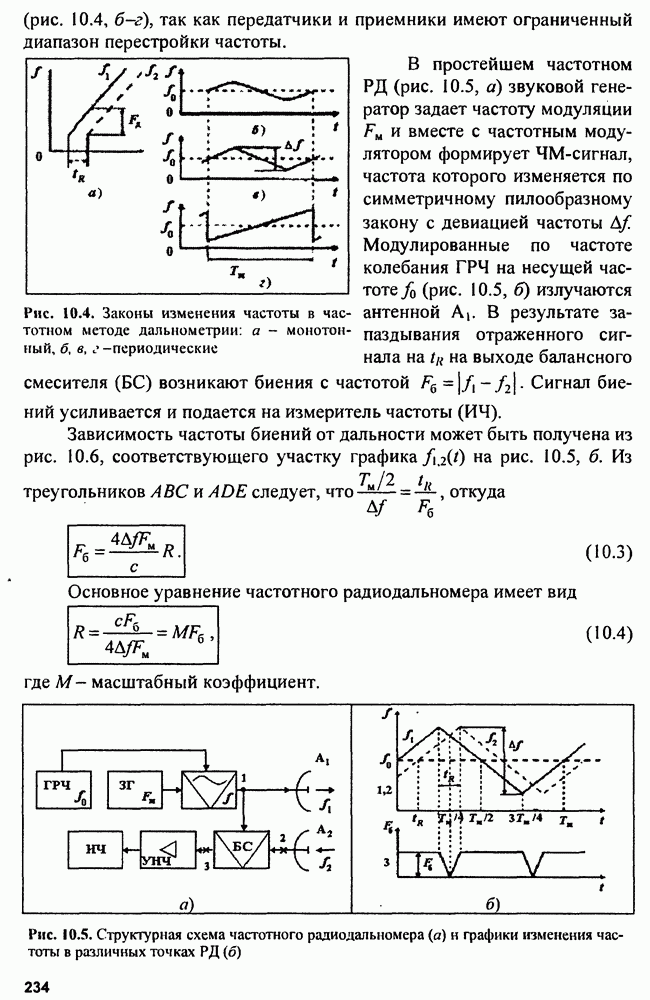
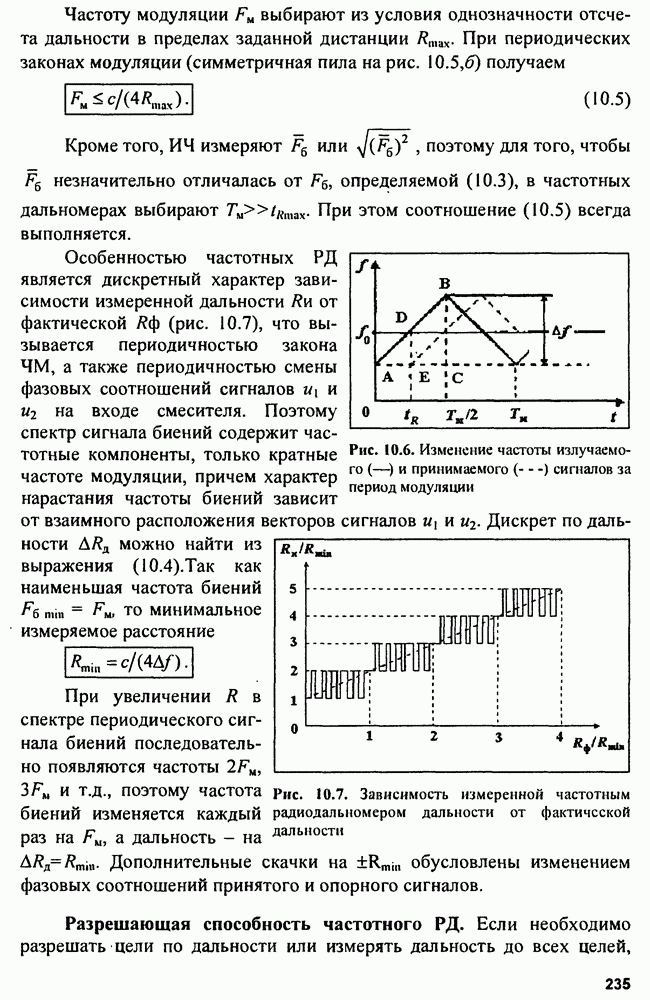
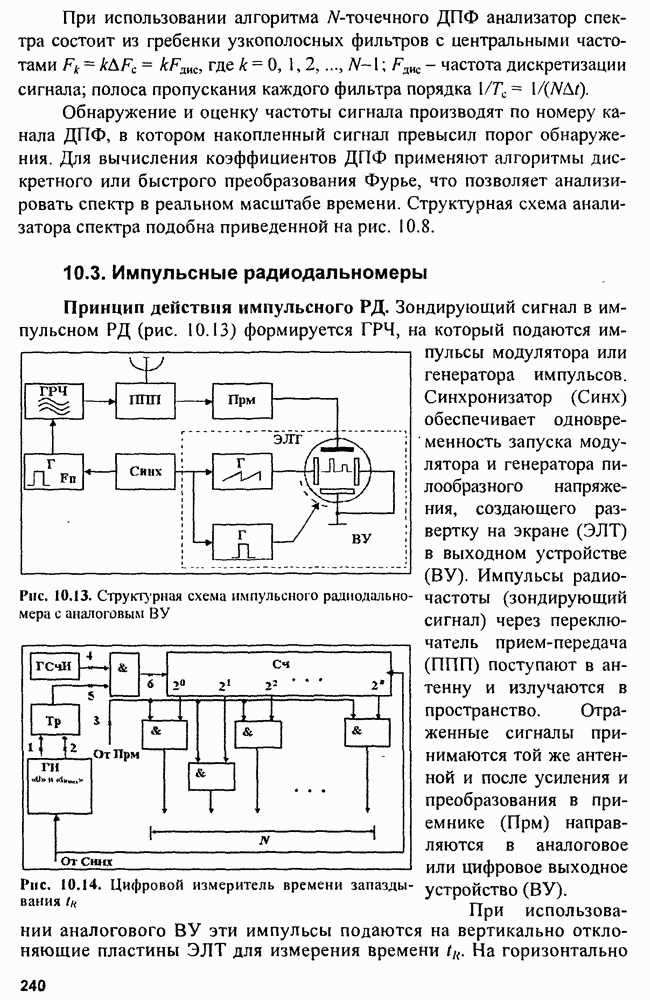
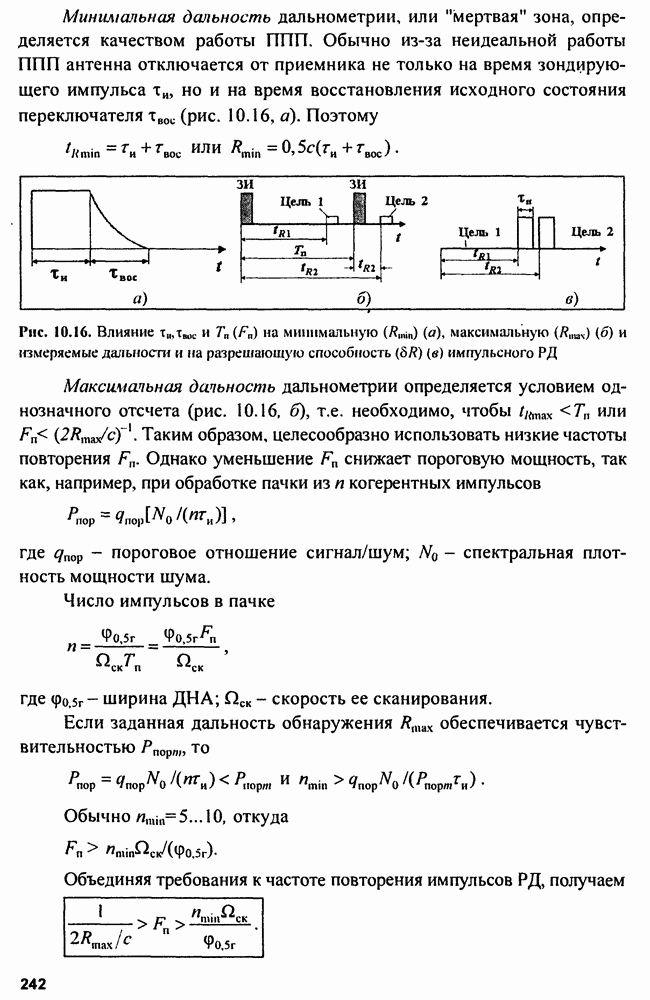
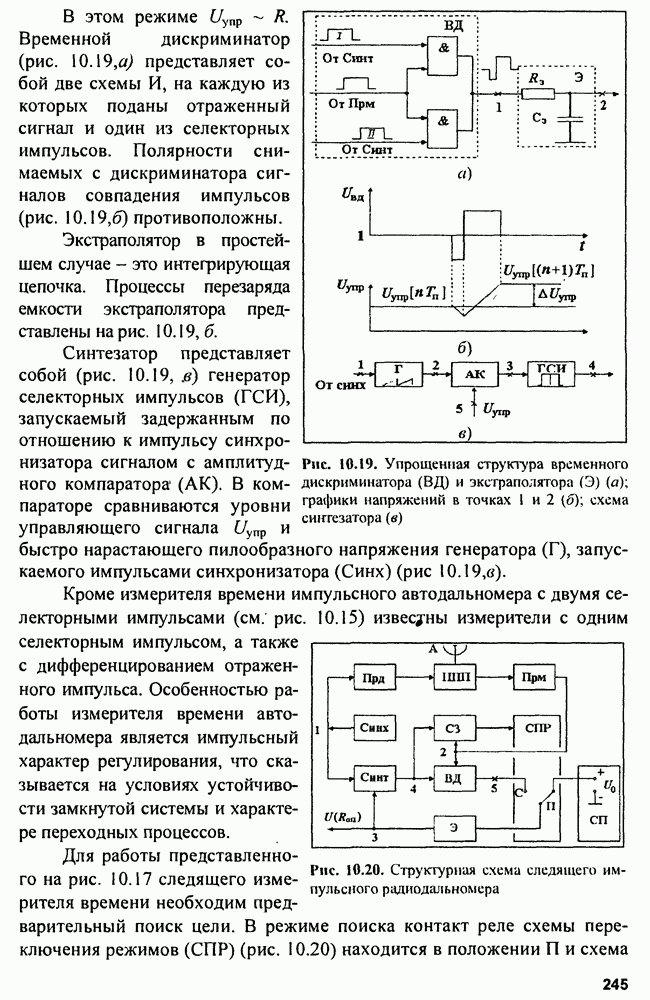
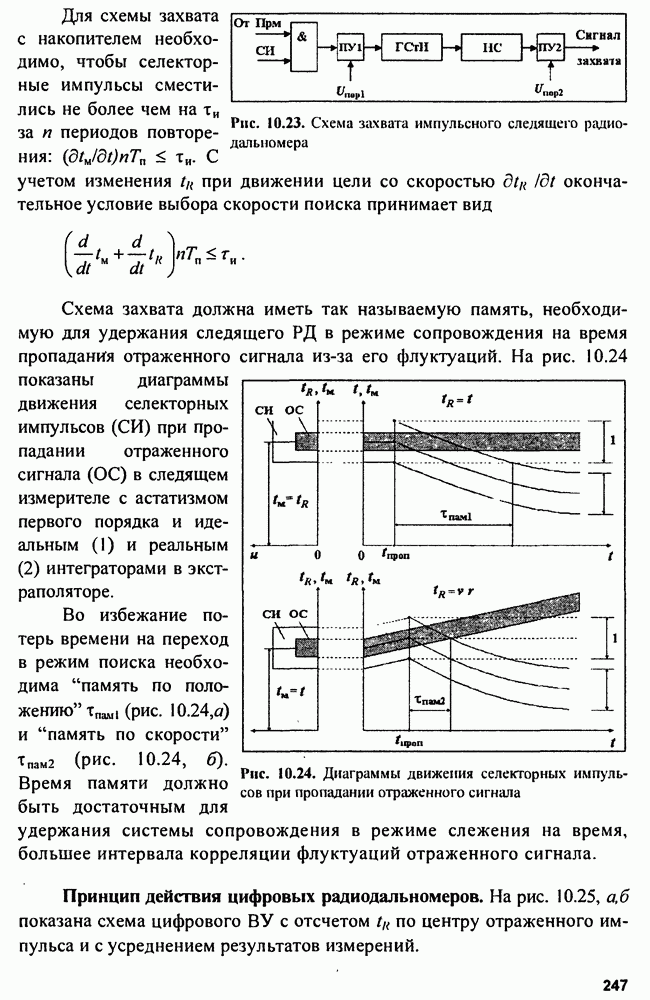
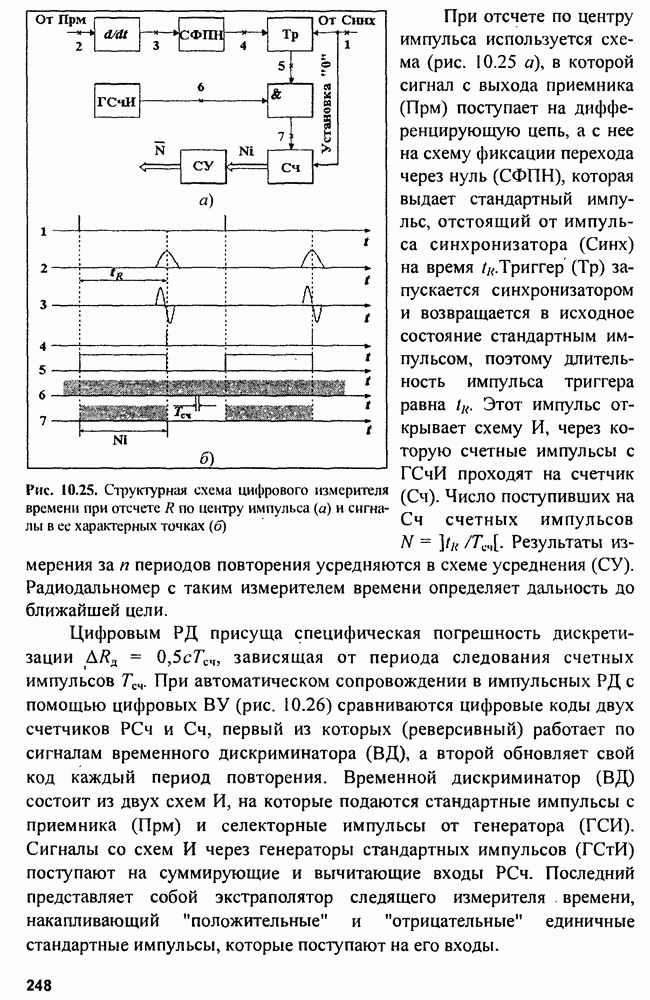
8.2. Устройства подавления пространственных активных помех
Изложенные принципы приема пространственного сигнала позволяют не только выполнять оптимальную обработку пространственно-временных сигналов на фоне пространственно-временных некоррелированных и равномерных по пространству шумов и помех, но и оптимально обнаруживать полезные сигналы на фоне пространственных коррелированных помех. Однако, как было показано, в общем случае решать эти задачи трудно. Поэтому на основе сведений об устройствах обработки пространственных сигналов (ФАР) рассмотрим более простые задачи компенсации мешающих пространственных сигналов —
разновидности пространственных коррелированных помех. Действительно, практика радиолокации показывает, что можно вполне успешно создавать устройства, способные подавлять пространственные активные помехи. Наиболее простые из таких устройств основаны на компенсации помехового сигнала или на деформировании ДНА и применимы при небольшом числе источников помех в пространстве. В более сложных ситуациях, когда число источников помех велико, используют более сложные системы обработки пространственно-временных сигналов.
Устройства компенсации помех. Когда направления на источники сигнала и активной помехи не совпадают, можно скомпенсировать помеху, применив устройство с основной и дополнительной антеннами. Пусть основная антенна  принимает помеху а дополнительная компенсационная антенна
принимает помеху а дополнительная компенсационная антенна  помеху
помеху  того же источника, отличающуюся на
того же источника, отличающуюся на  по фазе от (рис. 8.3).
по фазе от (рис. 8.3).

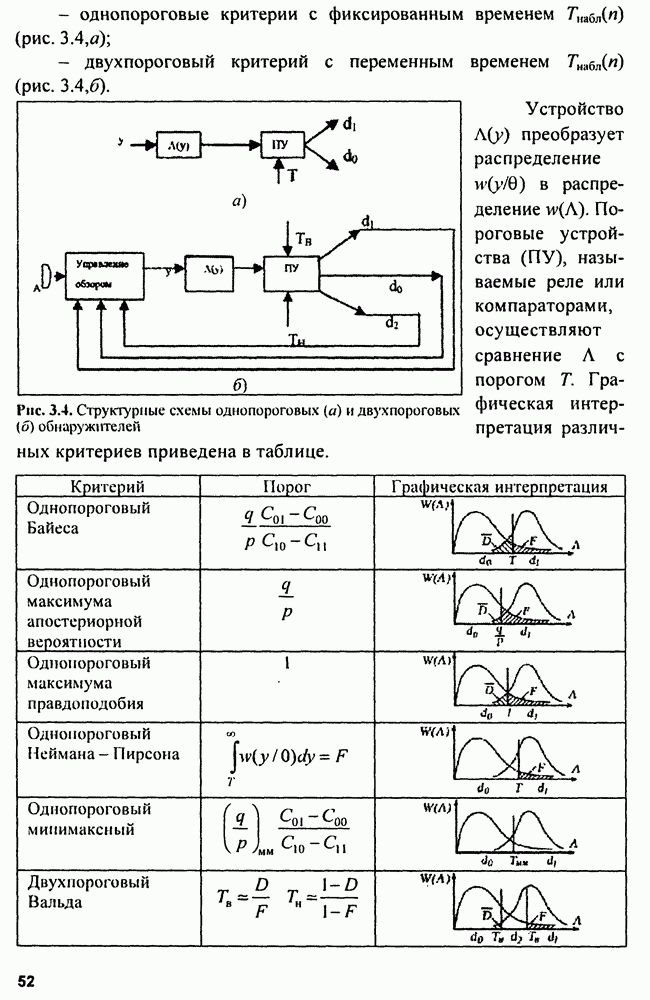
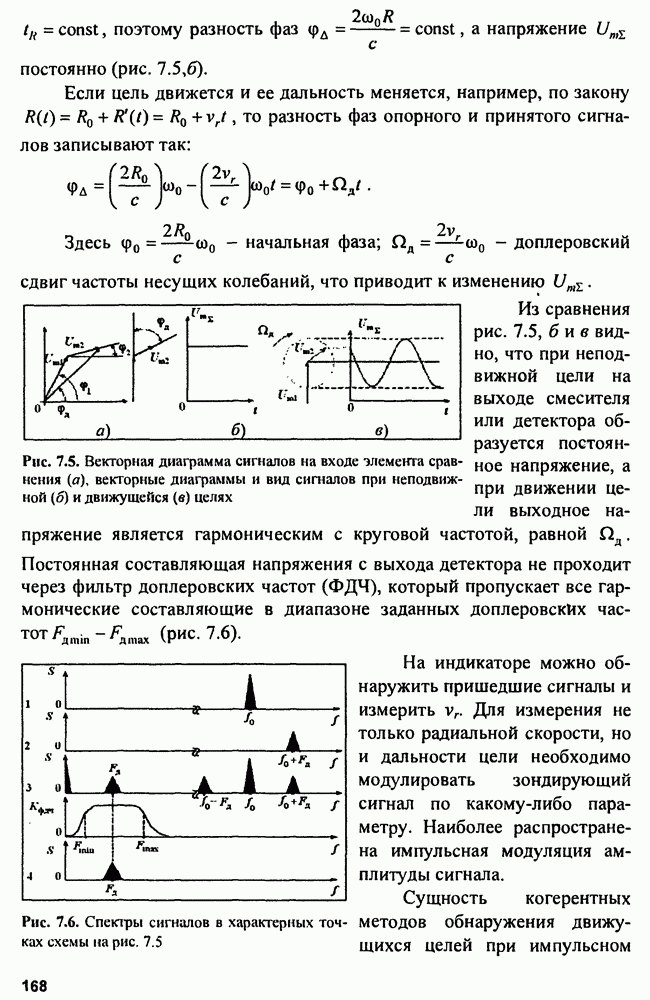
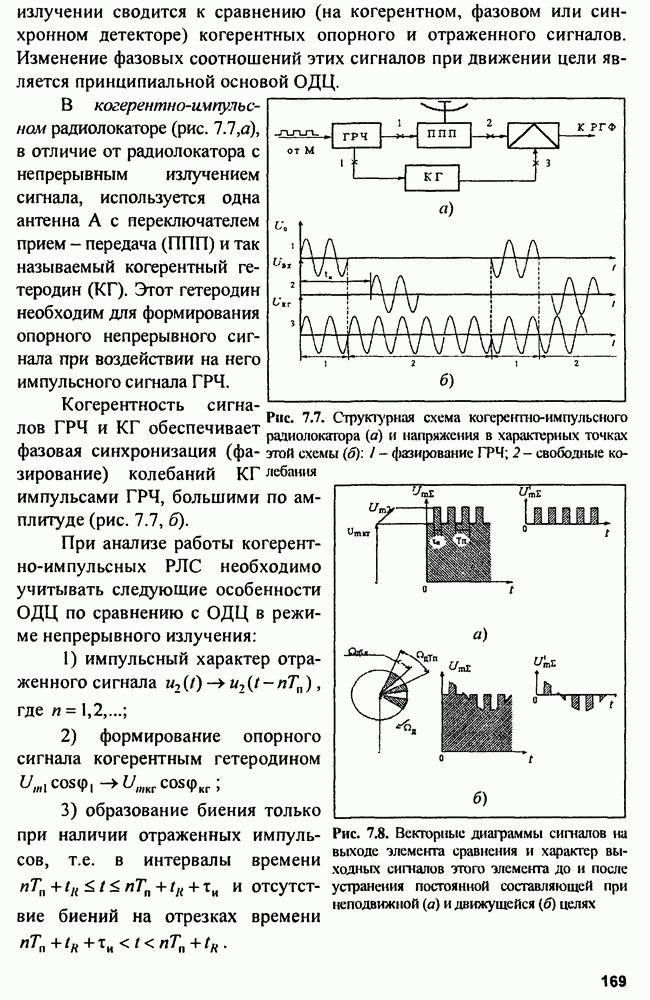
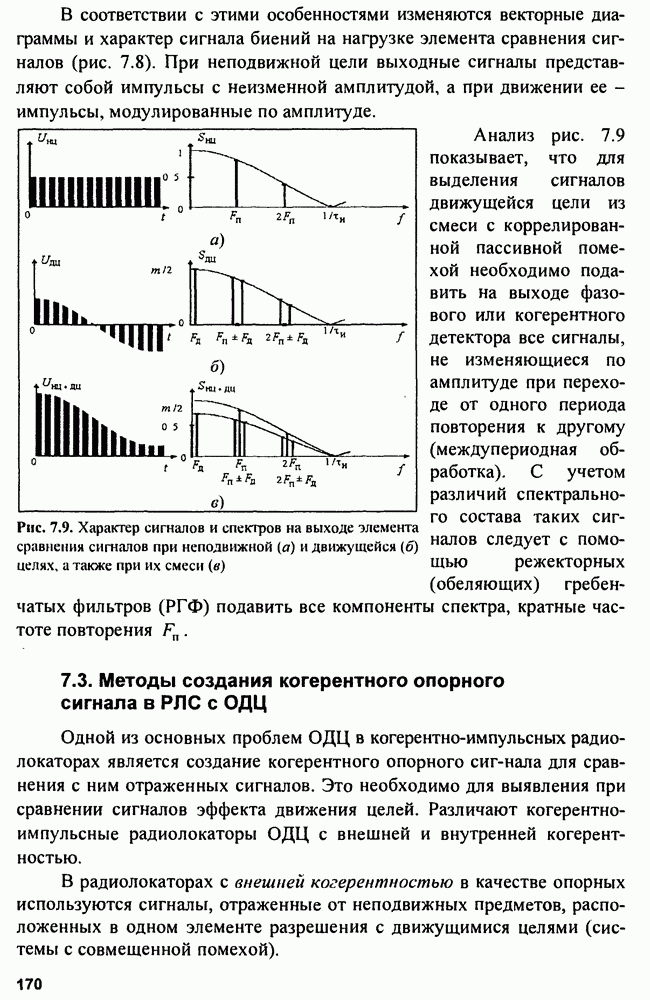
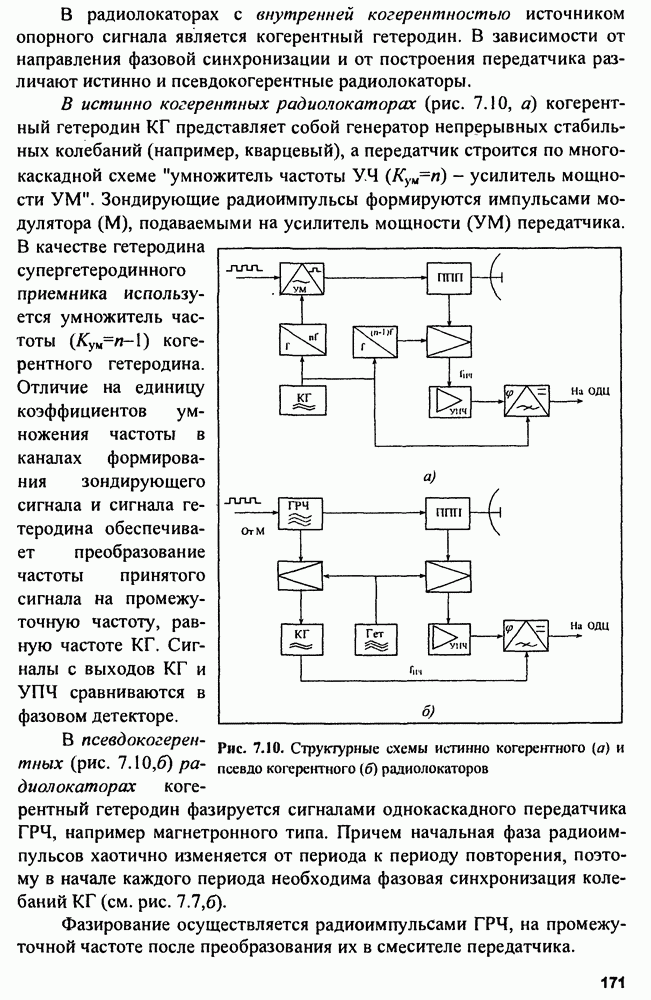
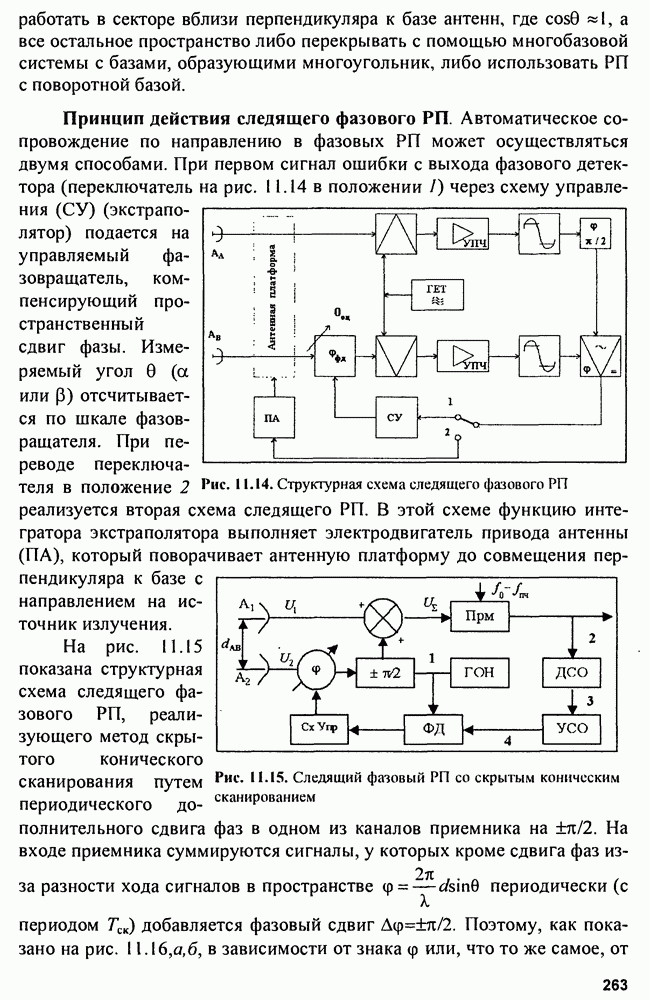
Рис. 8.3. Структурная схема (а) и векторная диаграмма сигналов (б) компенсатора активной помехи
Считаем, что на выходе сумматора образуется напряжение  где напряжение компенсирующего канала
где напряжение компенсирующего канала  Тогда
Тогда  где
где 
Весовые коэффициенты для компенсации помехи формируются в соответствии с алгоритмами  где
где  коэффициент усиления цепи компенсации помехи;
коэффициент усиления цепи компенсации помехи;  математическое ожидание.
математическое ожидание.
Подставив в эти соотношения значения  и проведя усреднение, получим
и проведя усреднение, получим

Составляющая  Кроме того,
Кроме того,  так как Компоненты
так как Компоненты  ортогональны. Поэтому
ортогональны. Поэтому  откуда
откуда

Весовой коэффициент  вычисляют с помощью формулы
вычисляют с помощью формулы

где  которая выводится аналогично предыдущей.
которая выводится аналогично предыдущей.
При  полученные выражения упрощаются и принимают вид
полученные выражения упрощаются и принимают вид

На основании этих соотношений можно синтезировать структуру квадратурного компенсатора с корреляционными обратными связями (рис. 8.4), в котором компенсируется помеха. Устройство обеспечивает минимум среднего квадрата напряжения (мощности) помехи на выходе:

где 

Рис. 8.4. Структурная схема компенсатора активной помехи с корреляционными обратными связями
Найдем минимум этого выражения при вариации 

откуда  Аналогично
Аналогично  Эти выражения совпадают с полученными ранее в предположении
Эти выражения совпадают с полученными ранее в предположении 
Если подставить  и
и  в выражение для
в выражение для 

Обозначим  поскольку
поскольку  Тогда окончательно получим
Тогда окончательно получим  откуда коэффициент подавления мощности
откуда коэффициент подавления мощности

При некоррелированной помехе  и подавления помехи нет. При сильно коррелированной помехе
и подавления помехи нет. При сильно коррелированной помехе  и подавление помехи максимально.
и подавление помехи максимально.
Весовой коэффициент можно представить в виде

и

При этом 
Устройство подавления с деформацией ДНА. Рассматриваемое устройство позволяет сформировать минимум диаграммы в направлении на источник помехи, требует дополнительной антенны (рис. 8.5) и является иллюстрацией функционирования устройства (см. рис. 8.3).

Рис. 8.5. Структурная схема устройства формирования провала в ДНА
Обозначим через  исходные диаграммы направленности основной и компенсирующей антенн, а через
исходные диаграммы направленности основной и компенсирующей антенн, а через  результирующую диаграмму антенной системы из антенн
результирующую диаграмму антенной системы из антенн  Тогда
Тогда  Если
Если  угловая координата источника помехи, то для компенсации помехи нужно выполнить условие
угловая координата источника помехи, то для компенсации помехи нужно выполнить условие  откуда
откуда  Подставив это соотношение в выражение для
Подставив это соотношение в выражение для  получим
получим  Видно, что при
Видно, что при  и в направлении на источник помехи образуется провал в ДНА. При действии нескольких помех с ряда направлений необходимо большее число антенн, чтобы антенна
и в направлении на источник помехи образуется провал в ДНА. При действии нескольких помех с ряда направлений необходимо большее число антенн, чтобы антенна  и одна из других антенн А, образовывали компенсирующее устройство активной помехи с
и одна из других антенн А, образовывали компенсирующее устройство активной помехи с  направления (рис. 8.6).
направления (рис. 8.6).

Рис. 8.6. Схема пространственной обработки для подавления нескольких  помех
помех
Построение оптимальных устройств подавления активных помех. Реализация оптимальной пространственной обработки при подавлении помехи от источника с угловой координатой  требует определения весовых коэффициентов
требует определения весовых коэффициентов  или при объединении последних - весового вектора
или при объединении последних - весового вектора  связанного с обратной корреляционной матрицей
связанного с обратной корреляционной матрицей  Если известны направления на источники помех и параметры антенны, а также если помеха очень интенсивна, то матрицу
Если известны направления на источники помех и параметры антенны, а также если помеха очень интенсивна, то матрицу  можно вычислить однозначно. Поскольку в общем случае
можно вычислить однозначно. Поскольку в общем случае  связана с корреляционными характеристиками помех и сигналов, нахождение
связана с корреляционными характеристиками помех и сигналов, нахождение  зависит от использованного при синтезе
зависит от использованного при синтезе  критерия оптимальности. При различных критериях, например, минимума среднего квадратичного отклонения или максимума отношения мощностей сигнала и помехи, вектор
критерия оптимальности. При различных критериях, например, минимума среднего квадратичного отклонения или максимума отношения мощностей сигнала и помехи, вектор  будет связан с различными корреляционными матрицами (функциями), как это показано далее.
будет связан с различными корреляционными матрицами (функциями), как это показано далее.
Пусть антенная решетка (рис. 8.7) состоит из одной основной  вспомогательных антенн. После взвешивания с весом
вспомогательных антенн. После взвешивания с весом  выходные сигналы антенн суммируются и результат сложения
выходные сигналы антенн суммируются и результат сложения  сравнивается с сигналом
сравнивается с сигналом  По результату сравнения
По результату сравнения  блок управления весовыми коэффициентами
блок управления весовыми коэффициентами  формирует веса
формирует веса  в каналах вспомогательных антенн.
в каналах вспомогательных антенн.

Рис. 8.7. Схема подавителя помех с корреляционной обратной связью на антенной решетке
Будем считать, что помеха является узкополосным гауссовским случайным процессом. В момент 

где  вектор-столбец компонентов сигналов элементов антенны;
вектор-столбец компонентов сигналов элементов антенны;  -знак транспонирования матрицы.
-знак транспонирования матрицы.
Каждый компонент  является вектором-строкой:
является вектором-строкой: 
Вектор-столбец весовых коэффициентов обозначим 
Используем критерий минимума среднего квадратического отклонения

где  вектор опорного сигнала. Следовательно,
вектор опорного сигнала. Следовательно,

откуда

Введем корреляционную матрицу выборок сигналов источников помех:

и вектор-столбец взаимно-корреляционной матрицы опорного сигнала и помех  Условия минимума
Условия минимума  можно отыскать, приравняв нулю градиент искомой матричной величины:
можно отыскать, приравняв нулю градиент искомой матричной величины:  С учетом того, что
С учетом того, что  квадрат скалярного произведения
квадрат скалярного произведения  где
где  градиент от нее выражается как
градиент от нее выражается как  Поэтому
Поэтому

откуда

или, умножая слева на  получим
получим

В результате

где I - единичная матрица.
Следовательно, алгоритм определения матрицы оптимальных весовых коэффициентов имеет вид

Последнее выражение есть уравнение Винера - Хопфа в матричной форме. Предполагается, что матрица  не вырождена, следовательно, существует обратная матрица
не вырождена, следовательно, существует обратная матрица 
Если для отыскания оптимального вектора весовых коэффициентов использовать критерий максимума отношения сигнала к помехам, то оптимальный вектор весовых коэффициентов

где К - некоторая константа;  шумовая составляющая входного сигнала.
шумовая составляющая входного сигнала.
Критерий максимума отношения мощностей сигнала и помехи применим в стационарных условиях, даже когда отсутствуют сигнал и внешние помехи, и не учитывает деформацию ДНА, особенно в области боковых лепестков.
Таким образом, при различных подходах к подавлению активных помех и любом критерии оптимальности приходим к схемам пространственной весовой обработки с компенсацией мешающих сигналов. При этом комплексные весовые коэффициенты можно формировать, обращая матрицу входных реализаций помех и сигналов. Существует два способа такого обращения: прямой и рекуррентный. При больших размерах корреляционных матриц  число источников помех) требуются большие вычислительные и временные затраты. Обычно корреляционные матрицы заранее неизвестны, поэтому их следует оценивать по входным реализациям, а затем получать обратную корреляционную матрицу с помощью, например, схем с корреляционной обратной связью.
число источников помех) требуются большие вычислительные и временные затраты. Обычно корреляционные матрицы заранее неизвестны, поэтому их следует оценивать по входным реализациям, а затем получать обратную корреляционную матрицу с помощью, например, схем с корреляционной обратной связью.
Использование антенных решеток с устройствами формирования весов  с учетом корреляционных связей (рис. 8.6) требует уменьшения длительности переходных процессов в устройстве или уменьшения времени установления, а также сходимости результатов оценивания к истинным значениям характеристик помех, т.е. адекватности измеренных характеристик помех истинным.
с учетом корреляционных связей (рис. 8.6) требует уменьшения длительности переходных процессов в устройстве или уменьшения времени установления, а также сходимости результатов оценивания к истинным значениям характеристик помех, т.е. адекватности измеренных характеристик помех истинным.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
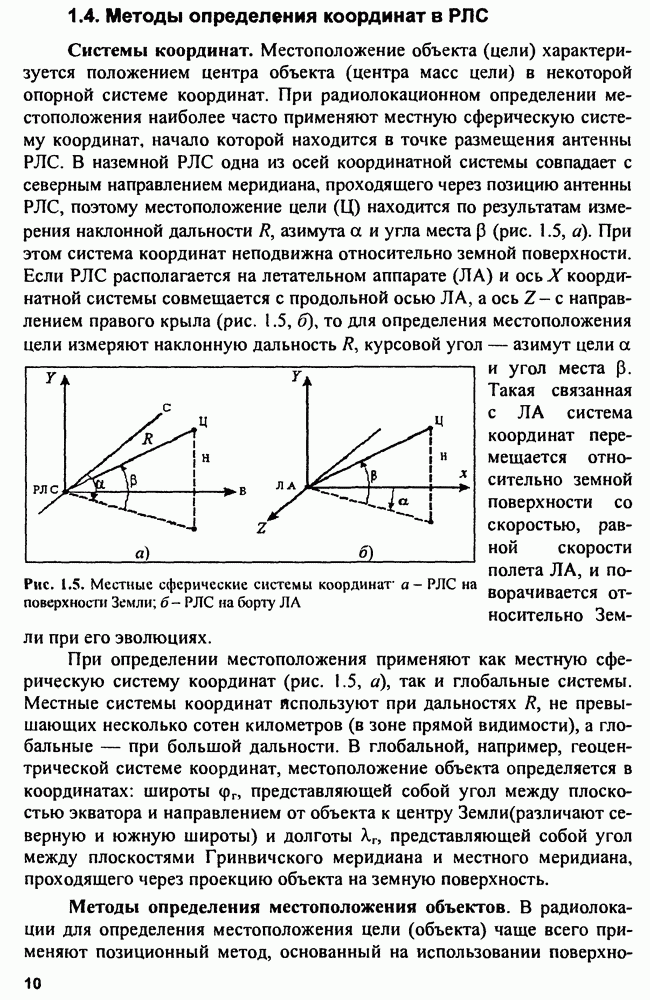
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
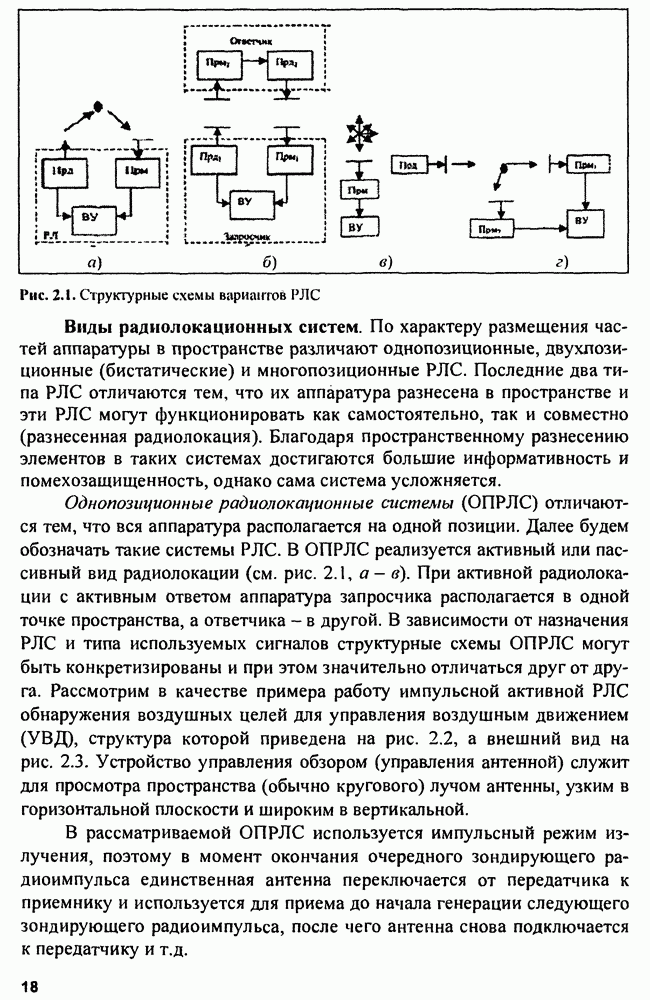
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
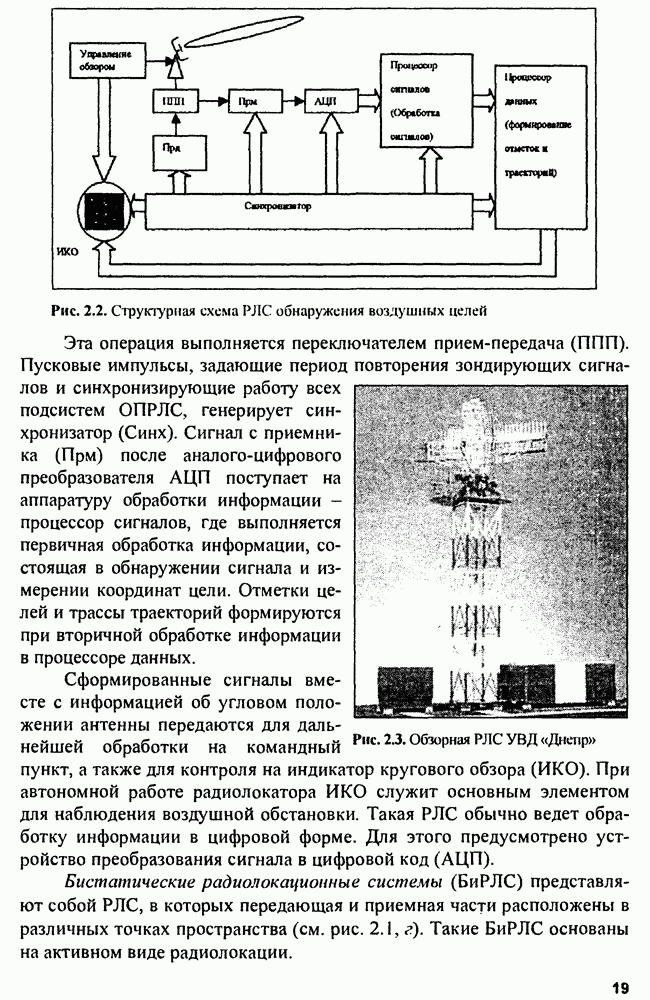
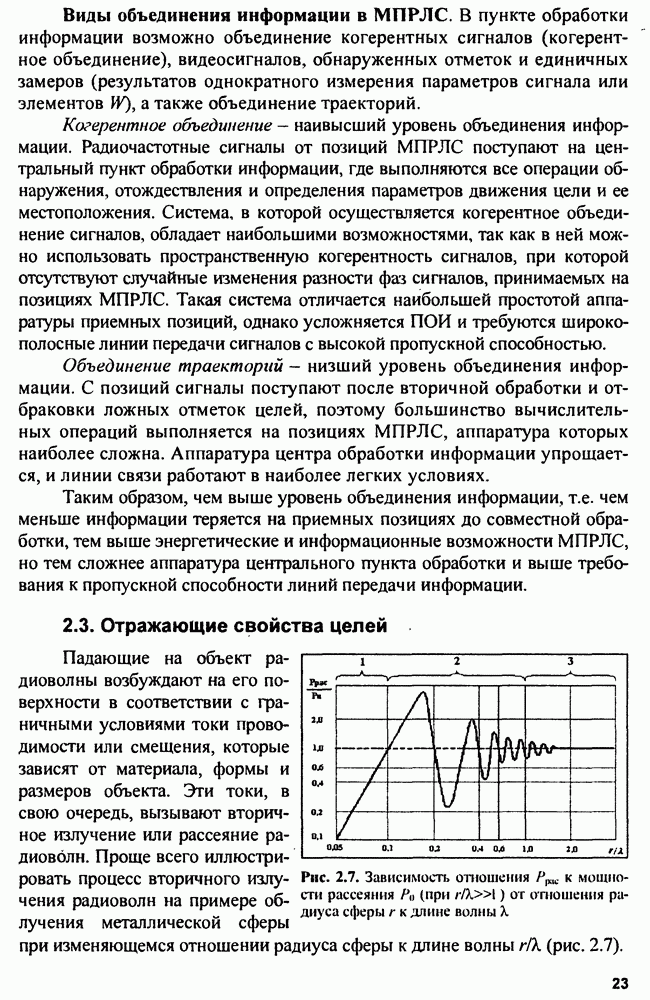
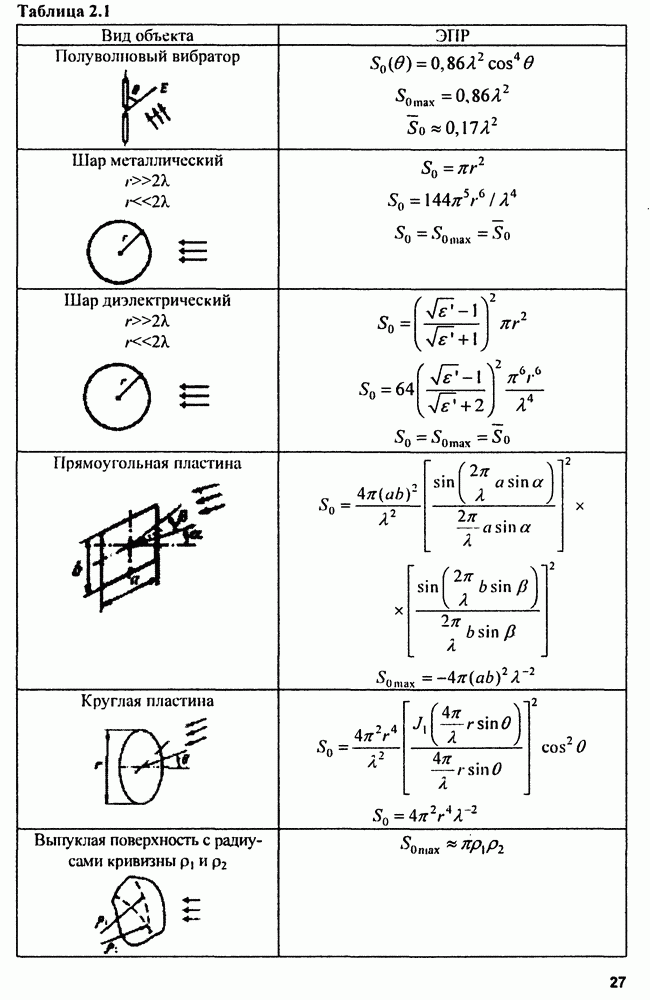
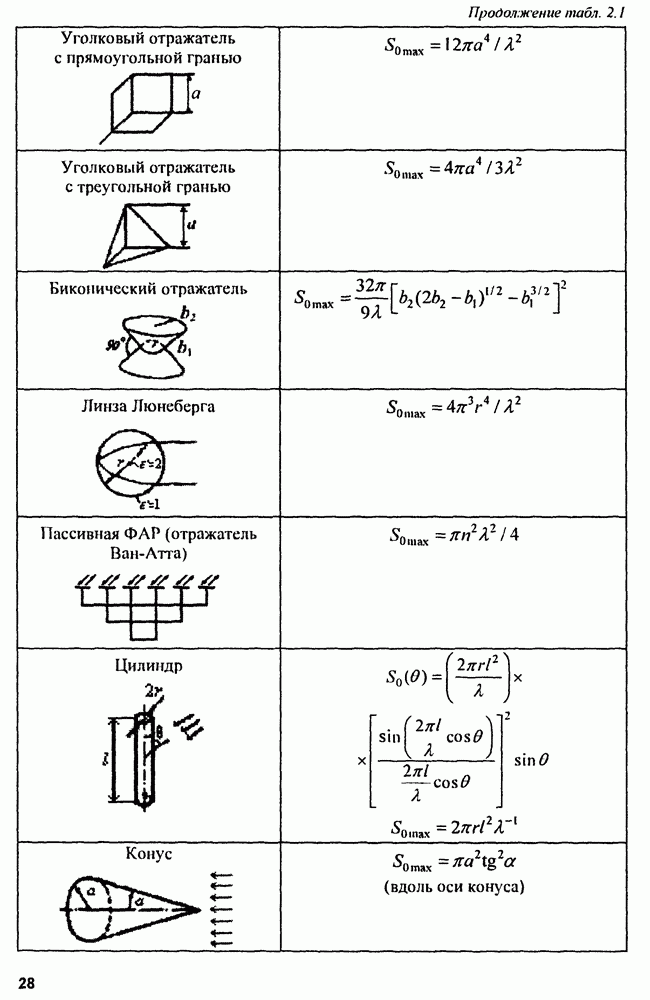
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
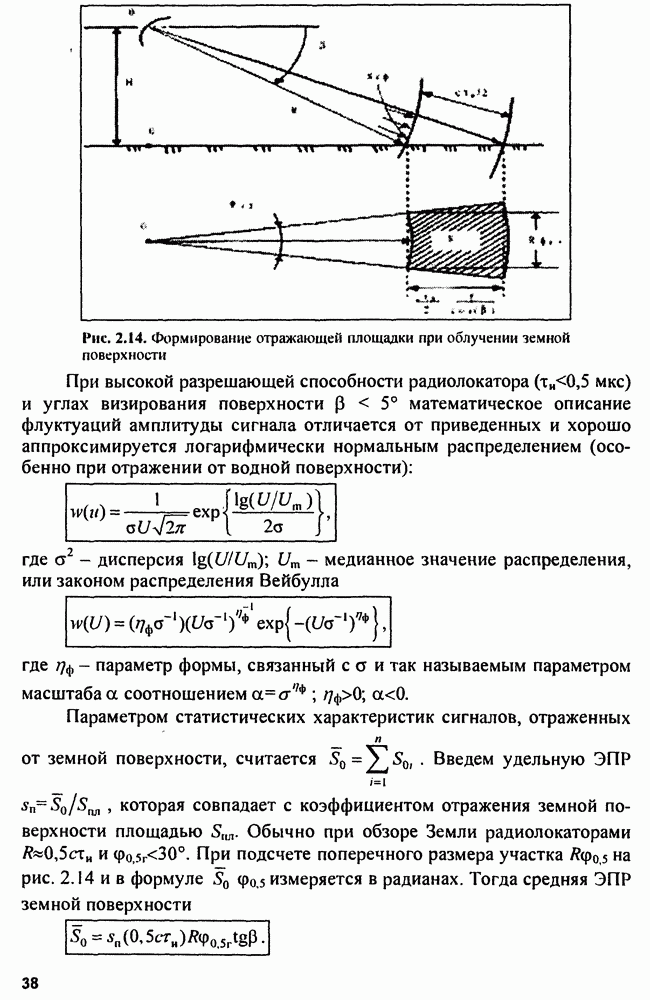
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение