| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
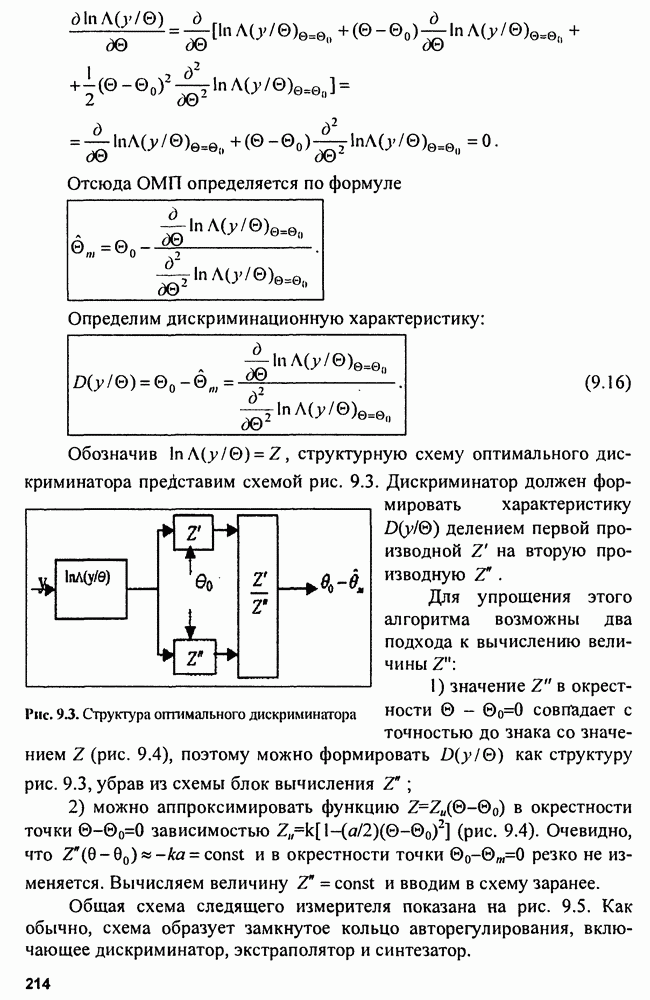
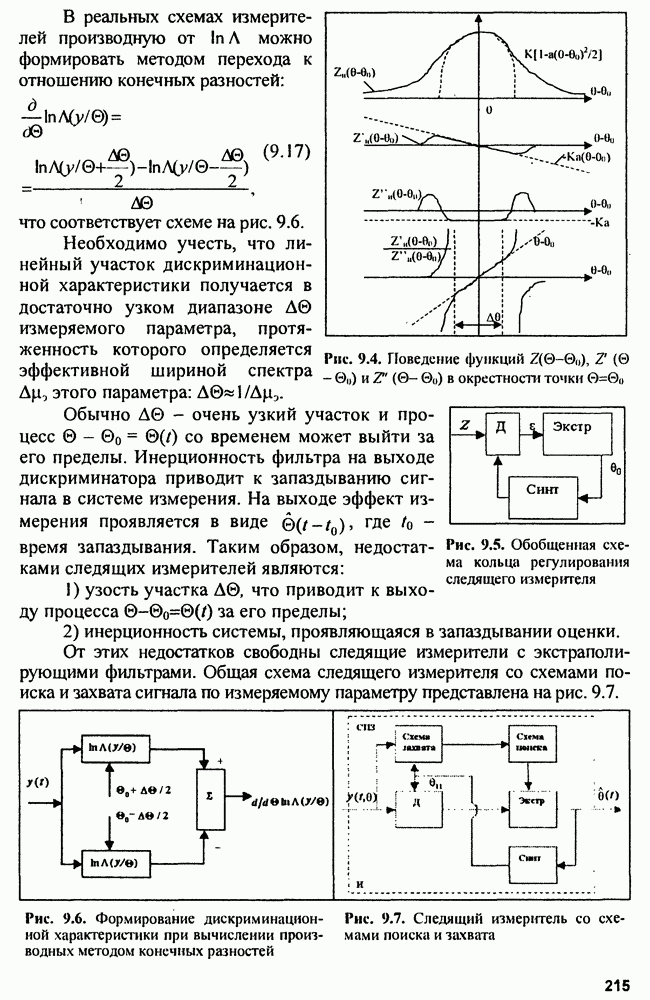
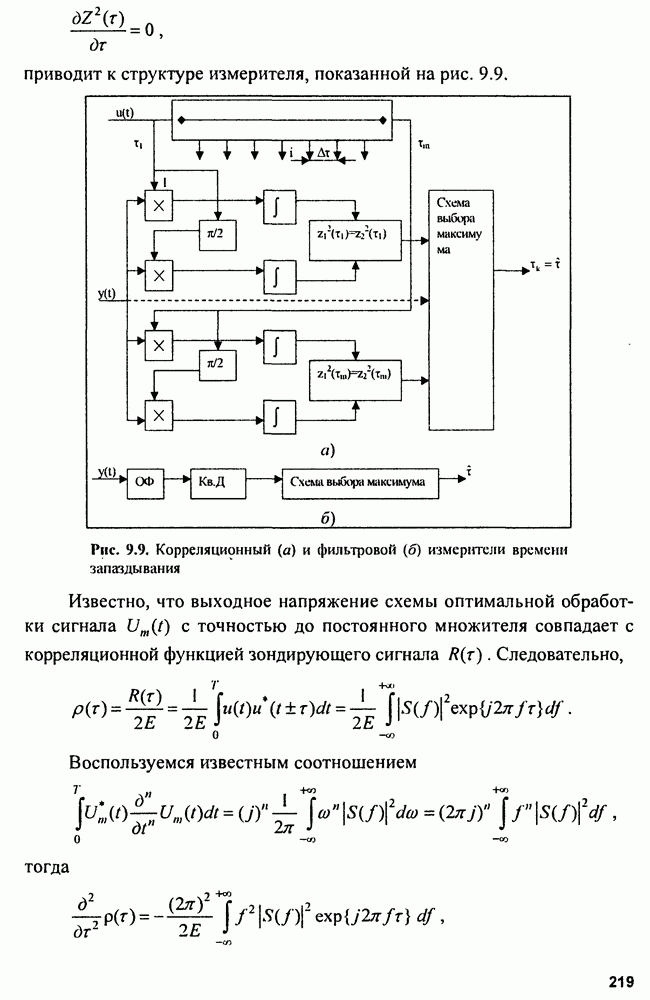
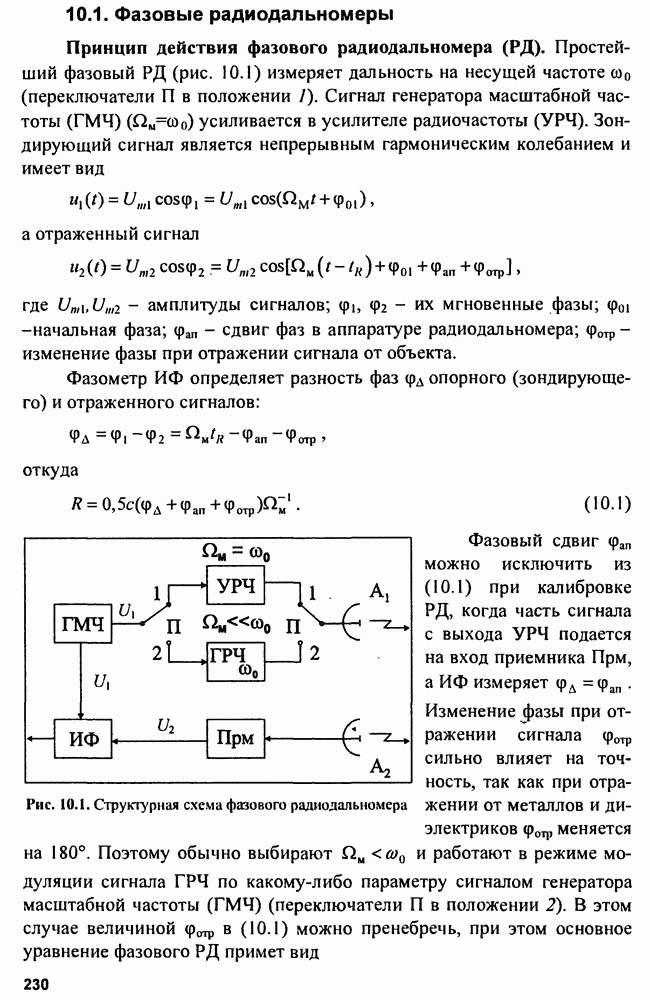
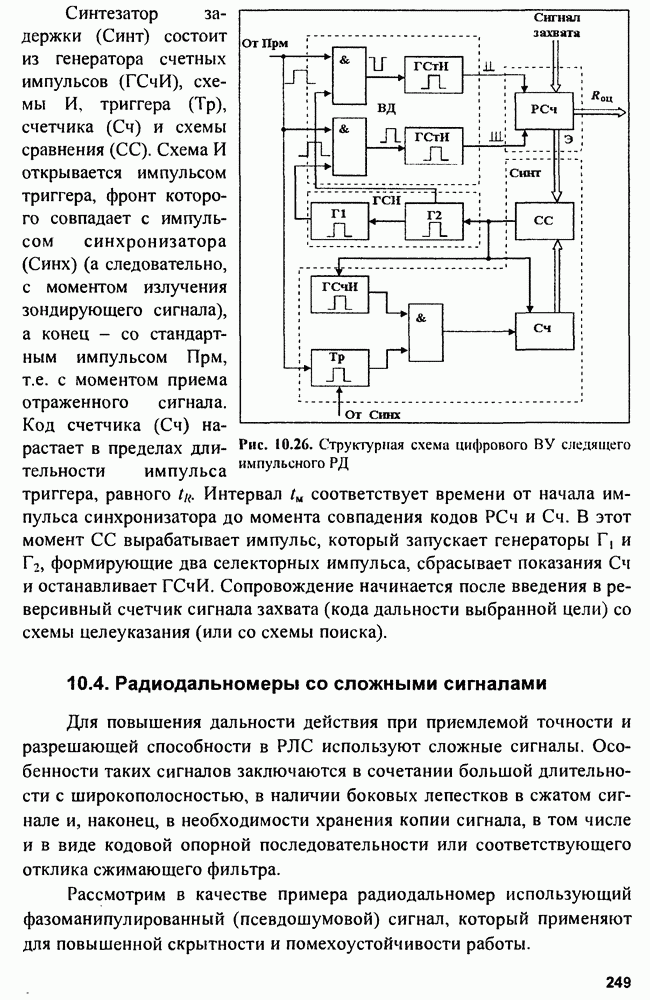
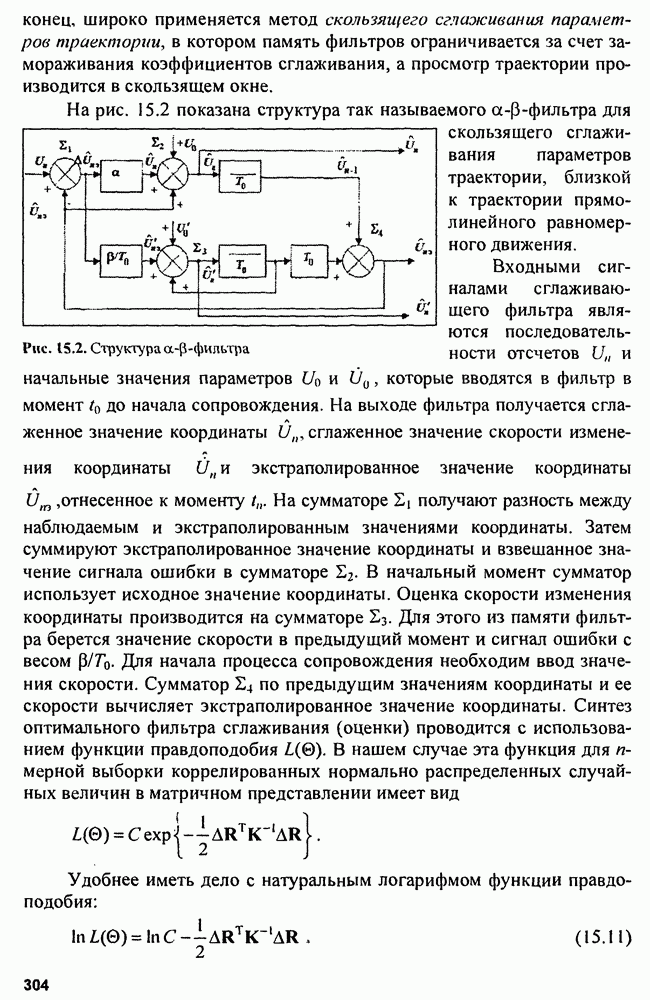
9.3. Качество оценок
Качество оценок характеризуется их состоятельностью, несмещенностью и эффективностью.
Состоятельность оценок  это сходимость по вероятности к оцениваемому параметру
это сходимость по вероятности к оцениваемому параметру  при неограниченном увеличении размера выборки
при неограниченном увеличении размера выборки  т.е. для любого малого наперед заданного положительного числа
т.е. для любого малого наперед заданного положительного числа 

Несмещенность оценки  это равенство среднего по совокупности выборок размера
это равенство среднего по совокупности выборок размера  значения оценки истинному значению оцениваемого параметра при любом значении
значения оценки истинному значению оцениваемого параметра при любом значении 

Следовательно, смещение оценки

Если  лишь при неограниченном увеличении
лишь при неограниченном увеличении  то такая оценка называется асимптотически несмещенной, т.е.
то такая оценка называется асимптотически несмещенной, т.е.

Оценки, которые можно получить из выборок размером  называются достаточными оценками (или достаточными статистиками). Используя достаточные статистики, в число которых входит и отношение правдоподобия
называются достаточными оценками (или достаточными статистиками). Используя достаточные статистики, в число которых входит и отношение правдоподобия  можно упростить процедуры оценки параметров или сократить процесс накопления входной информации для получения оценок.
можно упростить процедуры оценки параметров или сократить процесс накопления входной информации для получения оценок.
Эффективность оценки обеспечивается, если среднее значение квадрата отклонения оценки от истинного значения оцениваемого параметра не больше, чем для любой другой оценки:

Рассмотрим неравенство Крамера - Рао. Пусть  несмещенная оценка параметра
несмещенная оценка параметра  т.е.
т.е.

или

Дифференцируя это выражение по 0, получаем

Так как

В соответствии с соотношением  можно представить
можно представить  следовательно,
следовательно,

Применительно к последнему выражению, используя неравенство Буняковского - Коши - Шварца:

получаем

после чего переходим к неравенству

Таким образом, дисперсия несмещенной оценки

Нижний предел дисперсии, получаемый при условии

называется дисперсией наиболее эффективной оценки (НЭО). Если существует НЭО, то она совпадает с ОМП.
Оценка максимального правдоподобия асимптотически оптимальна, так как она состоятельна, асимптотически не смещена и асимптотически наиболее эффективна.
Асимптотическая наибольшая эффективность - это стремление в пределе (при  дисперсии оценки к нижнему пределу неравенства Крамера - Рао:
дисперсии оценки к нижнему пределу неравенства Крамера - Рао:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
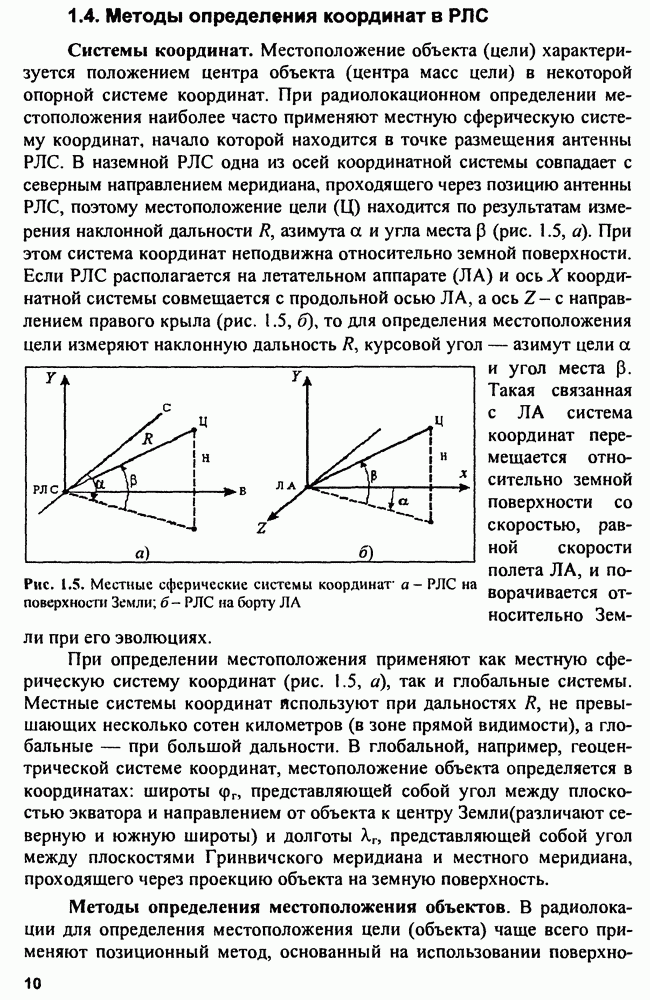
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
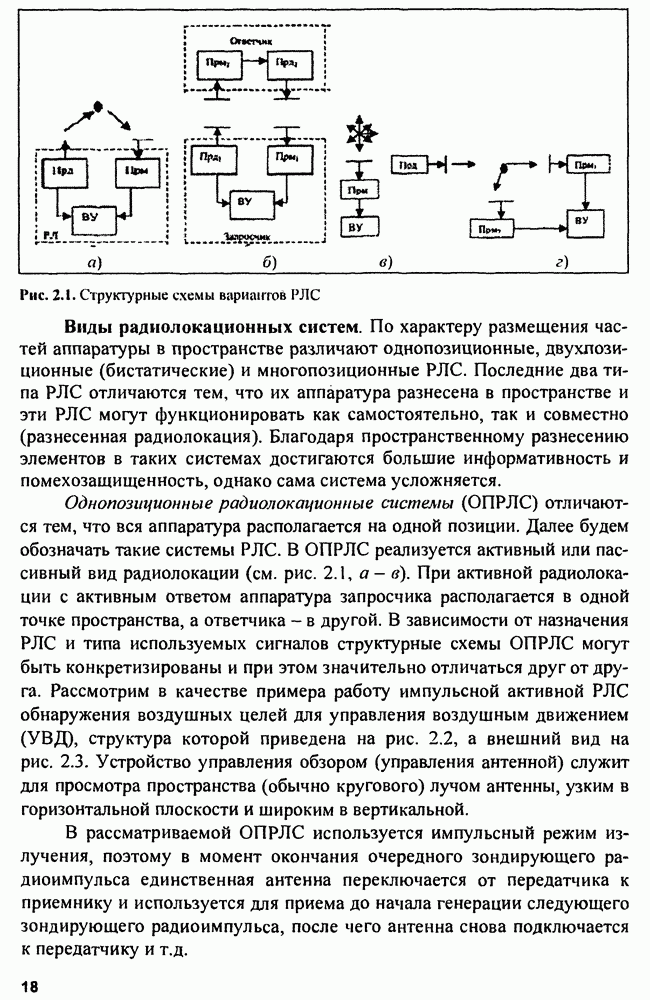
- 2.1. Виды радиолокации и радиолокационных систем
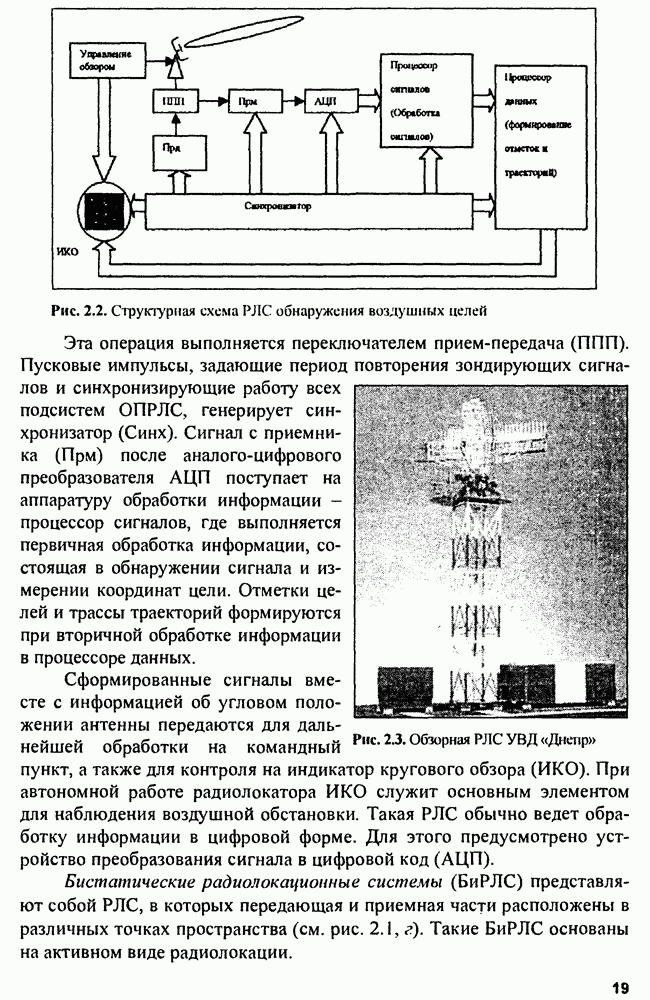
- 2.2. Многопозиционные радиолокационные системы
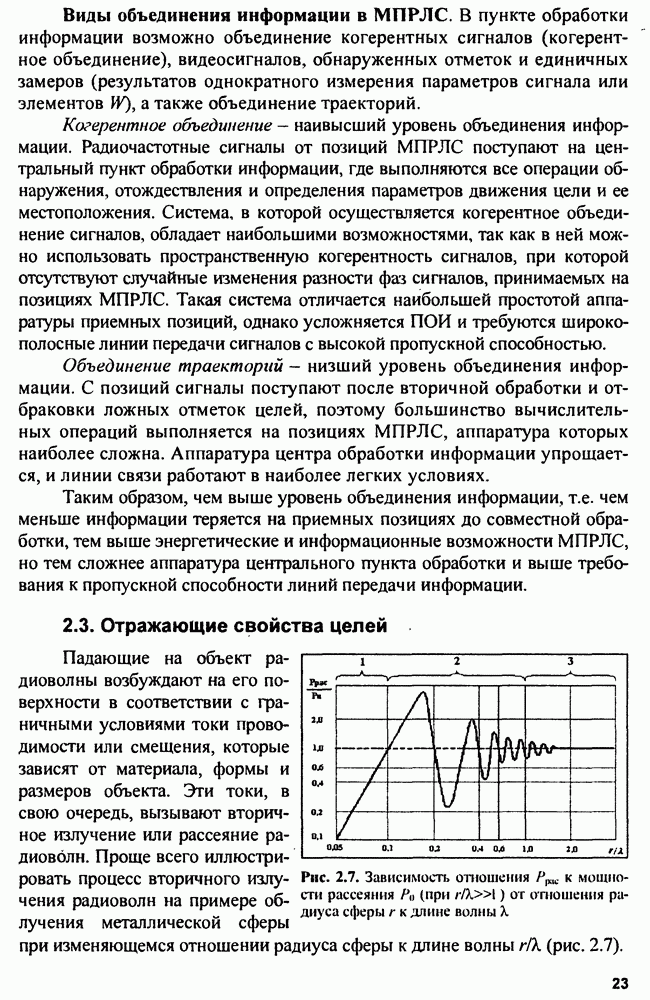
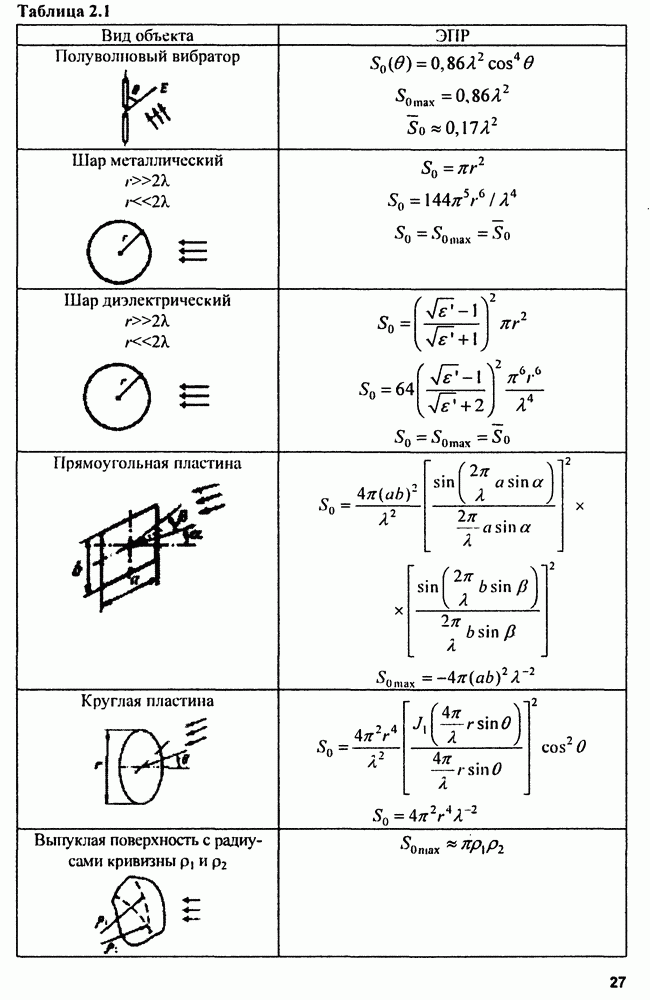
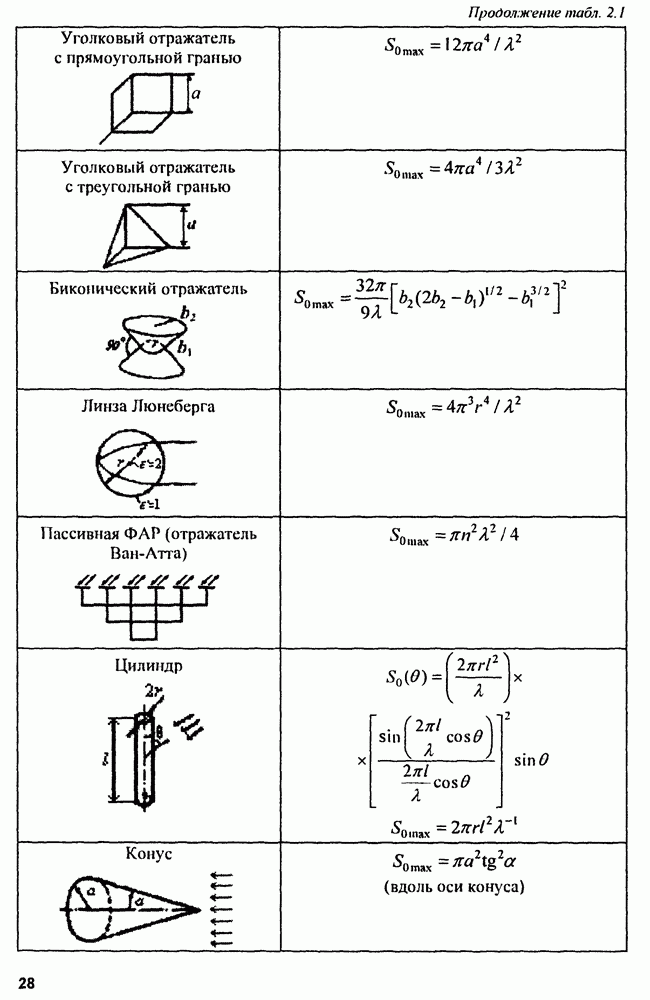
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
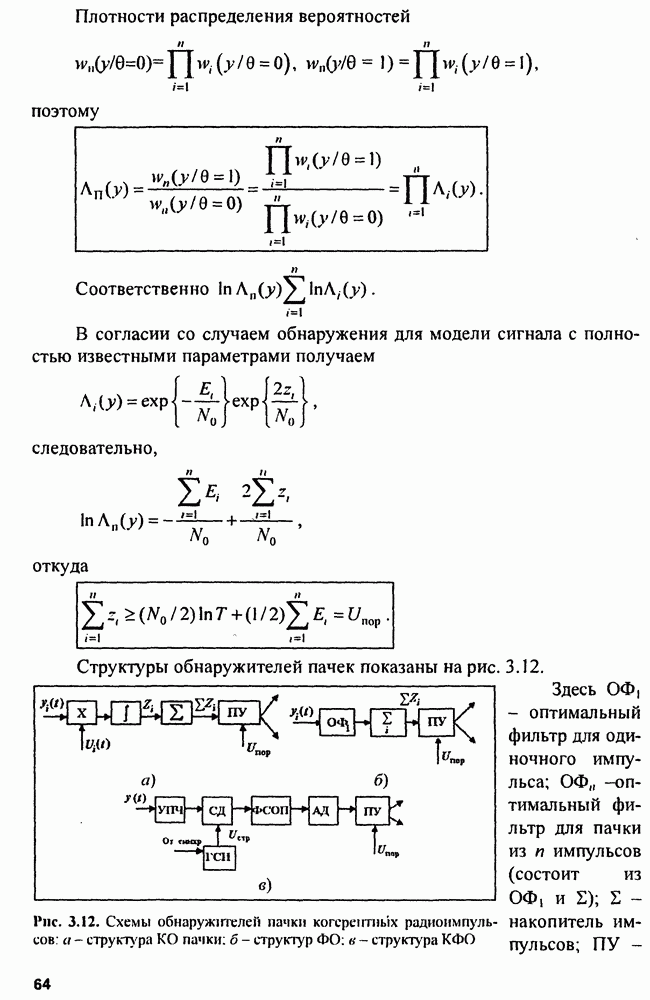
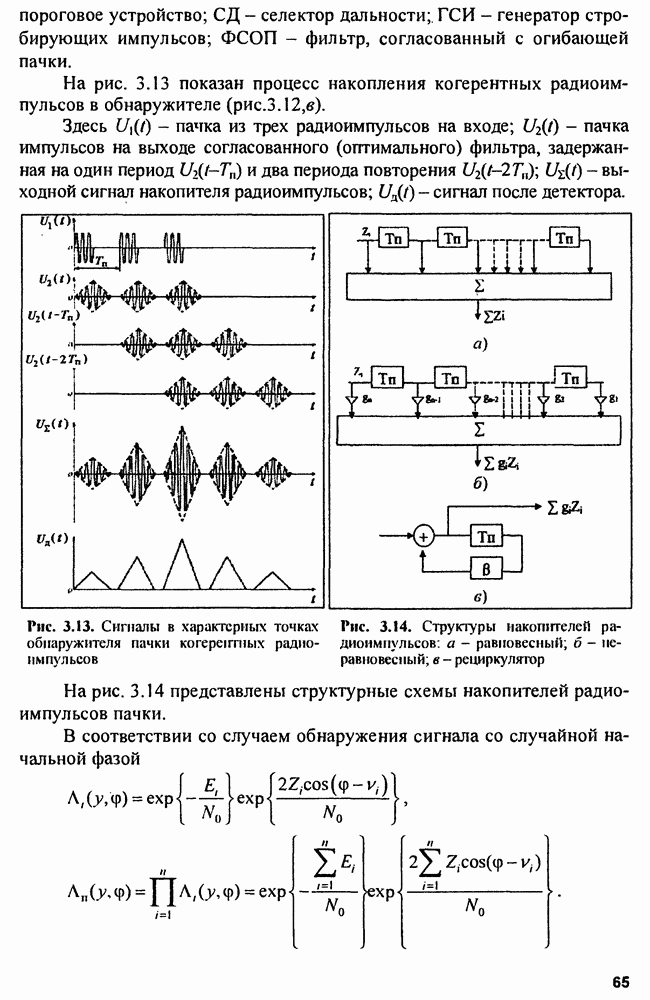
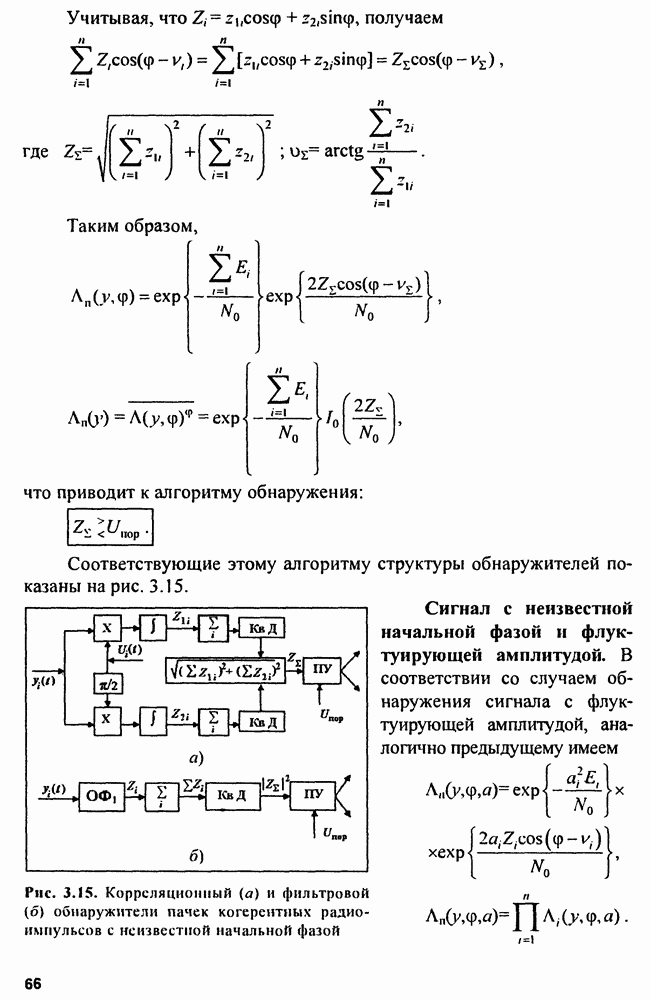
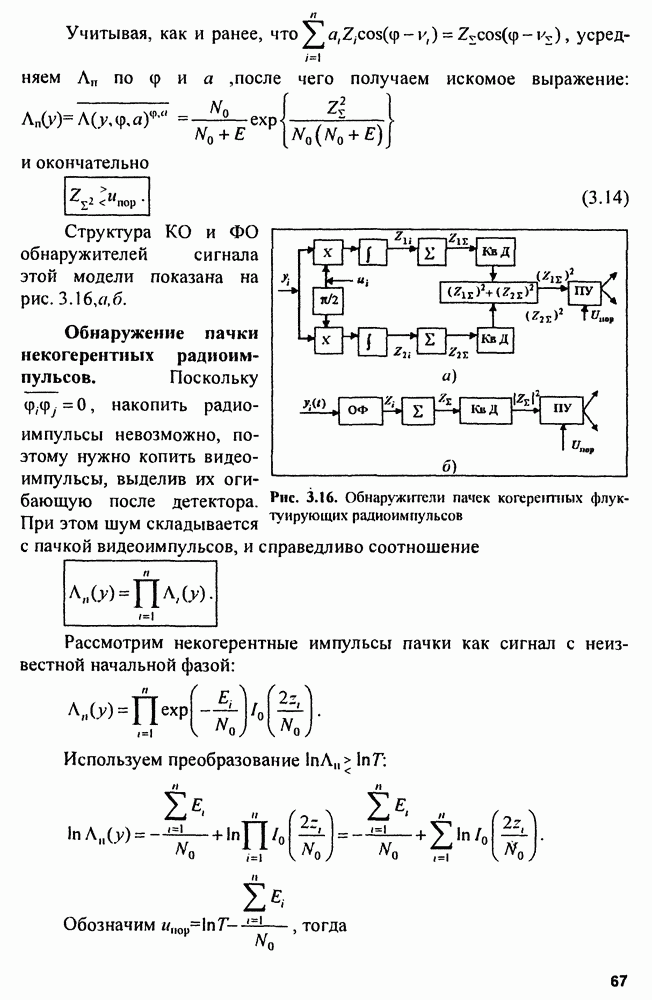
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
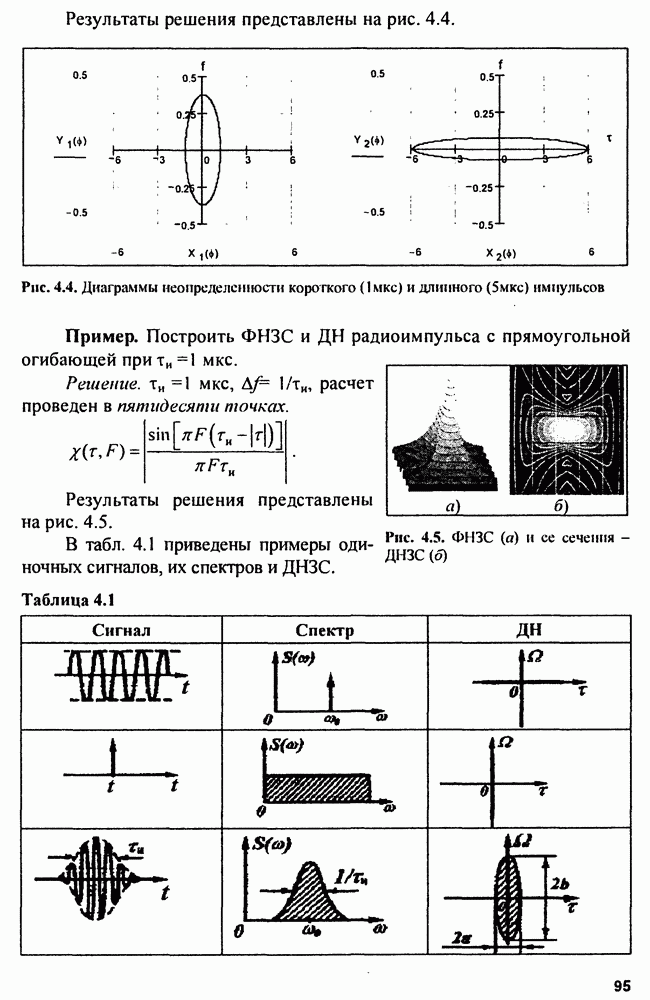
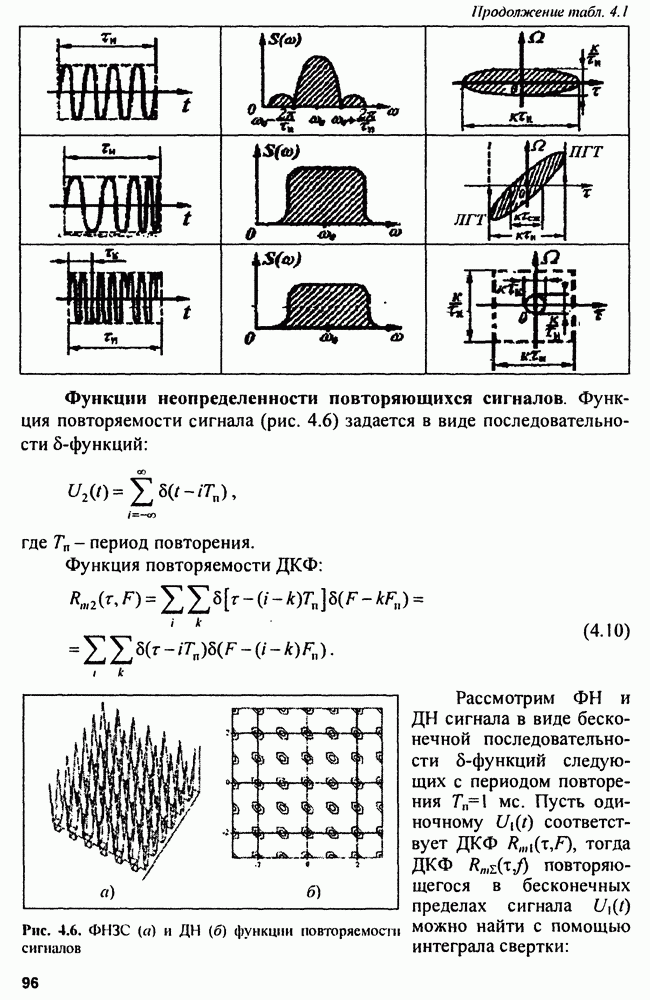
- 4.2. Диаграммы неопределенности
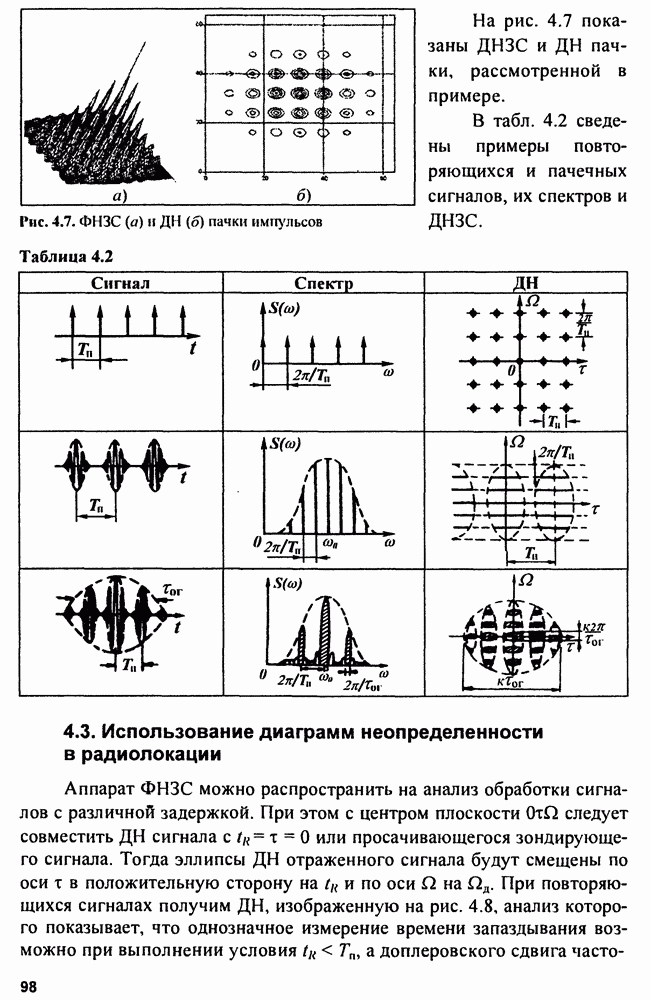
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
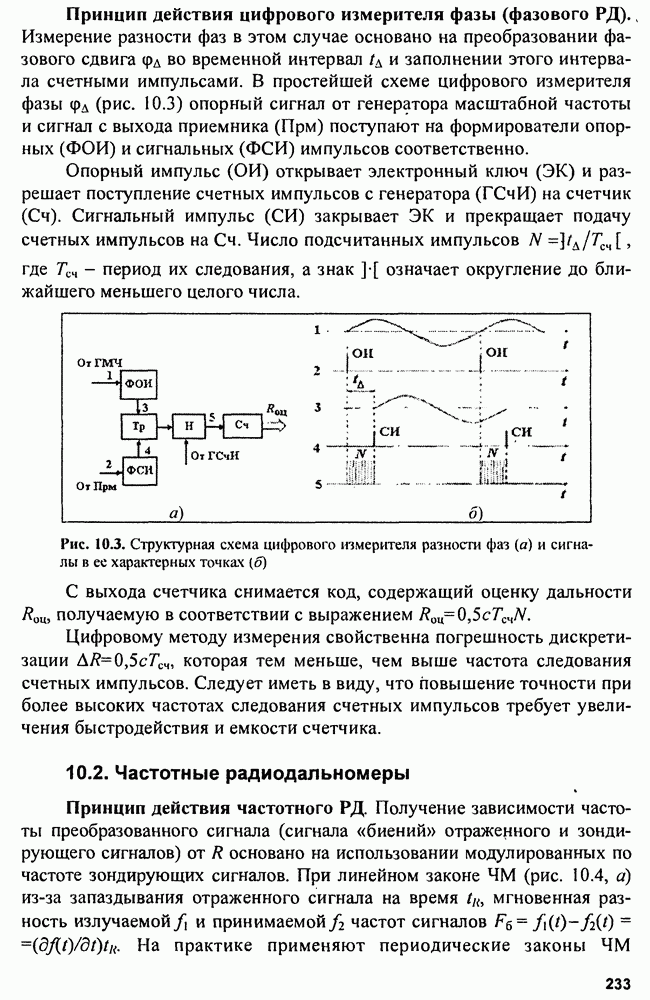
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
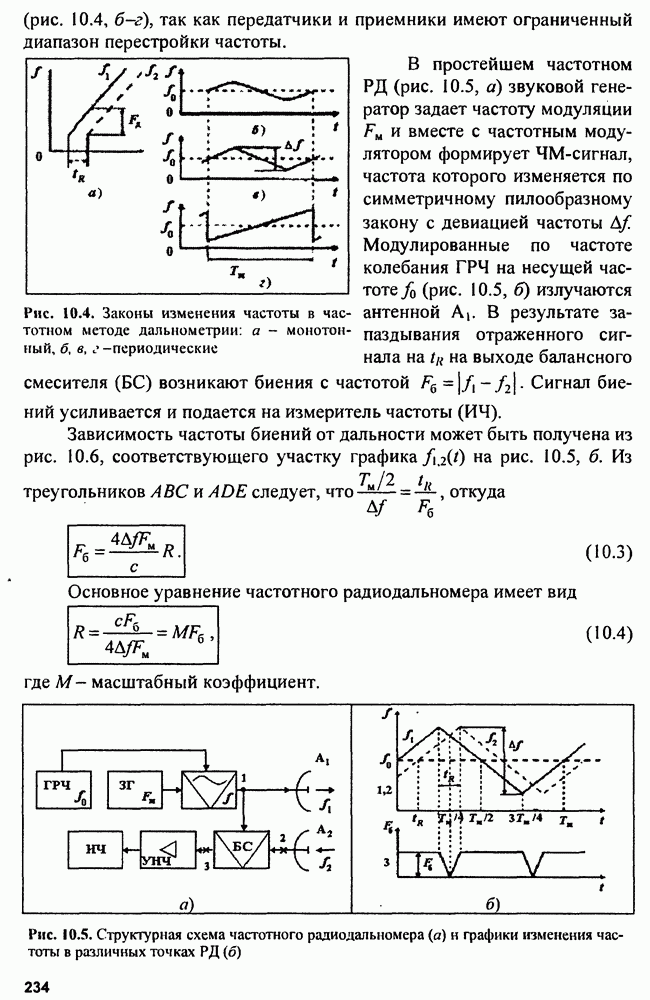
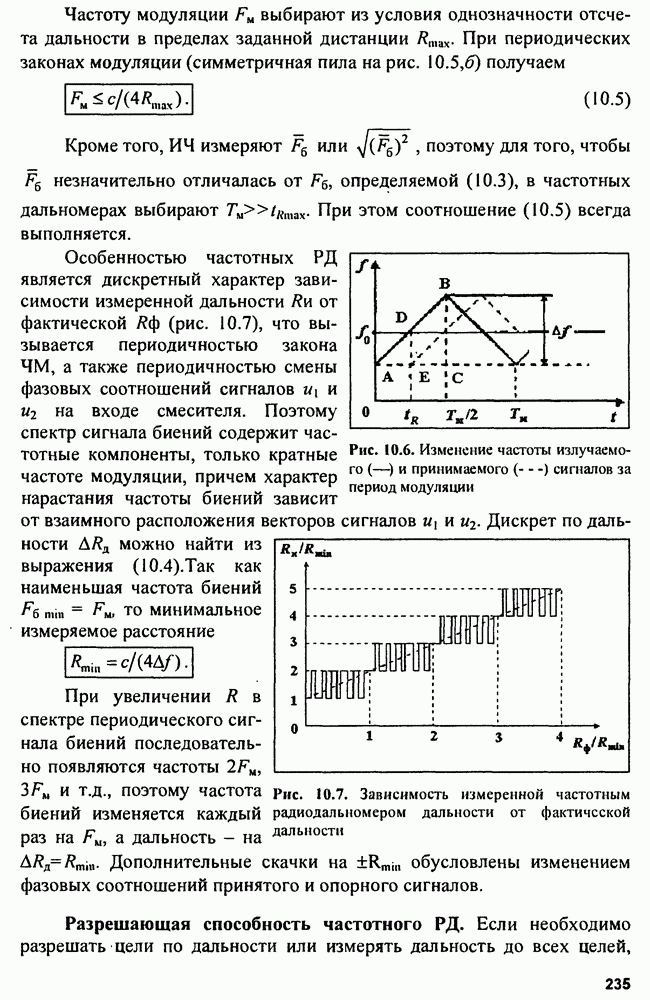
- 10.2. Частотные радиодальномеры
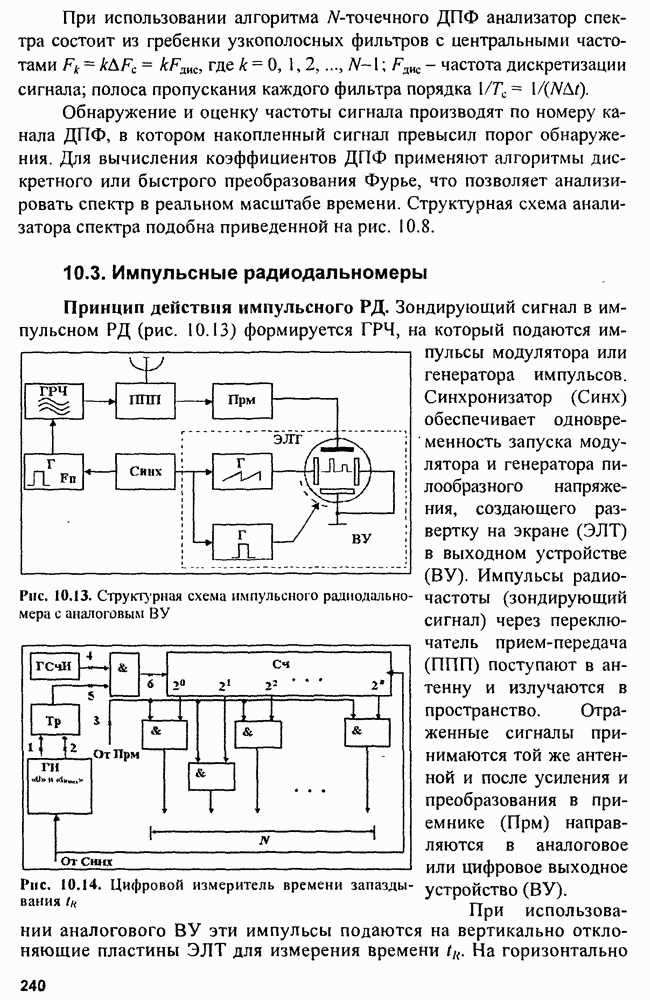
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
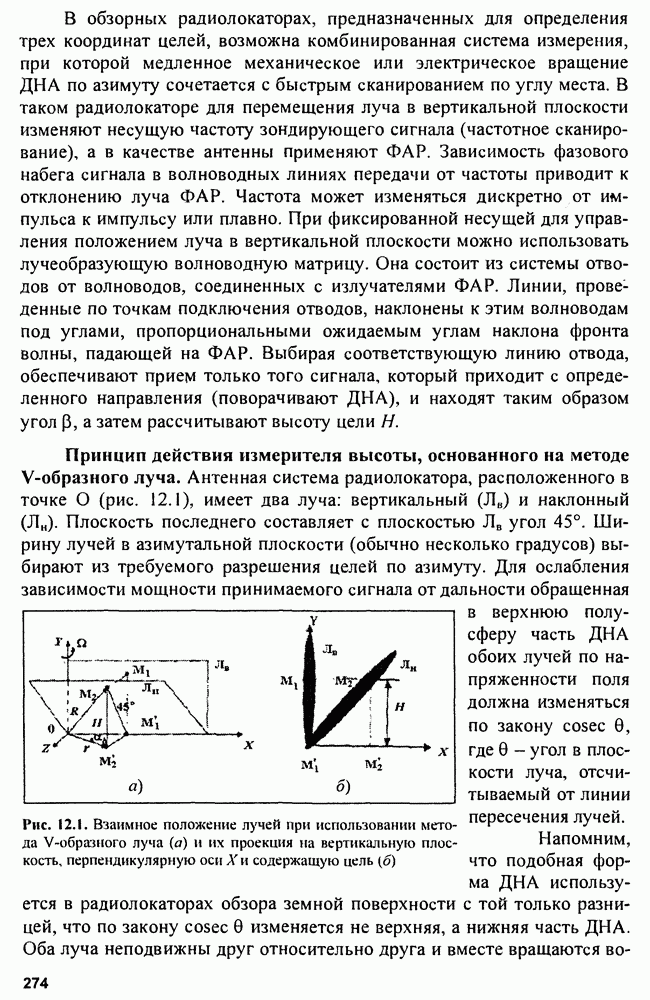
- Глава 12. Измерители высоты
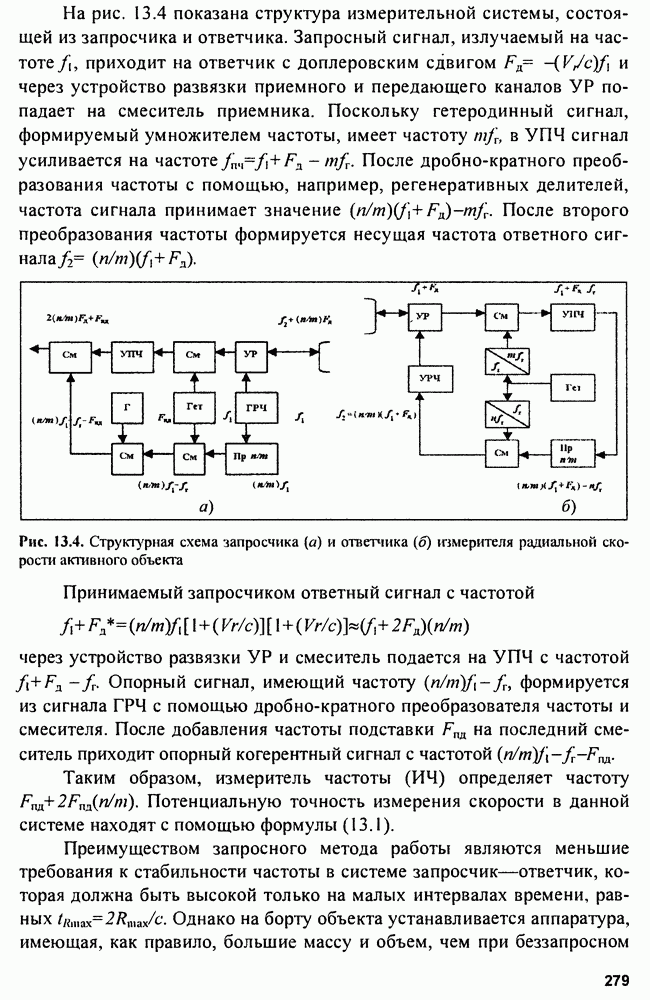
- Глава 13. Измерители скорости цели
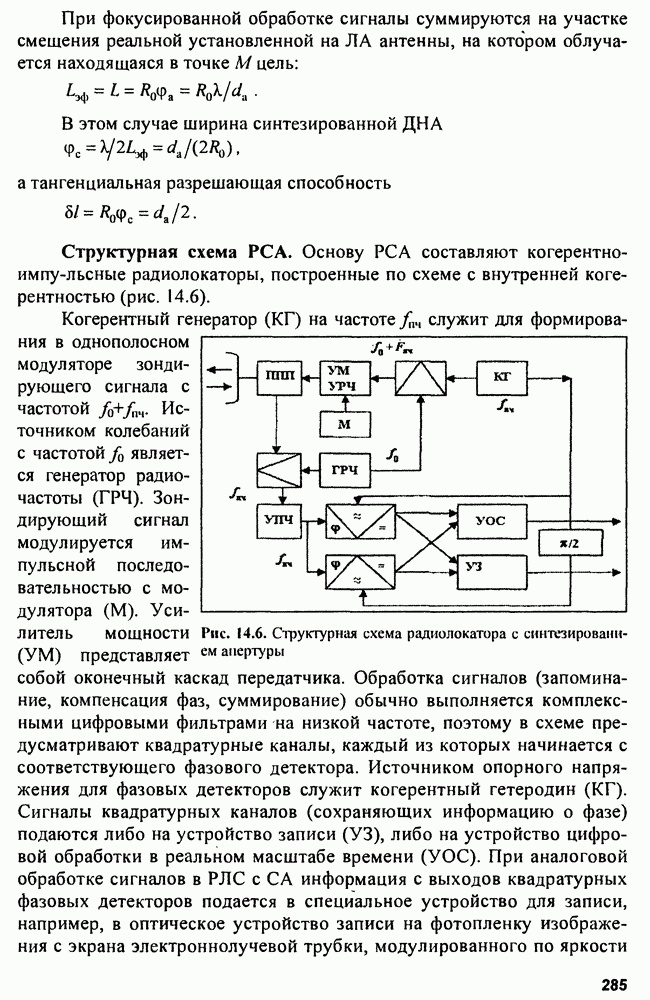
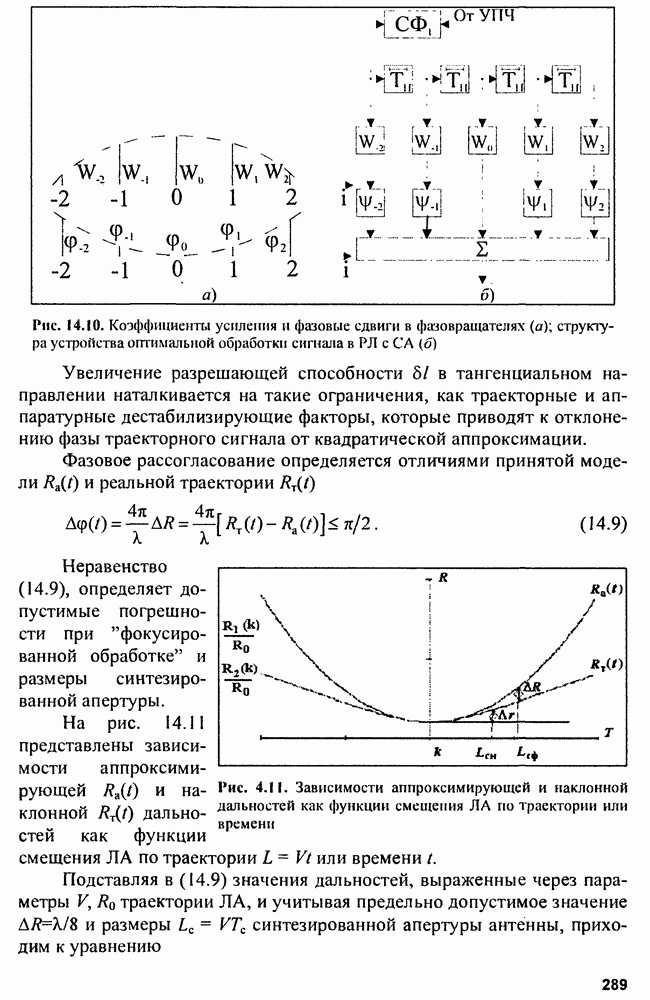
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение