| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
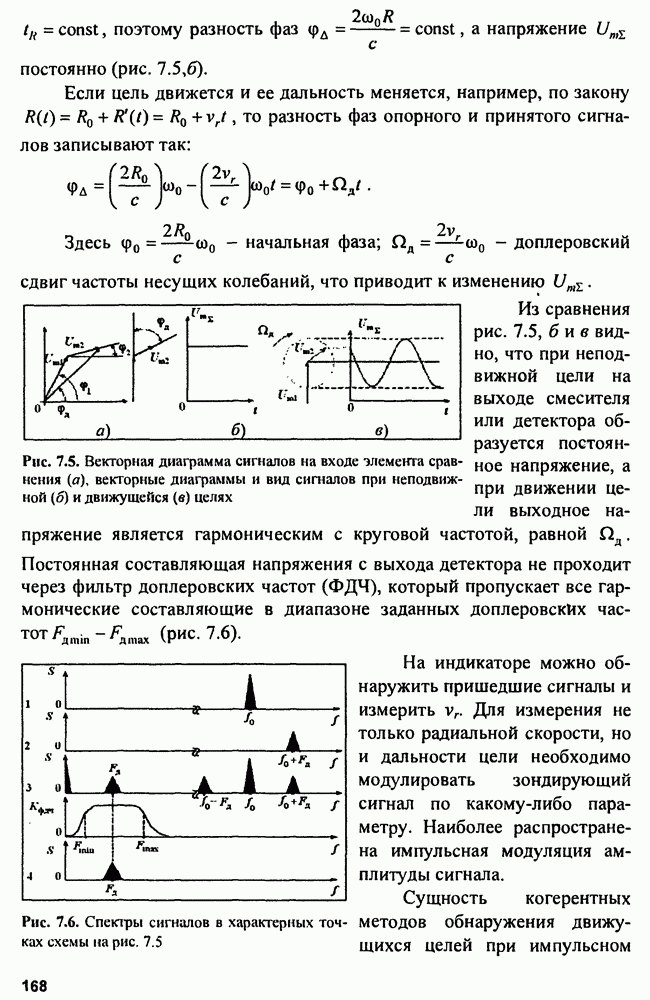
9.6. Оценка параметров сигнала на фоне «белого» шума
Используем метод максимального правдоподобия. Пусть  где
где  "белый" гауссов шум. В этом случае (см. гл. 3)
"белый" гауссов шум. В этом случае (см. гл. 3)

Все параметры сигнала делятся на энергетические, для которых  при
при  и неэнергетические, для которых
и неэнергетические, для которых  при
при 
Рассмотрим энергетический параметр - амплитуду  а точнее амплитудный множитель
а точнее амплитудный множитель  в соотношении
в соотношении 

При

или

Оценка несмещенная и наиболее эффективная. Потенциальная точность оценки амплитуды

или относительная дисперсия при реальных шумах в области положительных частот

К неэнергетическим параметрам относятся, например, фаза, частота, время запаздывания. Оценка неэнергетических параметров осуществляется по формуле

Если, как прежде, обозначить корреляционный интеграл  то условием оценки будет
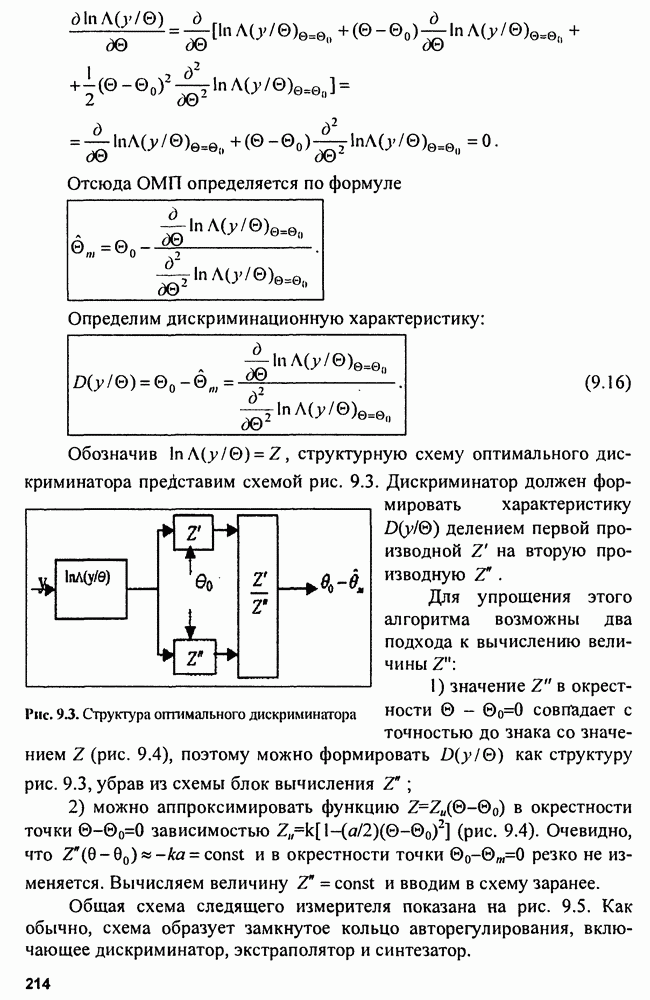
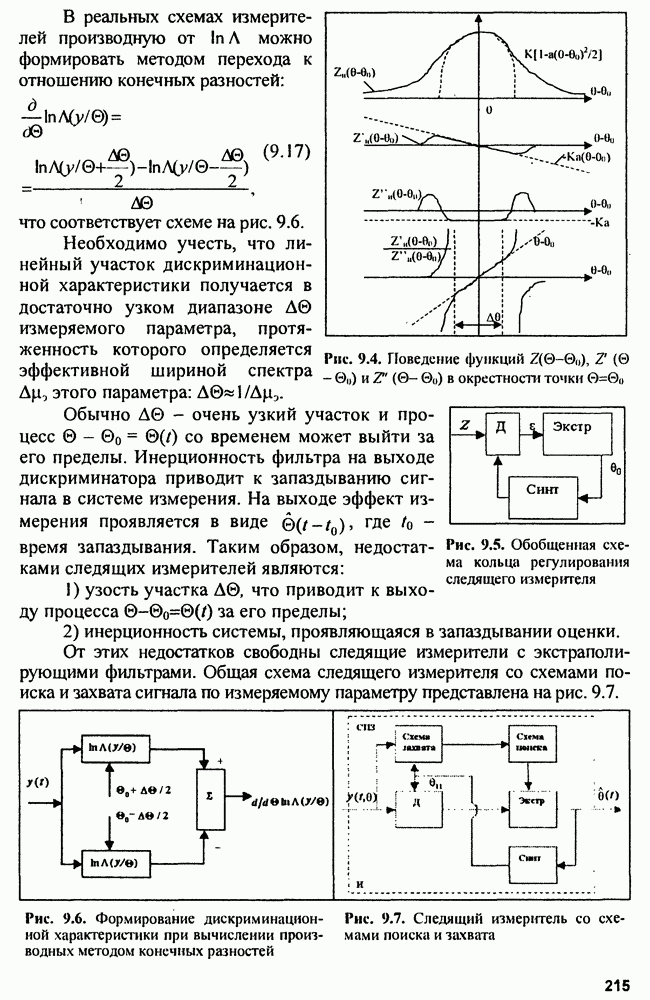
то условием оценки будет  что соответствует структуре измерителя, показанной на рис. 9.1.
что соответствует структуре измерителя, показанной на рис. 9.1.
Пример I. Для определения потенциальной точности оценки фазы воспользуемся соотношением (9.14) и найдем

Тогда для оценки фазы сигнала имеем соотношение

Поскольку при 

потенциальная точность

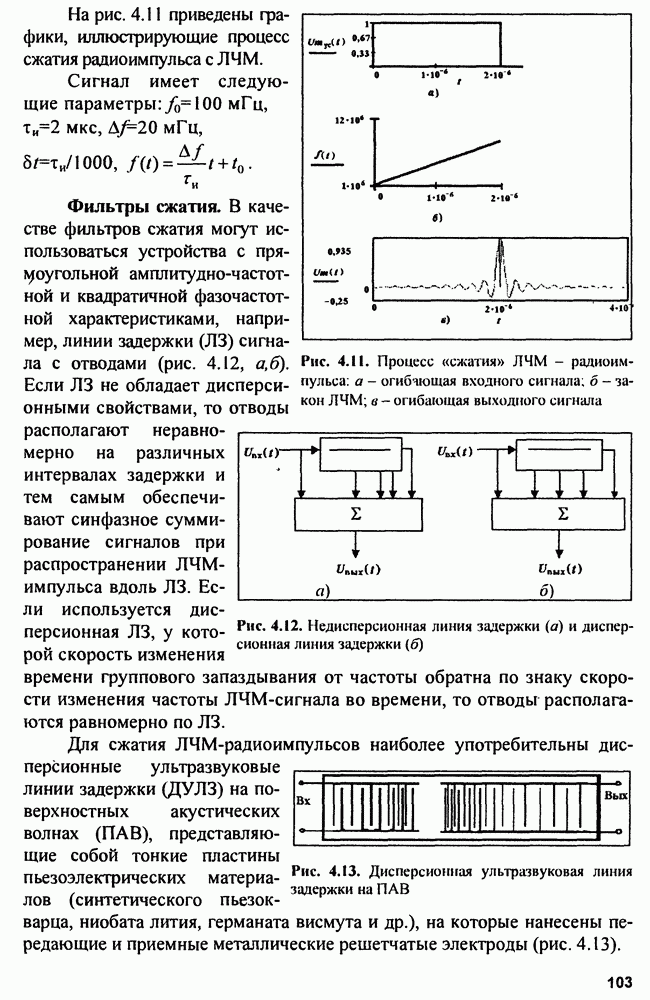
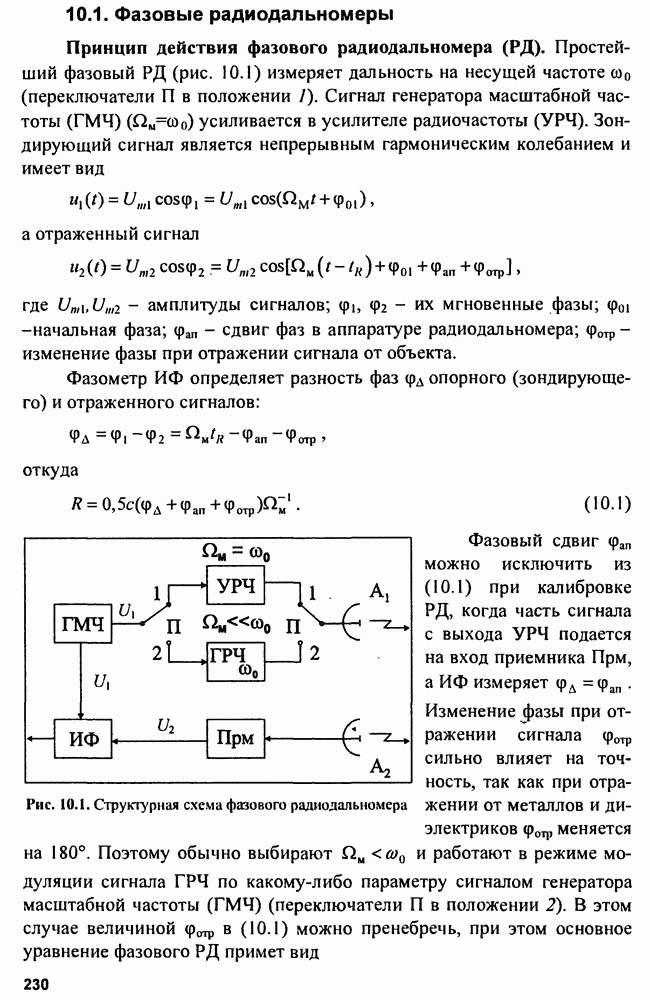
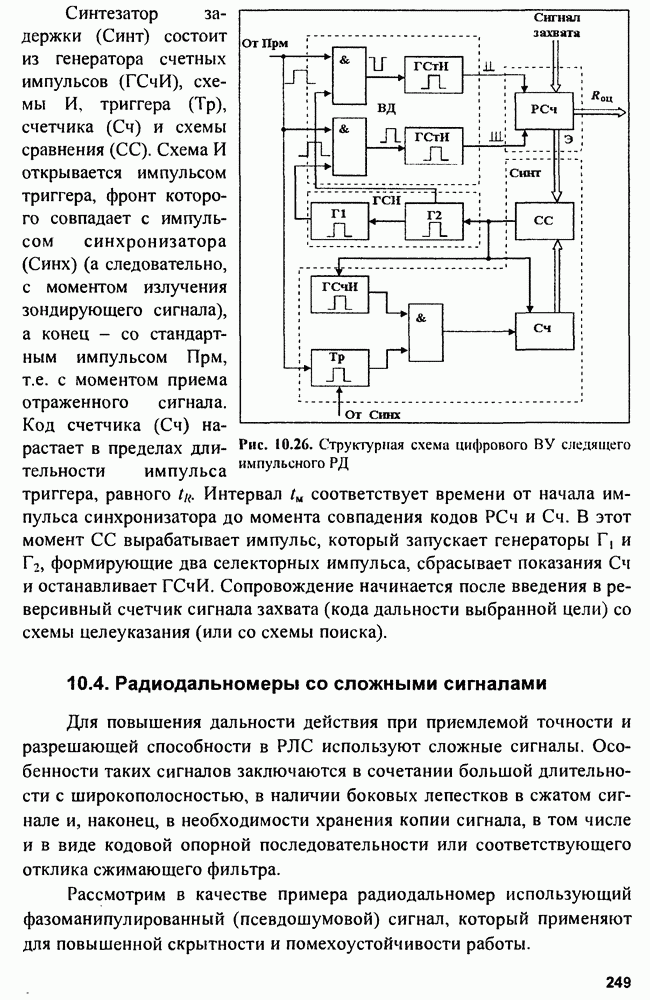
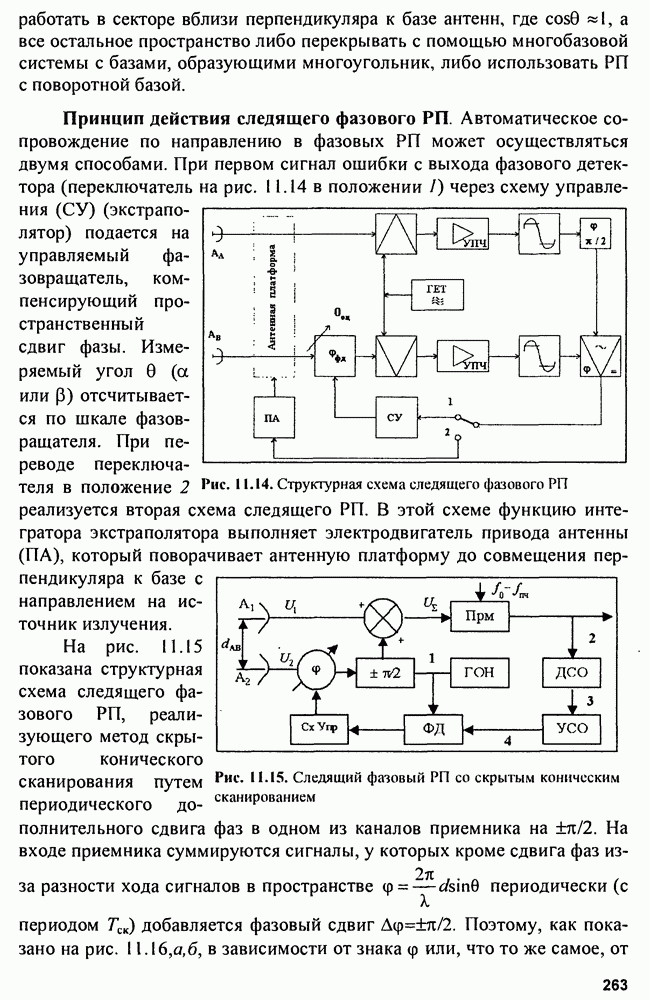
Для этого случая схема рис. 9.1 принимает вид, представленный на рис. 9.8.

Рис. 9.8. Измеритель фазы приходящего радиоимпульса
Здесь в многоканальный коррелятор опорный сигнал подается с линии задержки с отводами, обеспечивающими сдвиг фазы на величину  -Потенциальная точность оценки фазы приходящего радиоимпульса может быть вычислена по найденному значению
-Потенциальная точность оценки фазы приходящего радиоимпульса может быть вычислена по найденному значению 
Пример 2. Рассмотрим измеритель для оценки времени запаздывания сигнала со случайной начальной фазой и амплитудой

где  Пусть
Пусть

при

В соответствии с результатами гл. 3

где  квадратурные корреляционные интегралы имеют вид
квадратурные корреляционные интегралы имеют вид

Максимально правдоподобная оценка, получаемая из соотношения

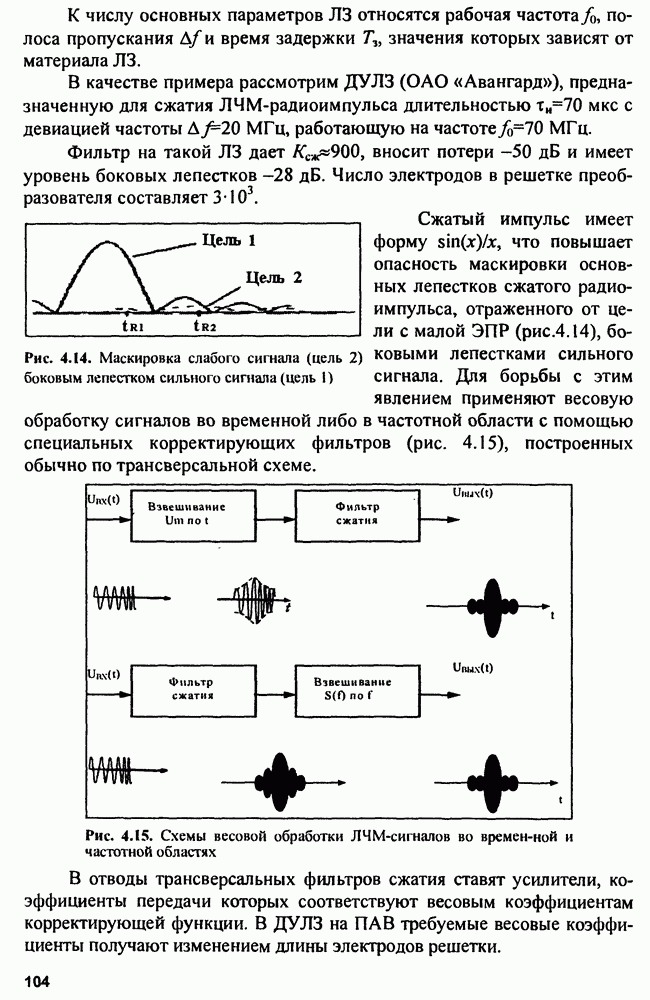
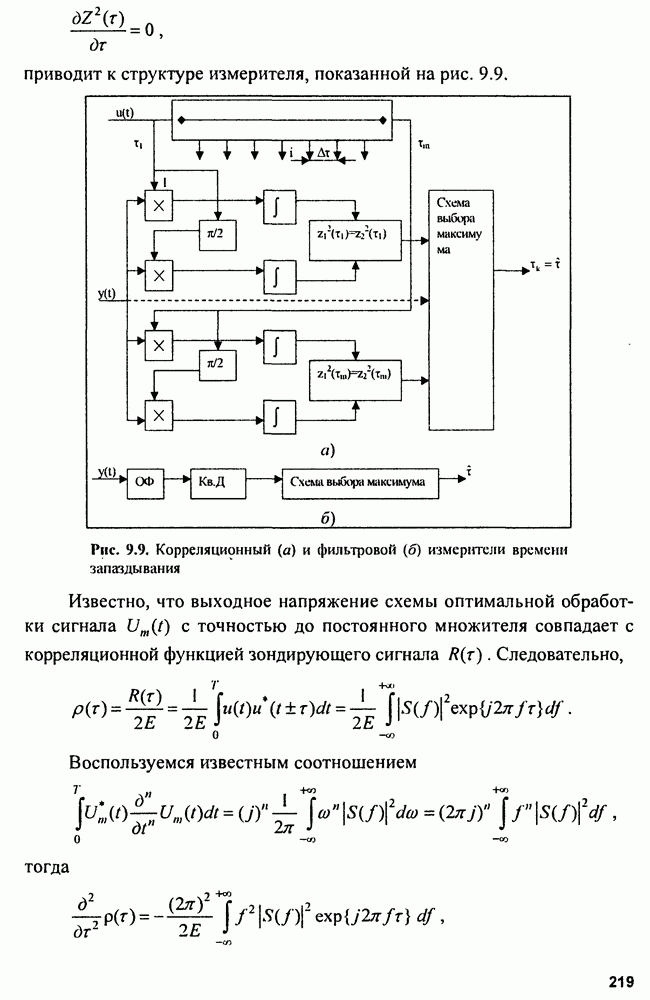
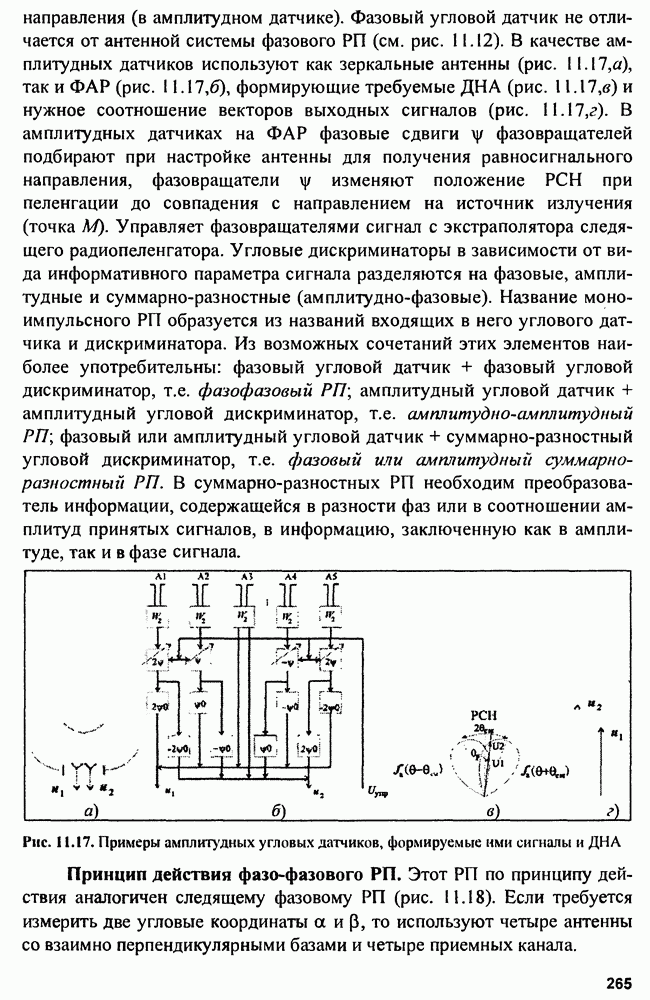
приводит к структуре измерителя, показанной на рис. 9.9.

Рис. 9.9. Корреляционный (а) и фильтровой (б) измерители времени запаздывания
Известно, что выходное напряжение схемы оптимальной обработки сигнала  с точностью до постоянного множителя совпадает с корреляционной функцией зондирующего сигнала
с точностью до постоянного множителя совпадает с корреляционной функцией зондирующего сигнала  Следовательно,
Следовательно,

Воспользуемся известным соотношением

тогда


Запишем выражение для среднеквадратической (эквивалентной) ширины спектра сигнала:

тогда

Обозначая, как всегда,  получаем
получаем

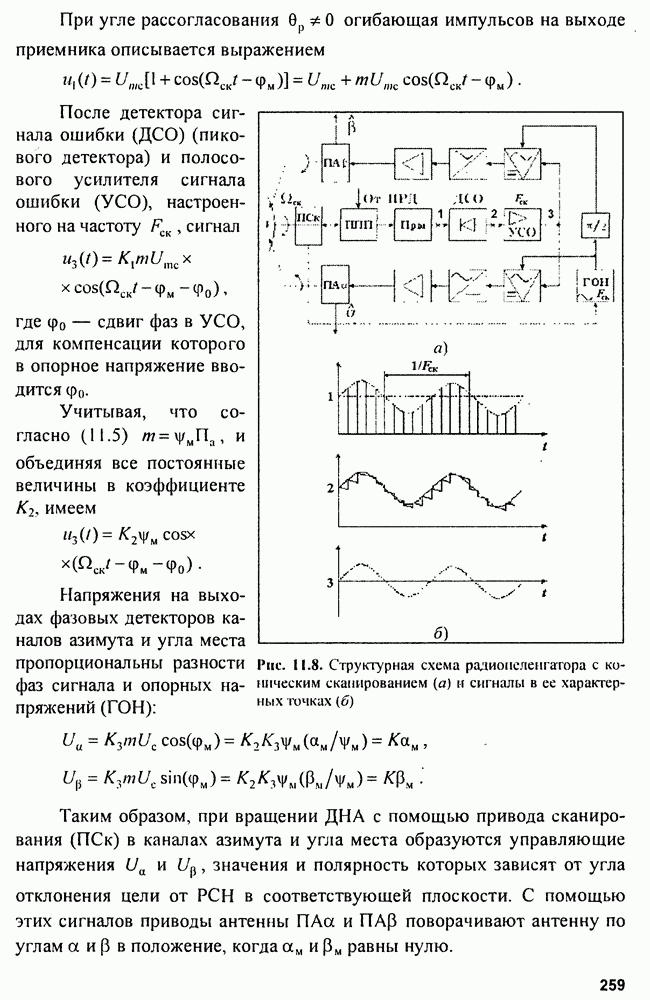
Пример 3. При расчете потенциальной точности измерителя смещения частоты сигнала со случайной фазой и флюктуирующей амплитудой (см. гл. 3)

составим отношение правдоподобия

где  модуль корреляционного интеграла.
модуль корреляционного интеграла.
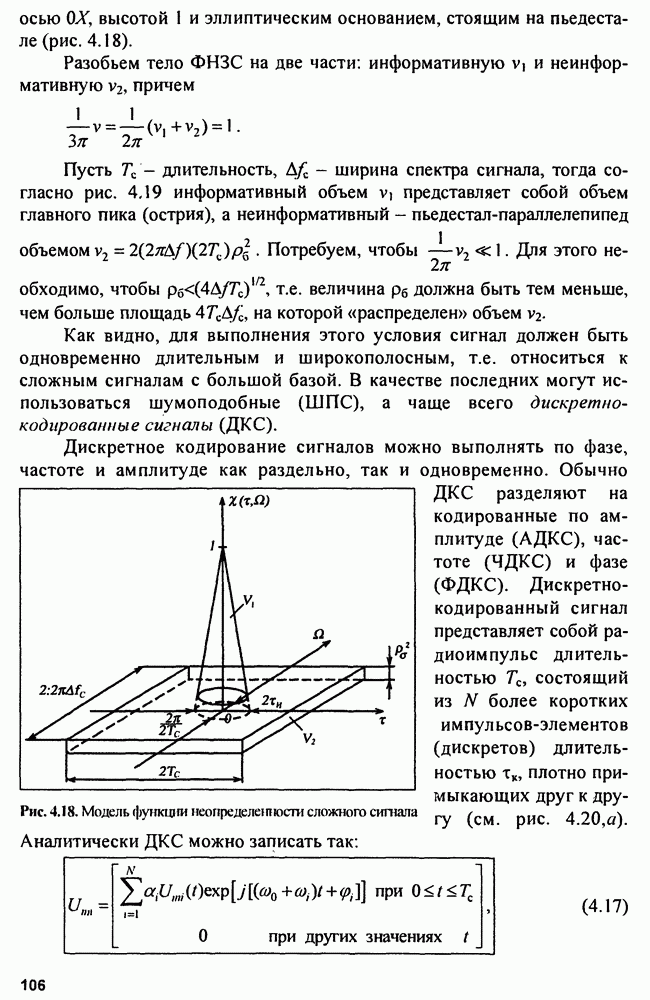
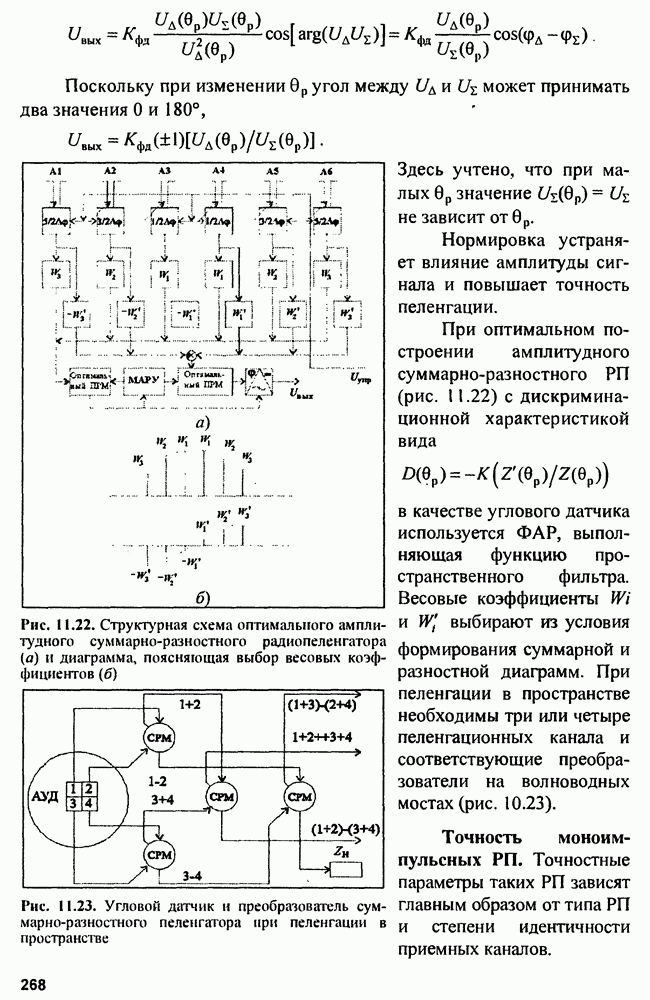
Оценка максимального правдоподобия определяется из уравнения  приводит к схеме измерителя (рис. 9.10), состоящей из
приводит к схеме измерителя (рис. 9.10), состоящей из  каналов, содержащих оптимальные фильтры, детекторы и схему выбора максимума. Аналогично расчету потенциальной точности измерителя времени запаздывания производится расчет потенциальной точности измерителя смещения частоты:
каналов, содержащих оптимальные фильтры, детекторы и схему выбора максимума. Аналогично расчету потенциальной точности измерителя времени запаздывания производится расчет потенциальной точности измерителя смещения частоты:

 среднеквадратическая (эквивалентная) длительность сигнала:
среднеквадратическая (эквивалентная) длительность сигнала:

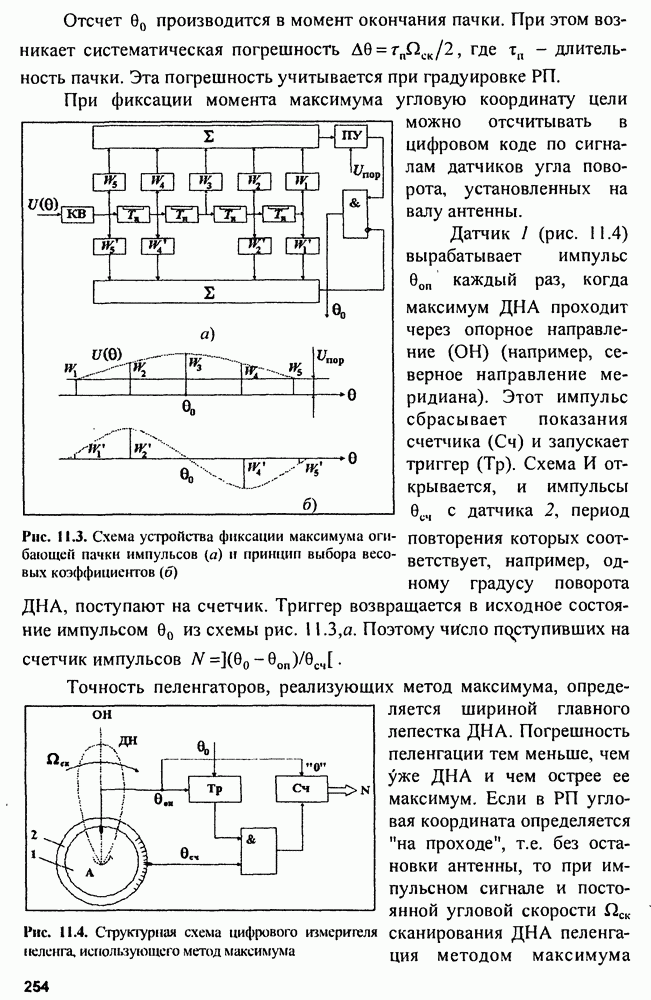
Пример 4. Рассмотрим измеритель угловой координаты при обзоре в горизонтальной плоскости и пеленгации по методу максимума. При плавном обзоре пространства  (а - угол поворота антенны;
(а - угол поворота антенны;  угловая скорость обзора) огибающая пачки на выходе приемника
угловая скорость обзора) огибающая пачки на выходе приемника  . Таким образом,
. Таким образом, 
Пеленгационная характеристика может быть представлена в виде

где  ширина пеленгационной характеристики на уровне 0,46. При этом
ширина пеленгационной характеристики на уровне 0,46. При этом


Рис. 9.10. Схема измерителя частоты
Следовательно, поскольку  получаем
получаем

Так как  где
где  диаметр антенны,
диаметр антенны,

Очевидно, что повышение точности оценки возможно за счет увеличения  или за счет
или за счет  , но
, но  не может быть больше чем
не может быть больше чем  и целесообразно использовать сигналы с максимальным
и целесообразно использовать сигналы с максимальным  Например, спектр сигнала с балансной модуляцией несущего колебания
Например, спектр сигнала с балансной модуляцией несущего колебания
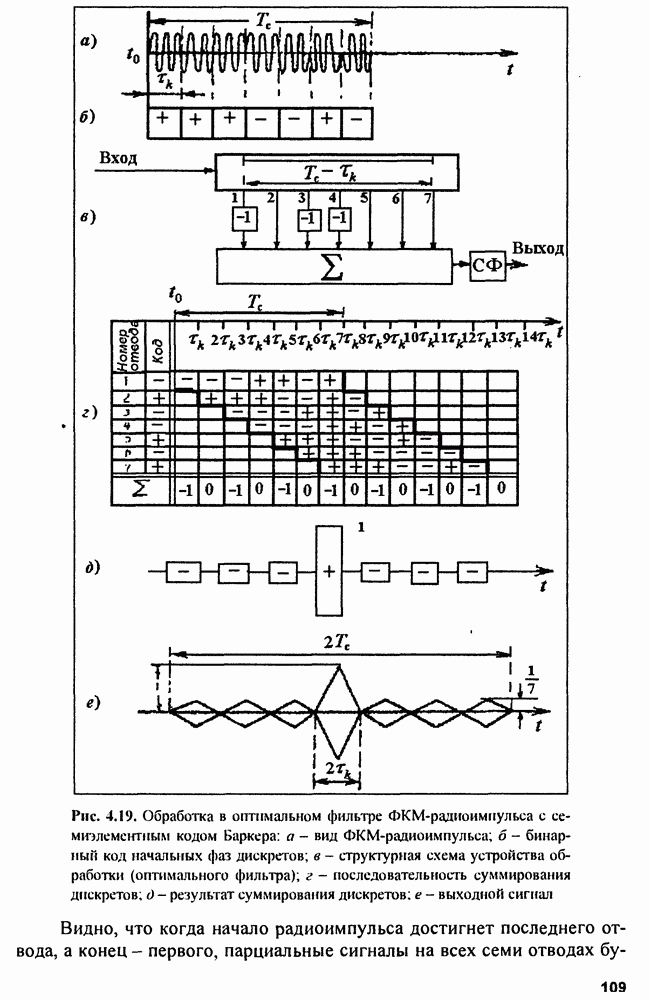
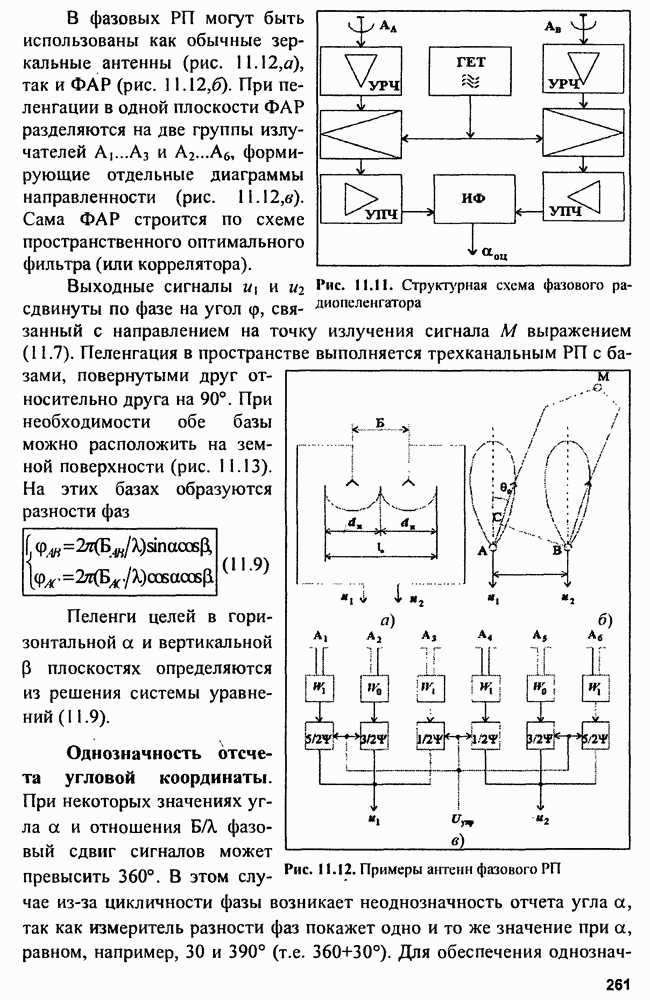
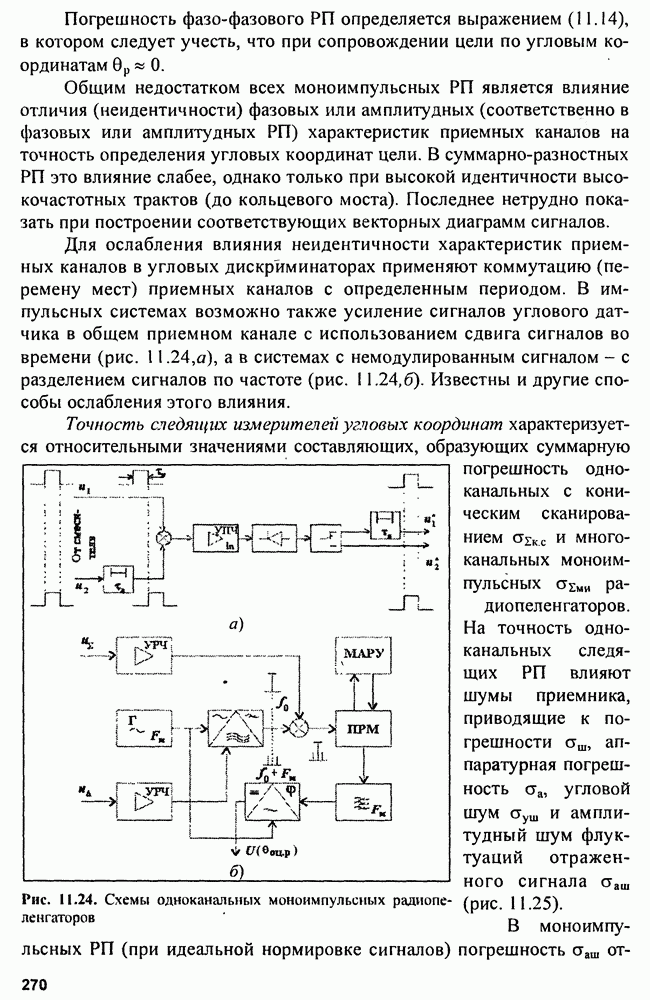
гармоническим колебанием состоит из двух компонент, расположенных по его краям (рис. 9.11, а). При этом энергия одной составляющей  а общая суммарная энергия сигнала
а общая суммарная энергия сигнала  Тогда эффективная ширина спектра этого сигнала
Тогда эффективная ширина спектра этого сигнала

Такой сигнал будет реализовывать наилучшую точность оценки, поскольку получаем наибольшее 
При использовании ЛЧМ-сигнала со сплошным равномерным спектром (рис. 9.11, б) в той же полосе частот, причем форма огибающей спектра может быть аппроксимирована прямоугольником, получаем  т.е. точность оценки при использовании ЛЧМ-сигнала в раз хуже по сравнению с балансно-модулированным сигналом.
т.е. точность оценки при использовании ЛЧМ-сигнала в раз хуже по сравнению с балансно-модулированным сигналом.

Рис. 9.11. Спектры сигналов оптимального для точных измерений  и оптимального для разрешения целей (б)
и оптимального для разрешения целей (б)
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
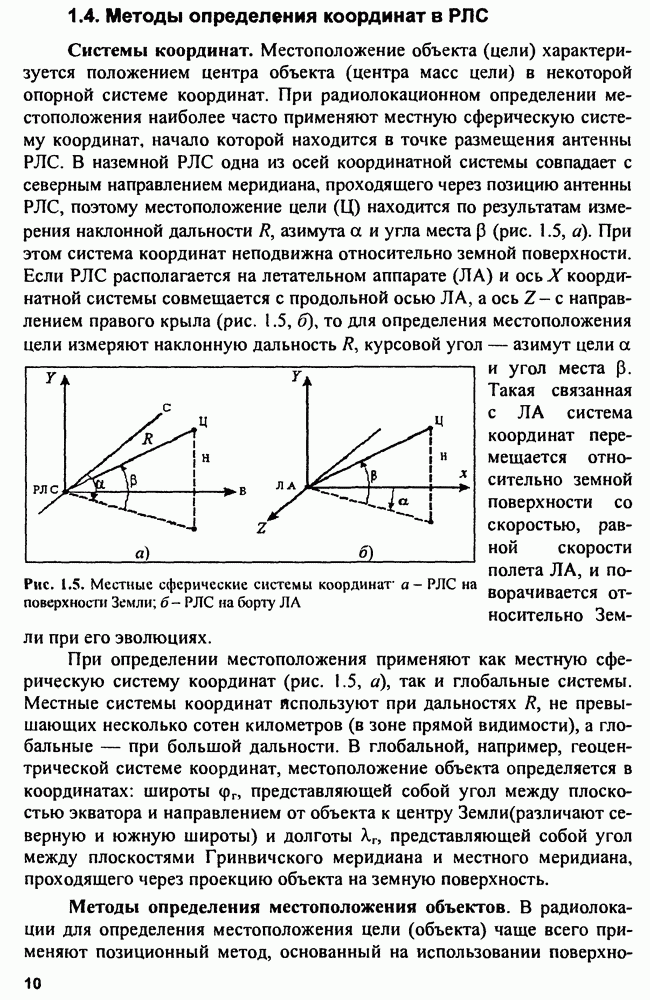
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
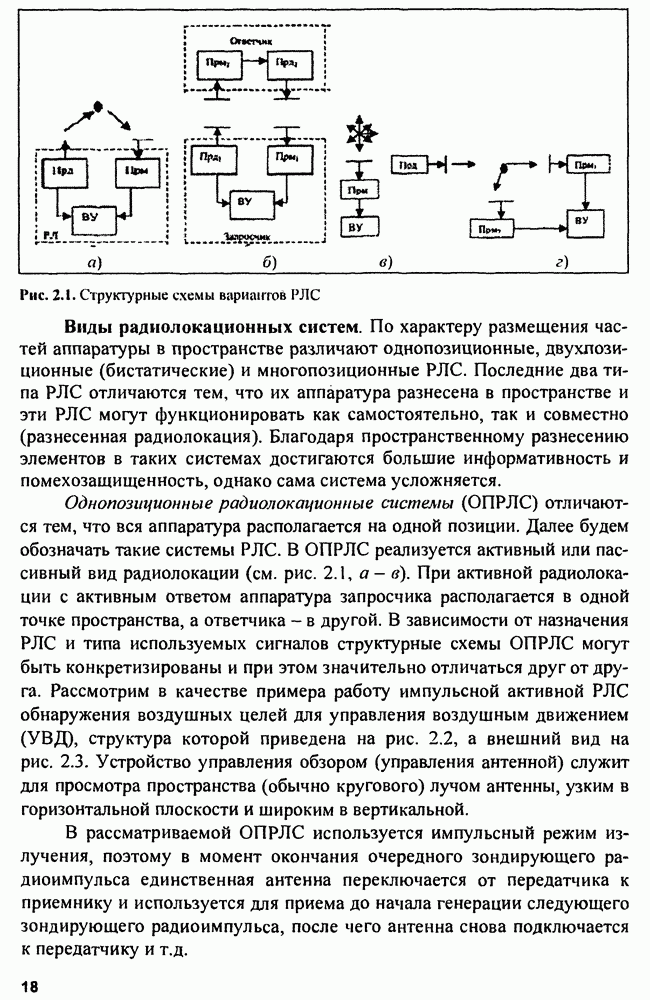
- 2.1. Виды радиолокации и радиолокационных систем
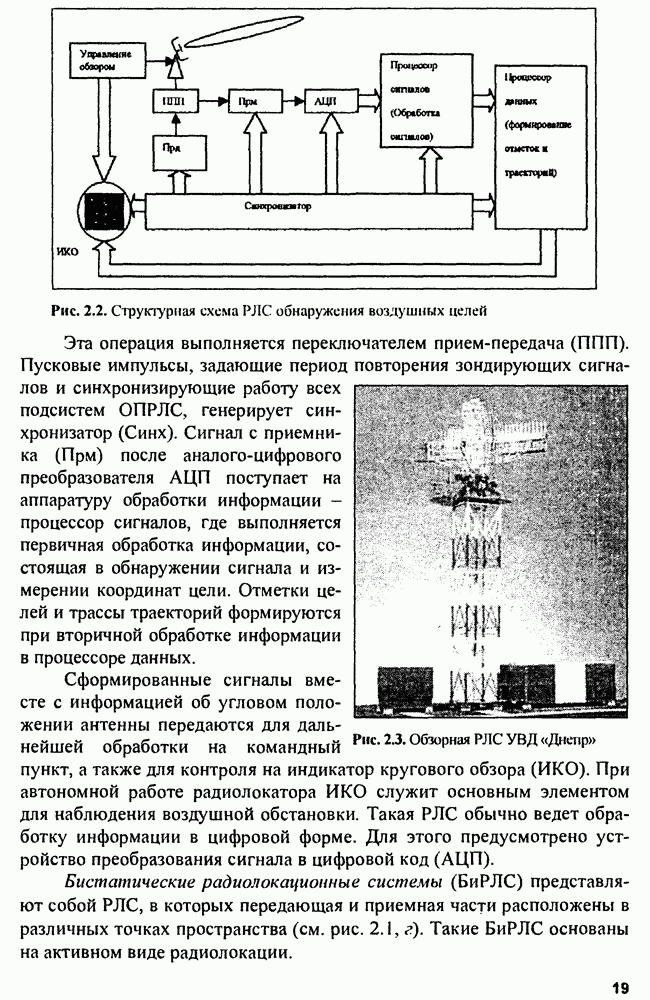
- 2.2. Многопозиционные радиолокационные системы
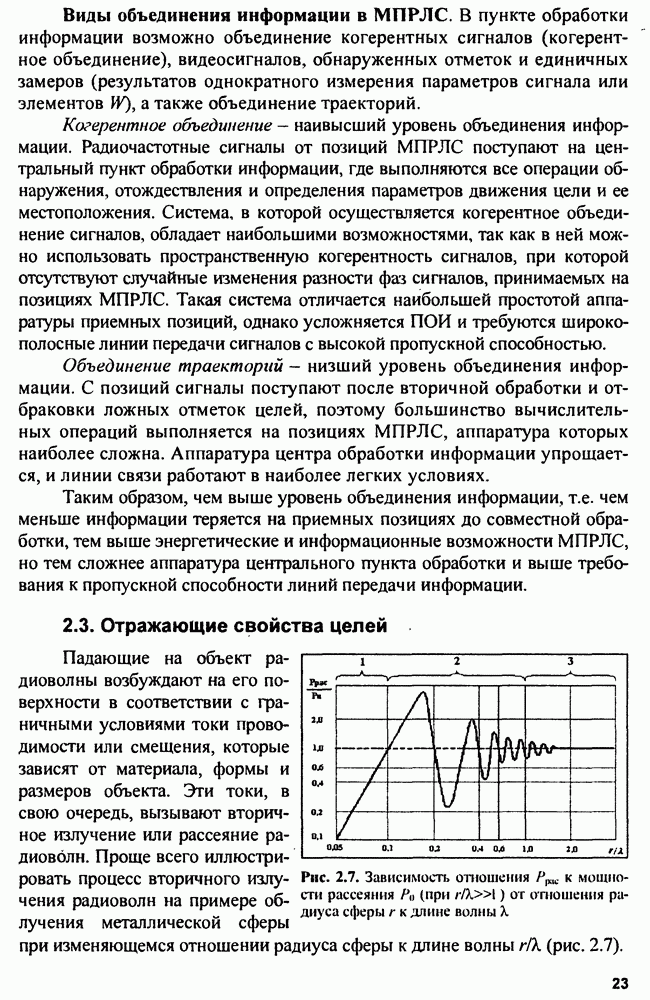
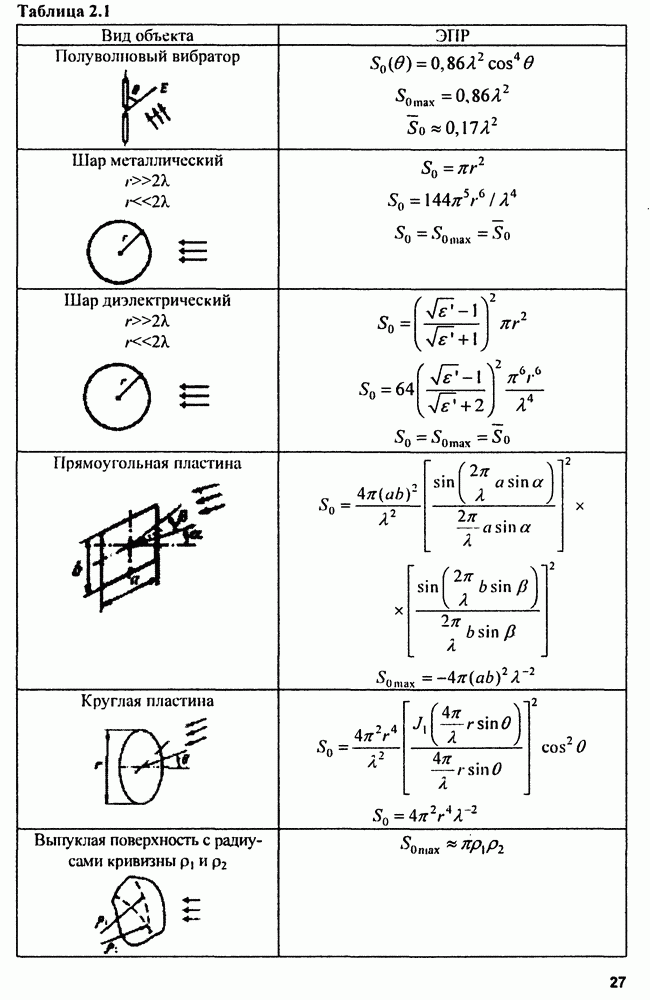
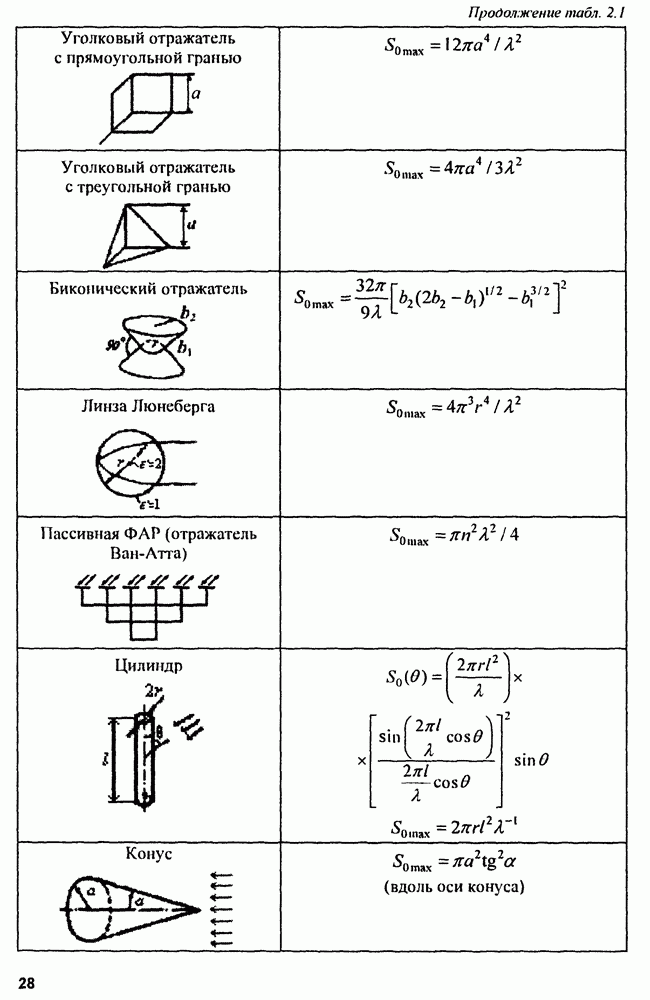
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
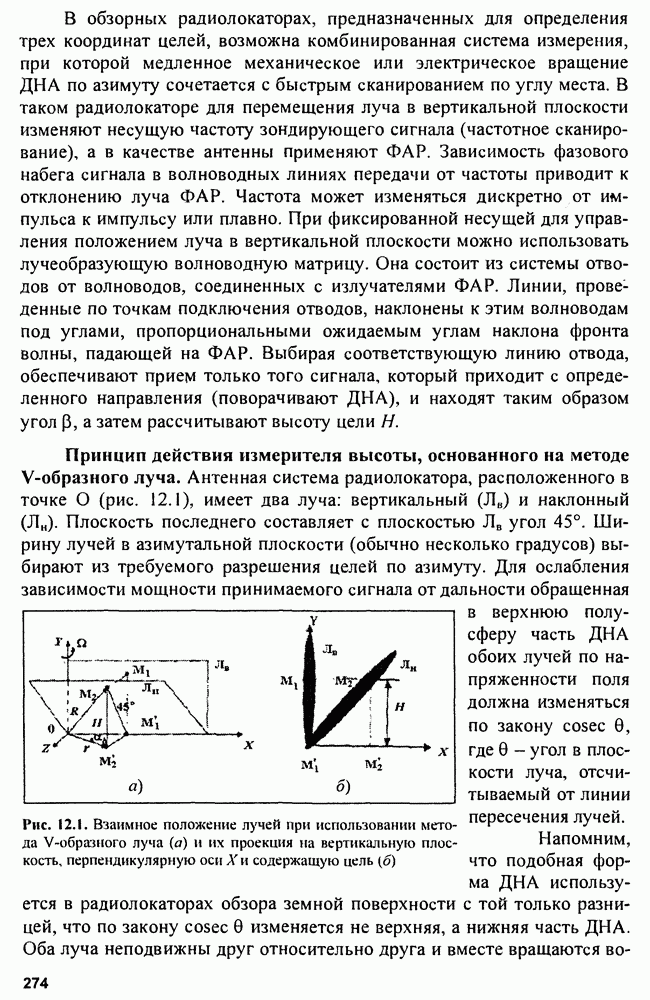
- Глава 12. Измерители высоты
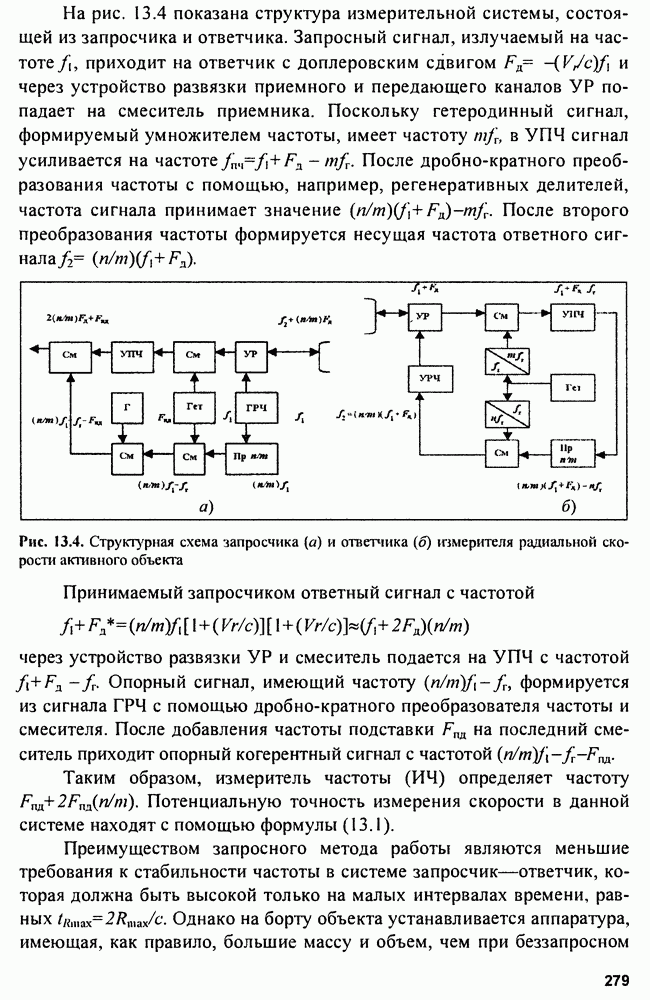
- Глава 13. Измерители скорости цели
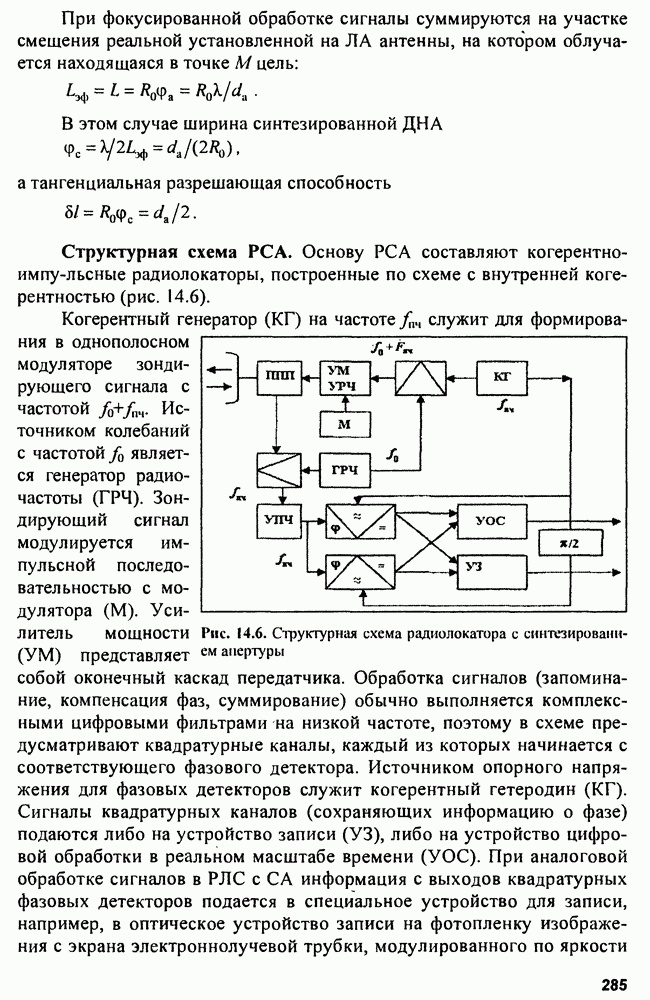
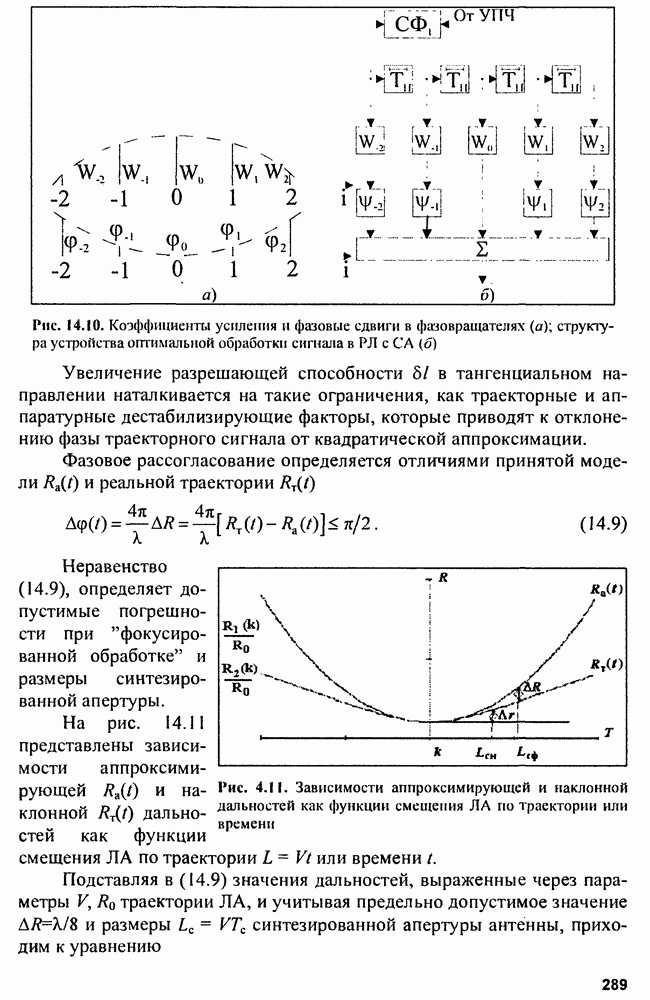
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение