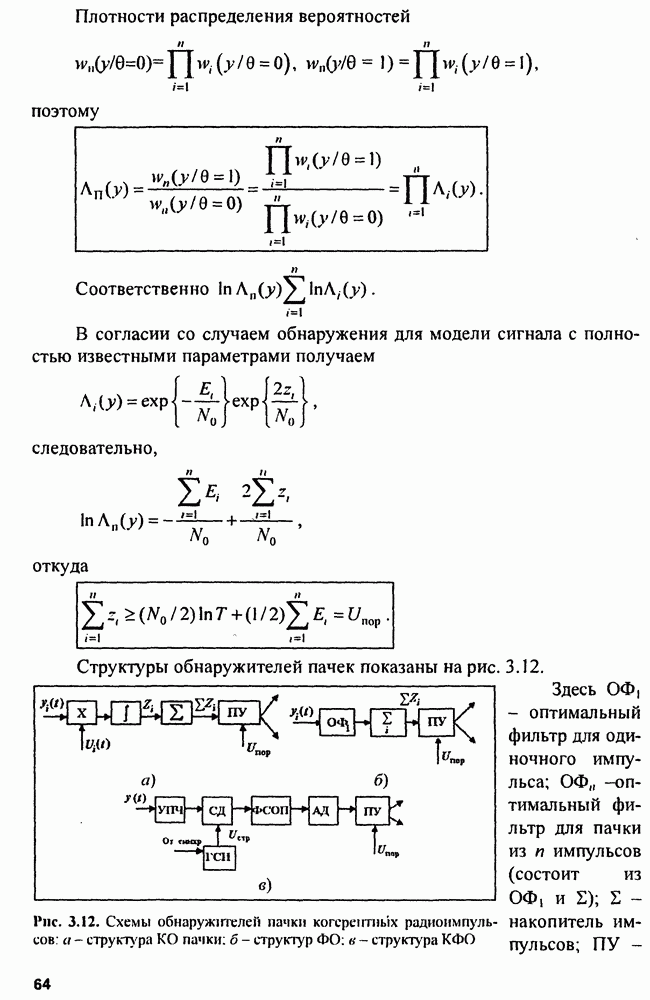
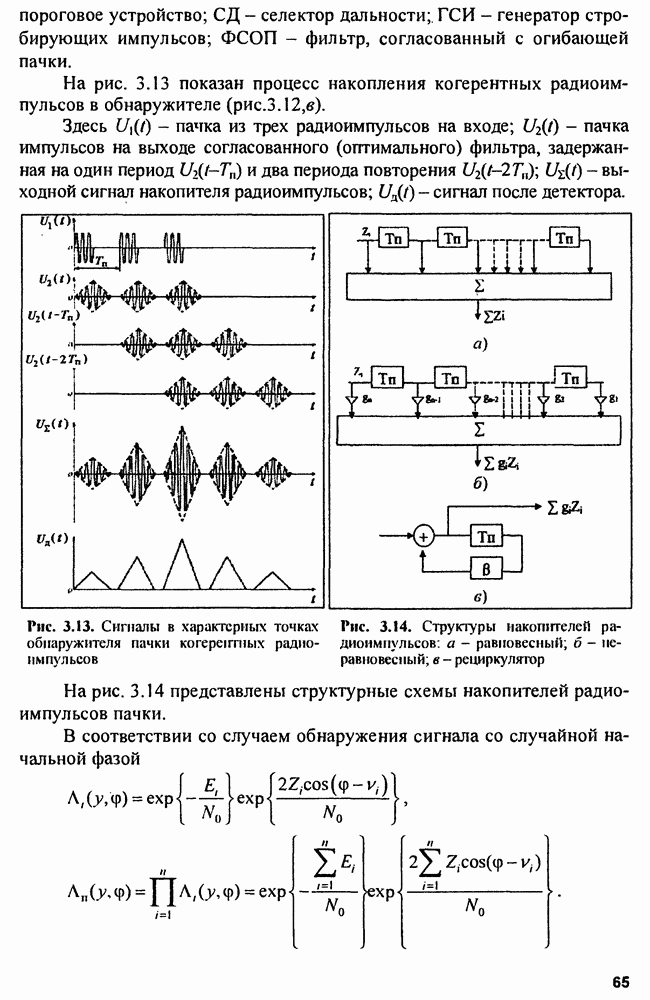
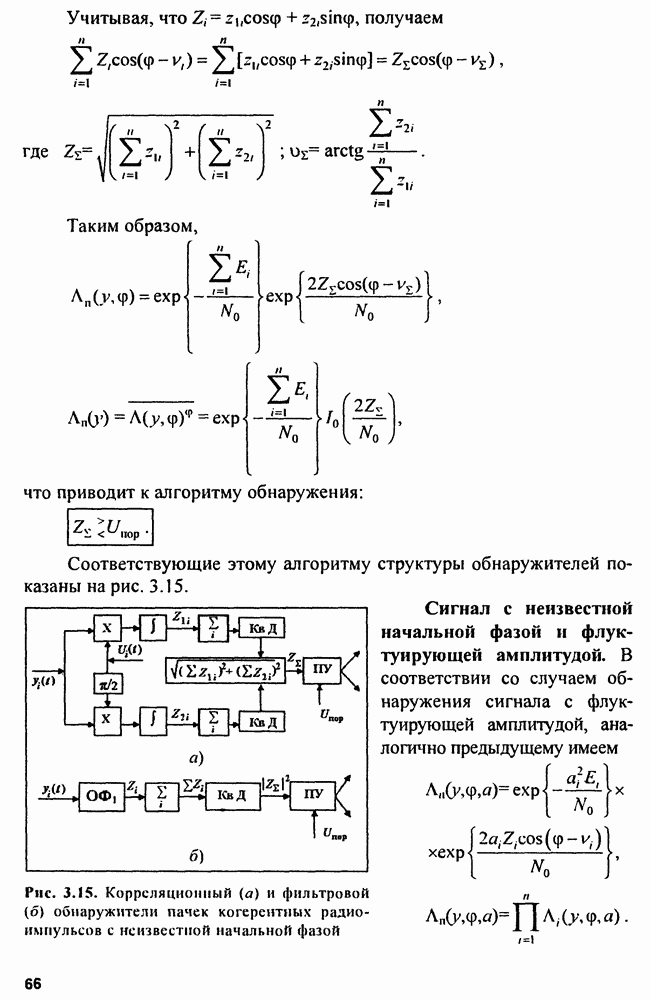
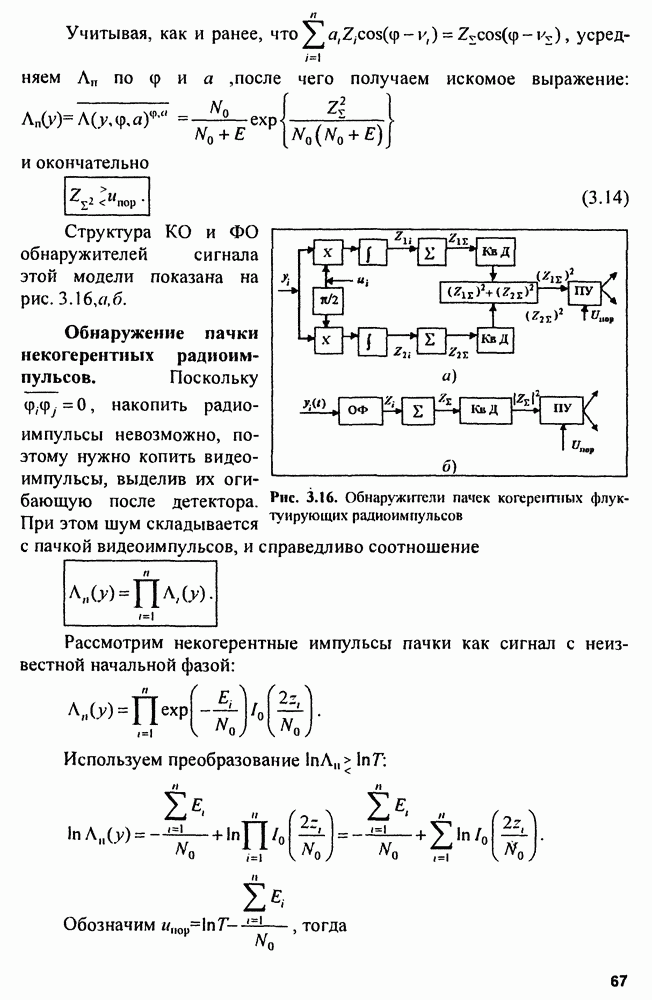
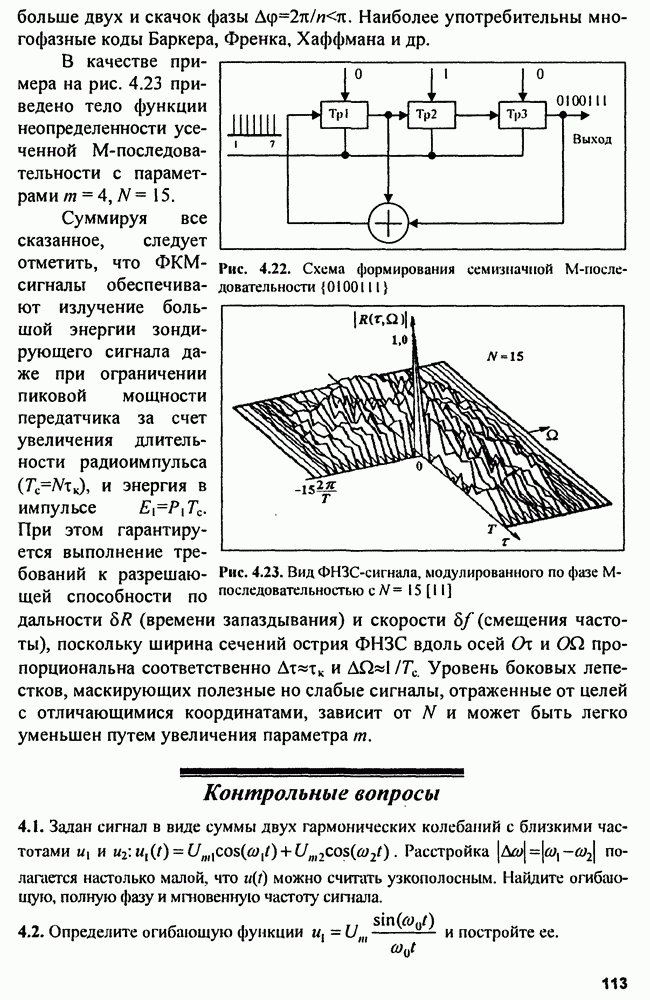
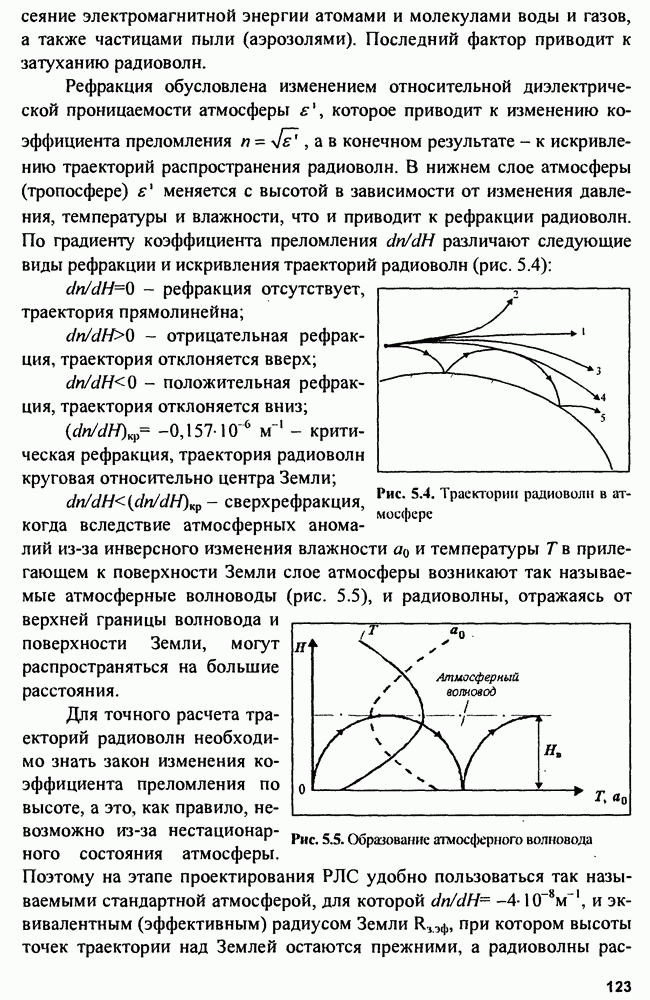
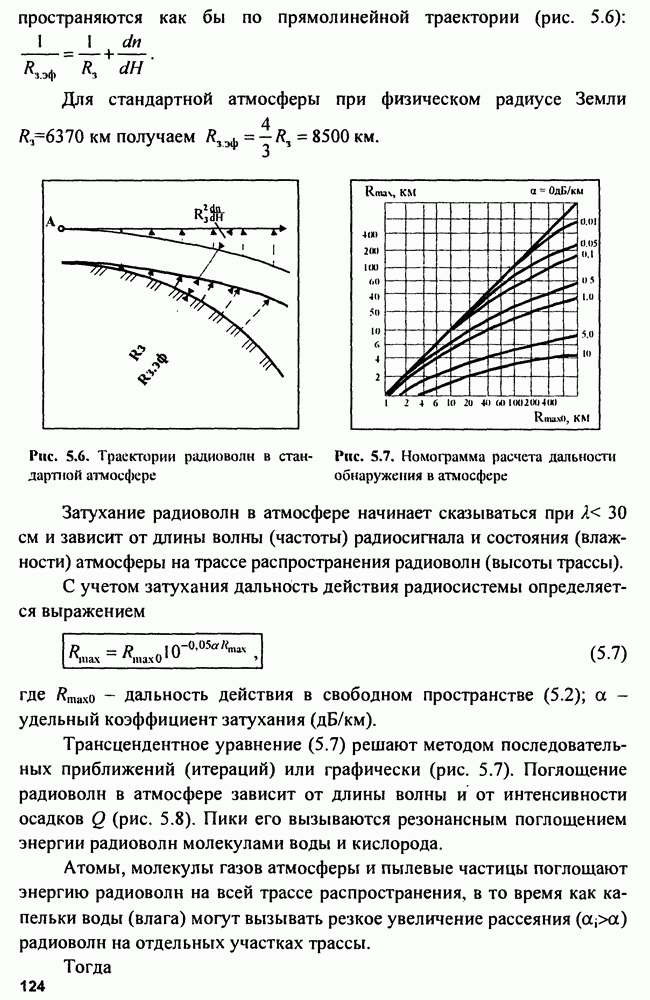
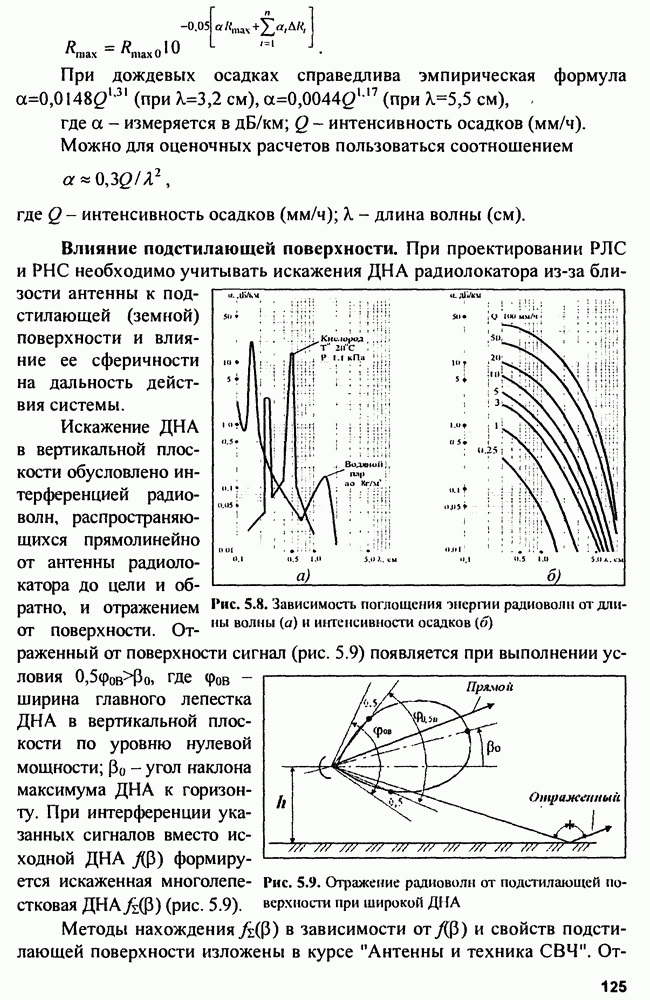
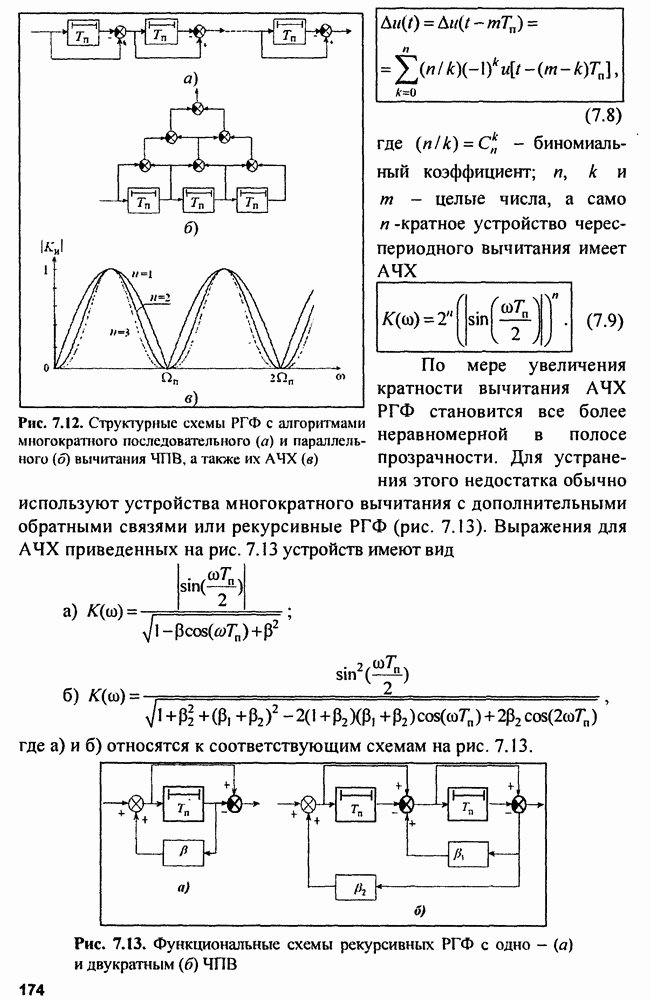
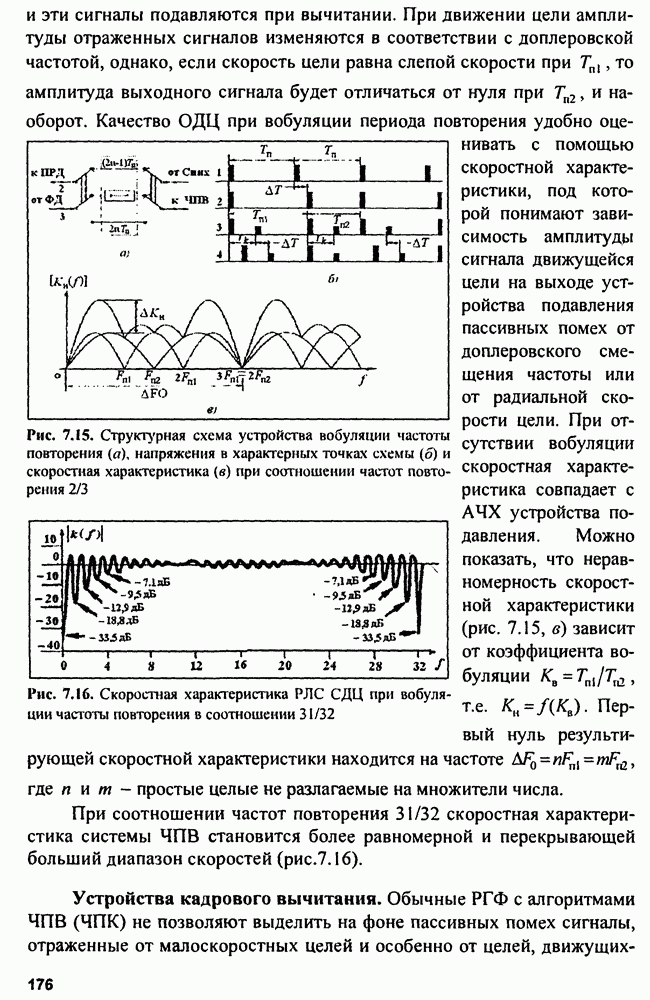
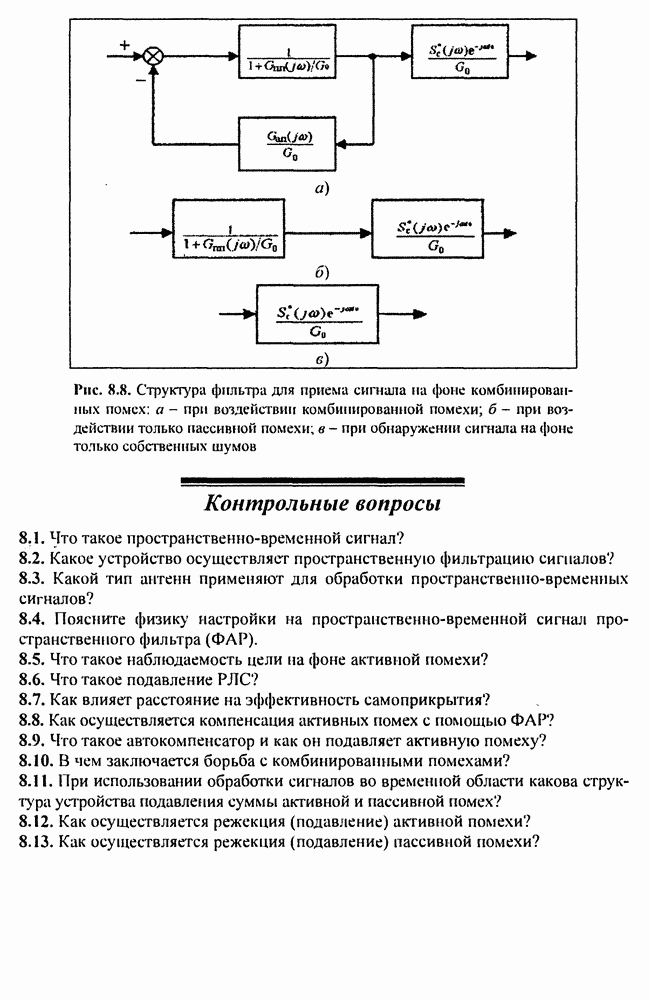
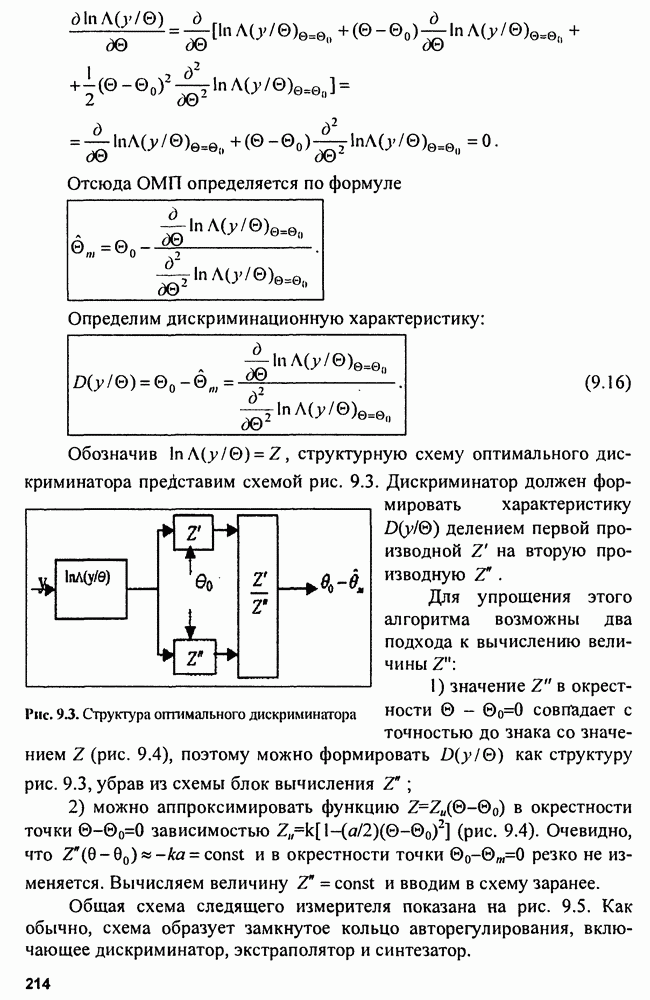
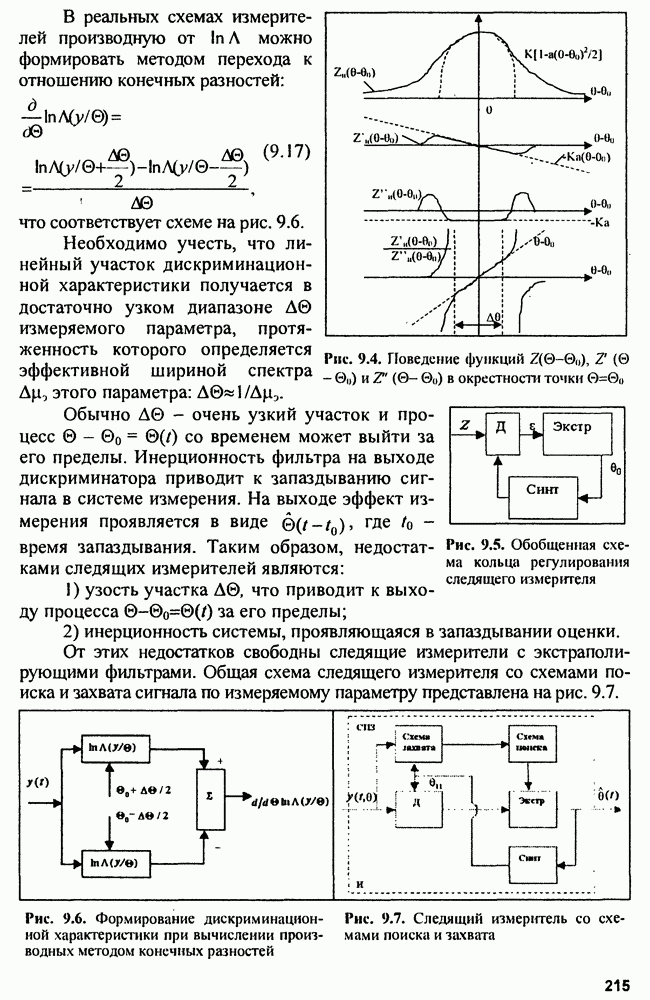
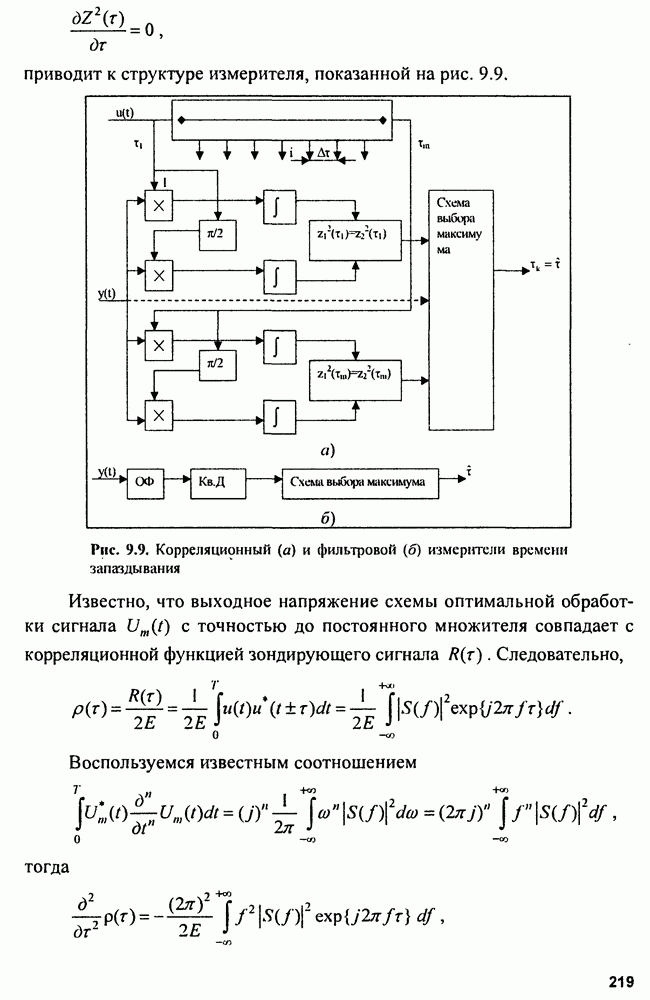
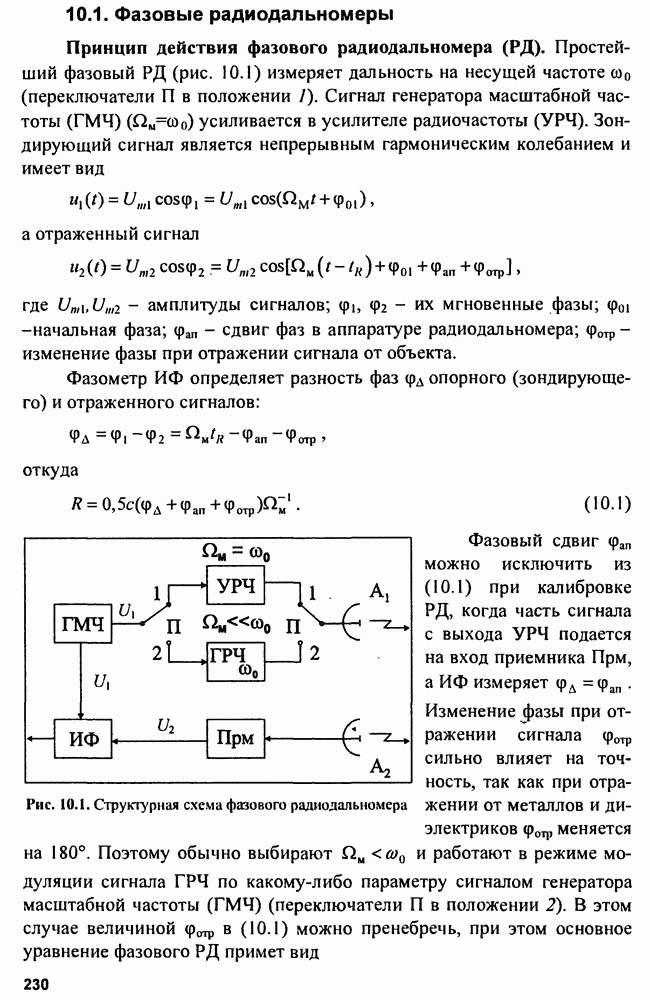
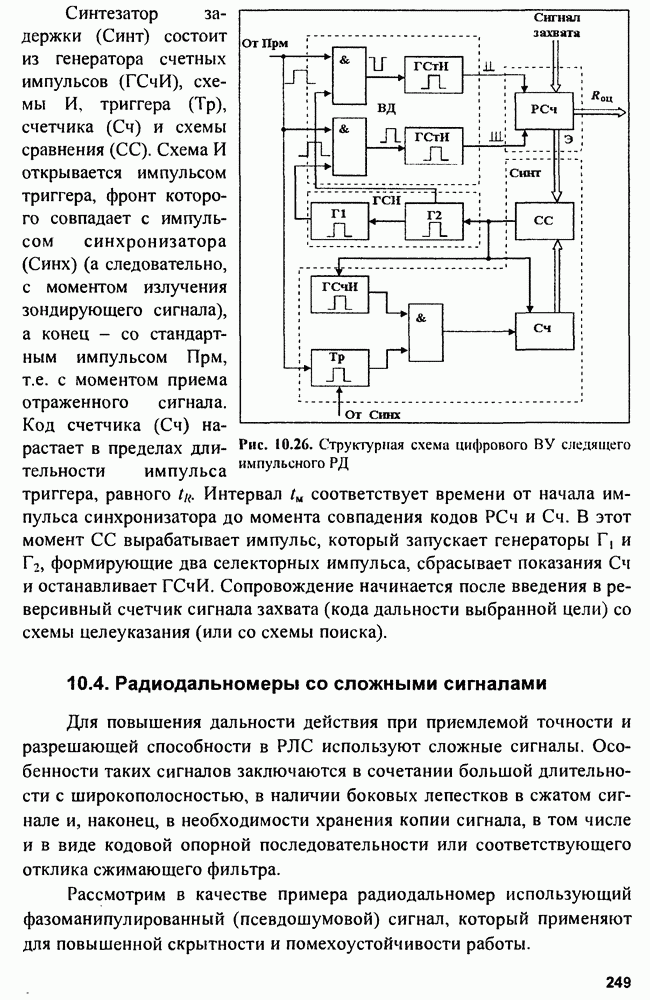
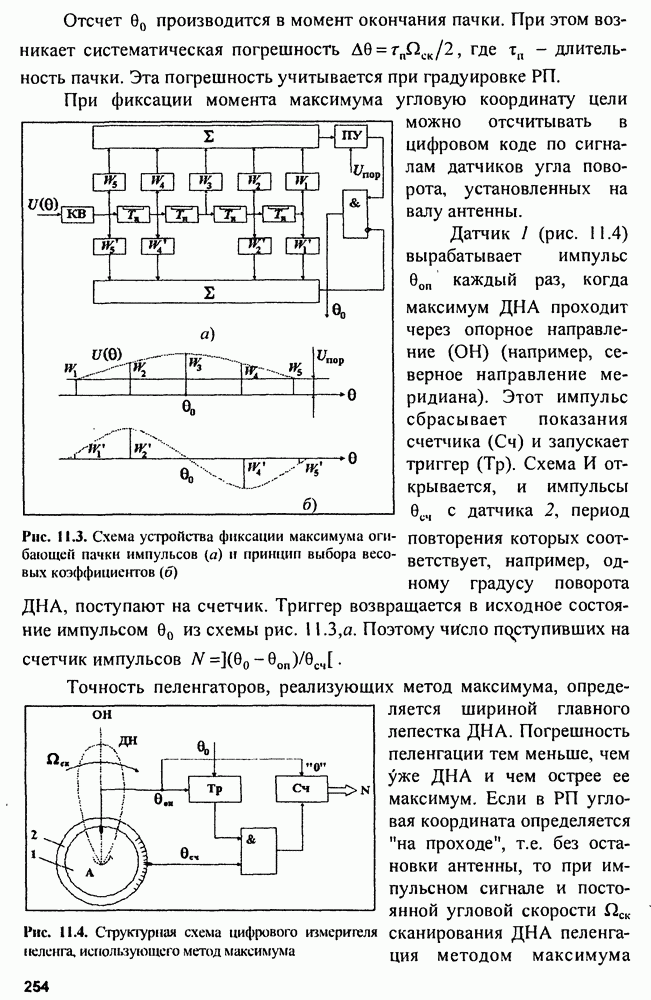
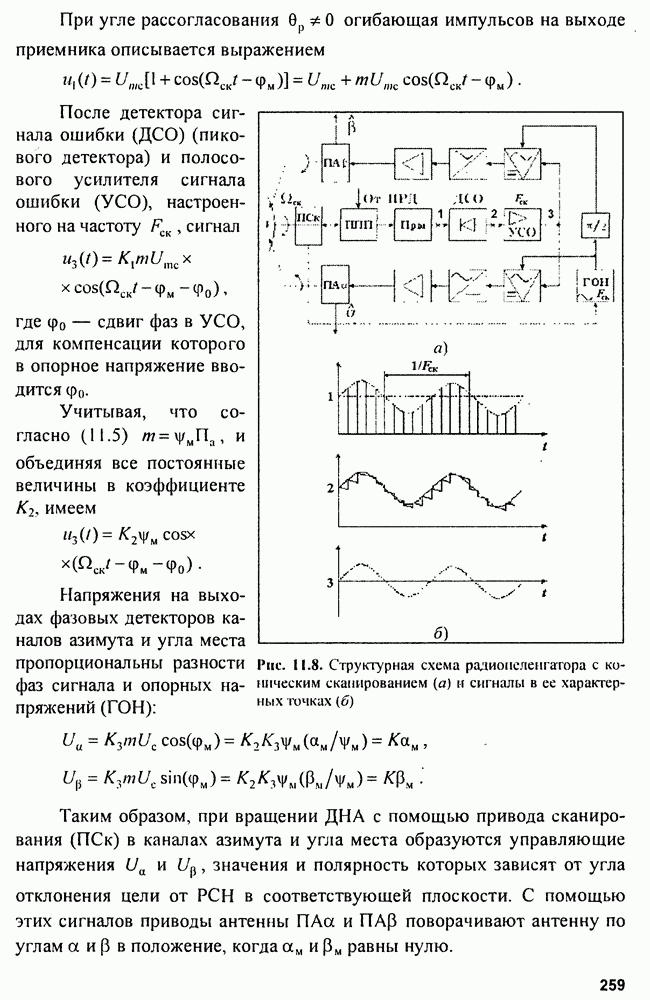
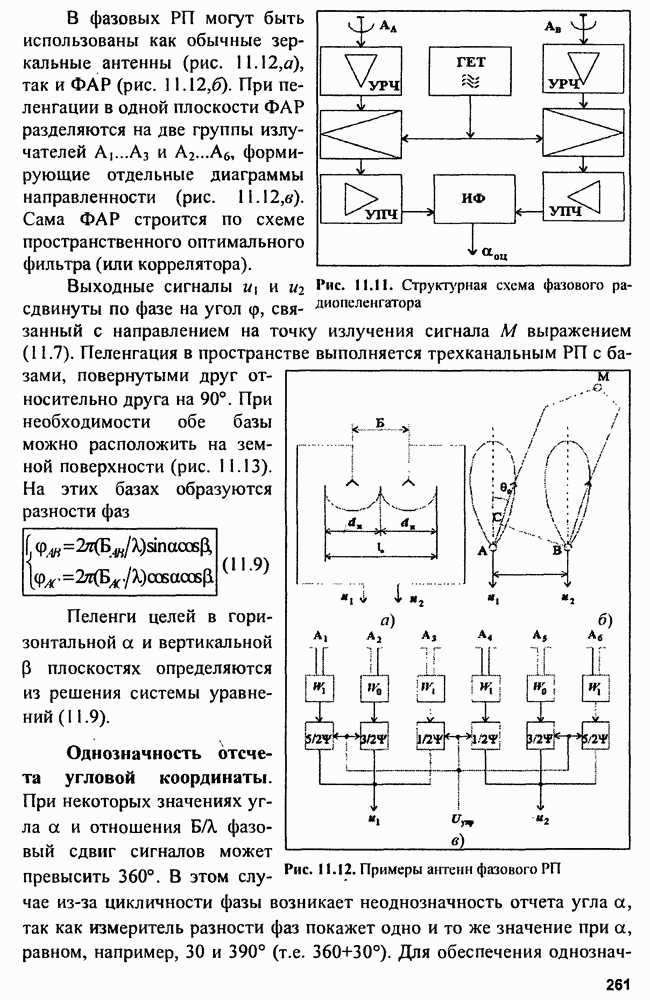
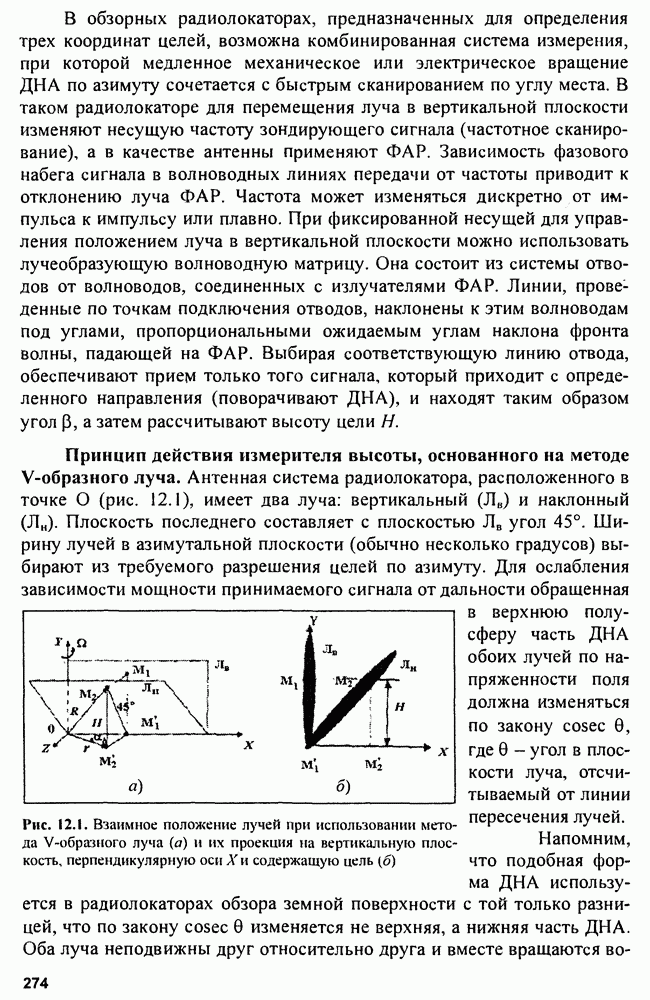
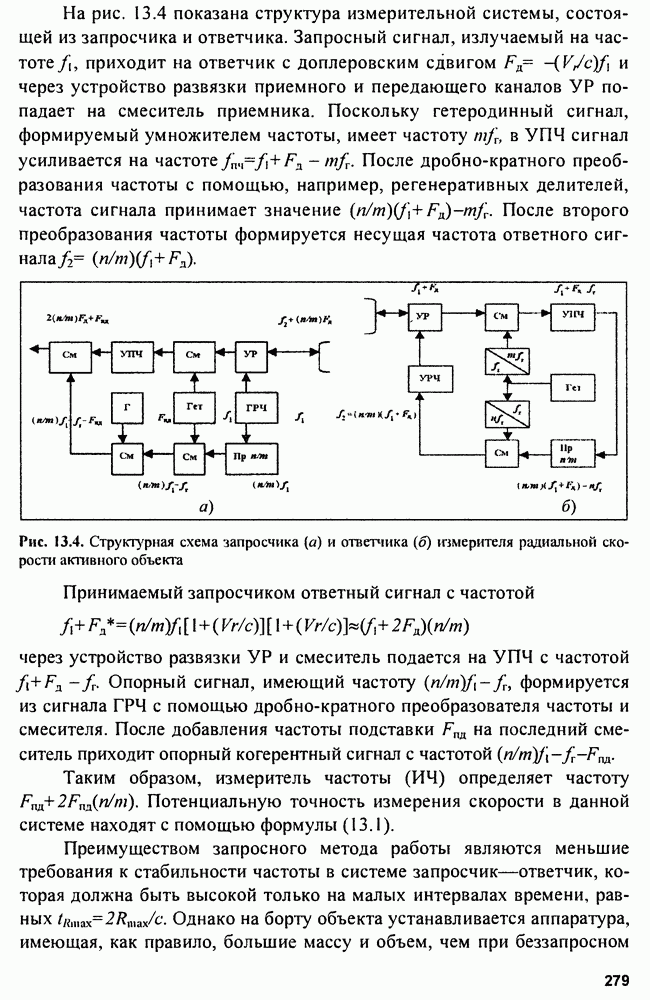
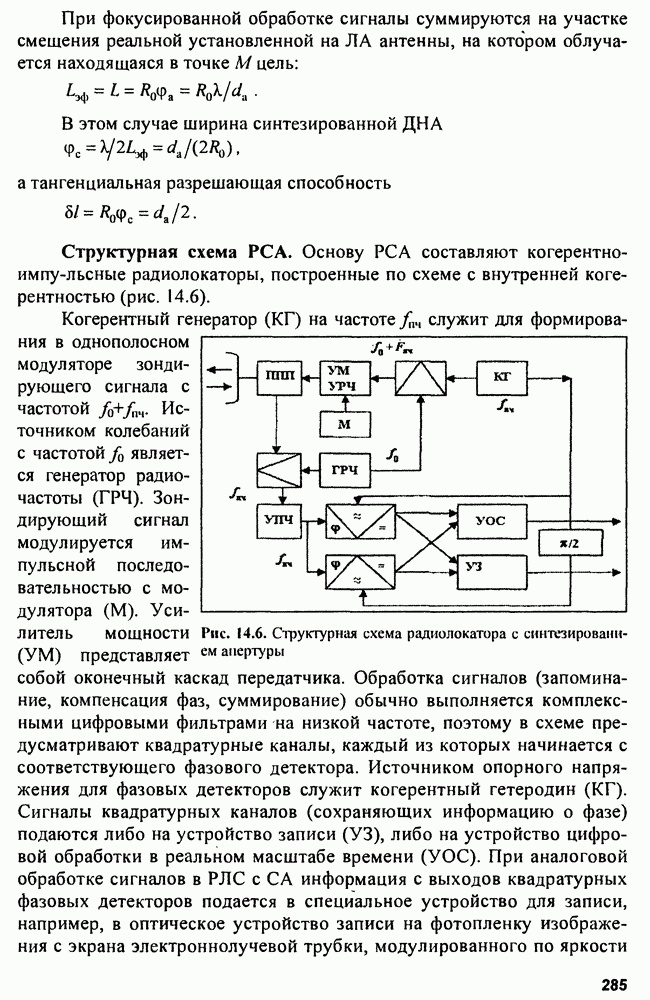
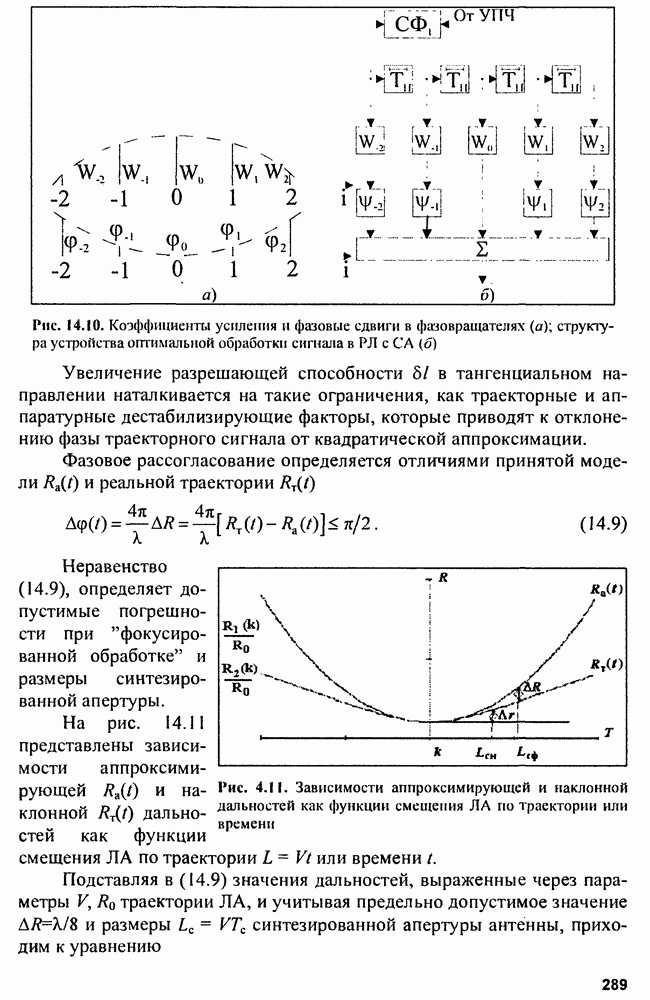
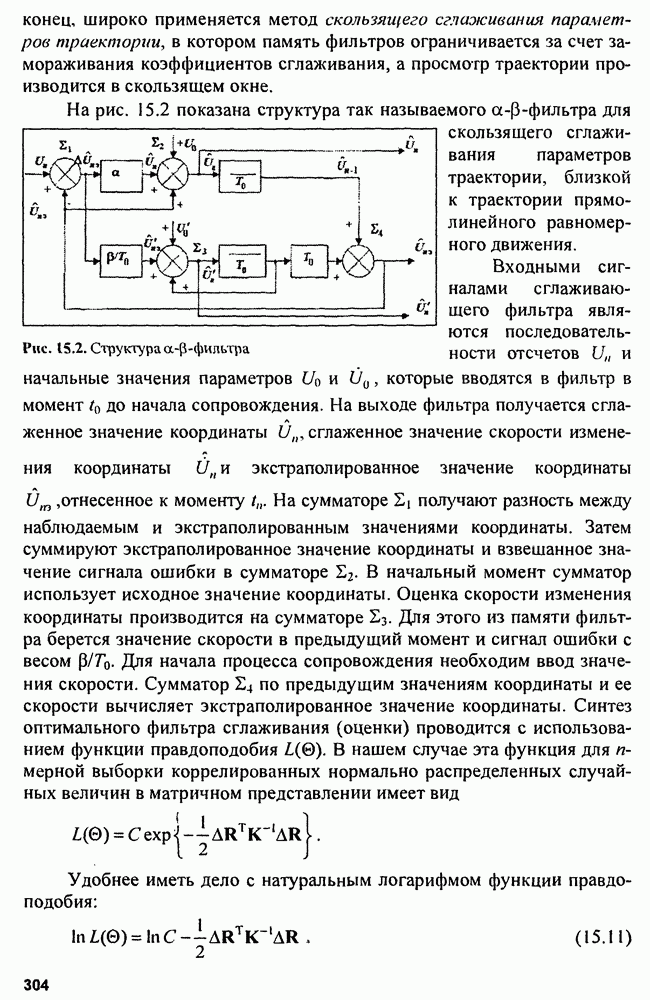
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
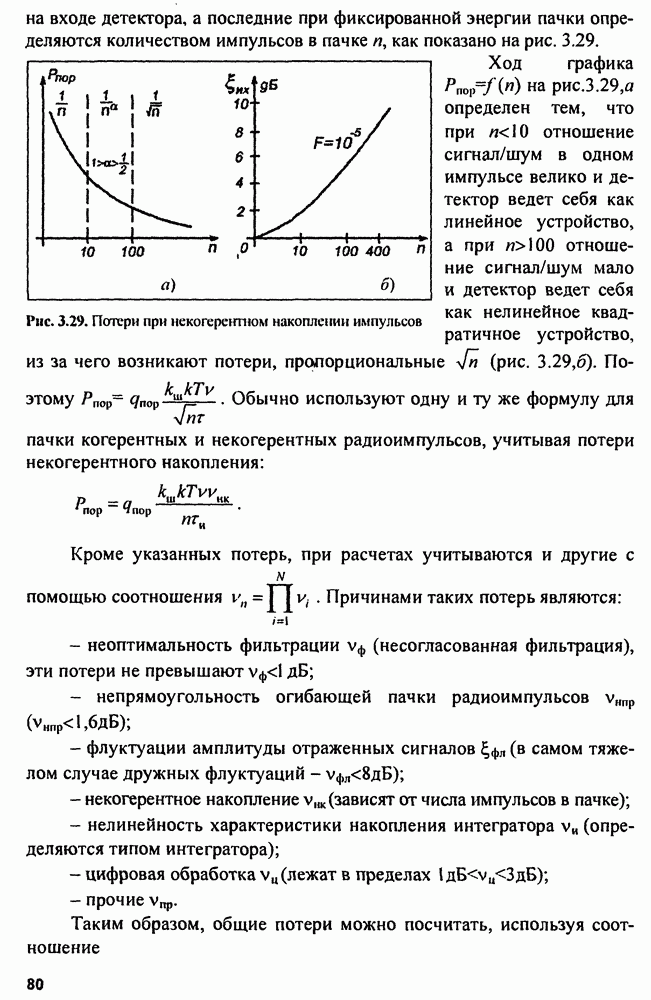
15.2. Сигналы и помехи в системах вторичной обработки
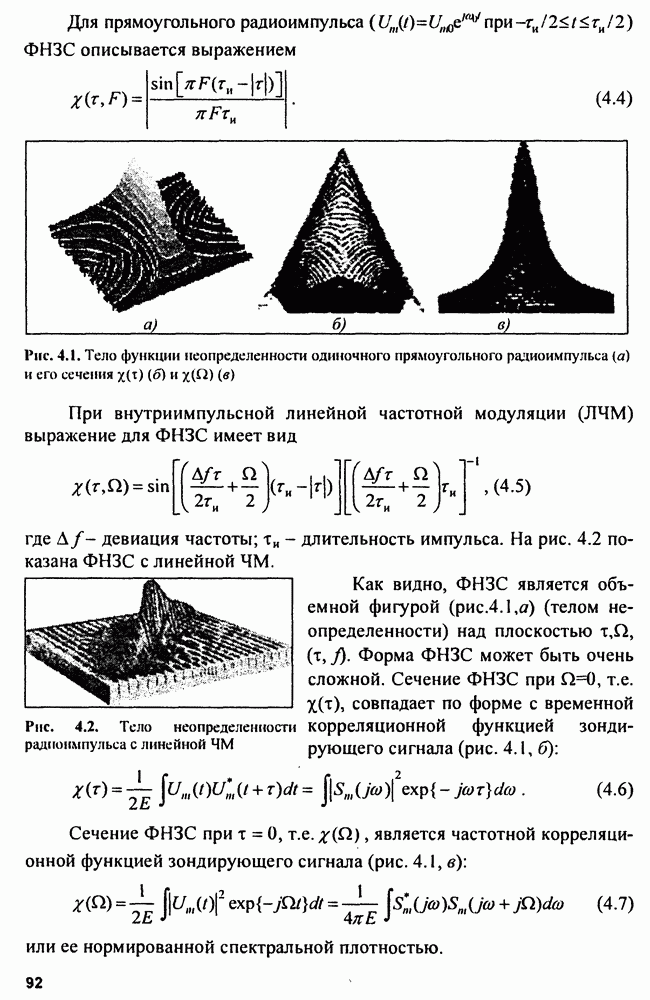
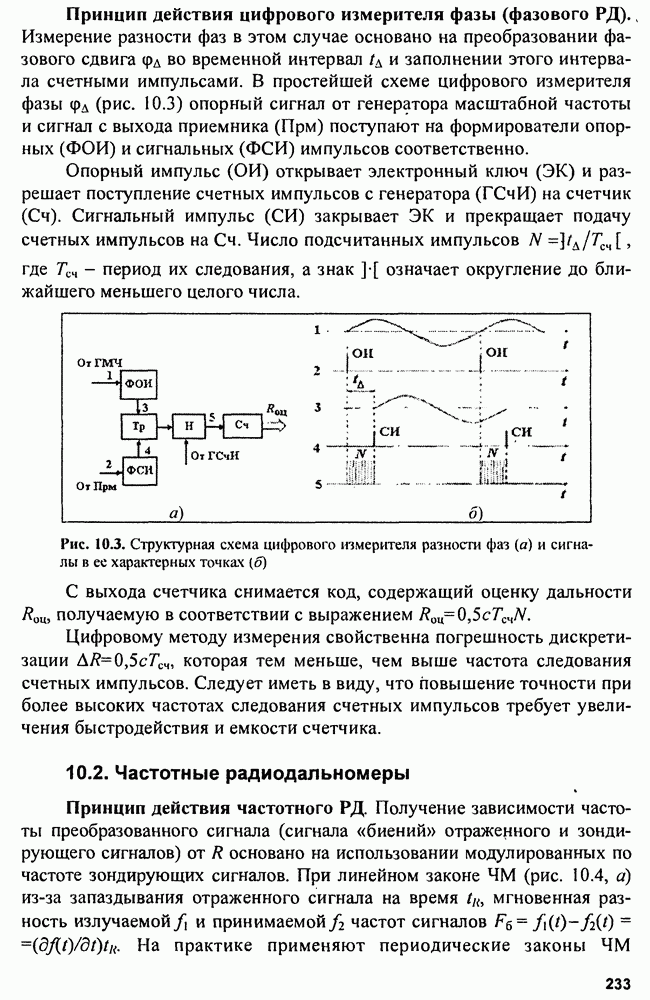
Как правило, на вход системы вторичной обработки поступают отметки целей в виде цифровых кодов, которые соответствуют координатам мгновенного положения как истинных, так и «ложных» целей.
Входную реализацию в системе вторичной обработки можно представить, как и в гл. 3, в виде суммы полезного сигнала и помехи:

где  полезный сигнал, представляющий собой траекторию движения цели;
полезный сигнал, представляющий собой траекторию движения цели;  помеха в виде случайного процесса, искажающего траекторию.
помеха в виде случайного процесса, искажающего траекторию.
При вторичной обработке радиолокационной информации помехами являются ошибки измерения координат и ложные отметки.
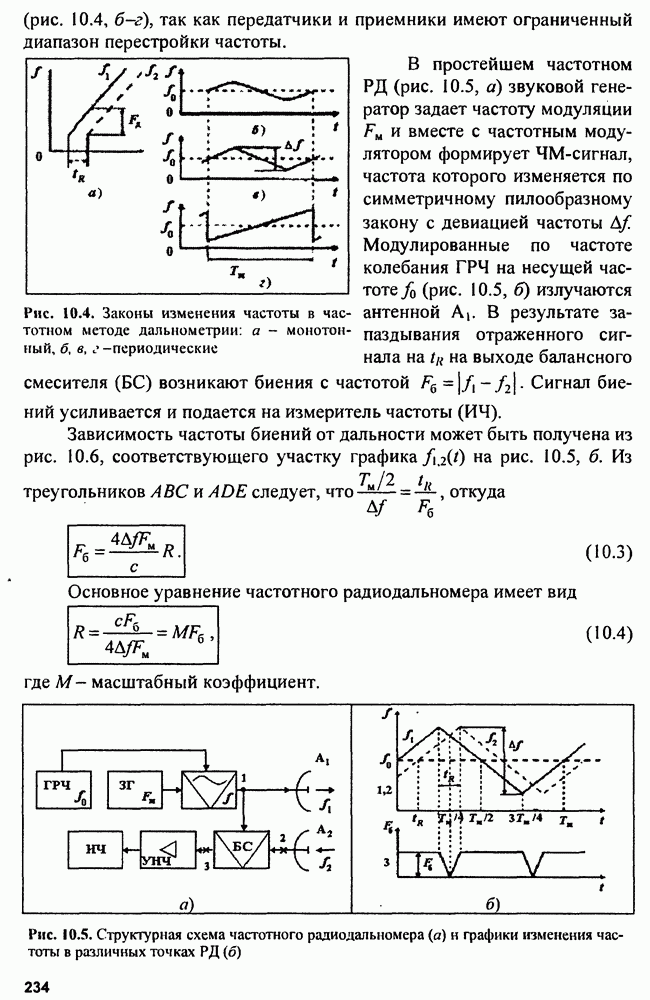
Рассмотрим возможные модели полезных сигналов и помех на примере сопровождения траектории летательного аппарата. Траектория летательного аппарата (воздушной цели - (ВЦ)) на больших интервалах времени не относится к классу детерминированных функций и может быть представлена в виде полинома на всех отрезках (участках) траектории полета. Коэффициенты полинома должны оцениваться по данным радиолокационных наблюдений. Обычно траекторию ВЦ делят на участки прямолинейного равномерного движения и участки маневрирования, которые чередуются случайным образом. Опыт показывает, что большую часть полета ЛА движется прямолинейно с постоянной скоростью. Маневрирование ВЦ - это изменение скорости и направления движения ЛА. Маневрирование по скорости ограничено допустимым
тангенциальным ускорением. При изменении направления (вираж) возникает перегрузка  Считается, что основным видом маневра ЛА является вираж с постоянным ускорением, минимальный радиус которого связан с допустимой перегрузкой идоп формулой
Считается, что основным видом маневра ЛА является вираж с постоянным ускорением, минимальный радиус которого связан с допустимой перегрузкой идоп формулой

Вираж считается равновероятным в обе стороны относительно направления движения в горизонтальной плоскости.
В полярной системе координат, используемой при радиолокационных измерениях, изменение координат даже для не маневрирующей цели может быть представлено только полиномами степени выше первой. Это затрудняет селекцию участков прямолинейного полета ЛА.
Если маневрирование ЛА осуществляется независимо по каждой координате, то процесс изменения отдельно взятой координаты маневрирующей ВЦ представим в виде суммы полинома, описывающего движение на линейном участке, и случайного процесса маневра с нулевым математическим ожиданием и корреляционной функцией вида

где  дисперсия интенсивности маневра; X — средняя частота изменения интенсивности маневра.
дисперсия интенсивности маневра; X — средняя частота изменения интенсивности маневра.
Такая модель соответствует марковскому случайному процессу.
Статистические характеристики ошибок измерения рассматриваются раздельно по каждой независимо измеряемой координате. В дальнейшем в качестве наблюдаемой координаты рассматривается дальность  и измеренное значение этой координаты представлется в виде
и измеренное значение этой координаты представлется в виде

где  значение координаты в момент времени
значение координаты в момент времени  ошибка измерения;
ошибка измерения;  вектор параметров траектории.
вектор параметров траектории.
Считается, что ошибки  измерений координаты имеют нормальную плотность распределения вероятностей, которую для одиночного значения
измерений координаты имеют нормальную плотность распределения вероятностей, которую для одиночного значения  записывают в виде
записывают в виде

где - дисперсия  отсчета координаты.
отсчета координаты.
Совокупность ошибок измерения координаты представляет собой n-мерную систему коррелированных, нормально распределенных случайных величин с корреляционной квадратной матрицой размерностью 

Матрица содержит математические ожидания  которые представлены в матрице дисперсиями
которые представлены в матрице дисперсиями  и корреляционными моментами
и корреляционными моментами 
Симметричные относительно диагонали элементы корреляционной матрицы ошибок равны между собой, т.е.  а диагональные равны дисперсиям
а диагональные равны дисперсиям  Когда ошибки некоррелированы, все элементы матрицы кроме диагональных равны нулю. Составляющими ошибок измерения координаты являются шумовая, флуктуационная и систематическая погрешности.
Когда ошибки некоррелированы, все элементы матрицы кроме диагональных равны нулю. Составляющими ошибок измерения координаты являются шумовая, флуктуационная и систематическая погрешности.
Шумовая составляющая обусловлена влиянием внешних и внутренних помех. Ее значения независимы от обзора к обзору  и характеризуются диагональной корреляционной матрицей
и характеризуются диагональной корреляционной матрицей  с элементами
с элементами

где  дальность, для которой определено значение
дальность, для которой определено значение 
Флуктуационная составляющая обусловлена возмущениями в измерительной системе РЛС, и ее величина не зависит от дальности, а корреляционная матрица имеет вид

где  дисперсия флуктуационной составляющей;
дисперсия флуктуационной составляющей;  единичная (диагональная) матрица.
единичная (диагональная) матрица.
Систематическая составляющая постоянна в течение одного сеанса измерений, но случайно изменяется от сеанса к сеансу. Корреляционную матрицу систематической составляющей записывают в виде

где  дисперсия систематической составляющей;
дисперсия систематической составляющей;  квадратная матрица порядка
квадратная матрица порядка  составленная из единиц.
составленная из единиц.
Суммарная корреляционная матрица ошибок измерения координаты равна сумме корреляционных матриц составляющих ошибок:

Условную плотность вероятности  -мерной выборки коррелированных нормально распределенных случайных величин записывают в виде
-мерной выборки коррелированных нормально распределенных случайных величин записывают в виде

где  определитель корреляционной матрицы К ошибок измерения координаты;
определитель корреляционной матрицы К ошибок измерения координаты;  алгебраическое дополнение элемента
алгебраическое дополнение элемента  в определителе представляющее собой определитель матрицы, полученной из матрицы К вычеркиванием
в определителе представляющее собой определитель матрицы, полученной из матрицы К вычеркиванием  строки
строки  столбца, умноженный на
столбца, умноженный на 
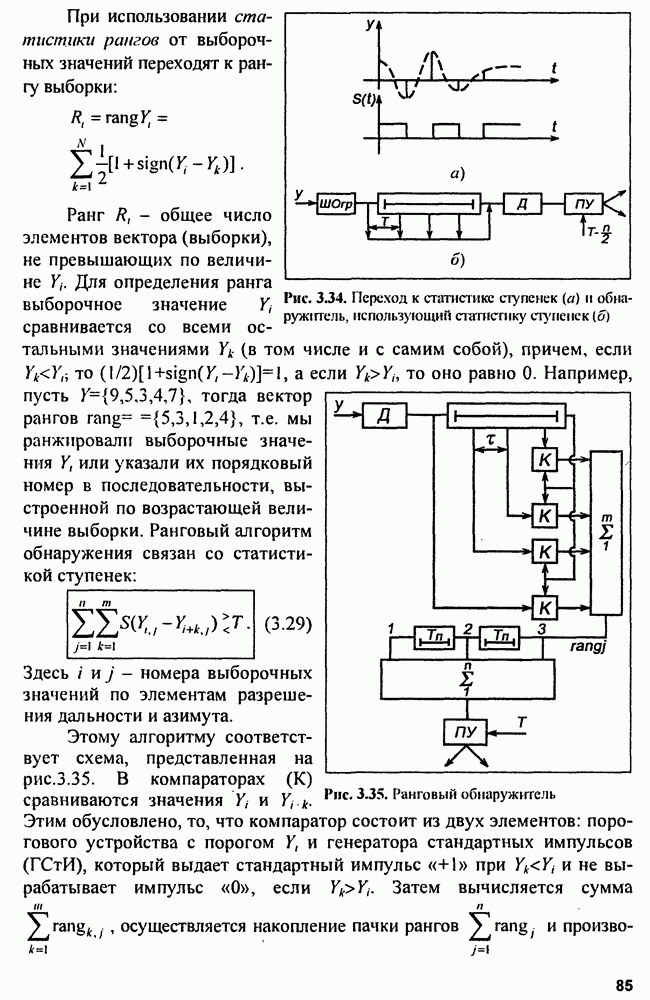
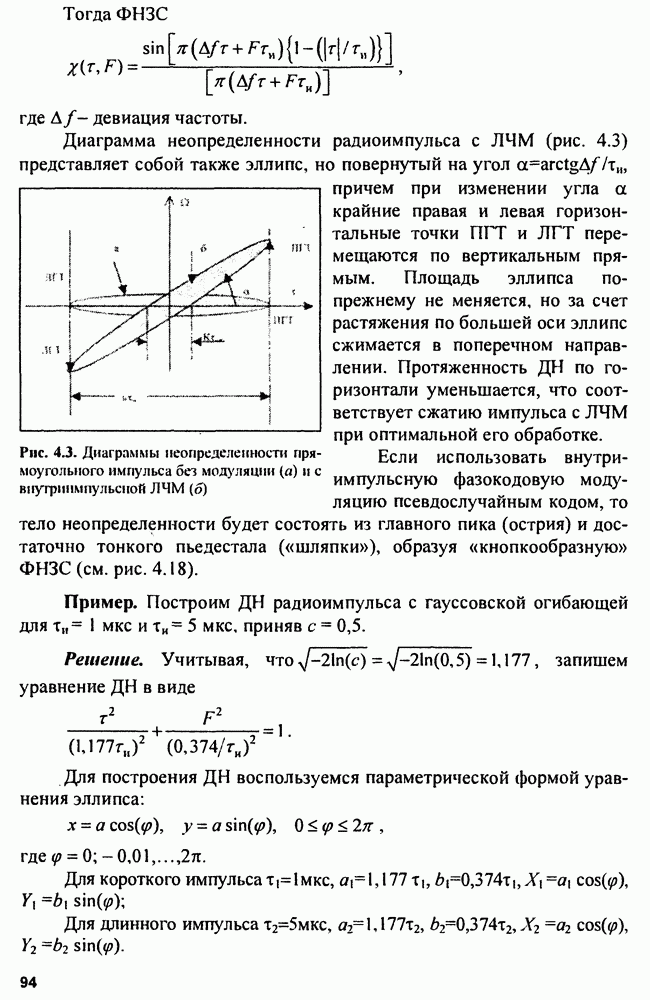
Квадратичная форма в показателе экспоненты выражения (15.5) может быть преобразована при использовании векторно-матричной записи. Ошибки измерения  представимы в виде n-мерного вектора-столбца
представимы в виде n-мерного вектора-столбца

где  знак транспонирования.
знак транспонирования.
Элементы  в выражении (15.5) образуют квадратную матрицу, обратную корреляционной матрице ошибок измерения, т.е.
в выражении (15.5) образуют квадратную матрицу, обратную корреляционной матрице ошибок измерения, т.е.  с элементами
с элементами  где
где 
Используя введенные обозначения, квадратичную форму в выражении (15.5) можно представить в виде следующего векторно-матричного произведения:

При таком представлении квадратичной формы условную плотность вероятности (15.5) записывают в виде

Это выражение является основным при синтезе оптимальных алгоритмов оценки параметров траектории.
Если помеха является стационарной, то ложные отметки возникают случайно и независимо друг от друга. При этом обычно считают, что во времени поток ложных отметок имеет постоянную плотность  При прокладке траекторий ложные отметки попадают в разные участки
При прокладке траекторий ложные отметки попадают в разные участки
области  строба независимым образом. Это приводит к распределению Пуассона числа ложных отметок
строба независимым образом. Это приводит к распределению Пуассона числа ложных отметок  попадающих в любой строб:
попадающих в любой строб:

где а - среднее число ложных отметок, попадающих в область строба  Для двухмерного случая
Для двухмерного случая

где  площадь строба
площадь строба  число ложных отметок, приходящихся на единицу площади.
число ложных отметок, приходящихся на единицу площади.
Для трехмерного случая (строба)

где  - объем строба
- объем строба  число ложных отметок, приходящихся на единицу объема.
число ложных отметок, приходящихся на единицу объема.
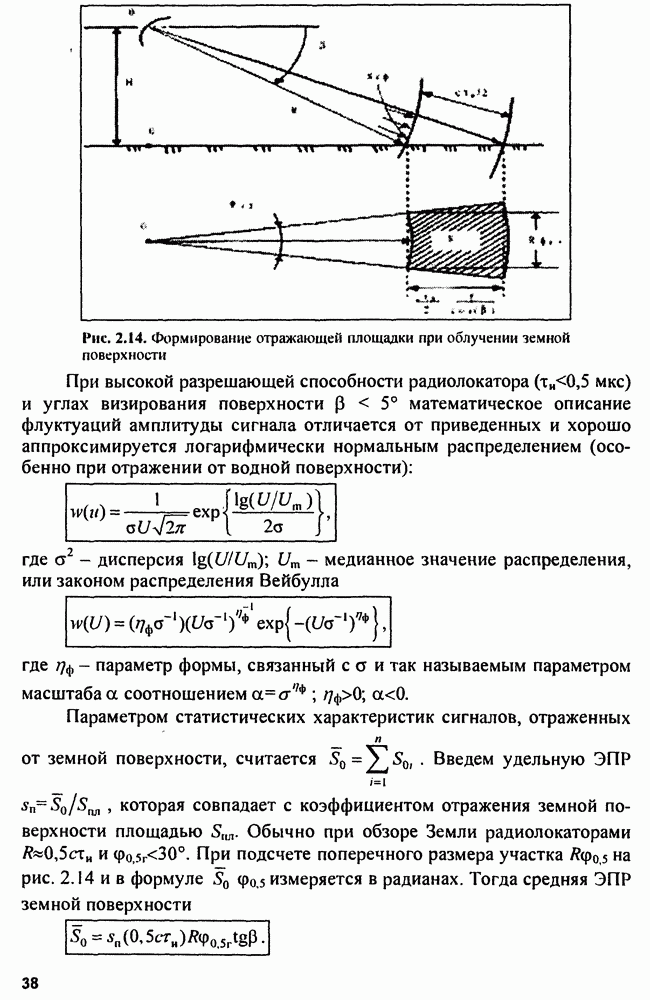
При круговом (секторном) обзоре плотность ложных отметок на единицу площади (объема) зоны не является постоянной, а зависит от дальности.
Рассмотрим эту зависимость для случая двухмерного строба  Разделим зону обзора РЛС на кольца, ширина
Разделим зону обзора РЛС на кольца, ширина  которых равна разрешающей способности по дальности
которых равна разрешающей способности по дальности  Число колец
Число колец  Зная общее число ложных отметок, возникающих в зоне обзора за период обзора Гобз, равное
Зная общее число ложных отметок, возникающих в зоне обзора за период обзора Гобз, равное  и учитывая тот факт, что среднее число ложных отметок в каждом кольце
и учитывая тот факт, что среднее число ложных отметок в каждом кольце  одинаково (обзор равномерный), можно определить число ложных отметок, приходящееся на одно кольцо
одинаково (обзор равномерный), можно определить число ложных отметок, приходящееся на одно кольцо

Площадь кольца на дальности 

поэтому на единицу площади обзора на дальности  приходится
приходится  отметок.
отметок.
Средняя плотность ложных отметок в области, ограниченной значениями дальности  определяется из выражения
определяется из выражения

Выражение (15.9) позволяем рассчитывать среднюю плотность ложных отметок в областях (стробах), протяженных по дальности. Расчет числа ложных отметок в стробе и в этом случае производится по
формуле (15.8), так как для наличия пуассоновского распределения условие постоянной плотности  несущественно. В процессе выполнения основных операций вторичной обработки влияние ложных отметок в основном сказывается на качестве селекции отметок в стробах. При этом неправильная селекция может привести к сбою сопровождения (сброс траектории).
несущественно. В процессе выполнения основных операций вторичной обработки влияние ложных отметок в основном сказывается на качестве селекции отметок в стробах. При этом неправильная селекция может привести к сбою сопровождения (сброс траектории).
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
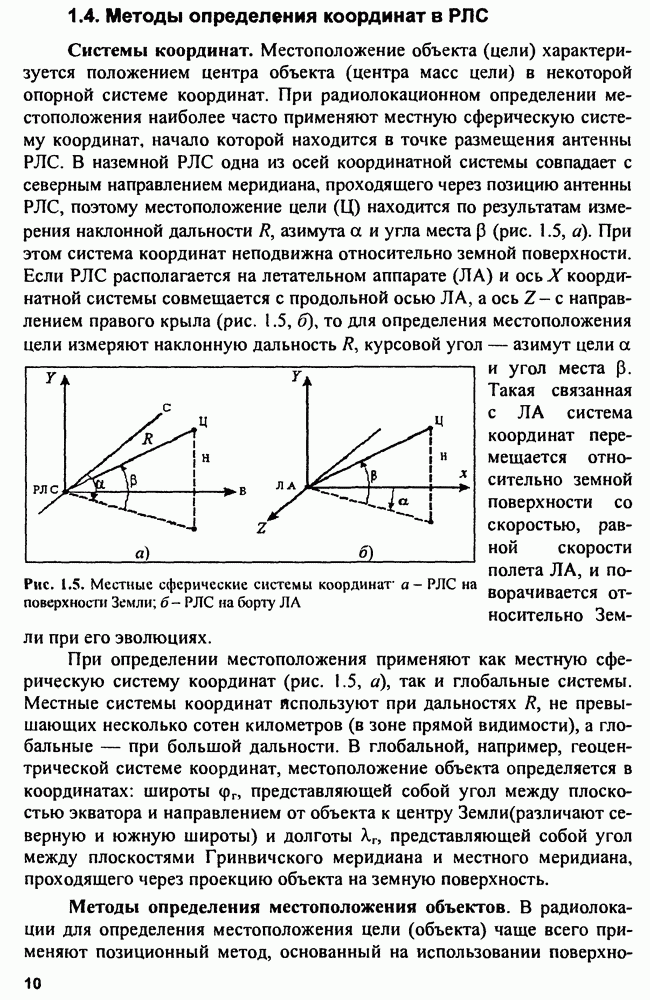
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
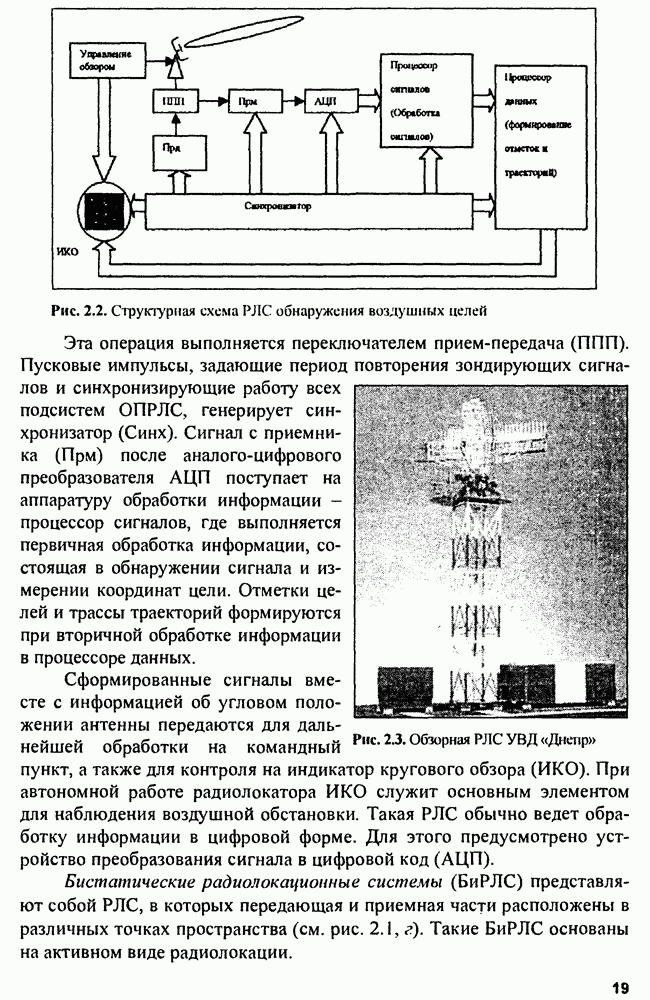
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
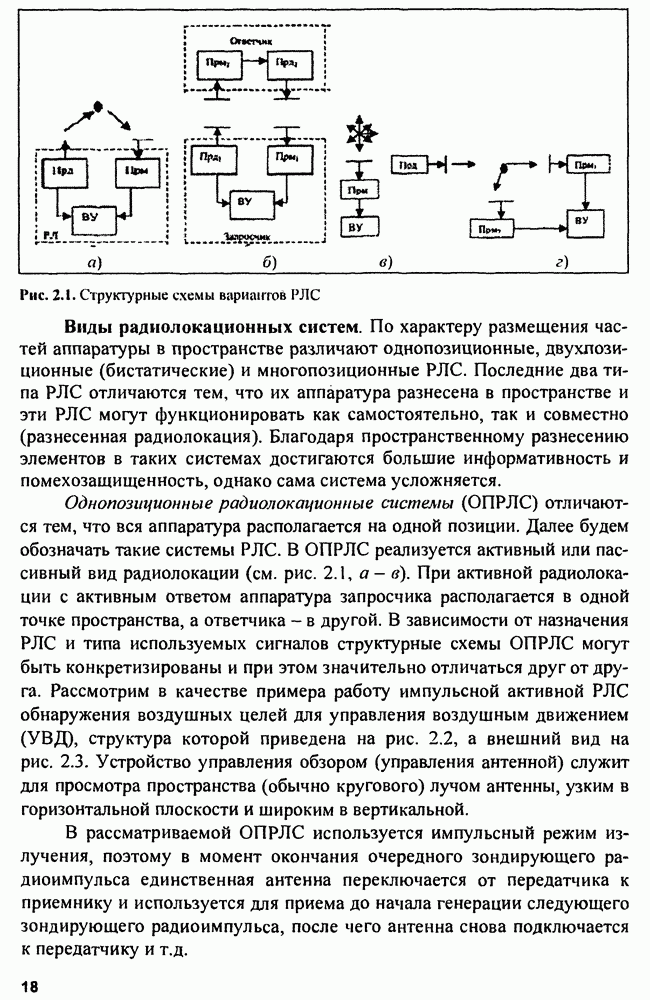
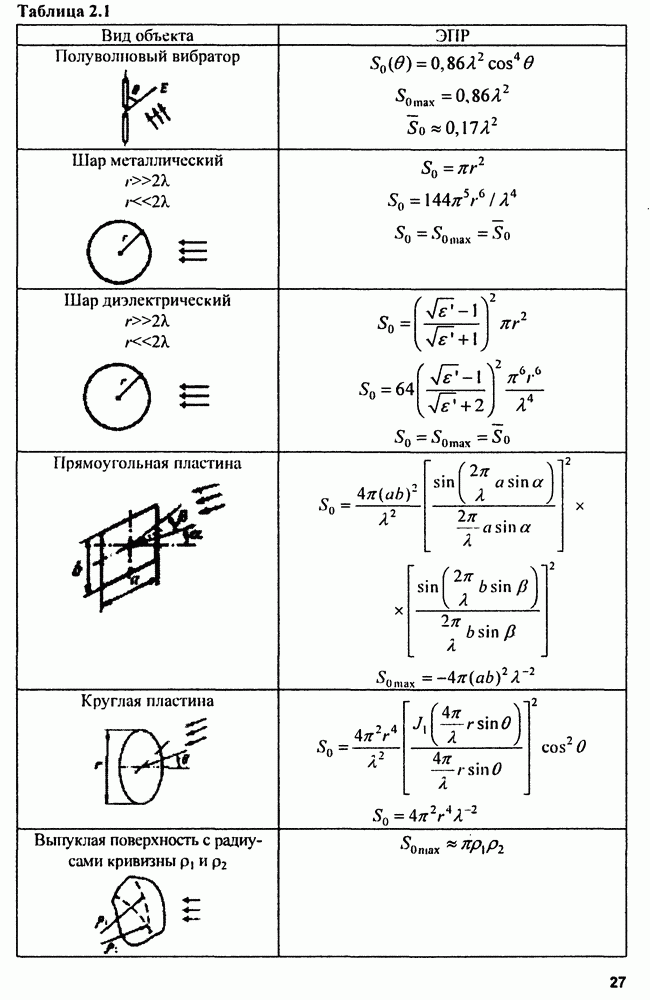
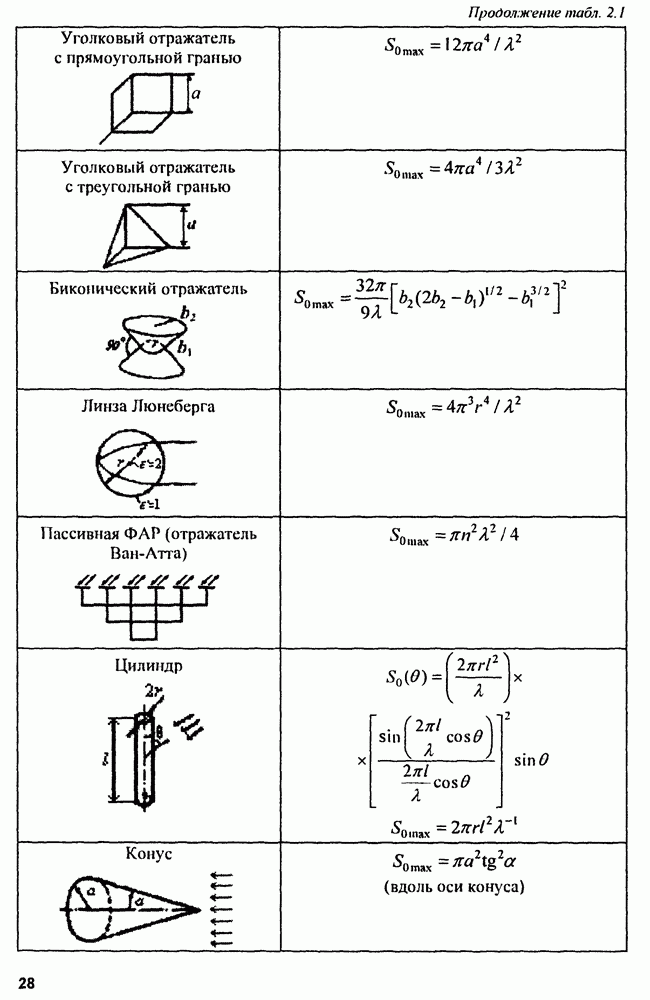
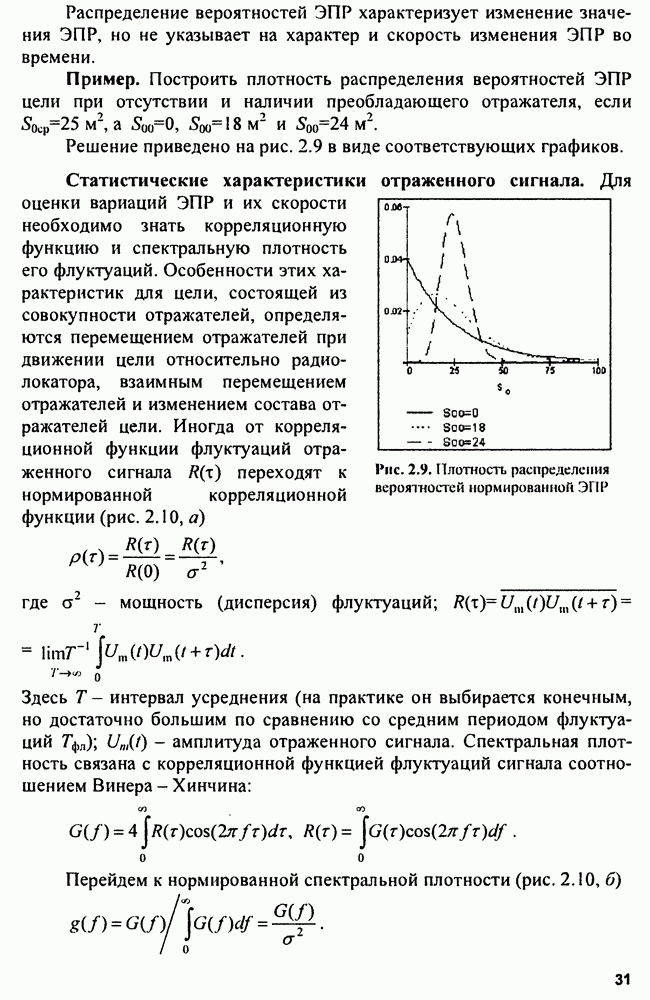
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
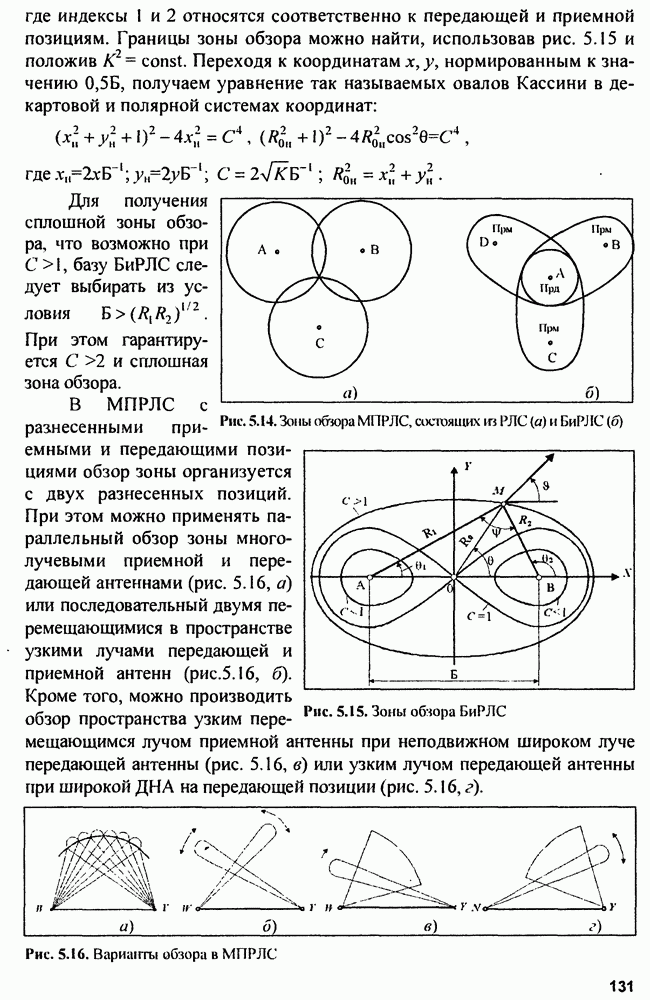
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
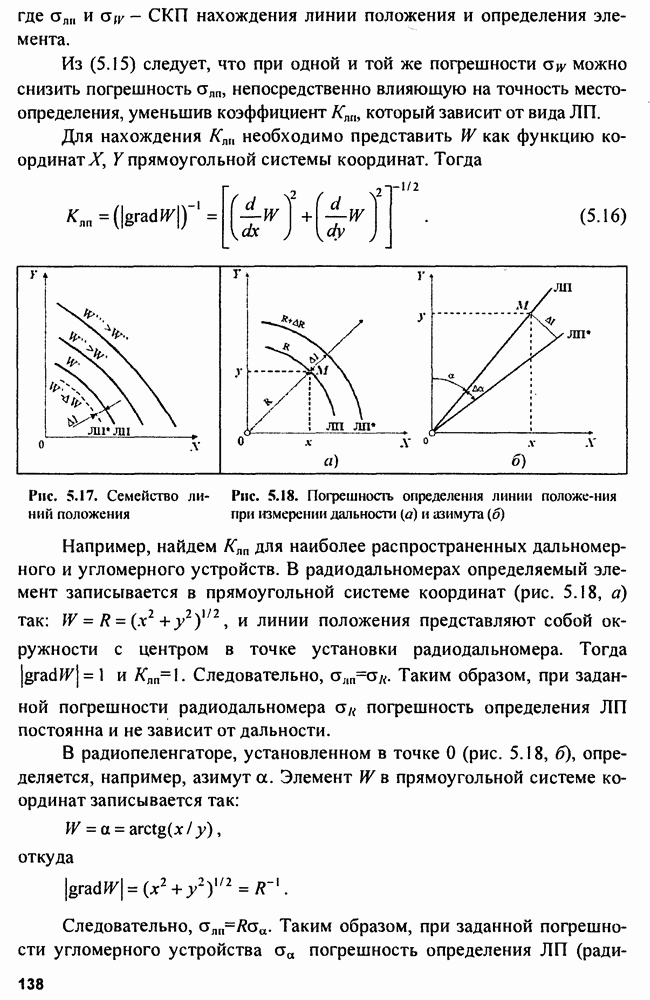
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
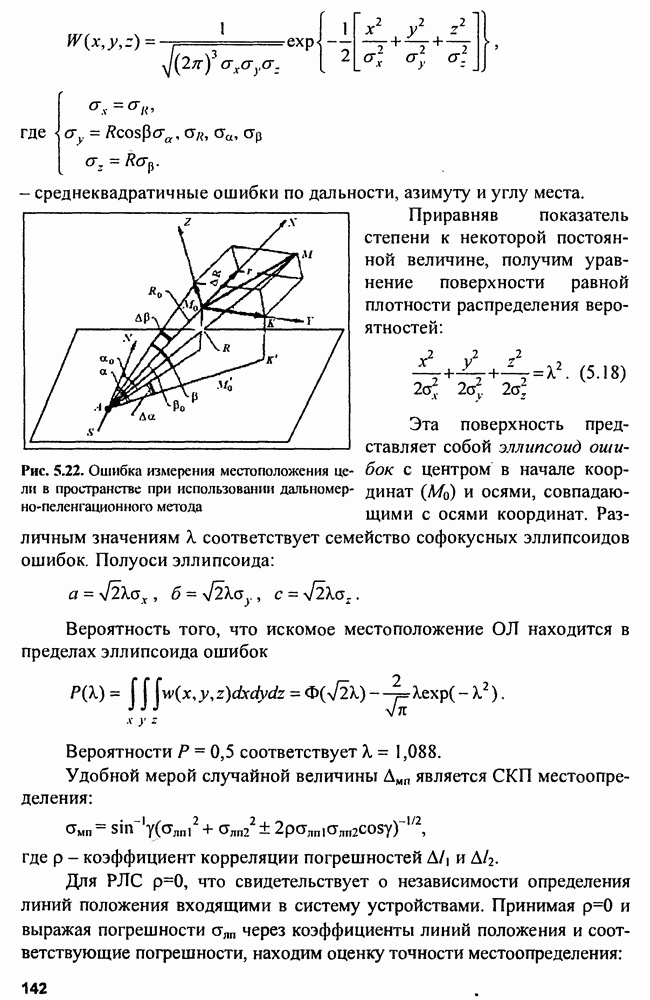
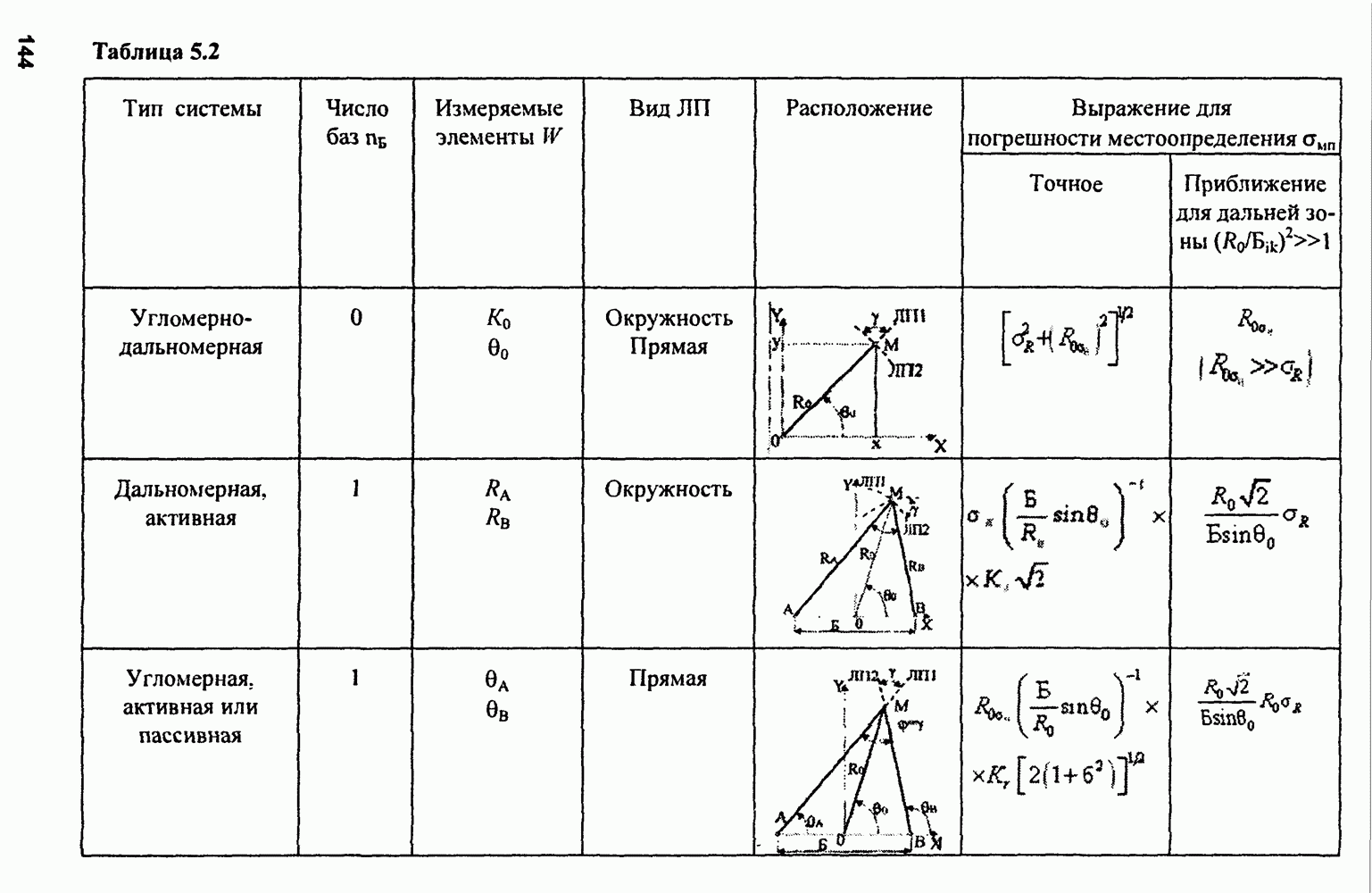
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение