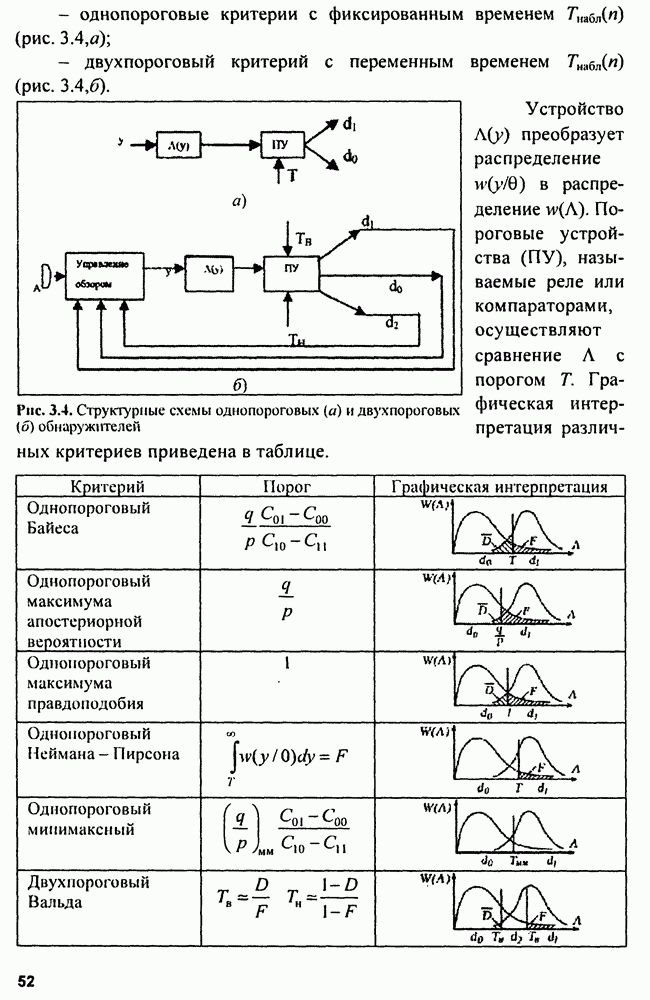
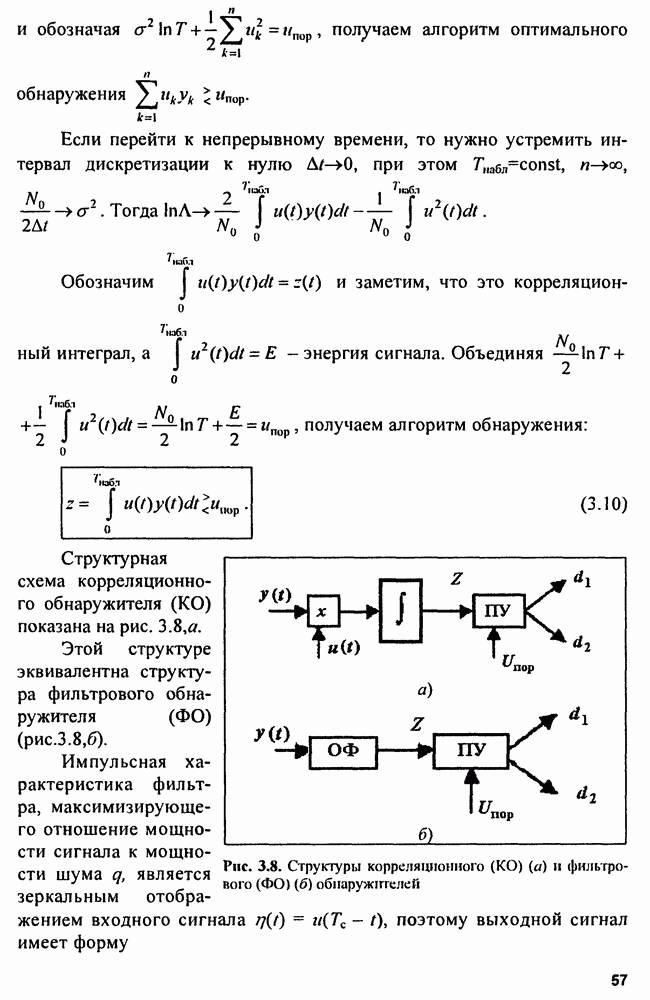
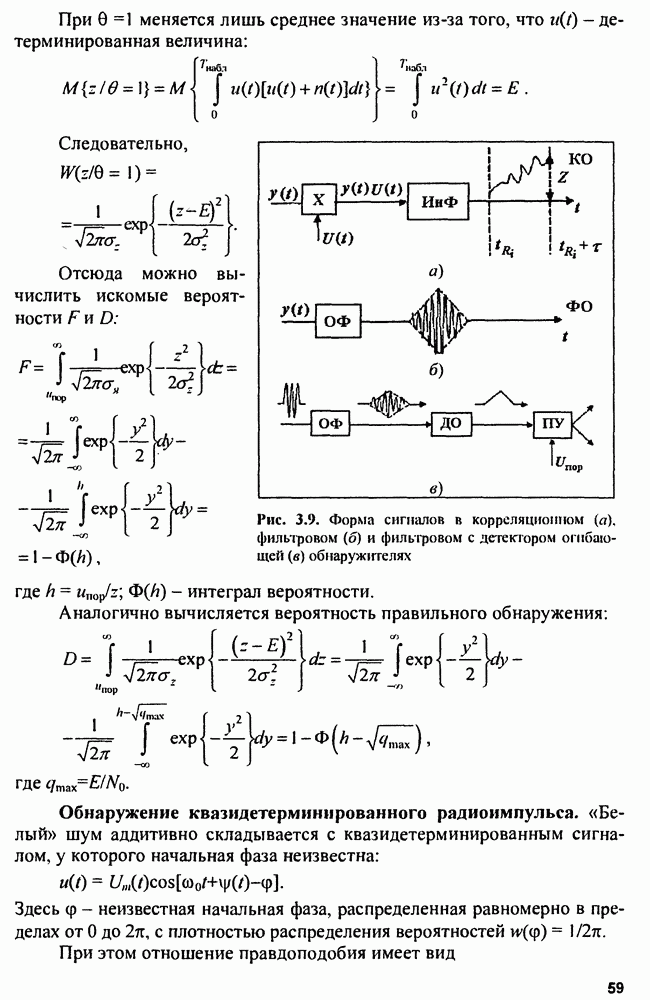
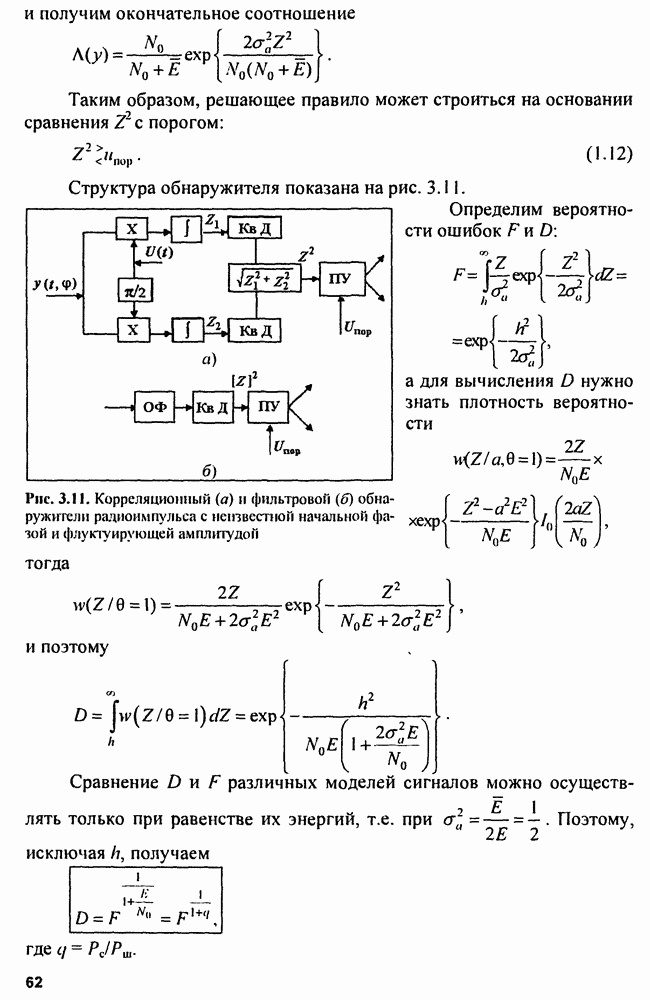
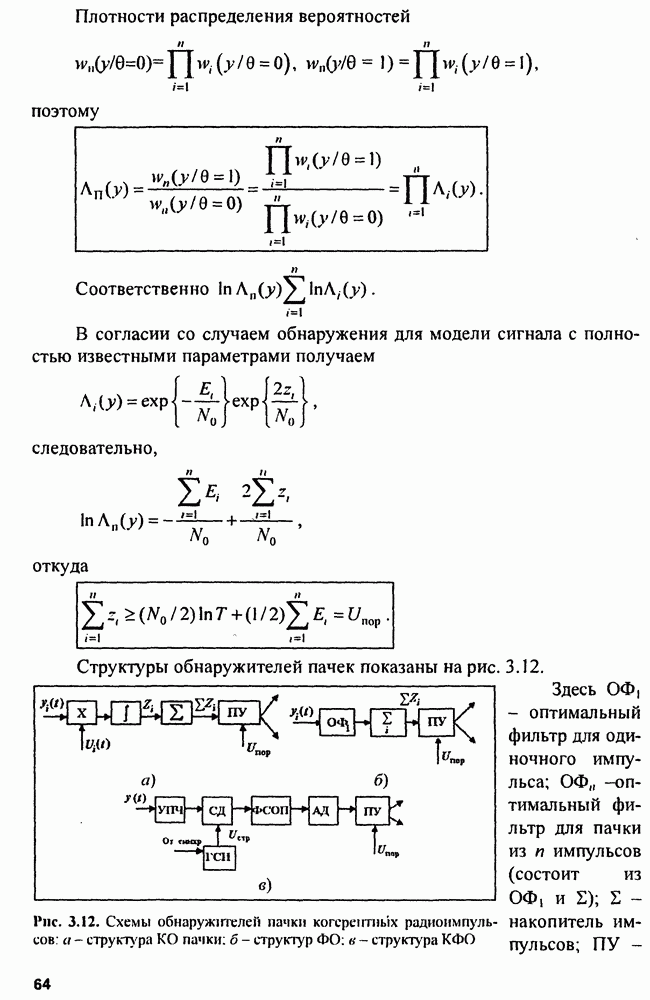
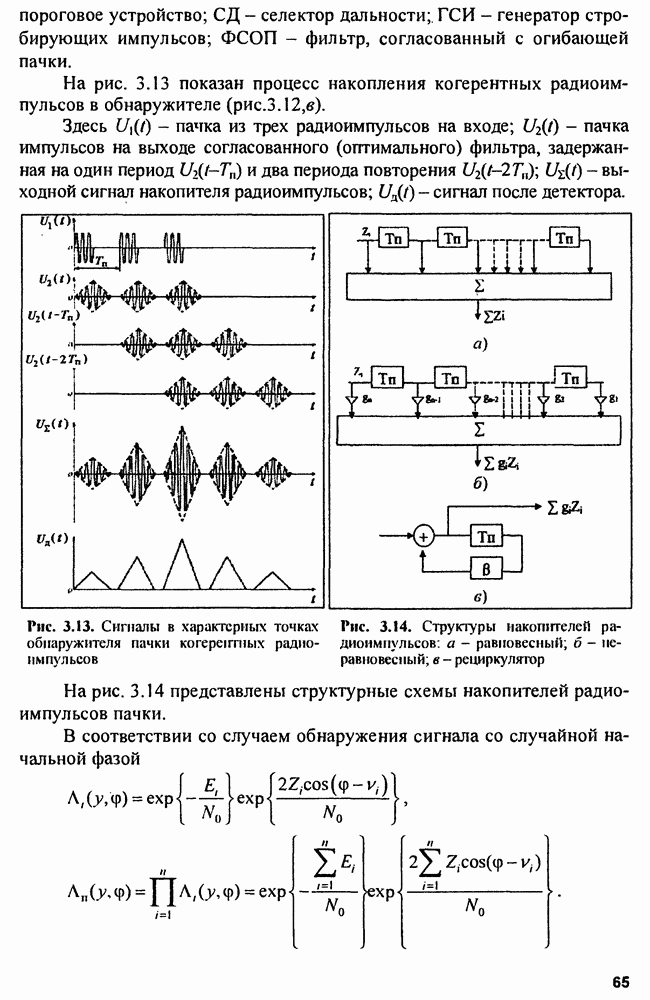
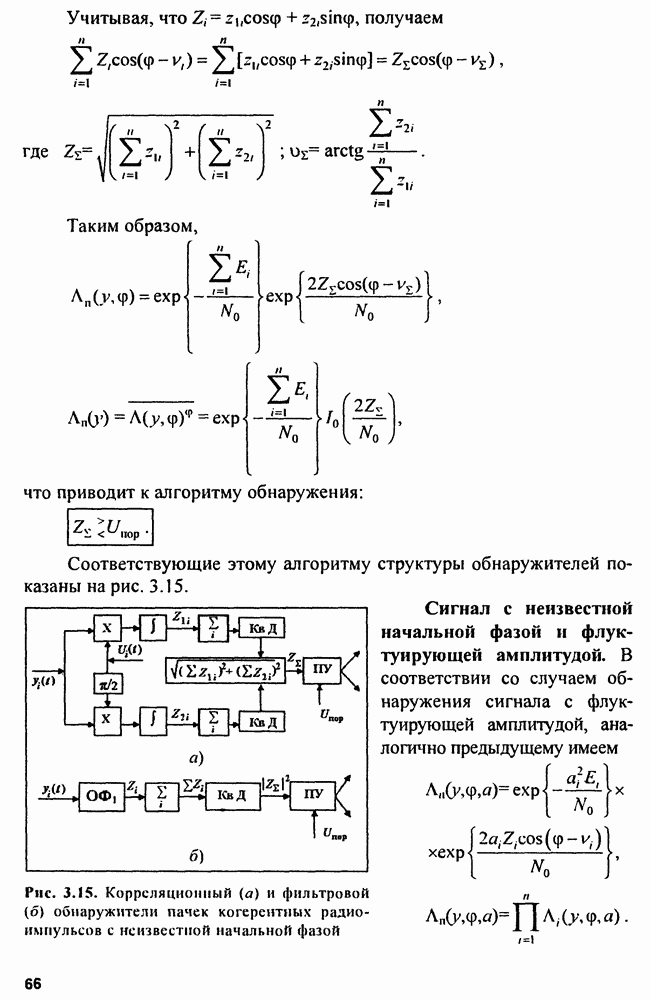
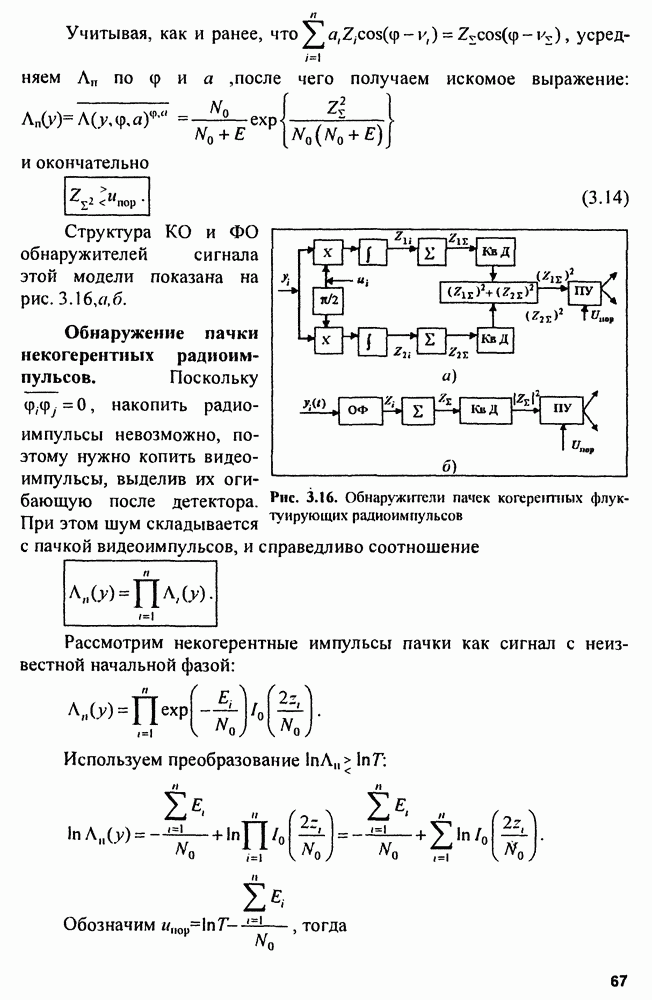
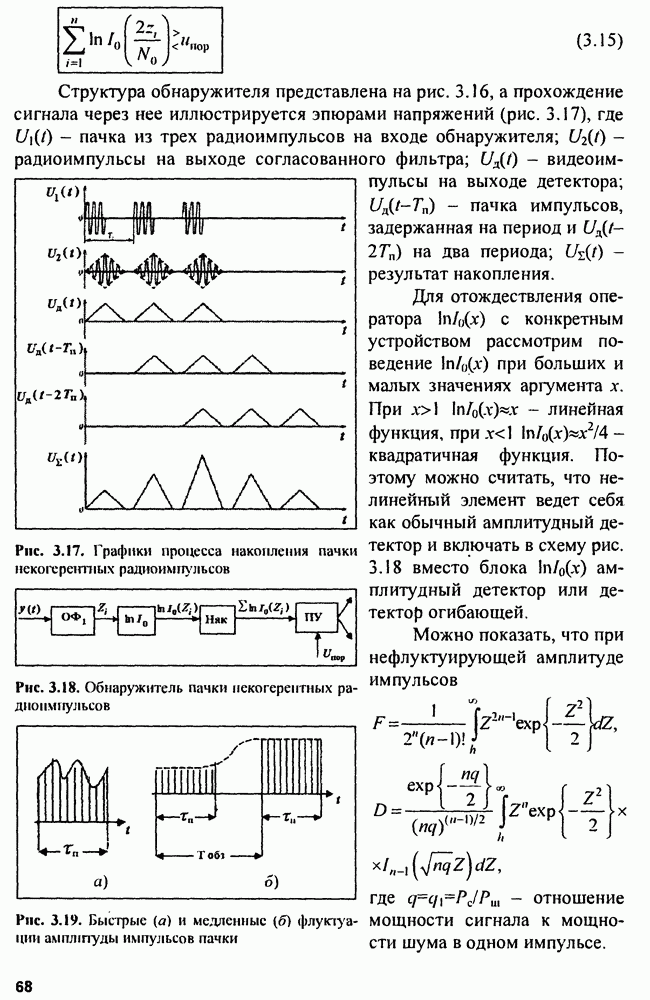
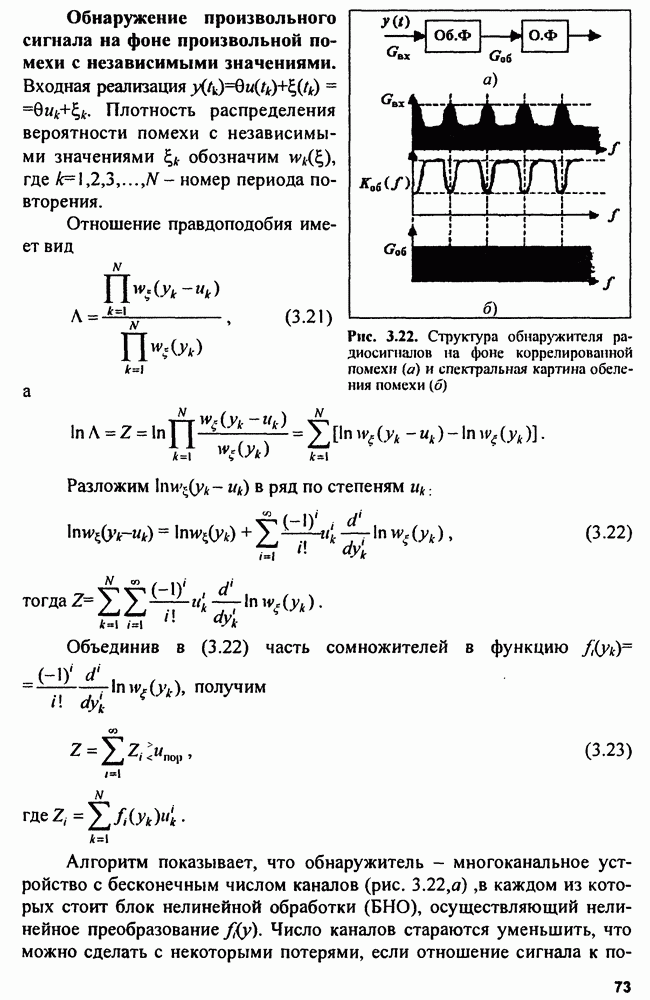
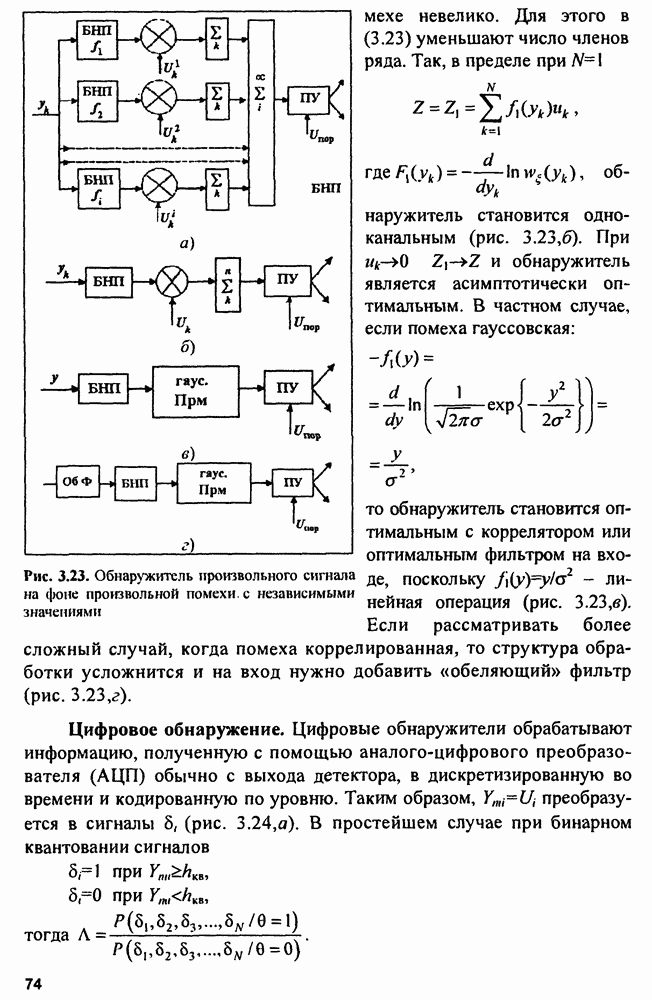
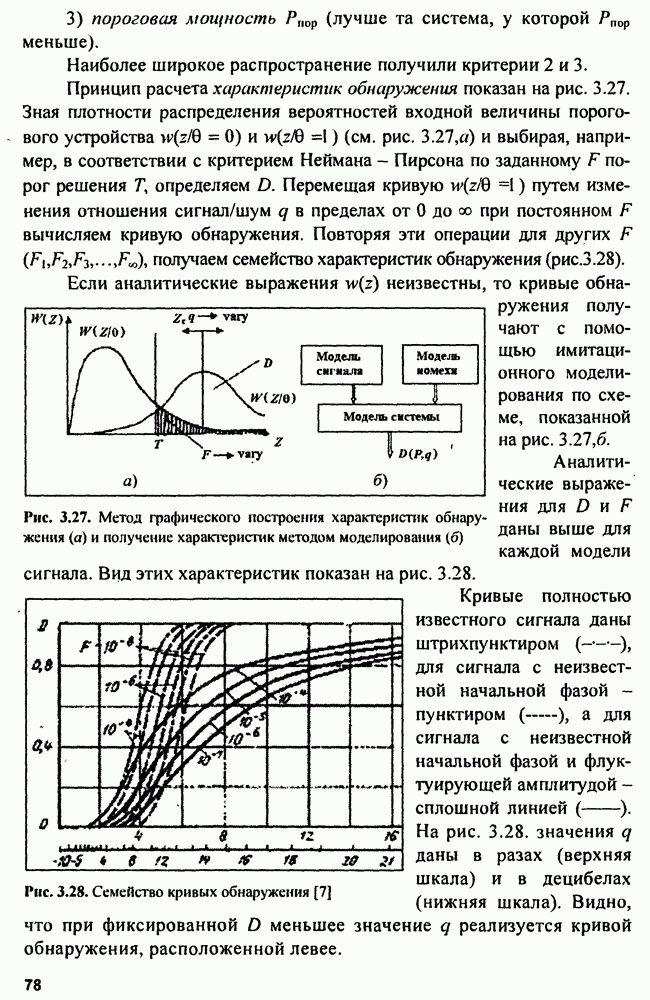
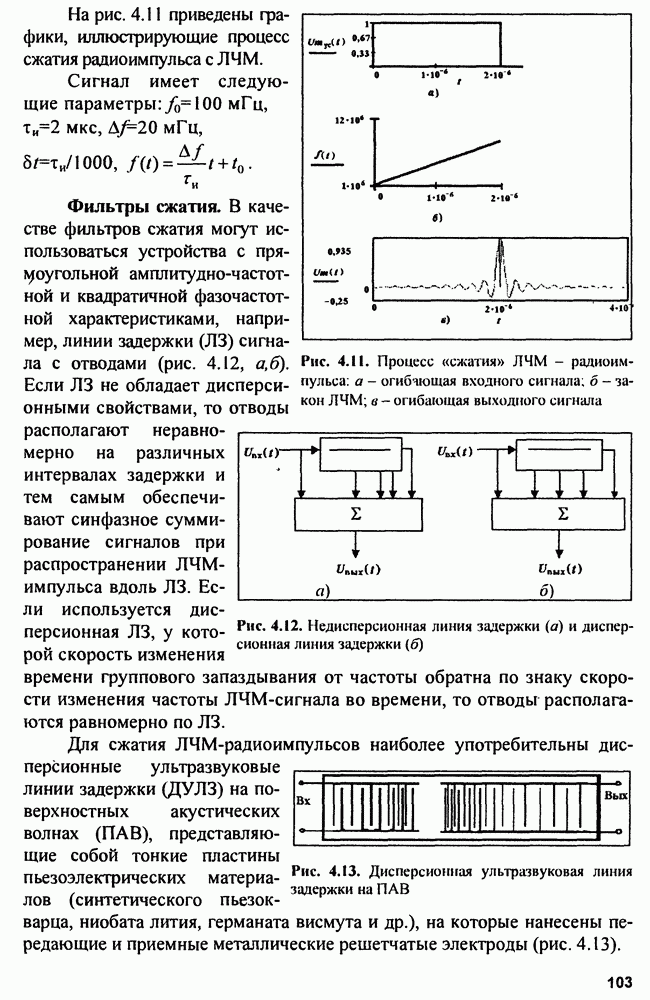
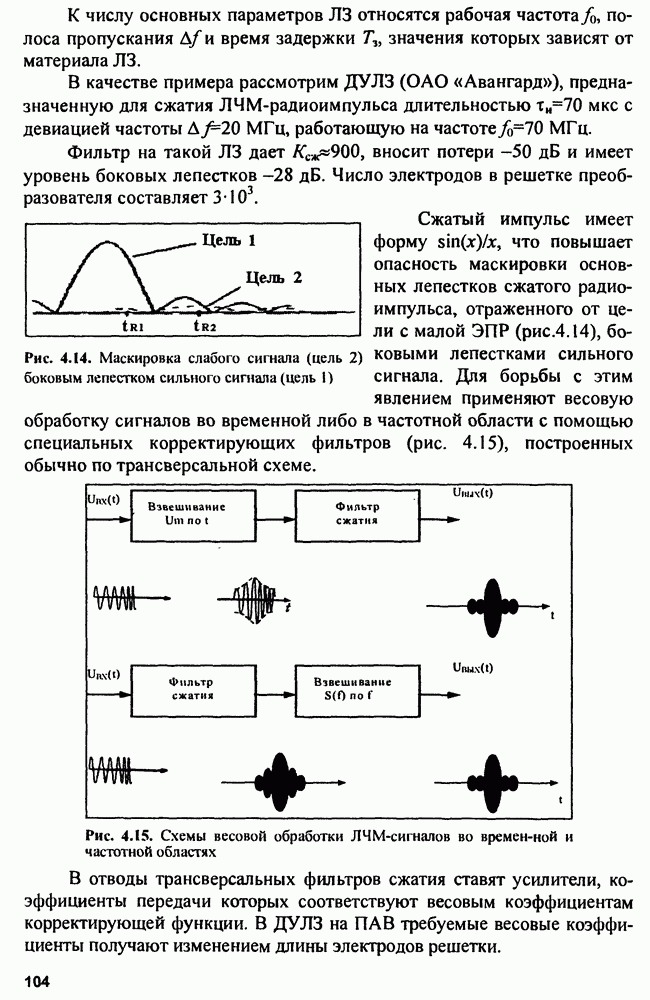
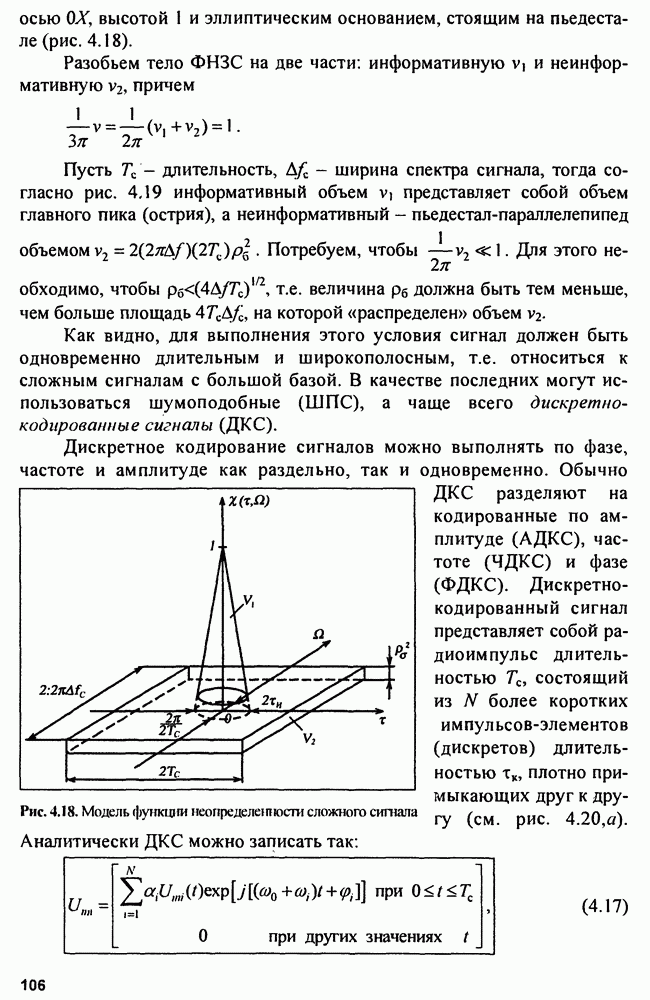
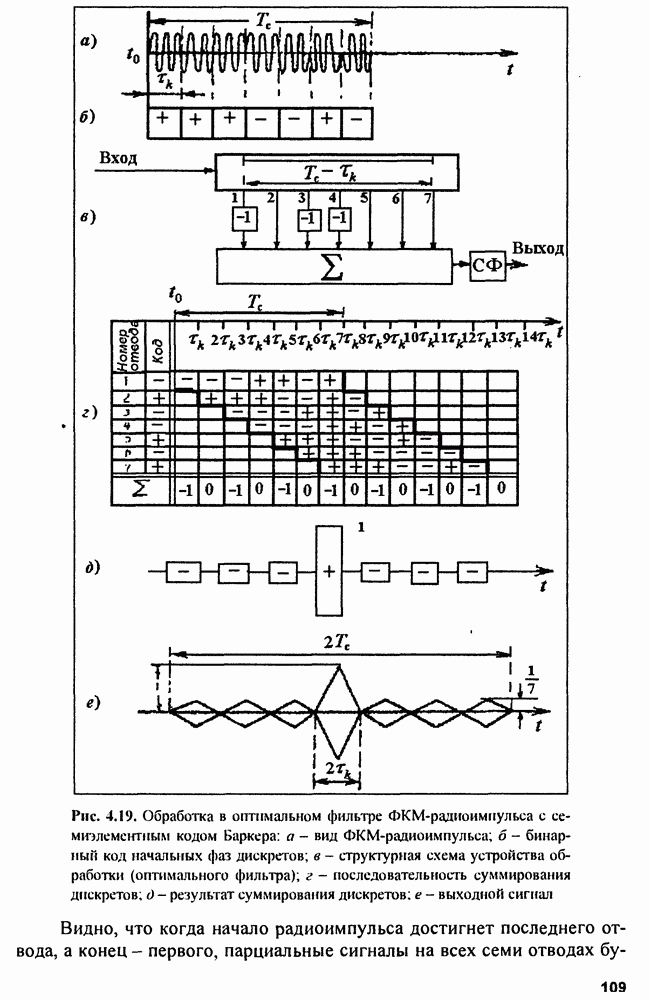
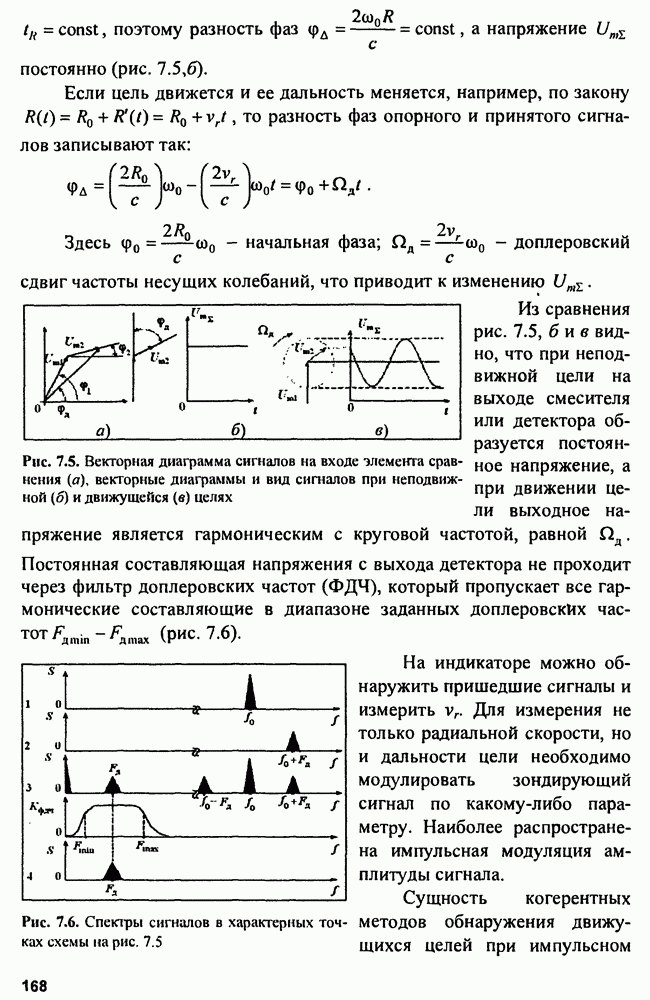
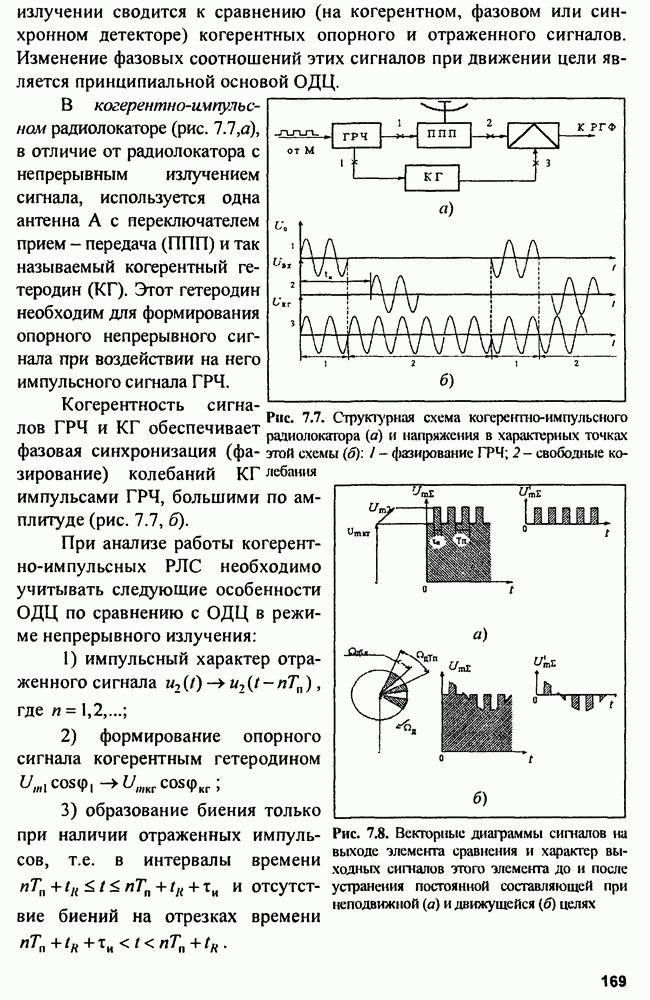
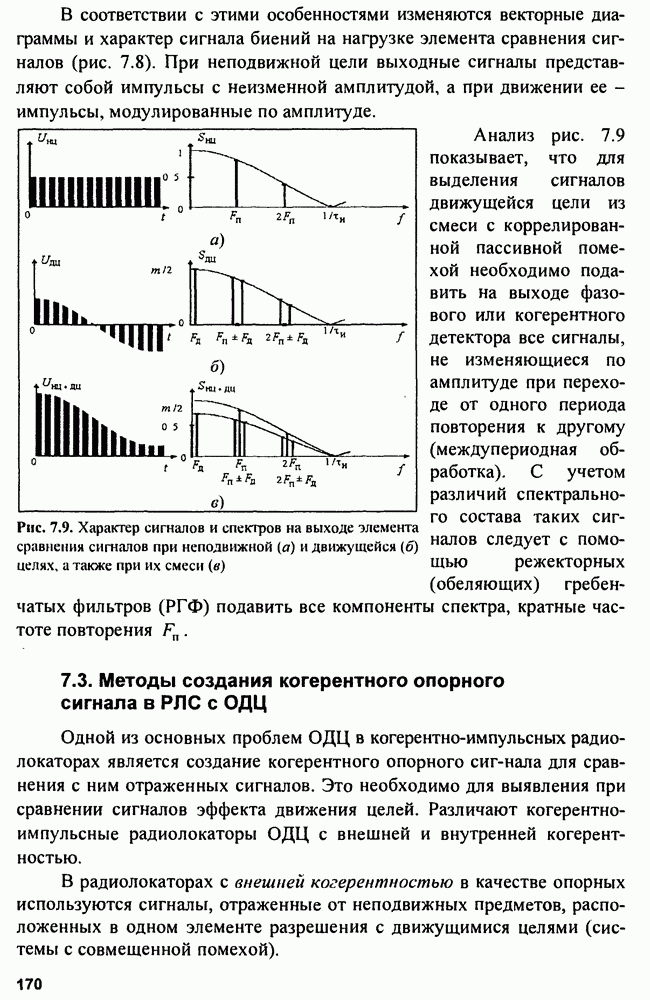
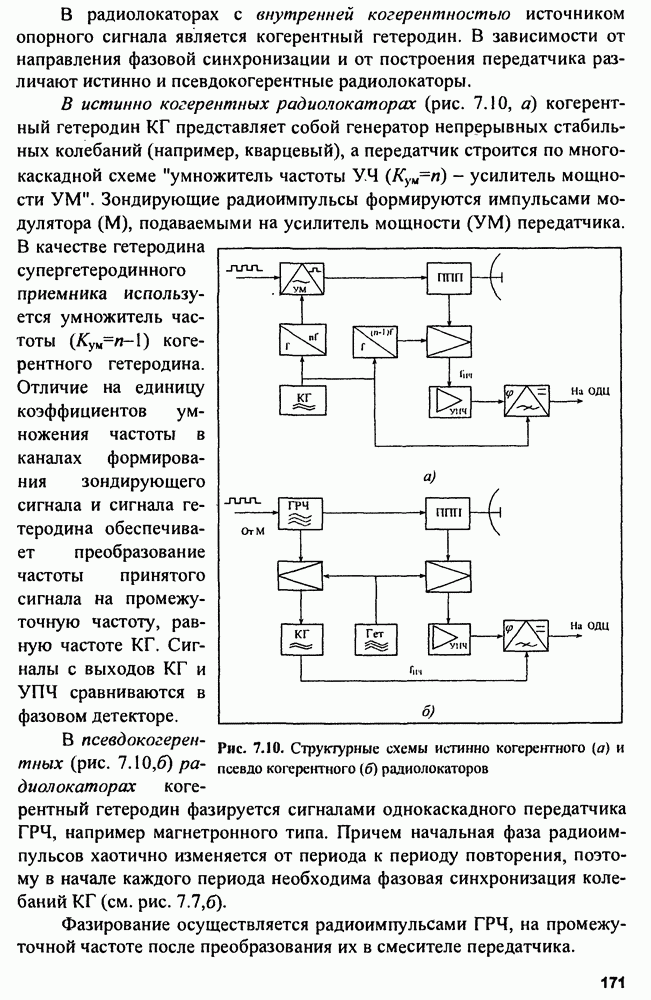
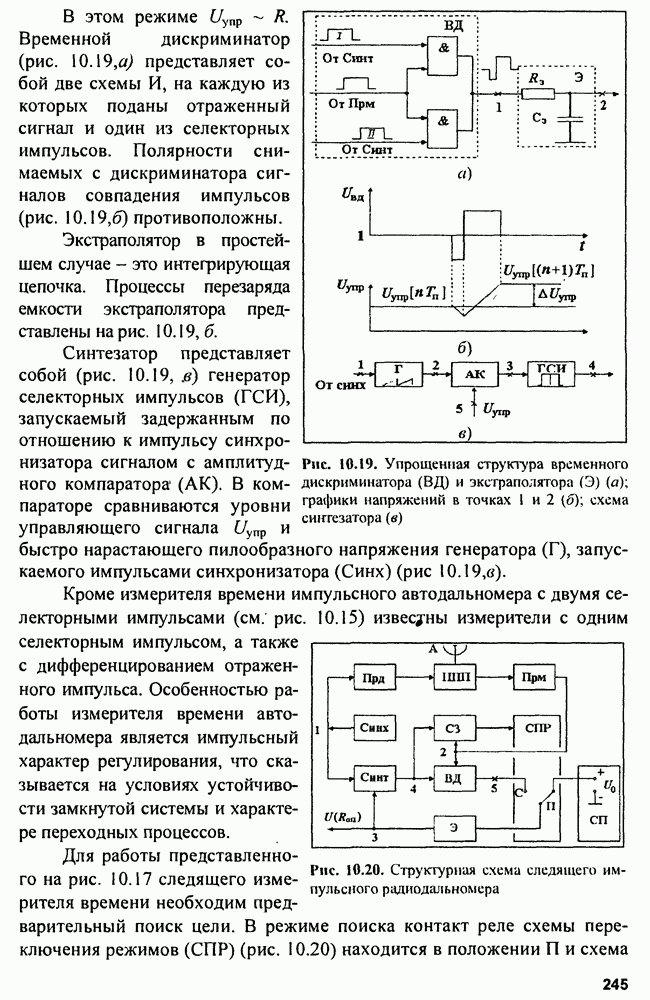
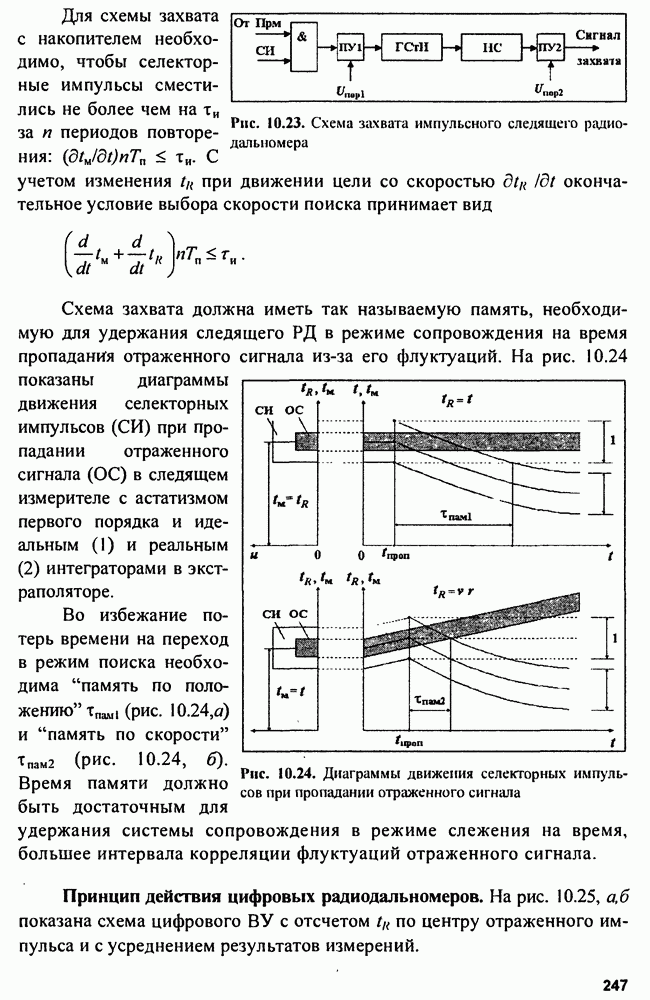
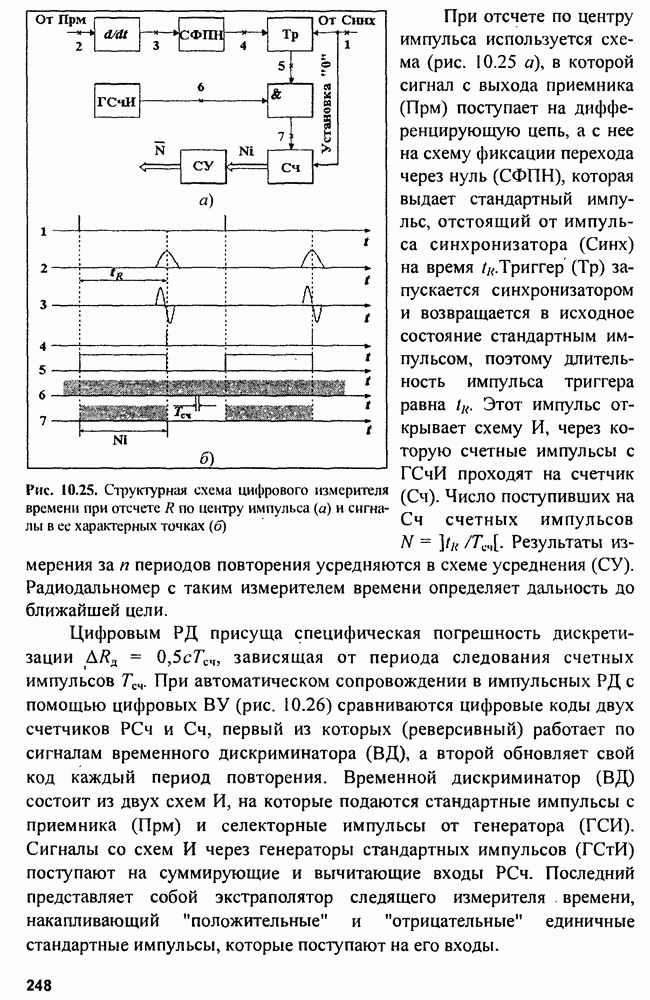
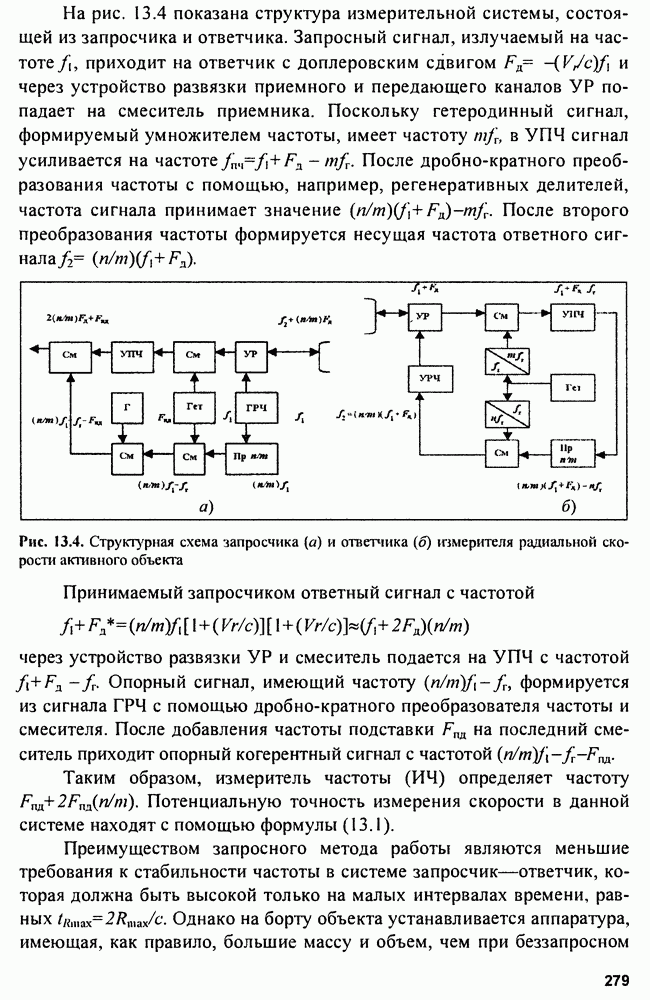
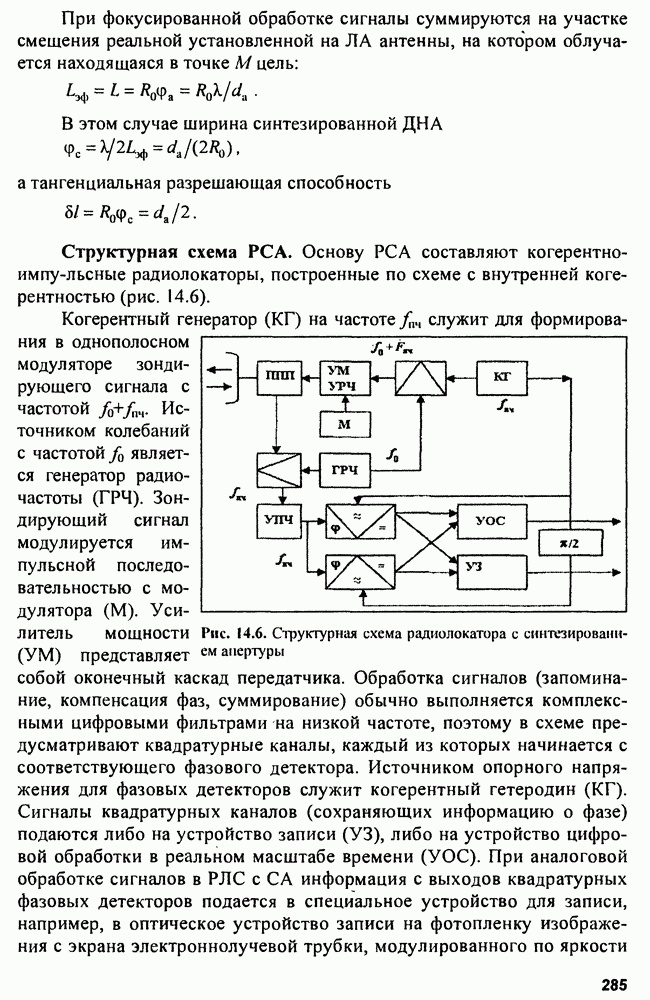
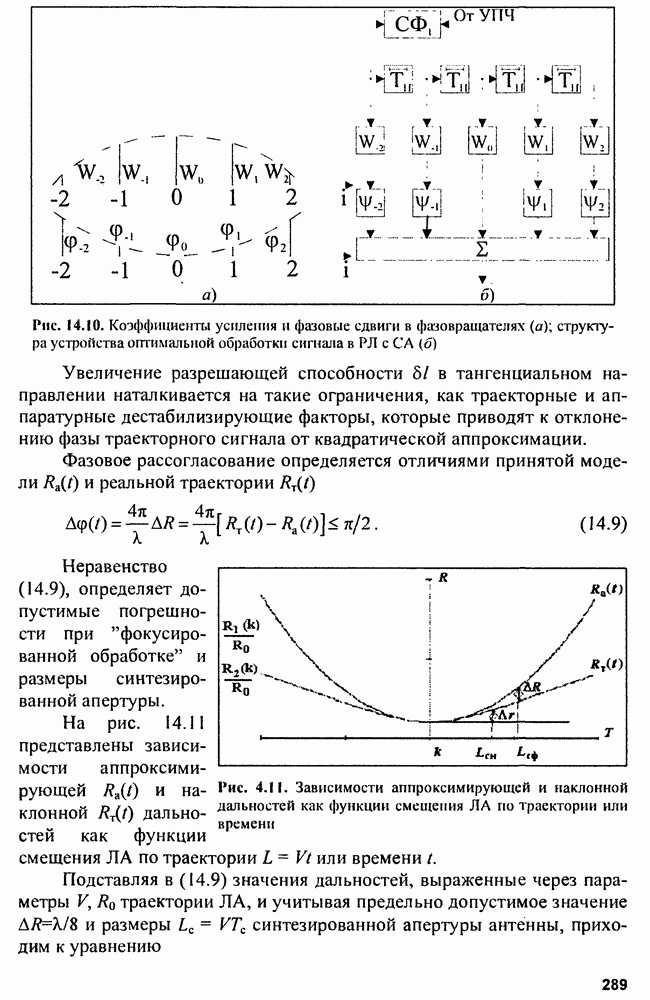
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
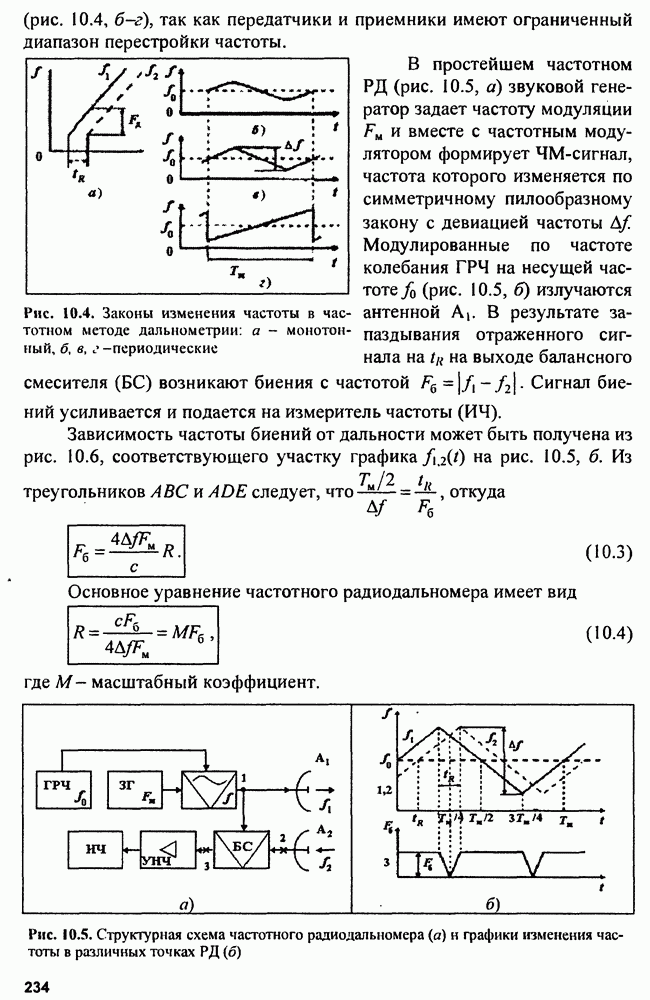
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
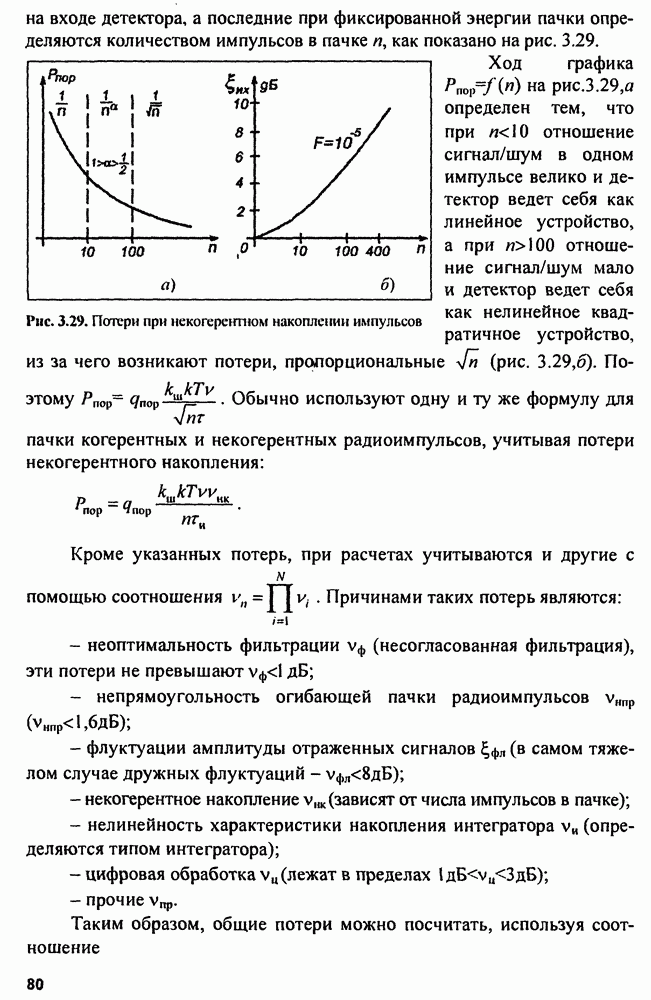
15.3. Оценка параметров траектории
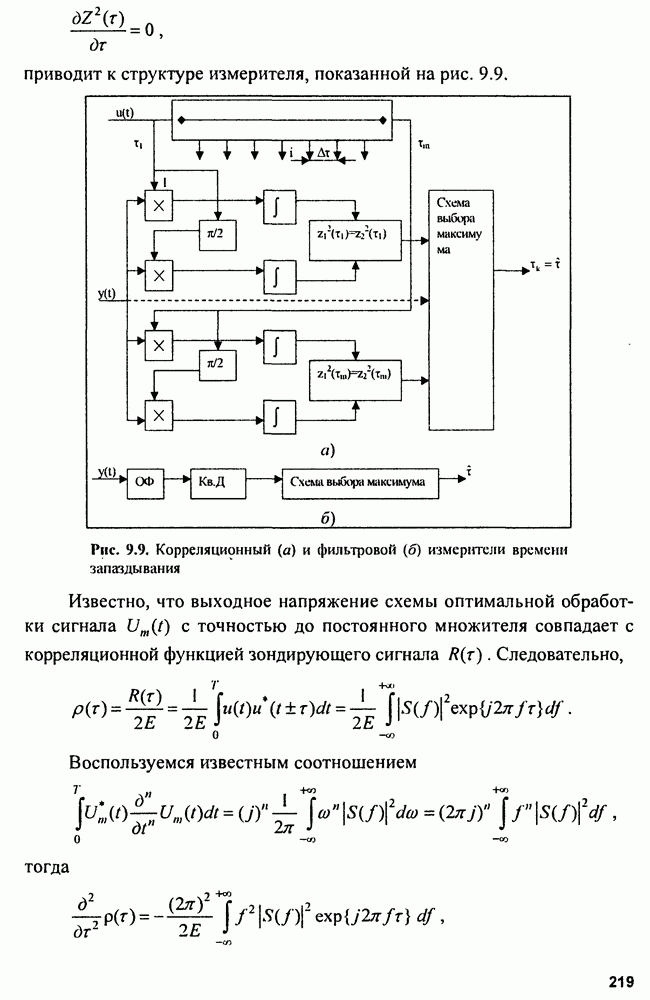
Пусть измеряемый параметр - дальность  случайный процесс, и является аддитивной смесью полезного сигнала
случайный процесс, и является аддитивной смесью полезного сигнала  и помехи
и помехи  Полезный сигнал - процесс изменения во времени независимой координаты цели - дальности представляется в виде полинома, степень которого определяется принятой моделью траектории:
Полезный сигнал - процесс изменения во времени независимой координаты цели - дальности представляется в виде полинома, степень которого определяется принятой моделью траектории:

Здесь коэффициенты полинома имеют смысл производных координаты (например дальности, скорости, ускорения и т.д.). Они называются параметрами траектории цели. Совокупность параметров  записанная в виде столбца, образует
записанная в виде столбца, образует  -мерный вектор параметров траектории
-мерный вектор параметров траектории 
Помеха, под которой понимают ошибки измерения координаты, представляет собой нормальный случайный процесс с известной корреляционной функцией и математическим ожиданием, равным нулю. Процесс измерения состоит в получении выборки значений  полинома
полинома  в моменты
в моменты 
Совокупность значений образует  -мерный вектор-столбец выборочных значений:
-мерный вектор-столбец выборочных значений:

Измерение или оценка  осуществляется в процессе фильтрации или сглаживания.
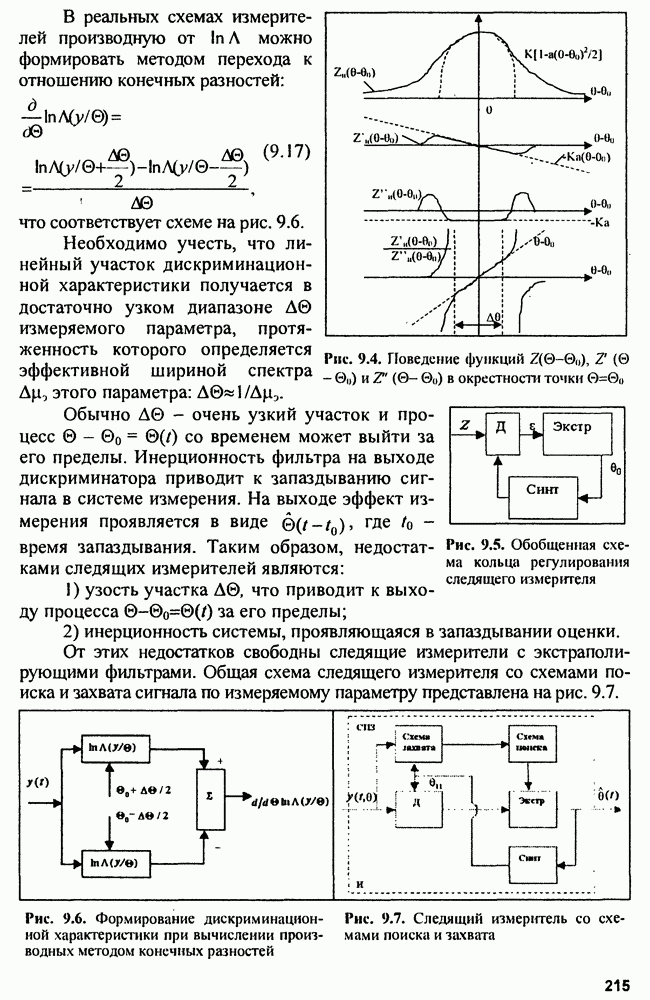
осуществляется в процессе фильтрации или сглаживания.
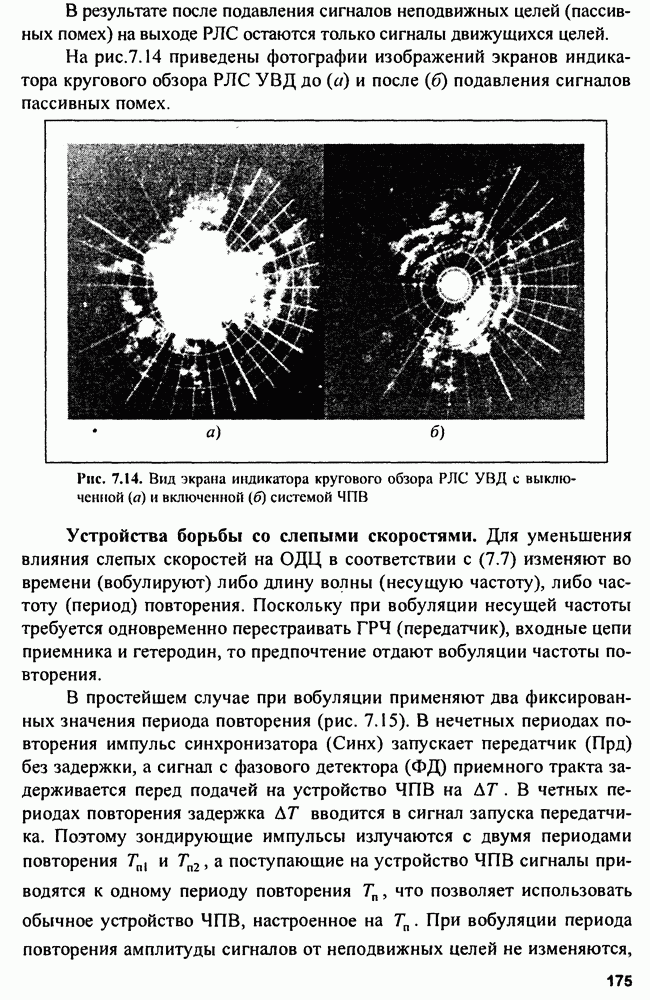
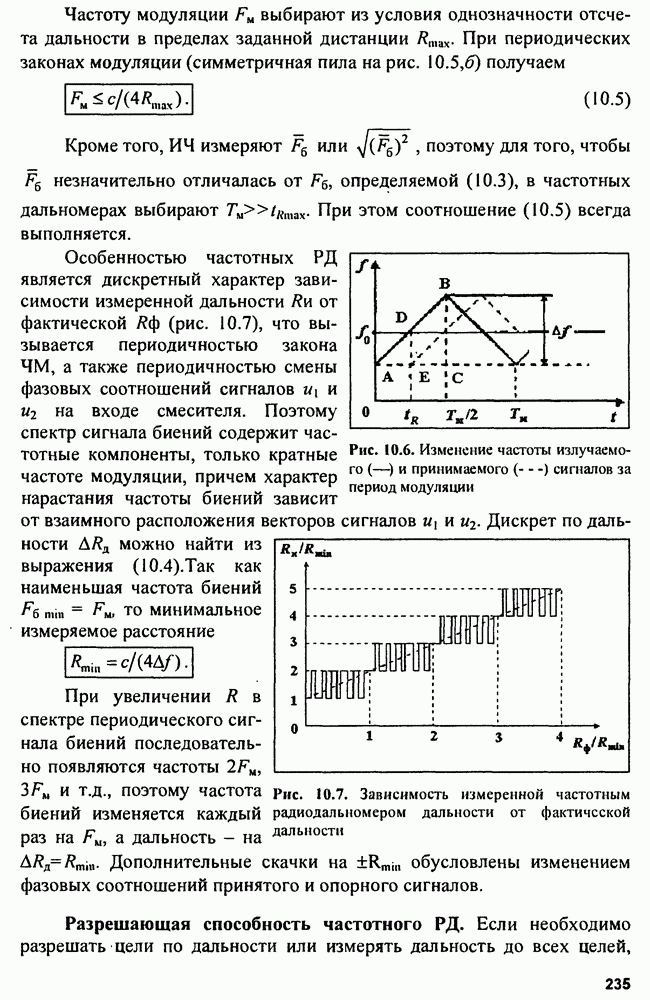
Существует ряд методов сглаживания параметров траектории. Наиболее простой метод - оценка параметров траектории по фиксированной выборке измеряемых координат, при этом для хранения обрабатываемых результатов нужен значительный объем памяти, а выдача результатов фильтрации происходит с задержкой. Более совершенен метод рекуррентного последовательного сглаживания параметров траектории, полученный на основе теории оптимальной фильтрации.
Наконец, широко применяется метод скользящего сглаживания параметров траектории, в котором память фильтров ограничивается за счет замораживания коэффициентов сглаживания, а просмотр траектории производится в скользящем окне.
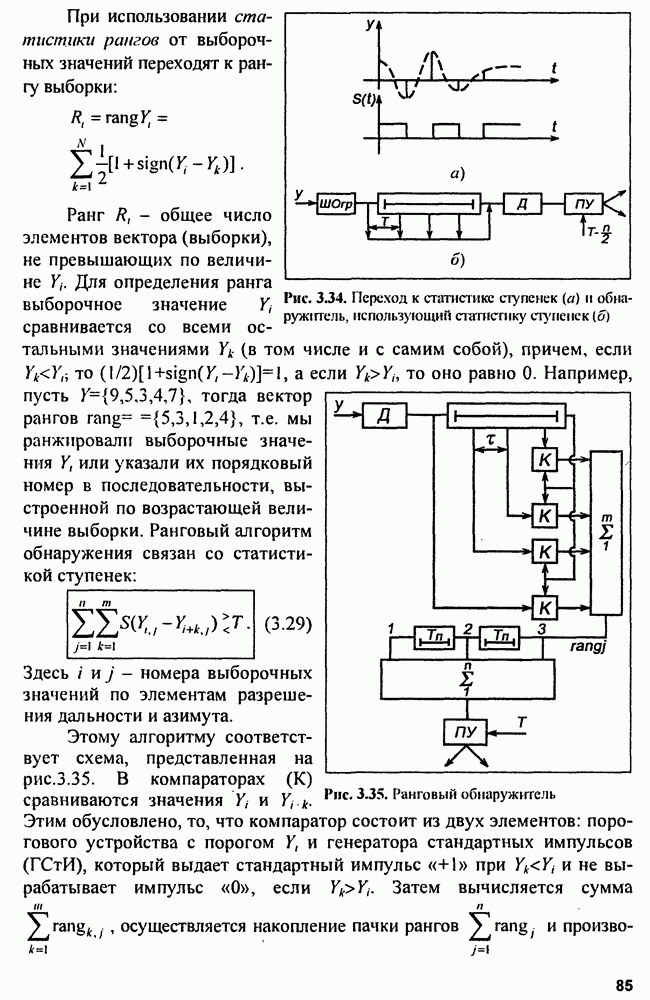
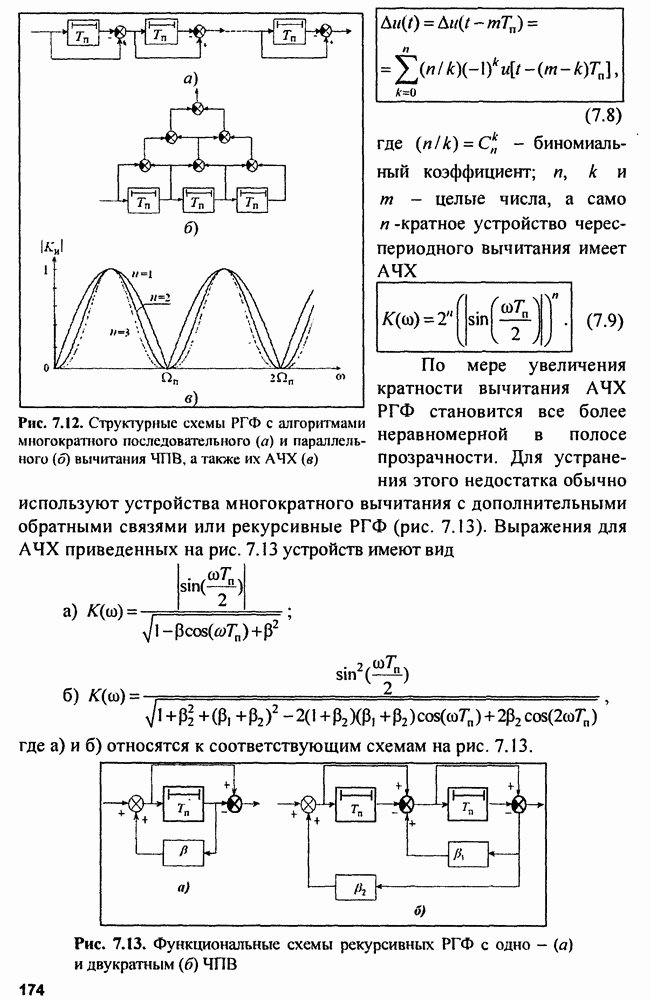
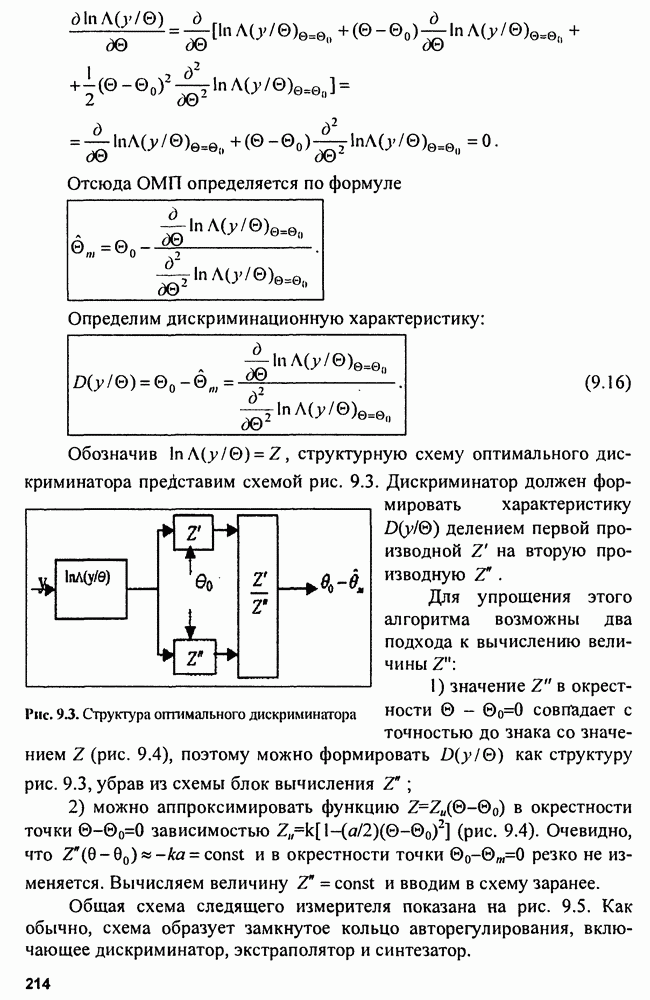
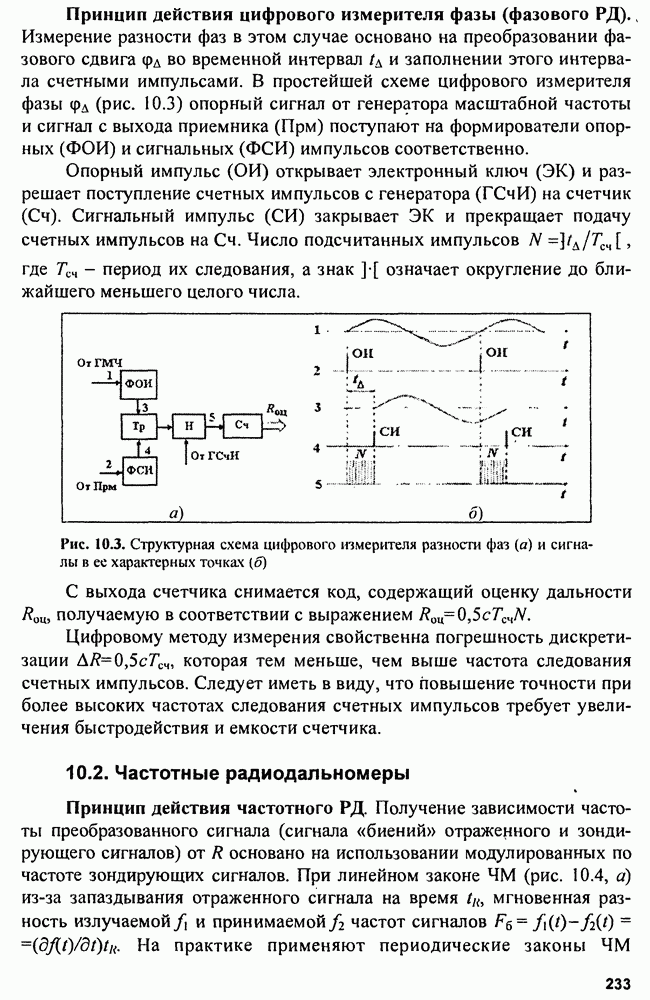
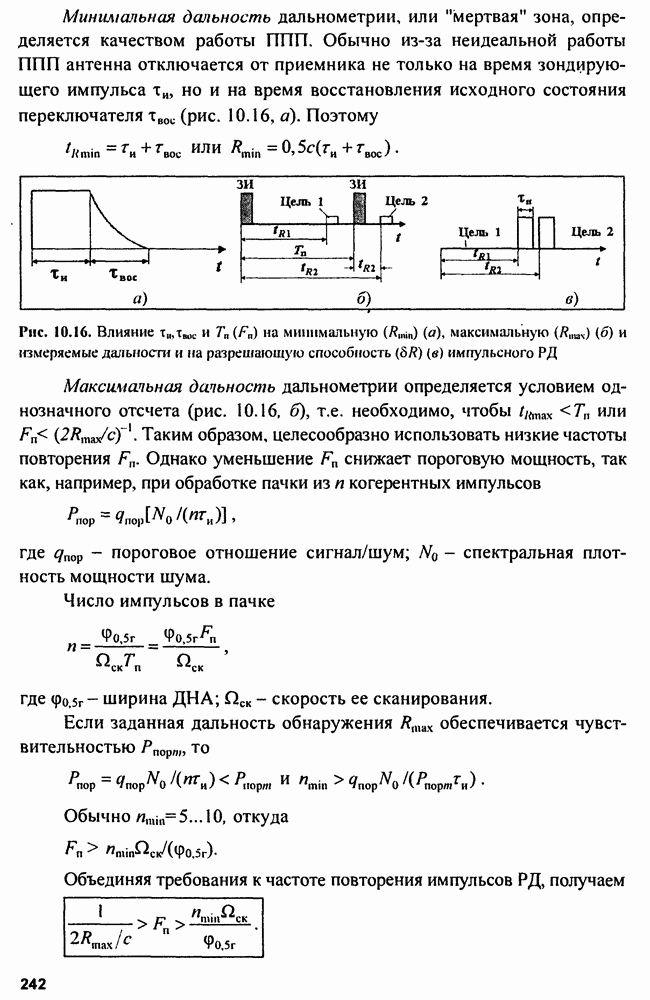
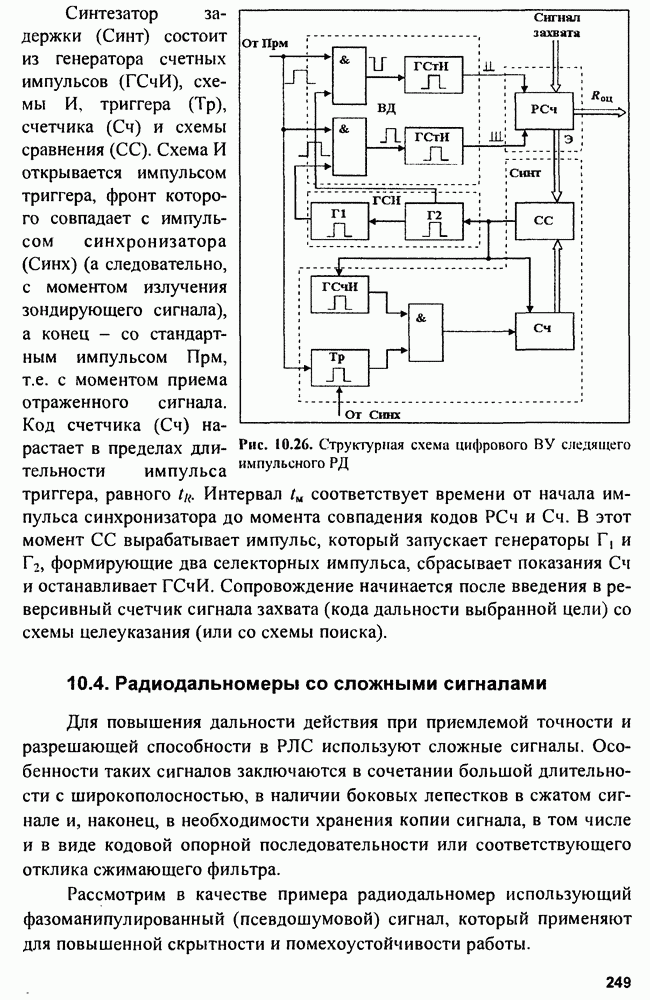
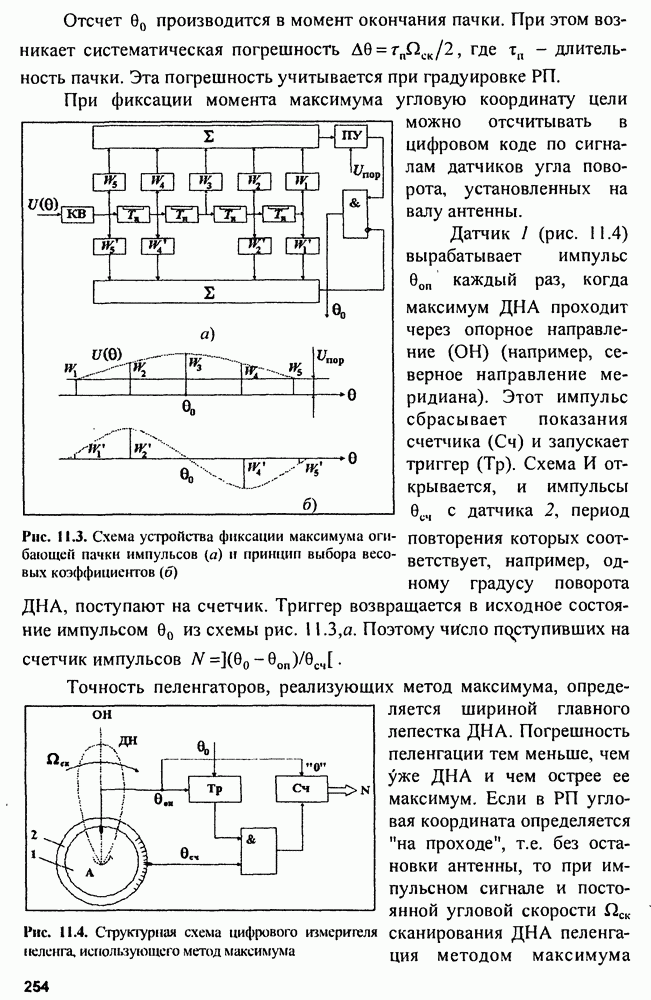
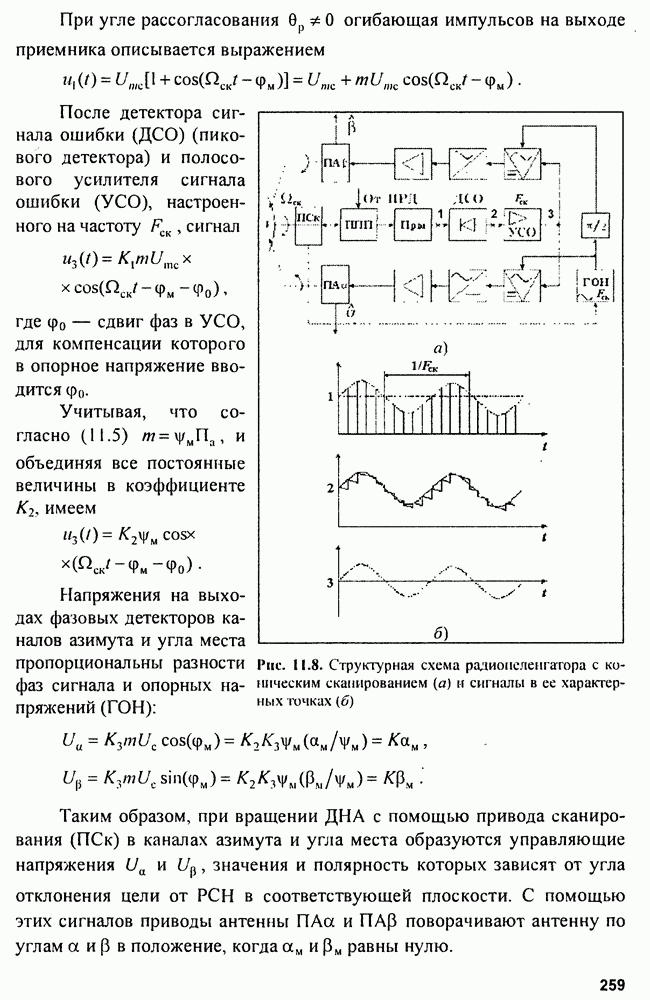
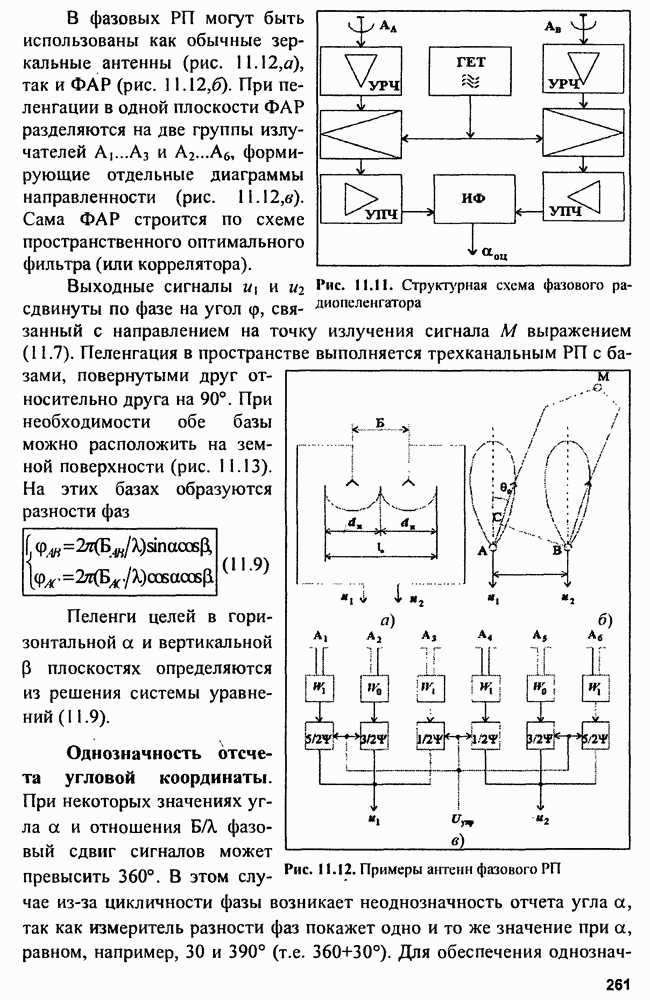
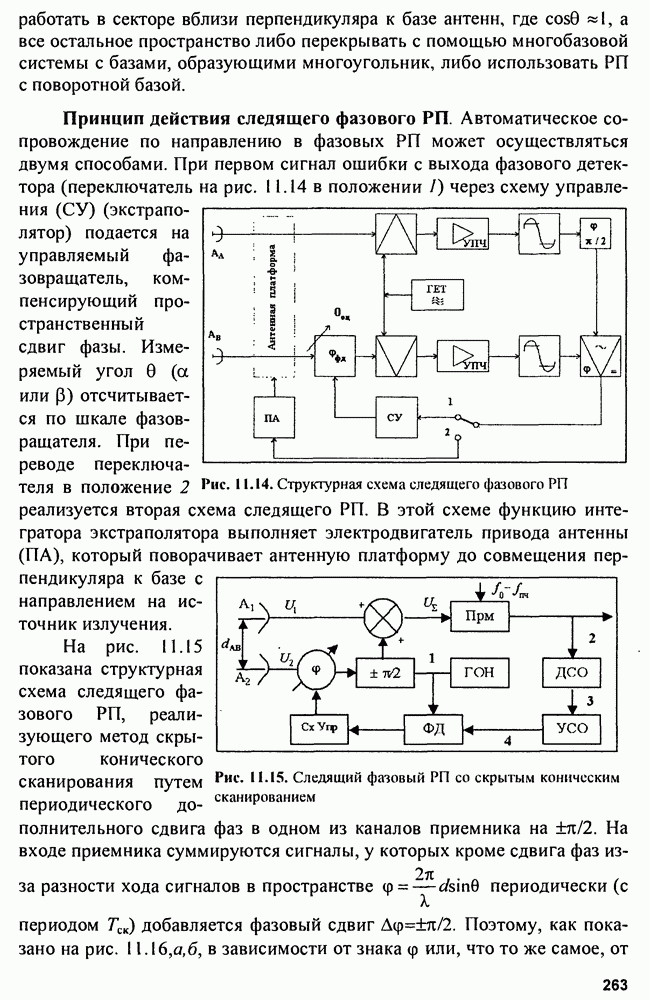
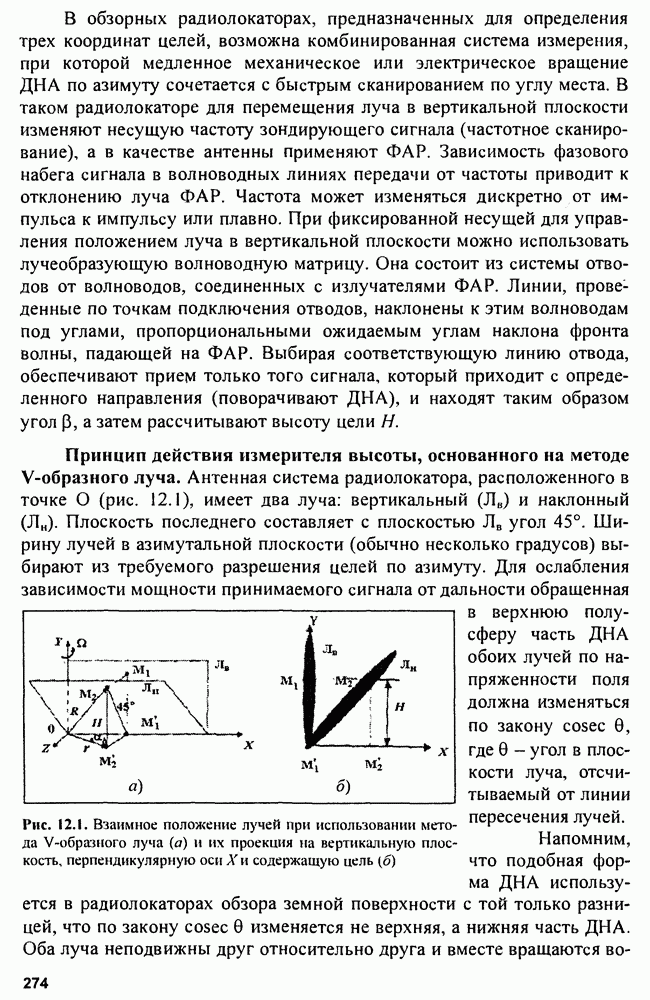
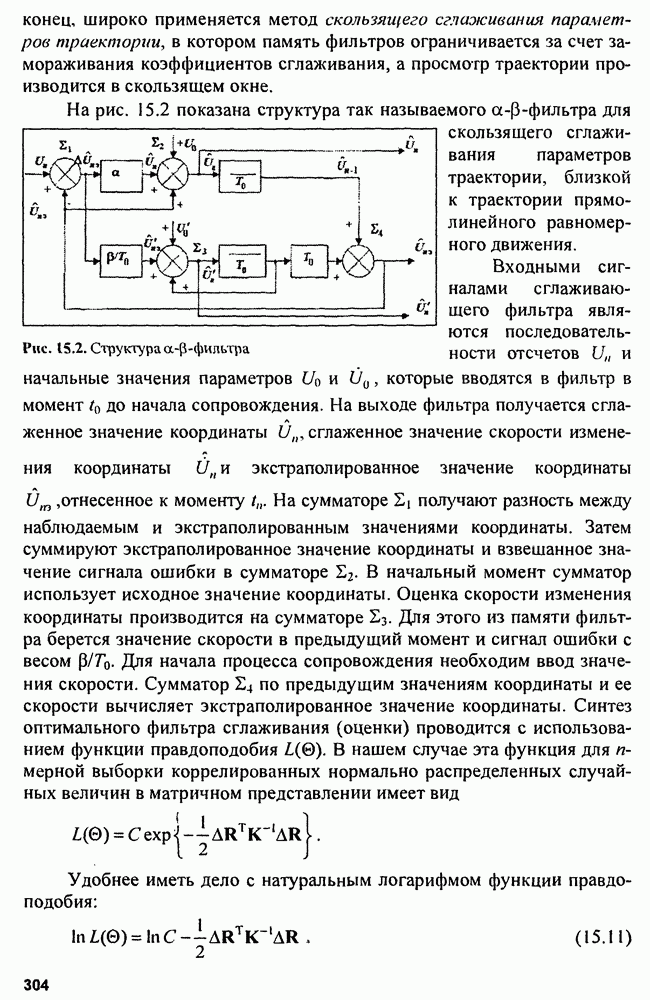
На рис. 15.2 показана структура так называемого  -фильтра для скользящего сглаживания параметров траектории, близкой к траектории прямолинейного равномерного движения.
-фильтра для скользящего сглаживания параметров траектории, близкой к траектории прямолинейного равномерного движения.

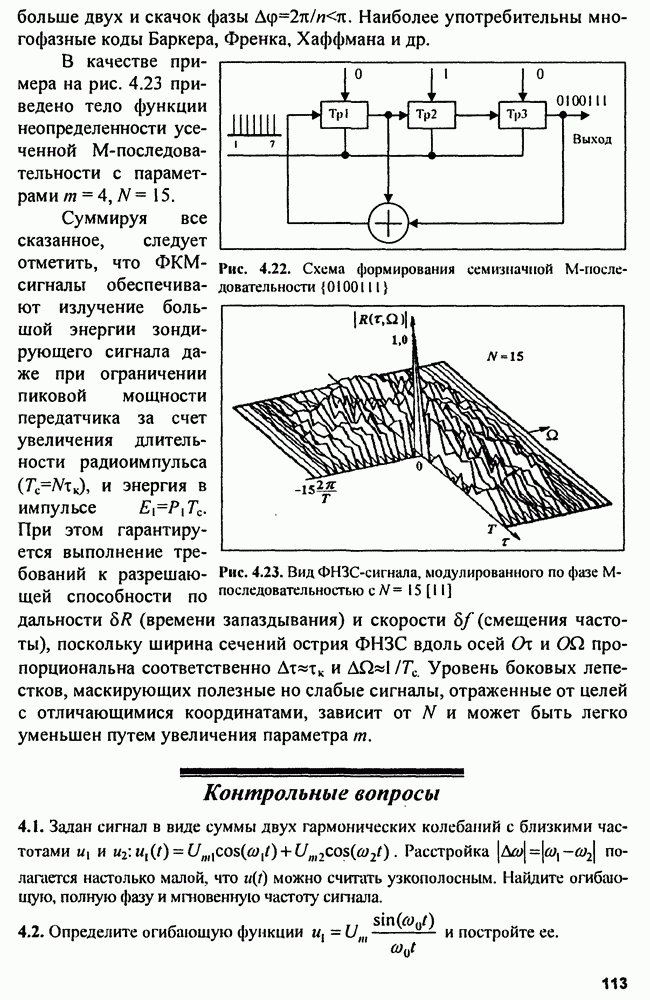
Рис. 15.2. Структура  -фильтра
-фильтра
Входными сигналами сглаживающего фильтра являются последовательности отсчетов  и начальные значения параметров
и начальные значения параметров  которые вводятся в фильтр в момент
которые вводятся в фильтр в момент  до начала сопровождения. На выходе фильтра получается сглаженное значение координаты
до начала сопровождения. На выходе фильтра получается сглаженное значение координаты  сглаженное значение скорости изменения координаты
сглаженное значение скорости изменения координаты  и экстраполированное значение координаты
и экстраполированное значение координаты  отнесенное к моменту
отнесенное к моменту  На сумматоре
На сумматоре  получают разность между наблюдаемым и экстраполированным значениями координаты. Затем суммируют экстраполированное значение координаты и взвешанное значение сигнала ошибки в сумматоре
получают разность между наблюдаемым и экстраполированным значениями координаты. Затем суммируют экстраполированное значение координаты и взвешанное значение сигнала ошибки в сумматоре  В начальный момент сумматор использует исходное значение координаты. Оценка скорости изменения координаты производится на сумматоре
В начальный момент сумматор использует исходное значение координаты. Оценка скорости изменения координаты производится на сумматоре  Для этого из памяти фильтра берется значение скорости в предыдущий момент и сигнал ошибки с весом
Для этого из памяти фильтра берется значение скорости в предыдущий момент и сигнал ошибки с весом  Для начала процесса сопровождения необходим ввод значения скорости. Сумматор
Для начала процесса сопровождения необходим ввод значения скорости. Сумматор  по предыдущим значениям координаты и ее скорости вычисляет экстраполированное значение координаты. Синтез оптимального фильтра сглаживания (оценки) проводится с использованием функции правдоподобия
по предыдущим значениям координаты и ее скорости вычисляет экстраполированное значение координаты. Синтез оптимального фильтра сглаживания (оценки) проводится с использованием функции правдоподобия  В нашем случае эта функция для n-мерной выборки коррелированных нормально распределенных случайных величин в матричном представлении имеет вид
В нашем случае эта функция для n-мерной выборки коррелированных нормально распределенных случайных величин в матричном представлении имеет вид

Удобнее иметь дело с натуральным логарифмом функции правдоподобия:

Для нахождения оценок продифференцируем (15.11) по 

Полагая  приравниваем производную нулю:
приравниваем производную нулю:

Поскольку  является вектор-строкой, производную представим в виде матрицы:
является вектор-строкой, производную представим в виде матрицы:

Векторное уравнение правдоподобия имеет вид 
Если обозначить  то решением этого уравнения будет соотношение
то решением этого уравнения будет соотношение

Алгоритм обработки получается при конкретизации статистики помех  Точность измерения параметров траектории зависит от корреляционной матрицы вектора
Точность измерения параметров траектории зависит от корреляционной матрицы вектора 

Поскольку  вектор пофешностей измерений) и
вектор пофешностей измерений) и  то
то 
Обычно матрица  симметрична относительно диагонали и, следовательно,
симметрична относительно диагонали и, следовательно, 
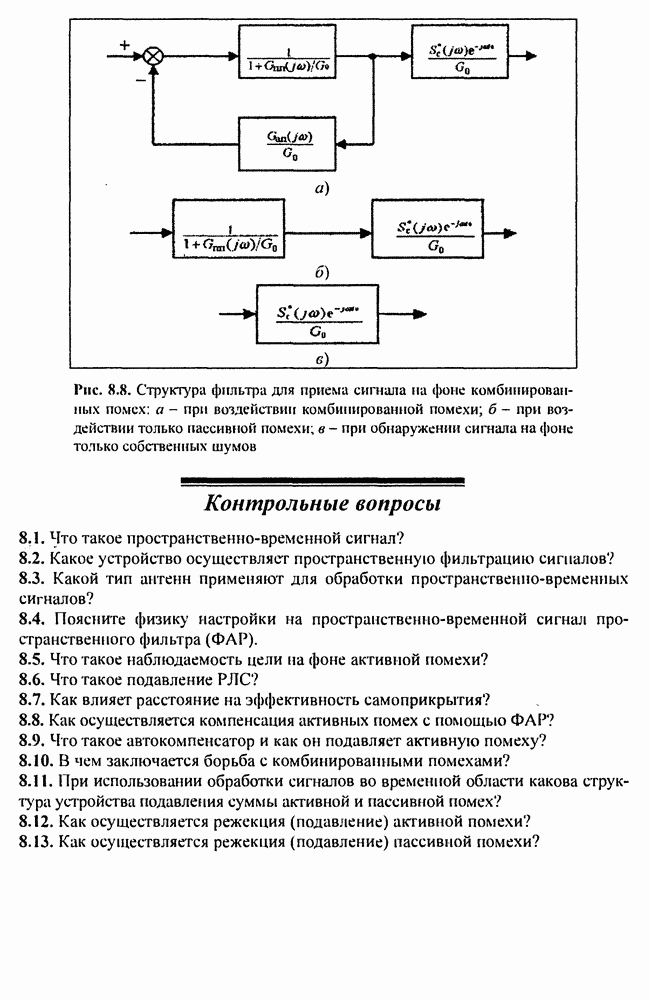
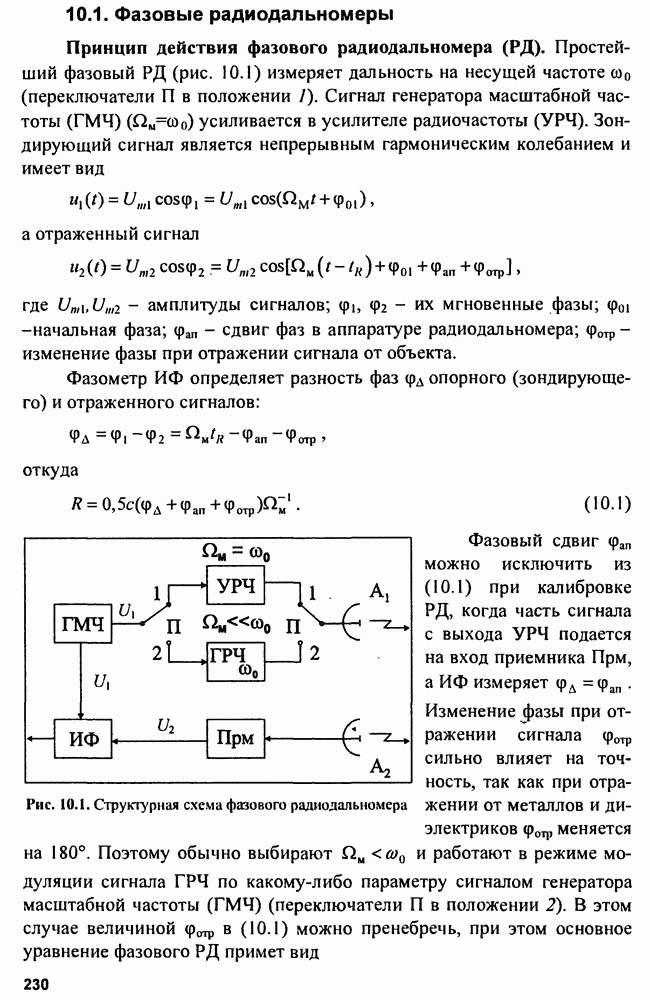
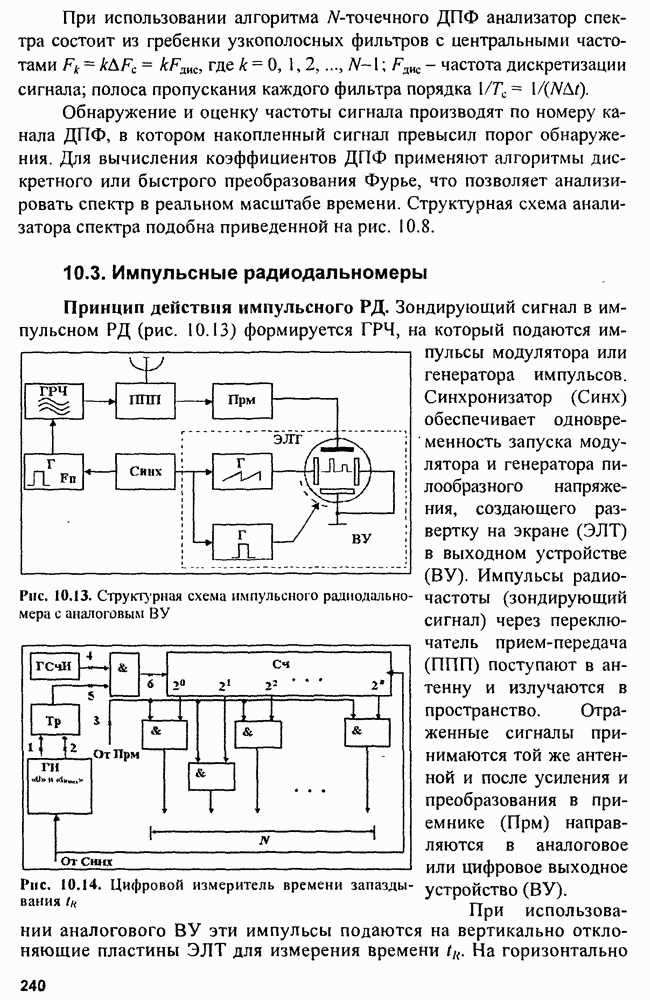
Если использовать многомерный фильтр Калмана, то его алгоритм и структура находят путем конкретизации оптимального соотношения рекуррентной фильтрации. Без вывода приведем результаты такого синтеза.
Пусть  -мерный вектор состояния
-мерный вектор состояния  задан линейным векторным разностным уравнением
задан линейным векторным разностным уравнением

где  переходная матрица состояния размера
переходная матрица состояния размера  матрица размера
матрица размера  -мерный вектор гауссовских величин, для которого
-мерный вектор гауссовских величин, для которого  матрица размера
матрица размера  - символ Кронекера;
- символ Кронекера;  задает начальное состояние.
задает начальное состояние.
Уравнение (15.15) характеризует движение  матрица
матрица  задает динамику движения, а матрица
задает динамику движения, а матрица  определяет преобразования возмущений, воздействующих на
определяет преобразования возмущений, воздействующих на  Наблюдаемый векторный процесс имеет вид
Наблюдаемый векторный процесс имеет вид

где  матрица размера
матрица размера  -мерный вектор погрешностей измерений (шум).
-мерный вектор погрешностей измерений (шум).
Процесс последовательного формирования оценки вектора состояния описывается соотношением

Например, если нужно оценить параметры прямолинейной траектории, то при равномерных и равноточных измерениях и мерности задачи, равной двум, получим

Совместное решение алгоритмов (15.16) и (15.17) позволяет найти соотношение

Алгоритму (15.18) соответствует структура фильтра Калмана (см. рис. 9.16). Работа такого фильтра рассмотрена в гл. 9.
Фильтр Калмана является линейным рекуррентным фильтром, что позволяет последовательно сглаживать параметры траекторий. Однако при реализации таких фильтров по мере вычисления коэффициентов  их величина уменьшается и стремится к нулю, поэтому они перестают зависеть от входных данных, что делает невозможным обнаружение маневров цели.
их величина уменьшается и стремится к нулю, поэтому они перестают зависеть от входных данных, что делает невозможным обнаружение маневров цели.
Кроме того, при больших к коэффициенты  соизмеримы с величиной вычислительных ошибок из-за многократного обращения матриц. В результате фильтры становятся неустойчивыми.
соизмеримы с величиной вычислительных ошибок из-за многократного обращения матриц. В результате фильтры становятся неустойчивыми.
Имеются приемы, препятствующие неустойчивости фильтра, например регуляризация, которая сводится к добавлению в фильтр шумов.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
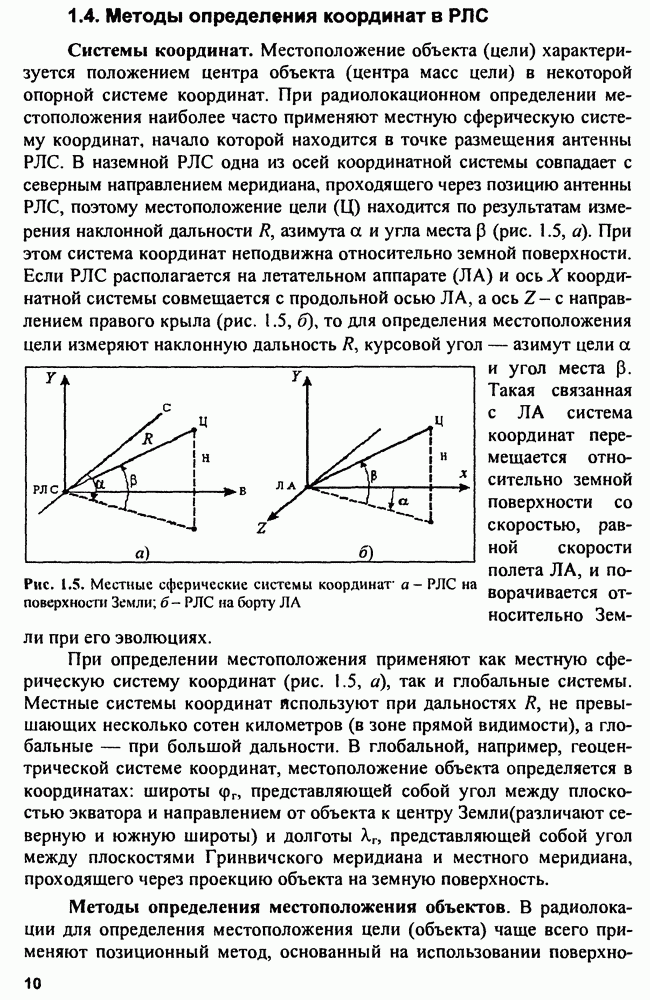
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
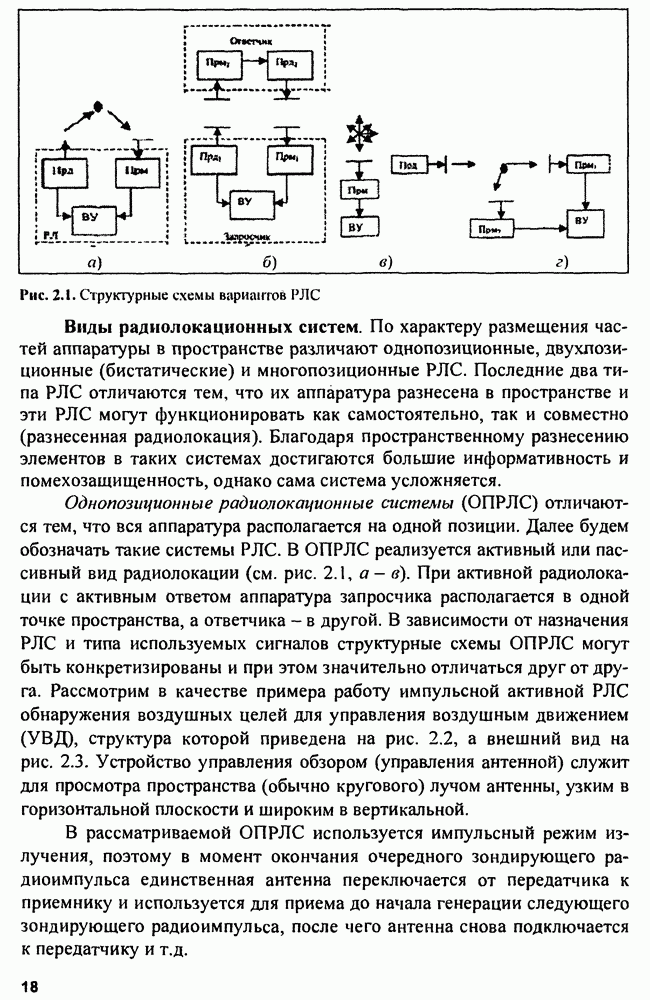
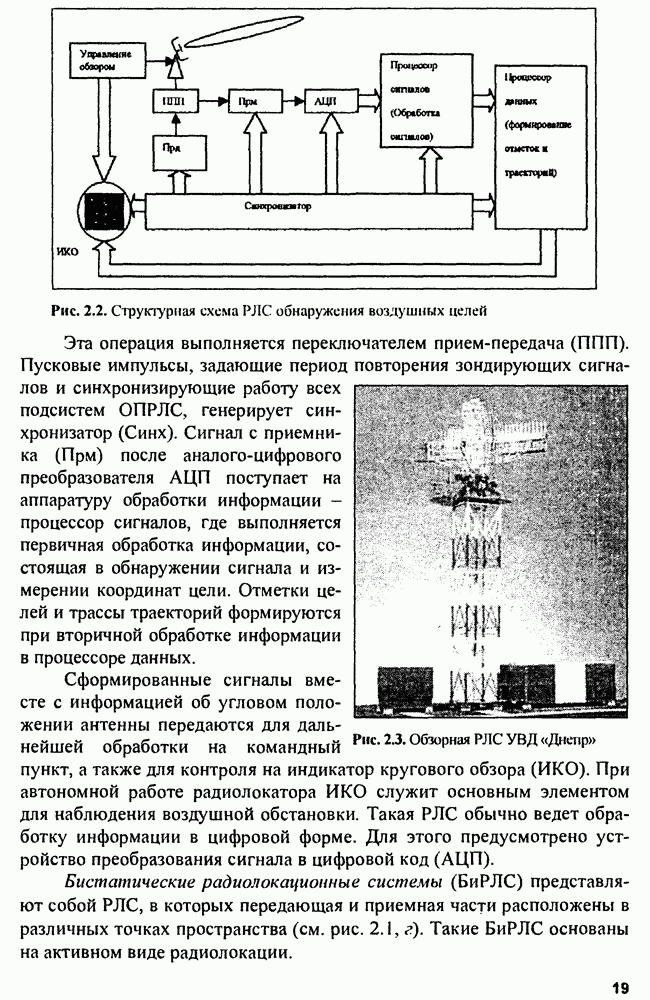
- Глава 2. Радиолокационные системы
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
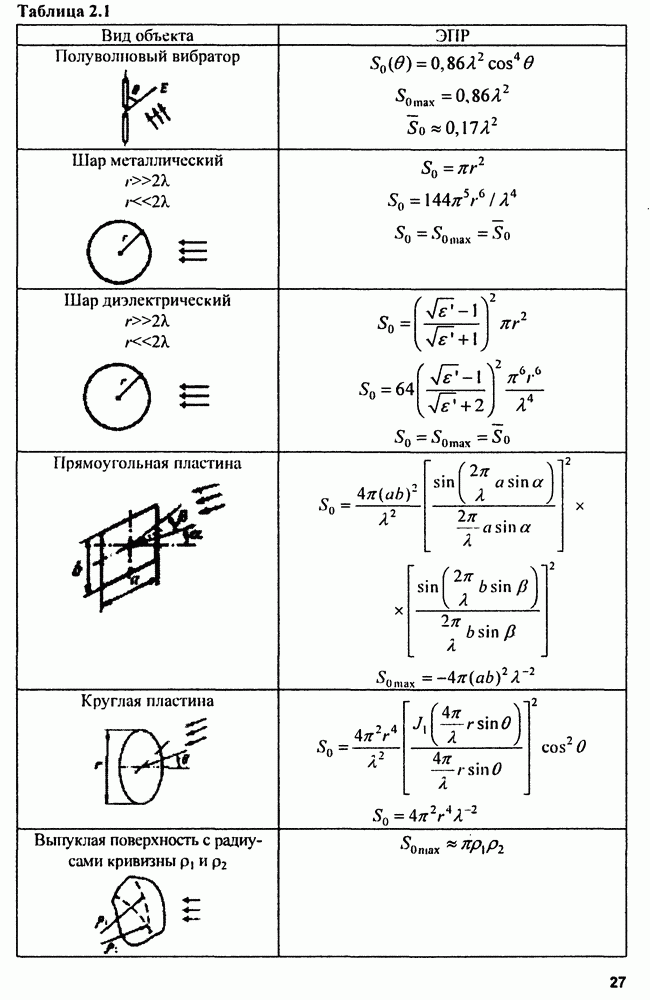
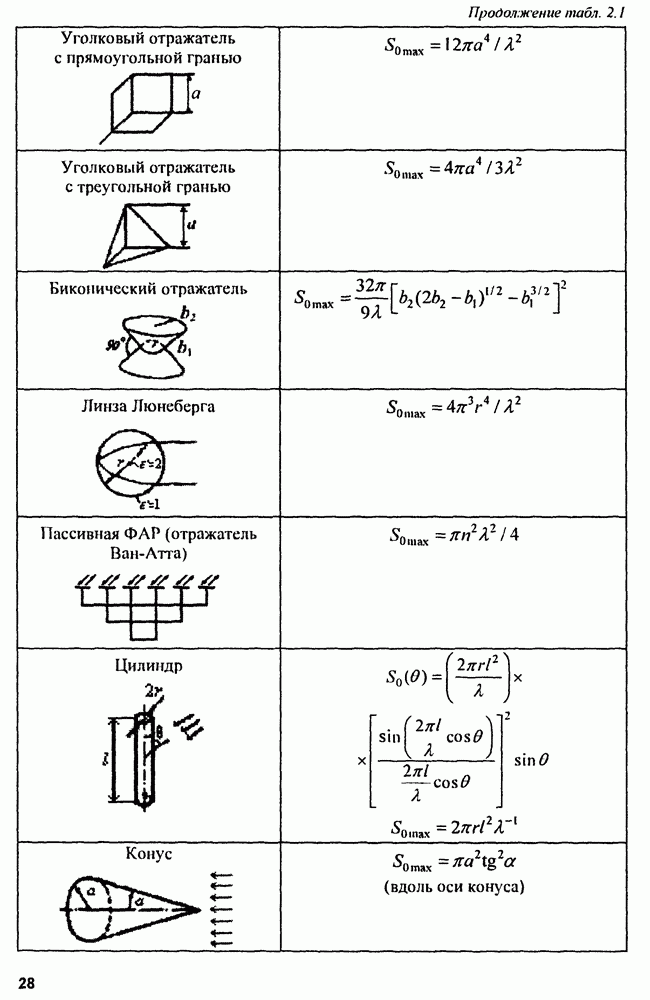
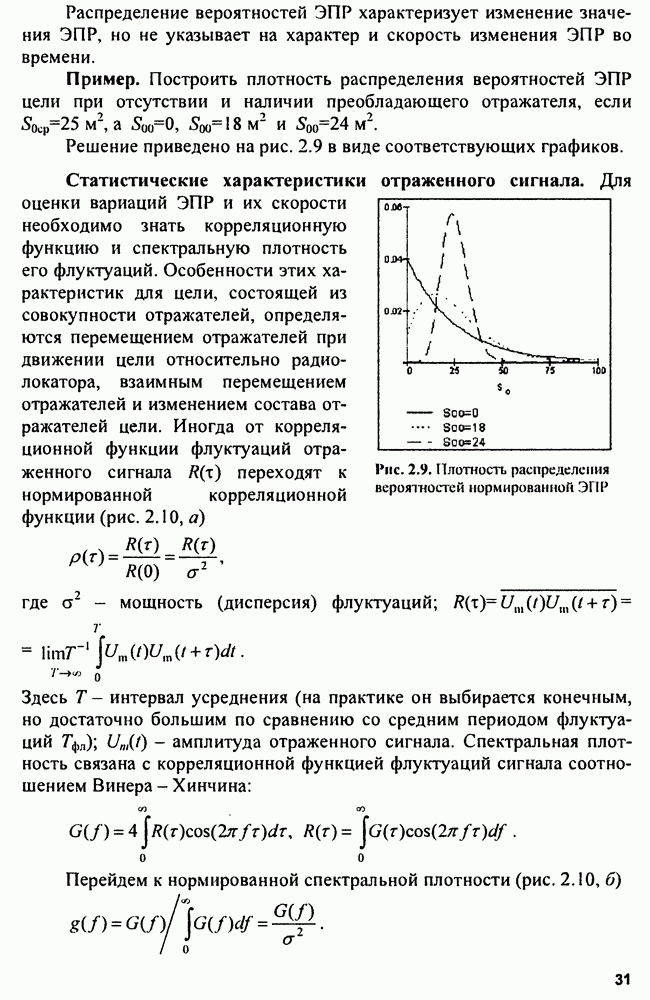
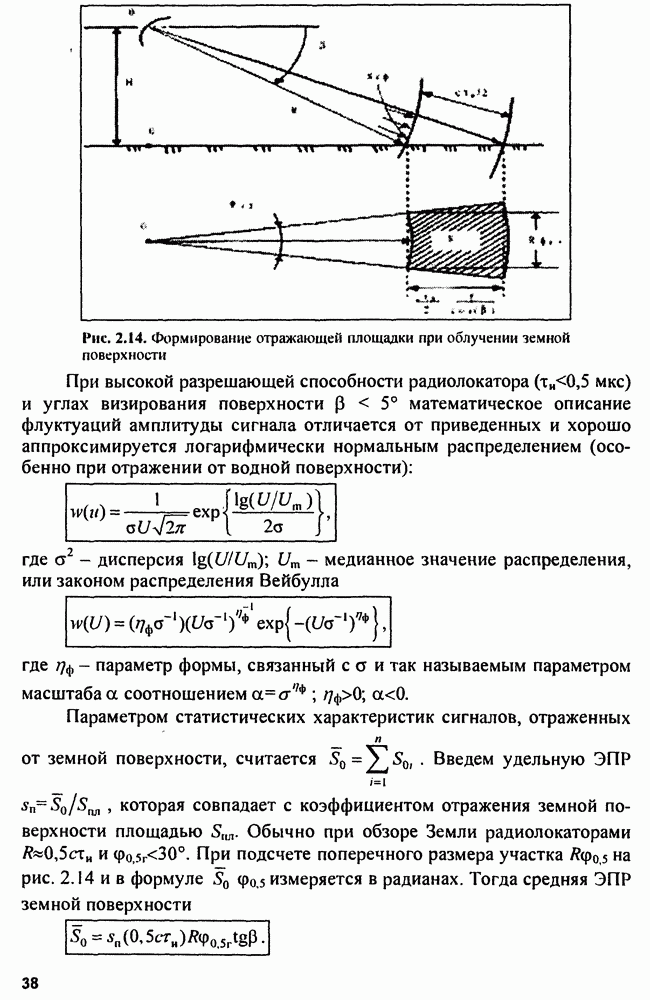
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
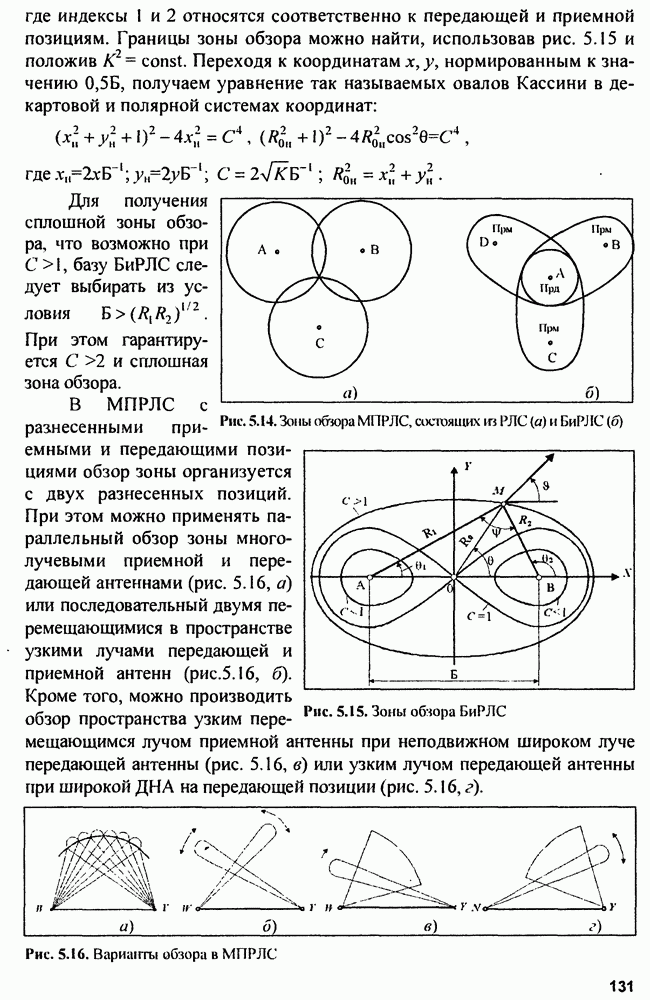
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
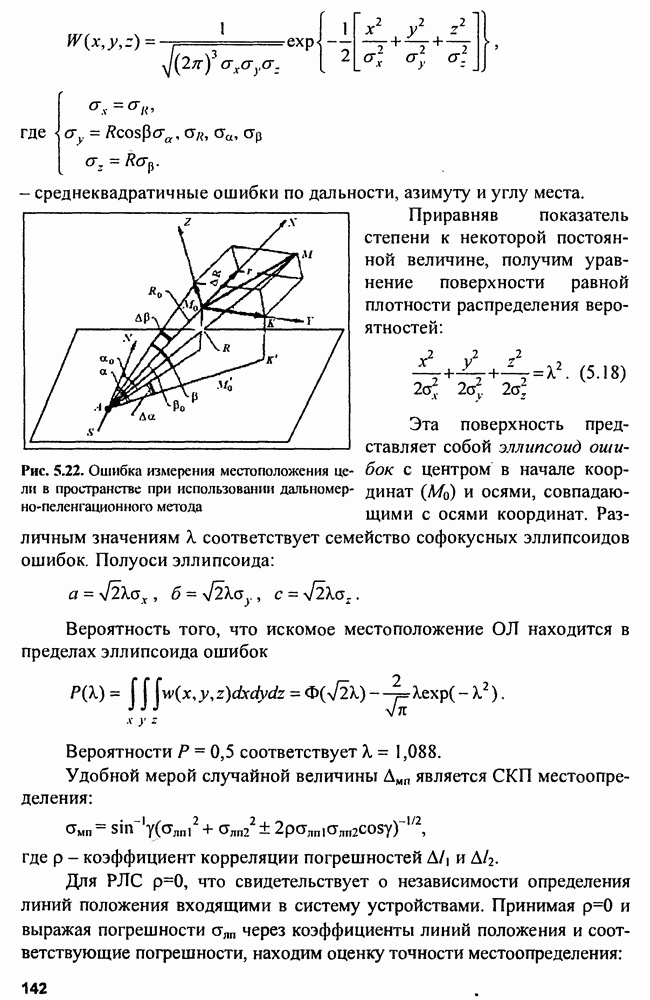
- 5.2. Точность определения местоположения цели в РЛС
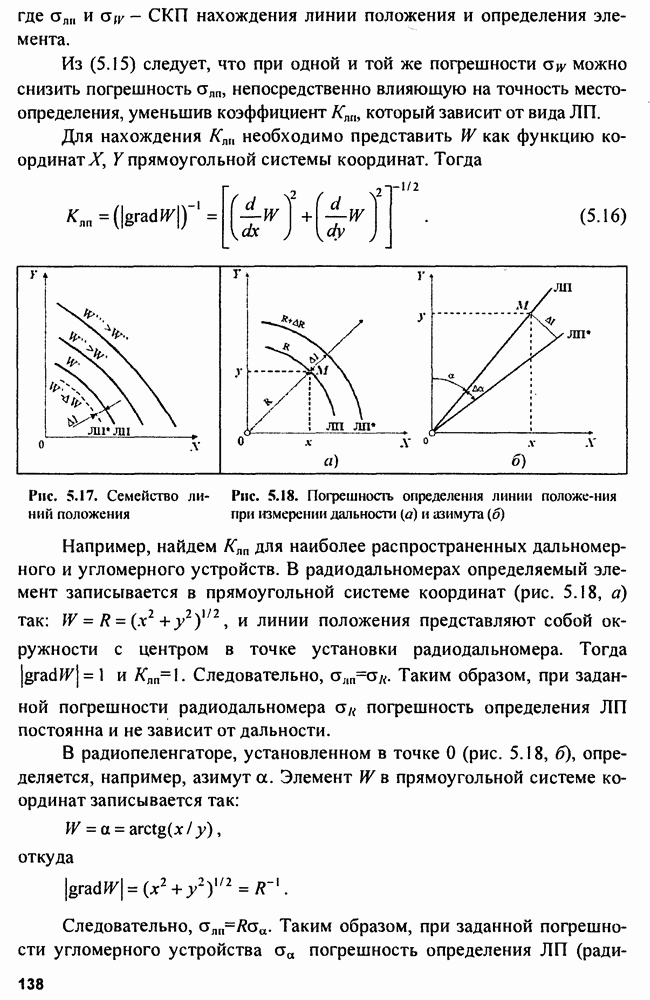
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
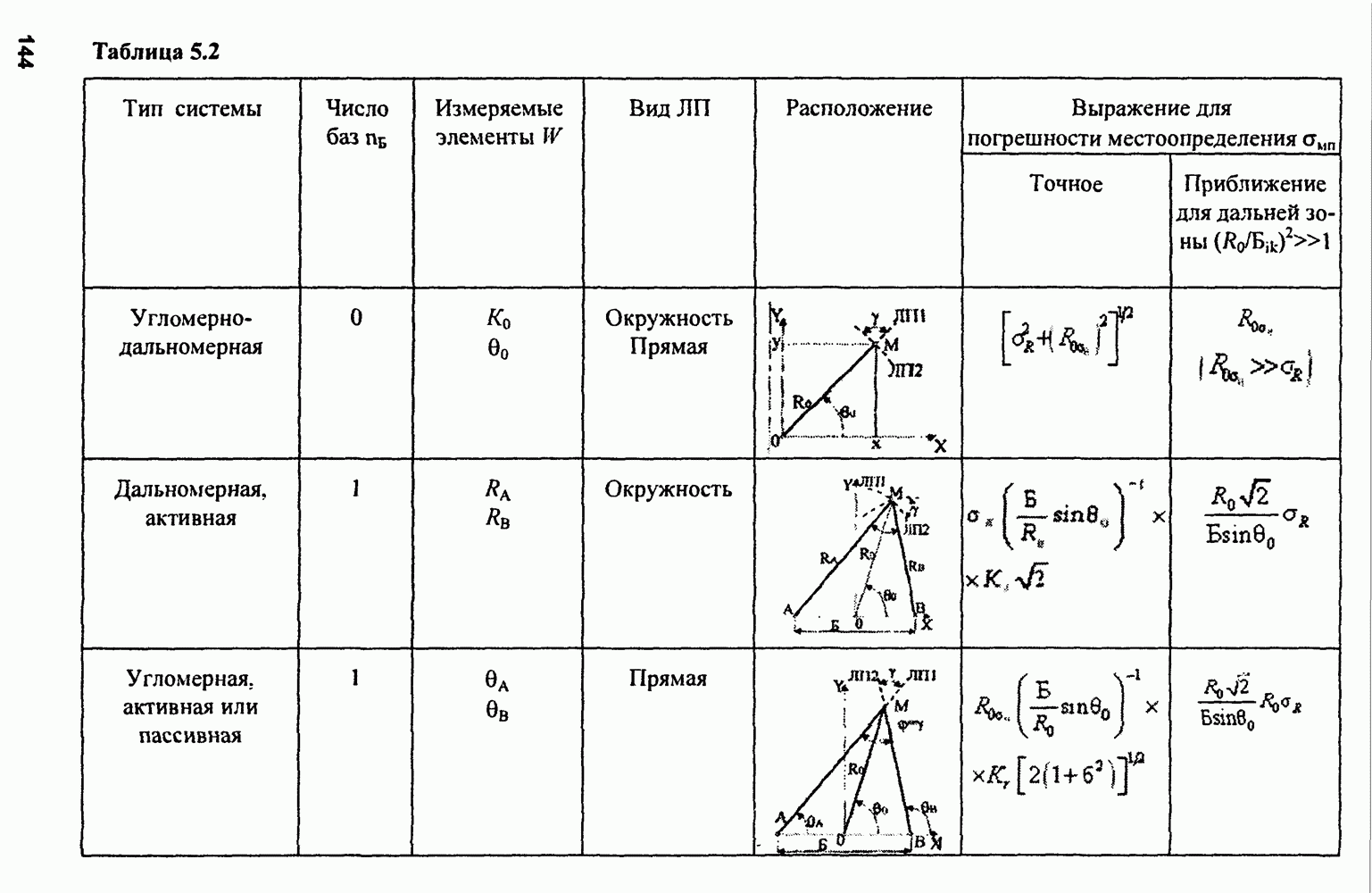
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
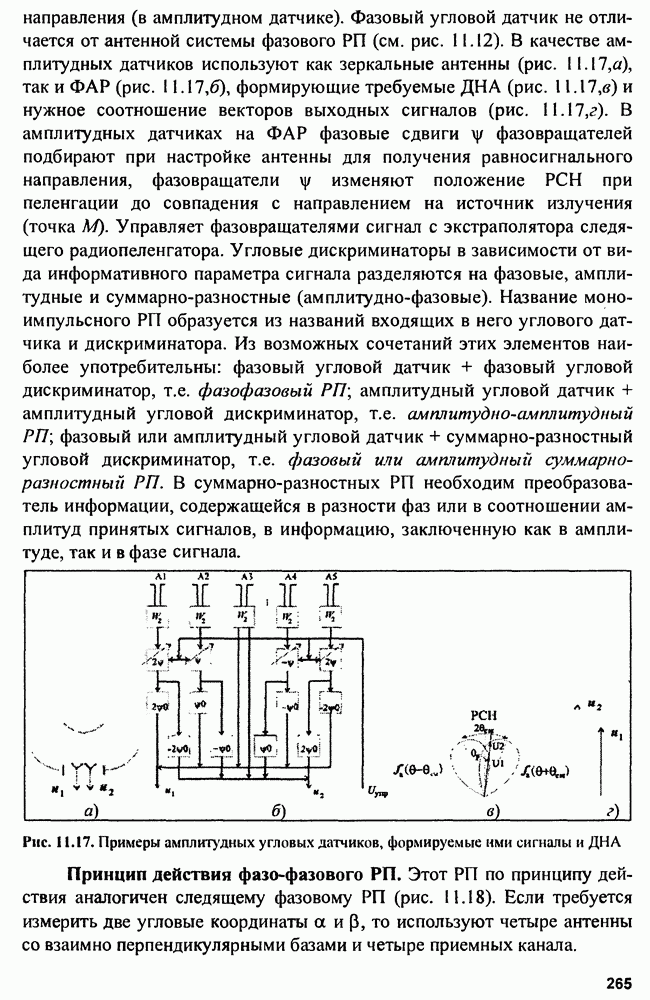
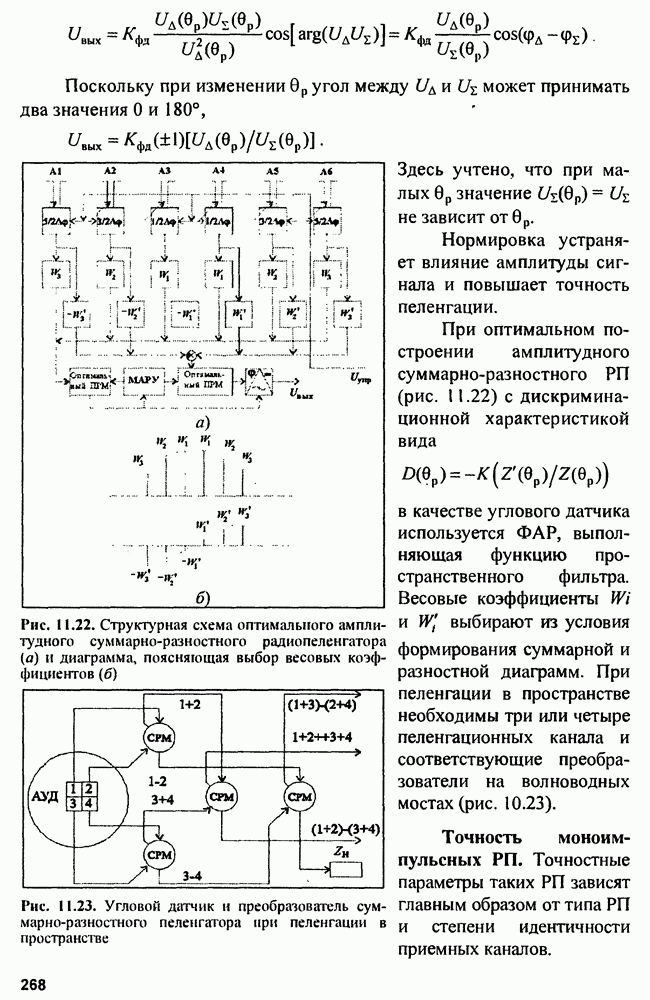
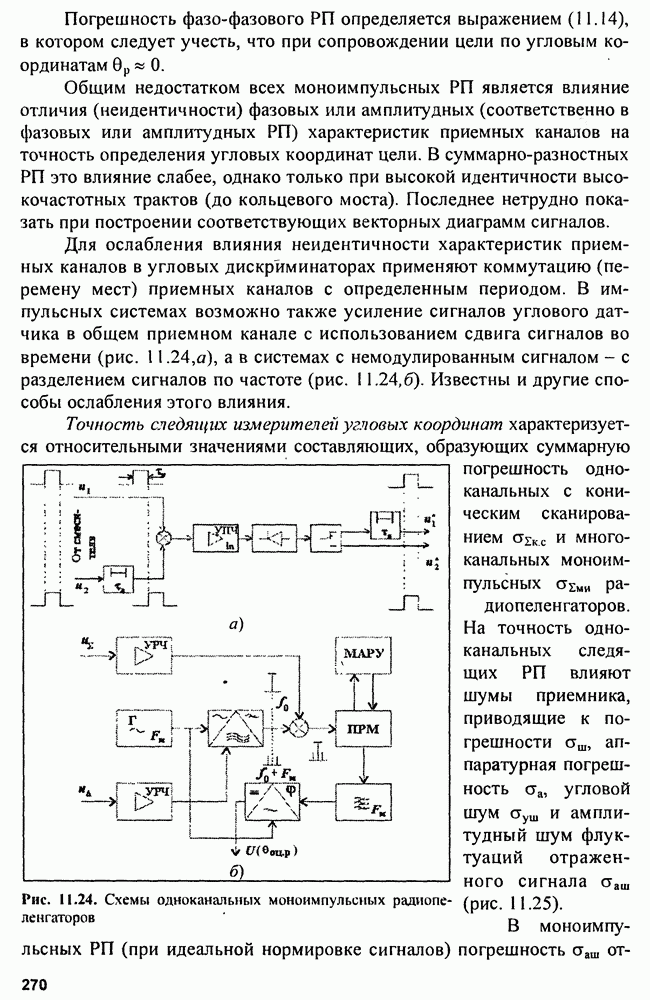
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение