| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.2.2. Точность определения геометрического элемента
В РЛС связь определяемого геометрического элемента  (координат объекта) с измеряемым параметром сигнала
(координат объекта) с измеряемым параметром сигнала  дается уравнением
дается уравнением

которое является исходным при нахождении погрешности определения  Находя полный дифференциал (5.11) и переходя к конечным приращениям, получим
Находя полный дифференциал (5.11) и переходя к конечным приращениям, получим

где  и
и  имеют смысл текущих значений погрешностей, обусловленных нестабильностью масштабного коэффициента и недостаточной точностью измерительного устройства.
имеют смысл текущих значений погрешностей, обусловленных нестабильностью масштабного коэффициента и недостаточной точностью измерительного устройства.
Возводя обе части выражения (5.12) в квадрат и усредняя полученный результат в предположении независимости погрешностей  и
и  получаем уравнение, связывающее дисперсию погрешности
получаем уравнение, связывающее дисперсию погрешности  определения элемента Же дисперсиями
определения элемента Же дисперсиями 

Из этого уравнения следуют два направления уменьшения погрешности  и в итоге повышения точности местоопределения. Первое связано с уменьшением погрешности
и в итоге повышения точности местоопределения. Первое связано с уменьшением погрешности  которая тем меньше, чем выше стабильность масштабного коэффициента. Поэтому при проектировании РЛС обычно принимают меры по стабилизации масштабного коэффициента (или учитывают, если это возможно, его нестабильность). При выполнении условия
которая тем меньше, чем выше стабильность масштабного коэффициента. Поэтому при проектировании РЛС обычно принимают меры по стабилизации масштабного коэффициента (или учитывают, если это возможно, его нестабильность). При выполнении условия  уравнение погрешностей (5.13) принимает вид
уравнение погрешностей (5.13) принимает вид 
При оптимальном построении измерителя  стремится к минимуму, называемому потенциальной точностью. Неоптимальность схемы измерителя информационного параметра сигнала приводит к росту погрешности по сравнению с потенциальной.
стремится к минимуму, называемому потенциальной точностью. Неоптимальность схемы измерителя информационного параметра сигнала приводит к росту погрешности по сравнению с потенциальной.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
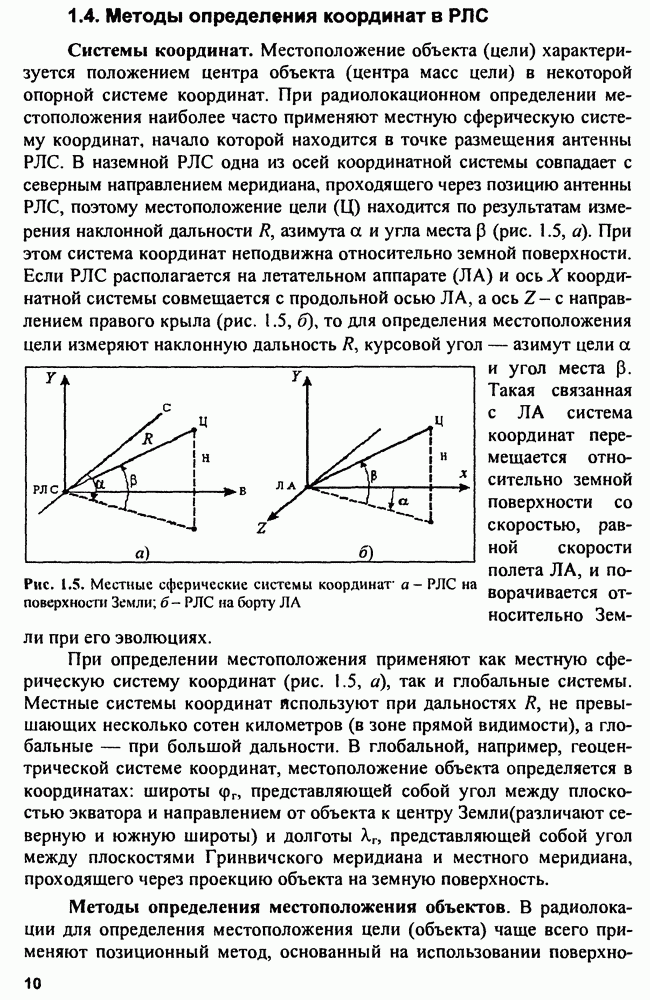
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
- Глава 2. Радиолокационные системы
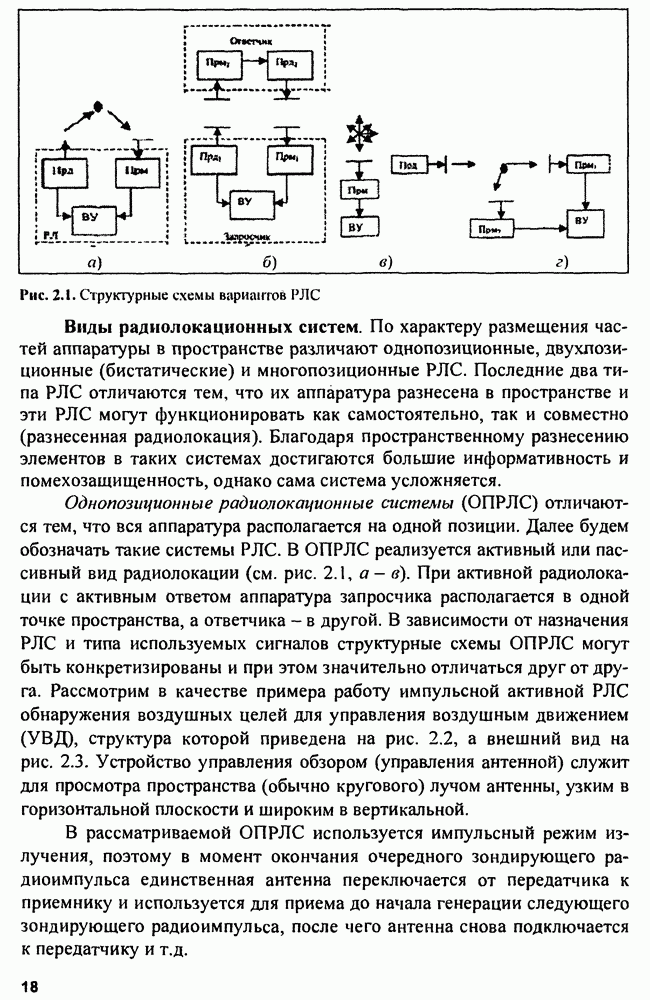
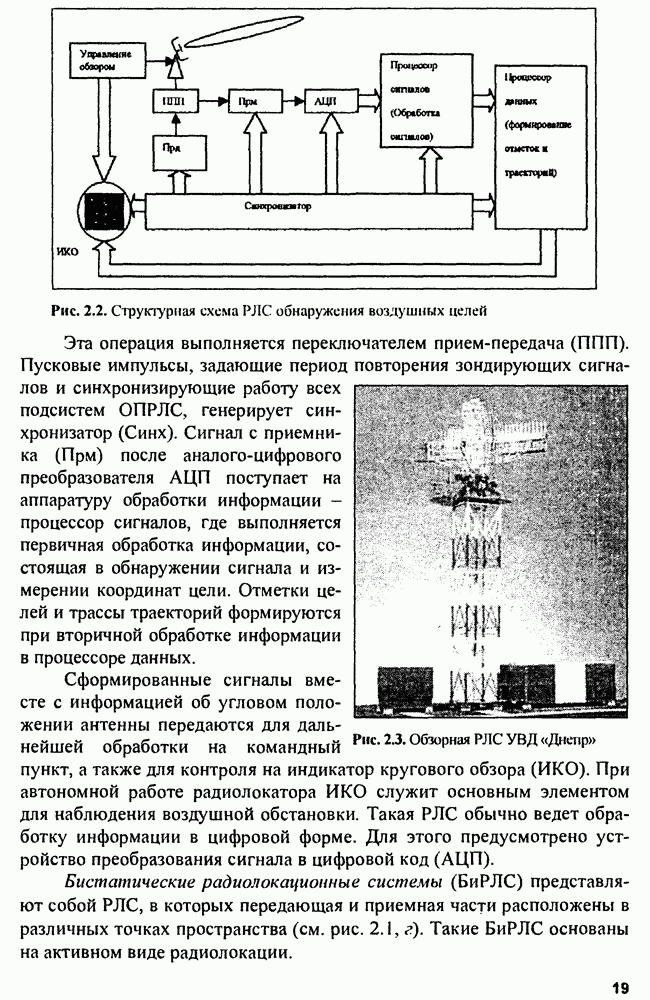
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
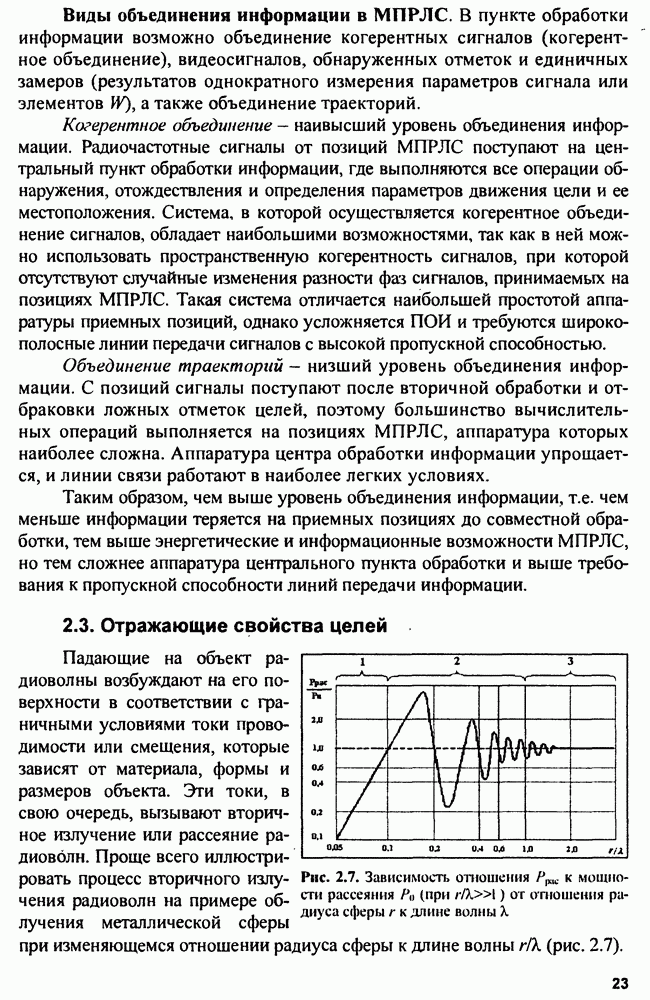
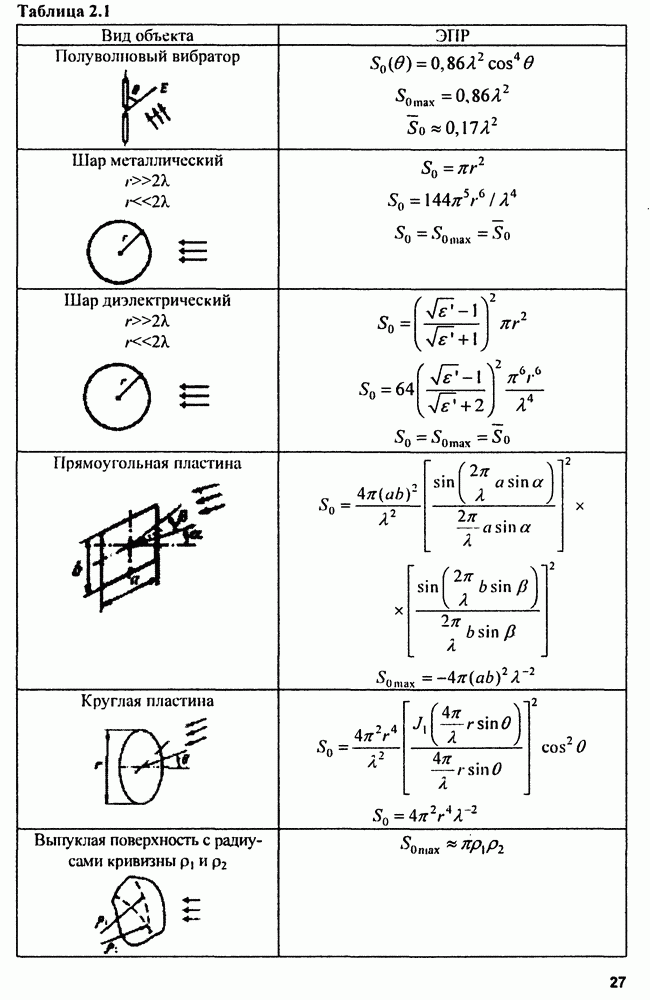
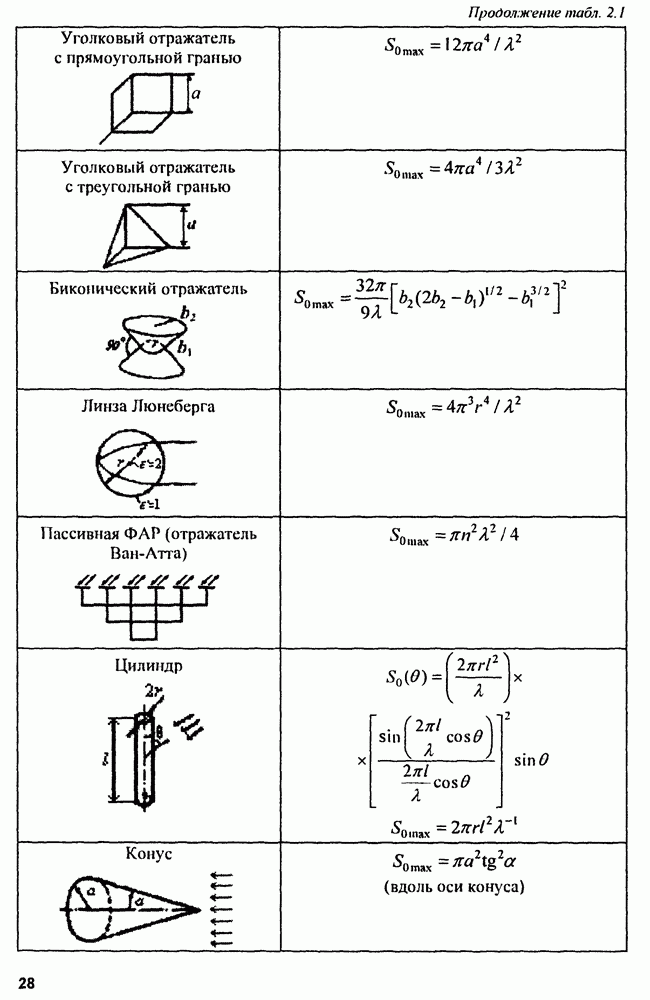
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
- 5.2.4. Погрешность местоположения определения
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
- 10.2. Частотные радиодальномеры
- 10.3. Импульсные радиодальномеры
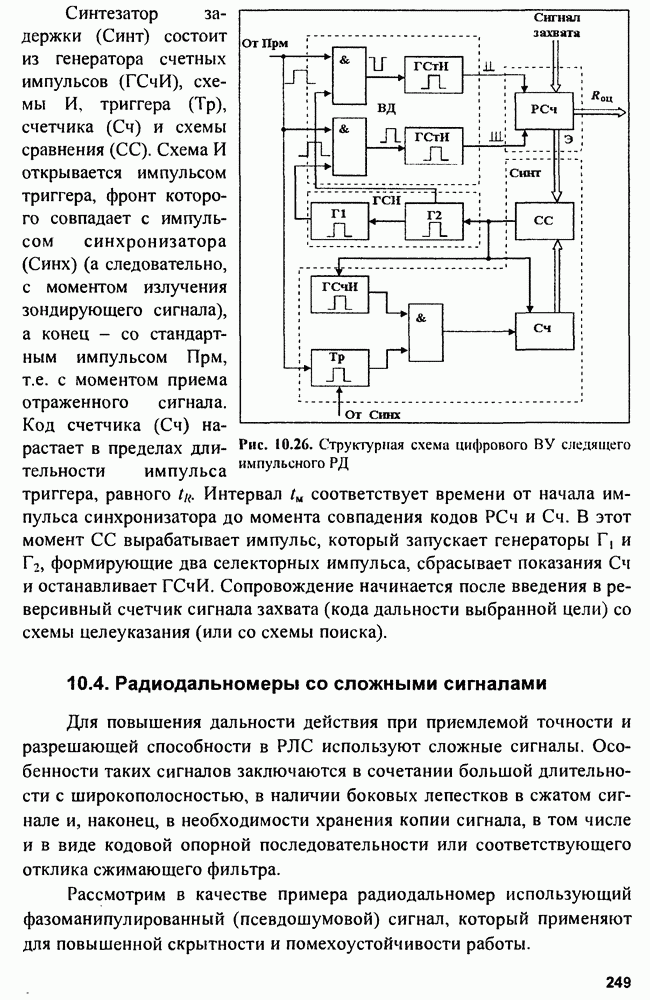
- 10.4. Радиодальномеры со сложными сигналами
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение