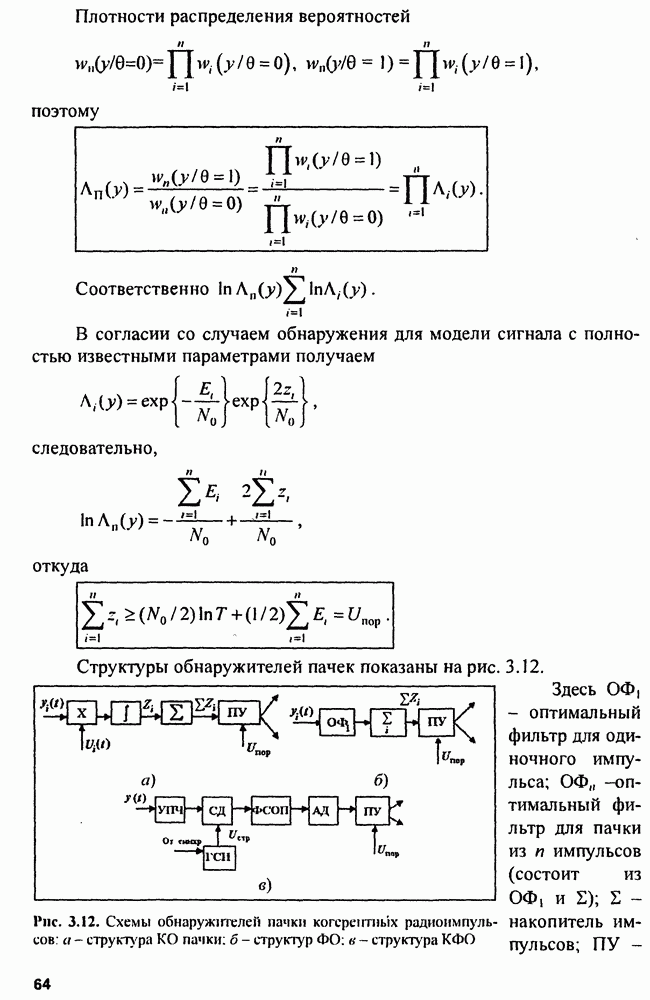
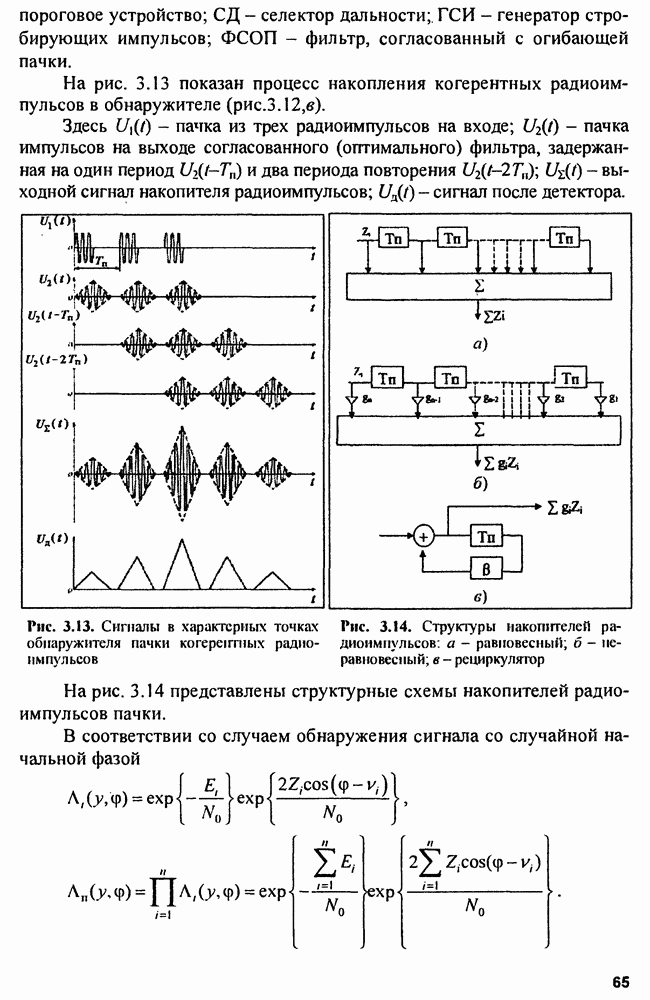
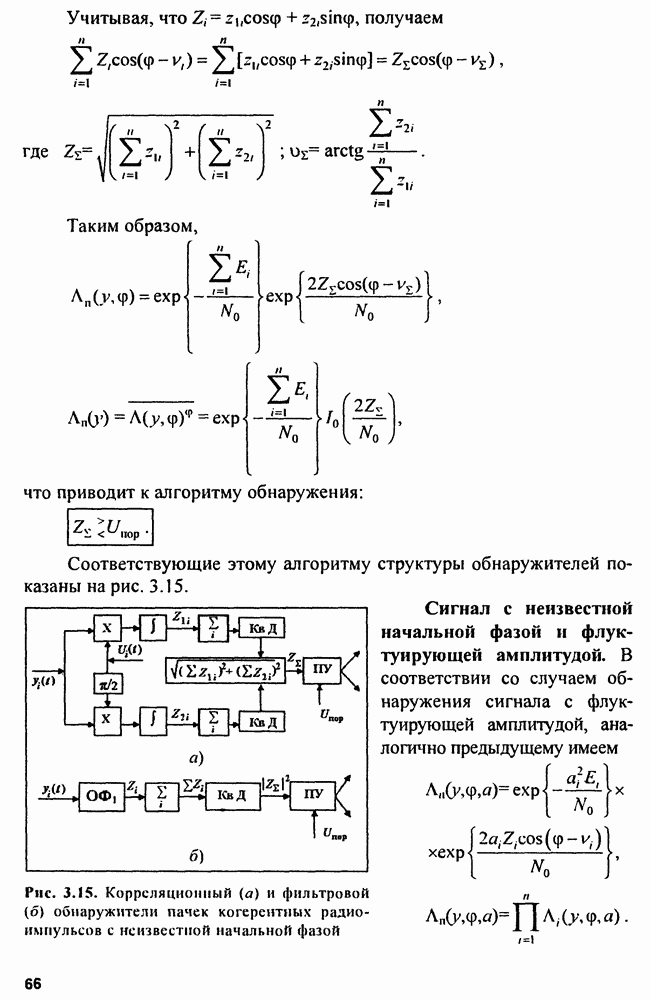
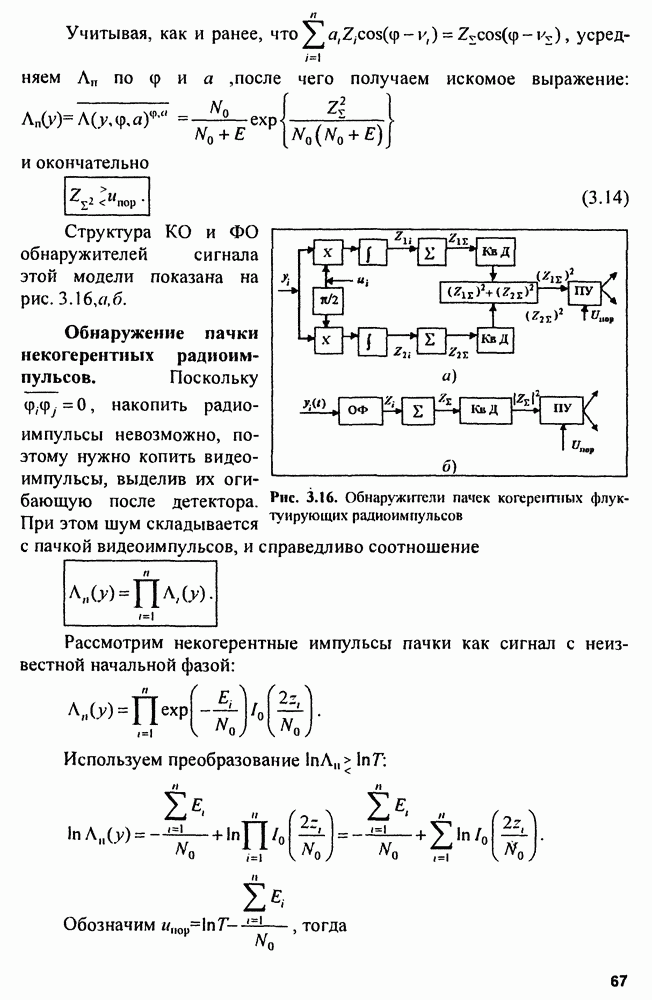
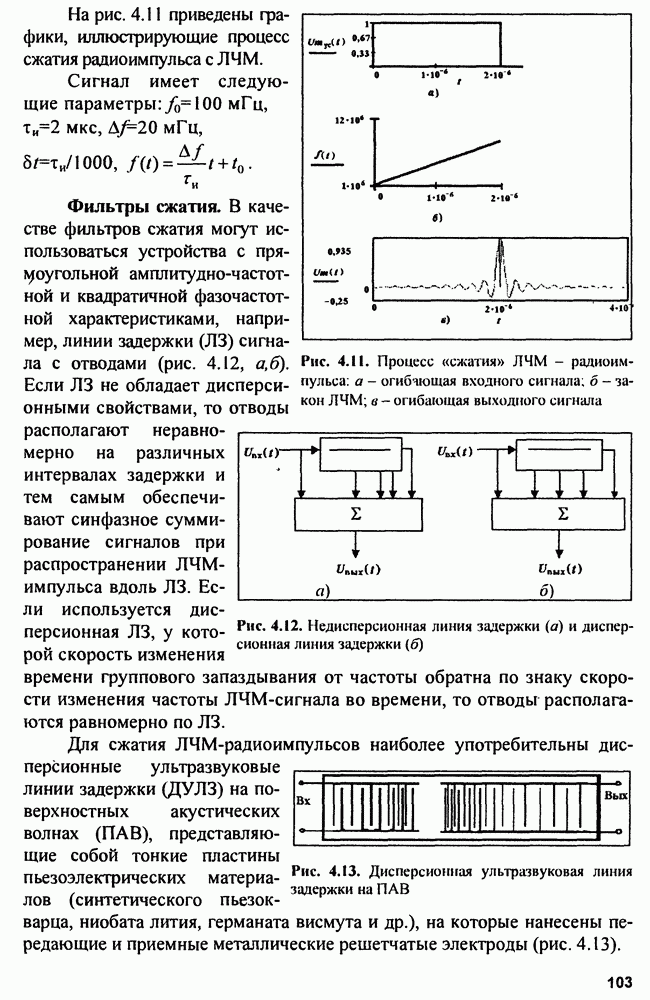
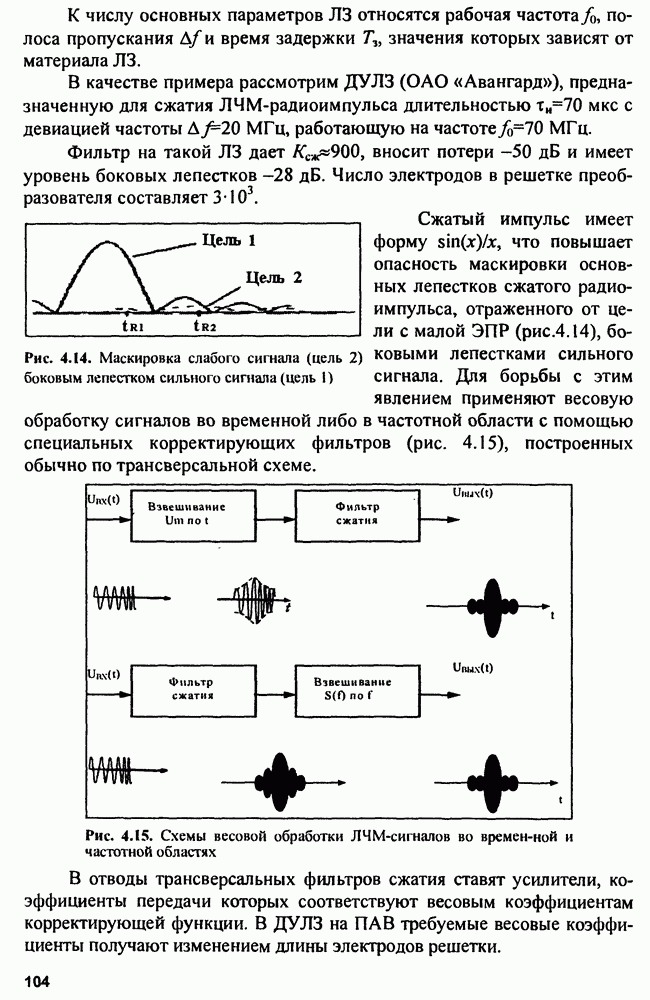
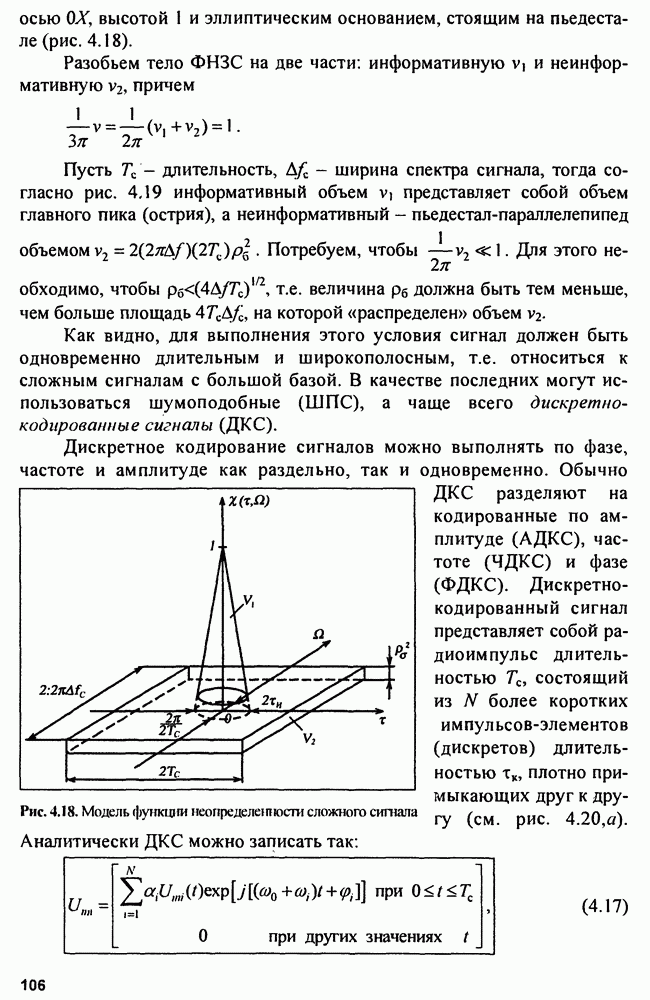
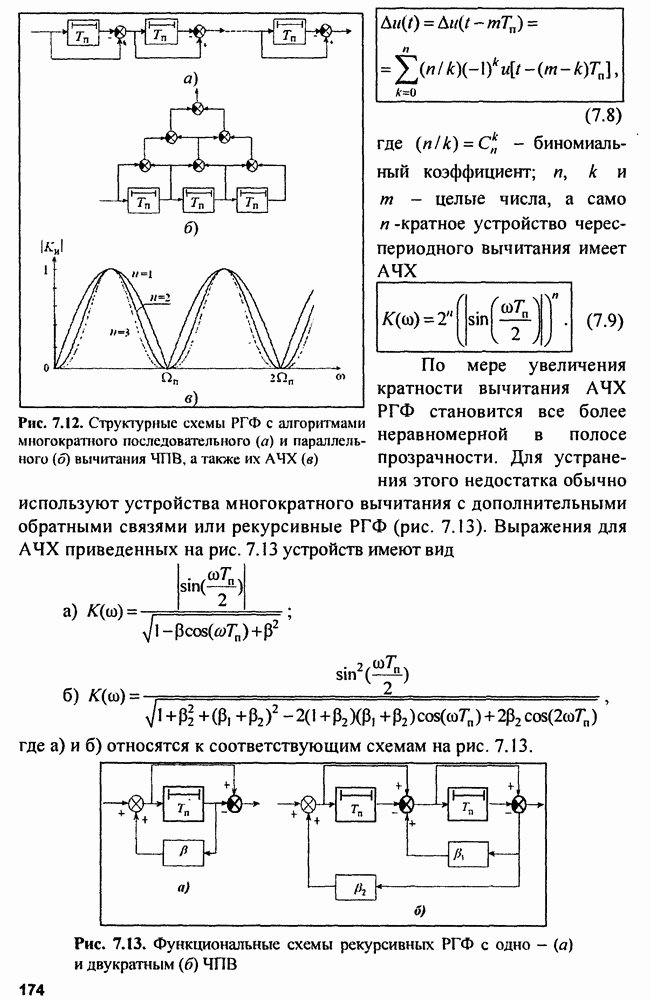
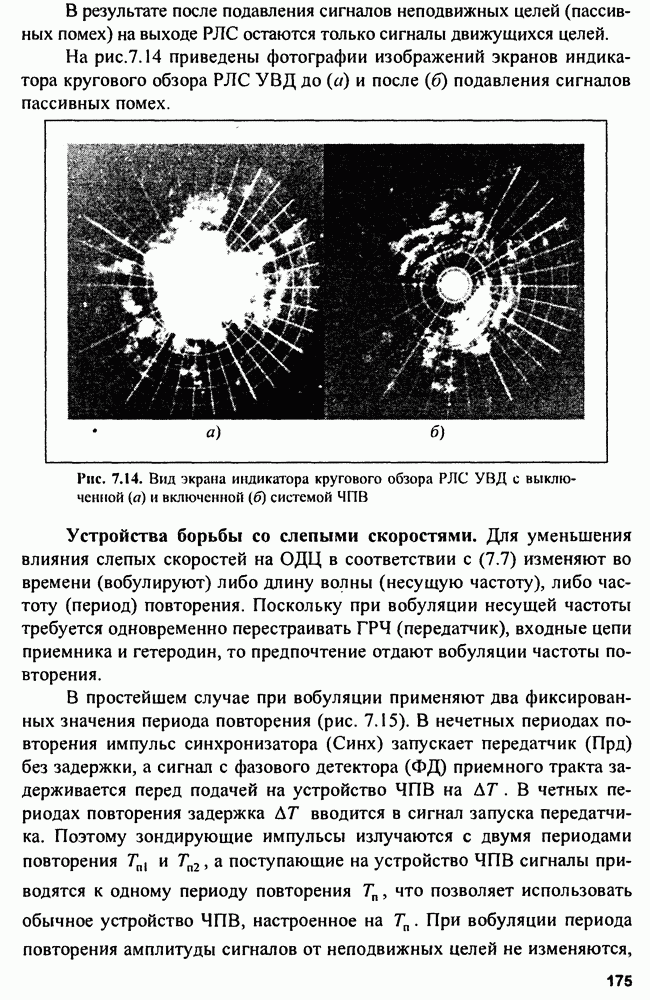
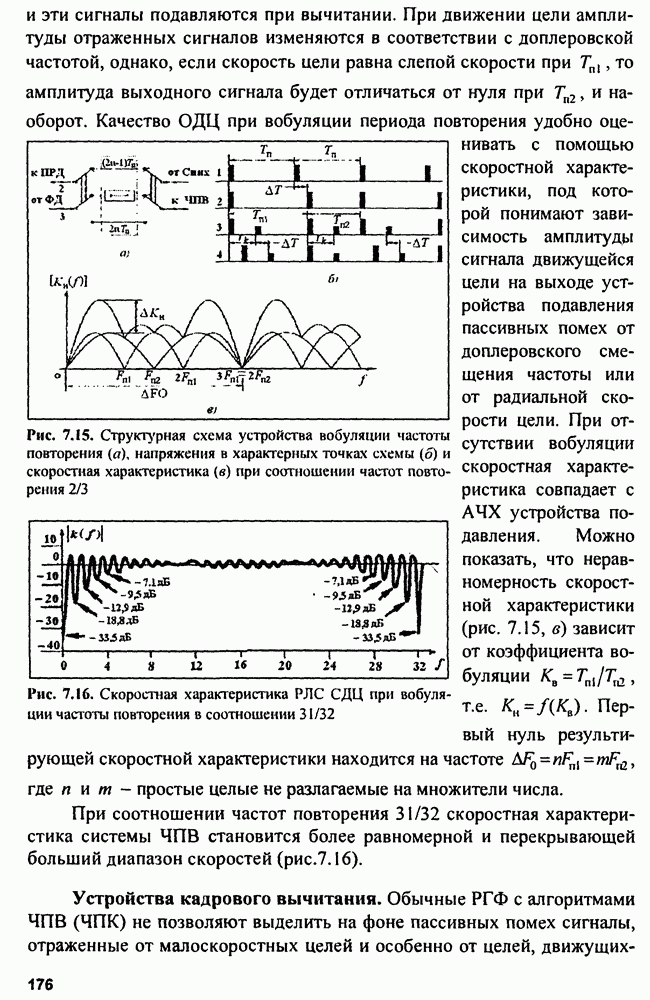
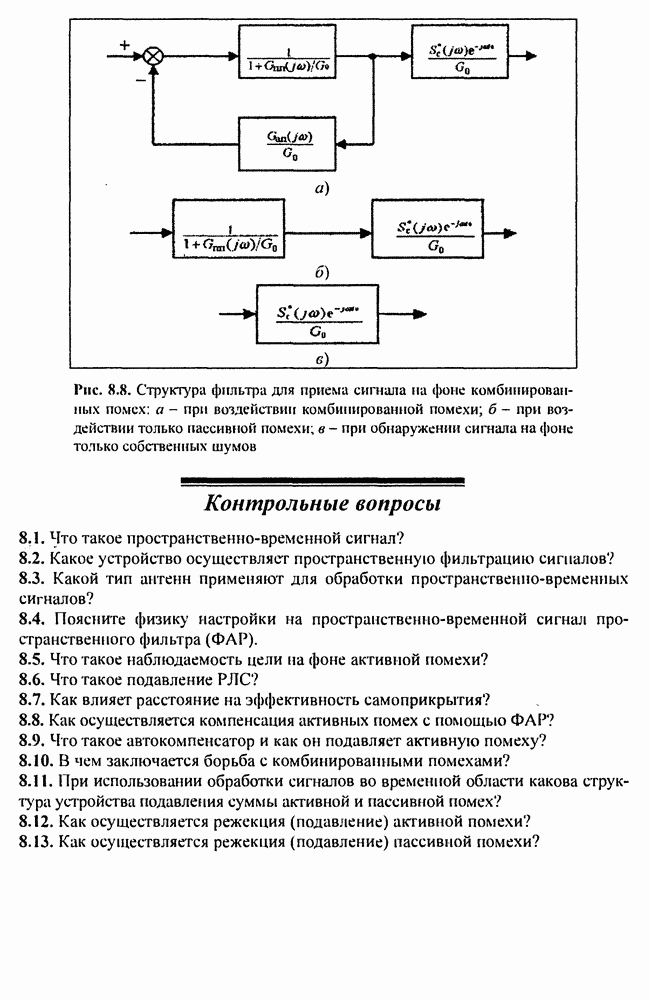
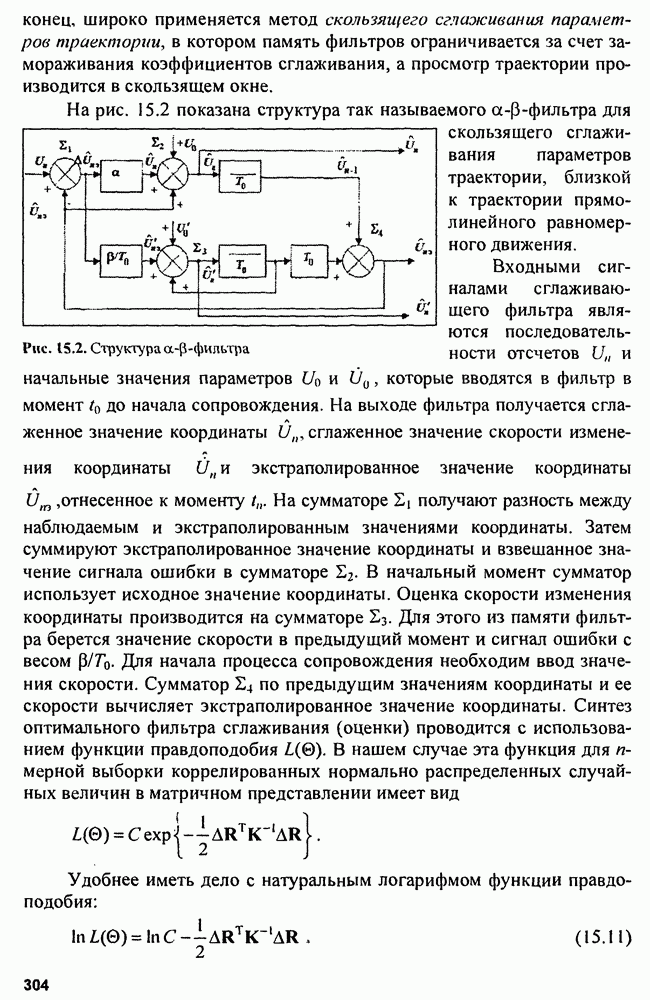
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
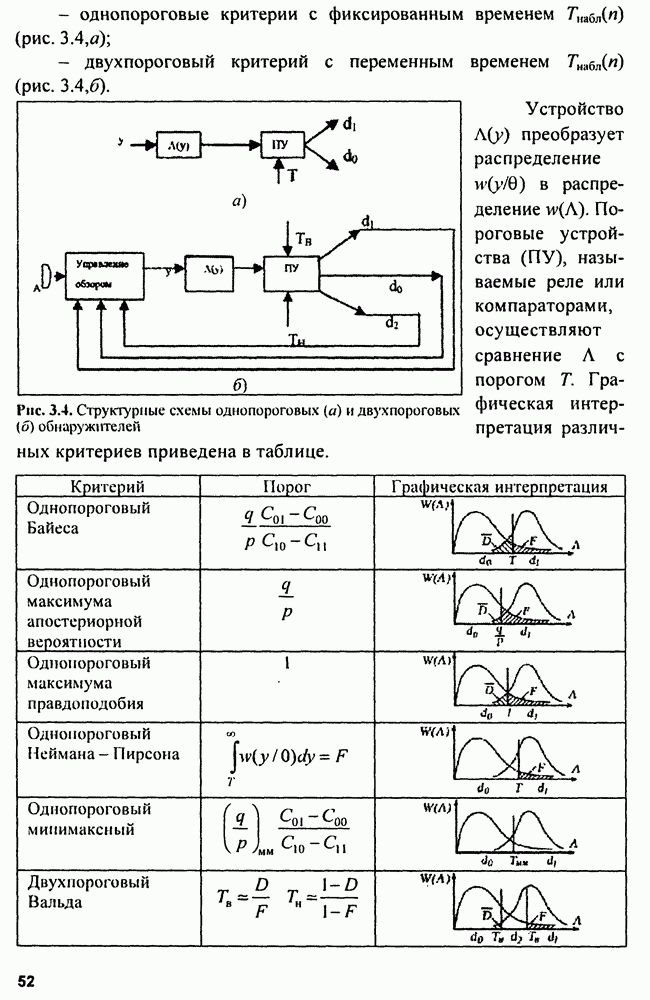
4.2. Диаграммы неопределенности
Несмотря на большую наглядность тел ФНЗС, использовать их изображения при синтезе и анализе зондирующих сигналов неудобно, поэтому переходят к сечениям ФНЗС плоскостью, параллельной плоскости  на некотором заданном уровне, например,
на некотором заданном уровне, например, 
Можно перейти к сечению плоскостью, параллельной плоскости  цилиндра, равновеликого по высоте и объему с ФНЗС. Полученные сечения, спроектированные на плоскость
цилиндра, равновеликого по высоте и объему с ФНЗС. Полученные сечения, спроектированные на плоскость  носят названия диаграмм неопределенности (ДН) и имеют следующие свойства:
носят названия диаграмм неопределенности (ДН) и имеют следующие свойства:
- центр ДН всегда находится в начале координат  является центрально-симметричной фигурой;
является центрально-симметричной фигурой;
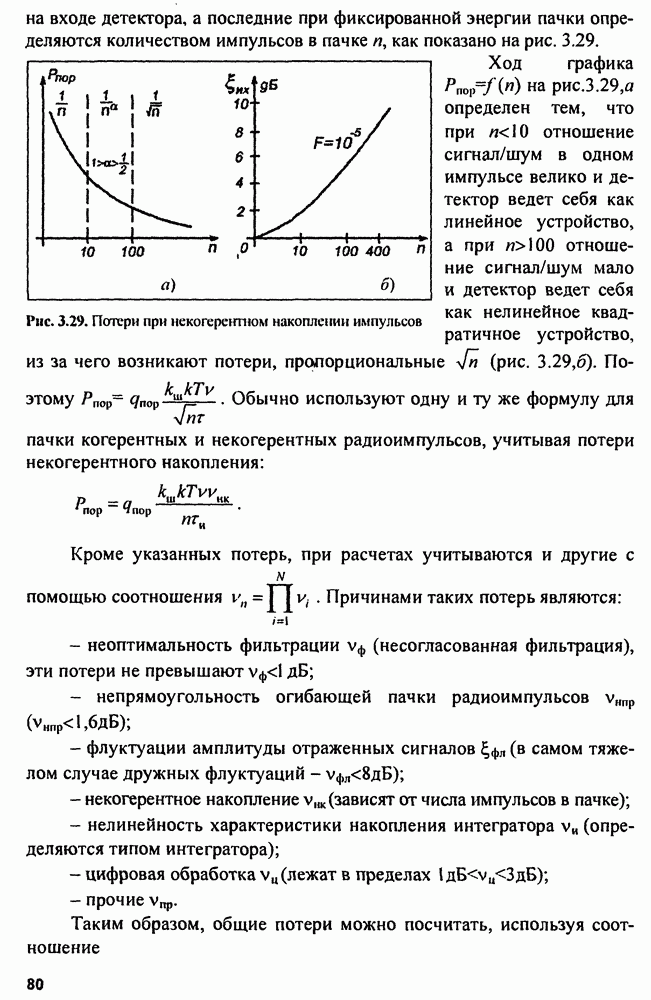
- площадь ДН при изменении параметров сигнала не меняется. Рассмотрим особенности ДН радиолокационных сигналов, разбив последние на три основные группы: одиночные; бесконечно повторяющиеся; пачки (ограниченные группы).
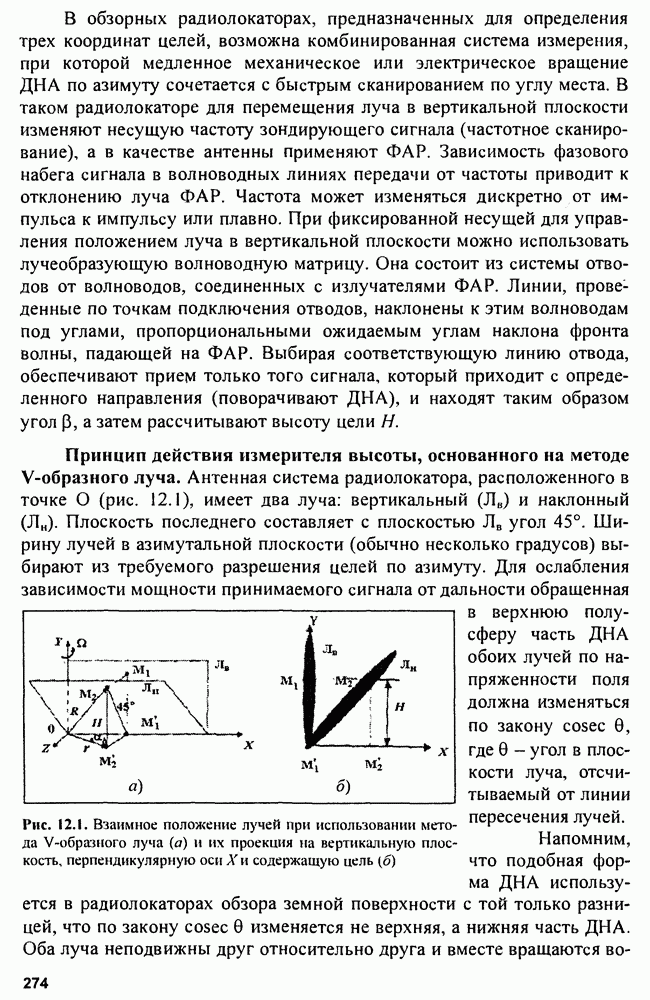
Функции неопределенности одиночных сигналов. Для радиоимпульса с гауссовской огибающей сечение тела неопределенности плоскостью, параллельной От/имеет форму эллипса:

где с - уровень, на котором проведена секущая плоскость.
Эллипс, симметричный относительно начала координат, имеет оси  Площадь эллипса не зависит от длительности импульса:
Площадь эллипса не зависит от длительности импульса:  Диаграмма неопределенности короткого импульса вытянута вдоль оси
Диаграмма неопределенности короткого импульса вытянута вдоль оси  а длинного - вдоль оси
а длинного - вдоль оси  .
.
Для прямоугольного радиоимпульса ДН при  по форме близка к эллипсу.
по форме близка к эллипсу.
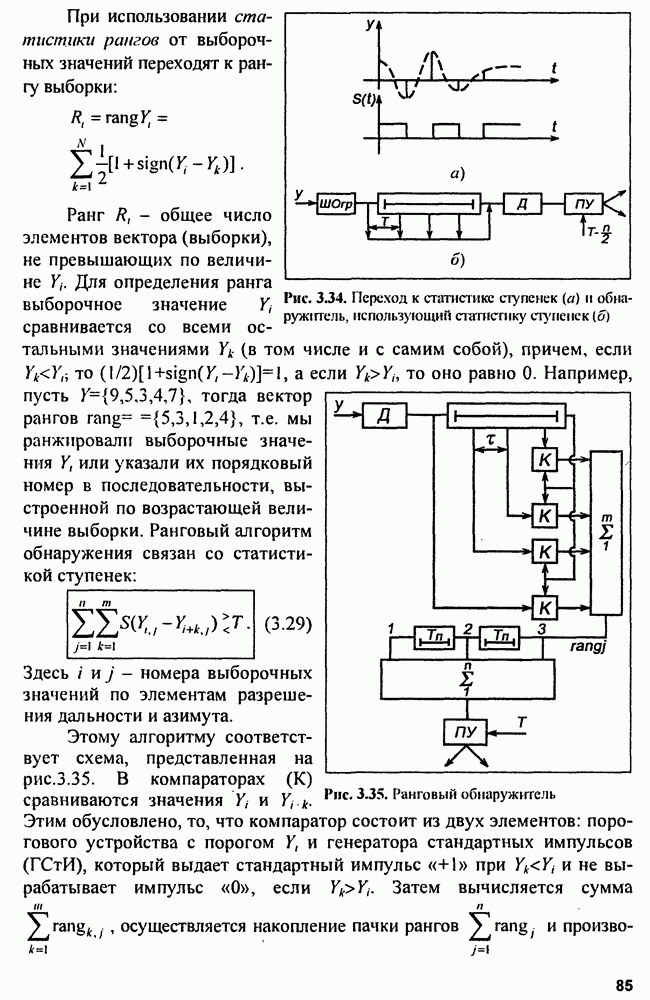
При внутриимпульсной  выражение для сигнала и ФНЗС имеет вид
выражение для сигнала и ФНЗС имеет вид

Тогда ФНЗС

где  девиация частоты.
девиация частоты.
Диаграмма неопределенности радиоимпульса с ЛЧМ (рис. 4.3) представляет собой также эллипс, но повернутый на угол  причем при изменении угла а крайние правая и левая горизонтальные точки
причем при изменении угла а крайние правая и левая горизонтальные точки  и
и  перемещаются по вертикальным прямым. Площадь эллипса по-прежнему не меняется, но за счет растяжения по большей оси эллипс сжимается в поперечном направлении. Протяженность ДН по горизонтали уменьшается, что соответствует сжатию импульса с
перемещаются по вертикальным прямым. Площадь эллипса по-прежнему не меняется, но за счет растяжения по большей оси эллипс сжимается в поперечном направлении. Протяженность ДН по горизонтали уменьшается, что соответствует сжатию импульса с  при оптимальной его обработке.
при оптимальной его обработке.

Рис. 4.3. Диаграммы неопределенности прямоугольного импульса без модуляции (а) и с виутринмпульсной ЛЧМ (б)
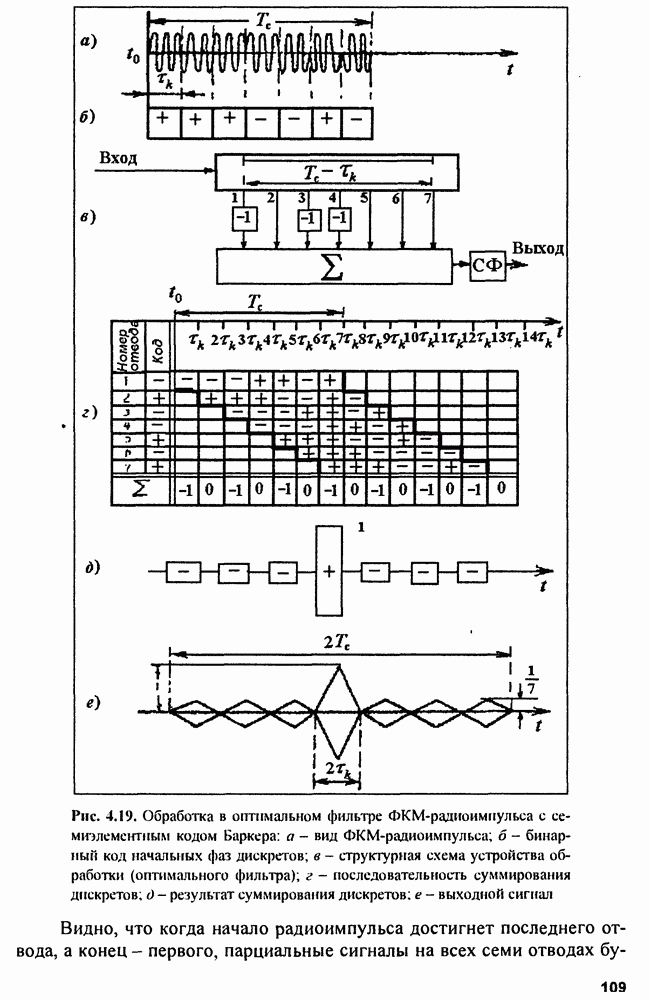
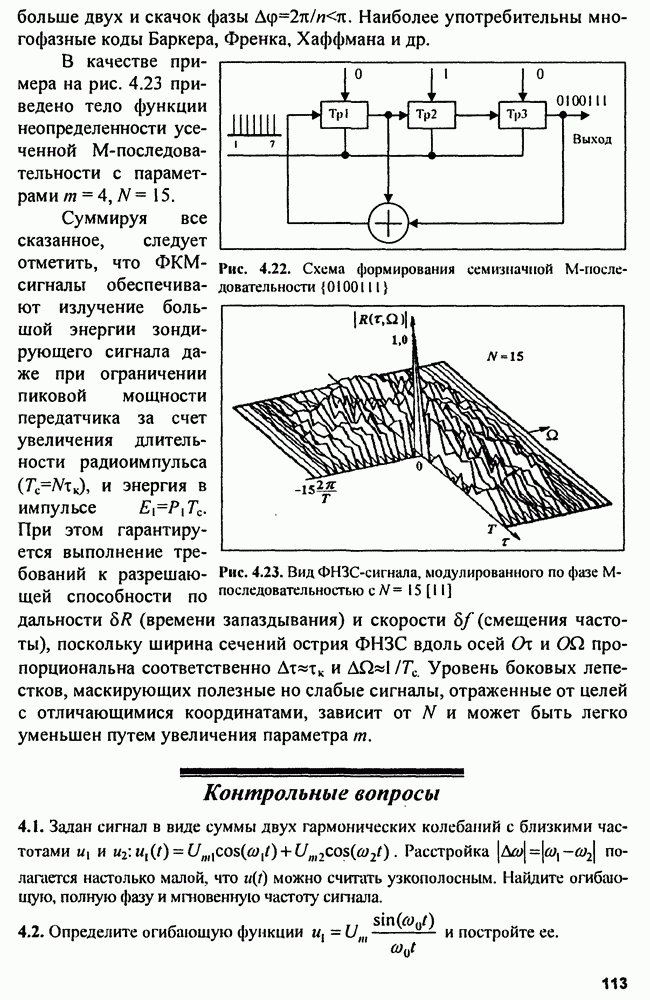
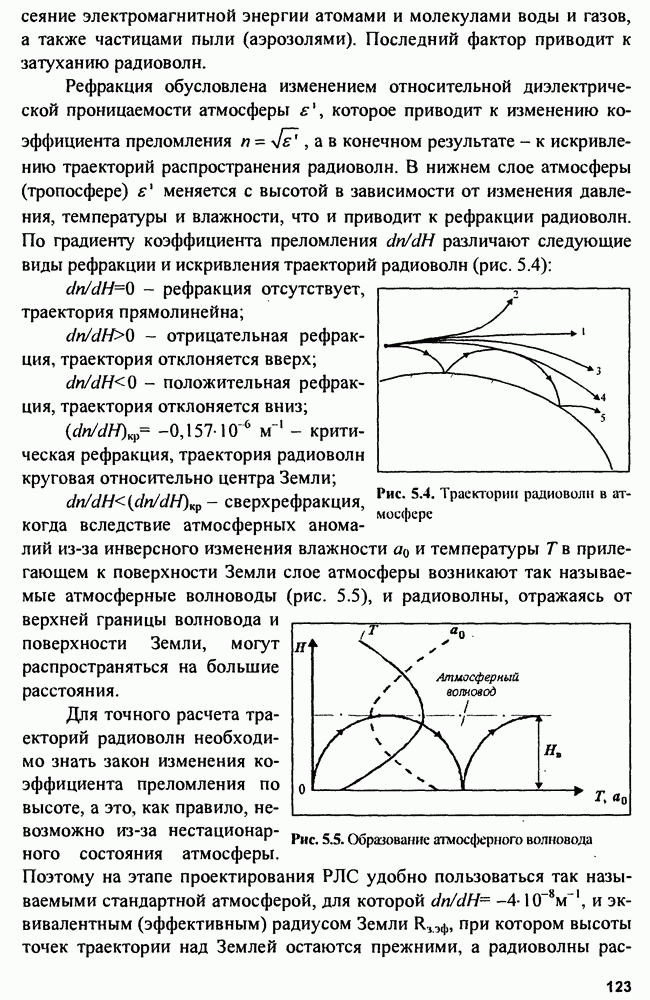
Если использовать внутри-импульсную фазокодовую модуляцию псевдослучайным кодом, то тело неопределенности будет состоять из главного пика (острия) и достаточно тонкого пьедестала («шляпки»), образуя «кнопкообразную» ФНЗС (см. рис. 4.18).
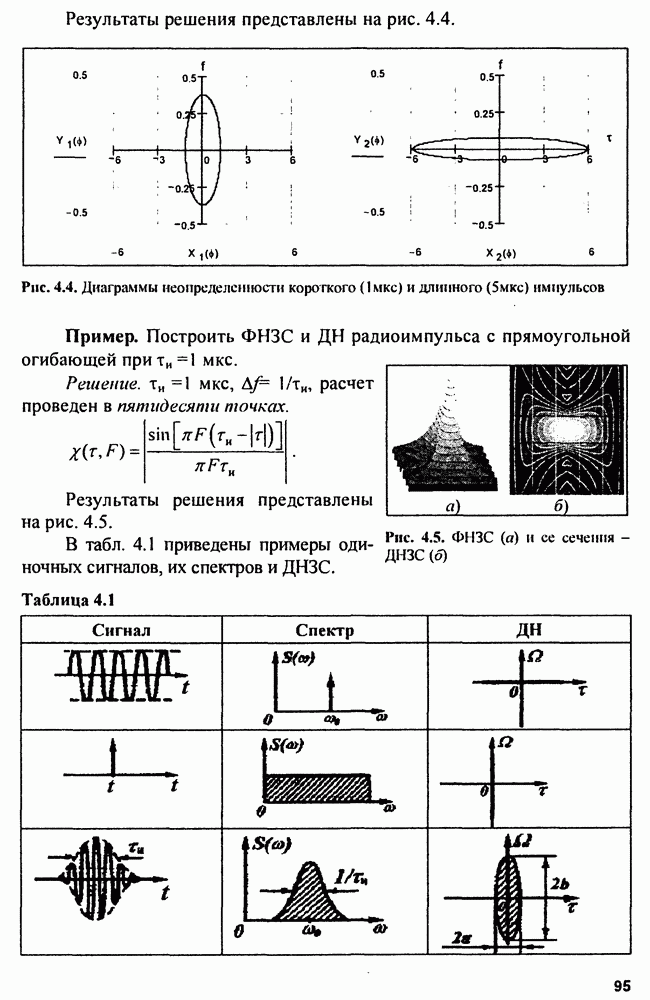
Пример. Построим ДН радиоимпульса с гауссовской огибающей для  приняв
приняв 
Решение. Учитывая, что  запишем уравнение ДН в виде
запишем уравнение ДН в виде

Для построения ДН воспользуемся параметрической формой уравнения эллипса:

где 
Для короткого импульса 
Для длинного импульса 
Результаты решения представлены на рис. 4.4.

Рис. 4.4. Диаграммы неопределенности короткого (1мкс) и длинного (5мкс) импульсов
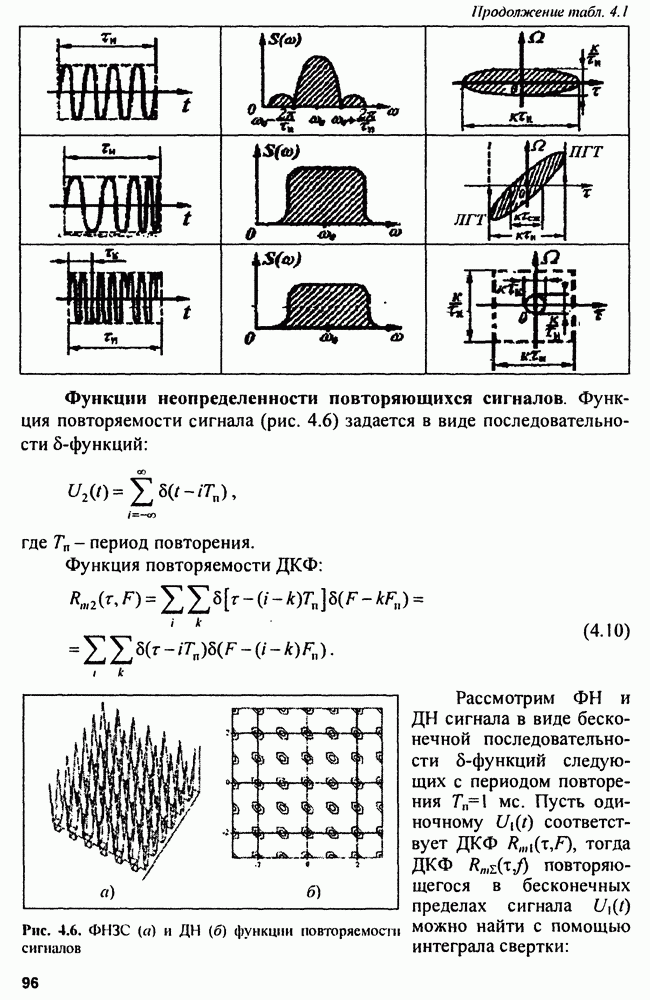
Пример. Построить ФНЗС и ДН радиоимпульса с прямоугольной огибающей при 

Рис. 4.5. ФНЗС (а) и ее сечения - ДНЗС (б)
Решение.  расчет проведен в пятидесяти точках.
расчет проведен в пятидесяти точках.

Результаты решения представлены на рис. 4.5.
В табл. 4.1 приведены примеры одиночных сигналов, их спектров и 
Таблица 4.1 (см. скан)
Продолжение табл. 4.1 (см. скан)
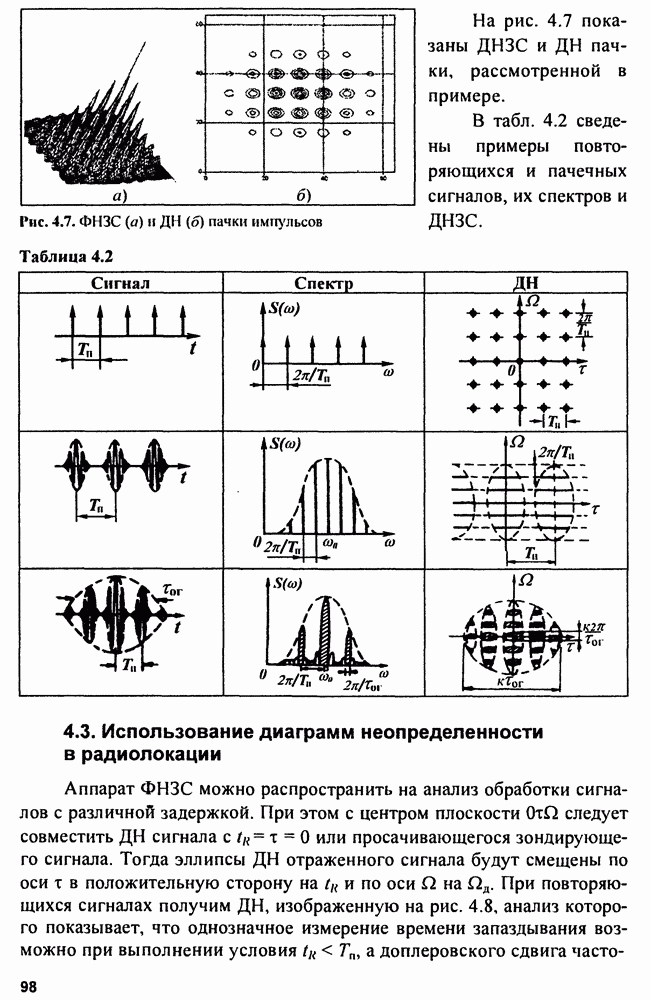
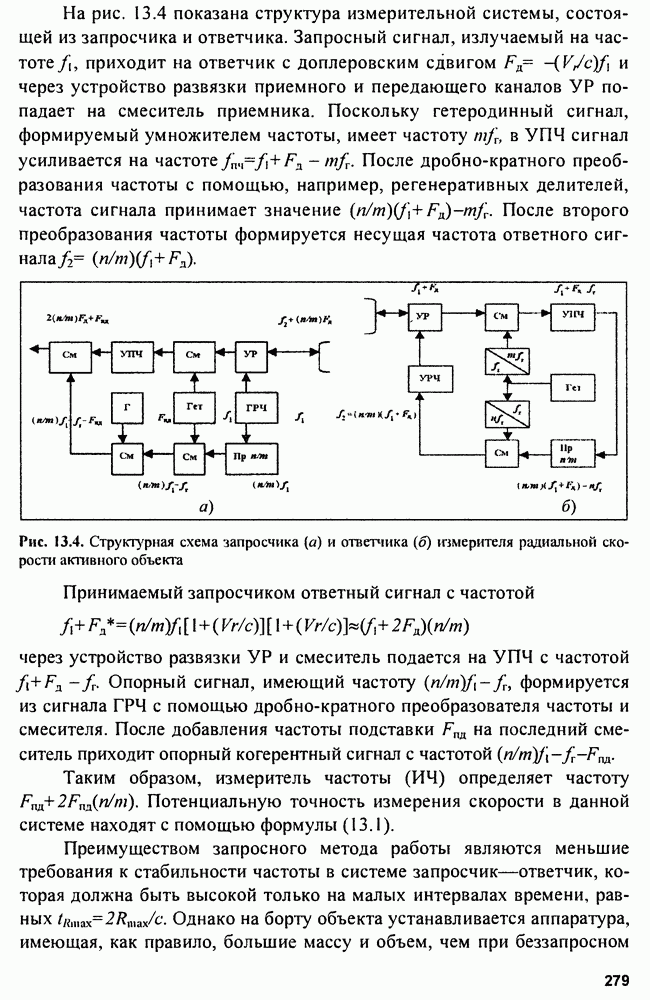
Функции неопределенности повторяющихся сигналов. Функция повторяемости сигнала (рис. 4.6) задается в виде последовательности  -функций:
-функций:

где  период повторения.
период повторения.
Функция повторяемости ДКФ:

Рассмотрим  и ДН сигнала в виде бесконечной последовательности
и ДН сигнала в виде бесконечной последовательности  -функций следующих с периодом повторения
-функций следующих с периодом повторения  Пусть одиночному
Пусть одиночному  соответствует
соответствует  тогда
тогда  повторяющегося в бесконечных пределах сигнала
повторяющегося в бесконечных пределах сигнала  можно найти с помощью интеграла свертки:
можно найти с помощью интеграла свертки:

Рис. 4.6. ФНЗС (а) и ДН (б) функции повторяемости сигналов

Следовательно, ДН представляет собой фигуру, образующуюся при пересечении двух семейств частных  и
и  -функций. Семейство
-функций. Семейство  является набором повторяющихся через
является набором повторяющихся через  вдоль оси
вдоль оси  эллипсов
эллипсов  а семейство
а семейство  -функций дает систему горизонтальных линий по оси
-функций дает систему горизонтальных линий по оси  через
через  Таким образом, ДН содержит отрезки прямых линий, вписанные в повторяющиеся эллипсы.
Таким образом, ДН содержит отрезки прямых линий, вписанные в повторяющиеся эллипсы.
Функция неопределенности пачки сигналов. Если представить огибающую пачки сигналов временной функцией,  , которой соответствует
, которой соответствует  то ДКФ пачки
то ДКФ пачки  можно определить путем свертки
можно определить путем свертки  т.е.
т.е.

Следовательно, ДН пачки сигналов формируется взаимным пересечением семейства повторяющихся через  по оси
по оси  эллипсов одиночных сигналов:
эллипсов одиночных сигналов:  и семейства повторяющихся по оси
и семейства повторяющихся по оси  через
через  эллипсов огибающей пачки:
эллипсов огибающей пачки:  Происходит дробление тела неопределенности на систему пиков, которая в сечении дает группу эллипсов малого размера с суммарной площадью, равной площади исходного эллипса одиночного сигнала.
Происходит дробление тела неопределенности на систему пиков, которая в сечении дает группу эллипсов малого размера с суммарной площадью, равной площади исходного эллипса одиночного сигнала.
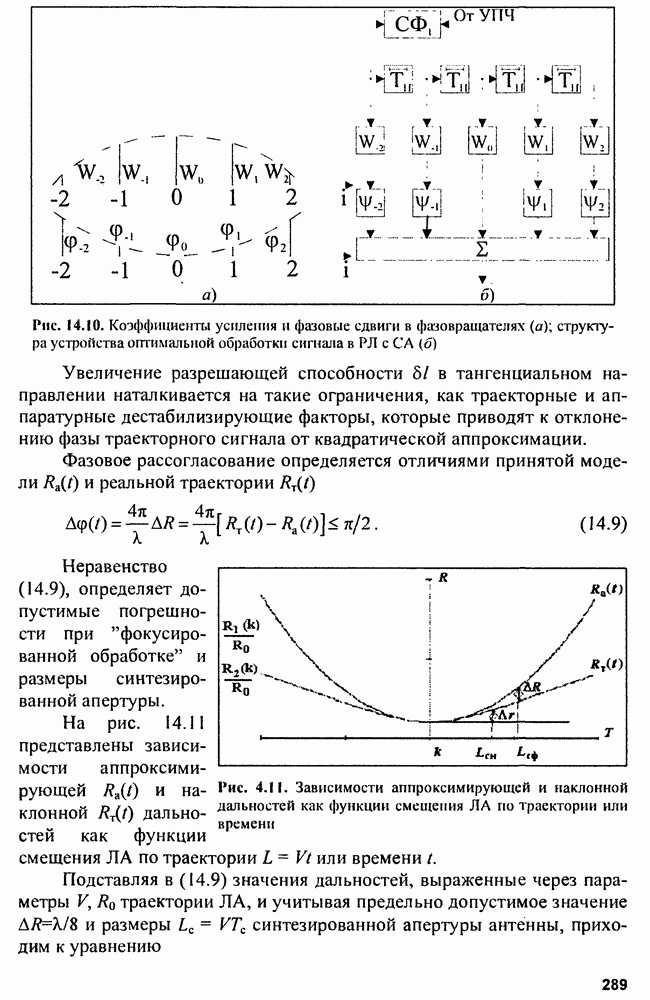
Пример. Рассмотрим  и ДН пачки когерентных гауссовских импульсов с гауссовской огибающей.
и ДН пачки когерентных гауссовских импульсов с гауссовской огибающей.
Длительность импульса  период повторения импульсов
период повторения импульсов  длительность пачки
длительность пачки  Тогда
Тогда

- ДКФ пачки импульсов.
Пусть  тогда
тогда

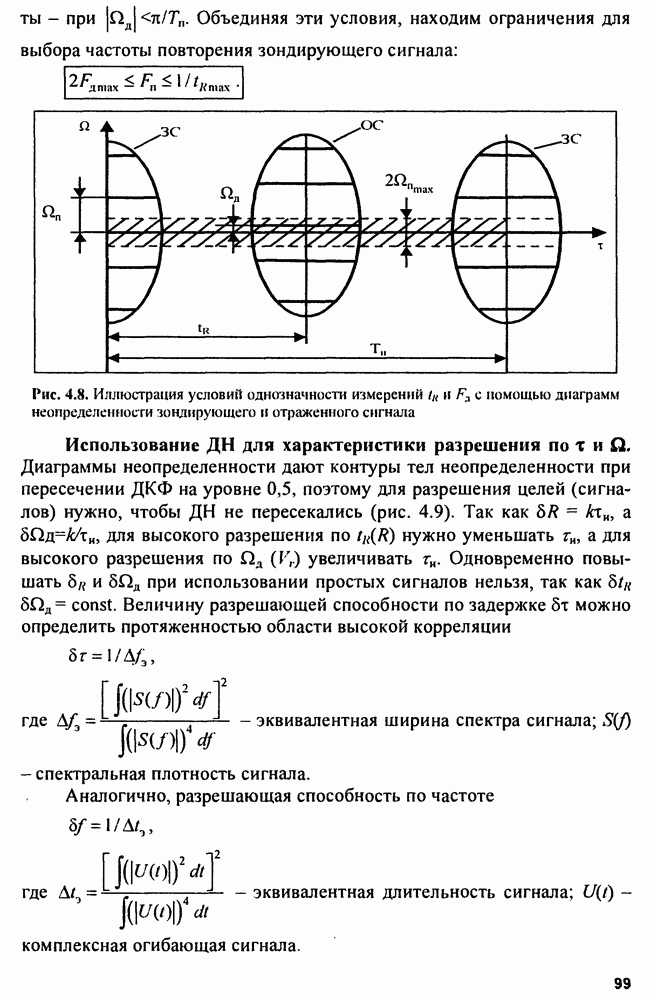
На рис. 4.7 показаны  и ДН пачки, рассмотренной в примере.
и ДН пачки, рассмотренной в примере.
В табл. 4.2 сведены примеры повторяющихся и пачечных сигналов, их спектров и 

Рис. 4.7. ФНЗС (а) и ДН (б) пачки импульсов
Таблица 4.2 (см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Глава 1. Общие сведения о радиолокационных системах
- 1.2. Физические основы радиолокации
- 1.3. Физические основы радиолокационных измерений
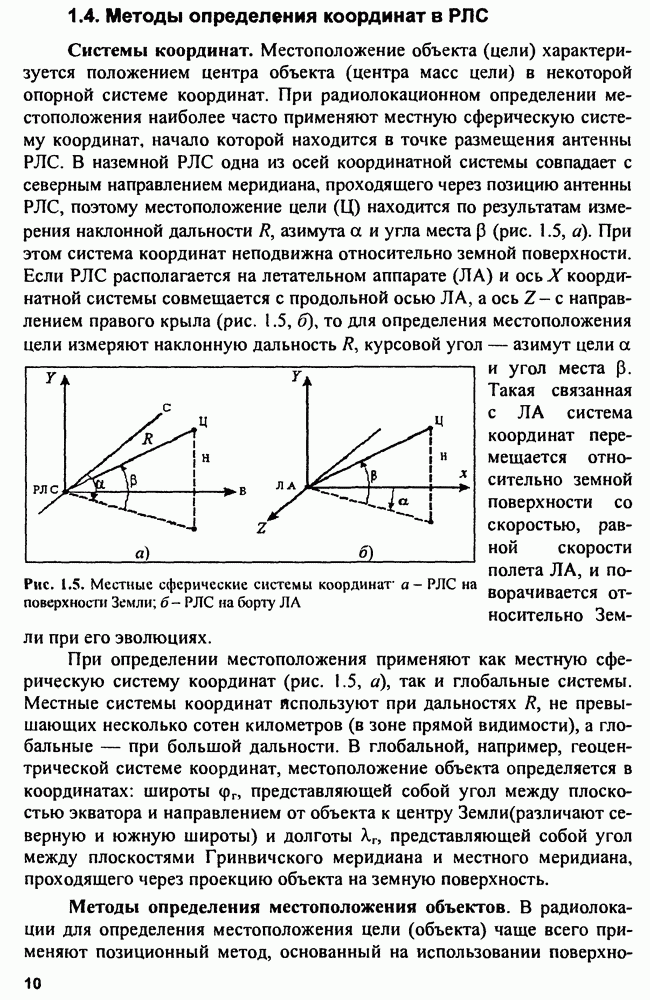
- 1.4. Методы определения координат в РЛС
- 1.5. Тактико-технические параметры РЛС
- 1.6. Классификация радиолокационных устройств и систем
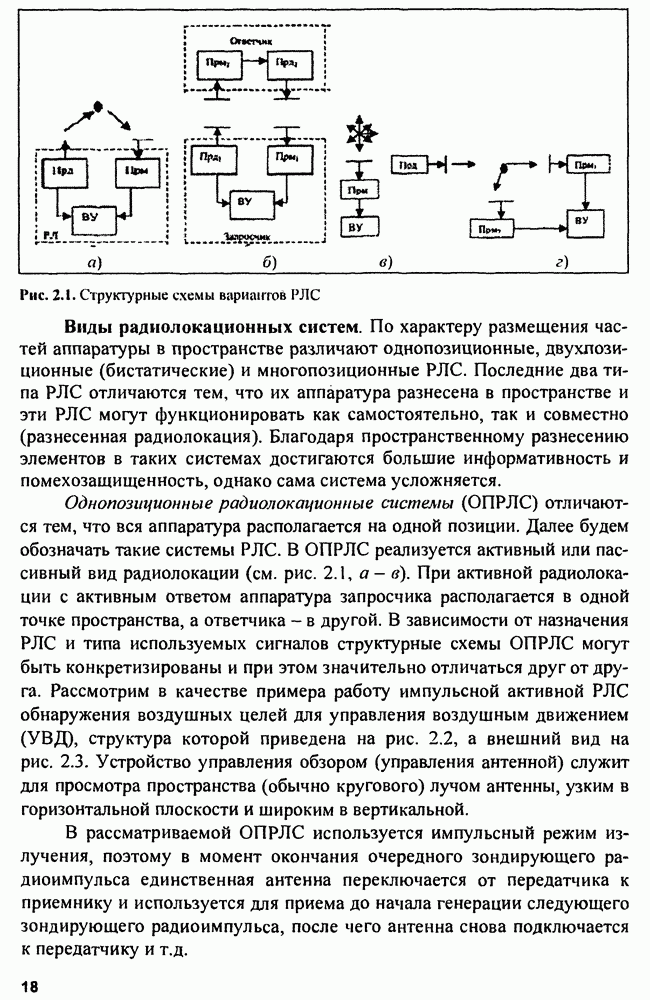
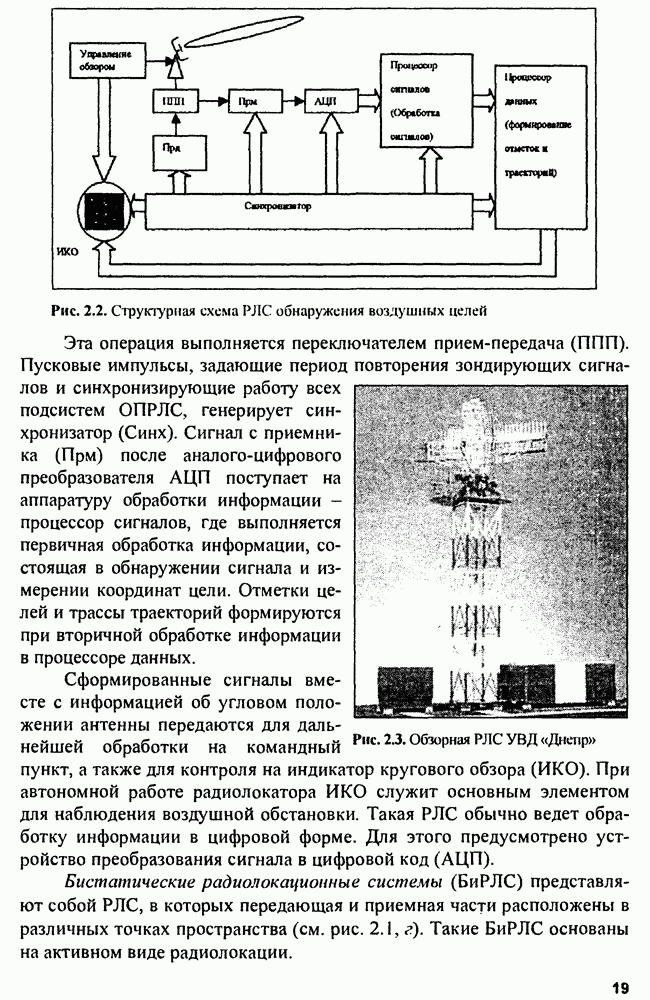
- Глава 2. Радиолокационные системы
- 2.1. Виды радиолокации и радиолокационных систем
- 2.2. Многопозиционные радиолокационные системы
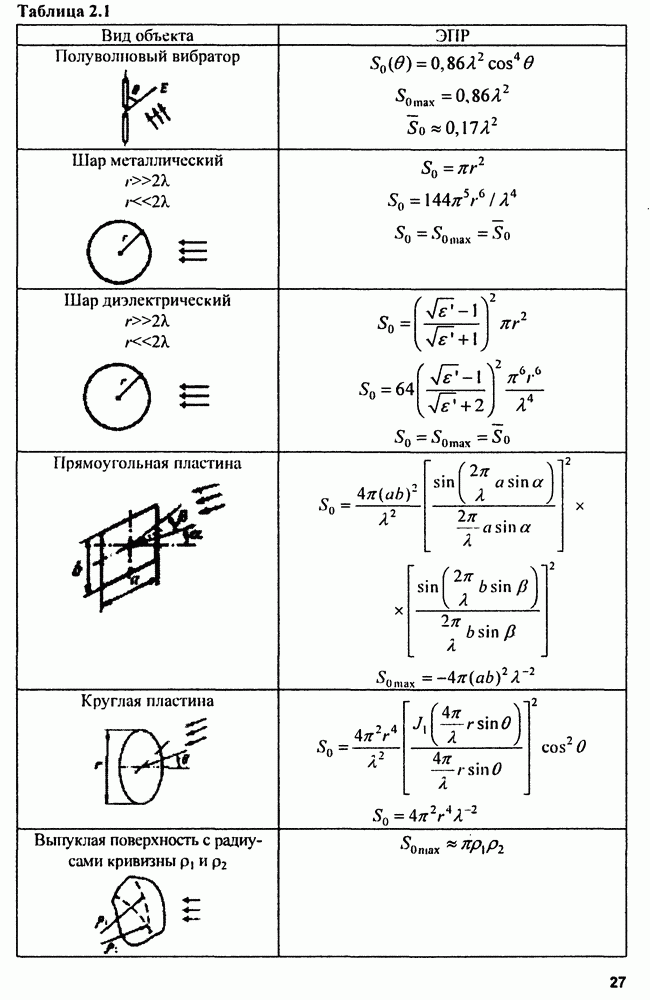
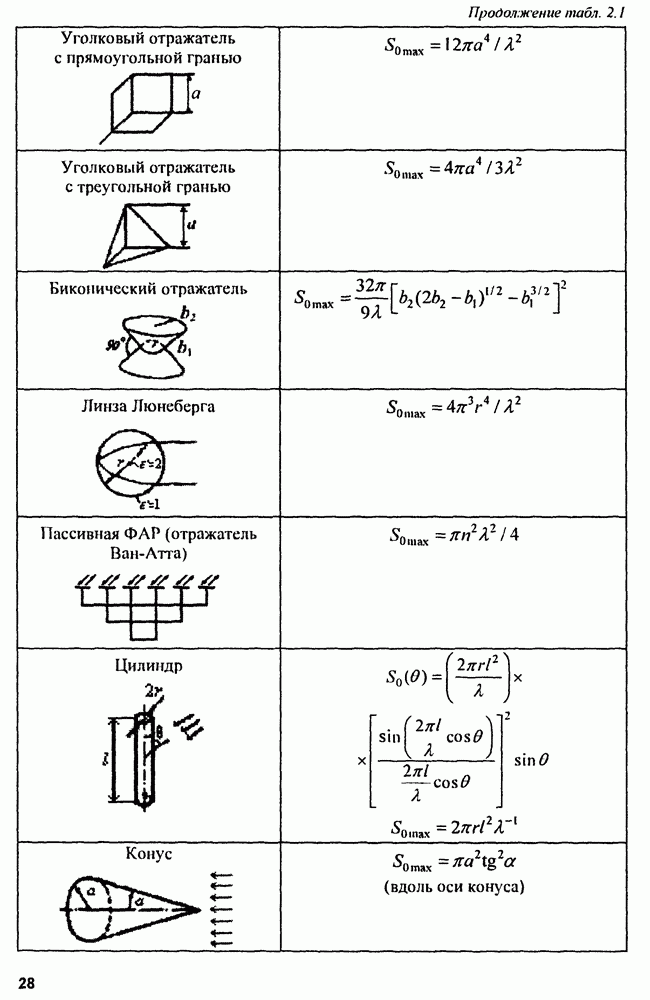
- 2.3. Отражающие свойства целей
- 2.3.1. Точечные цели
- 2.3.2. Особенности отражения радиоволн от реальных объектов
- 2.3.3. Методы определения ЭПР реальных целей
- 2.3.4. ЭПР протяженных целей
- Глава 3. Обнаружение радиосигналов
- 3.2. Критерии оптимального обнаружения
- 3.3. Модели радиолокационных сигналов
- 3.4. Синтез оптимальных обнаружителей
- 3.5. Эффективность систем обнаружения сигналов
- 3.6. Обнаружение радиосигналов при априорной неопределенности
- Глава 4. Выбор зондирующего сигнала в РЛС
- 4.2. Диаграммы неопределенности
- 4.3. Использование диаграмм неопределенности в радиолокации
- 4.4. Сложные сигналы
- Глава 5. Дальность действия и точность РЛС
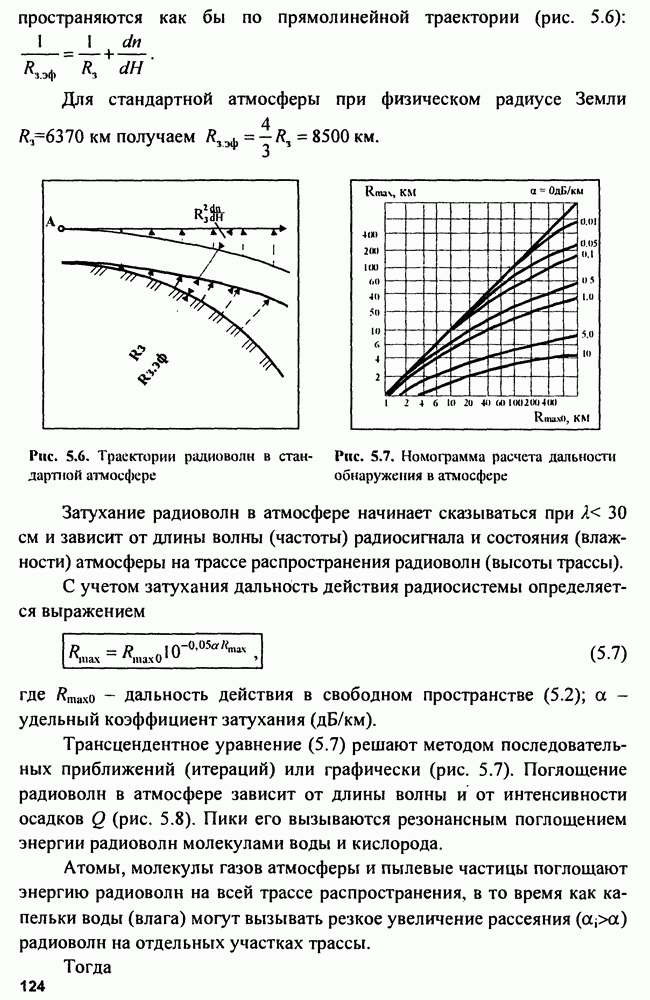
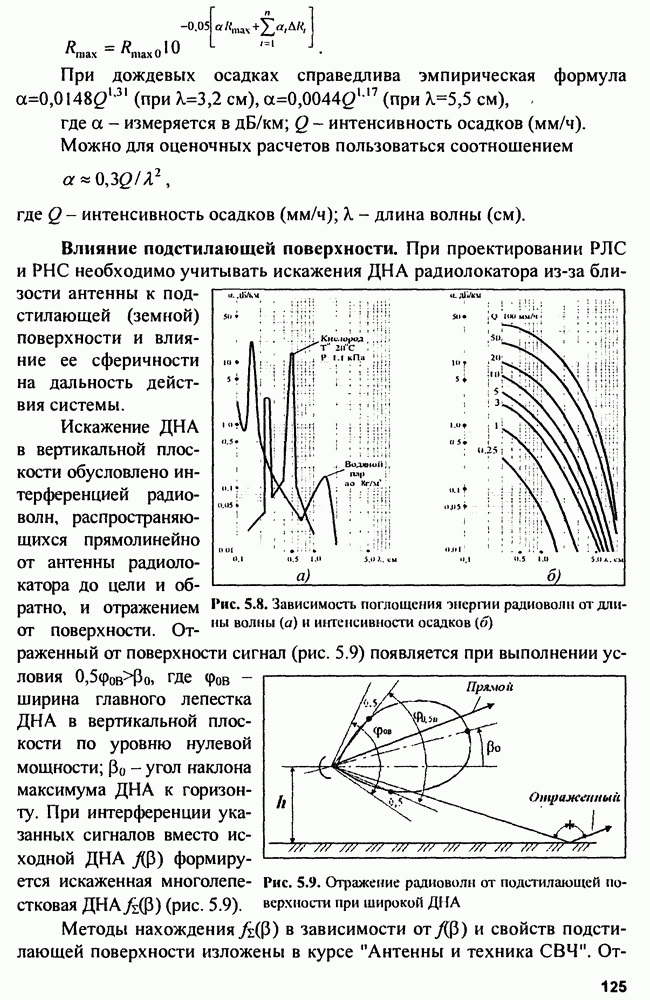
- 5.1.2. Влияние атмосферы и подстилающей поверхности на дальность действия РЛС
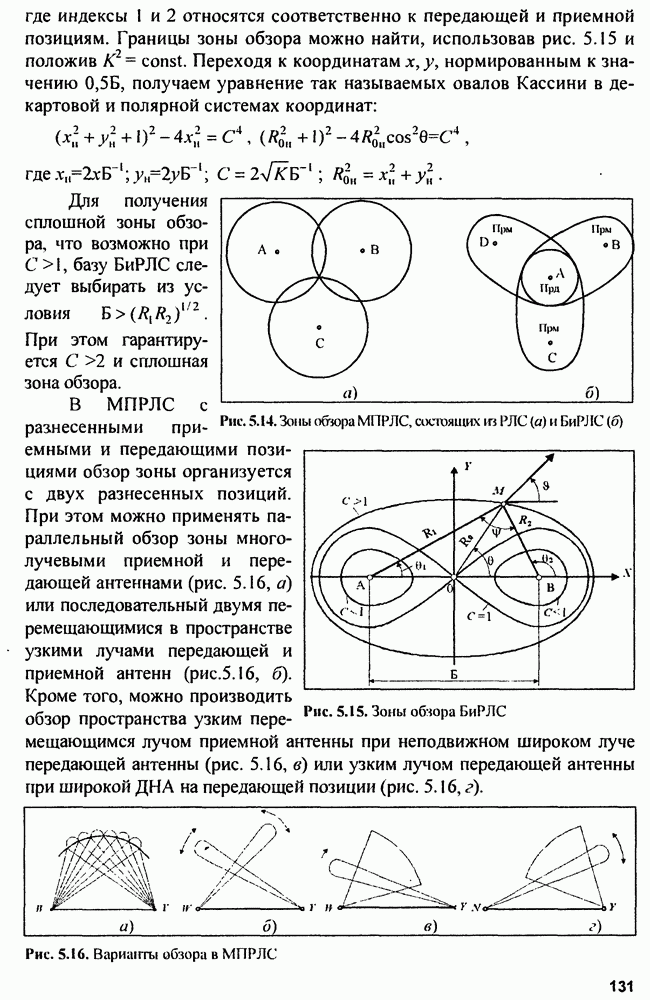
- 5.1.3. Обзор пространства в РЛС
- 5.1.4. Анализ факторов, определяющих дальность действия РЛС
- 5.2. Точность определения местоположения цели в РЛС
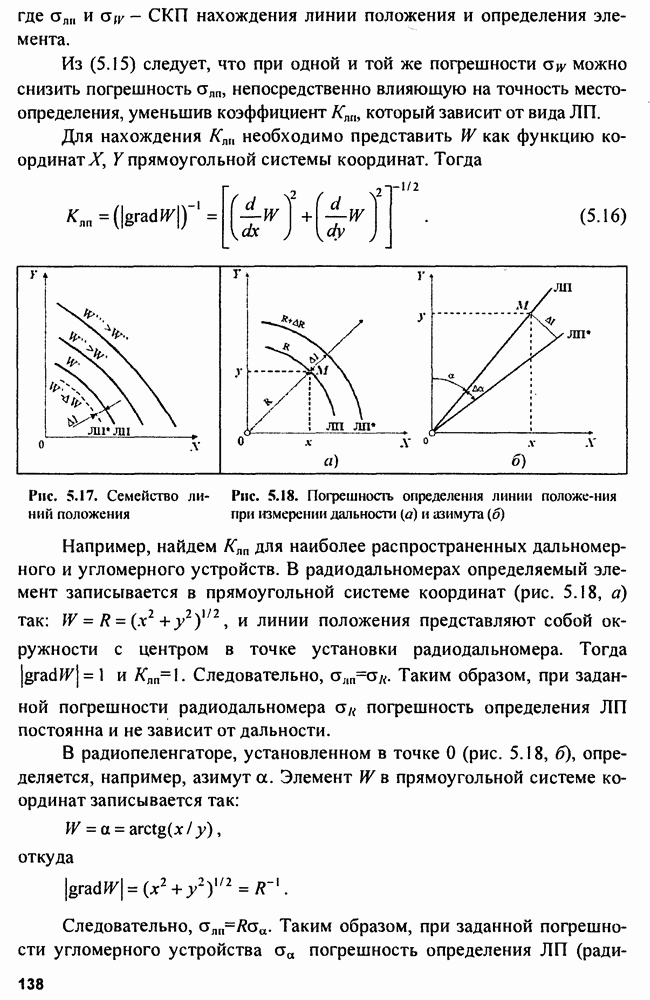
- 5.2.2. Точность определения геометрического элемента
- 5.2.3. Погрешность определения линии положения
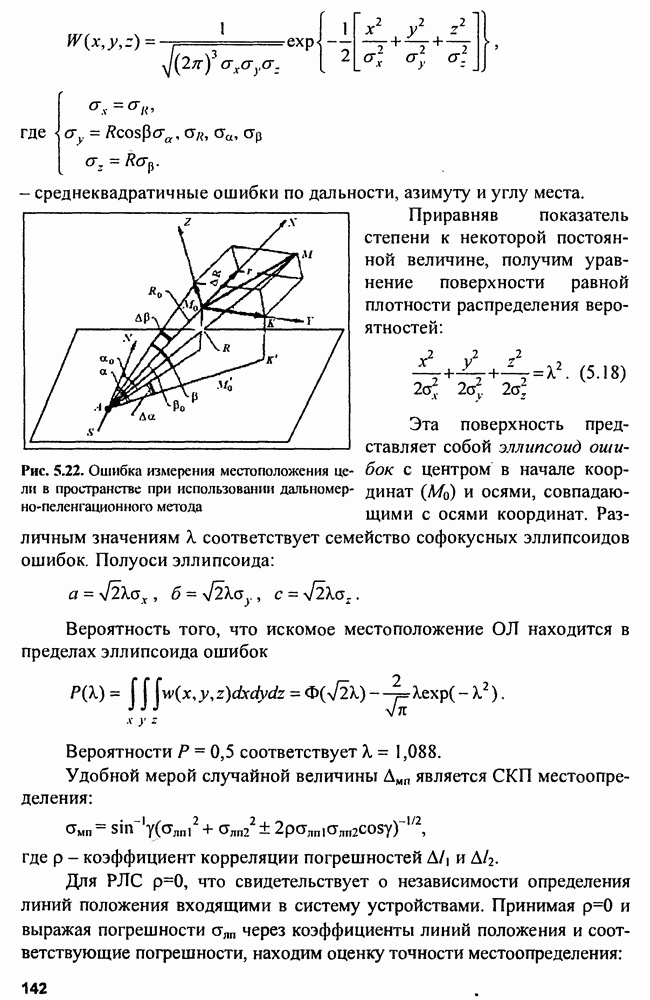
- 5.2.4. Погрешность местоположения определения
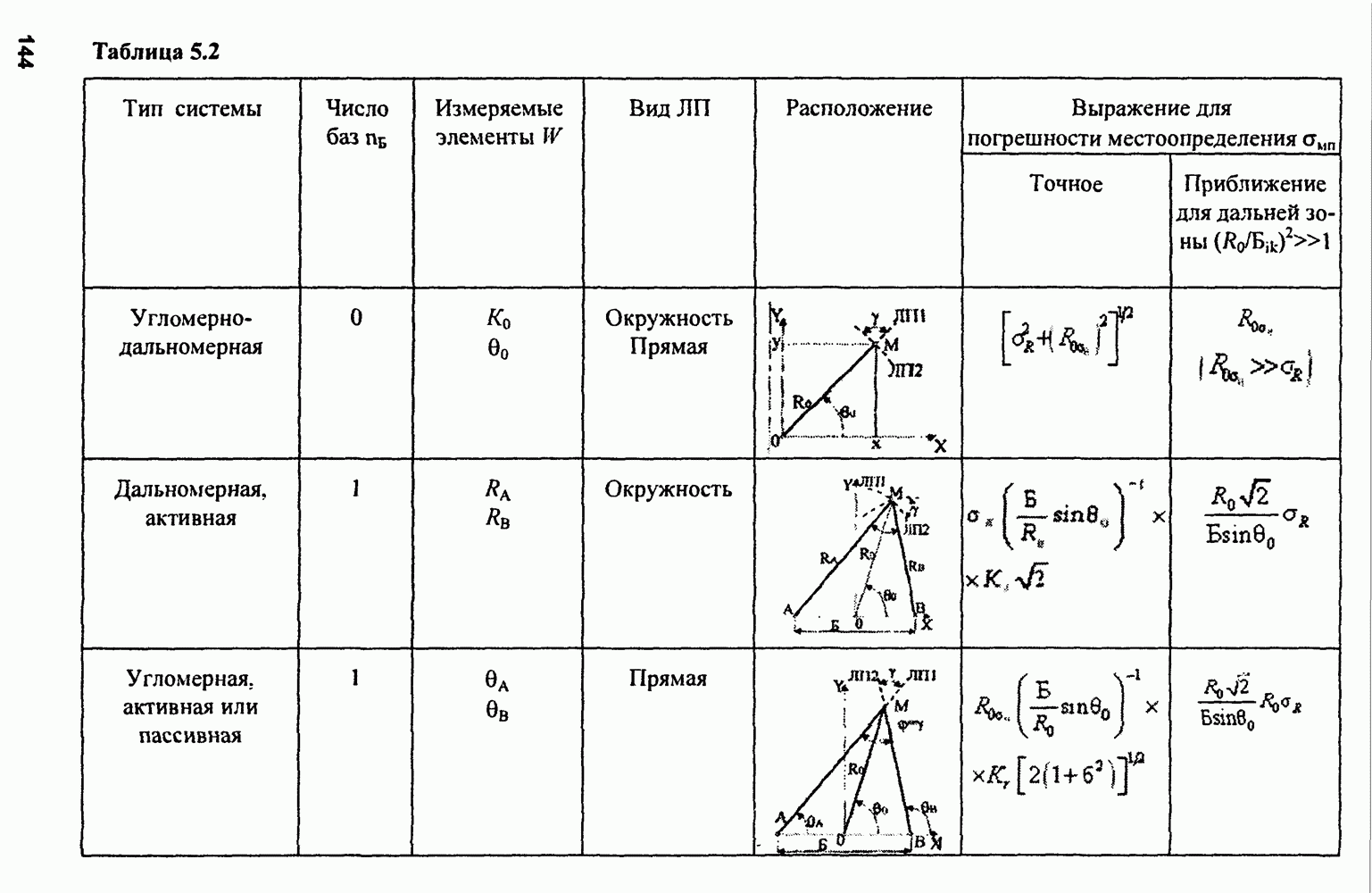
- 5.2.5. Рабочие зоны РЛС
- Глава 6. Помехи радиолокационным системам
- 6.2. Наблюдаемость целей при воздействии помех
- 6.2.3. Уменьшение ЭПР защищаемых объектов
- 6.2.4. Уменьшение собственного радиоизлучения объектов и влияние ионизированных областей атмосферы
- 6.2.5. Противорадиолокационная маскировка объектов
- 6.2.6. Наблюдаемость цели на фоне активной помехи
- 6.3. Радиотехническая разведка
- Глава 7. Борьба с пассивными помехами
- 7.1 Уменьшение влияния пассивных помех в приемном канале (на высокой и промежуточной частотах)
- 7.2. Обнаружение целей на фоне пассивных помех
- 7.3. Методы создания когерентного опорного сигнала в РЛС с ОДЦ
- 7.4. Построение устройств подавления пассивных помех в ОДЦ
- 7.5. Реализация устройств подавления пассивных помех
- 7.6. Критерии качества подавления пассивных помех в устройствах ОДЦ
- 7.7. Факторы, определяющие качество устройств ОДЦ
- Глава 8. Борьба с активными помехами
- 8.1. Прием и обработка пространственно-временных сигналов
- 8.2. Устройства подавления пространственных активных помех
- 8.3. Устройства борьбы с комбинированными помехами
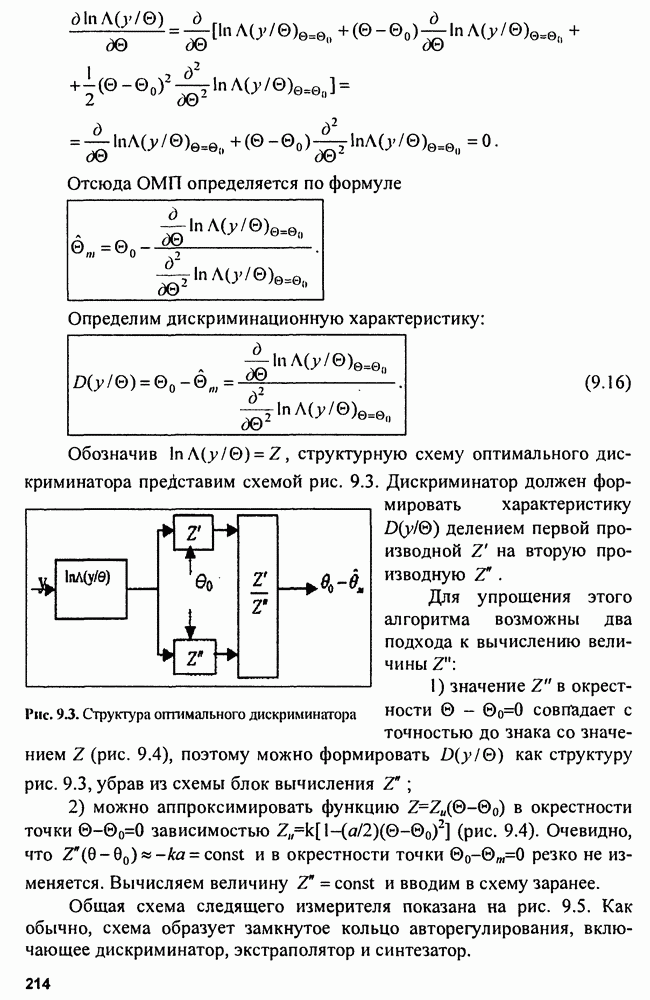
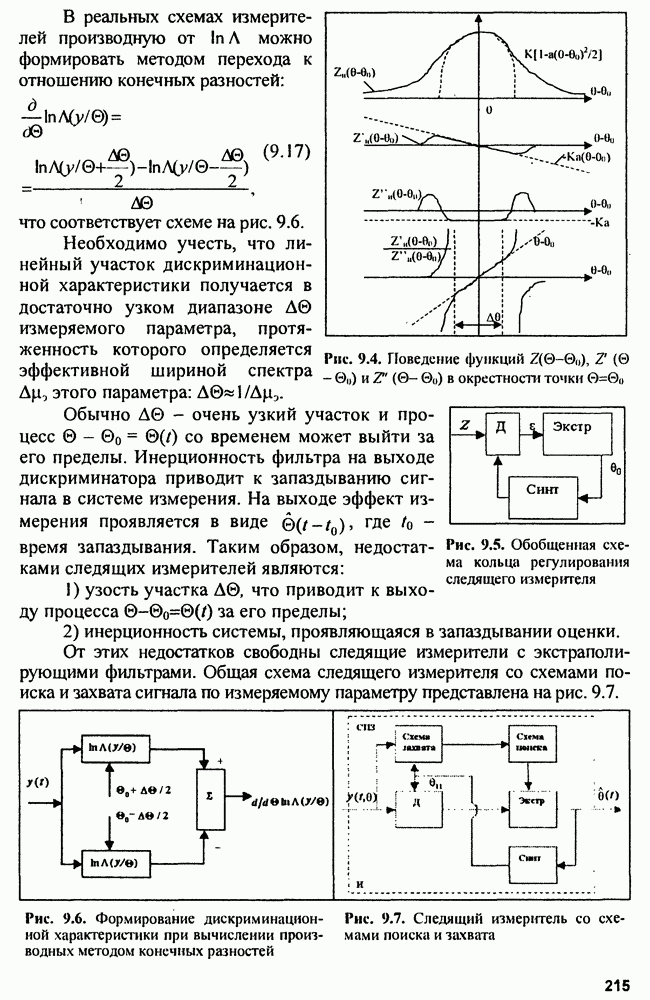
- Глава 9. Измерение параметров сигнала
- 9.1. Байесовы оценки
- 9.2. Оценки максимального правдоподобия
- 9.3. Качество оценок
- 9.4. Потенциальная точность измерений
- 9.5. Структура измерителей
- 9.6. Оценка параметров сигнала на фоне «белого» шума
- 9.7. Оптимальные дискриминаторы
- 9.8. Экстраполяторы
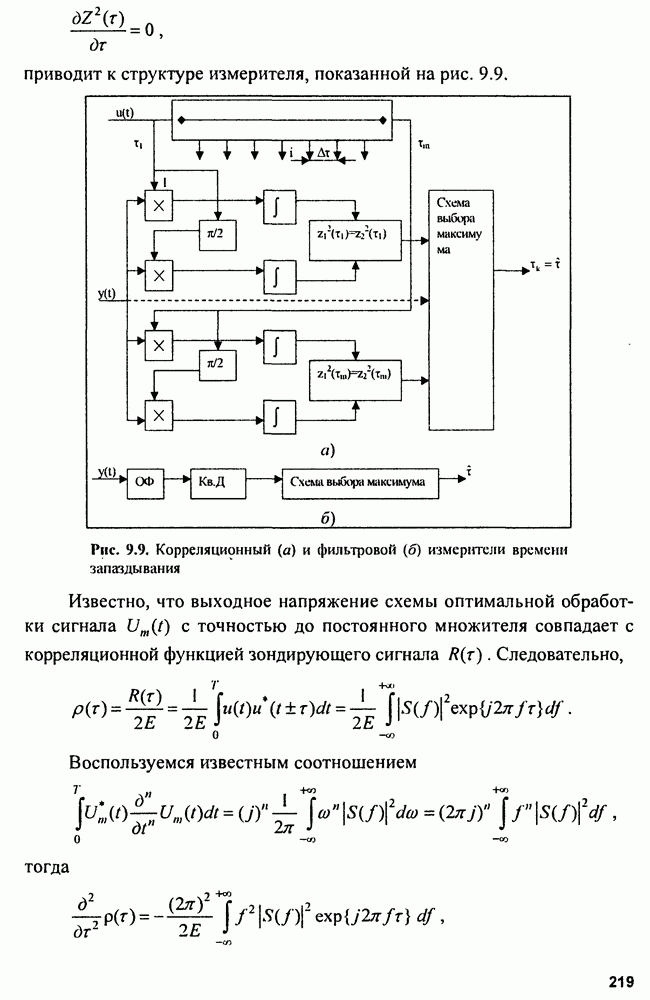
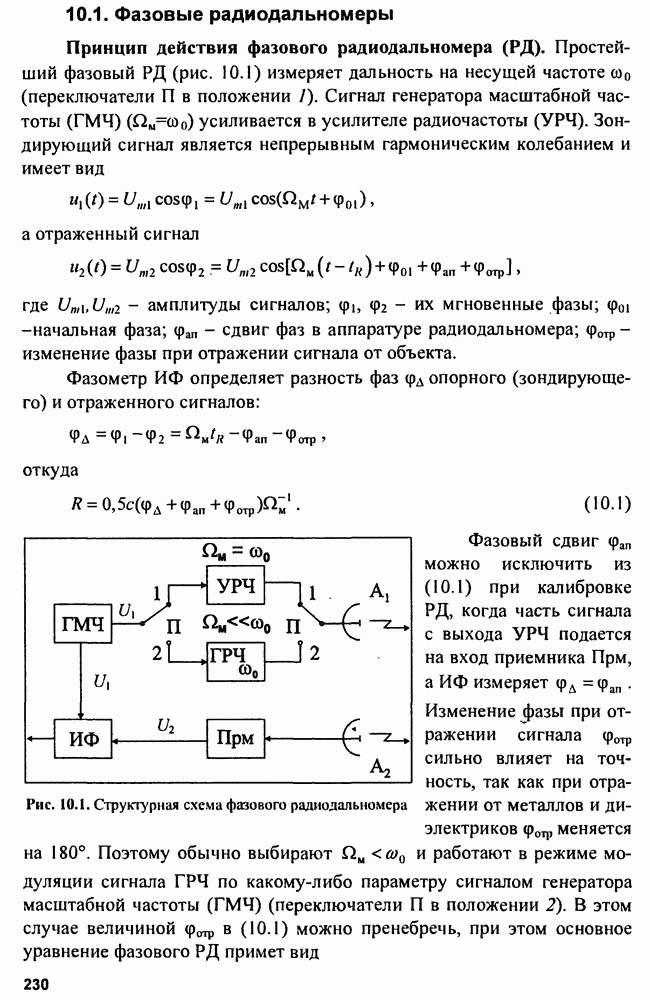
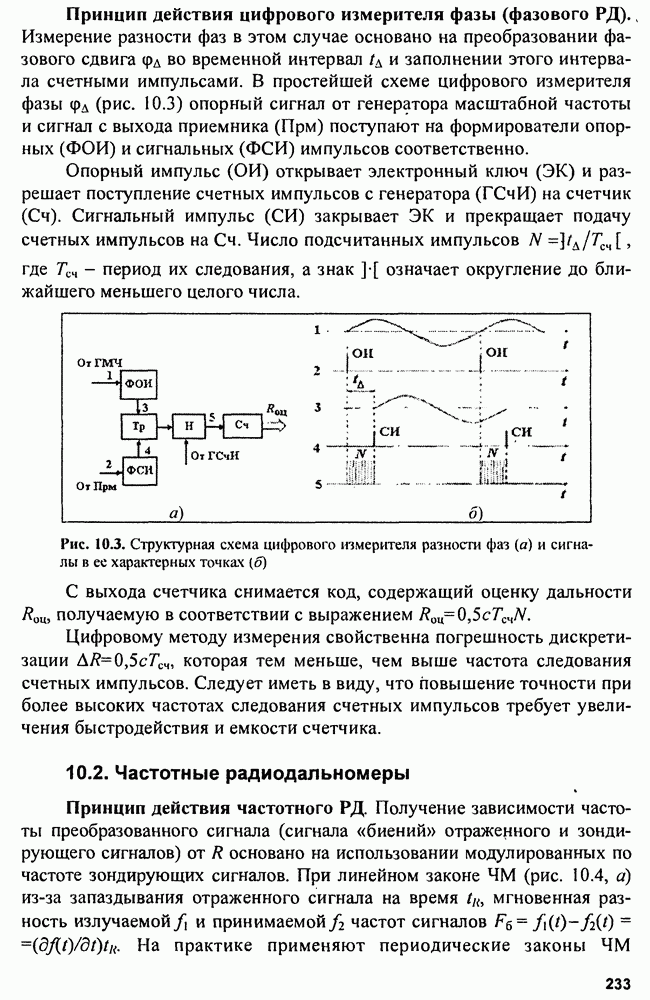
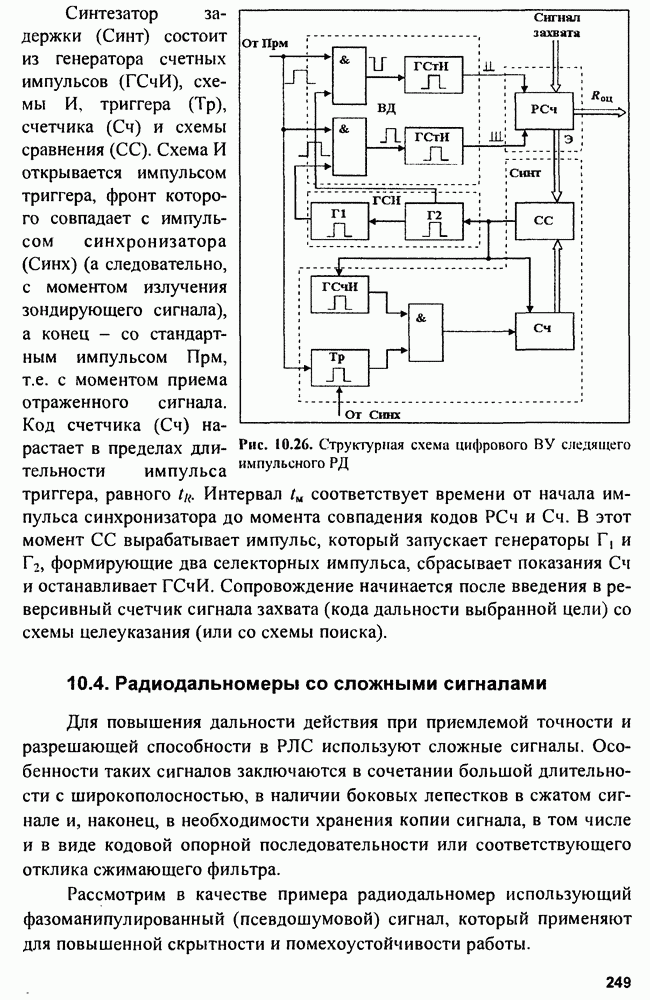
- Глава 10. Радиодальномеры
- 10.1. Фазовые радиодальномеры
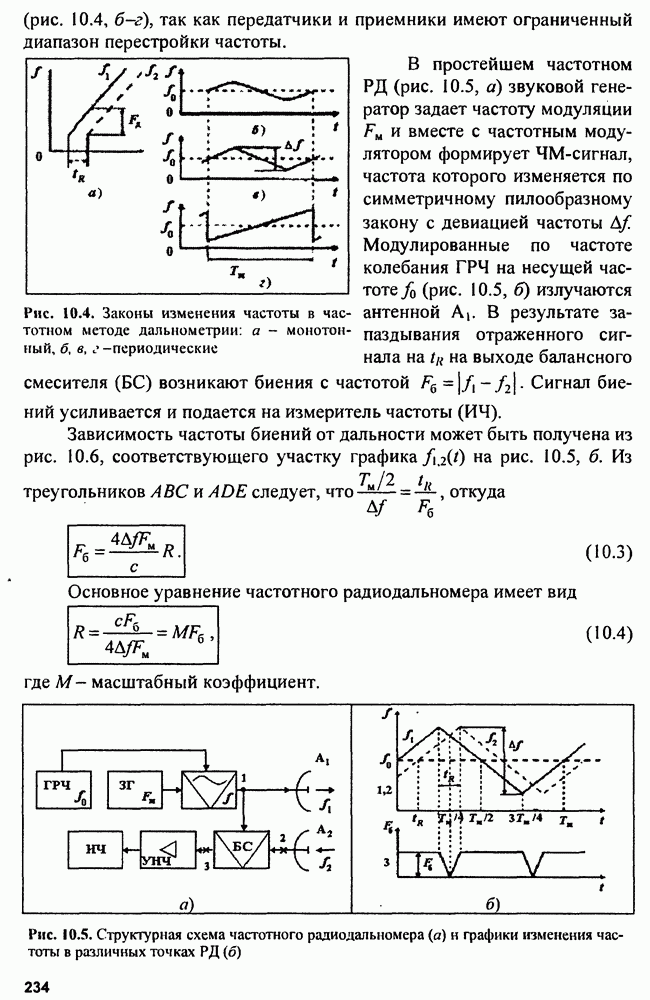
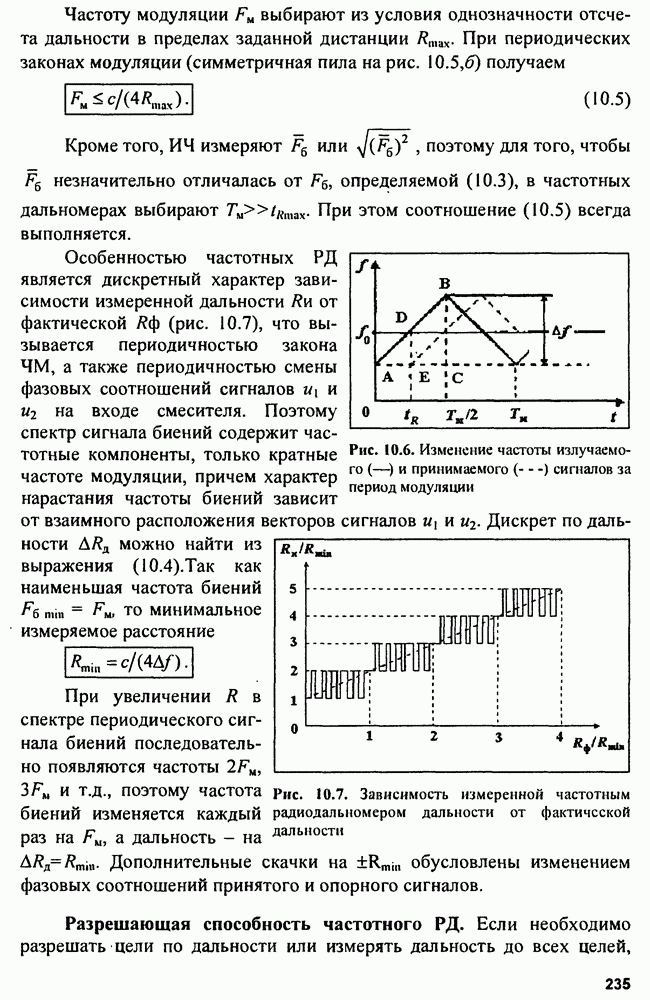
- 10.2. Частотные радиодальномеры
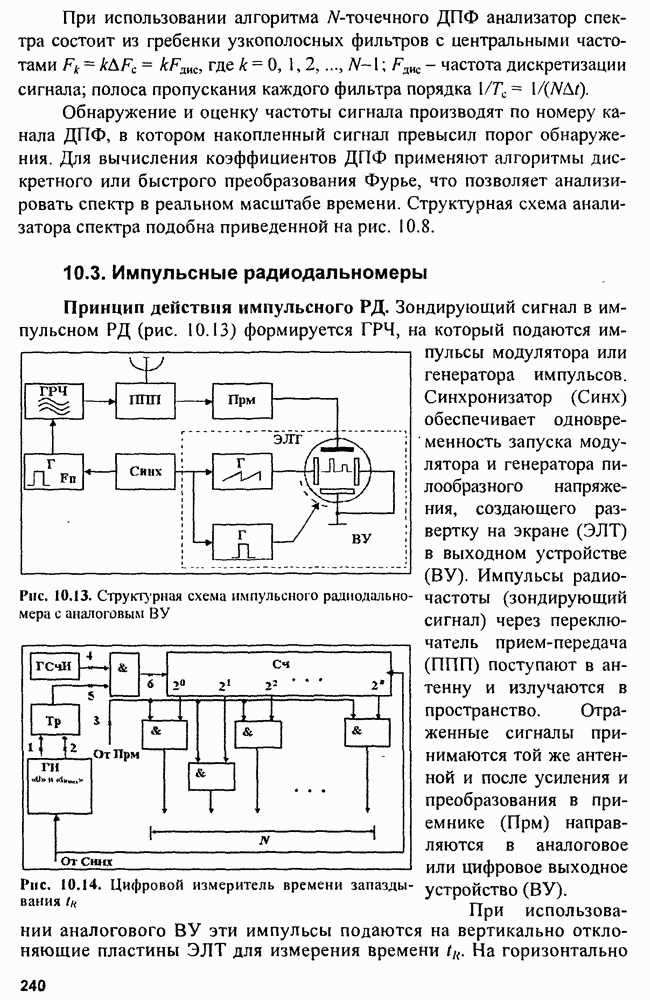
- 10.3. Импульсные радиодальномеры
- 10.4. Радиодальномеры со сложными сигналами
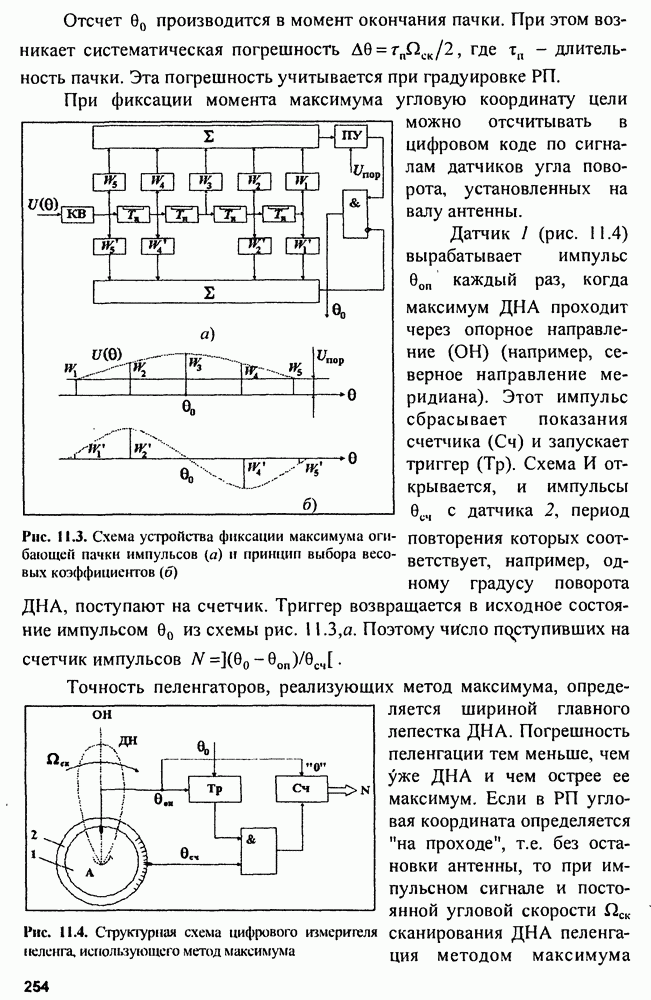
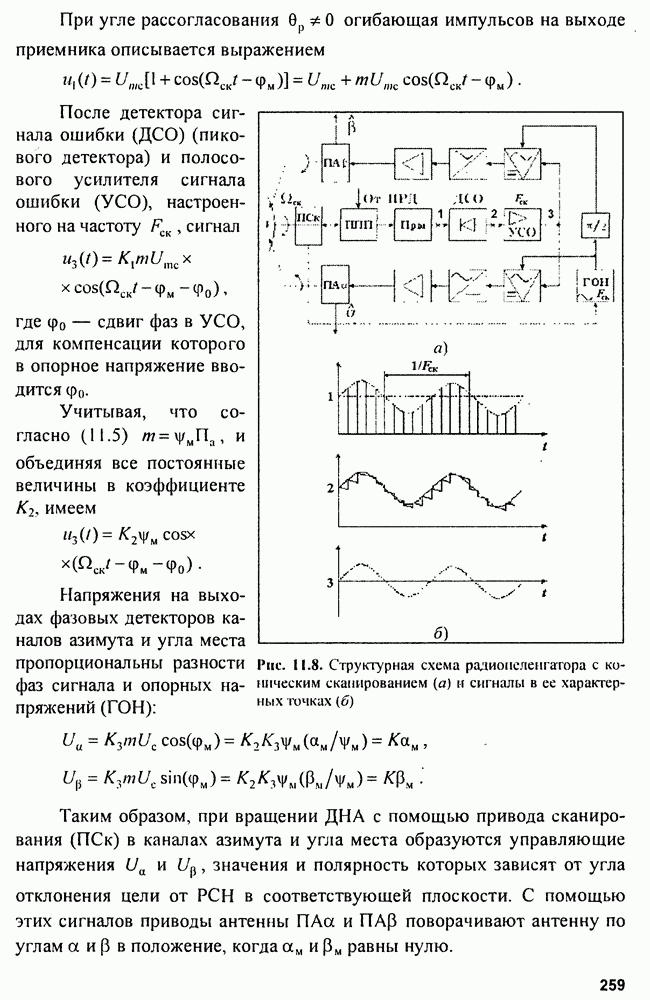
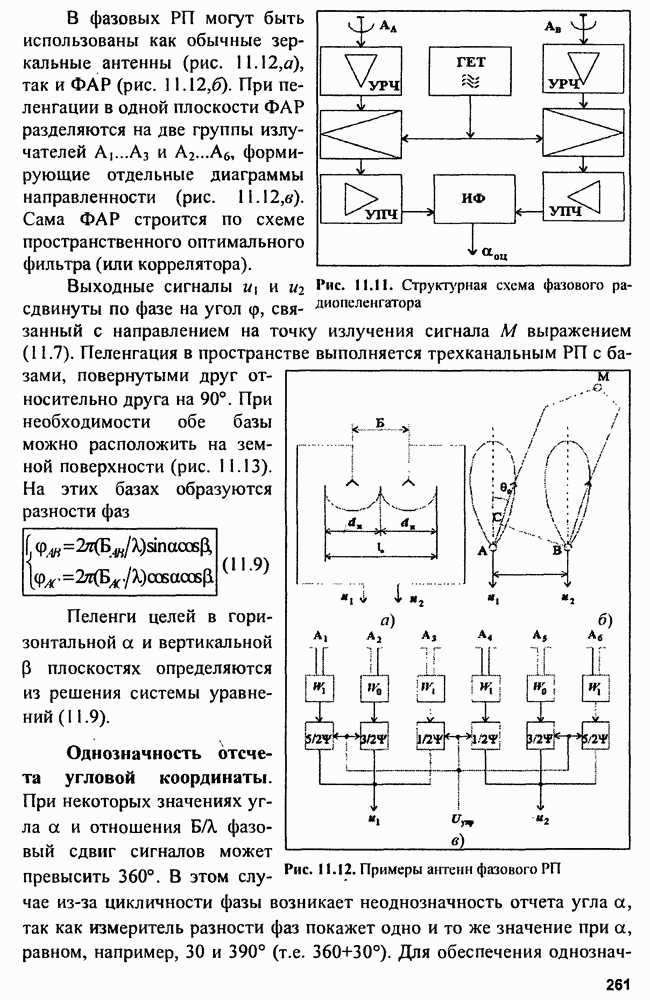
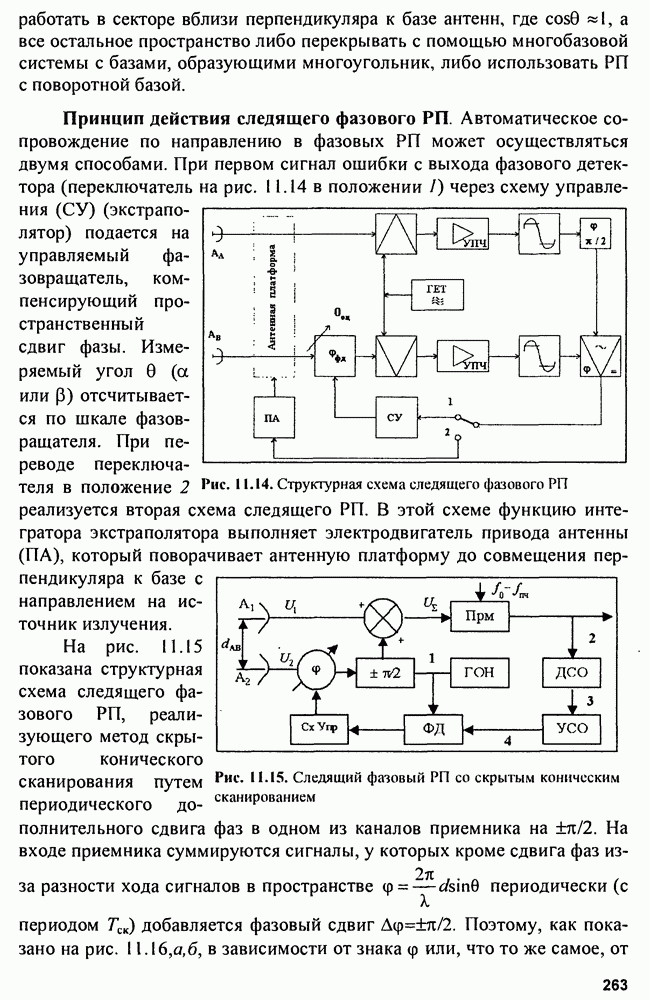
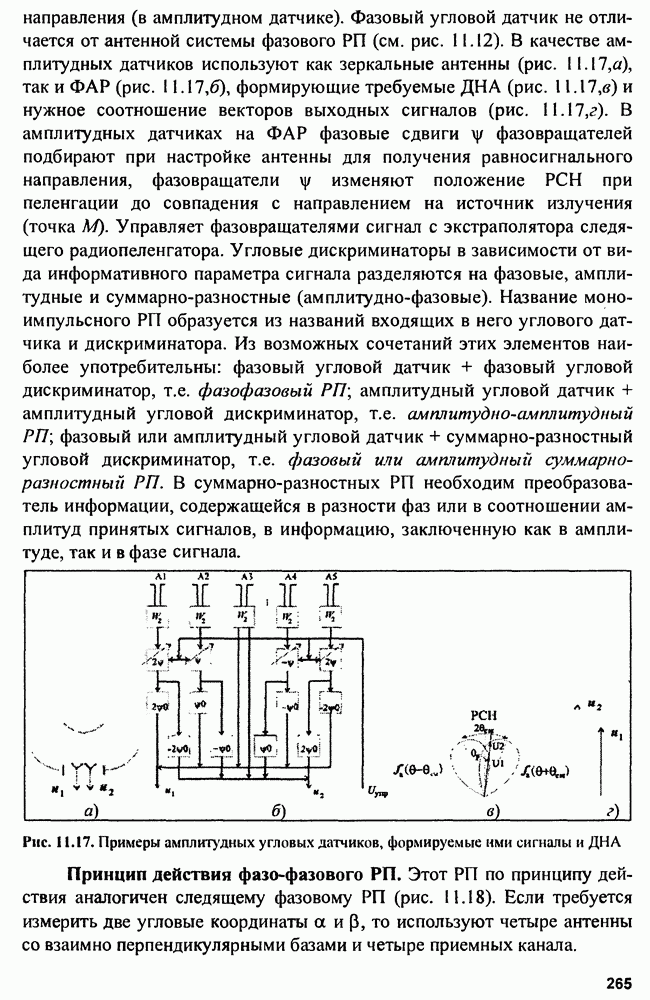
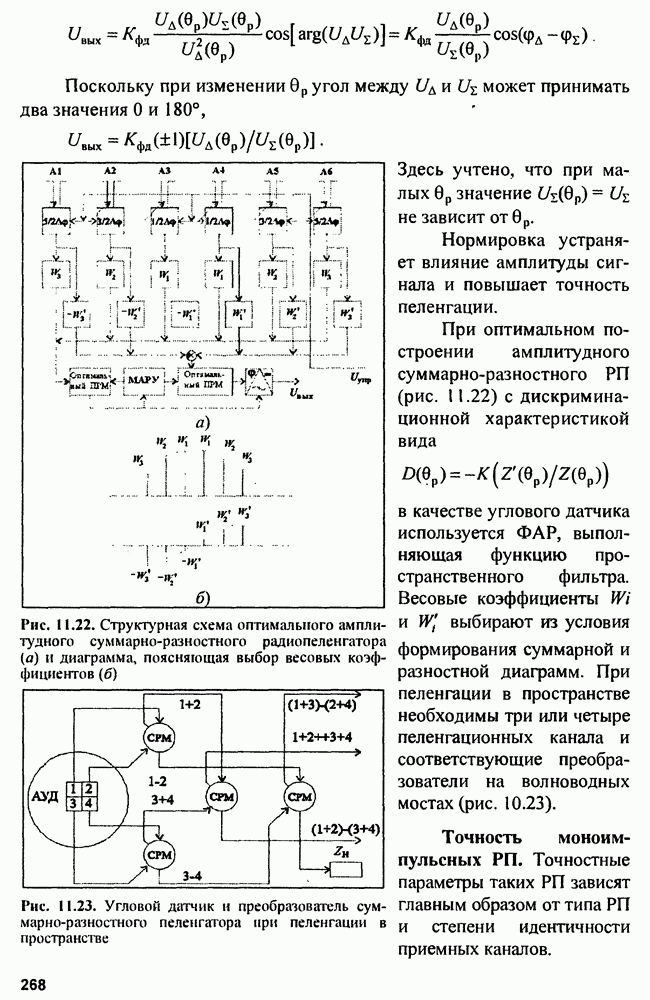
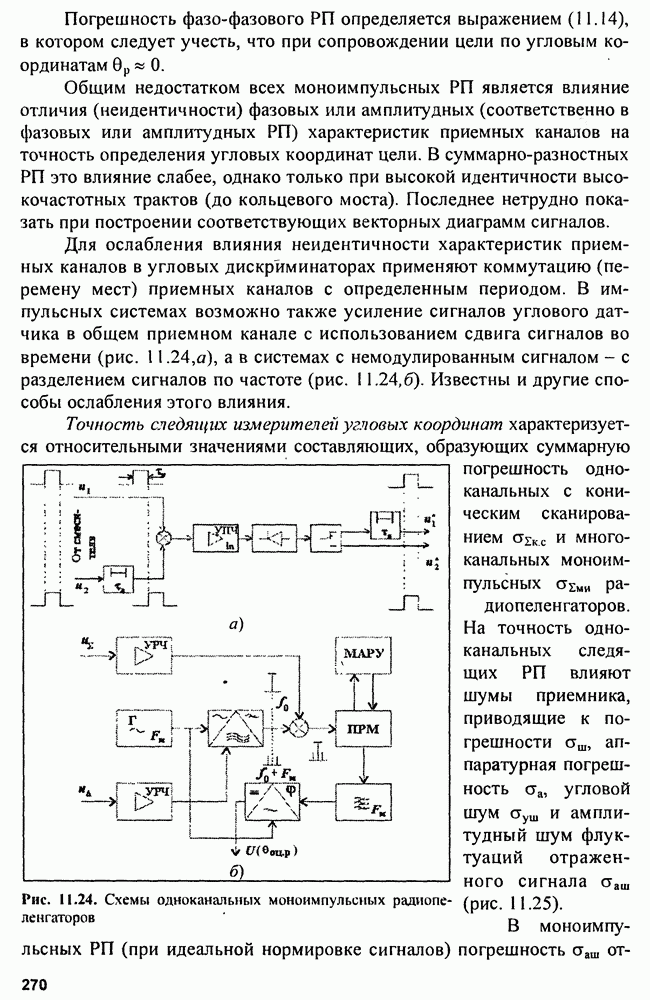
- Глава 11. Радиопеленгаторы
- 11.1. Амплитудные радиопеленгаторы
- 11.2. Фазовые радиопеленгаторы
- 11.3. Многоканальные (моноимпульсные) радиопеленгаторы
- Глава 12. Измерители высоты
- Глава 13. Измерители скорости цели
- Глава 14. Радиолокаторы с синтезированной апертурой
- 14.2. Цифровая обработка сигналов РСА
- Глава 15. Вторичная обработка радиолокационной информации
- 15.1. Обнаружение и сопровождение траекторий
- 15.2. Сигналы и помехи в системах вторичной обработки
- 15.3. Оценка параметров траектории
- 15.4. Стробирование отметок целей
- Заключение