| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. Вариационные проблемы на замкнутых многообразиях
Вспомогательные средства, подготовленные в двух первых главах, мы используем теперь для рассмотрения вариационных проблем в целом. Хотя метод приложим к произвольным положительным и положительно регулярным вариационным проблемам при общих граничных условиях, мы удовольствуемся тем, что применим его к типической проблеме геодезических линий на замкнутых многообразиях, причем будем рассматривать большей частью случай закрепленных концов, и только в последнем параграфе — случай произвольных граничных многообразий. Мы докажем предложения о существовании и минимальном числе таких геодезических линии. Начнем с точной формулировки задачи.
§ 11. Постановка проблемы
(Однородное)  -мерное многообразие
-мерное многообразие  есть окрестностное пространство, каждая точка которого обладает окрестностью, допускающей топологическое отображение на внутренность
есть окрестностное пространство, каждая точка которого обладает окрестностью, допускающей топологическое отображение на внутренность  -мерного шара. Допустим, что если каждой точке
-мерного шара. Допустим, что если каждой точке  поставлена в соответствие некоторая ее окрестность, то, как бы ни выбирались эти окрестности,
поставлена в соответствие некоторая ее окрестность, то, как бы ни выбирались эти окрестности,  всегда покрыто уже конечным их числом; тогда мы называем многообразие
всегда покрыто уже конечным их числом; тогда мы называем многообразие  замкнутым. Так как каждая точка многообразия
замкнутым. Так как каждая точка многообразия  обладает компактной окрестностью, например, топологическим образом замкнутого шара, то замкнутое многообразие компактно, т. е. всякое его бесконечное подмножество имеет по крайней мере одну предельную точку. Далее, мы предположим, что
обладает компактной окрестностью, например, топологическим образом замкнутого шара, то замкнутое многообразие компактно, т. е. всякое его бесконечное подмножество имеет по крайней мере одну предельную точку. Далее, мы предположим, что  трижды непрерывно
трижды непрерывно
дифференцируемо. Это означает, что подходящая открытая окрестность каждой точки  из
из  отнесена к локальным координатам
отнесена к локальным координатам  такого рода, что две системы координат
такого рода, что две системы координат  и
и  принадлежащие двум точкам
принадлежащие двум точкам  связаны, там где они перекрываются, трижды непрерывно дифференцируемым преобразованием
связаны, там где они перекрываются, трижды непрерывно дифференцируемым преобразованием  с отличным от нуля функциональным определителем. Тогда имеет смысл говорить о трижды непрерывно дифференцируемых функциях на
с отличным от нуля функциональным определителем. Тогда имеет смысл говорить о трижды непрерывно дифференцируемых функциях на  Наконец, мы превратим
Наконец, мы превратим  в риманово многообразие, приписав ему некоторую риманову метрику с линейным элементом
в риманово многообразие, приписав ему некоторую риманову метрику с линейным элементом 

Здесь  суть трижды непрерывно дифференцируемые функции локальных координат, и квадратичная форма является положительно определенной.
суть трижды непрерывно дифференцируемые функции локальных координат, и квадратичная форма является положительно определенной.
Наша задача состоит в отыскании на римановом многообразии  всех геодезических, соединяющих две данные точки
всех геодезических, соединяющих две данные точки 
Решение этой задачи требует исследования функционального пространства  всех кусочно-гладких кривых между
всех кусочно-гладких кривых между  Для того чтобы сделать это исследование возможным, мы должны ближе познакомиться с самим многообразием
Для того чтобы сделать это исследование возможным, мы должны ближе познакомиться с самим многообразием  (§ 12) и ввести в рассмотрение пространство
(§ 12) и ввести в рассмотрение пространство  всех вообще кусочно-гладких кривых многообразия
всех вообще кусочно-гладких кривых многообразия 
| << Предыдущий параграф | Следующий параграф >> |
- От переводчика
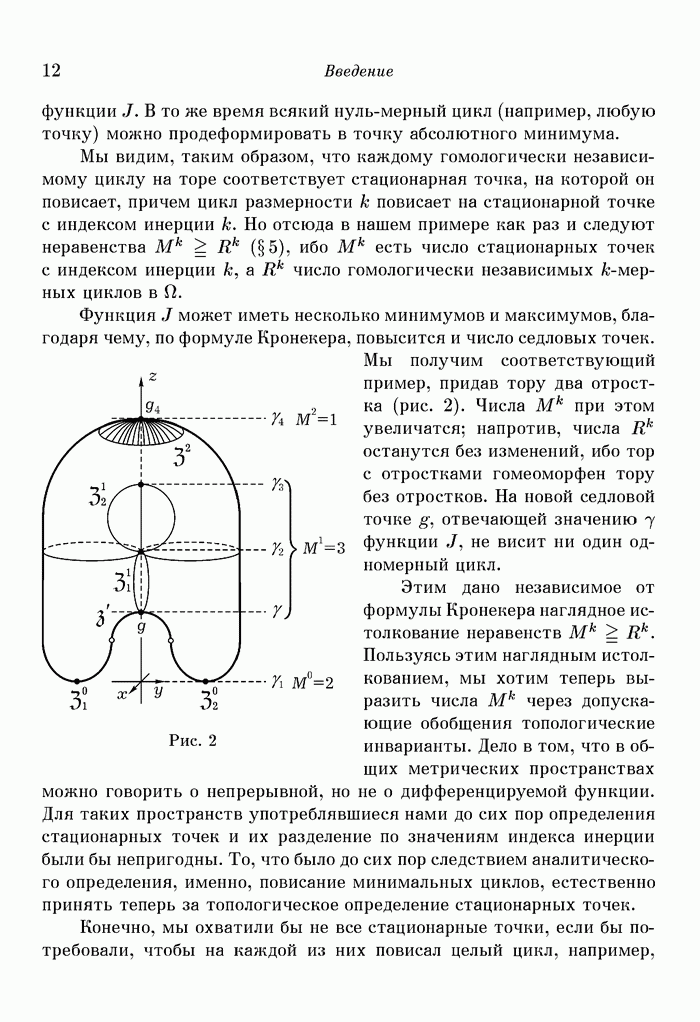
- Введение
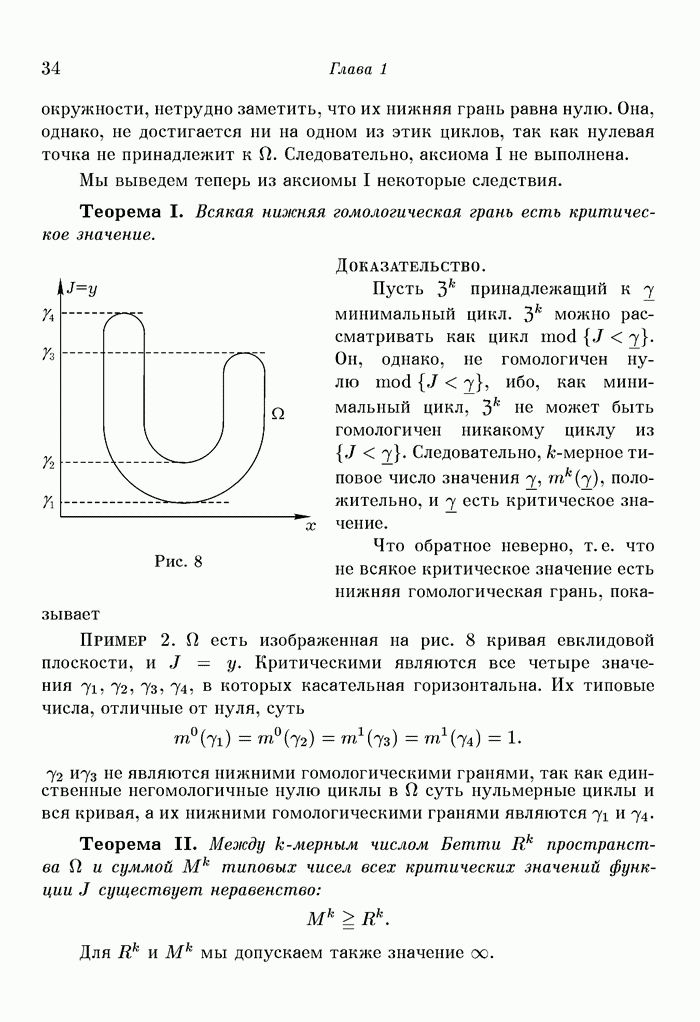
- Глава 1. Числа Бетти и типовые числа
- § 2. Абсолютные циклы и числа Бетти пространства «омега»
- § 3. Относительные циклы
- § 4. Типовые числа критических значений функции J на «омега»
- § 5. Неравенства между типовыми числами и числами Бетти
- § 6. Условие равенства чисел M^k и R^k
- Глава 2. Типовые числа стационарных точек
- § 8. Невырожденные стационарные точки
- § 9. J-деформация в окрестности стационарной точки
- § 10. Теорема о конечности типовых чисел
- Глава 3. Вариационные проблемы на замкнутых многообразиях
- § 12. Риманово многообразие
- § 13. Функциональное пространство
- § 14. Типовые числа изолированной геодезической
- § 15. Примеры типовых чисел (n-мерная сфера)
- § 16. Деформационные теоремы.
- § 17. Типовые числа критических значений и стационарных точек
- § 18. Действительность аксиом I и II
- § 19. Основная теорема
- § 20. Геодезические с закрепленными концами на n-мерной сфере
- § 21. Инвариантность чисел Бетти функционального пространства «омега»
- § 22. Произвольные граничные многообразия
- Прибавление. Стационарные точки на замкнутых многообразиях
- Примечания