§ 18. Действительность аксиом I и II

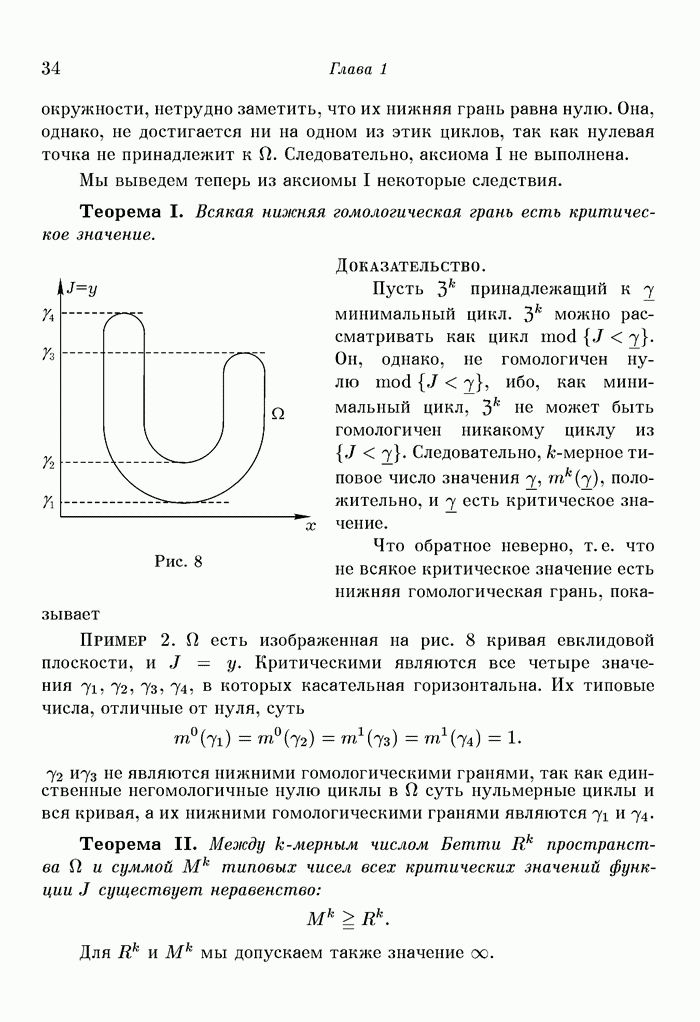
Теорема. Если в функциональном пространстве нашей вариационной проблемы для всякого значения функции область меньших значений содержит только конечное число стационарных точек, то аксиомы I (§ 5) и II (§ 6) выполнены.

Доказательство.

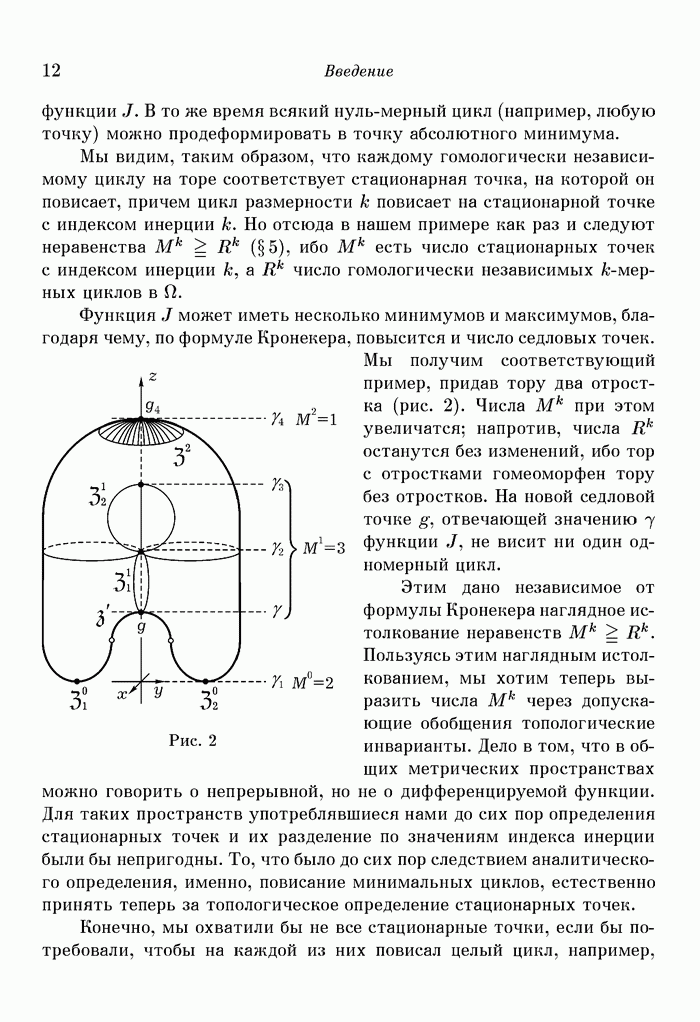
Пусть негомологичный нулю -мерный цикл в Рассмотрим максимум функции на каждом цикле, гомологичном Так как то эти максимумы имеют некоторую нижнюю грань . Нужно показать, что в имеется цикл, гомологичный или, другими словами, что есть нижняя гомологическая грань цикла Цикл из гомологичный заведомо существует, если Мы выберем а столь близким к чтобы в множестве не было никаких стационарных точек, и применим к множеству деформацию теоремы § 16 (стр. 90). Тогда цикл перейдет в некоторый гомологичный ему цикл из . Это доказывает справедливость аксиомы 1.

Пусть теперь гомологичный нулю -мерный цикл в Тогда гомологичен нулю уже в некотором множестве Пусть нижняя грань всех значений а, для которых это имеет место. заведомо не меньше, чем максимум функции на Чтобы убедиться в справедливости аксиомы II, нужно показать, что гомологичен нулю в что есть верхняя гомологическая грань цикла Для доказательства выберем а столь близким к чтобы множество не содержало стационарных точек. Тогда в найдется такая цепь что

Применяя здесь деформацию мы переведем цепь в некоторую цепь из а цикл в некоторый гомологичный ему в цикл При этом

Вместе с соотношением

это даст

что и требовалось доказать.