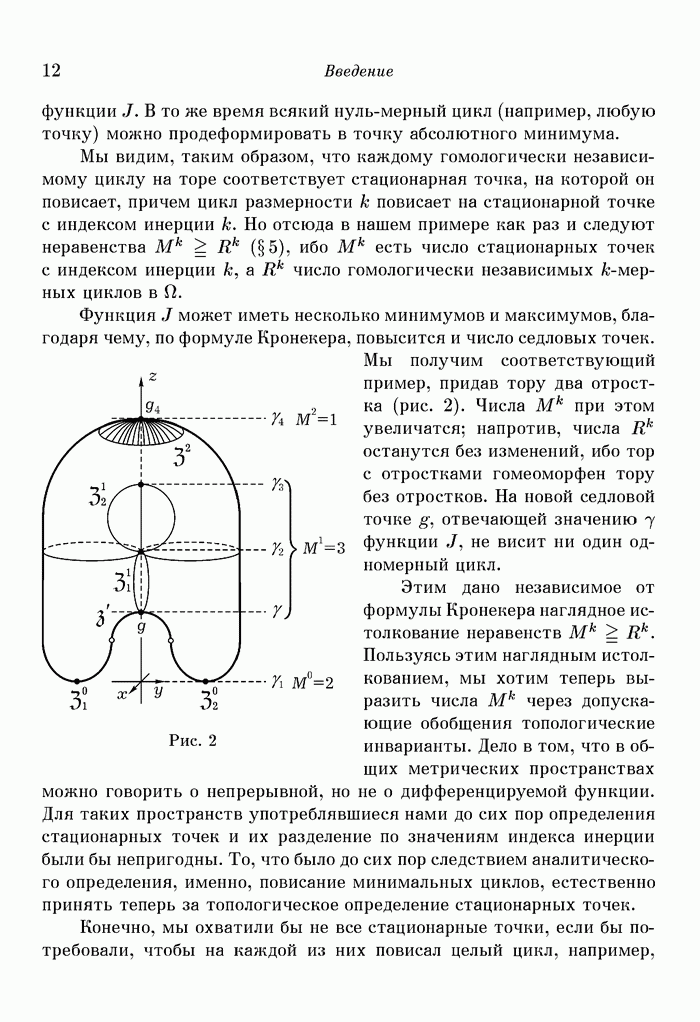
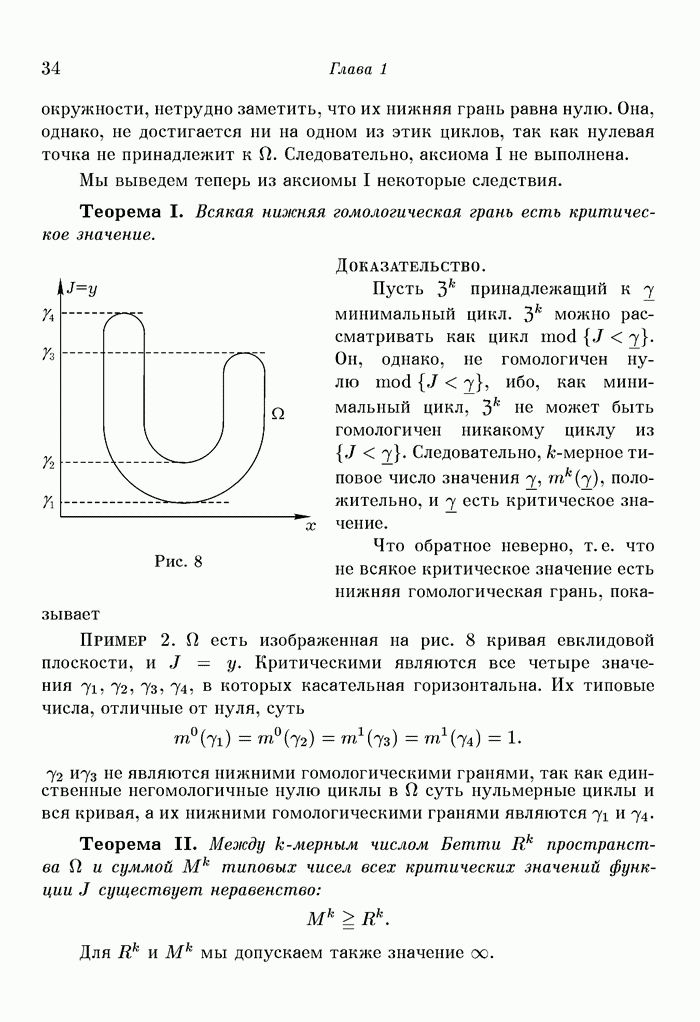
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 19. Основная теорема
Убедившись в том, что аксиомы I и II имеют место, мы можем перенести на функциональное пространство  те соотношении между типовыми числами и числами Бетти, которые были выведены в главе
те соотношении между типовыми числами и числами Бетти, которые были выведены в главе 
Теорема  Если на римановом многообразии
Если на римановом многообразии  существует только конечное число геодезических ограниченной длины, соединяющих две данные точки
существует только конечное число геодезических ограниченной длины, соединяющих две данные точки  то
то

при этом  есть
есть  -мерное число Бетти принадлежащего вариационной проблеме функционального пространства
-мерное число Бетти принадлежащего вариационной проблеме функционального пространства  сумма
сумма  -мерных типовых чисел всех геодезических на
-мерных типовых чисел всех геодезических на  соединяющих А с В, или, что по § 17 то же самое, сумма
соединяющих А с В, или, что по § 17 то же самое, сумма  -мерных типовых чисел всех критических значений функций
-мерных типовых чисел всех критических значений функций  на
на 
Это предположение есть не что иное, как следствие теоремы II § 5 (стр. 34), которая не требует иных предположении, кроме справедливости аксиомы 
В результате применения теоремы § 6 (стр. 37) получается другое предложение, которое в дальнейшем послужит нам для оценки чисел Бетти пространства 
Теорема II. Для того, чтобы в теореме I имел место знак равенства:

достаточно выполнение двух условий:
I. Существует только конечное число геодезических ограниченной длины, соединяющих А с В (что уже предположено в теореме  .
.
II. Все относительные циклы из  допускают дополнение.
допускают дополнение.
Условимся говорить, что  обладает бесконечной связностью, если сумма чисел Бетти всех размерностей бесконечна:
обладает бесконечной связностью, если сумма чисел Бетти всех размерностей бесконечна:

В этой сумме допускаются и бесконечные слагаемые.
Основной результат всех предпринятых нами до сих пор исследований может быть высказан теперь следующим образом:
Теорема III (Основная теорема). Если функциональное пространство вариационной проблемы имеет бесконечную связность, то существует бесконечное множество геодезических, соединяющих А с В.
Доказательство.
Если бы множество геодезических, соединяющих А с В, было конечно, то была бы применима теорема  По теореме II § 14 (стр. 74) каждая геодезическая, ведущая из
По теореме II § 14 (стр. 74) каждая геодезическая, ведущая из  увеличивает сумму
увеличивает сумму 
только на конечное число. Следовательно, эта сумма, а вместе с ней, по теореме I, и сумма  была бы конечна, что противоречит предположению бесконечной связности пространства
была бы конечна, что противоречит предположению бесконечной связности пространства 
| << Предыдущий параграф | Следующий параграф >> |
- От переводчика
- Введение
- Глава 1. Числа Бетти и типовые числа
- § 2. Абсолютные циклы и числа Бетти пространства «омега»
- § 3. Относительные циклы
- § 4. Типовые числа критических значений функции J на «омега»
- § 5. Неравенства между типовыми числами и числами Бетти
- § 6. Условие равенства чисел M^k и R^k
- Глава 2. Типовые числа стационарных точек
- § 8. Невырожденные стационарные точки
- § 9. J-деформация в окрестности стационарной точки
- § 10. Теорема о конечности типовых чисел
- Глава 3. Вариационные проблемы на замкнутых многообразиях
- § 12. Риманово многообразие
- § 13. Функциональное пространство
- § 14. Типовые числа изолированной геодезической
- § 15. Примеры типовых чисел (n-мерная сфера)
- § 16. Деформационные теоремы.
- § 17. Типовые числа критических значений и стационарных точек
- § 18. Действительность аксиом I и II
- § 19. Основная теорема
- § 20. Геодезические с закрепленными концами на n-мерной сфере
- § 21. Инвариантность чисел Бетти функционального пространства «омега»
- § 22. Произвольные граничные многообразия
- Прибавление. Стационарные точки на замкнутых многообразиях
- Примечания