| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 15. Примеры типовых чисел (n-мерная сфера)
Пример 1. Двумерная сфера.
Рассмотрим вариационную проблему геодезических линий на единичной сфере

евклидова пространства с декартовыми координатами  Закрепленными концами
Закрепленными концами  пусть будут точки со сферическим расстоянием
пусть будут точки со сферическим расстоянием

например,

Дуги геодезических, типовые числа которых мы хотим определить, суть дуги больших кругов с длинами:

Прежде всего мы должны установить на сфере элементарную длину  . В качестве
. В качестве  можно, очевидно, взять произвольное положительное число, меньшее чем
можно, очевидно, взять произвольное положительное число, меньшее чем  ; мы выберем какое-нибудь число, заключенное между
; мы выберем какое-нибудь число, заключенное между 
Первый способ. Начнем с дуги  длины Так как
длины Так как  есть вообще кратчайшая кривая, соединяющая
есть вообще кратчайшая кривая, соединяющая  то соответствующая ей точка пространства есть точка минимума функции
то соответствующая ей точка пространства есть точка минимума функции  Следовательно, ее типовые числа суть:
Следовательно, ее типовые числа суть:

Перейдем к следующей дуге  длины
длины  Чтобы ввести промежуточные многообразия, разобьем дугу
Чтобы ввести промежуточные многообразия, разобьем дугу  точками
точками  на три равные части, каждая из которых имеет длину В качестве (одномерных) промежуточных многообразий
на три равные части, каждая из которых имеет длину В качестве (одномерных) промежуточных многообразий  мы выберем отрезки дуг больших кругов, ортогонально пересекающих кривую
мы выберем отрезки дуг больших кругов, ортогонально пересекающих кривую  в точках
в точках  и в качестве гауссовой координаты
и в качестве гауссовой координаты  на
на  декартову координату
декартову координату  которую мы используем также как гауссову координату
которую мы используем также как гауссову координату  на
на  Рассмотрим на
Рассмотрим на  точки с координатами
точки с координатами  Эти точки определяют некоторый элементарный полигон с тремя сторонами, ведущий из
Эти точки определяют некоторый элементарный полигон с тремя сторонами, ведущий из  длина которого
длина которого  равна
равна

Поэтому при  функция
функция  имеет невырожденную стационарную точку с индексом инерции 1, и типовые числа суть:
имеет невырожденную стационарную точку с индексом инерции 1, и типовые числа суть:

Обратимся теперь к общему случаю. Пусть  дуга длины
дуга длины  соединяющая точки
соединяющая точки  Разобьем
Разобьем  на
на  дуг длины
дуг длины  при помощи точек
при помощи точек  и используем в качестве промежуточных многообразий
и используем в качестве промежуточных многообразий  ортогональные к
ортогональные к  отрезки дуг больших кругов, на которых числа
отрезки дуг больших кругов, на которых числа  примем за гауссовы координаты. Тогда длина геодезической ломаной, определенной
примем за гауссовы координаты. Тогда длина геодезической ломаной, определенной  точками этих промежуточных многообразий и соединяющей
точками этих промежуточных многообразий и соединяющей  будет:
будет:

 члены по меньшей мере третьего порядка.
члены по меньшей мере третьего порядка.
Квадратичные члены образуют здесь невырожденную квадратичную форму с индексом инерции  Поэтому типовые числа суть:
Поэтому типовые числа суть:

Второй способ. Мы укажем еще один метод определения типовых чисел, который мы заимствуем у Морса; он обходится вовсе без вычислений.
Мы рассматриваем сразу геодезическую линию  длины
длины  Пусть А есть точка, диаметрально противоположная точке А. Выберем
Пусть А есть точка, диаметрально противоположная точке А. Выберем  постоянных
постоянных  удовлетворяющих неравенствам:
удовлетворяющих неравенствам:

и обозначим через  расположенную на нашей сфере окружность со сферическим радиусом
расположенную на нашей сфере окружность со сферическим радиусом  и центром А! или А, в зависимости от того,
и центром А! или А, в зависимости от того,
нечетно  или четно. Пусть
или четно. Пусть  первая точка, в которой кривая
первая точка, в которой кривая  если перемещаться по ней от а к в, встречает окружность
если перемещаться по ней от а к в, встречает окружность  Дуги, на которые промежуточные точки
Дуги, на которые промежуточные точки  разбивают
разбивают  имеют длины:
имеют длины:

Так как все эти длины меньше  то точки
то точки  могут быть использованы как промежуточные точки на
могут быть использованы как промежуточные точки на  . В качестве промежуточного многообразия
. В качестве промежуточного многообразия  мы воспользуемся достаточно малой окрестностью точки
мы воспользуемся достаточно малой окрестностью точки  на окружности
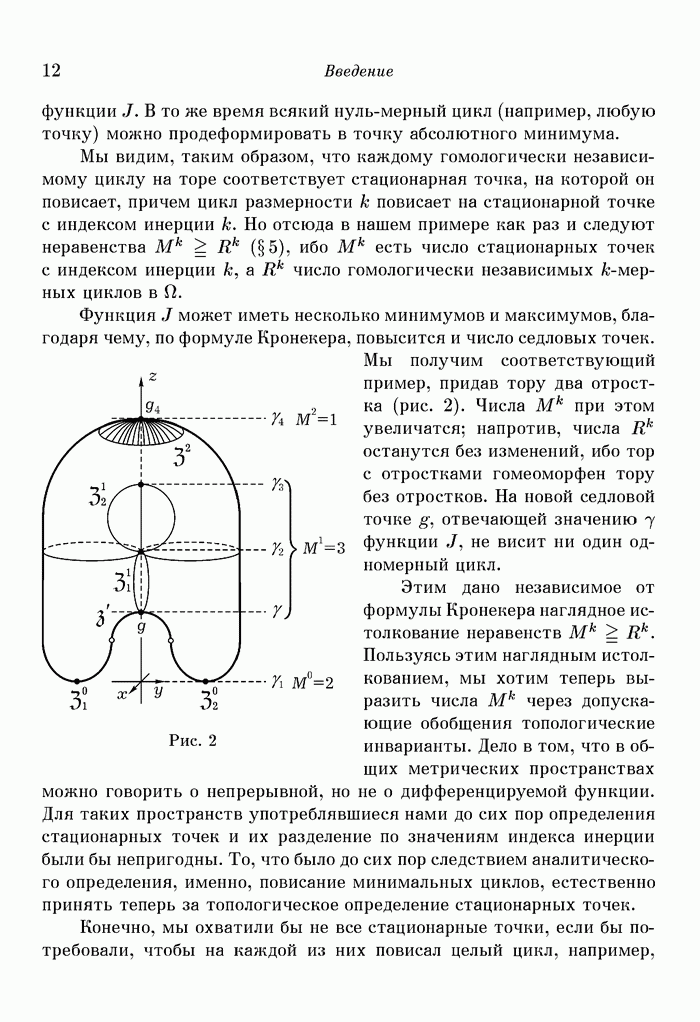
на окружности  На рис.
На рис.  показан случай
показан случай 

Рис. 
Если выбрать теперь на каждой окружности  по одной точке
по одной точке  то этим будет определен элементарный полигон с вершинами:
то этим будет определен элементарный полигон с вершинами:

Длины его сторон, взятых по порядку, не превосходят соответствующих выражений (1). Поэтому длина элементарного полигона (2) не превосходит  Она равна этому числу только в том случае, если
Она равна этому числу только в том случае, если  в чем можно убедиться, проходя элементарный полигон в обратном порядке. Следовательно, функция
в чем можно убедиться, проходя элементарный полигон в обратном порядке. Следовательно, функция  имеет на содержащемся в
имеет на содержащемся в  топологическом произведении
топологическом произведении

(представляющем собой элемент в  -мерном числовом пространстве) изолированный максимум в точке
-мерном числовом пространстве) изолированный максимум в точке  Отсюда следует, по теореме II § 7, что
Отсюда следует, по теореме II § 7, что  -мерное типовое число в точке
-мерное типовое число в точке  равно единице, в то время как все остальные типовые числа равны нулю.
равно единице, в то время как все остальные типовые числа равны нулю.
В качестве негомологичного нулю относительного  -мерного цикла множества
-мерного цикла множества  можно взять само как-либо триангулированное топологическое произведение
можно взять само как-либо триангулированное топологическое произведение  . Сверх того, мы видим,
. Сверх того, мы видим,
что каждый относительный цикл допускает дополнение в смысле § 6 (стр. 36). Именно, дополнение заданного  -мерного цикла есть непрерывный образ в
-мерного цикла есть непрерывный образ в  топологического произведения
топологического произведения

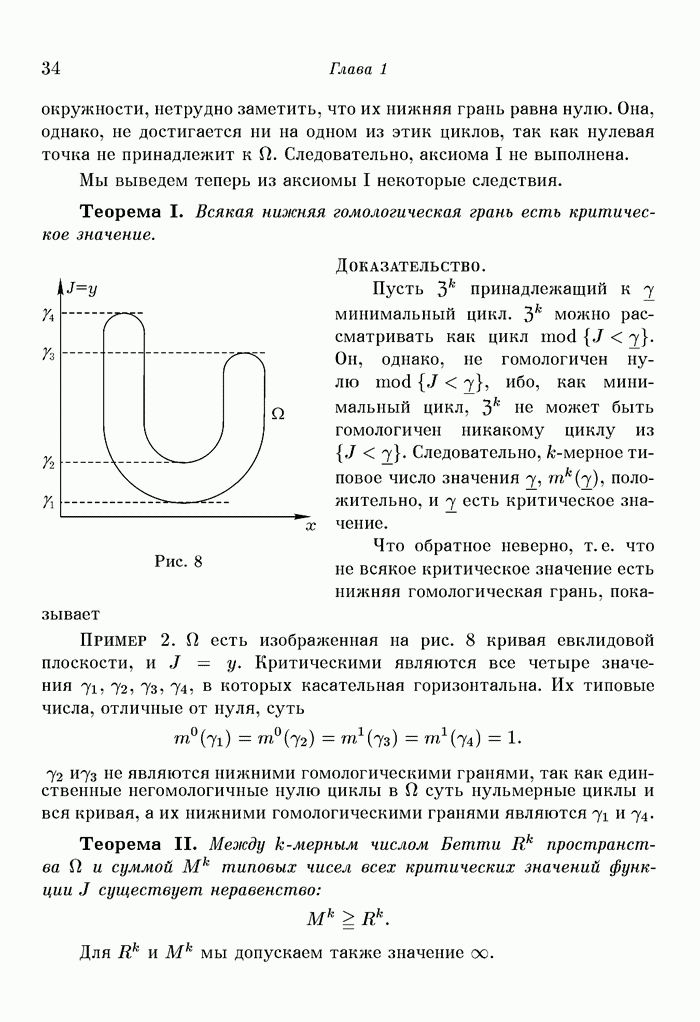
 окружностей), — замечание, которое позже будет нам полезно. Пример
окружностей), — замечание, которое позже будет нам полезно. Пример  -мерная сфера.
-мерная сфера.
Только что использованный метод может быть без существенных изменений применен к решению вариационной проблемы геодезических линий с закрепленными концами на единичной  -мерной сферы.
-мерной сферы.
На месте окружностей  оказываются тогда
оказываются тогда  -мерные сферы. Топологическое произведение окрестностных многообразий получает, таким образом, размерность
-мерные сферы. Топологическое произведение окрестностных многообразий получает, таким образом, размерность  Типовые числа геодезической
Типовые числа геодезической  суть поэтому:
суть поэтому:

Мы считаем нелишним подтвердить этот результат путем перенесения на  -мерный случай также и первого способа примера 1. Пусть
-мерный случай также и первого способа примера 1. Пусть

уравнение  -мерной сферы
-мерной сферы  -мерного евклидова пространства. Пусть координаты закрепленных концов
-мерного евклидова пространства. Пусть координаты закрепленных концов  суть:
суть:

так что их сферическое расстояние равно  Мы начнем с геодезической линии
Мы начнем с геодезической линии  представляющей собой дугу большого круга длины
представляющей собой дугу большого круга длины 
Разобьем  двумя точками
двумя точками  на три дуги, каждая из которых имеет длину и выберем в качестве промежуточных многообразий куски ортогональных к
на три дуги, каждая из которых имеет длину и выберем в качестве промежуточных многообразий куски ортогональных к  больших гиперсфер (размерности
больших гиперсфер (размерности  с гауссовыми координатами:
с гауссовыми координатами:

Соединяющий  элементарный полигон, определенный точками
элементарный полигон, определенный точками

имеет длину:

Чтобы вычислить квадратичные члены тейлоровского разложения функции  в окрестности нулевой точки, нам вовсе не нужно знать функцию
в окрестности нулевой точки, нам вовсе не нужно знать функцию  во всех подробностях; достаточно воспользоваться следующими ее свойствами:
во всех подробностях; достаточно воспользоваться следующими ее свойствами:

Соотношения 2 и 3 очевидны, соотношение 4 следует из того, что при зеркальном отображении евклидова пространства

соединяющий  элементарный полигон, определенный промежуточными точками
элементарный полигон, определенный промежуточными точками

переходит в соединяющий  элементарный полигон, определенный точками
элементарный полигон, определенный точками

и что при этом зеркальном отображении длины остаются неизменными. Из формул 14 следует, что, за исключением производных

которые могут быть вычислены из 1, все производные второго порядка функции  равны нулю. Поэтому тейлоровское разложение функции
равны нулю. Поэтому тейлоровское разложение функции  в окрестности нулевой точки ее
в окрестности нулевой точки ее  аргументов выглядит следующим образом:
аргументов выглядит следующим образом:
 члены не ниже третьего порядка.
члены не ниже третьего порядка.
Вообще, тейлоровское разложение функции  в окрестности геодезическои линии
в окрестности геодезическои линии  длины
длины  имеет вид:
имеет вид: 

При этом предполагается, что  промежуточных многообразий выбраны на равных расстояниях друг от друга, и что локальные координаты установлены на них так же, как в случае двух промежуточных многообразий. Так как квадратичная форма, образованная квадратичными членами этого разложения, невырождена, и ее индекс инерции равен
промежуточных многообразий выбраны на равных расстояниях друг от друга, и что локальные координаты установлены на них так же, как в случае двух промежуточных многообразий. Так как квадратичная форма, образованная квадратичными членами этого разложения, невырождена, и ее индекс инерции равен  то типовые числа суть:
то типовые числа суть:

| << Предыдущий параграф | Следующий параграф >> |
- От переводчика
- Введение
- Глава 1. Числа Бетти и типовые числа
- § 2. Абсолютные циклы и числа Бетти пространства «омега»
- § 3. Относительные циклы
- § 4. Типовые числа критических значений функции J на «омега»
- § 5. Неравенства между типовыми числами и числами Бетти
- § 6. Условие равенства чисел M^k и R^k
- Глава 2. Типовые числа стационарных точек
- § 8. Невырожденные стационарные точки
- § 9. J-деформация в окрестности стационарной точки
- § 10. Теорема о конечности типовых чисел
- Глава 3. Вариационные проблемы на замкнутых многообразиях
- § 12. Риманово многообразие
- § 13. Функциональное пространство
- § 14. Типовые числа изолированной геодезической
- § 15. Примеры типовых чисел (n-мерная сфера)
- § 16. Деформационные теоремы.
- § 17. Типовые числа критических значений и стационарных точек
- § 18. Действительность аксиом I и II
- § 19. Основная теорема
- § 20. Геодезические с закрепленными концами на n-мерной сфере
- § 21. Инвариантность чисел Бетти функционального пространства «омега»
- § 22. Произвольные граничные многообразия
- Прибавление. Стационарные точки на замкнутых многообразиях
- Примечания