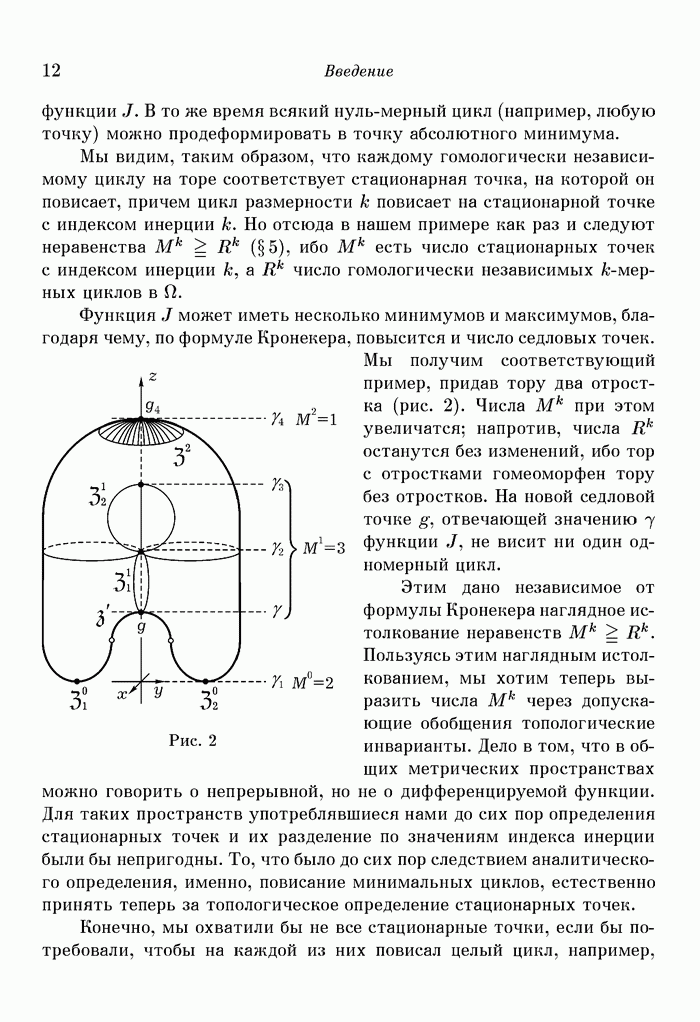
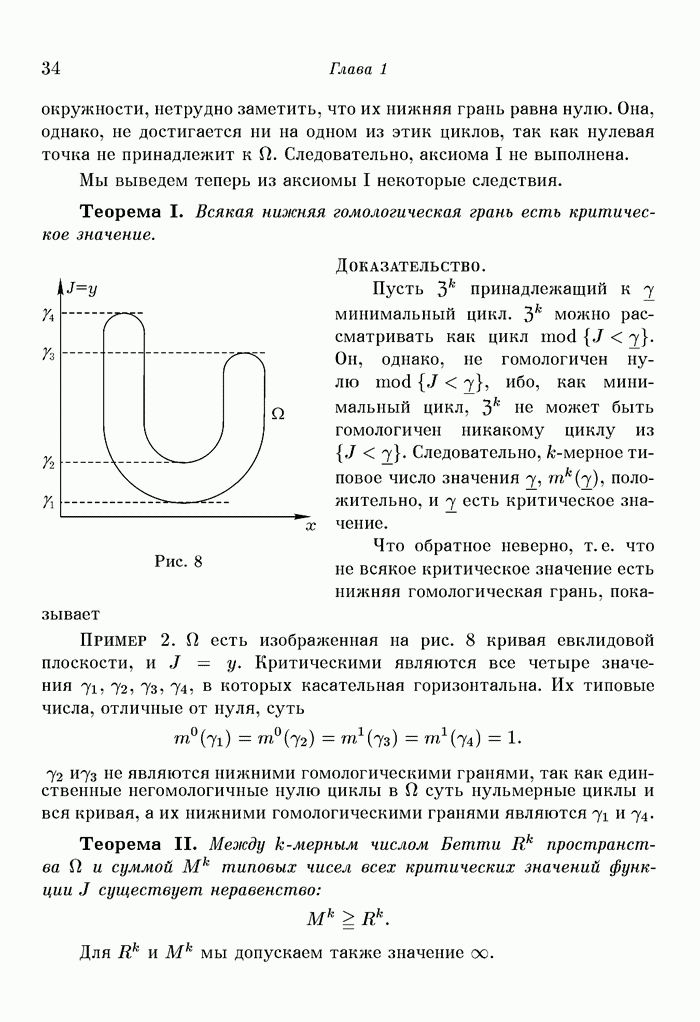
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. Числа Бетти и типовые числа
§ 1. Окрестностное пространство и непрерывное отображение
Напомним те топологические средства, которые существенны для вариационного исчисления в целом.
1. Окрестностное пространство  есть множество элементов, называемых точками, в котором для каждой точки
есть множество элементов, называемых точками, в котором для каждой точки  определены окрестности
определены окрестности

Окрестности суть подмножества множества  удовлетворяющие следующим двум аксиомам:
удовлетворяющие следующим двум аксиомам:
a) Каждая окрестность точки  содержит точку
содержит точку  .
.
b) Каждое множество, содержащее некоторую окрестность точки  также есть окрестность точки
также есть окрестность точки 
2. Этого определения достаточно, чтобы ввести в  понятие непрерывной функции: вещественная функция
понятие непрерывной функции: вещественная функция  непрерывна в точке
непрерывна в точке  пространства
пространства  если для каждого положительного числа
если для каждого положительного числа  существует окрестность точки
существует окрестность точки  в которой
в которой  уклоняется от
уклоняется от  менее чем на
менее чем на  Функция непрерывна на всем пространстве
Функция непрерывна на всем пространстве  если она непрерывна в каждой его точке.
если она непрерывна в каждой его точке.
3. Пусть  другое окрестностное пространство, и каждой точке из
другое окрестностное пространство, и каждой точке из  поставлена в соответствие некоторая точка из
поставлена в соответствие некоторая точка из  (обратное не предполагается). Это отображение
(обратное не предполагается). Это отображение  называется непрерывным в
называется непрерывным в
точке  из
из  если для каждой окрестности
если для каждой окрестности  образа
образа  точки
точки  существует окрестность
существует окрестность  точки
точки  образ которой лежит в
образ которой лежит в  Если отображение непрерывно в каждой точке пространства
Если отображение непрерывно в каждой точке пространства  то оно называется непрерывным отображением
то оно называется непрерывным отображением 
4. В силу изложенного, непрерывная функция может рассматриваться как непрерывное отображение пространства  в числовую прямую, представляющую собой особое окрестностное пространство. Это понятие функции мы должны обобщить на другие окрестностные пространства, отличные от числовой прямой, и на случай нескольких независимых переменных точек. Пусть даны окрестностные пространства
в числовую прямую, представляющую собой особое окрестностное пространство. Это понятие функции мы должны обобщить на другие окрестностные пространства, отличные от числовой прямой, и на случай нескольких независимых переменных точек. Пусть даны окрестностные пространства  и пусть
и пусть  система переменных точек в них. Пусть далее каждой такой «системе аргументов», взятой из некоторой совокупности, соответствует определенная точка у окрестностного пространства
система переменных точек в них. Пусть далее каждой такой «системе аргументов», взятой из некоторой совокупности, соответствует определенная точка у окрестностного пространства  Мы называем тогда у функцией от
Мы называем тогда у функцией от 

Функция непрерывна для системы аргументов  если для каждой окрестности
если для каждой окрестности  существуют окрестности
существуют окрестности  такого рода, что при любом выборе системы
такого рода, что при любом выборе системы  в этих окрестностях, для которой
в этих окрестностях, для которой  вообще определена,
вообще определена,  лежит в
лежит в  Если функция
Если функция  непрерывна для каждой системы аргументов, для которой она определена, то мы говорим также, что точка у непрерывно зависит от точек
непрерывна для каждой системы аргументов, для которой она определена, то мы говорим также, что точка у непрерывно зависит от точек  Позже мы будем иметь дело с известными кривыми на многообразии
Позже мы будем иметь дело с известными кривыми на многообразии  которые явятся «точками» некоторого функционального пространства
которые явятся «точками» некоторого функционального пространства  и значениями функции у, в то время как аргументами будут варьирующиеся на
и значениями функции у, в то время как аргументами будут варьирующиеся на  концы кривых.
концы кривых.
5. Отображение называется топологическим, если оно взаимно-однозначно и взаимно-непрерывно. Два окрестностных пространства, которые могут быть топологически отображены друг на друга, называются гомеоморфными.
6. Любое подмножество  окрестностного пространства
окрестностного пространства  само превращается в окрестностное пространство, если объявить окрестностями
само превращается в окрестностное пространство, если объявить окрестностями  точки
точки  из
из  по отношению к
по отношению к  пересечения всевозможных окрестностей
пересечения всевозможных окрестностей  (и, следовательно, все подмножества
(и, следовательно, все подмножества  содержащие такие окрестности).
содержащие такие окрестности).
7. В главе III мы будем иметь дело с особыми окрестностными пространствами — с метрическими пространствами. Множество «точек» называется метрическим пространством, если между каждыми двумя точками  определено неотрицательное расстояние
определено неотрицательное расстояние  удовлетворяющее следующим аксиомам:
удовлетворяющее следующим аксиомам:
a) Аксиома тождества:  тогда и только тогда, когда
тогда и только тогда, когда 
b) Аксиома симметрии: 
c) Аксиома треугольника: 
Метрическое пространство  становится окрестностным пространством, если принять следующее определение окрестности: множество тогда и только тогда есть окрестность точки
становится окрестностным пространством, если принять следующее определение окрестности: множество тогда и только тогда есть окрестность точки  когда существует такое положительное число
когда существует такое положительное число  что все точки, удаленные от
что все точки, удаленные от  менее чем на
менее чем на  принадлежат этому множеству. В частности, множество точек
принадлежат этому множеству. В частности, множество точек  для которых
для которых  называется сферической окрестностью точки
называется сферической окрестностью точки  точнее, ее (открытой)
точнее, ее (открытой)  -окрестностью. Мы обозначаем эту окрестность через
-окрестностью. Мы обозначаем эту окрестность через

Каждое подмножество метрического пространства есть, очевидно, опять метрическое пространство.
8. Простейшими примерами метрических пространств являются  -мерное евклидово пространство
-мерное евклидово пространство  и его подмножества, например, кривые и поверхности. В под расстоянием двух точек с декартовыми координатами
и его подмножества, например, кривые и поверхности. В под расстоянием двух точек с декартовыми координатами  понимают число
понимают число

В главе III мы должны будем рассматривать также метрические пространства, не гомеоморфные подмножествам эвклидова пространства, например, такие, точками которых являются кривые на многообразиях. Эти пространства значительно отличаются от пространств, привычных нашему наглядному представлению, например, они не компактны в малом, т.е. содержат в сколь угодно малой окрестности точки бесконечные подмножества без предельных точек.
9. Мы хотим теперь определить деформацию некоторого подмножества  окрестностного пространства
окрестностного пространства  Пусть каждой точке
Пусть каждой точке  из
из  и каждому числу
и каждому числу  единичного интервала
единичного интервала 

отнесена некоторая точка  из
из  пусть
пусть  и пусть точка
и пусть точка  непрерывно зависит от
непрерывно зависит от  в смысле
в смысле  Каждой окрестности
Каждой окрестности  отвечают, следовательно, такие окрестности
отвечают, следовательно, такие окрестности  что принадлежит к
что принадлежит к  всякий раз, как
всякий раз, как  лежит в
лежит в  естественно в
естественно в 
Пусть  множество всех точек
множество всех точек  отвечающих всем
отвечающих всем  из
из  и всем
и всем  из и
из и  множество точек
множество точек  Тогда мы скажем, что
Тогда мы скажем, что  деформируется в
деформируется в  на множестве
на множестве  (а также на каждом множестве, содержащем
(а также на каждом множестве, содержащем  Для каждого
Для каждого  соответствием
соответствием

определяется непрерывное отображение множества  которое, как подмножество пространства
которое, как подмножество пространства  само есть окрестностное пространство, в
само есть окрестностное пространство, в  При этом
При этом  называется параметром деформации. Если это требуется, он может пробегать и другие замкнутые интервалы, отличные от интервала
называется параметром деформации. Если это требуется, он может пробегать и другие замкнутые интервалы, отличные от интервала 
В случае, когда  есть метрическое пространство, определению непрерывной зависимости точки
есть метрическое пространство, определению непрерывной зависимости точки  от
от  целесообразно придать следующую форму: если
целесообразно придать следующую форму: если  последовательность точек из
последовательность точек из  сходящаяся к
сходящаяся к  последовательность значений
последовательность значений  сходящаяся к
сходящаяся к  , то последовательность
, то последовательность  всегда сходится к
всегда сходится к 
10. Далее в метрическом пространстве справедлива теорема, что две деформации, выполненные одна за другой, снова дают деформацию. Точнее: если

деформация  и
и

деформация  в некоторое множество
в некоторое множество  то, полагая
то, полагая

мы получим деформацию  в при которой параметр деформации изменяется от О до
в при которой параметр деформации изменяется от О до 
11. Мы воспользуемся также следующим предложением: если  замкнутые подмножества метрического пространства
замкнутые подмножества метрического пространства  и
и

деформация  а
а

деформация  причем для каждой точки
причем для каждой точки  пересечения
пересечения  и для всех
и для всех 

то соответствия (4) и (5) определяют некоторую деформацию множества 
12. Позже мы будем иметь дело с окрестностными пространствами, на которых определена непрерывная функция  Если для некоторого подмножества
Если для некоторого подмножества  определена деформация
определена деформация  и
и

для всех точек  из
из  при условии, что
при условии, что

то мы говорим об  -деформации множества
-деформации множества  Таким образом, при
Таким образом, при  -деформации значения функции
-деформации значения функции  в точке никогда не возрастают при движении этой точки по пути деформации. Если, например, наше окрестностное пространство есть дважды непрерывно дифференцируемое многообразие, и
в точке никогда не возрастают при движении этой точки по пути деформации. Если, например, наше окрестностное пространство есть дважды непрерывно дифференцируемое многообразие, и  дважды непрерывно дифференцируемая функция на нем, то деформация, при которой точки скользят вниз по ортогональным траекториям (§ 9) функции
дважды непрерывно дифференцируемая функция на нем, то деформация, при которой точки скользят вниз по ортогональным траекториям (§ 9) функции  есть
есть  -деформация.
-деформация.
| << Предыдущий параграф | Следующий параграф >> |
- От переводчика
- Введение
- Глава 1. Числа Бетти и типовые числа
- § 2. Абсолютные циклы и числа Бетти пространства «омега»
- § 3. Относительные циклы
- § 4. Типовые числа критических значений функции J на «омега»
- § 5. Неравенства между типовыми числами и числами Бетти
- § 6. Условие равенства чисел M^k и R^k
- Глава 2. Типовые числа стационарных точек
- § 8. Невырожденные стационарные точки
- § 9. J-деформация в окрестности стационарной точки
- § 10. Теорема о конечности типовых чисел
- Глава 3. Вариационные проблемы на замкнутых многообразиях
- § 12. Риманово многообразие
- § 13. Функциональное пространство
- § 14. Типовые числа изолированной геодезической
- § 15. Примеры типовых чисел (n-мерная сфера)
- § 16. Деформационные теоремы.
- § 17. Типовые числа критических значений и стационарных точек
- § 18. Действительность аксиом I и II
- § 19. Основная теорема
- § 20. Геодезические с закрепленными концами на n-мерной сфере
- § 21. Инвариантность чисел Бетти функционального пространства «омега»
- § 22. Произвольные граничные многообразия
- Прибавление. Стационарные точки на замкнутых многообразиях
- Примечания