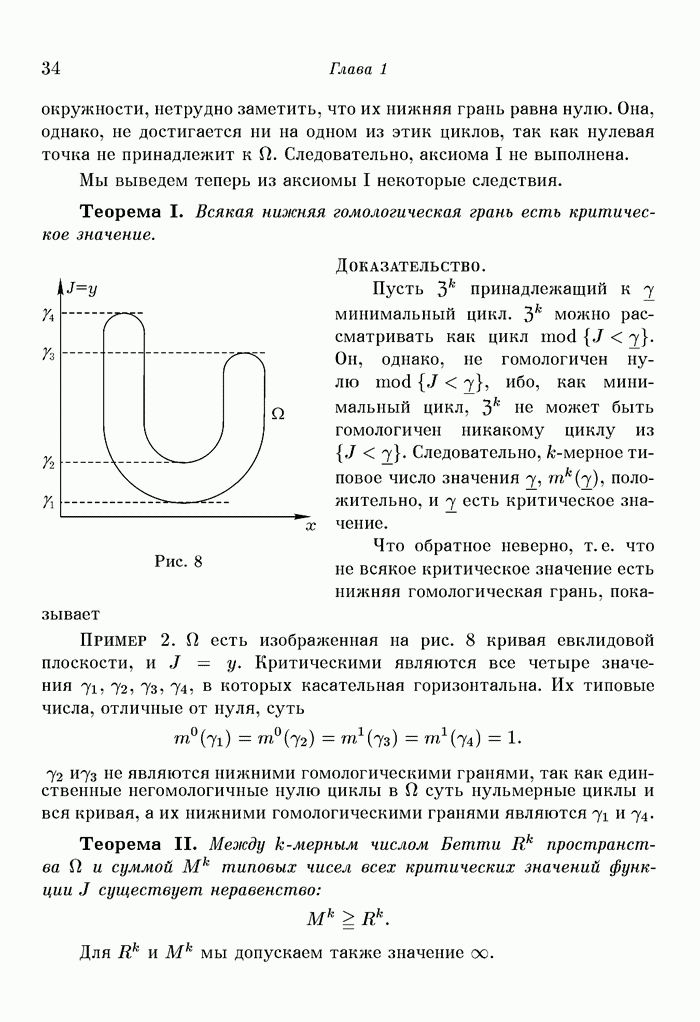
Введение

Вариационное исчисление в малом имеет дело с непосредственной окрестностью экстремали. Одной из его задач является, например, установление необходимых и достаточных условий для того, чтобы экстремаль, по сравнению с известными соседними кривыми, давала минимум. Вариационное исчисление в целом рассматривает все многообразие на котором дана вариационная проблема. Пусть, например, есть поверхность связности сферы с некоторой римановой метрикой. Тогда ищутся все геодезические, соединяющие две данные точки

Идея Морса, ведущая к решению этой и других проблем вариационного исчисления в целом, состоит в следующем. Рассмотрим всевозможные кусочно-гладкие кривые, которые могут быть проведены на из (§ 12). Они образуют, при соответствующем определении расстояния между двумя кривыми некоторое метрическое пространство, функциональное пространство вариационной проблемы. Длина кривой представляет собой непрерывную функцию на Геодезическим линиям многообразия отвечают такие точки в в которых имеет «стационарное» значение Так мы приходим к следующей задаче: в метрическом пространстве дана непрерывная функция требуется определить стационарные точки этой функции и привести их род и число в связь с топологической структурой

Что такая связь существует, не так уже трудно усмотреть. В особенно простых случаях она давно известна; например, когда пространство есть замкнутая поверхность рода дважды непрерывно дифференцируемая функция на этой поверхности. Под стационарными точками понимаются в этом случае этакие точки поверхности, в которых все частные производные первого порядка по локальным координатам равны нулю.

Остановимся несколько на поверхностях. Мы еще упростим нашу проблему, предположив, что стационарные точки невырождены т.е. что квадратичная форма, образованная квадратичными членами

тейлоровского разложения функции по локальным координатам, невырождена. Тогда, в соответствии с возможными значениями индекса инерции, можно различить три рода стационарных точек. Если локальные координаты в стационарной точке, которую мы будем считать их нулевой точкой, и если квадратичная форма приведена к нормальной форме, то эти три случая суть:

Три введенные здесь числа не являются независимыми друг от друга. Они связаны с эйлеровой характеристикой поверхности кронекеровской формулой:

Мы знаем, что ибо на замкнутой поверхности имеется по крайней мере один минимум и один максимум. Поэтому формула Кронекера учит, что существует по меньшей мере седловых точек. Таким образом,

Поясним эти соотношения на примере тора, представленного как поверхность вращения окружности (рис. 1). Пусть ось вращения есть ось т.е. есть высота над плоскостью Тогда имеются четыре горизонтальные касательные плоскости, соответствующие четырем стационарным точкам: минимуму, нижней седловой точке, верхней седловой точке и максимуму. Пусть принимает в них значения . Все стационарные точки здесь невырождены. Род тора равен единице: Три соотношения (2) действительно имеют место, и притом со знаками равенства.

Неравенства (2) показывают, что в случае замкнутых поверхностей топологическая структура метрического пространства определяет нижние границы для чисел стационарных точек. Это и есть те неравенства, которые мы хотим перенести на произвольные метрические пространства. Мы начнем с того, что придадим им несколько иной вид, более пригодный для обобщения.

С этой целью вспомним подобное формуле Кронекера (1) соотношение между числами Бетти по модулю есть число Бетти размерности к) нашей поверхности и ее эйлеровой характеристикой:

Под -мерным числом Бетти понимается при этом, как известно, максимальное число гомологически независимых -мерных циклов в Не входя здесь в точное определение гомологически независимых циклов, мы заметим только, что к одномерным циклам принадлежат замкнутые кривые и системы таких кривых, к двумерным — замкнутые поверхности, и что -мерный цикл во всяком случае гомологичен нулю или «гомологически не независим», если его можно стянуть на в одну точку. Далее, два -мерных цикла во всяком случае гомологически зависимы, если их можно перевести друг в друга деформацией, или, более общим образом, если они ограничивают -мер-ную часть пространства Так, нульмерное число Бетти поверхности рода равно единице, существует один единственный гомологически независимый нульмерный цикл, который состоит из одной единственной точки; всякая другая точка может быть в него продеформирована. Одномерное число Бетти поверхности рода равно в качестве гомологически независимых одномерных циклов могут быть

Рис. 1

использованы циклических сечений канонической системы разрезов поверхности. Наконец, единственный двумерный цикл есть сама поверхность. Этот цикл гомологически независим, так как не ограничивает на поверхности никакого трехмерного образа.

Поэтому из (2) следуют неравенства Морса:

Мы вывели эти неравенства, несколько искусственно, из формулы Кронекера. Теперь мы хотим подтвердить их, не обращаясь к формуле Кронекера. При этом сейчас же окажется, что в более общих случаях, чем случай поверхностей, левые части неравенств (4), т.е. род и число стационарных точек, определяются топологически. Правые части числа Бетти, уже являются топологическими инвариантами, которые для любых метрических пространств могут быть определены так же, как для поверхностей.

Для ориентации в этих вопросах нам снова послужит тор. Рассмотрим на нем некоторый негомологичный нулю и потому не стягиваемый в точку одномерный цикл, например, меридиан (рис. 1). На каждом гомологичном ему цикле, в частности, на каждом цикле, который может быть получен из него деформацией, мы рассмотрим максимум функции Из этих циклов мы выберем тот, для которого максимум является наименьшим, например, меридиан на рис. 1. Этот цикл не гомологичен никакому нижележащему циклу. Мы называем его поэтому минимальным циклом

Минимальный цикл всегда проходит через стационарную точку. Действительно, в окрестности всякой нестационарной точки ортогональные траектории функции образуют «параллельное расслоение» поверхности; поэтому всякий одномерный цикл, не содержащий стационарных точек, может быть продеформирован вдоль ортогональных траекторий в другой, лежащий еще ниже, цикл, т.е. не является минимальным. При более точном рассмотрении обнаруживается, что одномерный минимальный цикл повисает наседловой точке, так как очевидно, что с точки максимума функции его всегда можно стянуть, а точка минимума не может быть точкой максимума негомологичного нулю одномерного цикла.

Например, минимальный цикл меридианов проходит через нижнюю седловую точку. Напротив, параллели повисают на верхней седловой точке. Единственный двумерный цикл висит на точке максимума

функции . В то же время всякий нуль-мерный цикл (например, любую точку) можно продеформировать в точку абсолютного минимума.

Мы видим, таким образом, что каждому гомологически независимому циклу на торе соответствует стационарная точка, на которой он повисает, причем цикл размерности к повисает на стационарной точке с индексом инерции k. Но отсюда в нашем примере как раз и следуют неравенства ибо есть число стационарных точек с индексом инерции число гомологически независимых -мерных циклов в

Функция может иметь несколько минимумов и максимумов, благодаря чему, по формуле Кронекера, повысится и число седловых точек.

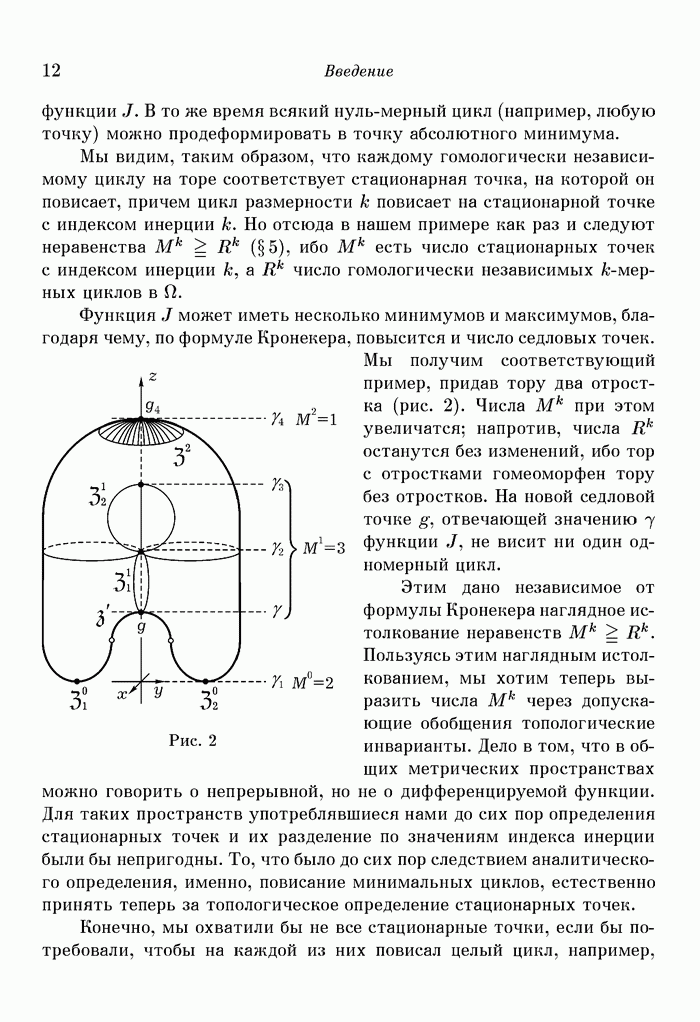
Мы получим соответствующий пример, придав тору два отростка (рис. 2). Числа при этом увеличатся; напротив, числа останутся без изменений, ибо тор с отростками гомеоморфен тору без отростков. На новой седловой точке отвечающей значению 7 функции не висит ни один одномерный цикл.

Рис. 2

Этим дано независимое от формулы Кронекера наглядное истолкование неравенств Пользуясь этим наглядным истолкованием, мы хотим теперь выразить числа через допускающие обобщения топологические инварианты. Дело в том, что в общих метрических пространствах можно говорить о непрерывной, но не о дифференцируемой функции. Для таких пространств употреблявшиеся нами до сих пор определения стационарных точек и их разделение по значениям индекса инерции были бы непригодны. То, что было до сих пор следствием аналитического определения, именно, повисание минимальных циклов, естественно принять теперь за топологическое определение стационарных точек.

Конечно, мы охватили бы не все стационарные точки, если бы потребовали, чтобы на каждой из них повисал целый цикл, например,

мы упустили бы нижнюю седловую точку тора с отростками (рис. 2). Так как свойство точки быть стационарной есть локальное свойство, то мы должны ограничиться достаточно малыми участками циклов. Например, на нижней седловой точке висит небольшая часть одномерного цикла (жирно обозначенная на рис. 2), мы можем сказать также: одномерная цепь, которая, если не считать ее самой верхней точки целиком лежит в области меньших значений функции по отношению к значению 7 этой функции в точке Мы выражаем это также следующим образом: одномерная цепь лежит в множестве а ее граница в множестве Такая одномерная цепь называется в топологии относительным одномерным циклом множества Это обозначение находится в полном согласии с обычной математической терминологией: относительный цикл определен лишь с точностью до своих частей, целиком лежащих в области меньших значении.

Заметим теперь, что если закрепить границу нашей одномерной цепи, то ее нельзя продеформировать в другую цепь, целиком лежащую в области меньших значений. В множестве вообще нет ни одной одномерной цепи, гомологичной нашей цепи. Этот факт выражают, говоря, что наш относительный одномерный цикл негомологичен нулю

Нечто аналогичное имеет место и для максимума. Относительным одномерным циклом является там дуга кривой, проходящей через точку максимума. Теперь, однако, эта дуга, также и при закрепленных концах, деформируема в другую, лежащую в области меньших значений, и потому гомологична нулю Зато теперь часть поверхности, содержащая точку максимума внутри, например, заштрихованная на рис. 2, есть относительный двумерный цикл множества негомологичный нулю Наконец, в точке минимума имеется только один относительный нульмерный цикл: сама точка минимума, и этот цикл негомологичен нулю.

Тем самым мы научились различать типы стационарных точек при помощи топологических инвариантов. Для всякой невырожденной стационарной точки с индексом инерции существует относительный гомологически независимый цикл размерности Индекс инерции стационарной точки, определение которого основано на предположении дифференцируемости функции мы можем заменить теперь допускающими топологическое определение типовыми числами

размерностей -мерное типовое число тк стационарной точки в которой функция принимает значение 7, есть максимальное число гомологически независимых -мерных циклов множества

Например, одномерное типовое число седловой точки равно единице, все остальные равны нулю. Действительно, существует в точности один гомологически независимый относительный одномерный цикл множества но ни одного нульмерного и ни одного двумерного. Негомологичных нулю относительных циклов размерности выше двух не существует и подавно; поэтому все типовые числа старших размерностей также равны нулю. Число удовлетворяющее неравенству есть сумма -мерных типовых чисел, распространенная на все стационарные точки:

Заметим сейчас же, что эта топологическая классификация стационарных точек при помощи типовых чисел не дает ничего нового по сравнению с их классификацией при помощи индексов инерции, пока речь идет о невырожденных стационарных точках дважды непрерывно дифференцируемой функции на многообразии. В самом деле, в этом случае типовые числа тк определяются индексом инерции по формуле:

(§8). Однако, топологическое определение типовых чисел действует в следующих трех случаях, в которых аналитический метод отказывает:

I. Когда стационарная точка вырождена. Известно, насколько запутанным может быть поведение даже аналитической функции в окрестности стационарной точки, если не сделаны никакие предположения о коэффициентах, с которых начинается ее разложение. Простой пример вырожденной стационарной точки дает обезьянье седло, имеющее, как известно, в задней части вырез для обезьяньего хвоста, — седловая точка, в которой сходятся три впадины; его одномерное типовое число Как значительный результат, который получается с помощью типовых чисел, упомянем здесь формулы Морса,

представляющие собой точный аналог формулы Кронекера для дважды непрерывно дифференцируемой функции на -мерном замкнутом многообразии Мы рассмотрим их в прибавлении.

II. Когда стационарные точки не изолированы. Рассмотрим, например, единичную сферу пространства и на ней функцию При т.е. в плоскости она имеет абсолютный минимум. Поэтому вся экваториальная окружность стационарна. Определение типовых чисел может быть, если это нужно, перенесено и на такие стационарные множества.

III. Топологическое введение типовых чисел делает прежде всего возможным исследование стационарных точек в любых метрических пространствах. С помощью типовых чисел удается оценить числа геодезических в проблемах вариационного исчисления в целом. Как производится эта оценка, мы и хотим теперь показать.

Вернемся к упомянутому в самом начале функциональному пространству нашей вариационной проблемы, т.е. к метрическому пространству всех кусочно-гладких кривых, соединяющих две фиксированные точки нашего, снабженного римановой метрикой, многообразия Длина лежащей на кривой есть непрерывная функция на Мы будем понимать теперь под стационарными точками функции на те точки, которые соответствуют геодезическим, ведущим из Таким образом, мы не пользуемся здесь типовыми числами для определения стационарных точек; мы воспользуемся ими для классификации стационарных точек Мы предполагаем, что между существует только конечное число геодезических ограниченной длины.

Пусть одна из этих геодезических. Обозначим через также соответствующую ей точку пространства Пусть длина кривой Рассмотрим в всевозможные относительные -мерные циклы множества

Максимальное число гомологически независимых среди них называется -мерным типовым числом тк геодезической

Если теперь опять обозначить через сумму всех -мерных типовых чисел тк, распространенную на все геодезические, соединяющие А с В, то и в функциональном пространстве будет иметь место неравенство

Далее, справедлива теорема о конечности типовых чисел (II, § 14, стр. 68), в силу которой каждая геодезическая увеличивает лишь на конечное число. Точнее: все типовые числа изолированной геодезической конечны, и среди них имеется только конечное число отличных от нуля.

Но отсюда при некоторых обстоятельствах получается оценка для числа геодезических, соединяющих А с В, именно, в том случае, когда функциональное пространство имеет бесконечную связность т.е. когда сумма чисел Бетти всех размерностей бесконечна. Тогда с необходимостью должно существовать бесконечное множество геодезических.

Таким образом, в конце концов вопрос сводится к определению чисел Бетти функционального пространства нашей вариационной проблемы. Общего метода их вычисления не существует. Однако иногда удается определить их при помощи теоремы, в силу которой они не зависят от римановой метрики на и положения концов (§ ). Тем самым мы получаем возможность выбирать метрику и концы удобным образом. Но и после этого числа Бетти определяются не непосредственно: сначала мы убеждаемся в том, что при нашем специальном выборе выполняется некоторое условие (§ 6), достаточное для того, чтобы в неравенстве наступило равенство, и затем определяем при помощи уже доступных вычислению типовых чисел этой специальной вариационной проблемы

Оценка числа геодезических требует поэтому доказательства неравенств теоремы о конечности типовых чисел и определения чисел Бетти Мы начнем наши исследования с неравенств которые докажем при очень общих предположениях.

Так как при этом мы не будем делать никаких предположений о роде стационарных точек и вовсе не будем пользоваться тем, что позже стационарными станут точки пространства соответствующие геодезическим, то мы поведем доказательство неравенств несколько иначе, чем делали это выше на примере тора. Сначала мы введем вовсе не типовые числа стационарных точек пространства а типовые числа критических значений функции Связь между критическими значениями и стационарными точками будет раскрыта только в § 17.