§ 8. Невырожденные стационарные точки

В качестве функции мы рассмотрим теперь квадратичную форму переменных . С точностью до невырожденного линейного преобразования переменных она вполне определяется своим рангом или, если угодно, дефектом ранга и своим индексом инерции Мы ограничимся случаем, когда дефект ранга равен нулю; в этом случае квадратичная форма называется невырожденной. Как известно, соответствующим линейным преобразованием координат квадратичную форму

можно привести к нормальной форме

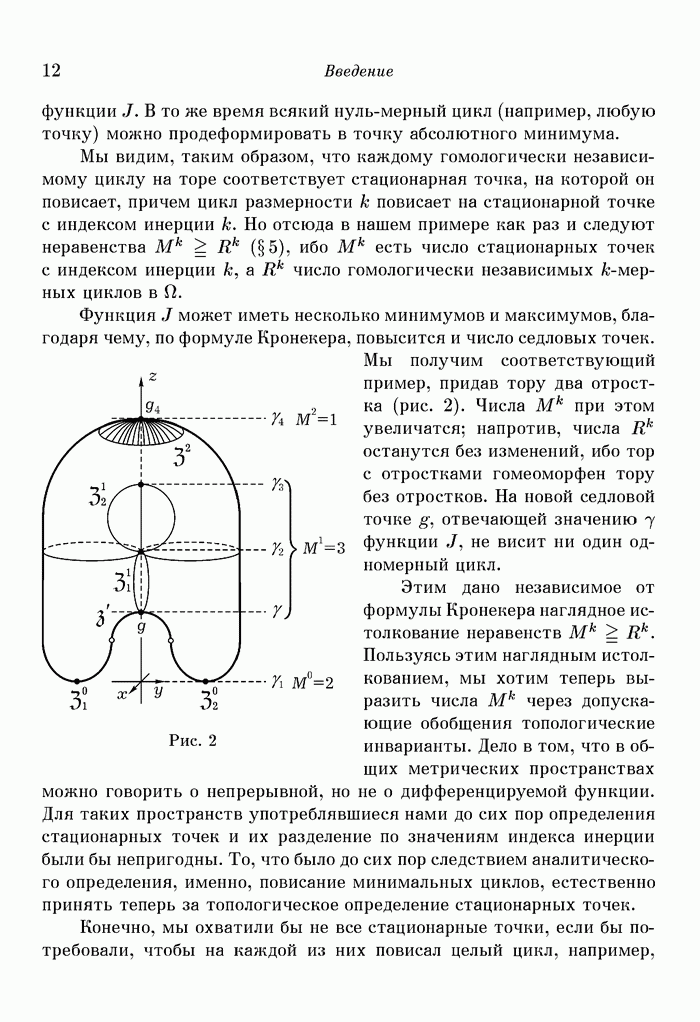
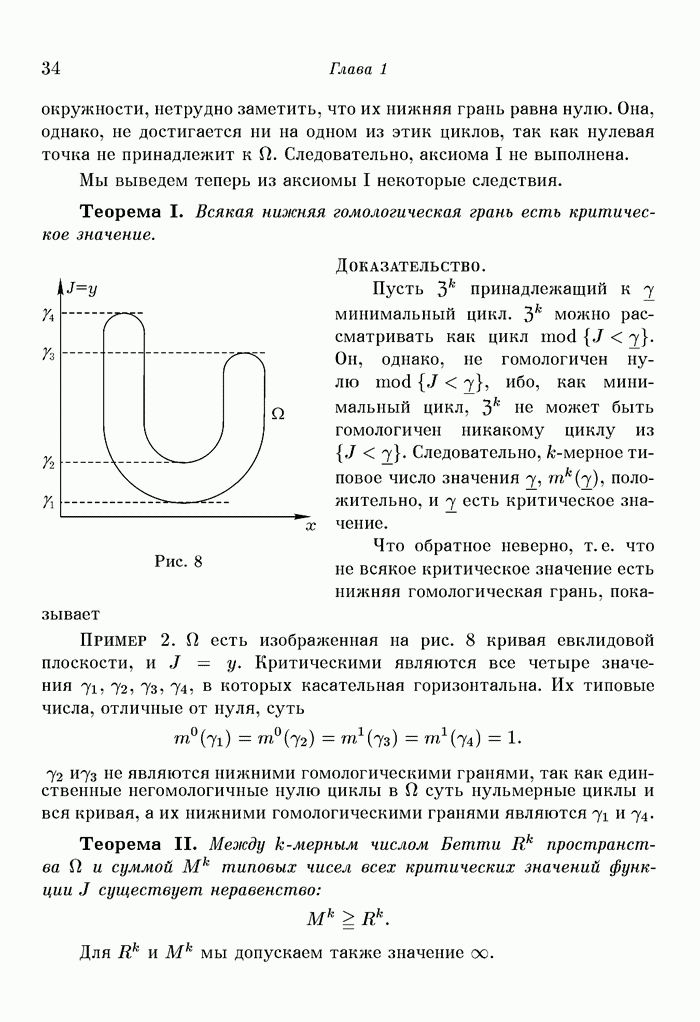
Нулевая точка есть, очевидно, стационарная точка, и притом единственная стационарная точка функции во всем евклидовом пространстве. Мы обозначим ее снова через Чтобы определить ее типовые числа, примем во внимание, что множество может быть стянуто путем деформации на гиперплоскость определяемую равенством Рассмотрим следующий пример:

Здесь внутри нижнего и верхнего конусов, в «промежуточной области». Плоскость есть плоскость (рис. 11).

Чтобы произвести упомянутую деформацию, опустим из каждой точки промежуточной области перпендикуляр на и заставим эту точку перемещаться вдоль него с постоянной скоростью в течение промежутка времени 1 к плоскости Позже (стр. 47,48) мы должны будем рассмотреть другого рода деформацию, приводящую к тому же результату. При этой деформации относительные циклы множества переходят в относительные циклы множества и притом гомологически независимые — в гомологически независимые. Поэтому числа Бетти множества совпадают с числами Бетти множества Но на функция имеет в нулевой точке изолированный максимум. Поэтому, в силу теоремы II (стр. 43), а все остальные типовые числа равны нулю.

Точно так же проводится рассуждение и в случае измерений. Мы сейчас же приведем результат:

Теорема 1. Если невырожденная квадратичная форма переменных с индексом инерции то для типовых чисел стационарной

Рис. 11. Стационарная точка функции

нулевой точки справедлива формула

В случае перед нами изолированный минимум, в случае изолированный максимум; теорема находится, таким образом, в согласии с теоремой II стр. 43.

Теорема 1 может быть перенесена на так называемые невырожденные стационарные точки произвольной дважды непрерывно дифференцируемой функции Стационарная точка такой функции называется невырожденной, если детерминант Гесса

отличен в ней от нуля. Таким образом, тейлоровское разложение функции в окрестности невырожденной стационарной точки, которую мы без ограничения общности можем переместить в нулевую точку и в которой мы можем считать выглядит, после соответствующего преобразования координат, следующим образом:

Здесь

есть квадратическая часть разложения. Число отрицательных квадратов формы называется индексом инерции невырожденной стационарной точки есть дважды непрерывно дифференцируемая функция, обращающаяся в нулевой точке в нуль вместе со своими первыми двумя производными.

Поэтому, вводя сокращенное обозначение

мы будем иметь:

В частности, отсюда следует, что невырожденная стационарная точка изолирована. Действительно, при

Исчезновение этого выражения эквивалентно равенству

из которого, путем возвышения в квадрат и суммирования, мы получаем:

В силу (1), при достаточно малом правая часть заведомо меньше 4, так что равенство не может иметь места. Но это значит, что в достаточной близости нулевой точки нет никаких других стационарных точек.

Чтобы определить типовые числа нулевой точки рассмотрим множество состоящее из тех точек некоторой сферической окрестности 11 точки в которых и самой точки Мы покажем, что если окрестность 11 достаточно мала, то существует деформация, переводящая множество внутрь -мерной гиперплоскости и притом так, что в процессе деформации точки гиперплоскости остаются неподвижными, а точки множества не выходят за пределы этого множества. Отсюда, в точности так же, как в случае квадратичных форм, будет следовать

Теорема II. Типовые числа невырожденной стационарной точки с индексом инерции суть

Чтобы построить названную деформацию, введем функцию

которая определена всюду, кроме нулевой точки, и значения которой лежат в интервале Семейство

есть семейство гиперконусов с вершинами в нулевой точке, в котором значению отвечает гиперконус

Сначала мы покажем, что ортогональные траектории функции т. е. ортогональные траектории семейства гиперконусов, суть четверти окружностей, соединяющие точки -мерной гиперплоскости с точками -мерной гиперплоскости Пусть а — единичный вектор второй, и единичный вектор первой гиперплоскости; тогда каждый вектор, лежащий в плоскости, натянутой на может быть представлен в виде где а и (5 вещественные числа. Приложенный к концу этого вектора вектор имеет компоненты

и, следовательно, лежит в плоскости, натянутой на Так как, с другой стороны, ортогонален к гиперконусу проходящему через его начало, то ортогональные траектории суть одновременно плоские и сферические кривые, т. е. дуги окружностей, и притом, очевидно, четверти окружностей указанного вида.

Предположим теперь, что лежит в интервале и выберем сферическую окрестность 11 нулевой точки столь малой, чтобы в 11 имело место неравенство

что, в силу (2.6), возможно. Тогда в

так что лежит целиком в области Путем дальнейшего, если это необходимо, уменьшения окрестности 11 мы можем добиться того, чтобы вдоль проходящих в 11 ортогональных траекторий функции для функция монотонно убывала, т. е. чтобы имело место неравенство:

В самом деле,

Но так как то последний же член, в силу (1), путем уменьшения окрестности И может быть сделан сколь угодно малым, так что в достаточно малой окрестности Если 11 такая окрестность, то, в силу (2) и (3), на каждой проходящей в И ортогональной траектории функции имеется в точности одна точка, в которой Перед этой точкой за нею . В ней в силу (2). Отсюда следует, что если мы будем равномерно стягивать ортогональные траектории функции начиная со значения и кончая значением к их концам, то этим будет определена деформация с нужными нам свойствами. Тем самым доказательство теоремы II доведено до конца.