§ 4. Типовые числа критических значений функции J на «омега»

Мы подходим теперь к главному предмету нашего исследования. Пусть в окрестностном пространстве О задана непрерывная функция Под

где а произвольное значение мы понимаем множество всех точек из О, в которых Это множество называется областью меньших значений функции относительно а. Соответствующий смысл имеют и такие символы, как

Мы рассматриваем лежащие в циклы и называем их коротко относительными циклами, принадлежащими значению а. Может случиться, что все они гомологичны нулю Если это так, то а называется обыкновенным значением . В противном случае значение а называется критическим, и максимальное число гомологически независимых -мерных циклов значения а — мы можем сказать также: -мерное число Бетти множества называется -мерным типовым числом значения а:

тк может быть и бесконечным. Обыкновенное значение функции характеризуется, таким образом, тем, что все его типовые числа равны нулю.

Следующие примеры пояснят значение этих понятий.

Рис. 7. Критическое значение (седловая точка) с линиями уровня

Пример 1. Пусть произвольное окрестностное пространство. Если имеет на абсолютный минимум то есть критическое значение. Действительно, множество пусто, и любая точка из есть, очевидно, нульмерный цикл, не гомологичный нулю Поэтому нульмерное типовое число значения наверное, больше нуля. Вообще, типовые числа значения совпадают с числами Бетти множества

Напротив, максимум может не быть критическим значением. Пример: есть замкнутый отрезок оси Все типовые числа максимального значении равны нулю, так как каждый относительный цикл может быть переведен деформацией в область меньших значений.

Пример есть снова произвольное окрестностное пространство, и функция постоянна на Как минимальное

значение, 7 является критическим (пример 1). Относительные циклы совпадают с абсолютными циклами пространства -мерное типовое число — с -мерным числом Бетти пространства

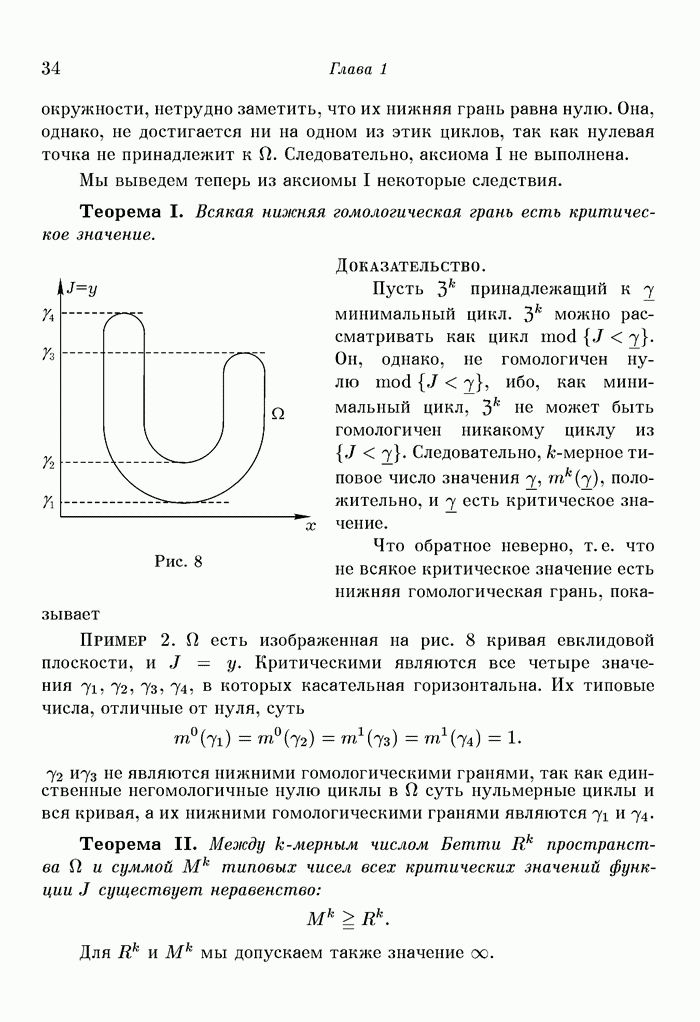
Пример есть эвклидова плоскость и

Все значения являются обыкновенными, ибо всякий относительный цикл, принадлежащий любому значению а, может быть продеформирован при помощи сдвига в направлении отрицательной оси у в область меньших значении и, следовательно, гомологичен нулю в (ср. § 3, абз. 5).

Пример 4. Седловая точка. Пусть снова эвклидова плоскость и

Всякое отличное от нуля значение а есть обыкновенное значение, так как любой принадлежащий ему относительный цикл может быть продеформирован по ортогональным траекториям функции внутрь области меньших значений; ортогональные траектории ортогональны к изображенным на рис. 7 линиям уровня. Напротив, есть критическое значение, ибо отрезок оси есть одномерный цикл в не гомологичный нулю Действительно, множество состоит из двух непересекающихся областей (квадрантов, заштрихованных на рисунке), в силу чего концы отрезка не гомологичны друг другу в

Чтобы определить типовые числа рассмотрим в множестве какой-нибудь цикл Пользуясь ортогональным проектированием на ось мы можем продеформировать его в гомологичный ему относительный цикл Последний мы симплициально аппроксимируем на оси некоторым относительным циклом Но есть -мерный нулевой цикл, откуда следует, что

что же касается цикла то он либо целиком лежит в либо представляет собой отрезок оси содержащий точку внутри. Следовательно,

Наконец,

так как каждый нульмерный симплекс из гомологичен некоторому нульмерному симплексу из

Пример есть окружность Критическими являются значения . Значение является критическим как абсолютный минимум; значение является критическим, так как сама окружность (а также любая ее дуга, содержащая внутри точку есть негомологичный нулю относительный одномерный цикл . В самом деле, окружность, которая является одновременно абсолютным одномерным циклом в О и относительным одномерным циклом не гомологична нулю в себе и, следовательно, негомологична никакому циклу из т.е. не гомологична нулю Поэтому

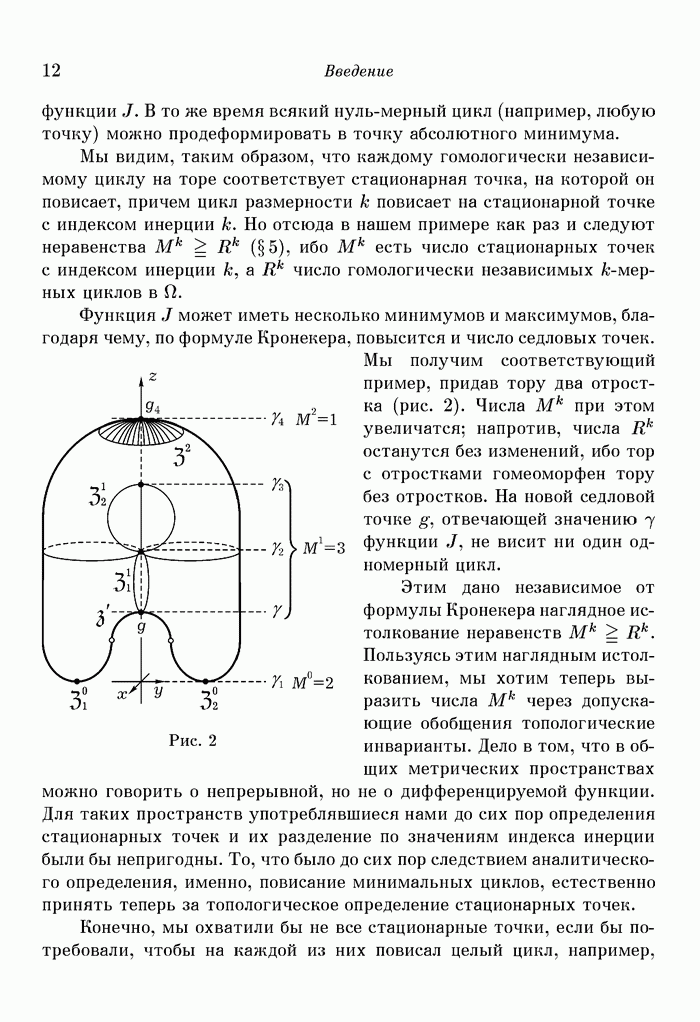
Пример есть тор, расположенный в пространстве как поверхность вращения окружности радиуса 1 вокруг о При этом плоскость есть плоскость симметрии. Пусть

Критическими являются значения (абсолютный минимум) и (абсолютный максимум). Типовые числа значения совпадают с числами Бетти множества (пример 1). Это множество состоит здесь из двух окружностей: наименьшей параллели и наибольшей параллели. Поэтому (§ 2, примеры 1 и 2)

Множество также состоит из двух параллелей: самой нижней и самой верхней. Мы имеем:

Чтобы получить, например, два гомологически независимых относительных двумерных цикла нужно так триангулировать

тор, чтобы наименьшая и наибольшая параллели состояли из одномерных симплексов триангуляции. Тогда обе части, на которые эти параллели разбивают тор, будут относительными двумерными циклами Они гомологически независимы, ибо их сумма есть абсолютный двумерный цикл (именно, весь тор), не гомологичный никакому циклу из