§ 6. Условие равенства чисел M^k и R^k

Мы исследуем теперь тот важный для приложений случай, когда неравенство теоремы II § 5 переходит в равенство:

Мы укажем условия, при которых это равенство заведомо имеет место. Прежде всего, мы потребуем, чтобы выполнялась еще одна аксиома.

Аксиома II. Для каждого гомологичного нулю абсолютного -мерного цикла существует такое число гомологичен нулю в но не гомологичен нулю в

7 называется верхней гомологической гранью цикла

Этой аксиоме можно придать также следующую форму. Рассмотрим максимум функции на некоторой -мерной цепи, натянутой на цикл и затем нижнюю грань таких максимумов. Аксиома II требует, чтобы эта нижняя грань достигалась .

Что аксиома II не является следствием аксиомы I, показывает следующий

Пример есть полукруг , из которого удалена нулевая точка Аксиома I выполнена, так как единственные негомологичные нулю циклы суть нульмерные циклы, и их нижней гомологической гранью является значение Напротив, гомологичный нулю нульмерный цикл, состоящий из точек оси не имеет верхней гомологической грани. Заметим, что в этом примере следовательно, имеет место неравенство

Точно так же аксиома I не является следствием аксиомы II, как что видно из следующею примера:

Пример есть полуинтервал оси Верхняя гомологическая грань совпадает для любого цикла с максимумом, который принимает на этом цикле функция Напротив, аксиома I не выполнена для нульмерных циклов.

Обратимся теперь к нашему второму условию. Пусть некоторый лежащий в цикл Может случиться, что его граница гомологична нулю в Если, в соответствии с этим, есть натянутая на цепь, лежащая в то есть замкнутая цепь, следовательно, абсолютный -мерный цикл. Мы можем сказать, что относительный цикл допускает дополнение в области меньших значений до абсолютного цикла. Если значение а не является критическим, то такое дополнение всегда возможно, ибо в этом случае цикл гомологичен некоторой цепи, лежащей в области меньших значений, и эту цепь мы можем использовать в качестве Однако, если а есть критическое значение, то дополнение может оказаться невозможным, как показывает следующий пример.

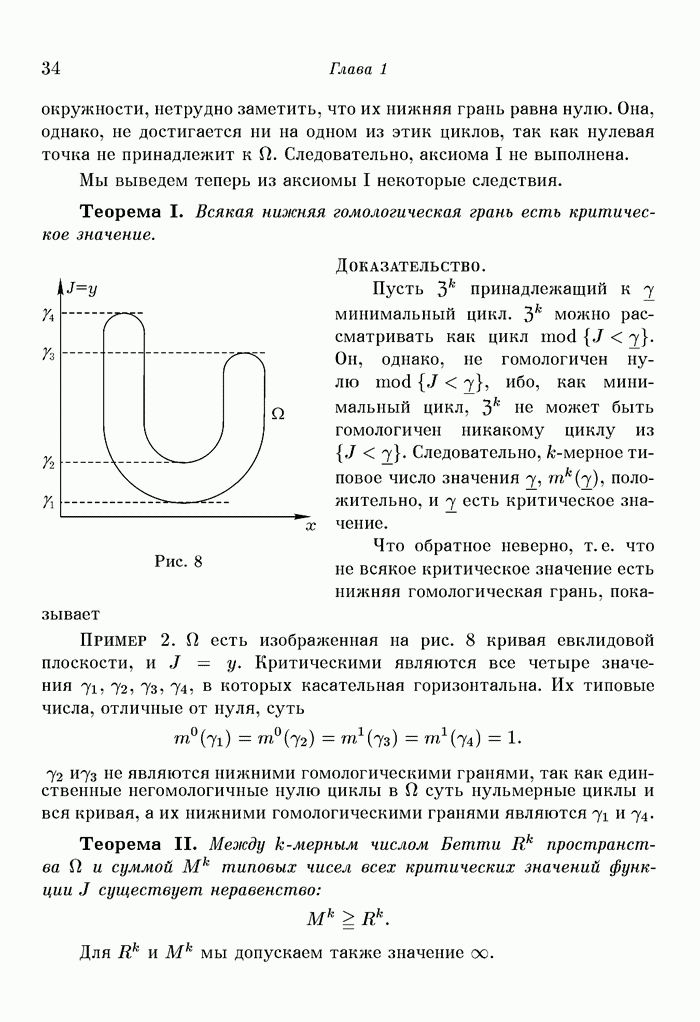
Пример есть полуокружность . Сама полуокружность есть одномерный цикл не допускающий дополнения.

Наше второе условие состоит в том, что для любого значения а функции всякий лежащий в цикл допускает дополнение в области меньших значений

Теорема. Если аксиомы I и II выполнены, и для любого значения а функции все относительные циклы всех размерностей допускают дополнение, то

т. е. -мерное число Бетти пространства равно сумме -мерных типовых чисел, распространенной на все критические значения функции

Эта теорема послужит нам в главе III для вычисления чисел Бетти.

Доказательство.

Пусть означает если конечно, и произвольное натуральное число в противном случае. Тогда существует такая система относительных циклов что есть цикл принадлежащий к критическому значению и циклы принадлежащие одинаковым критическим значениям гомологически независимы По предположению, относительный цикл

может быть дополнен в до абсолютною цикла может случиться, что уже есть абсолютный цикл. Мы утверждаем, что циклы гомологически независимы в Если бы это было не так, то некоторые из этих циклов, скажем, в сумме были бы гомологичны нулю:

Пусть 7 наибольшее из критических значений Выписанное соотношение не может иметь места в так как принадлежащие к 7 циклы системы рассматриваемые как относительные циклы гомологически независимы Следовательно, существующая в силу аксиомы II верхняя гомологическая грань цикла должна быть больше 7. Пусть такая цепь в что

Так как можно дополнить в до абсолютного цикла, то цикл должен был бы быть гомологичен нулю уже в в то время как есть его верхняя гомологическая грань. Из этого противоречия вытекает, что циклы гомологически независимы; следовательно, и потому Вместе с неравенством теоремы II § 5 это дает:

Для иллюстрации теорем § 5 и § 6 нам послужит тор с отростками и без отростков.

Пример 4. Пусть лежащая в пространстве поверхность вращения окружности, с осью в качестве оси вращения, и пусть (рис. 1, стр. 9). Мы имеем четыре критических значения 71, 72, 73, 74, которые соответствуют четырем касательным плоскостям, параллельным плоскости Отличные от нуля значения типовых чисел суть:

Принадлежащие к ним относительные циклы суть соответственно: точка 3°, меридиан параллель и сама как либо триангулированная поверхность Эти относительные циклы являются одновременно абсолютными циклами, и притом минимальными циклами. Так как

аксиомы I и II и условие дополнимости выполнены, то применима теорема этого параграфа. И действительно:

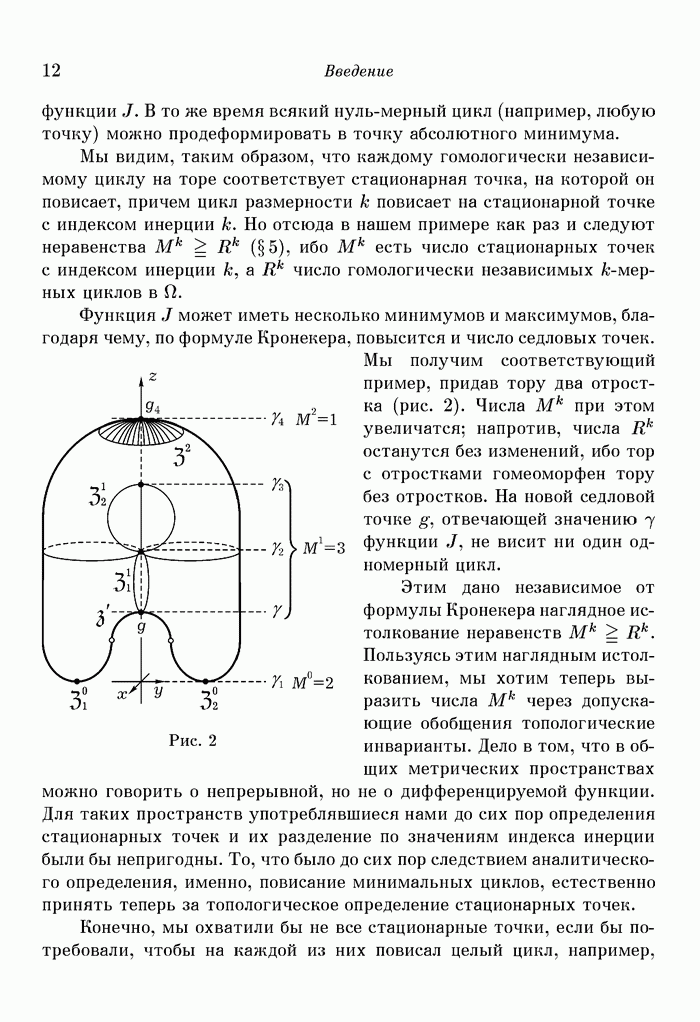
Пример 5. Мы изменим предыдущий пример, присоединив к поверхности два отростка, схематически показанные на рис. 2 стр. 12. Теперь имеются критические значения 71 (минимум), 71, 72, 73, 74 (максимум). Соответствующие гомологически независимые относительные циклы суть:

для обе точки ,

для сечение поверхности плоскостью в окрестности седловой точки (жирная линия на рис. 2),

для меридиан для параллель

для триангулированная поверхность или изображенная на рисунке шапка.

Аксиомы I и II выполнены. Напротив, условие дополнимости нарушено для относительного цикла Вследствие этого числа больше соответствующих чисел Бетти. Именно,

Задача. Функция

есть регулярная аналитическая функция в евклидовом пространстве, какой бы знак, или мы ни взяли, есть критическое значение. Требуется отыскать принадлежащие ему гомологически независимые относительные циклы и типовые числа и исследовать относительные циклы на дополнимость.