Глава 2. Типовые числа стационарных точек

До сих пор мы имели дело с типовыми числами критических значений непрерывной функции в окрестностном пространстве VI. Это были рассмотрения в целом; они распространялись на все множество, на котором принимает критическое значение. Следующий шаг, который мы должны сделать, есть изучение окрестности отдельной точки. К нему мы теперь и обратимся. При этом многое изменится. Вместо произвольного окрестностного пространства мы положим в основу евклидово пространство Вместо того, чтобы предполагать функцию просто непрерывной, мы предположим ее дважды непрерывно дифференцируемой. Вместо критических значений функции мы будем рассматривать теперь стационарные точки в

§ 7. Определение типовых чисел стационарных точек

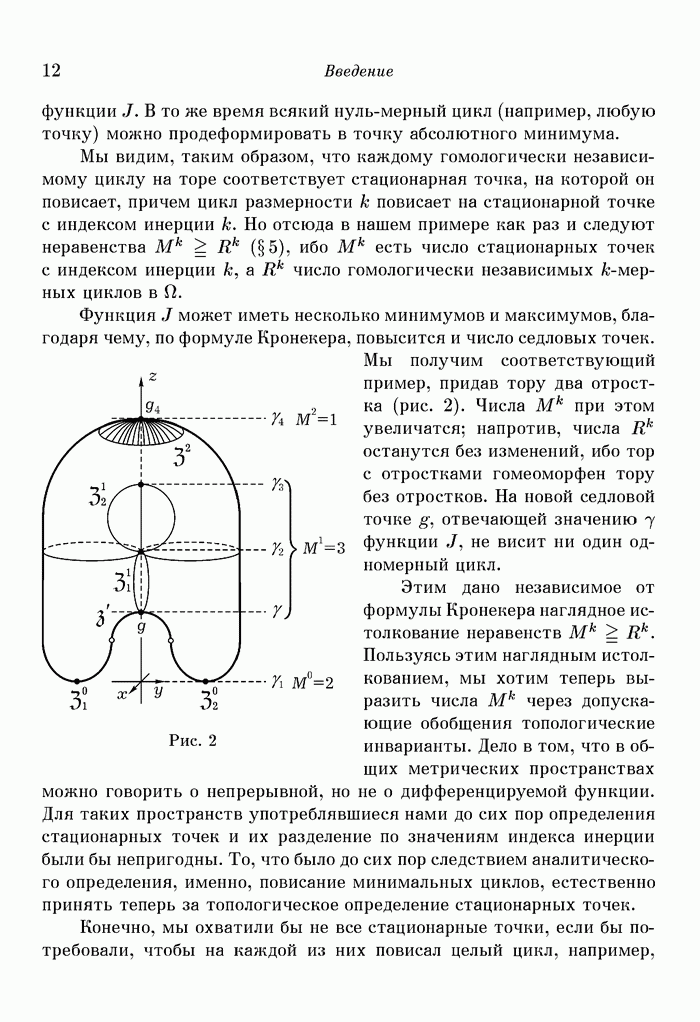
Пусть в некоторой области эвклидова пространства с декартовыми координатами задана дважды непрерывно дифференцируемая функция Если нет оснований опасаться недоразумений, то вместо мы будем писать сокращенно

Под стационарной точкой пространства мы понимаем точку, в которой исчезают все частные производные первого порядка функции

В дальнейшем мы исследуем изолированную стационарную точку это значит, что есть единственная стационарная точка в некоторой своей окрестности которую мы предполагаем целиком принадлежащей к области определения функции

Для того чтобы проклассифицировать различные возможные типы изолированных точек, рассмотрим множество тех точек из в которых Мы определяем -мерное типовое число тк точки как

-мерное число Бетти множества как максимальное число гомологически независимых относительных -мерных циклов множества с присоединенной к нему точкой по модулю

Типовые числа определяются уже сколь угодно малой окрестностью точки Именно, имеет место

Теорема 1. Если произвольная лежащая в окрестность точки и — множество тех точек из в которых то числа Бетти множества совпадают с числами Бетти множества На рис. 9 показаны эти окрестности для стационарной точки функции

Рис. 9. Функция

Доказательство.

Мы обозначаем относительные -мерные циклы из через относительные -мерные циклы из через

1. Для каждого относительного цикла существует такой относительный цикл , что

Действительно, построим настолько мелкое подразделение цикла чтобы все симплексы этого подразделения, содержащие точку лежали в 0. Составленная из этих последних цепь и есть нужный нам относительный цикл, так как по § 3 (абзацы 4 и 1), в результате подразделения цикла и удаления не содержащих симплексов должен получиться относительный цикл, гомологичный Если теперь относительные

циклы гомологически независимы в то то же верно для гомологичных им циклов Но последние будут тогда гомологически независимы и в Таким образом, из 1 следует, что -мерное число Бетти множества не больше -мерного числа Бетти множества Из соотношения

следует соотношение:

Действительно, (1) эквивалентно соотношению:

Пусть столь мелкое подразделение цепи что все его симплексы, содержащие лежат в Подразделяя в мы тем самым подразделили и в некоторые цепи и причем, в силу (3),

Удалив из все симплексы, не содержащие точки мы получим новую цепь Для нее имеет место соотношение

эквивалентное соотношению

из которого, благодаря тому что

и следует (2).

Если теперь относительные циклы гомологически независимы в то они гомологически независимы и в Таким образом, из II следует, что -мерное число

Бетти множества не меньше -мерного числа Бетти множества Этим теорема 1 доказана.

Важные примеры стационарных точек доставляют изолированный минимум и изолированный максимум. Если есть точка изолированного минимума функции т.е. если принимает в точке меньшее значение, чем во всех остальных точках некоторой ее окрестности то множество пусто, и типовые числа точки совпадают с (абсолютными) числами Бетти множества, состоящего из единственной точки Но числа Бетти множества, состоящего из одной точки, суть:

Пусть теперь есть точка изолированного максимума функции т. е. пусть принимает в точке большее значение, чем во всех остальных точках некоторой ее окрестности которую мы можем предположить открытой. Пусть, далее некоторый -мерный цикл Мы произведем (прямолинейное) симплициальное разбиение Это возможно, ибо есть открытое множество в евклидовом пространстве и, следовательно, может быть исчерпано бесконечным множеством прямолинейных симплексов. Пусть разбиение выбрано так, что есть внутренняя точка некоторого -мерного симплекса столь малого, что он не имеет общих точек с границей относительного цикла это также возможно, ибо представляет собою замкнутое множество, не содержащее точки Аппроксимируя в этом симплициальном разбиении, мы получим гомологичный ему симплициальный цикл Если то не содержит следовательно, Если то есть -мерная нулевая цепь, следовательно, опять Если, однако, то после удаления всех симплексов, лежащих в может остаться симплекс который не гомологичен нулю так как его граница не гомологична нулю в пространстве, в которое превращается после удаления точки следовательно, существует в точности один гомологически независимый -мерный цикл Таким образом,

Мы объединим полученные результаты в следующем предложении:

Теорема II. Типовые числа изолированного минимума функции суть

изолированного максимума —

при этом

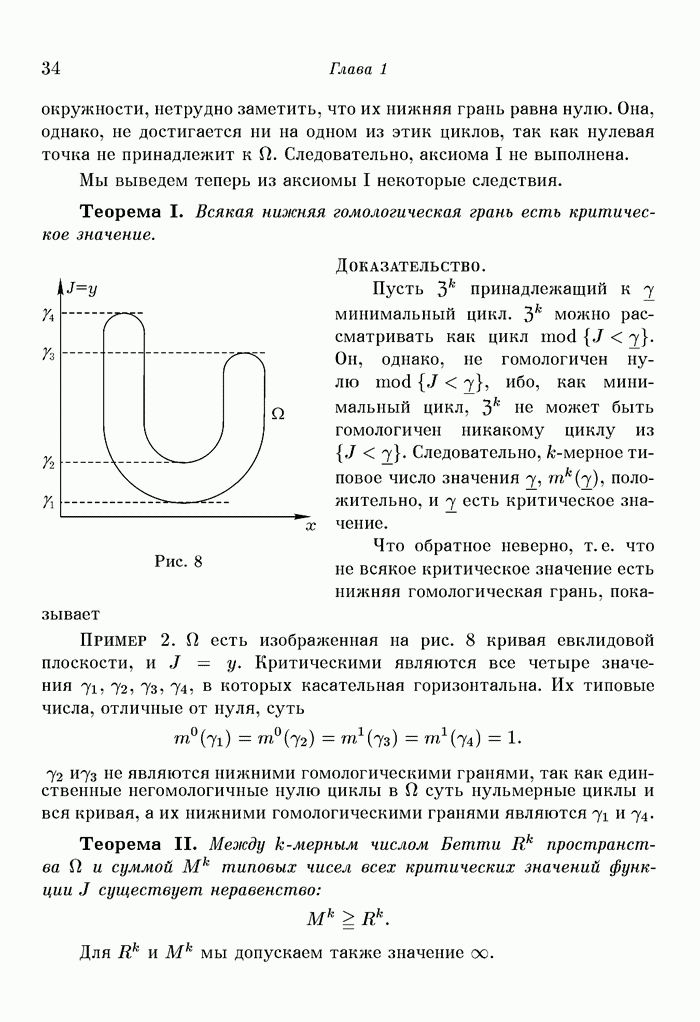
Что точка может быть стационарной, хотя все ее типовые числа равны нулю, показывает пример функции для которой окрестностным пространством служит ось Здесь точка очевидно, стационарна, но все ее типовые числа равны нулю. Последнее видно из того, что всякий принадлежащий значению относительный цикл может быть сдвигом в направлении отрицательной оси деформация, переведен в некоторый цикл из Следовательно, нулевая точка стационарна, хотя соответствующее значение не является критическим в смысле § 4. Что размерность не играет здесь роли, показывает пример «кресла» у функции (рис. 10).

Рис. 10. «Кресло»