§ 5. Неравенства между типовыми числами и числами Бетти

Чтобы установить связь между типовыми числами и числами Бетти, нужно сделать следующее предположение относительно уточняющее упомянутое во введении повисание циклов:

Аксиома Для каждого негомологичного нулю абсолютного -мерного цикла существует такое число 7, что гомологичен в О некоторому циклу из но не гомологичен никакому числу из называется нижней гомологической гранью цикла

Если цикл сам лежит в то он называется принадлежащим к значению 7 минимальным циклом. В силу этого аксиома I может быть формулирована следующим образом: для каждого негомологичного нулю цикла существует гомологичный ему минимальный цикл.

Вот еще одна эквивалентная формулировка. Так как цикл состоит из конечного числа особых симплексов, то имеет максимум на -Рассмотрим нижнюю грань таких максимумов, соответствующих всевозможным циклам, гомологичным Аксиома I требует, чтобы эта нижняя грань достигалась.

Что аксиома I не всегда выполнена, показывает пример 3 § 4: для единственных негомологичных нулю в плоскости циклов — нульмерных циклов — аксиома I нарушается. Мы приведем еще один пример.

Пример есть круг

из которого удалена точка Пусть Рассматривая максимумы функции на одномерных циклах, гомологичных граничной

окружности, нетрудно заметить, что их нижняя грань равна нулю. Она, однако, не достигается ни на одном из этик циклов, так как нулевая точка не принадлежит к Следовательно, аксиома I не выполнена.

Мы выведем теперь из аксиомы I некоторые следствия.

Теорема Всякая нижняя гомологическая грань есть критическое значение.

Доказательство.

Пусть принадлежащий к минимальный цикл. можно рассматривать как цикл Он, однако, не гомологичен нулю ибо, как минимальный цикл, не может быть гомологичен никакому циклу из Следовательно, -мерное типовое число значения положительно, и 7 есть критическое значение.

Рис. 8

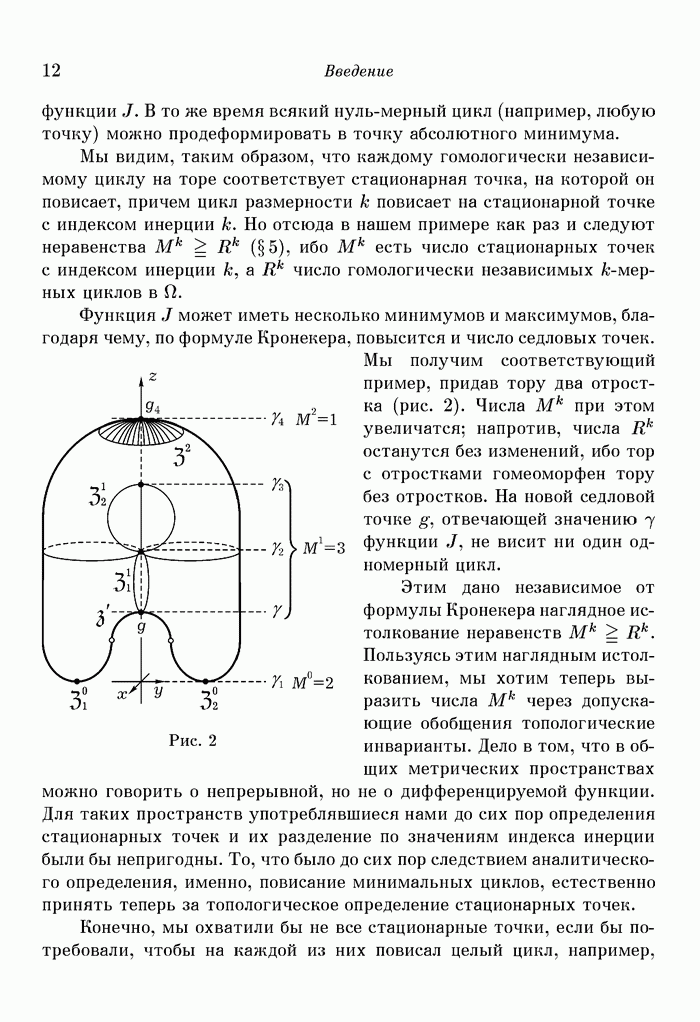
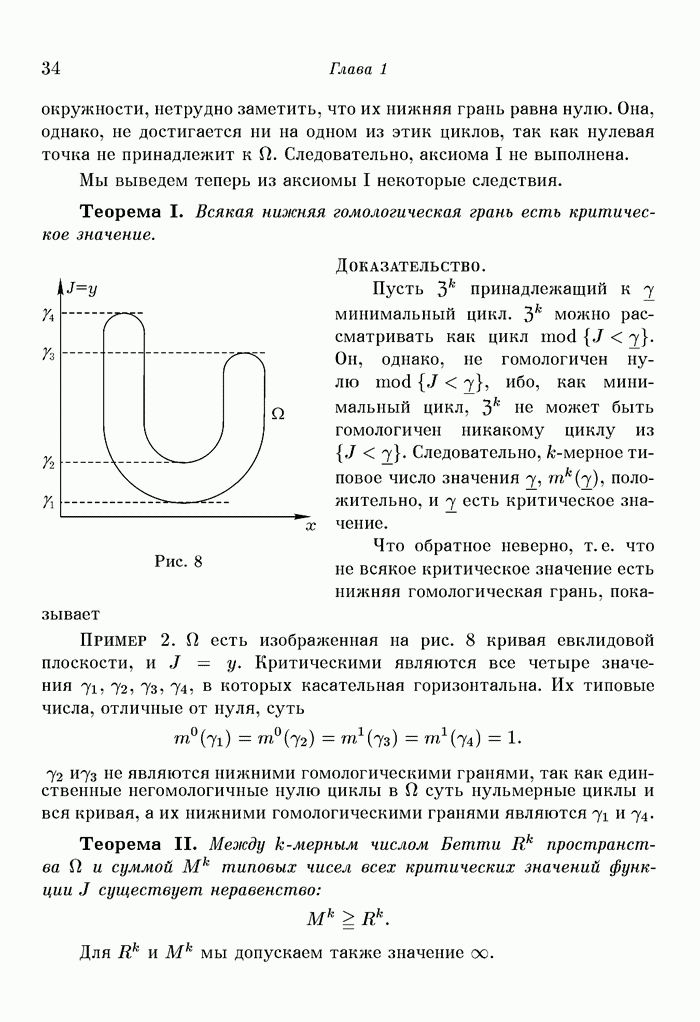
Что обратное неверно, т. е. что не всякое критическое значение есть нижняя гомологическая грань, показывает

Пример 2. О есть изображенная на рис. 8 кривая евклидовой плоскости, и . Критическими являются все четыре значения , в которых касательная горизонтальна. Их типовые числа, отличные от нуля, суть

не являются нижними гомологическими гранями, так как единственные негомологичные нулю циклы в суть нульмерные циклы и вся кривая, а их нижними гомологическими гранями являются 71 и 74.

Теорема II. Между -мерным числом Бетти пространства И и суммой типовых чисел всех критических значений функции существует неравенство:

Для мы допускаем также значение

Доказательство.

Пусть означает если конечно, и произвольное натуральное число, если Тогда в можно найти гомологически независимых -мерных циклов . В силу аксиомы I мы вправе считать их минимальными. Каждый из них принадлежит к определенному критическому значению. Пусть 71 наибольшее из этих значений. Рассмотрим те из наших циклов, которые принадлежат к 71. Если какая-нибудь линейная комбинация этих циклов, скажем гомологична некоторому циклу из области меньших значений то мы заменяем систему циклов системой циклов причем мы вправе также считать минимальным циклом. Так мы получим гомологически независимых минимальных циклов среди которых уже только принадлежат к критическому значению 71. Если снова существует линейная комбинация этих циклов, гомологичная некоторому циклу из области меньших значений то мы применяем к ней тот же прием; в конце концов мы получим гомологически независимых минимальных циклов такого рода, что все линейные комбинации циклов, принадлежащих к 71, суть минимальные циклы, также принадлежащие к 71, в то время как остальные лежат в области меньших значений Из последних мы выберем те, которые принадлежат к следующему наибольшему критическому значению 72, и применим к ним тот же прием. В конце концов мы получим гомологически независимых минимальных циклов такого рода, что никакая линейная комбинация циклов, принадлежащих к одному и тому же критическому значению не гомологична циклу, лежащему к области меньших значений Но тогда эти циклы, рассматриваемые как относительные циклы в гомологически независимы, и их число самое большее равно типовому числу Следовательно, сумма всех -мерных типовых чисел

что и требовалось доказать.