§ 9. J-деформация в окрестности стационарной точки

Мы обращаемся к наиболее общим изолированным стационарным точкам; для этого мы должны произвести некоторые вспомогательные рассмотрения.

1. В каждой точке некоторой открытой окрестности стационарной точки которую мы снова предположим нулевой точкой эвклидова пространства и которая должна быть единственной стационарной точкой в функция имеет определенный вектор-градиент с компонентами:

Векторы-градиенты образуют в векторное поле, интегральные кривые которого суть решения системы дифференциальных уравнений

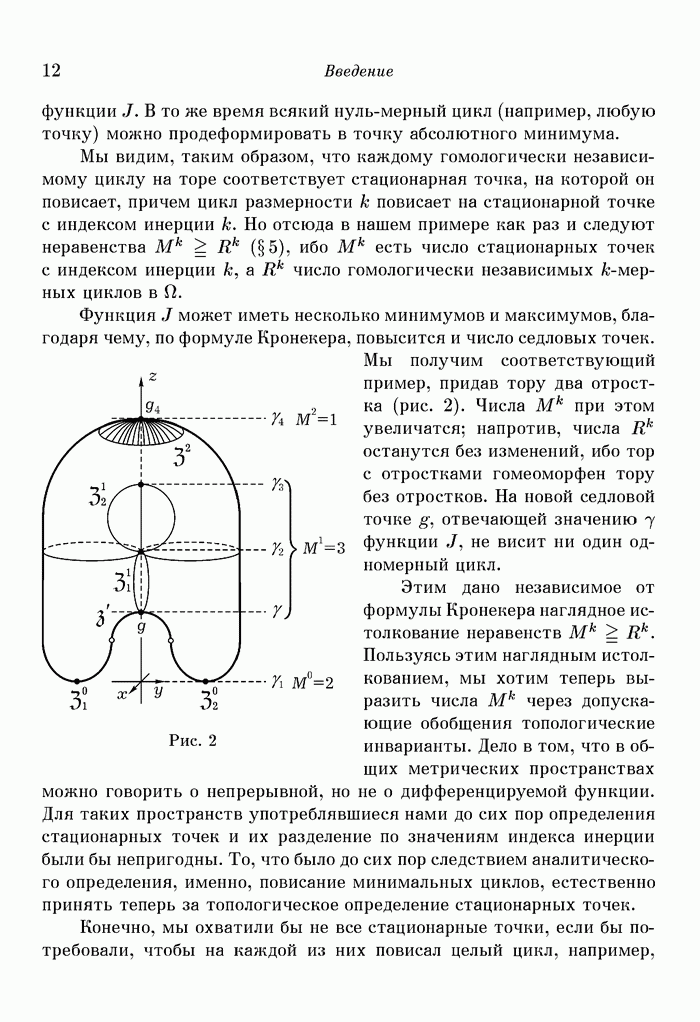
При этом должна быть исключена точка так как в ней (и только в ней) знаменатель правой части обращается в нуль. Решения системы (1) имеют вид:

где функция непрерывно дифференцируема по всем аргументам и

есть начальная точка нашей интегральной кривой. Из (1) следует, что

так что вдоль интегральной кривой

Поэтому вместо в качестве параметра на интегральной кривой можно ввести Тогда из (2) получится:

Функция снова непрерывно дифференцируема по своим аргументам и имеет место тождество:

Мы называем интегральные кривые, проходимые в направлении убывающих значений функции ортогональными траекториями нашей функции Через каждую точку множества проходит в точности одна ортогональная траектория; через самое точку не проходит ни одна, так как для нулевой точки система (1) не определена вовсе.

2. Пусть теперь некоторая отличная от точка окрестности 0. Таким образом, есть нестационарная точка. Поэтому при достаточно малых для всех точек -окрестности точки и всех значений функции удовлетворяющих неравенству имеют место равенства (3). Выберем на гиперповерхности некоторую окрестность с точки лежащую в названной (-окрестности точки точки ) (на рис. 12 окрестность с изображена жирной линией), проведем через все точки окрестности с ортогональные траектории и вырежем на каждой из них сегмент:

Множество, состоящее из всех точек всех этих сегментов, есть некоторая окрестность точки она называется цилиндрической окрестностью нестационарной точки высоты

Рис. 12. Цилиндрическая окрестность нестационарной точки

3. Рассмотрим теперь стационарную точку Ради простоты положим Мы скажем, что ортогональная траектория входит в если она определена для всех достаточно малых значений и если всякая последовательность ее точек, для которой

соответствующие значения функции убывая, сходятся к нулю, сходится к Напротив, мы скажем, что ортогональная траектория выходит из если она, рассматриваемая как ортогональная траектория функции при прохождении в обратном направлении), входит в

Пусть открытая окрестность точки замыкание которой лежит в 0. Пусть некоторая точка из Через проходит в точности одна ортогональная траектория Возможны только два случая: либо траектория проходимая в направлении убывающих значений не выходит за пределы тогда входит либо достигает границы окрестности в некоторой определенной точке.

Доказательство.

Так как функция ограничена на то существует наименьшее число а такого рода, что траектория лежит в 11 и определена для всех значений функции удовлетворяющих неравенствам:

Пусть

последовательность точек на для которой соответствующие значения функции убывая, сходятся к а. Покажем, что последовательность (4) сходится. В противном случае она имеет по крайней мере две предельные точки, из которых одна — обозначим ее через отлична от и потому нестационарна. В сколь угодно малой цилиндрической окрестности точки и притом на сегменте, который высекается этой окрестностью на должно лежать тогда бесконечное множество точек последовательности (4); а так как то на том же сегменте должны лежать и почти все точки последовательности (4), т.е. эта последовательность, в противоположность нашему предположению, должна сходиться к Точка окрестности отличная от не может быть пределом последовательности (4), так как окрестность , будучи открытой, содержала бы вместе с такой точкой также точки траектории в которых Следовательно, предел последовательности (4) есть либо либо некоторая точка на границе окрестности Соответствующее предложение имеет место и для кривой проходимой в обратном направлении.

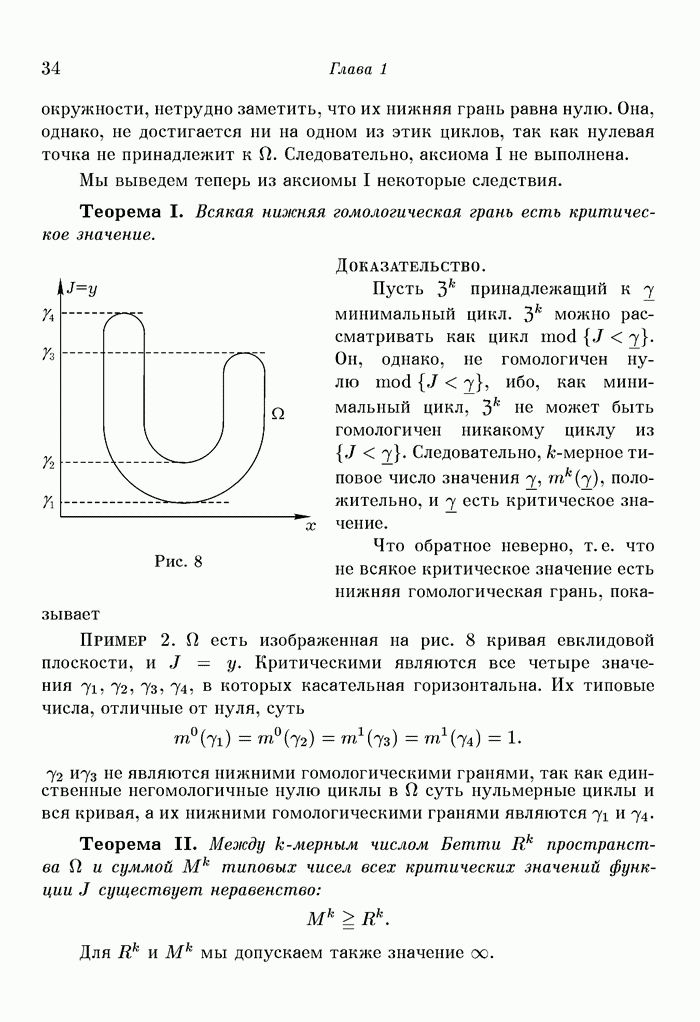
Рис. 13. Цилиндрическая окрестность стационарной точки;

4. Теперь мы можем определить цилиндрическую окрестность и для стационарной точки Пусть с окрестность точки на гиперповерхности лежащая в вместе со своим замыканием (на рис. 13 окрестность с жирно обозначена). Тогда существует столь малое положительное число что к принадлежат следующие точки:

1) Точки на всех входящих в ортогональных траекториях.

2) Точки на всех выходящих из ортогональных траекториях.

3) Точки на всех ортогональных траекториях, проходящих через отличные от точки окрестности с.

Эти точки вместе с самой точкой образуют цилиндрическую окрестность стационарной точки высоты Название «цилиндрическая окрестность» оправдано, так как есть действительно некоторая окрестность точки

5. Мы определим деформацию нашей цилиндрической окрестности 0, переводящую в подмножество тех ее точек, где Из всякой точки окрестности 0, в которой выходит определенная ортогональная траектория, ведущая в определенную точку гиперповерхности совпадает с тогда и только тогда, когда эта ортогональная траектория входит в Мы заставим перемещаться вдоль этой траектории к точке в течение единицы времени с постоянной относительно скоростью. Это значит, что к моменту времени точка должна перейти в точку проходящей через нее ортогональной траектории, отвечающую значению параметра Если мы еще примем, что точки окрестности 0, в которых остаются неподвижными, то этим будет определена деформация окрестности в пересечении

6. Вслед за только что указанной деформацией мы произведем еще одну деформацию, при которой множество перейдет в некоторое подмножество множества . С этой целью рассмотрим систему дифференциальных уравнений:

где есть высота цилиндрической окрестности 0. Правые части (5) непрерывно дифференцируемы во всей окрестности они исчезают все одновременно только в нулевой точке и на гиперповерхности Интегральные кривые системы имеют вид

где означает точку интегральной кривой. Если есть нулевая точка или какая-нибудь точка гиперповерхности то т.е. интегральная кривая (6) вырождается в точку Для всякой другой точки интегральная кривая совпадает с проходящей через ортогональной траекторией функции потому что

Если теперь обозначить точку через и точку определенную формулой (6), через то соответствие

даст деформацию желаемого рода.

7. Произведя последовательно деформации абз. 5 и 6, мы можем высказать следующее предложение (ср. §1, абз. 10):

Теорема. Всякая цилиндрическая окрестность изолированной стационарной точки дважды непрерывно дифференцируемой функции переменных может быть переведена -деформацией в некоторое подмножество множества во время деформации ни одна точка не покидает цилиндрической окрестности, и сама точка остается неподвижной.

Если не бояться несколько неточного способа выражения, то можно сказать, что цилиндрическая окрестность скользит вдоль ортогональных траекторий и останавливается, только натолкнувшись на стационарную точку.