| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Относительные циклы
1. Помимо определенных в предыдущем параграфе абсолютных циклов мы будем пользоваться в дальнейшем введенными в топологию Лефшецем относительными циклами. Рассмотрим все цепи, лежащие в некотором определенном подмножестве  пространства
пространства  Цепь из
Цепь из  равна нулю по модулю
равна нулю по модулю  где
где  некоторое подмножество множества
некоторое подмножество множества  если она целиком лежит в
если она целиком лежит в  Более общим образом, две цепи
Более общим образом, две цепи  равны
равны  если они отличаются только особыми
если они отличаются только особыми  -мерными симплексами, целиком лежащими в
-мерными симплексами, целиком лежащими в 

Далее, мы говорим, что цепь  из
из  замкнута
замкнута  или есть цикл
или есть цикл  если
если

Циклы  называются относительными циклами. Не изменяя относительного цикла, можно выбросить из него все симплексы, целиком лежащие в
называются относительными циклами. Не изменяя относительного цикла, можно выбросить из него все симплексы, целиком лежащие в  или, что то же, не имеющие точек в
или, что то же, не имеющие точек в 
Если, например,  есть эвклидова плоскость,
есть эвклидова плоскость,  та же плоскость после удаления из нее точки
та же плоскость после удаления из нее точки  то двумерный симплекс (треугольник) с центром
то двумерный симплекс (треугольник) с центром  есть двумерный цикл
есть двумерный цикл 
2. Цикл  называется гомологичным нулю
называется гомологичным нулю  если он гомологичен в
если он гомологичен в  некоторой цепи
некоторой цепи  из
из  Равенство
Равенство

эквивалентно, следовательно, соотношению

В соответствии с этим приведенный в качестве примера двумерный цикл  не гомологичен нулю
не гомологичен нулю  Однако одномерный цикл, состоящий из отрезка с серединой
Однако одномерный цикл, состоящий из отрезка с серединой  гомологичен нулю
гомологичен нулю  так как он гомологичен сумме двух сторон треугольника, имеющего этот отрезок своей третьей стороной (рис. 6).
так как он гомологичен сумме двух сторон треугольника, имеющего этот отрезок своей третьей стороной (рис. 6).

Рис. 6
3. Относительные циклы  называется гомологически независимыми
называется гомологически независимыми  если из соотношения
если из соотношения

где  есть
есть  или 1, следует, что
или 1, следует, что  Максимальное число гомологически независимых
Максимальное число гомологически независимых  -мерных циклов из
-мерных циклов из  называется
называется  -мерным числом Бетти множества
-мерным числом Бетти множества  Заметим еще, что, как и в случае абсолютных циклов, при подразделении относительного цикла
Заметим еще, что, как и в случае абсолютных циклов, при подразделении относительного цикла  получается гомологичный ему цикл
получается гомологичный ему цикл  . В самом деле, в силу изложенного в предыдущем параграфе, в множестве, покрытом циклом
. В самом деле, в силу изложенного в предыдущем параграфе, в множестве, покрытом циклом  можно найти такую цепь
можно найти такую цепь  а в множестве, покрытом циклом
а в множестве, покрытом циклом  такую цепь
такую цепь  что
что

А так как  лежит в
лежит в  как и
как и  то
то

что и требовалось доказать.
5. Далее, при деформации относительного цикла  получается гомологичный ему в
получается гомологичный ему в  цикл
цикл  если только в процессе деформации
если только в процессе деформации  остается в
остается в  а в
а в  Если
Если  суть соединяющие цепи, которые обметаются при деформации циклами
суть соединяющие цепи, которые обметаются при деформации циклами  то
то

Но так как  лежит в
лежит в  а
а  то
то

или

| << Предыдущий параграф | Следующий параграф >> |
- От переводчика
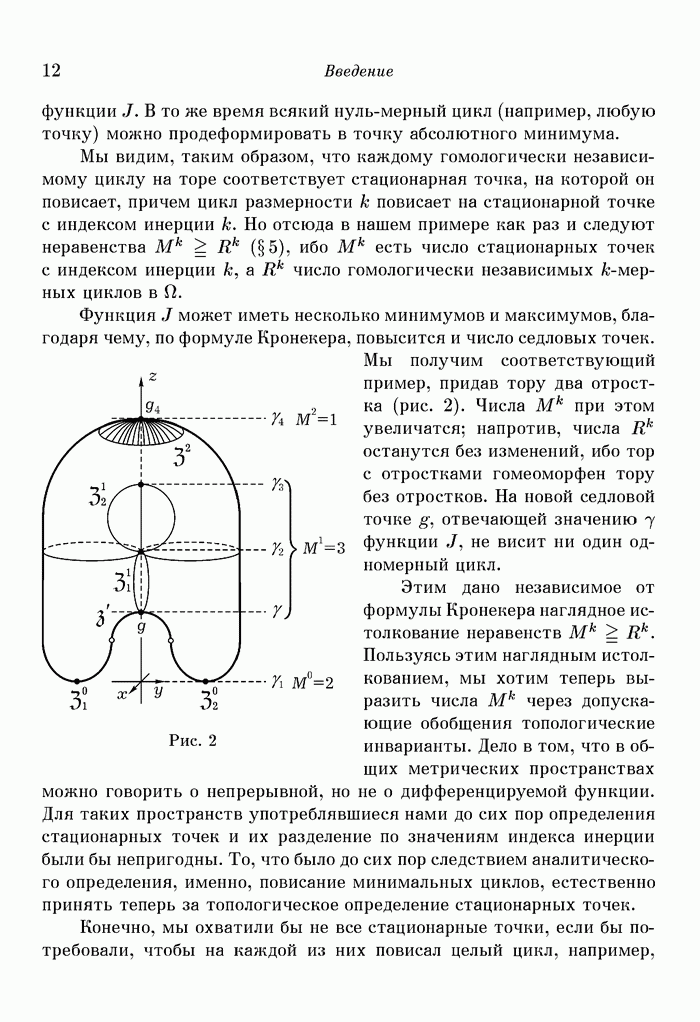
- Введение
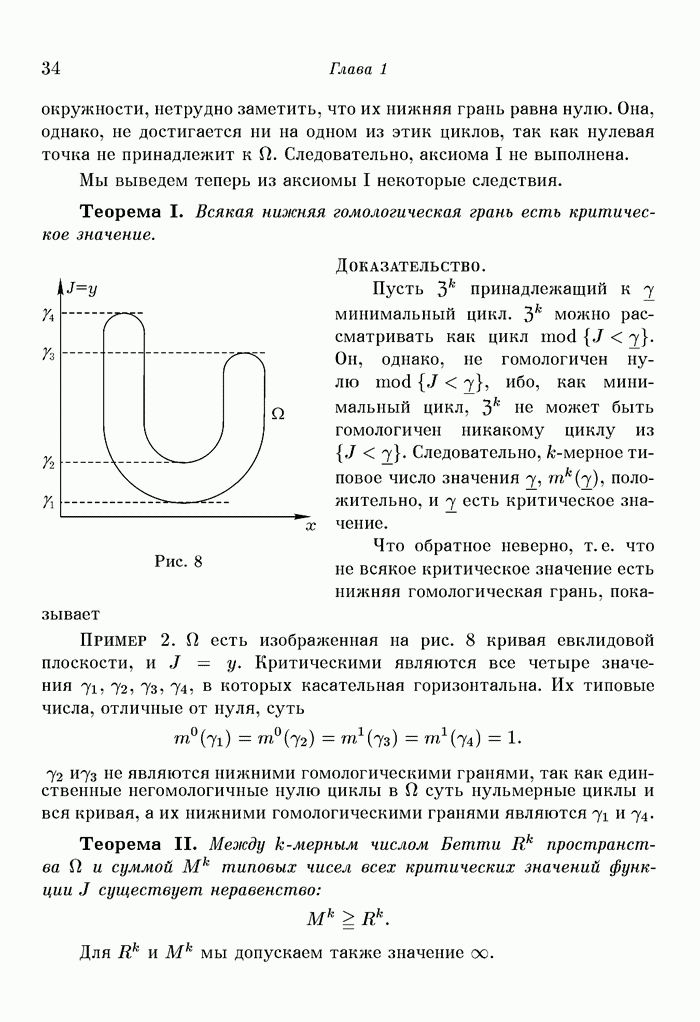
- Глава 1. Числа Бетти и типовые числа
- § 2. Абсолютные циклы и числа Бетти пространства «омега»
- § 3. Относительные циклы
- § 4. Типовые числа критических значений функции J на «омега»
- § 5. Неравенства между типовыми числами и числами Бетти
- § 6. Условие равенства чисел M^k и R^k
- Глава 2. Типовые числа стационарных точек
- § 8. Невырожденные стационарные точки
- § 9. J-деформация в окрестности стационарной точки
- § 10. Теорема о конечности типовых чисел
- Глава 3. Вариационные проблемы на замкнутых многообразиях
- § 12. Риманово многообразие
- § 13. Функциональное пространство
- § 14. Типовые числа изолированной геодезической
- § 15. Примеры типовых чисел (n-мерная сфера)
- § 16. Деформационные теоремы.
- § 17. Типовые числа критических значений и стационарных точек
- § 18. Действительность аксиом I и II
- § 19. Основная теорема
- § 20. Геодезические с закрепленными концами на n-мерной сфере
- § 21. Инвариантность чисел Бетти функционального пространства «омега»
- § 22. Произвольные граничные многообразия
- Прибавление. Стационарные точки на замкнутых многообразиях
- Примечания