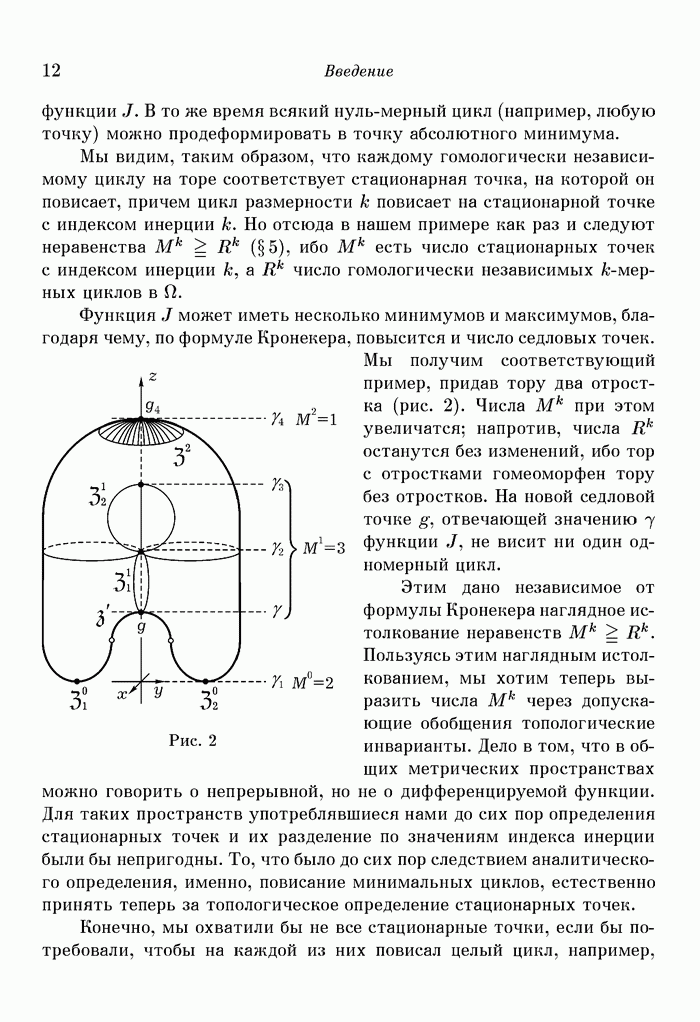
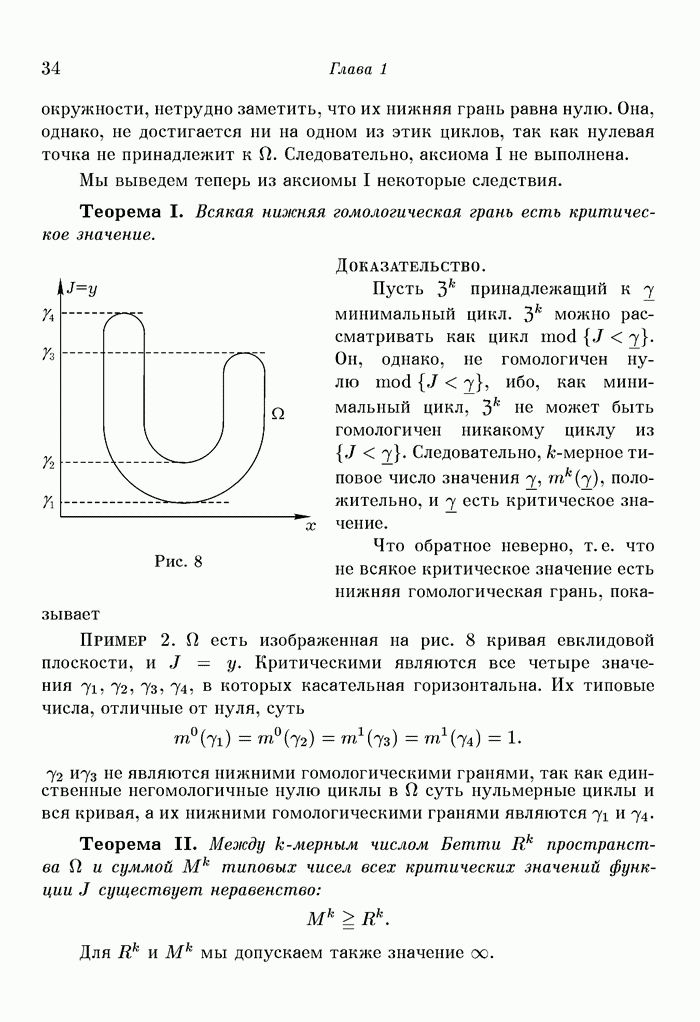
§ 21. Инвариантность чисел Бетти функционального пространства «омега»

В предыдущем параграфе мы использовали предложение, утверждающее, что числа Бетти функционального пространства остаются неизменными при изменении концов так же как и метрики риманова многообразия Теперь мы докажем это предложение.

I. Пусть сначала метрика многообразия остается неизменной, и только концы заменяются другими концами Точки могут быть при этом как различными, так и совпадающими. Соответствующие функциональные пространства, для которых мы хотим доказать совпадение чисел Бетти, пусть будут

Проведем из кусочно-гладкую кривую а и, точно так же, из кусочно-гладкую кривую Произвольной кусочно-гладкой

кривой с, ведущей из поставим в соответствие кривую:

где есть проходимая в противоположном направлений кривая а. Это соответствие, которое мы обозначим через есть, очевидно, непрерывное отображение пространства в пространств Совершенно так же, произвольной кусочно-гладкой кривой с, ведущей из мы поставим в соответствие кусочно-гладкую кривую:

Этим определяется непрерывное отображение пространства в пространство которое мы обозначим через Если теперь применить сначала отображение а затем отображение то получится непрерывное преобразование пространства при котором имеет место соответствие:

Это преобразование может быть продеформировано в тождественное преобразование пространства Пусть а параметр, убывающий от 1 до 0; рассмотрим семейство отображений:

(обозначения см. в абз. 6 § 13). Очевидно, что при это есть преобразование при тождественное преобразование. Точно так же можно убедиться в том, что и преобразование пространства может быть продеформировано в тождественное преобразование

Но отсюда уже следует совпадение чисел Бетти пространств Действительно, если -мерные циклы

гомологически независимы в то то же должно быть справедливо для их образов

в ибо гомологическое соотношение между последними в повлекло бы за собой такое же соотношение между циклами

в Между тем, эти циклы гомологичны циклам (1) и потому гомологически независимы. Таким образом, -мерное число Бетти пространства не меньше -мерного числа Бетти пространства Точно так же можно убедиться в том, что -мерное число Бетти пространства не меньше -мерного числа Бетти пространства Следовательно, эти числа совпадают.

II. Предположим теперь, что концы закреплены. Чтобы освободиться от предположений дифференцируемости, мы будем рассматривать вместо кусочно-гладких кривых многообразия произвольные непрерывные параметрические кривые, ведущие из При этом параметр должен меняться вдоль кривой от до 1. Две параметрические кривые считаются равными, если одинаковым значениям параметра отвечают одинаковые точки на кривых (этим определением равенства параметрические кривые отличаются от кривых § 13). Соответственные точки двух параметрических кривых суть точки, отвечающие одному и тому же значению параметра. Мы превратим множество всех параметрических кривых, соединяющих А с В, в метрическое пространство X, приняв за расстояние двух параметрических кривых максимум расстояний между соответственными точками.

Мы докажем, что пространства имеют одинаковые числа Бетти. Отсюда будет следовать независимость чисел Бетти от выбора римановой метрики многообразия . В самом деле, хотя X определено при помощи определенной римановой метрики на нетрудно видеть, что изменение этой метрики повлекло бы за собой только переход от пространства X к некоторому гомеоморфному ему метрическому пространству. Чтобы убедиться в этом, рассмотрим другое трижды непрерывно дифференцируемое риманово многообразие и предположим, что допускает топологическое отображение на переводящее две заданные точки (концы) на в две заданные точки (концы) А! и В на Тогда, по теореме о равномерной непрерывности, для всякого существует такое что две точки из расстояние которых меньше всегда переходят в две точки из расстояние которых меньше Отсюда следует, что если две параметрические кривые на соединяющие А с В, удалены друг от друга менее чем на то их образы на (соединяющие А с В) удалены друг от друга менее чем на Но это означает, что соответствующее взаимно-однозначное отображение пространства X на пространство X непрерывно. Более того, оно является топологическим, ибо в этом рассуждении можно поменять местами.

Что числа Бетти пространства не зависят от метрики многообразия будет установлено, если мы докажем, что обладают одинаковыми числами Бетти. Доказательство основывается на возможности продеформировать параметрическую кривую в полигон, составленный из ее хорд.

Пусть параметр параметрической кривой с, ведущей из . С помощью точек

разобьем с на частей, причем выберем столь большим, чтобы диаметр каждой части не превышал элементарной длины многообразия Далее, для каждого числа из интервала заменим участок кривои с между точками со значениями параметра элементарным отрезком, соединяющим эти две точки На этом элементарном отрезке мы введем параметр, изменяющийся от и до который линейно связан с длиной дуги и однозначно этим определяется. Так из с получится параметрическая кривая При совпадает с при с элементарным полигоном вершинами которого являются точки ) кривой с. Параметр на кривой не есть, вообще говоря, приведенная длина дуги; он возрастает, на вдоль каждой стороны элементарного полигона.

Так как непрерывно зависит от то перед нами деформация, которую мы обозначим через Конечно, деформация только в том случае применима к некоторой точке с пространства если этой точке соответствует параметрическая кривая, разбиваемая точками ) на частей с диаметрами, не превосходящими Следовательно, определена заведомо не на всем Однако для всякого компактного подмножества пространства можно указать столь большое что деформация применима к этому подмножеству.

Нам потребуется еще одна деформация цель которой состоит в переведении параметра на элементарном полигоне в приведенную длину дуги. Она будет определена на подмножестве пространства точки которого соответствуют -спгоронним параметрическим элементарным полигонам. Под этим мы понимаем следующее:

Разобьем единичный отрезок внутренними точками на частичных отрезков (не обязательно равной длины) и отобразим подразделенный таким образом единичный отрезок непрерывно в так, чтобы каждый частичный отрезок перешел в элементарный отрезок, и чтобы длина дуги на каждом элементарном отрезке была линейной функцией параметра. Сверх того, концы единичного отрезка должны, конечно, перейти в точки Получающаяся таким образом кривая называется -сторонним параметрическим элементарным полигоном. Этим определением не исключается и тот случай, когда некоторые из частичных отрезков единичного отрезка переходят в точки (стороны длины 0). -сторонним параметрическим элементарным полигонам многообразия отвечает некоторое подмножество пространства Одной и той же точке множества могут соответствовать различные -сторонние параметрические элементарные полигоны. Так как каждый -сторонний параметрический элементарный полигон разбиением одной стороны может быть сделан -сторонним, то содержится в

Итак, пусть с -сторонний параметрический элементарный полигон с параметром Если мы предположим, что не является ограничением, что то с заведомо не будет вырожденной кривой. Приведенная длина дуги будет тогда непрерывной функцией на Отнесем точке интервала точку на кривой с значением приведенной длины дуги, равным

Этим для каждого будет определена параметрическая кривая Кривые отличаются от с только своей параметризацией. При получается первоначальный параметр при приведенная длина дуги. непрерывно зависит от при условии, что с принадлежит к Это и есть деформация множества

Так как кусочно-гладкие кривые, на которых в качестве параметра введена приведенная длина дуги, могут рассматриваться как особые параметрические кривые, то каждой точке пространства соответствует определенная точка пространства Это соответствие представляет собою непрерывное отображение в Действительно, если расстояние двух кусочно-гладких кривых рассматриваемых как точки пространства меньше (в это расстояние должна быть

включена, по §13, абсолютная величина разности длин), то расстояние любых двух соответственных точек этих кривых на во всяком случае меньше рассматриваемые как точки пространства удалены друг от друга также меньше, чем на Следовательно, отображение пространства на его образ взаимно-однозначно и непрерывно. Однако оно не является топологическим, как показывает пример, приведенный на стр. 63: расходящаяся последовательность точек из может перейти в сходящуюся последовательность точек из

При этих условиях важно, что по крайней мере компактные подмножества пространства отображаются в топологически. Таким компактным подмножеством является, например, множество всех точек из которым отвечают на -сторонние элементарные полигоны. Действительно, из всякого бесконечного множества -сторонних элементарных полигонов можно выбрать подмножество, вершины всех полигонов которого имеют в точности одну предельную точку Точки Но, определяют некоторый -сторонний элементарный полигон, представляющий собой, как точка пространства предельную точку множества Но это значит, что компактно. есть часть множества так как всякий -сторонний элементарный полигон разбиением одной стороны может быть превращен в -сто-ронний.

Пусть теперь -мерное число Бетти пространства если конечно, и произвольное натуральное число в противном случае. Тогда в можно найти гомологически независимых -мерных циклов:

Мы вправе предположить, что эти циклы лежат в одном из множеств так как в противном случае можно было бы (применением первого шага деформации описанной на стр. 80-82) продеформировать их в некоторые циклы из Пусть

соответствующие циклы в образе множества в пространстве Мы покажем, что гомологически независимы в Отсюда следует, что если то -мерное число Бетти пространства также бесконечно.

Если, напротив, конечно, то

b) Всякий -мерный цикл из гомологически зависим от циклов Из а) и следует совпадение -мерных чисел Бетти пространств VI и

Чтобы доказать продеформируем сначала заданный -мерный цикл из в некоторый гомологичный ему цикл из где достаточно велико; это можно сделать путем последовательного применения деформаций Так как соответствие между является топологическим, то в циклу отвечает некоторый цикл гомологически зависим от и эта зависимость переносится непрерывным отображением VI в VI на циклы

Доказательство а): Пусть

т.е. существует -мерная цепь для которой

Применим к деформацию с достаточно большим тогда перейдет в некоторую цепь из При этой деформации цикл обметет некоторую цепь Так как точкам из отвечают -сторонние элементарные полигоны, которые во время деформации переходят в параметрические элементарные полигоны с менее чем сторонами, то заведомо лежит в и ввиду того, что

мы имеем:

Применяя еще деформацию мы переведем в то время как точки множества в частности, точки из останутся неподвижными. Поэтому также

Но соответствие между является топологическим. Следовательно,

откуда, ввиду независимости циклов следует: что и требовалось доказать.