| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
§ 1. КАЧЕСТВЕННЫЕ СООБРАЖЕНИЯ
Задача преобразования изображения означает необходимость сохранения при переводе в видимую область возможно более широкого пространственного спектра при взаимно однозначном соответствии отдельных его компонент в видимой и ИК-об-ластях. Наиболее удобным для перевода ИК-излучеиия в видимый диапазон является эффект сложения частот в нелинейной оптической среде. Но сравнению с вычитанием частот этот эффект предпочтительнее, поскольку в этом варианте отсутствует прямая спонтанная параметрическая люминесценция, которая является мощным источником шума. Сказанное приводит к следующей общей схеме нелинейно-оптического преобразователя ИК-излучения. В нелинейную среду, где сформирована нужным образом световая волна (волны) накачки, попадает сигнальное ИК-излучение. Благодаря эффекту сложения частот в среде генерируется излучение суммарной частоты, т. е. видимого диапазона [14—16, 29—253]. Пространственное распределение накачки, благодаря явлению синхронизма, обеспечивает:
— относительно большую интенсивность выходного сигнала;
— взаимно однозначное соответствие компонент пространственного спектра ИК-изучения и выходного излучения (в случае преобразования изображения) и/или частотного спектра (в случае нелинейного спектрографа),
— относительно большое отношение иитенсивностей полезного сигнала и паразитных полей (разностная частота, оптические гармоники и т. д.).
Линейная оптическая система на входе и выходе преобразователя оптимальным для процесса преобразования образом формирует ИК-излучение и делает сигнальное излучение удобным для дальнейшего использования.
Нелинейная поляризация при сложении частот пропорциональна амплитуде каждой из волн в первой степени (см. (1.24)). Поэтому и амплитуда рожденного в преобразователе излучения суммарной частоты зависит от амплитуды ИК-сигнала линейно. Иными словами, при заданном распределении электромагнитного поля накачки по отношению к ИК-излучению остается справедливым принцип суперпозиции. Сказанное означает, что, как и в линейной оптике, для построения теории нелинейно-оптических преобразователей изображения достаточно найти отклик на излучение точечного ИК-источника.
Качественный анализ преобразователя может быть проведен на основе «лучевого» подхода, когда считается, что лучи взаимодействуют так же, как и плоские волны. Поскольку угловая ширина синхронизма, как правило, мала, то выбор накачки в виде плоской волны в направлении критичного синхронизма обеспечивает эффективное преобразование узкого пространственного спектра, грубо говоря, одной плоской волны (луча) ИК-излучения. Угловую ширину синхронизма  можно увеличить, уменьшая длину кристалла
можно увеличить, уменьшая длину кристалла  Однако при этом неизбежно падает коэффициент преобразования. Поэтому более естественно сформировать излучение накачки так, чтобы эффективное взаимодействие в синхронизме (или почти в синхронизме) имело место для большого углового диапазона ИК-лучей без уменьшения размеров кристалла. Сделать это можно либо за счет увеличения угловой ширины синхронизма
Однако при этом неизбежно падает коэффициент преобразования. Поэтому более естественно сформировать излучение накачки так, чтобы эффективное взаимодействие в синхронизме (или почти в синхронизме) имело место для большого углового диапазона ИК-лучей без уменьшения размеров кристалла. Сделать это можно либо за счет увеличения угловой ширины синхронизма  либо с помощью формирования достаточно большого числа лучей накачки, каждый из которых преобразует свой инфракрасный луч.
либо с помощью формирования достаточно большого числа лучей накачки, каждый из которых преобразует свой инфракрасный луч.
Итак, существуют две основные возможные схемы нелинейно-оптического преобразователя — схема касательного (некритичного) синхронизма (КС) [14—16, 156—203] и схема критичного векторного синхронизма (КВС) [16, 204—228].
Преобразуемый угловой спектр можно увеличить третьим способом, если ИК-излучение иемоиохроматично. Тогда в каждом направлении распространяется много спектральных компонент ИК-излучения и находится спектральная компонента для каждого направления — своя, взаимодействующая с плоской волной накачки в точном синхронизме. В силу очевидных недостатков этот способ пока не получил распространения.
Начнем со схемы некритичного синхронизма (рис. 1.4, в). В простейшем варианте направление накачки в виде плоской волны выбирается так, чтобы взаимодействие с центральным лучом ИК-сигнала происходило в точном синхронизме и в направлении синхронизма имело место касание (а не перенесение, как обычно) волновых поверхностей. Очевидно, что при этом угловая ширина синхронизма резко возрастает. В самом деле,  С другой стороны,
С другой стороны,  где
где  угол пересения волновых поверхностей. Отсюда следует, что
угол пересения волновых поверхностей. Отсюда следует, что  при
при 
В случае касательного синхронизма  Поэтому
Поэтому  При длине кристалла
При длине кристалла  см угол зрения преобразователя может быть порядка нескольких градусов, что позволяет говорить о реальном преобразовании изображения.
см угол зрения преобразователя может быть порядка нескольких градусов, что позволяет говорить о реальном преобразовании изображения.
Для простоты рассмотрения будем считать нелинейную среду изотропной, тогда понятия касательного и линейного
синхронизма совпадают. В этом приближении угловую ширину синхронизма можно рассчитать точно (рис. 2.1):

Таким образом, в схеме касательного синхронизма преобразователь представляет собой некоторую эффективную диафрагму, вырезающую из пучка инфракрасных лучей конус  Размер диафрагмы 3, очевидно, оценивается формулой
Размер диафрагмы 3, очевидно, оценивается формулой

Здесь возможны два случая:
1. Точечный источник находится вблизи кристалла на расстоянии  меньшем
меньшем  (рис. 2.2, а):
(рис. 2.2, а):

 это расстояние от нелинейного кристалла до ИК-источника, при котором размер эффективной диафрагмы
это расстояние от нелинейного кристалла до ИК-источника, при котором размер эффективной диафрагмы  сравнивается с апертурой кристалла
сравнивается с апертурой кристалла  Тогда размытие изображения определяется дифракцией на этой эффективной диафрагме. Разрешающая способность преобразователя
Тогда размытие изображения определяется дифракцией на этой эффективной диафрагме. Разрешающая способность преобразователя  определяется
определяется

Поле зрения  в этом случае по порядку величины совпадает с апертурой
в этом случае по порядку величины совпадает с апертурой  нелинейной среды. При
нелинейной среды. При  в точности совпадает с
в точности совпадает с  Число разрешаемых элементов
Число разрешаемых элементов  определяется выражением
определяется выражением

2. Если источник ИК-излучения находится на

Рис. 2.1. Расчет угловой ширины касательного синхронизма в модели изотропной среды.
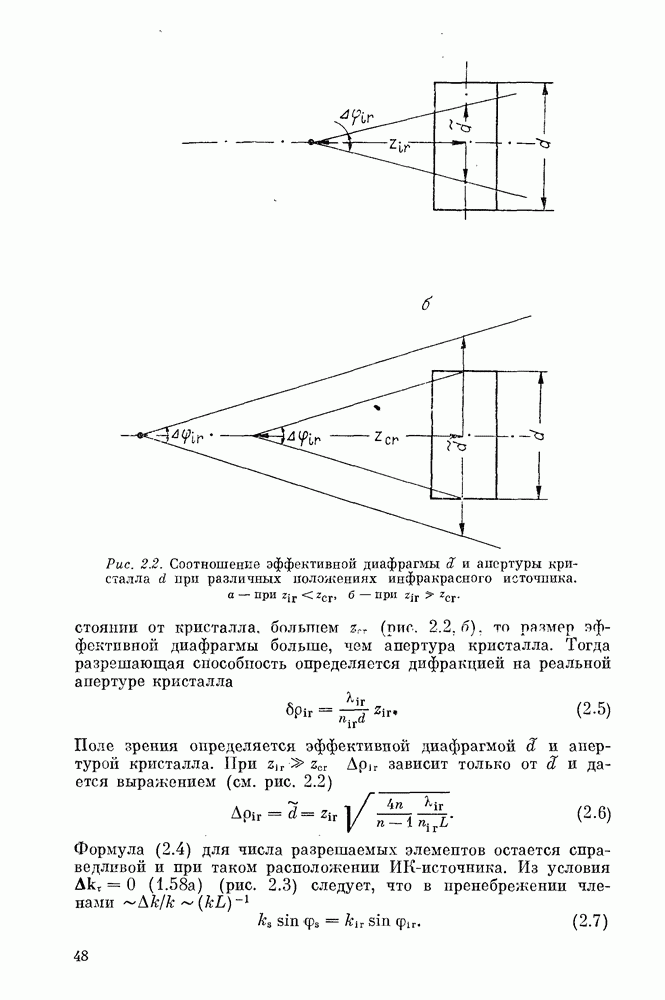
Рис. 2.2. (см. скан) Соотношение эффективной диафрагмы  и апертуры кристалла
и апертуры кристалла  при различных положениях инфракрасного источника. а — при
при различных положениях инфракрасного источника. а — при  при
при 
расстоянии от кристалла, большем  (рис. 2.2.6). то размер эффективной диафрагмы больше, чем апертура кристалла. Тогда разрешающая способность определяется дифракцией на реальной апертуре кристалла
(рис. 2.2.6). то размер эффективной диафрагмы больше, чем апертура кристалла. Тогда разрешающая способность определяется дифракцией на реальной апертуре кристалла

Поде зрения определяется эффективной диафрагмой 3 и апертурой кристалла. При  зависит только от
зависит только от  и дается выражением (см. рис. 2.2)
и дается выражением (см. рис. 2.2)

Формула (2.4) для числа разрешаемых элемептов остается справедливой и при таком расположении ИК-источника. Из условия  (1.58а) (рис. 2.3) следует, что в пренебрежении членами
(1.58а) (рис. 2.3) следует, что в пренебрежении членами 


Рис. 2.3. Направление луча суммарной частоты, рожденного ИК-лучом, идущим под углом  к направлению распространения накачки.
к направлению распространения накачки.
Это означает, что с точки зрения закона формирования изображения преобразователь в схеме КС эквивалентен преломляющей поверхности, разделяющей оптические среды с показателем преломления 

В некоторых случаях в схеме касательного синхронизма целесообразно фокусировать накачку [16, 166, 169, 170, 175, 177]. При этом угол фокусировки, конечно, должен быть не слишком велик, чтобы условие касательного синхронизма нарушалось для крайних лучей накачки не слишком сильно. Лучевой анализ позволяет и в этом случае оценить основные параметры преобразователя. Волновая расстройка как функция угла  под которым идет данный ИК-луч, дается формулой (рис. 2.4, а)
под которым идет данный ИК-луч, дается формулой (рис. 2.4, а)

Из условия  синхронизма имеем выражение для угловой ширины
синхронизма имеем выражение для угловой ширины

которое позволяет оценить размер эффективной диафрагмы:

и

После этого нетрудно получить формулы для разрешающей способности и поля зрения

при 

при  Число разрешаемых элементов в обоих вариантах одинаково и совпадает с
Число разрешаемых элементов в обоих вариантах одинаково и совпадает с  в случае плоской волны накачки (см. (2.4)).
в случае плоской волны накачки (см. (2.4)).
Закон (2.7) выполняется и для случая сферической волны накачки (см. рис.  если углы
если углы  отсчитывать от направления соответствующего луча накачки:
отсчитывать от направления соответствующего луча накачки:

Это означает, что с точки зрения формирования изображения преобразователь в схеме КС с фокусированной накачкой эквивалентен сферической преломляющей поверхности с показателем преломления (2.8) и радиусом кривизны, совпадающим с 
Коэффициент преобразования для центрального ИК-луча можно оценить по формуле (1.73):

Перейдем к схеме критичного векторного синхронизма: широкий диапазон эффективно преобразуемого пространственного спектра реализуется за счет фокусировки накачки, когда для каждого ИК-луча имеется соответствующий луч накачки, взаимодействие с которым идет в точном синхронизме. Каждый луч накачки взаимодействует с одномерным многообразием ИК-лучей, лежащих на образующих конуса, осью которого является данный луч накачки, а угол при вершине равен углу 

Рис. 2.4. К оценке волновой расстройки как функции угла  в схеме касательного синхронизма с фокусированной накачкой.
в схеме касательного синхронизма с фокусированной накачкой.
векторного критичного синхронизма между  при взаимодействии плоских волн (см. рис. 4.1). Поэтому для перевода двумерного многообразия ИК-лучей достаточно сфокусировать накачку в одном направлении (фокусировка цилиндрической линзой). Для упрощения качественного анализа ограничимся здесь двумерной моделью преобразования, когда ИК-изображение представляет собой систему полос, параллельных оси фокусировки (оси цилиндрической волны) накачки. В изотропной модели нелинейной среды диаграмма волновых векторов приведена на рис. 1.4, а, а ход лучей, идущих от цилиндрического (точечного в плоскости
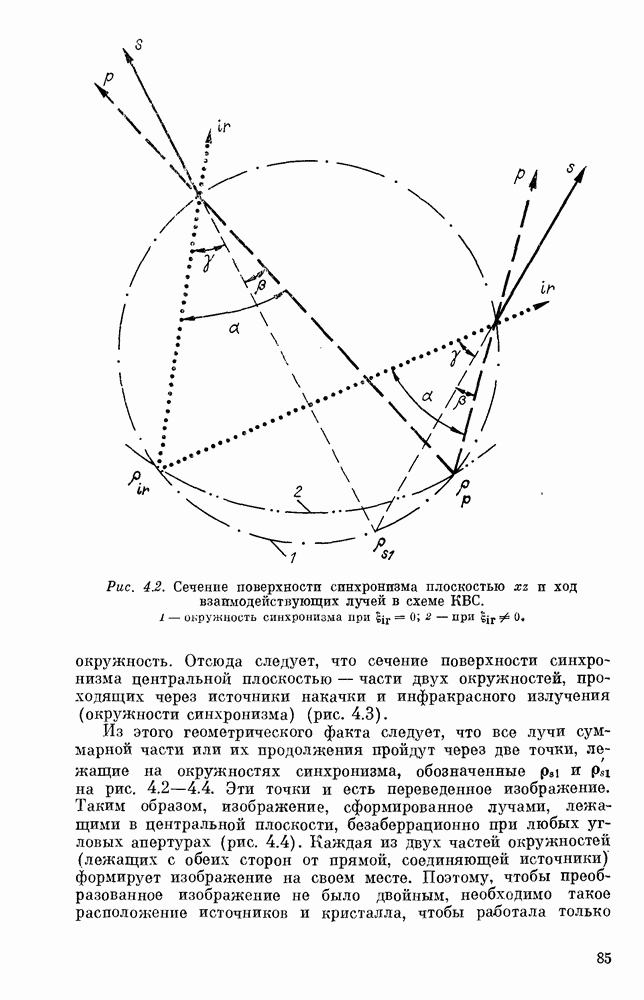
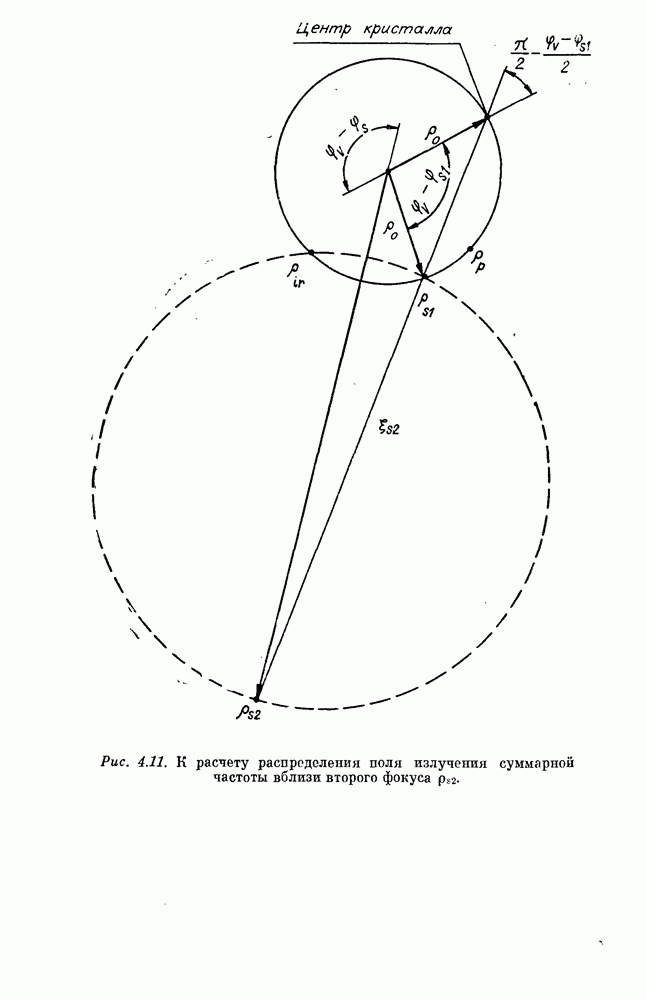
при взаимодействии плоских волн (см. рис. 4.1). Поэтому для перевода двумерного многообразия ИК-лучей достаточно сфокусировать накачку в одном направлении (фокусировка цилиндрической линзой). Для упрощения качественного анализа ограничимся здесь двумерной моделью преобразования, когда ИК-изображение представляет собой систему полос, параллельных оси фокусировки (оси цилиндрической волны) накачки. В изотропной модели нелинейной среды диаграмма волновых векторов приведена на рис. 1.4, а, а ход лучей, идущих от цилиндрического (точечного в плоскости  ИК-источника и цилиндрического же источника накачки, показан на рис. 4.2. В том месте кристалла, где луч накачки пересекается с ИК-лучом под углом а, генерируется сигнальный луч суммарной частоты. Совокупность этих лучей и формирует видимое изображение ИК-источника. Оцеиим разрешающую способность
ИК-источника и цилиндрического же источника накачки, показан на рис. 4.2. В том месте кристалла, где луч накачки пересекается с ИК-лучом под углом а, генерируется сигнальный луч суммарной частоты. Совокупность этих лучей и формирует видимое изображение ИК-источника. Оцеиим разрешающую способность  из следующих соображений. Поскольку все лучи суммарной частоты имеют примерно одинаковую яркость, можно предположить, что
из следующих соображений. Поскольку все лучи суммарной частоты имеют примерно одинаковую яркость, можно предположить, что  определяется углом раствора суммарных лучей, формирующих видимое изображение. Этот угол определяется углом раствора эффективно преобразующихся ИК-лучей, т. е. апертурой кристалла и расстоянием от кристалла до ИК-источника (см. рис. 4.2). Таким образом, при отсутствии (или устранении) геометрических аберраций следует ожидать, что разрешающая способность определяется дифракционным размытием ИК-источника на апертуре нелинейной среды. Наиболее простой для рассмотрения случай соответствует ситуации, когда ИК-исгочник находится на бесконечности. Тогда
определяется углом раствора суммарных лучей, формирующих видимое изображение. Этот угол определяется углом раствора эффективно преобразующихся ИК-лучей, т. е. апертурой кристалла и расстоянием от кристалла до ИК-источника (см. рис. 4.2). Таким образом, при отсутствии (или устранении) геометрических аберраций следует ожидать, что разрешающая способность определяется дифракционным размытием ИК-источника на апертуре нелинейной среды. Наиболее простой для рассмотрения случай соответствует ситуации, когда ИК-исгочник находится на бесконечности. Тогда

а угловое поле зрения

где  угол фокусировки накачки. Число разрешаемых элементов
угол фокусировки накачки. Число разрешаемых элементов

может быть существенно больше (по параметру  чем в схеме касательного синхронизма.
чем в схеме касательного синхронизма.
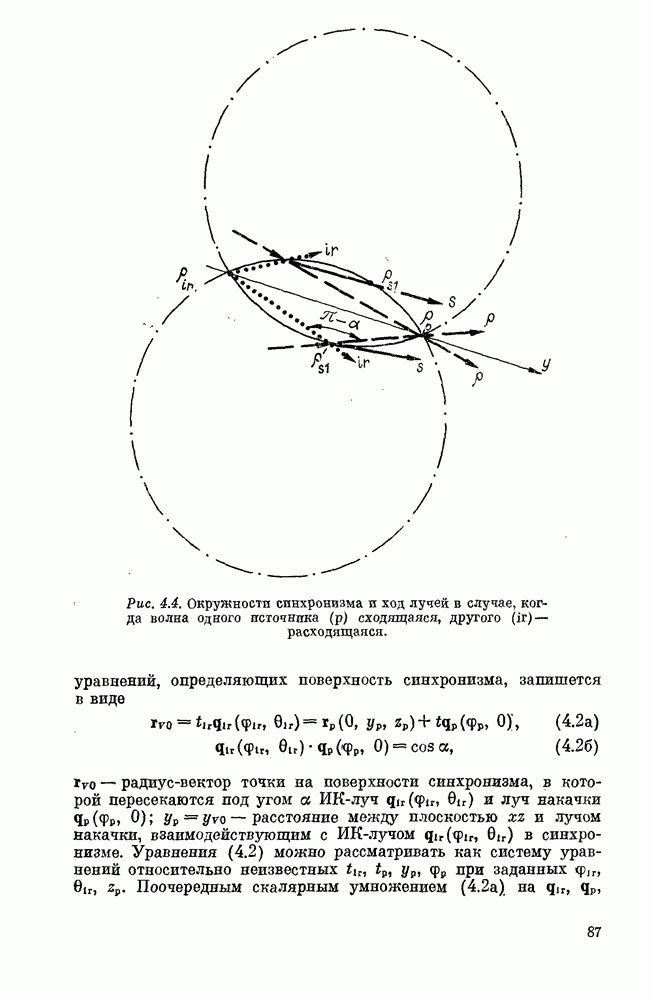
Для приближенного расчета коэффициента преобразования оценим толщину слоя в нелинейной среде, эффективно генерирующего сигнальное излучение из следующих соображений. Лучи накачки и ИК-излучения, идущие от двух точечных (в плоскости  источников, пересекаются под заданным углом а на линии, которая является окружностью (см. рис. 4.2). При уходе от окружности на величину
источников, пересекаются под заданным углом а на линии, которая является окружностью (см. рис. 4.2). При уходе от окружности на величину  угол пересечения меняется
угол пересечения меняется
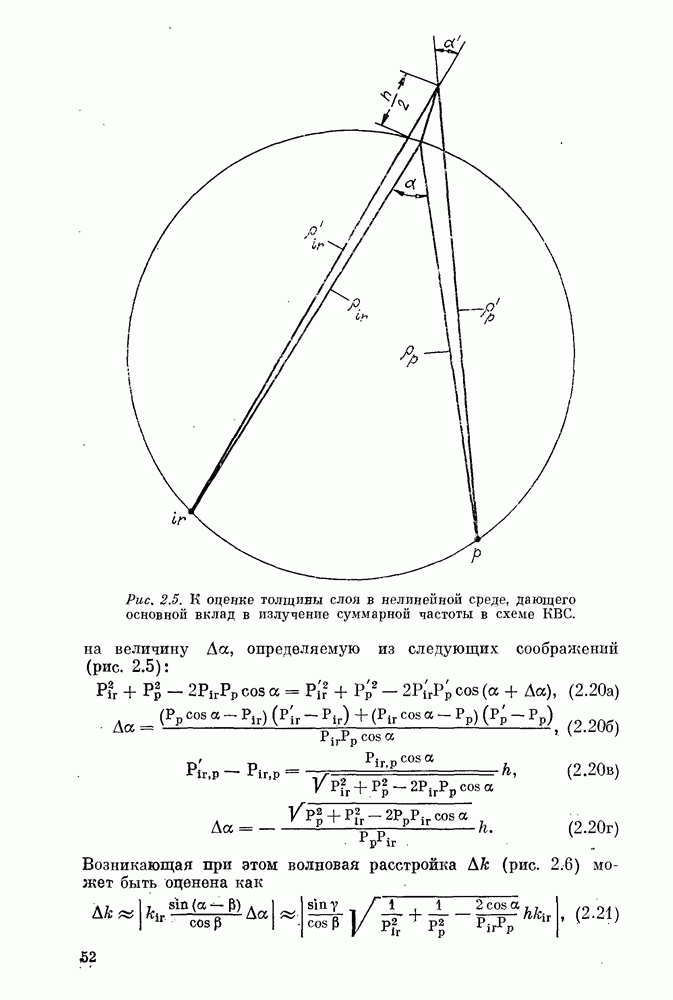
Рис. 2.5. (см. скан) К оценке толщины слоя в нелинейной среде, дающего основной вклад в излучение суммарной частоты в схеме КВС.
на величину  определяемую из следующих соображений (рис. 2.5):
определяемую из следующих соображений (рис. 2.5):

Возникающая при этом волновая расстройка  (рис. 2.6) может быть оценена как
(рис. 2.6) может быть оценена как


Рис. 2.6. К оценке волновой расстройки, возникающей при распространении ИК-луча под углом а к направлению распространения луча накачки.
где  соответствующие углы в треугольнике синхронизма при взаимодействии плоских волн (см. рис. 4.1). Поскольку
соответствующие углы в треугольнике синхронизма при взаимодействии плоских волн (см. рис. 4.1). Поскольку  толщина эффективно генерирующего слоя, условие
толщина эффективно генерирующего слоя, условие  выхода из синхронизма в пределах его главного максимума можно записать в виде
выхода из синхронизма в пределах его главного максимума можно записать в виде

В итоге из формул  (2.21), (2.22) цмеем
(2.21), (2.22) цмеем

Можно предположить, что коэффициент преобразования оценивается формулой (1.73) для плоских волн, в которой роль толщины кристалла  играет толщина эффективного слоя
играет толщина эффективного слоя  Ограничившись для упрощения формул случаем бесконечно удаленного ИК-объекта
Ограничившись для упрощения формул случаем бесконечно удаленного ИК-объекта  из (1.73) и (2,23) имеем
из (1.73) и (2,23) имеем

Формула (2.24) позволяет предположить, что коэффициент преобразования в схеме КВС меньше, чем в схеме КС при тех же размерах кристалла.
Рассмотренный лучевой подход нестрогий. Отождествление лучей с плоскими волнами в нелинейной оптике гораздо более проблематично, чем в теории обычных оптических приборов (приближение геометрической оптики). Например, один из основных вопросов связан с тем, что для нелинейных процессов существенна толщина (объем) среды. Поэтому эффективность взаимодействия пересекающихся лучей явным образом зависит от их «толщины». Приведенный пример показывает, что полученные на основе интуитивного лучевого подхода результаты не являются априорно достоверными, даже в качестве оценочных. Эти результаты должны восприниматься как предварительные, помогающие скорее строгой постановке задачи, чем ее решению. Весьма заманчиво строить теорию нелинейно-оптических преобразователей в терминах обычных оптических систем: понятия геометрической оптики — законы идеального изображения, геометрические аберрации, дифракционные эффекты, светосила и т. д. Не видно, однако, возможности обобщить эти понятия на нелинейную оптику с помощью интуитивных
соображений. Такое обобщение нуждается в строгом подходе, основанном на волновом уравнении, включающем в себя нелинейную поляризацию. Развитие подхода и является целью дальнейшего рассмотрения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
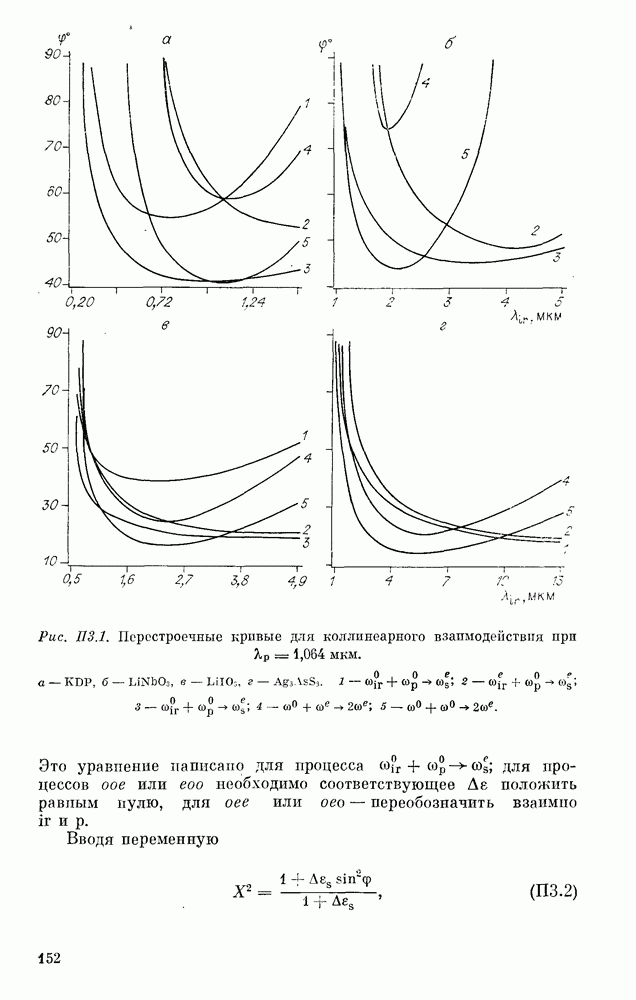
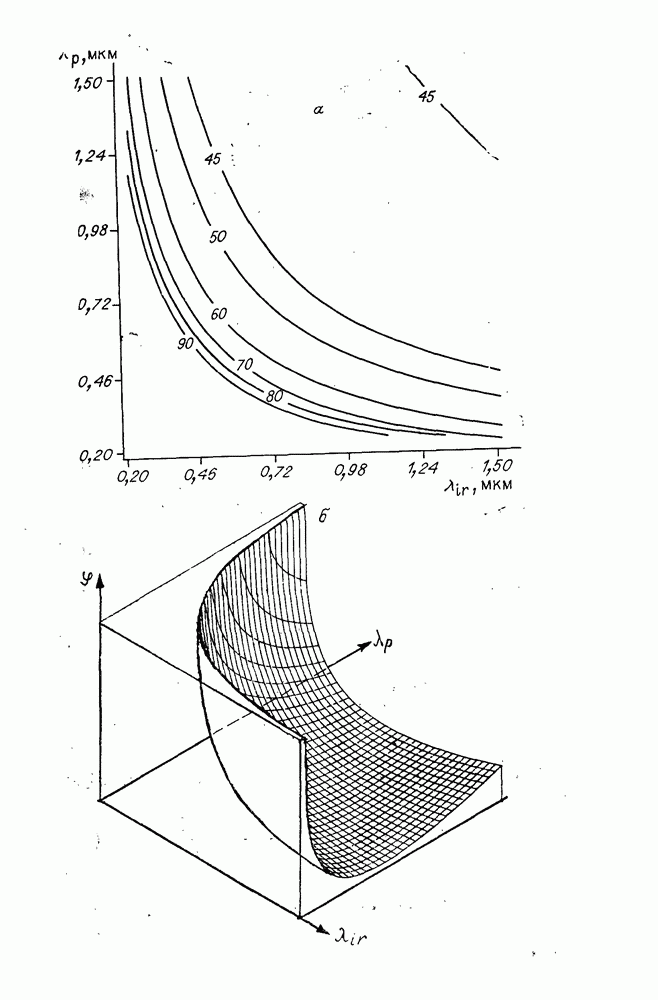
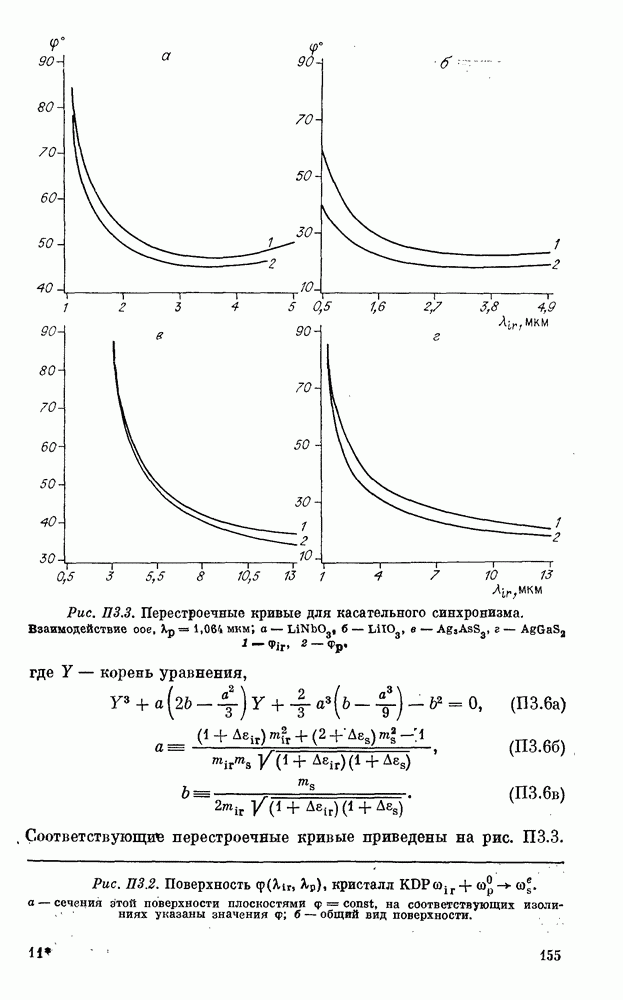
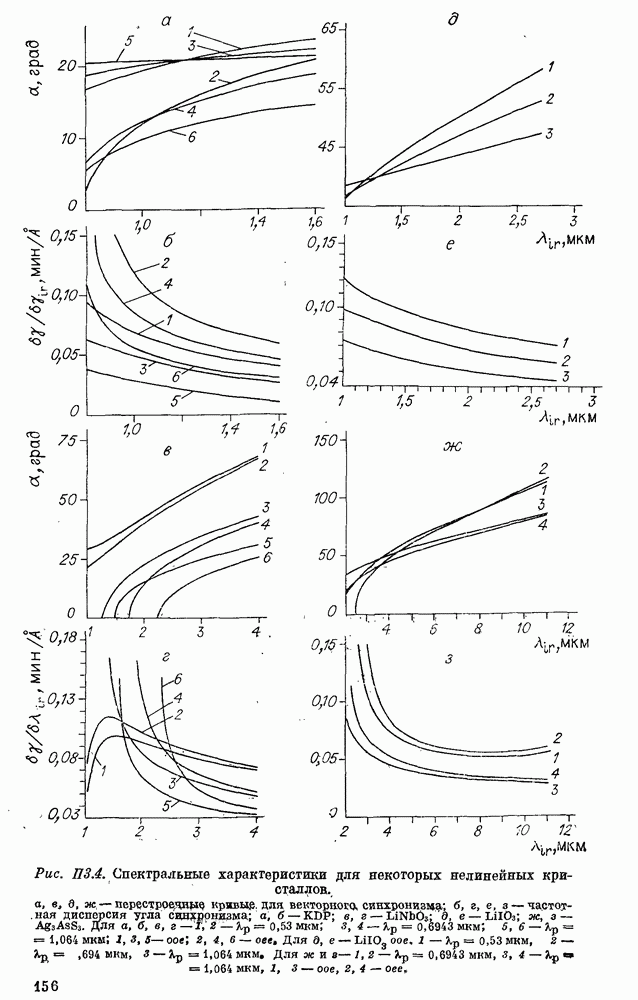
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)