| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
Есть два способа построения геометрической оптики. Первый, наиболее общий, связан с уравнением эйконала [1, 7, 8]. Второй — с вычислением интеграла Френеля — Кирхгофа методом стационарной фазы. Преимущество этого способа состоит в том, что он позволяет рассматривать геометрические и дифракционные эффекты с единой точки зрения (см. приложение 1). Именно таким образом строится дифракционная теория аберраций [7]. В нелинейной оптике первому способу соответствует
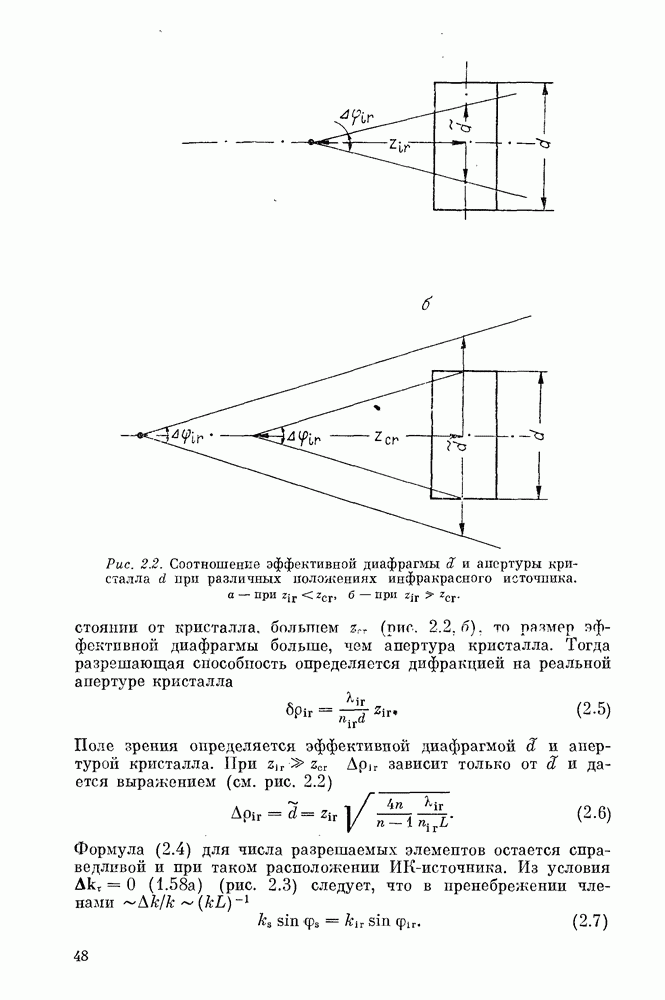
приближение, когда пренебрегают вторыми производными в уравнениях для медленных амплитуд взаимодействующих волн (см. гл. 1, § 4). Сформулированный выше подход функций Грина (2.27), (2.35) позволяет ввести приближение геометрической оптики в форме, удобной для расчета параметрических преобразователей излучения [177, 223]. Для этого перепишем (2.27) в виде

где  медленная амплитуда,
медленная амплитуда,  фаза ИК-излучения. Далее, разделим нелинейный кристалл на области, большие по сравнению с длиной волны,
фаза ИК-излучения. Далее, разделим нелинейный кристалл на области, большие по сравнению с длиной волны,  столь малые, чтобы фазу
столь малые, чтобы фазу  в подынтегральном выражении (2.36)
в подынтегральном выражении (2.36)

можно было считать линейной функцией координат.
Разлагая функцию (2.37) внутри каждой такой области в ряд Тейлора и принимая во внимание, что  где к
где к  -волновое число,
-волновое число,  единичный вектор в направлении луча, находим
единичный вектор в направлении луча, находим

Интегрирование в формуле (2.36) проведем теперь в таком порядке: сначала возьмем интегралы по координатам  внутри каждой области, затем сложим поля от всех таких областей. Наибольший вклад в поле излучения на суммарной частоте для данной точки наблюдения дадут те области, в которых
внутри каждой области, затем сложим поля от всех таких областей. Наибольший вклад в поле излучения на суммарной частоте для данной точки наблюдения дадут те области, в которых

Вклады от областей, где равенство (2.38) не выполняется, в пределе  обращаются в нуль из-за быстрой осцилляции фазового множителя подынтегрального выражения (2.36). Рассмотренный подход аналогичен обычному приближению геометрической оптики (см. (П1.15)) с той лишь разницей, что теперь интеграл трехмерный. Этим, в частности, обусловлена следующая особенность формирования изображения. Если при интегрировании по поверхности для каждого участка найдется точка наблюдения, по отношению к которой фаза на этом участке стационарна, то в трехмерном случае некоторые области вообще не излучают на суммарной частоте, и их можно не рассматривать.
обращаются в нуль из-за быстрой осцилляции фазового множителя подынтегрального выражения (2.36). Рассмотренный подход аналогичен обычному приближению геометрической оптики (см. (П1.15)) с той лишь разницей, что теперь интеграл трехмерный. Этим, в частности, обусловлена следующая особенность формирования изображения. Если при интегрировании по поверхности для каждого участка найдется точка наблюдения, по отношению к которой фаза на этом участке стационарна, то в трехмерном случае некоторые области вообще не излучают на суммарной частоте, и их можно не рассматривать.
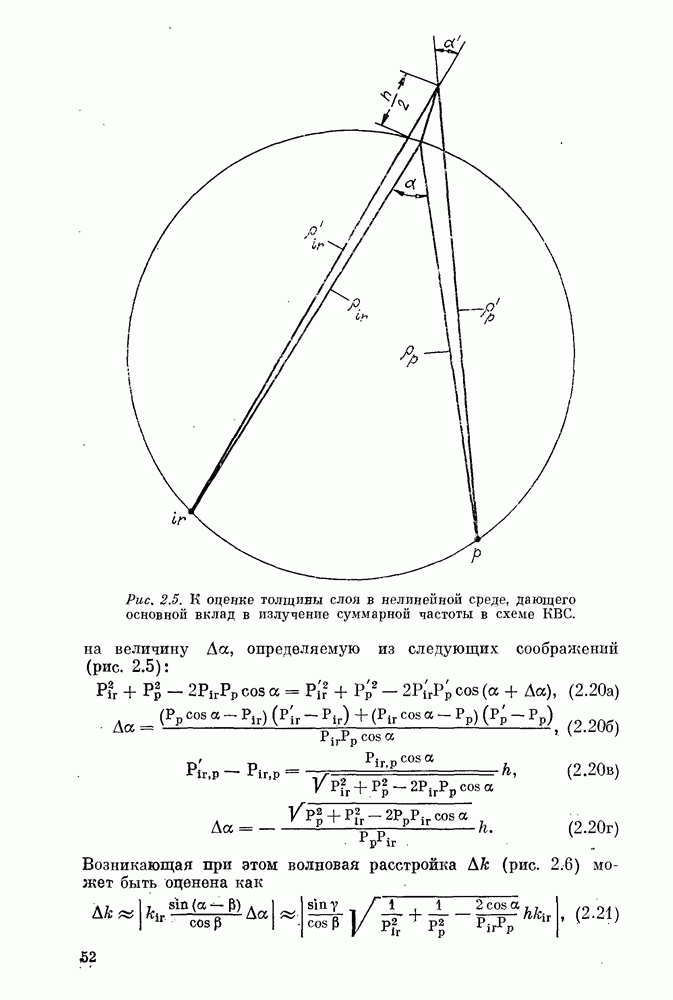
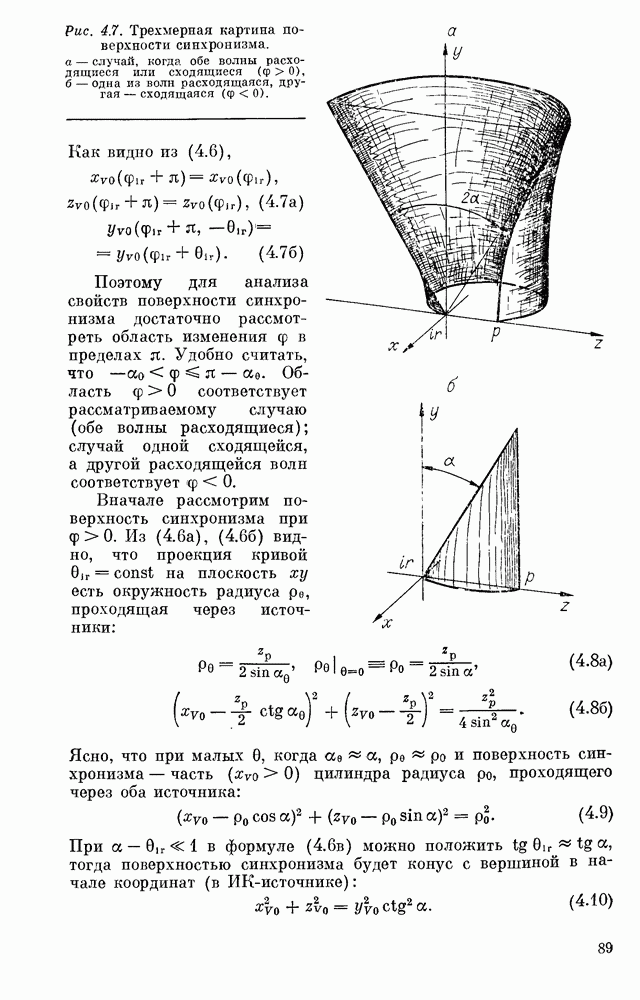
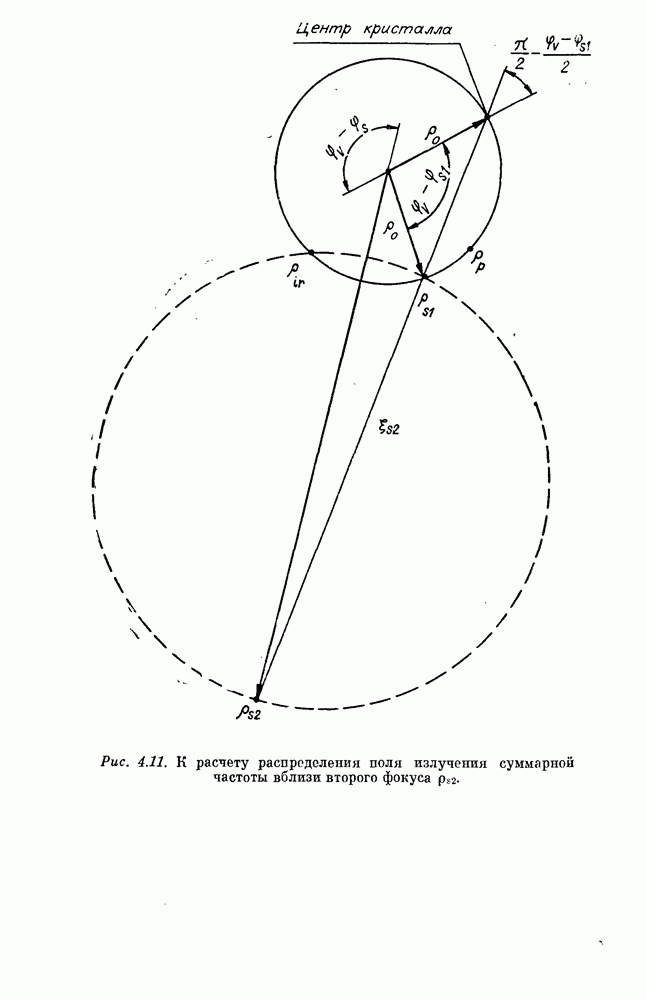
Формула (2.38) описывает пространственное распределение преобразованного излучения. Она показывает, что излучение на суммарной частоте генерируется главным образом в тех областях нелинейного кристалла, где лучи накачки и инфракрасного излучения пересекаются под углом синхронизма между накачкой и ИК-излучением, как при векторном взаимодействии плоских волн (см. рис. 4.1):

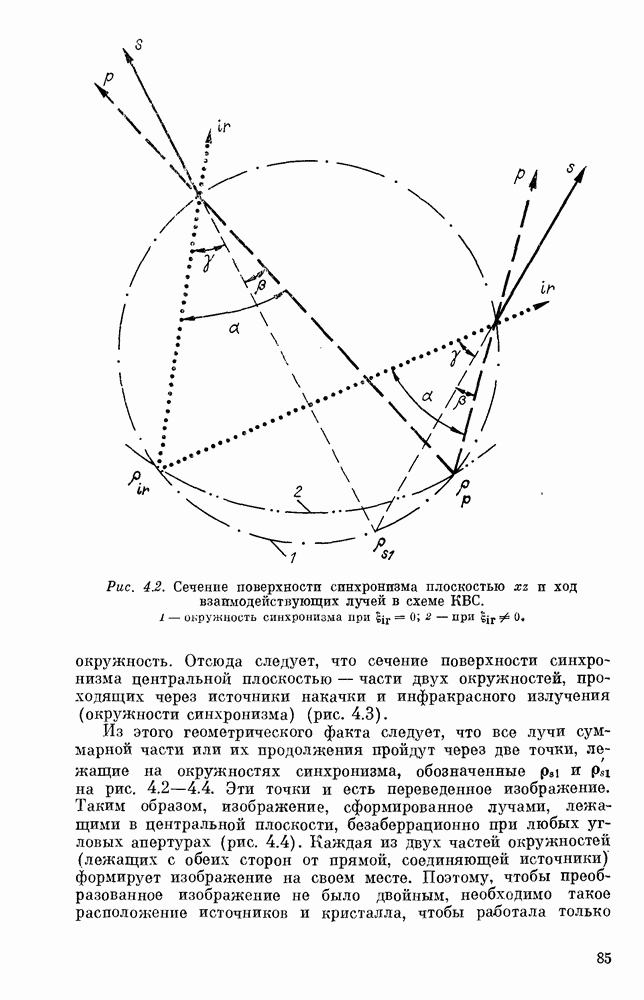
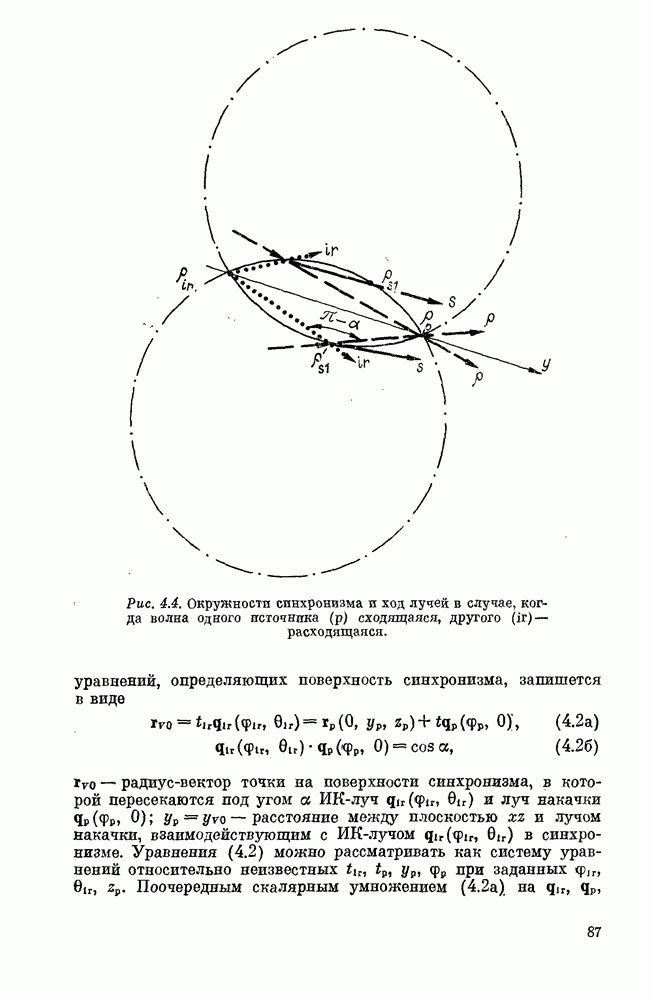
Уравнение (2.39) в общем случае определяет некоторую поверхность в кристалле, называемую поверхностью синхронизма [212, 223]. Генерация преобразованного излучения происходит в основном слое, непосредственно примыкающем к поверхности (2.39) (слой синхронизма). Каждая элементарная область, расположенная на поверхности синхронизма, генерирует луч  частоты
частоты  направленный по отношению к лучам ИК-сигнала
направленный по отношению к лучам ИК-сигнала  и накачки
и накачки  так, что
так, что

Уравнение луча  идущего из данной точки поверхности синхронизма, удобно записать в виде
идущего из данной точки поверхности синхронизма, удобно записать в виде

Равенства (2.39), (2.41) полностью описывают работу преобразователя в приближении геометрической оптики.
Отметим, что в случае касательного синхронизма поверхность (2.39) вырождается в отрезок прямой линии вдоль оси  Таким образом, в рассматриваемом приближении нелинейный кристалл генерирует только один луч, идущий вдоль оси
Таким образом, в рассматриваемом приближении нелинейный кристалл генерирует только один луч, идущий вдоль оси  . В этом смысле преобразователь в схеме касательного синхронизма напоминает камеру обскуру.
. В этом смысле преобразователь в схеме касательного синхронизма напоминает камеру обскуру.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
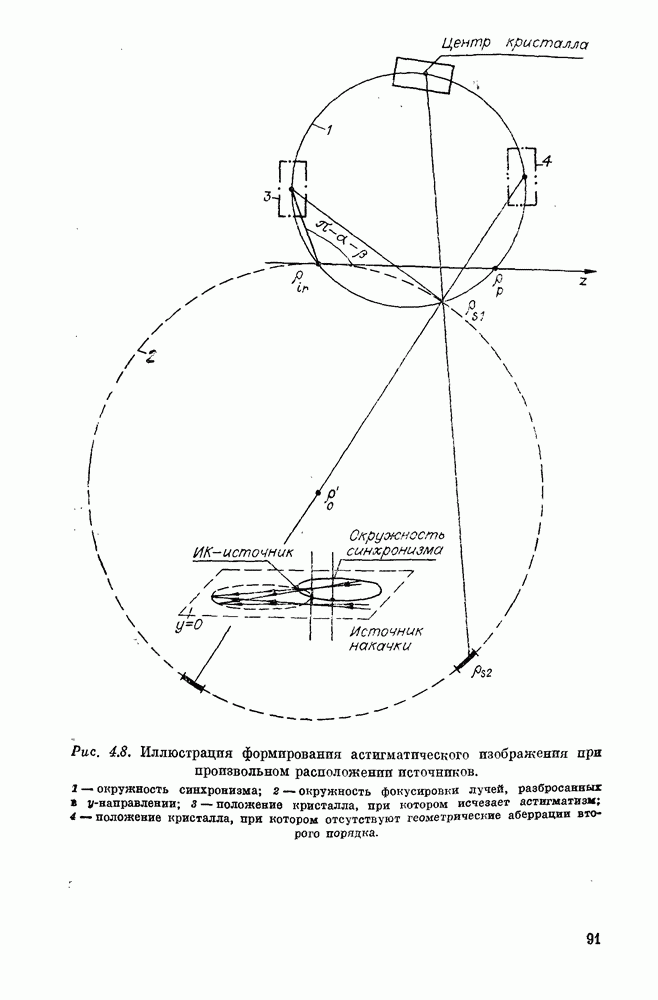
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
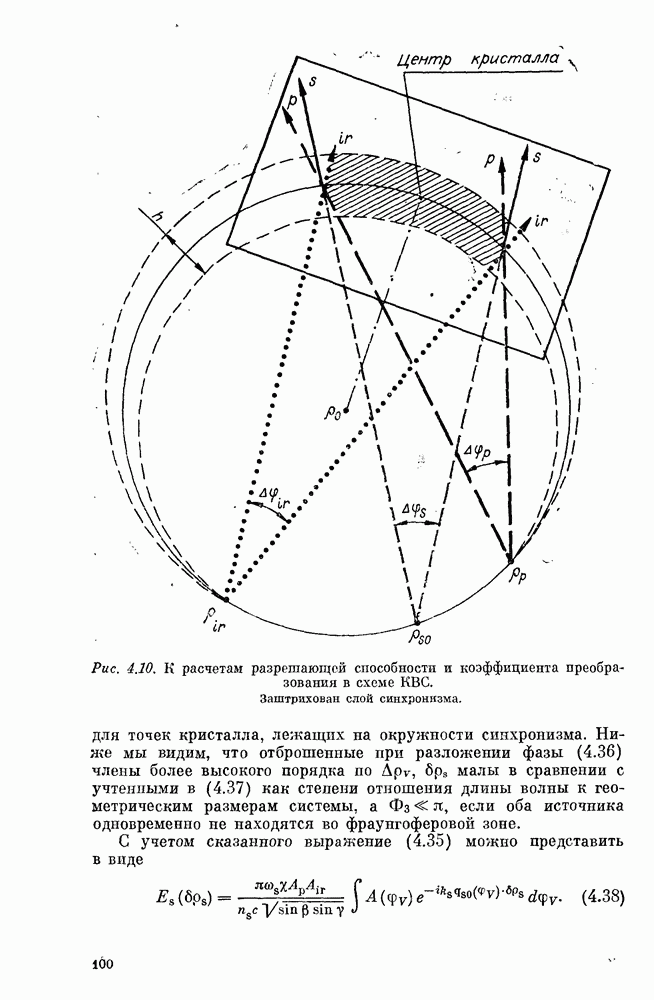
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
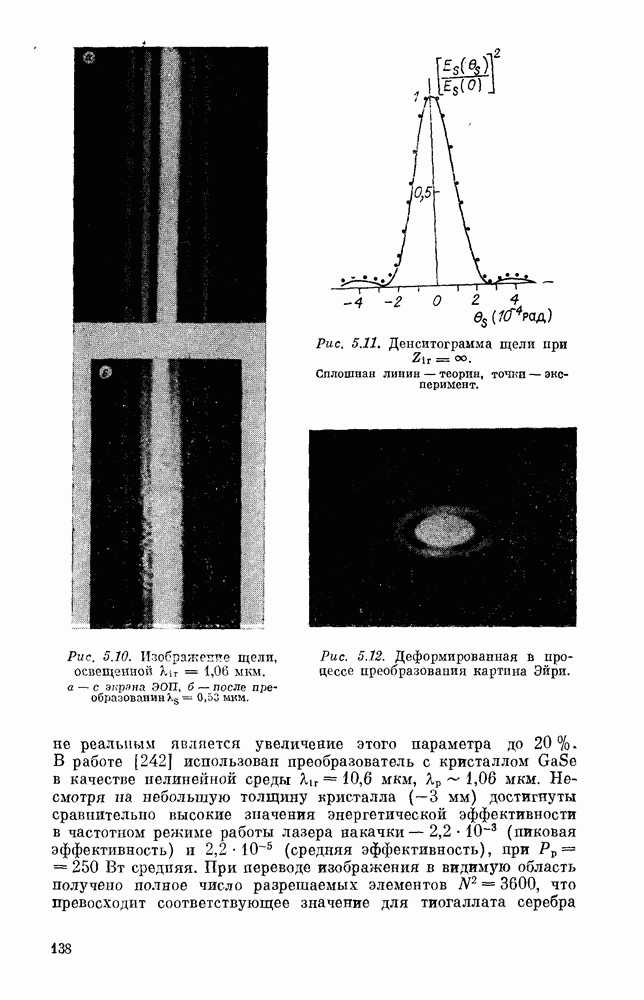
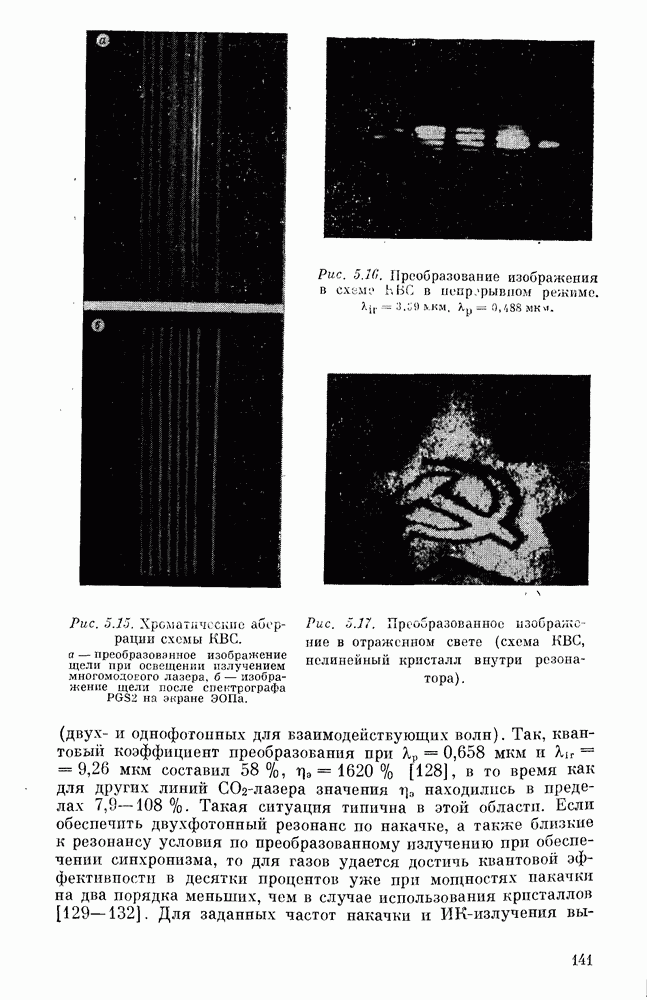
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
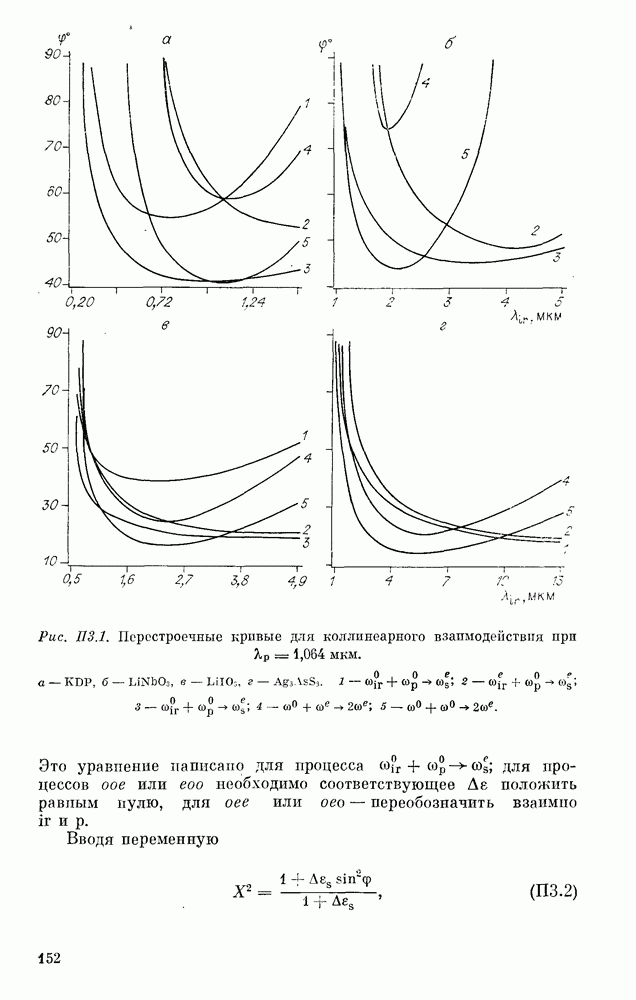
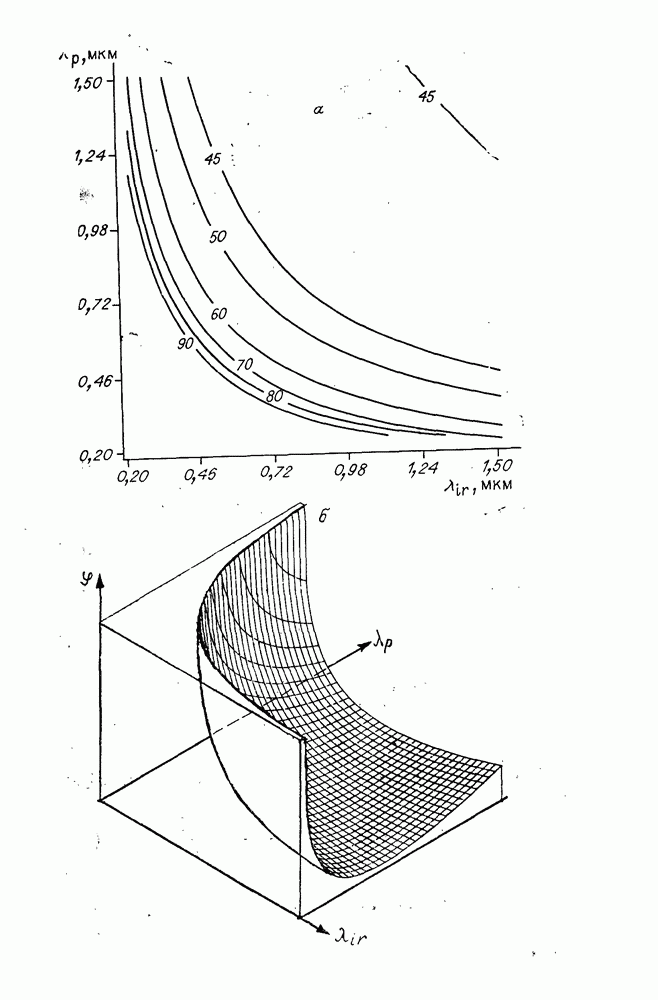
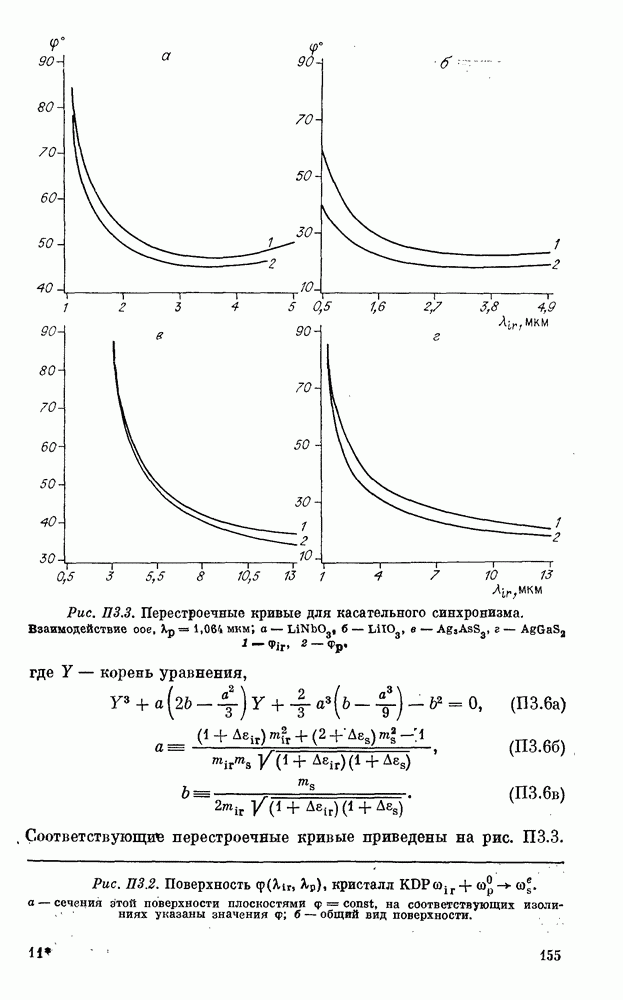
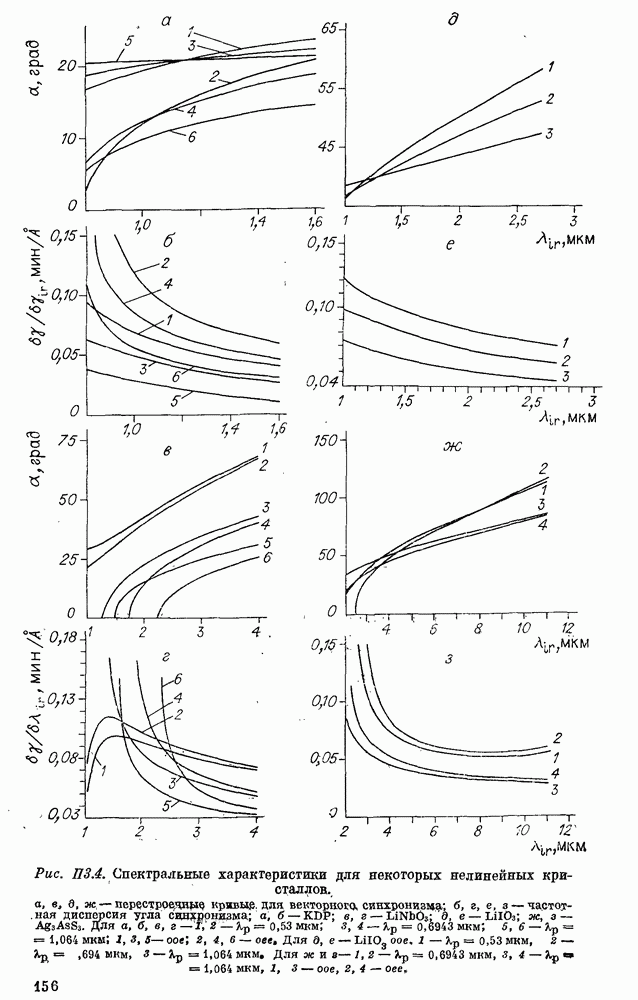
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)