| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
В силу линейности уравнений Максвелла при заданных значениях зарядов и токов нелинейность в оптике связана со свойствами отклика среды на поле. Это действительно так, пока можно пренебрегать рождением электронно-позитронных пар, т. е. нелинейностью самого вакуума. Один из вариантов традиционного подхода в нелинейной оптике состоит в том, что любая среда описывается с помощью диэлектрической проницаемости  которая для нелинейной среды сама зависит от электромагнитного поля. Ясно, что при этом волновое уравнение оказывается с математической точки зрения сугубо нелинейным. В книге в дальнейшем будем использовать другой подход, задавая свойства среды вектором поляризации, фигурирующим в правой части волнового уравнения. Очевидно, что волновое уравнение остается линейным относительно поля и поляризации, а все «нелинейности» выносятся за рамки этого уравнения и определяются зависимостью вектора поляризации в данной среде от электромагнитного поля (материальными уравнениями). Такой подход, математически эквивалентный первому, физически более естественен и, как следствие, позволяет сформулировать некоторые свойства нелинейно-оптических явлений (например, синхронизм) безотносительно к конкретным свойствам среды, типу нелинейного процесса, величине поля и т. д. Кроме того, он облегчает введение приближений заданного поля в случае достаточно слабых полей.
которая для нелинейной среды сама зависит от электромагнитного поля. Ясно, что при этом волновое уравнение оказывается с математической точки зрения сугубо нелинейным. В книге в дальнейшем будем использовать другой подход, задавая свойства среды вектором поляризации, фигурирующим в правой части волнового уравнения. Очевидно, что волновое уравнение остается линейным относительно поля и поляризации, а все «нелинейности» выносятся за рамки этого уравнения и определяются зависимостью вектора поляризации в данной среде от электромагнитного поля (материальными уравнениями). Такой подход, математически эквивалентный первому, физически более естественен и, как следствие, позволяет сформулировать некоторые свойства нелинейно-оптических явлений (например, синхронизм) безотносительно к конкретным свойствам среды, типу нелинейного процесса, величине поля и т. д. Кроме того, он облегчает введение приближений заданного поля в случае достаточно слабых полей.
§ 1. КАЧЕСТВЕННАЯ КАРТИНА
Для понимания физических явлений нелинейной оптики рассмотрим традиционную в оптике модель среды, состоящей из неподвижных, взаимодействующих между собой, осцилляторов во внешнем световом поле. В ней учет нелинейных эффектов означает учет энгармонизма осцилляторов (либо нелинейную зависимость сил трения от поля).
В простейшем варианте одномерного осциллятора с кубическим энгармонизмом уравнение движения имеет вид

Ограничимся такими полями, при которых нелинейность  Полезно рассмотреть поведение такого осциллятора в бигармоническом поле:
Полезно рассмотреть поведение такого осциллятора в бигармоническом поле:  В первом приближении теории возмущений
В первом приближении теории возмущений  имеем
имеем

(для определенности 
Уравнение для  принимает вид
принимает вид

Вынуждающая сила для  здесь имеет гармоники на частотах
здесь имеет гармоники на частотах  Нас будут интересовать суммарные и разностные компоненты
Нас будут интересовать суммарные и разностные компоненты  Тогда
Тогда

Поскольку спектр излучаемого диполем поля воспроизводит спектр колебаний этого диполя, то происходит генерация средой электромагнитного излучения суммарной и разностной гармонии. Как следует из уравнений Максвелла, амплитуда гармоник определяется плотностью дипольного момента единицы объема  где
где  число осцилляторов в единице объема. Оценим
число осцилляторов в единице объема. Оценим  в резонансной и нерезонансной ситуациях. В первом случае
в резонансной и нерезонансной ситуациях. В первом случае  а во втором
а во втором  Для оценки параметра 3 будем считать, что в нерезонансном случае х порядка боровского радиуса
Для оценки параметра 3 будем считать, что в нерезонансном случае х порядка боровского радиуса  при значениях амплитуды внешнего поля порядка
при значениях амплитуды внешнего поля порядка  амплитуда атомного поля). Отсюда
амплитуда атомного поля). Отсюда  Нелинейная восприимчивость
Нелинейная восприимчивость  определяемая равенством
определяемая равенством  оценивается как
оценивается как  в нерезонансном случае, а в резонансном случае она больше в
в нерезонансном случае, а в резонансном случае она больше в  раз.
раз.
Оценим максимально возможную амплитуду поля  на суммарной (разностной) частоте
на суммарной (разностной) частоте  Для этого нужно учесть интерференцию излучения, рожденного в разных частях среды. Поскольку фаза наведенной поляризации
Для этого нужно учесть интерференцию излучения, рожденного в разных частях среды. Поскольку фаза наведенной поляризации  определяется фазами полей
определяется фазами полей  характерный размер фазовой структуры
характерный размер фазовой структуры  порядка К. Если добиться в каком-либо направлении когерентного сложения полей
порядка К. Если добиться в каком-либо направлении когерентного сложения полей  от разных точек среды, то произойдет усиление амплитуды поля в число излучающих на размере среды слоев в
от разных точек среды, то произойдет усиление амплитуды поля в число излучающих на размере среды слоев в  раз. Конкретные условия такого согласования разобраны в § 3.
раз. Конкретные условия такого согласования разобраны в § 3.
Таким образом, максимально возможная интенсивность (плотность потока энергии) суммарного (разностного) излучения

Коэффициент преобразования  при
при  см и
см и  может быть порядка единицы для накачки
может быть порядка единицы для накачки  с интенсивностью порядка
с интенсивностью порядка 
Отметим, что коэффициент преобразования  линейно зависит от интенсивности накачки. При использовании в качестве накачки излучения непрерывных лазеров с интенсивностью
линейно зависит от интенсивности накачки. При использовании в качестве накачки излучения непрерывных лазеров с интенсивностью  следует ожидать значений
следует ожидать значений 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
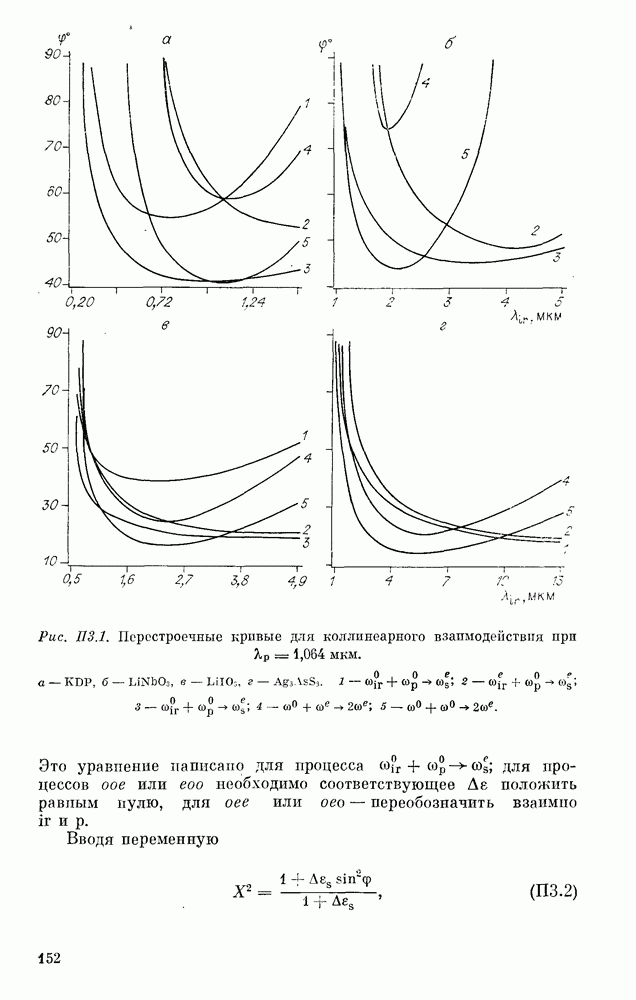
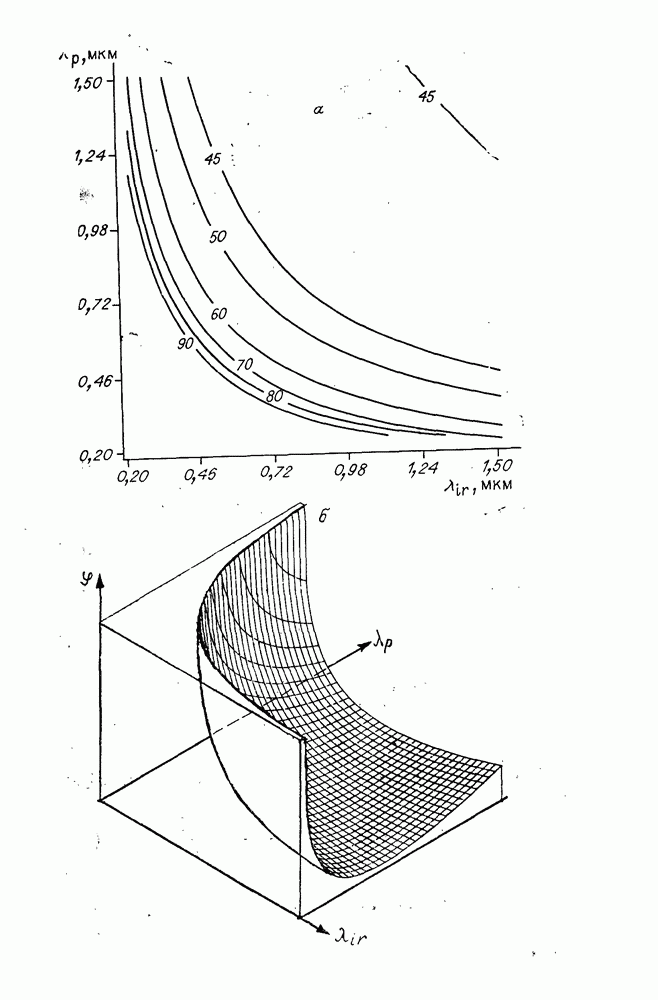
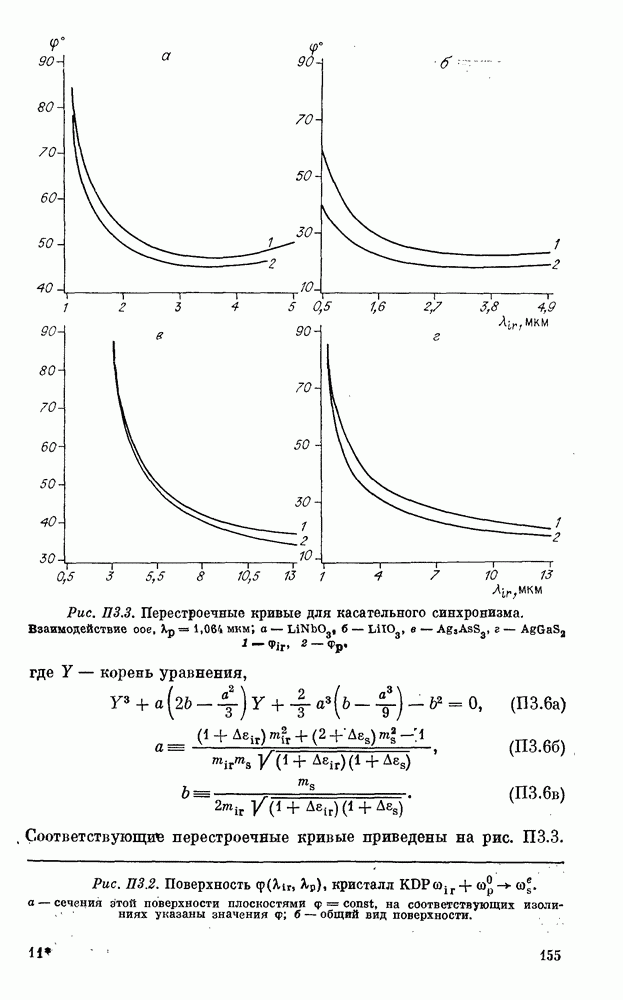
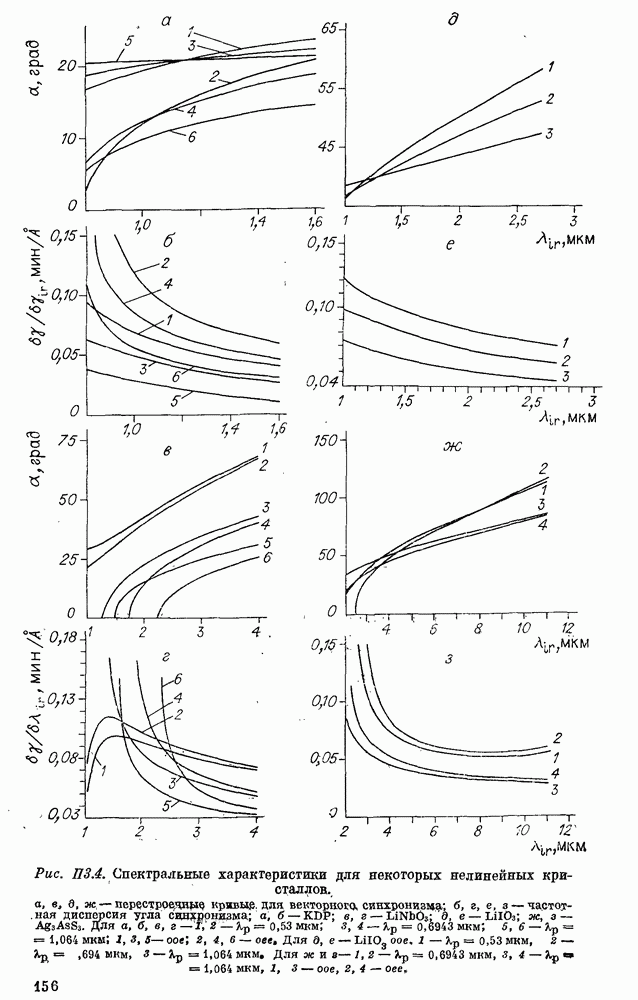
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)