§ 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ

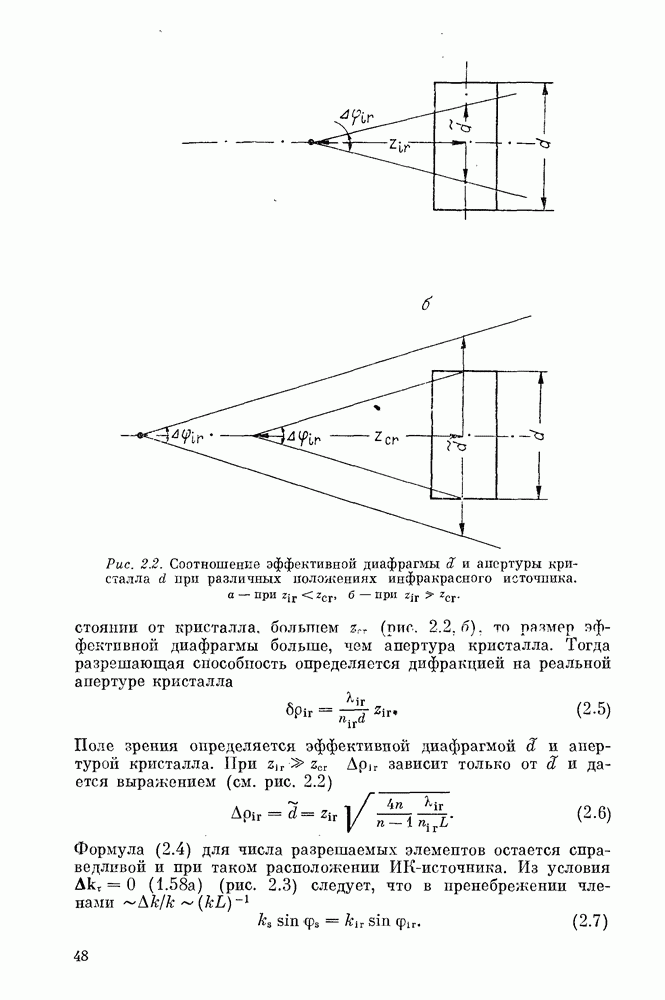
Для анализа дифракционных эффектов необходимо учесть области нелинейного кристалла, волны от которых интерферируют не в фазе. Очевидно, достаточно ограничиться теми областями, для которых разброс фазы не превышает . Последнее существенно упрощает задачу и позволяет в ряде случаев распространить установленную в приближении геометрической оптики аналогию с линейными системами на дифракционную теорию. Таким образом, задачи о пространственном распределении преобразованного излучения сводятся к рассмотренным в линейной оптике. Определение размеров почти когерентно (фаза колеблется в пределах излучающей области и дает возможность вычислить коэффициент преобразования по мощности (эффективность преобразования).

Взаимодействие двух цилиндрических волн (двумерная модель преобразователя изображения с схеме КВС)

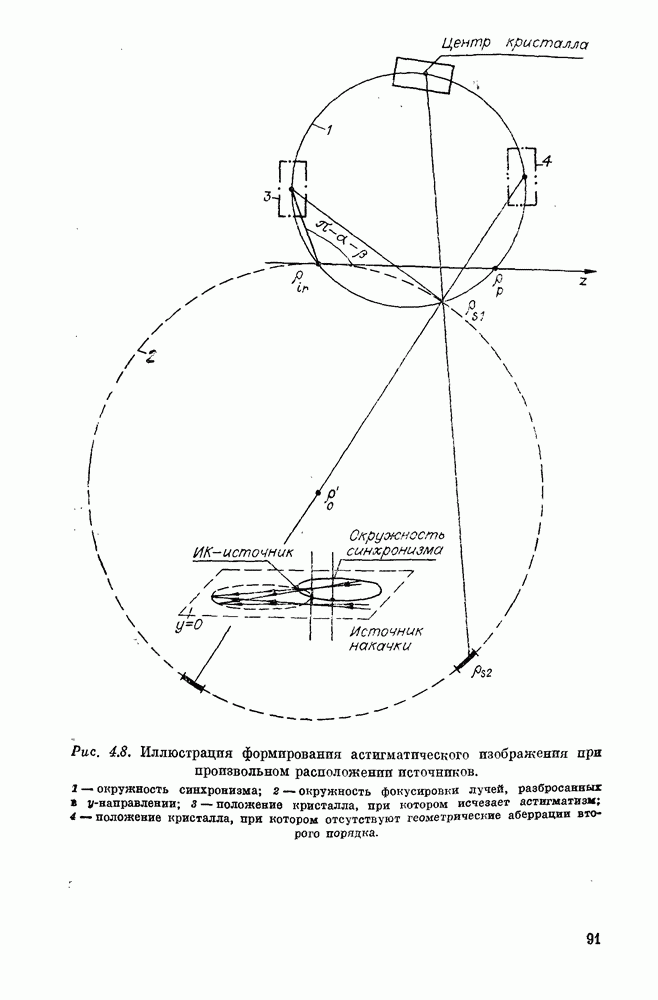
Дифракционная теория особенно важна в тех случаях, когда с точки зрения геометрической оптики изображение идеально. В схеме КВС лучи, лежащие в плоскости фокусировки накачки формируют безаберрационное изображение при произвольных апертурах. Поэтому естественно рассмотреть вначале двумерную модель преобразователя. В этой модели задача сводится к анализу взаимодействия двух цилиндрических волн, линейные источники которых параллельны друг другу (и координатной оси :

где радиус-векторы источников ИК-излучения, накачки и точки наблюдения соответственно; функция Грина двумерного волнового уравнения амплитуды линейных источников взаимодействующих волн. Система координат выбрана следующим образом. Начало лежит на оси поверхности синхронизма (из результатов § 1 следует, что поверхность синхронизма в рассматриваемом случае — цилиндр, проходящий через линейные источники взаимодействующих волн, причем ось цилиндра параллельна этим источникам). Ось также параллельна линейным источникам. Ось направлена на источник накачки.

Формула (2.27), описывающая распределение поля в преобразованном излучении, заменяется на

показатель преломления кристалла на частоте

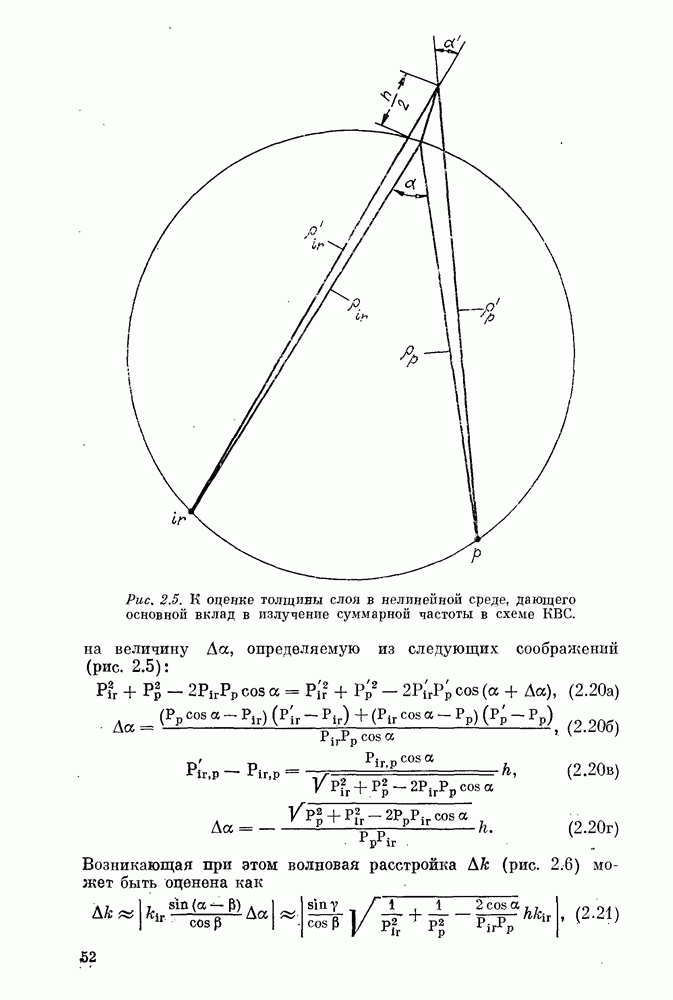
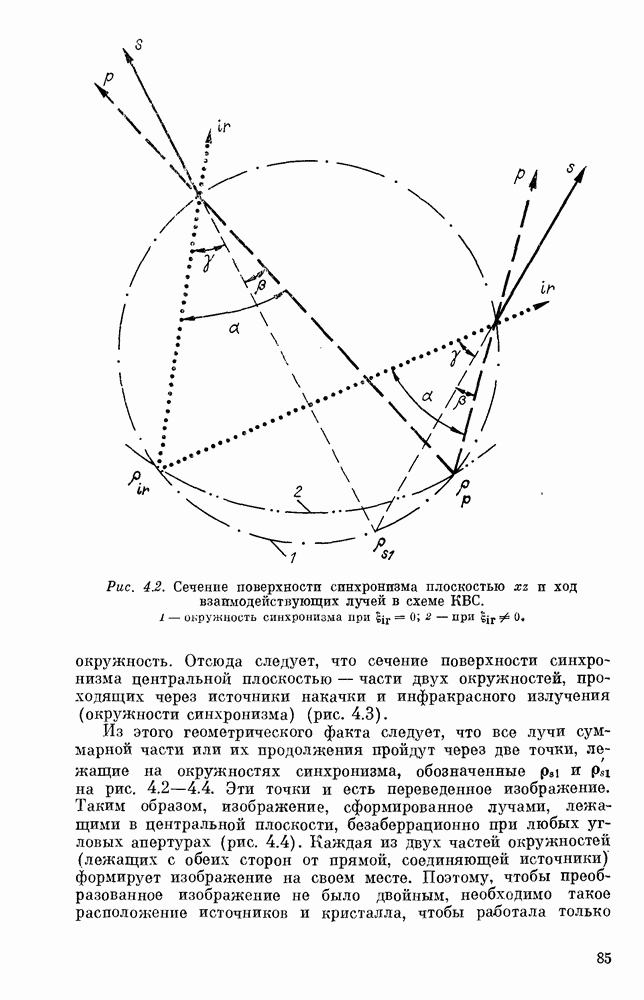
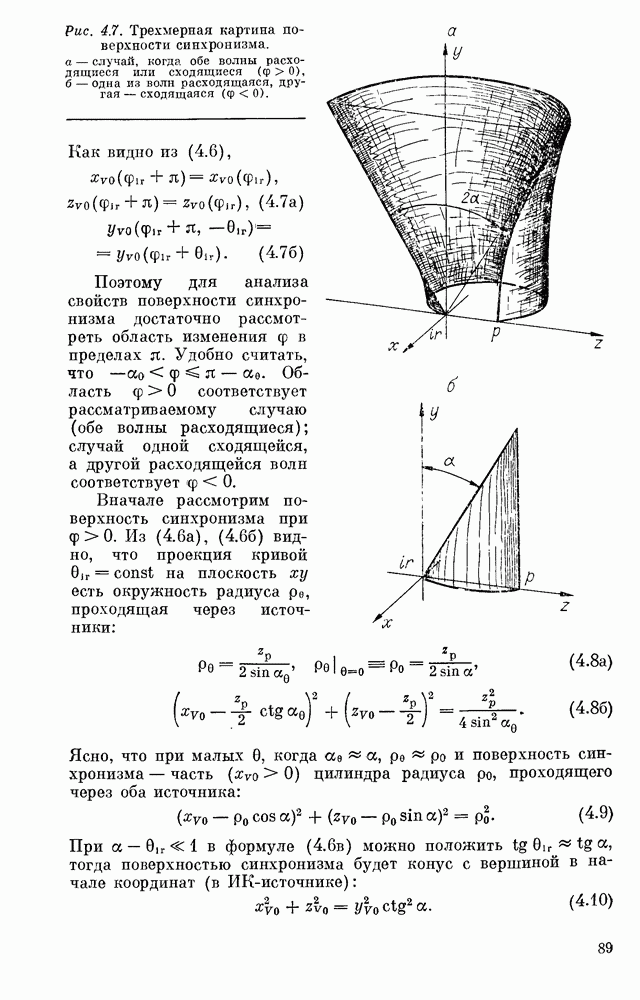
Преобразователь в данном случае формирует безаберрационное геометрическое изображение в точке (см. рис. 4.2), лежащей на окружности синхронизма (проекция цилиндрической поверхности синхронизма на плоскость (см. § 1, 2). Поэтому в приближении геометрической оптики преобразованное излучение представляет собой цилиндрическую волну, ось которой параллельна линейным источникам взаимодействующих волн и пересекает плоскость в точке

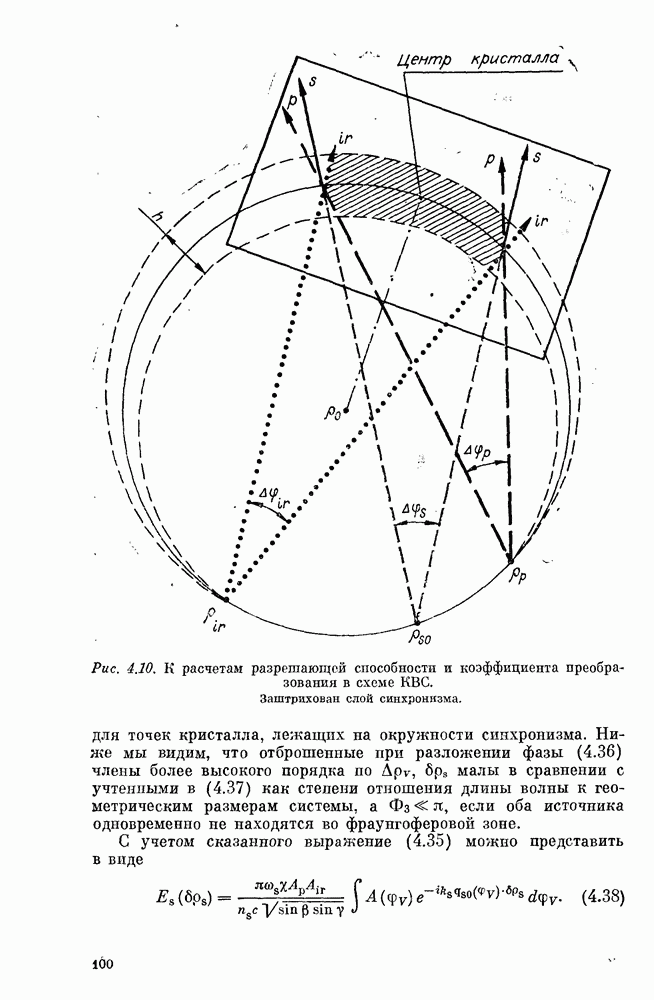
Найдем дифракционное распределение поля вблизи точки Для этого заметим (см. гл. 2, § 4), что излучение суммарной частоты генерируется в основном в слое, непосредственно прилегающем к поверхности синхронизма (рис. 4.10), и разложим фазу (4,36) в ряд Тейлора по степеням отклонений где радиус-вектор точки на окружности синхронизма. С точностью до членов второго порядка по это разложение имеет вид

где первое, второе и третье слагаемые в правой части (4.37) соответственно; единичные векторы. Индекс показывает, что значения величин берутся

Рис. 4.10. (см. скан) К расчетам разрешающей способности и коэффициента преобразования в схеме КВС. Заштрихован слой синхронизма.

для точек кристалла, лежащих на окружности синхронизма. Ниже мы видим, что отброшенные при разложении фазы (4.36) члены более высокого порядка по малы в сравнении с учтенными в (4.37) как степени отношения длины волны к геометрическим размерам системы, а если оба источника одновременно не находятся во фраунгоферовой зоне.

С учетом сказанного выражение (4.35) можно представить в виде

Здесь эффективная апертурная диафрагма:

где интеграл вероятности [226]:

толщина слоя синхронизма.

Выражая через формулы (4.40) можно переписать следующим образом:

С изменением отношения толщина слоя синхронизма меняется от минимального значения при или

до максимального при

то и выражение (4.38) принимает вид

где угол, под которым видна точка на поверхности синхронизма из точки формирования геометрического изображения Интегрирование в (4.45) ведется по всей апертуре кристалла 3.

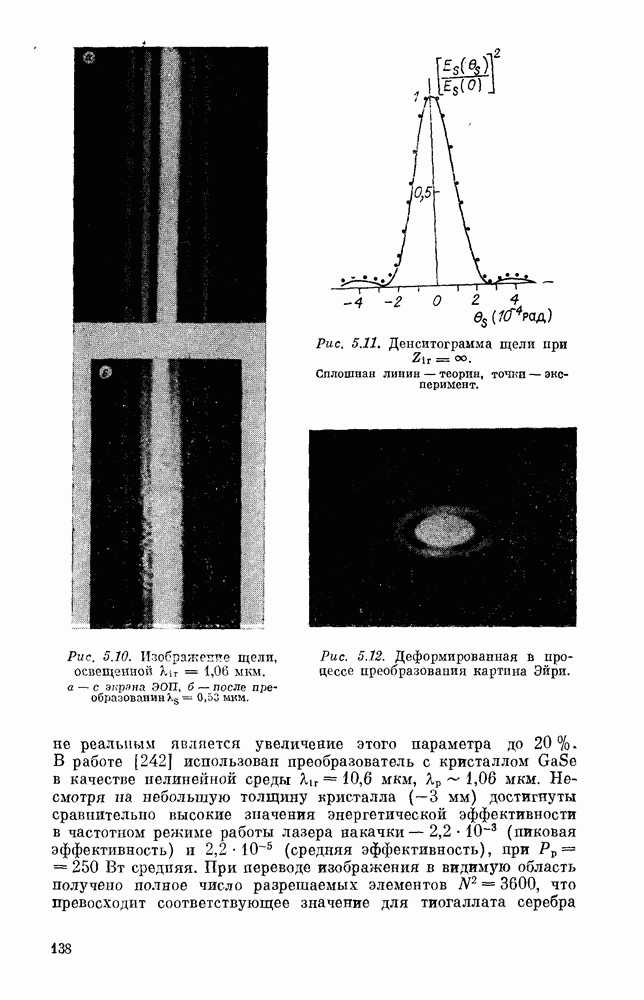
Из выражения (4.45) видно, что распределение поля в преобразованном изображении описывается интегралом Дебая [7], т. е. совпадает с дифракционным. Полуширина этого распределения в отношений меньше, чем полуширина дифракционного распределения в инфракрасном свете. Однако система обладает линейным увеличением, равным Таким образом, преобразователь в схеме критичного синхронизма в рассматриваемом случае не вносит искажений, а его разрешение определяется дифракцией инфракрасного излучения на апертуре кристалла:

где апертурные углы, под которыми виден кристалл из ИК-источника, и точки соответственно.

Выражения позволяют оценить отброшенные при вычислении члены.

Нетрудно убедиться, что если

Условие (4.47) можно ослабить, заметив, что учет приводит просто к изменению пределов интегрирования в меняется не от до а от до где определяется выражением

Если то вместо можно потребовать, чтобы т. е.

и приведенные результаты не изменятся.

Меняя знак знак как это обычно делается в оптике [7, 8], условия (4.44) и (4.47) можно записать в виде

Неравенства (4.50) означают, что оба источника одновременно не должны находиться в «поперечной» (связанной с и «продольной» (связанной с зонах Фраунгофера.

Из (4.36), (4.46) следует, что отброшенные в (4.37) члены высших степеней по малы в сравнении с учтенными, как соответствующие степени (точно так же, как и в линейной оптике). Непосредственным вычислением можно убедиться, что член относится к слагаемому как

Таким образом, приближение, связанное с переходом от (4.36) к (4.37), справедливо, когда характерные геометрические размеры системы велики по сравнению с длиной волны.

Рассмотрим предельные переходы к взаимодействию плоских волн и преобразованию в схеме касательного синхронизма Вычисления показывают, что при взаимодействии плоских волн в синхронизме и формула (4.35) с фазой приводит к известному в теории плоских волн (см. гл. 1) выражению для поля суммарной частоты. Если условия синхронизма не выполнены, то расстояние от центра кристалла до поверхности синхронизма при возрастает до бесконечности с той же скоростью, что и В результате не равно нулю, но становится линейной функцией координат точек внутри кристалла:

Нетрудно убедиться, что в этом случае совпадает с волновой расстройкой А к при взаимодействии в нелинейном кристалле плоских волн, пересекающихся под углом а, отличным от угла синхронизма а.

В случае касательного синхронизма , как видно из (4.8), (4.41), радиус окружности синхронизма стремится к бесконечности, а толщина слоя синхронизма остается конечной величиной. В итоге и фаза принимает вид, типичный для касательного синхронизма (см. § 2, гл. 3).

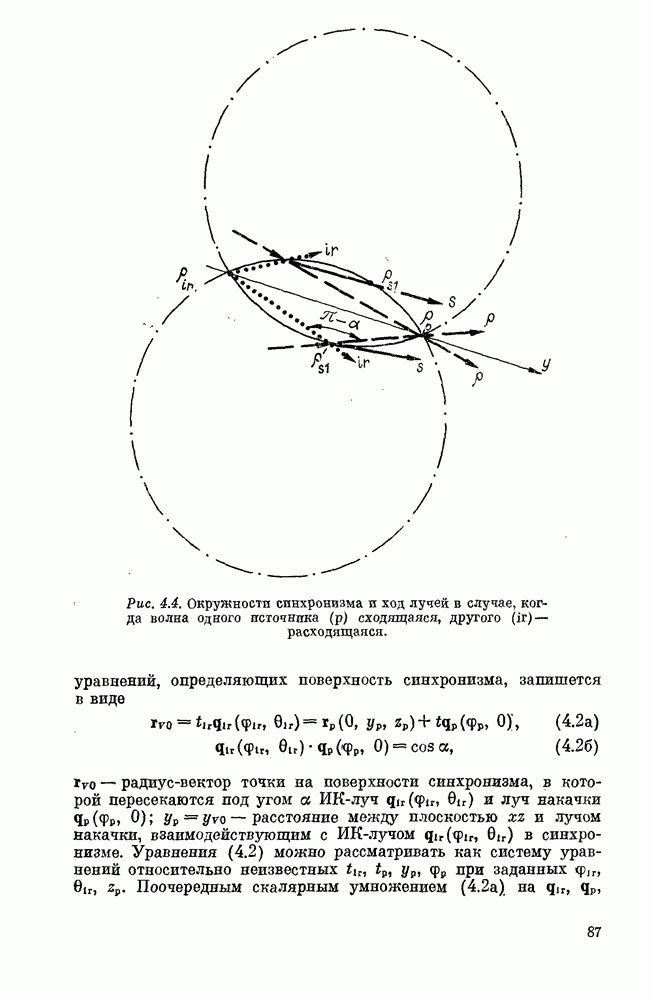
Взаимодействие сферической и цилиндрической волн в параксиальном приближении (преобразователь изображения в схеме КВС в случае малых углов зрения)

Причина, по которой рассмотренный в этом разделе вопрос представляет интерес для дифракционной теории, та что и в предыдущем разделе: в приближении геометрической оптики формируемое изображение является идеальным.

Интеграл (2.27) в данном случае принимает вид

где амплитуда сферической ИК-волны

Разложим фазу (4.5) в ряд Тейлора по аналогично тому, как это было сделано в предыдущем разделе. Дополнительно считаем, что мало и ограничимся учетом первого исчезающего (квадратичного) члена по этим параметрам. В указанном разложении, по сравнению с формулой (4.37), появятся два новых члена. Первый — связан с появлением зависимости от у:

Поскольку величина малая, в (4.54) считается, что концы векторов лежат на поверхности сипхронизма Значения величии, относящихся к изображению, формируемому лучами, разбросанными в плоскости (плоскость фокусировки накачки), будем обозначать индексом 1. Величины, относящиеся ко второму фокусу (см. гл. 4, § 3), обозначены далее индексом 2.

Второй, новый по отношению к (4.37), член связан с тем, что отклонение точки наблюдения от теперь нельзя считать малым, поскольку возникает необходимость вычислять распределение поля вблизи второго фокуса где сходятся лучи, разбросанные в плоскости Расстояние между этими фокусами может быть велико, так как система обладает астигматизмом:

Поскольку вычисляется распределепие поля в области фокусов, представляют интерес значения вблизи первого фокуса для всех членов (4.55), кроме первого, и вблизи второго

Очевидно, что в области первого фокуса

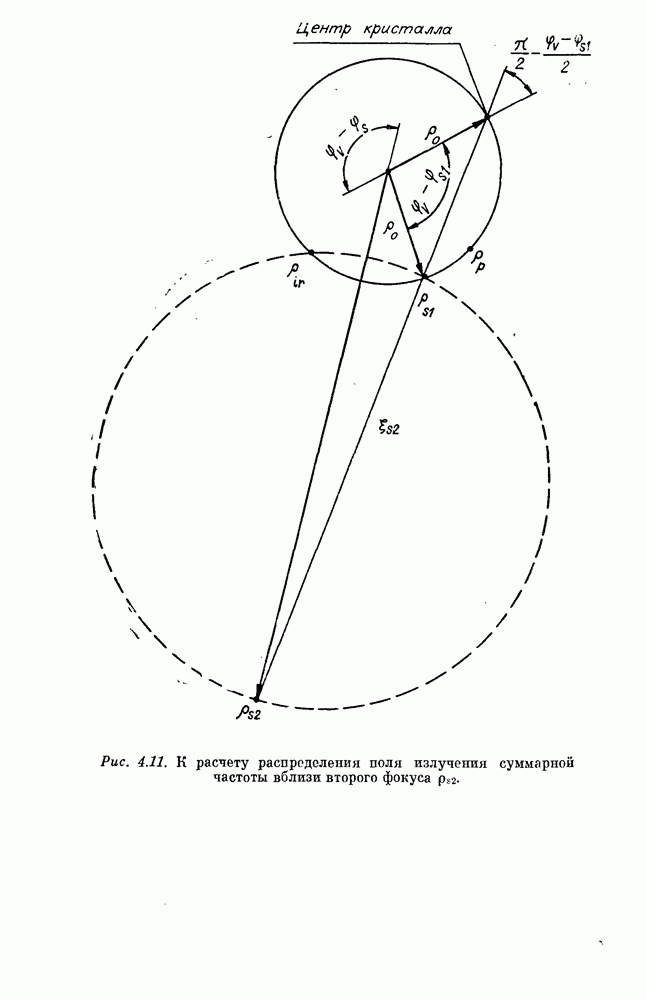
Значение в области второго фокуса можно вычислить, используя результаты, приведенные в § 3 гл. 4, и рис. 4.11. Оказывается, что линейный по член обращается в нуль,

(кликните для просмотра скана)

а квадратичный определяется выражением

В итоге, вблизи первого фокуса, как видно из выражений (4.37), (4.54), (4.56), интеграл в формуле (4.53) разбивается на произведение двух интегралов:

Последний сомножитель в выражении (4.58) только видом медленной амплитудной функции отличается от рассмотренного в предыдущем разделе интеграла (4.35). Это позволяет утверждать, что распределение электромагнитного поля частоты в плоскости фокусировки накачки имеет дифракционный характер при малых апертурах в направлении оси параллельной линейному источнику накачки, а при произвольных апертурах — в перпендикулярном направлении. В самом деле, если даже апертура велика, так что нельзя пренебрегать зависимостью фазы экспоненты в первом интепрале (4.58) от то этот интеграл не зависит от положения точки наблюдения Следовательно, зависимость его от приведет к появлению дополнительной апертурной диафрагмы. Характер распределения остается дифракционным.

Иначе обстоит дело во втором фокусе Ясно, что правая часть выражения (4.58) разобьется на произведение двух интегралов, один из которых — интеграл Дебая, если только апертуры малы в обоих направлениях:

где некоторая диафрагма, совпадающая с (4.39), когда центр нелинейного кристалла и являются концами одного и того же диаметра окружности синхронизма.

Действительно, при выводе формулы (4.59) использовалось равенство

полученное с учетом Последнее означает, что выражение (4.59) имеет место только если в можно заменить на где угловая координата центра кристалла.

Итак, распределение поля суммарной частоты в направлении оси у имеет дифракционный характер, если апертура преобразователя ограничена в обоих направлениях. Это, очевидно, является отражением установленного выше факта (если апертура велика, хотя бы в одном направлении, то изображение в фокусе формируется при наличии геометрических аберраций (гл. 4, § 3)).

Взаимодействие плоской и цилиндрической волн, произвольно ориентированных друг относительно друга (преобразование изображения бесконечно удаленного ИК-объекта в схеме КВС)

В § 1—3 показано, что при переводе изображения ИК-объекта, находящегося на бесконечности, геометрические аберрации (кроме дисторсии) отсутствуют при произвольных апертурах преобразования и произвольном положении ИК-объекта. Поэтому преобразование изображения бесконечно удаленного объекта заслуживает самостоятельного рассмотрения. В ситуациях, когда плоская ПК-волна распространяется в направлении, перпендикулярном линейному источнику, а также при неперпендикулярных, но близких к оптической оси в пространстве объектов направлениях и малых апертурах преобразования, вопрос фактически решен ранее (предыдущие два раздела параграфа). Попытаемся обобщить полученные результаты на случай произвольного распространения ИК-волны и произвольных апертур. Задача сводится к анализу взаимодействия в нелинейной среде цилиндрической волны накачки и плоской волны ИК-излучения с волновым вектиром Из формулы (4.60) следует, что геометрическое изображение на суммарной частоте расположено на бесконечности. Функция Грина в этом случае принимает вид плоской волны, волновой вектор которой определяет направление наблюдения. Фаза экспоненты в подынтегральном выражении в (2.27) может быть записана следующим образом:

Тогда распределение поля суммарной частоты дается произведением двух интегралов:

Последний сомножитель в (4.62) описывает дифракцию Фраунгофера плоской волны, преломленной на плоском преломляющем слое с показателем преломления Интеграл по форме точно совпадает с интегралом, описывающим рассмотренное выше взаимодействие двух цилиндрических волн (4.35) в предельном случае бесконечно удаленных ИК-объекта и точки наблюдения. При этом роль играют Последнее означает, что углы преломления (преобразования ИК-волны в волну частоты в плоскости при другие, чем при угол между направлением распространения и плоскостью Из формулы (4.62) и результатов, приведенных в § 2, 3, следует, что положение идеальпого изображепия дается выражениями

Формула (4.63д) включает дисторсию (см. § 3). При этом распределение поля в преобразованном излучении дифракционное в обоих направлениях.

Даже при малых углах когда дисторсией можно пренебречь, преобразованное изображение нуждается в исправлении. Дело в том, что, как видно из формул (4.63), формирование изображения в двух направлениях идет по-разному: вдоль оси происходит сжатие в раз, а в направлении оси X масштаб не меняется. Поэтому для получения изображения с правильным масштабом необходимо применять коррегирующую оптику. Изображение каждой точки в отдельности идеально и разрешающая способность определяется дифракцией на апертуре кристалла.

С учетом формул (4.31) делаем вывод, что число разрешаемых элементов параметрического преобразователя изображения в схеме КВС определяется выражением

размеры нелинейного кристалла в направлениях соответственно.