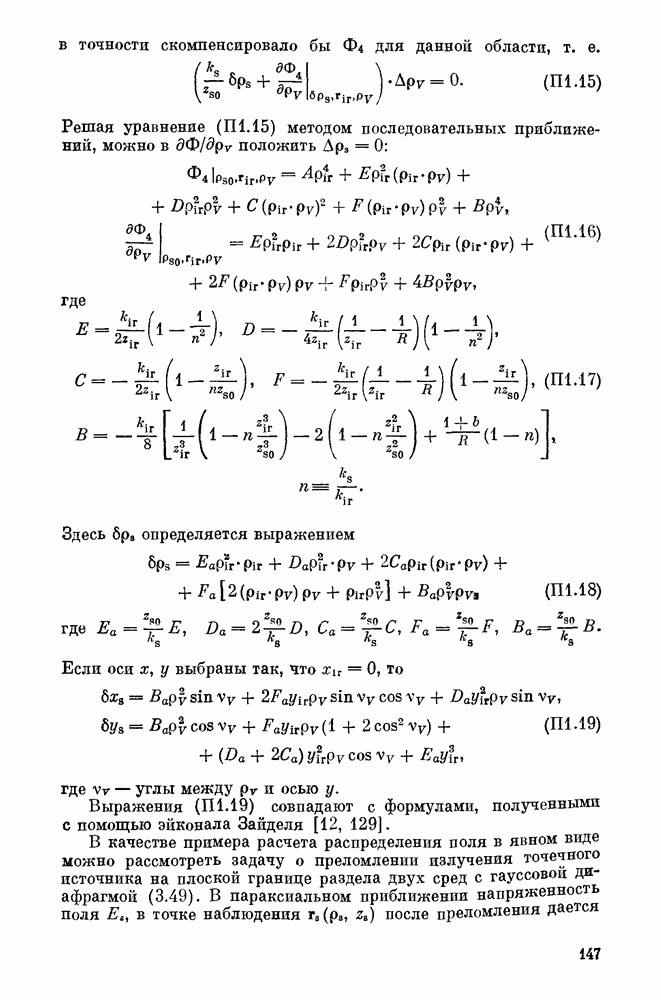| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
Для исследования преобразователя как оптического прибора удобно из специальной системы координат, введенной выше, перейти в неподвижную систему, не зависящую от положения ИК-источника и определяемую положением кристалла и источником накачки. Ясно, что в качестве оптической оси в пространстве объектов удобно выбрать прямую, проходящую через центр кристалла под углом синхронизма к направлению из кристалла на источник накачки и лежащую в плоскости  . Эта прямая является осью
. Эта прямая является осью  в пространстве объектов в неподвижной системе координат. Ось
в пространстве объектов в неподвижной системе координат. Ось  перпендикулярна к ней и лежит в плоскости
перпендикулярна к ней и лежит в плоскости  Ось
Ось  направлена по-прежнему. Начало координат совпадает с центром кристалла. Ось
направлена по-прежнему. Начало координат совпадает с центром кристалла. Ось  в пространстве изображений проходит через центр кристалла под углом
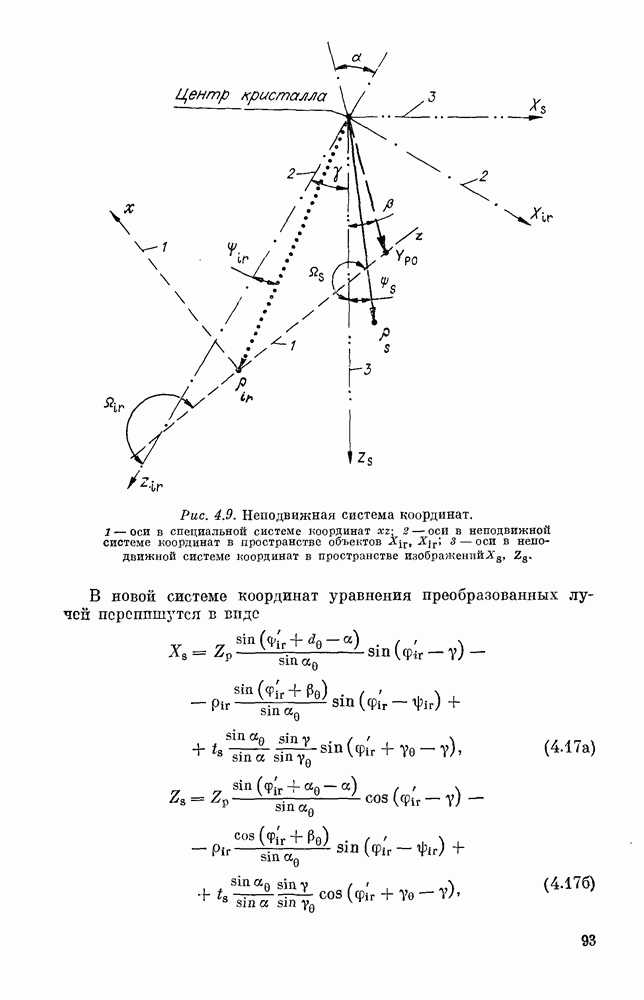
в пространстве изображений проходит через центр кристалла под углом  к направлению из кристалла на источник накачки (рис. 4.9). Положение ИК-источника в системе координат пространства объектов характеризуется вектором
к направлению из кристалла на источник накачки (рис. 4.9). Положение ИК-источника в системе координат пространства объектов характеризуется вектором

где  угол между проекцией
угол между проекцией  на плоскость
на плоскость  радиус вектора
радиус вектора  и осью
и осью 

Рис. 4.9. Неподвижная система координат. 1 — оси в специальной системе координат  2 - оси в неподвижной системе координат в пространстве объектов
2 - оси в неподвижной системе координат в пространстве объектов  3 - оси в неподвижной системе координат в пространстве изображений,
3 - оси в неподвижной системе координат в пространстве изображений, 
В новой системе координат уравнения преобразованных лучей перепишутся в виде


где  расстояние от центра кристалла до источника накачки;
расстояние от центра кристалла до источника накачки;  полярный угол ИК-луча относительно оси
полярный угол ИК-луча относительно оси 

Безаберрационное астигматическое изображение определяется формулами (см. также [217]):

Положение фокусов дается выражениями:

Как видно из равенства (4.196), изображения точек, лежащих на разных расстояниях  от оси, формируются при разных
от оси, формируются при разных  Этот факт можно трактовать как наличие у системы аберрации типа кривизны поля:
Этот факт можно трактовать как наличие у системы аберрации типа кривизны поля:

При получении (4.20) использованы формулы связи  и координат в плоскости входного зрачка
и координат в плоскости входного зрачка  координаты пересечения данного ИК-луча с плоскостью
координаты пересечения данного ИК-луча с плоскостью 

Формулы (4.19а), (4.196) являются частным случаем  в (2.53) соотношений, описывающих взаимодействие двух астигматических пучков.
в (2.53) соотношений, описывающих взаимодействие двух астигматических пучков.
Из выражений (4.19) следует, что изображение становится стигматическим в двух случаях — когда  либо если
либо если  источник расположен в точке
источник расположен в точке 

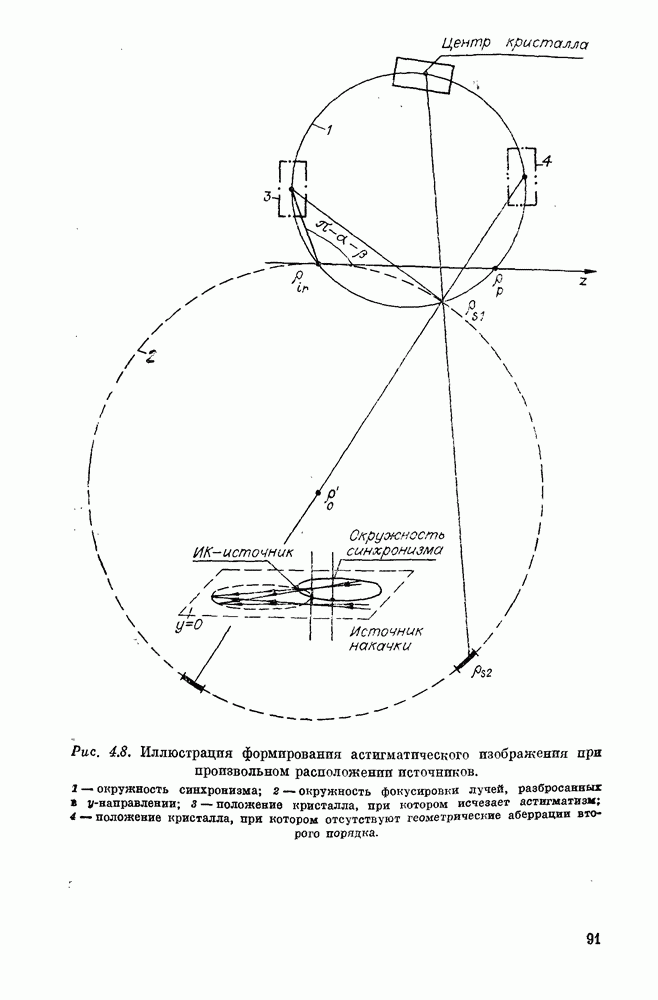
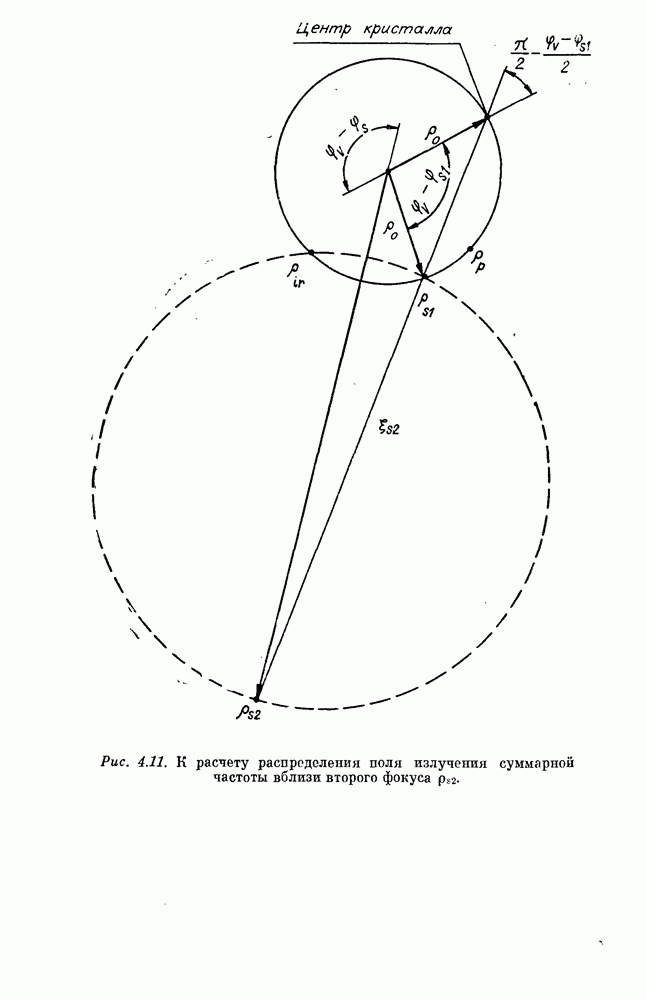
Формула (4.22) может быть получена также из простых геометрических соображений (см. рис. 4.8).
Рассмотрим геометрические аберрации преобразователя. Для простоты расчетов ограничимся только осевыми аберрациями. Заметим, что в силу симметрии задачи внеосевые аберрации, связанные с отклонением ИК-источника от оптической оси в направлении  можно получить заменой в формулах для осевых аберраций
можно получить заменой в формулах для осевых аберраций  на
на  Единственная, связанная с отклонением в направлении X, внеосевая аберрация второго порядка определяется формулой (4.20). Поэтому фактически не рассматриваются только внеосевые аберрации третьего порядка, связанные с отклонением вдоль оси
Единственная, связанная с отклонением в направлении X, внеосевая аберрация второго порядка определяется формулой (4.20). Поэтому фактически не рассматриваются только внеосевые аберрации третьего порядка, связанные с отклонением вдоль оси  Общий вид аберраций третьего порядка включительно в системах без оси симметрии выражается следующими формулами:
Общий вид аберраций третьего порядка включительно в системах без оси симметрии выражается следующими формулами:

Симметрия системы приводит к тому, что часть аберраций в (4.23) обращается в нуль. Во-первых, при  изображение в первом фокусе безаберрационно.
изображение в первом фокусе безаберрационно.  Следовательно.
Следовательно.  Далее, при замене
Далее, при замене  на
на  не должно меняться, а
не должно меняться, а  должен смениться знак. Поэтому
должен смениться знак. Поэтому  Окончательно
Окончательно

Вычисления, основанные на равенствах (4.17), дают:


 могут быть получены из геометрических соображений (см. рис. 4.8). Аберрация
могут быть получены из геометрических соображений (см. рис. 4.8). Аберрация  связана с тем, что отрезок окружности, на которой лучи фокусируются в направлении У, не перпендикулярен направлению к центру кристалла. Параметр
связана с тем, что отрезок окружности, на которой лучи фокусируются в направлении У, не перпендикулярен направлению к центру кристалла. Параметр  учитывает кривизну этого отрезка. Из формулы (4.25) видно, что обе аберрации второго порядка исчезают одновременно при
учитывает кривизну этого отрезка. Из формулы (4.25) видно, что обе аберрации второго порядка исчезают одновременно при

Аберрации третьего порядка в такой конфигурации определяются выражениями

Из формул (4.27) следует, что при преобразовании изображения бесконечно удаленного объекта все аберрации, кроме дисторсии, обращаются в нуль.
Дисторсия описывается формулой

 угол между направлением из кристалла в бесконечно удаленный ИК-источник и плоскостью
угол между направлением из кристалла в бесконечно удаленный ИК-источник и плоскостью 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
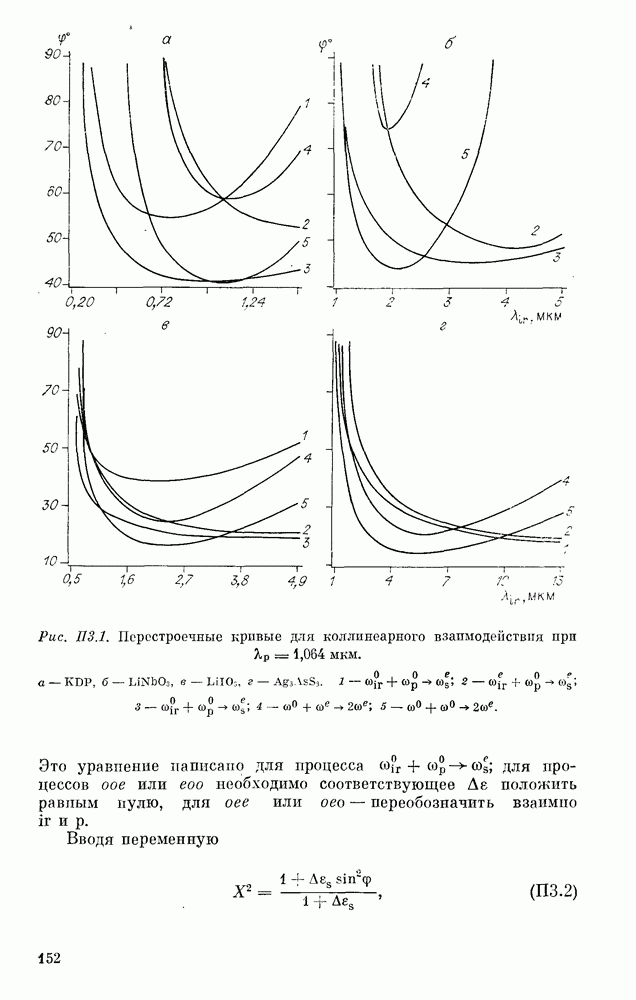
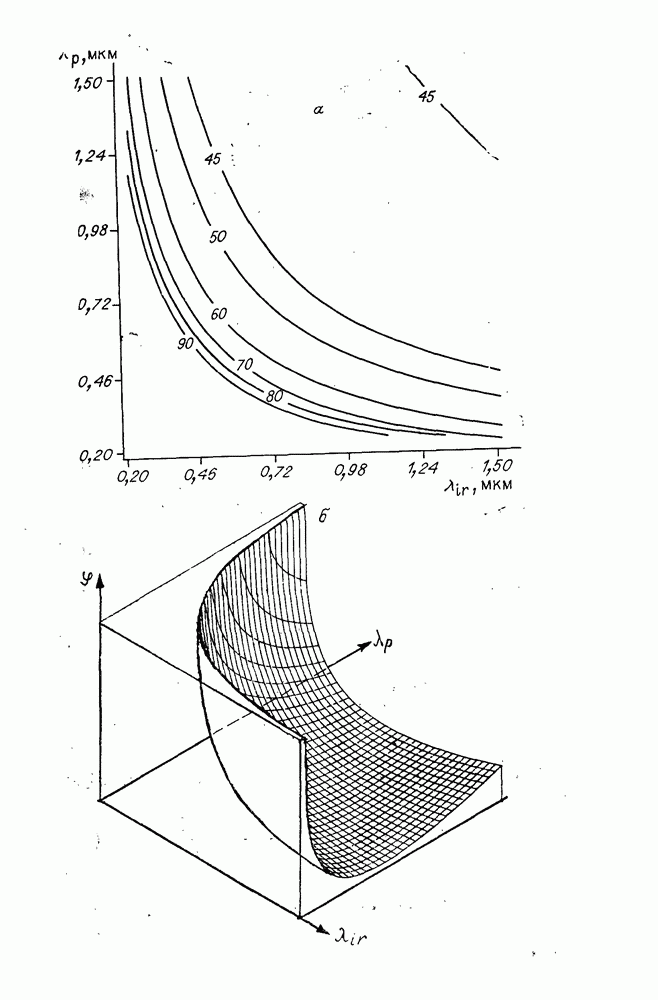
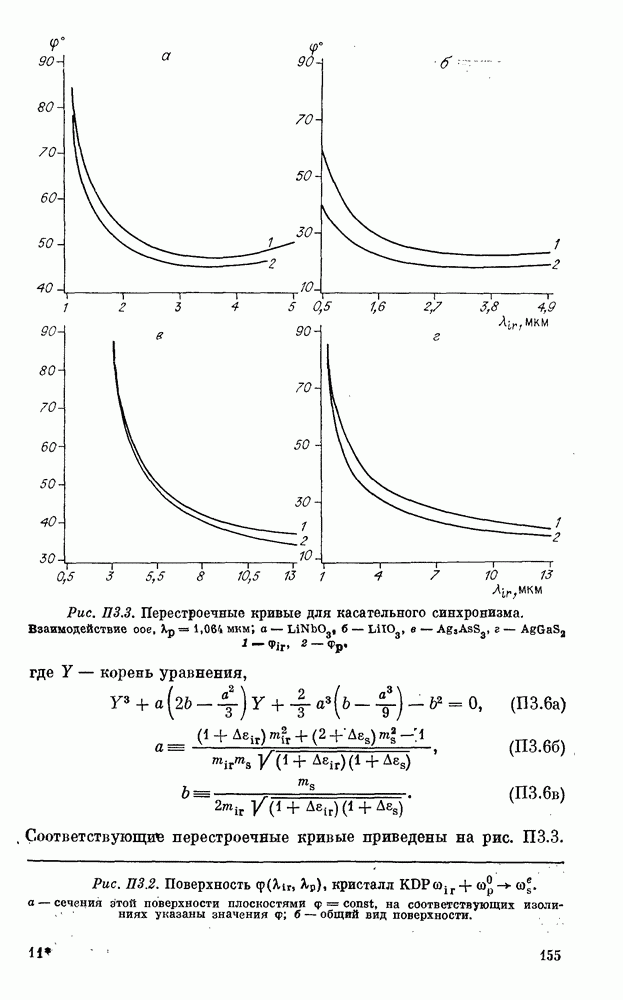
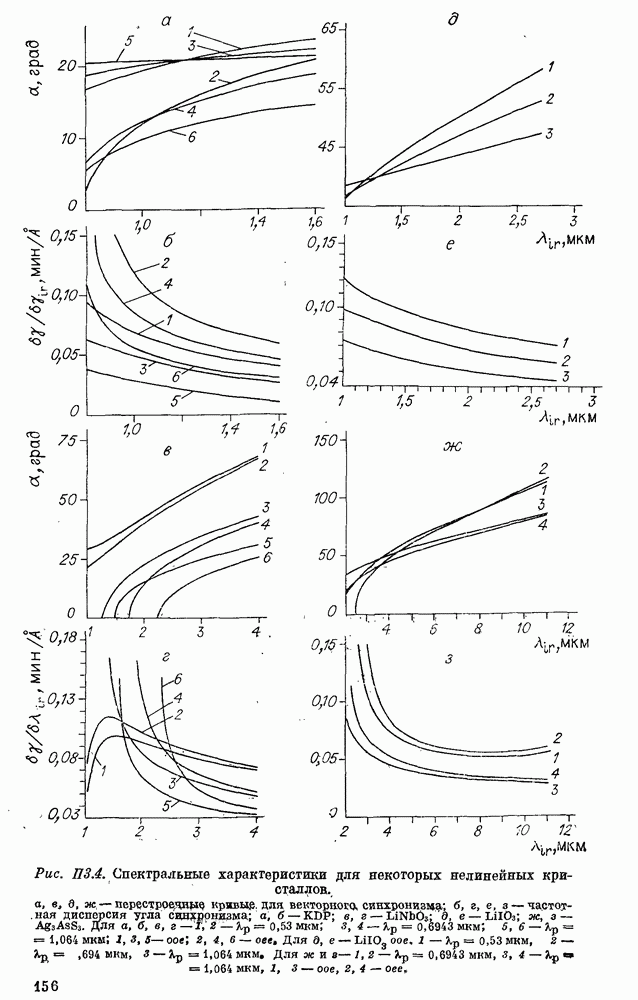
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)