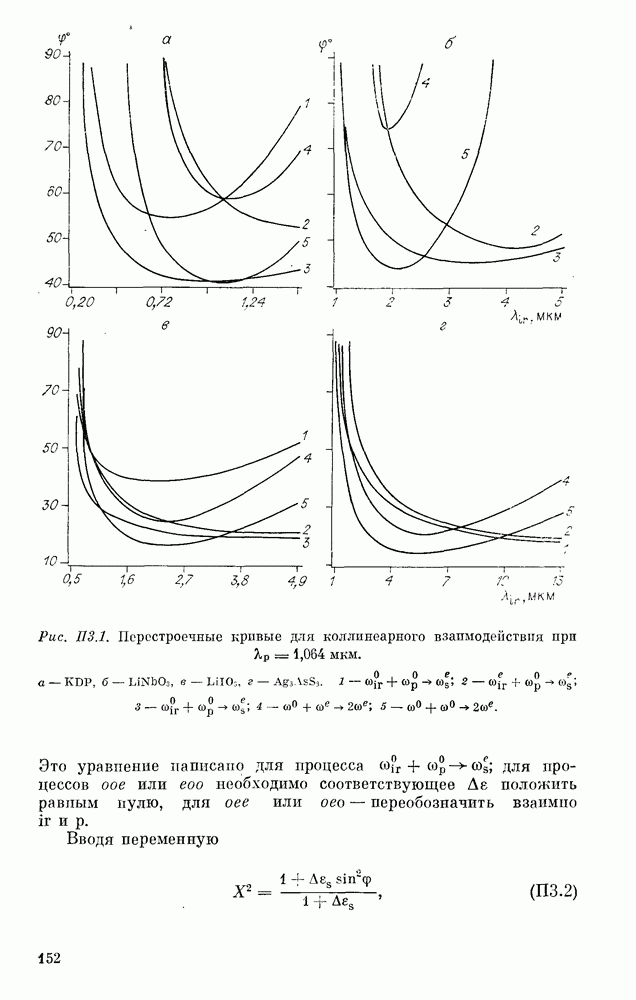
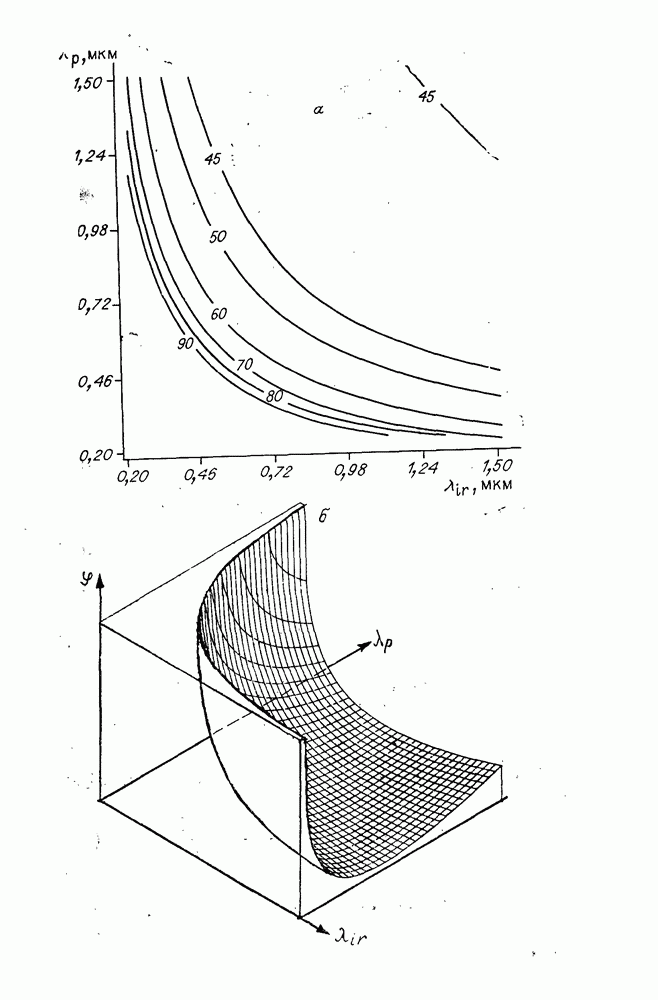
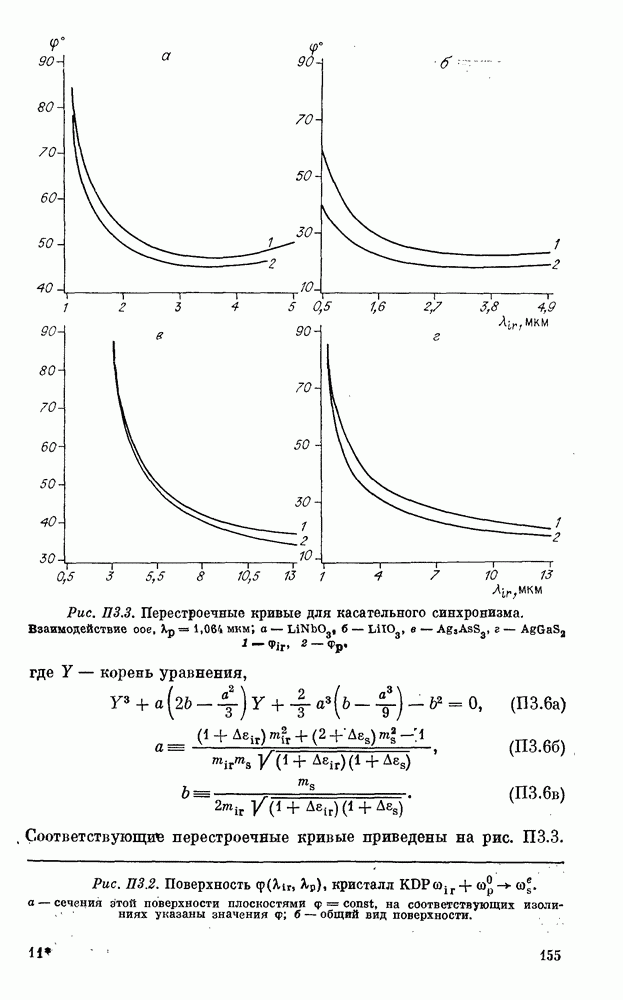
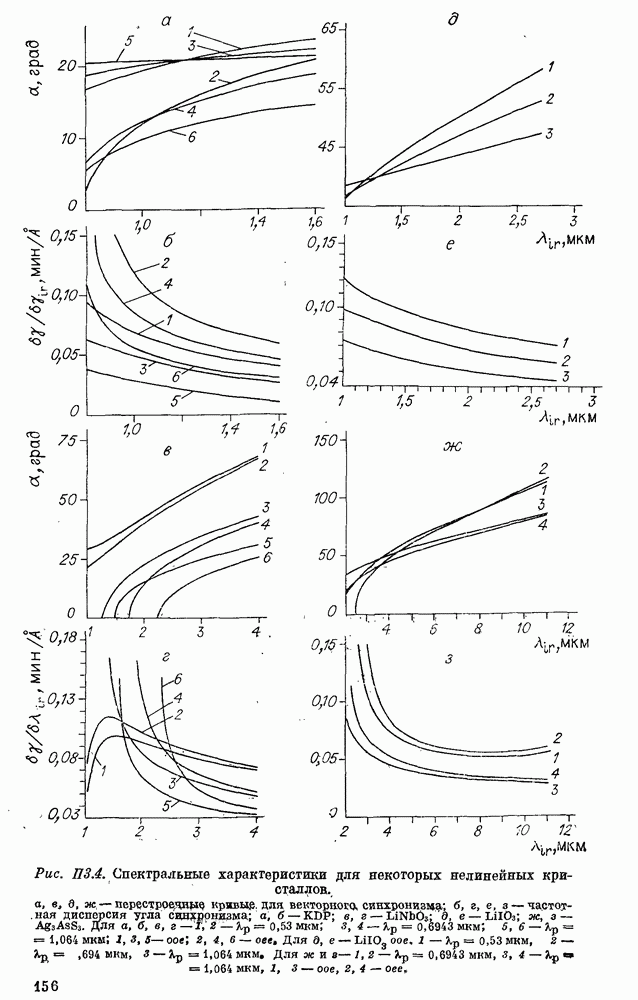
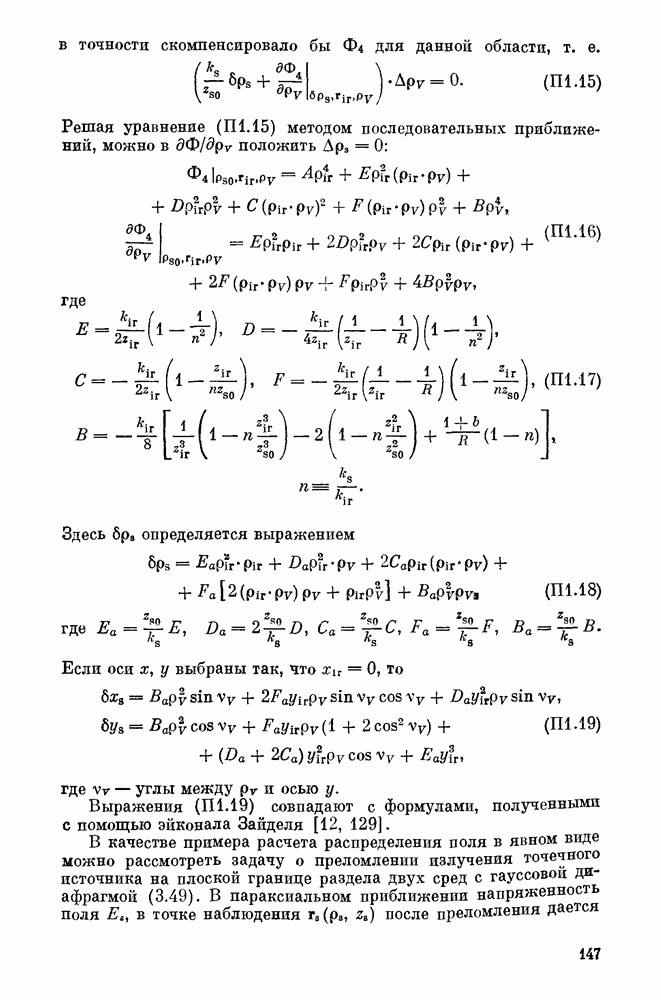| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
Подход функций Грина позволил проследить аналогию между нелинейно-оптическим преобразователем и определенной линейной оптической системой. Тем самым выяснены основные свойства преобразователей. Однако для решения некоторых конкретных вопросов более удобен подход, связанный с разложением по плоским волнам взаимодействующих полей. Все это относится прежде всего к расчету преобразователей с большими коэффициентами преобразования, когда становится несправедливым приближение заданного поля по ИК-сигналу. Для упрощения вычислений рассмотрим случай несфокусированной накачки (плоская волна, распространяющаяся вдоль оси  и ограничимся параксиальным приближением
и ограничимся параксиальным приближением  что означает сравнительно большие
что означает сравнительно большие  Именно в такой ситуации прежде всего могут реализовываться большие коэффициенты преобразования. Процедура расчета состоит в следующем. Разлагаем электрическое поле ИК-излучення в плоскости объекта
Именно в такой ситуации прежде всего могут реализовываться большие коэффициенты преобразования. Процедура расчета состоит в следующем. Разлагаем электрическое поле ИК-излучення в плоскости объекта  в двумерный пространственный
в двумерный пространственный  интеграл Фурье. Пользуясь дисперсионной связью
интеграл Фурье. Пользуясь дисперсионной связью  находим распределение ИК-излучения на входной грапи нелинейной среды. С помощью формул (1.128), (1.130) или (1.132) находим распределение рожденного сигнального излучения частоты
находим распределение ИК-излучения на входной грапи нелинейной среды. С помощью формул (1.128), (1.130) или (1.132) находим распределение рожденного сигнального излучения частоты  на выходной грани нелинейной среды. Дисперсионная связь
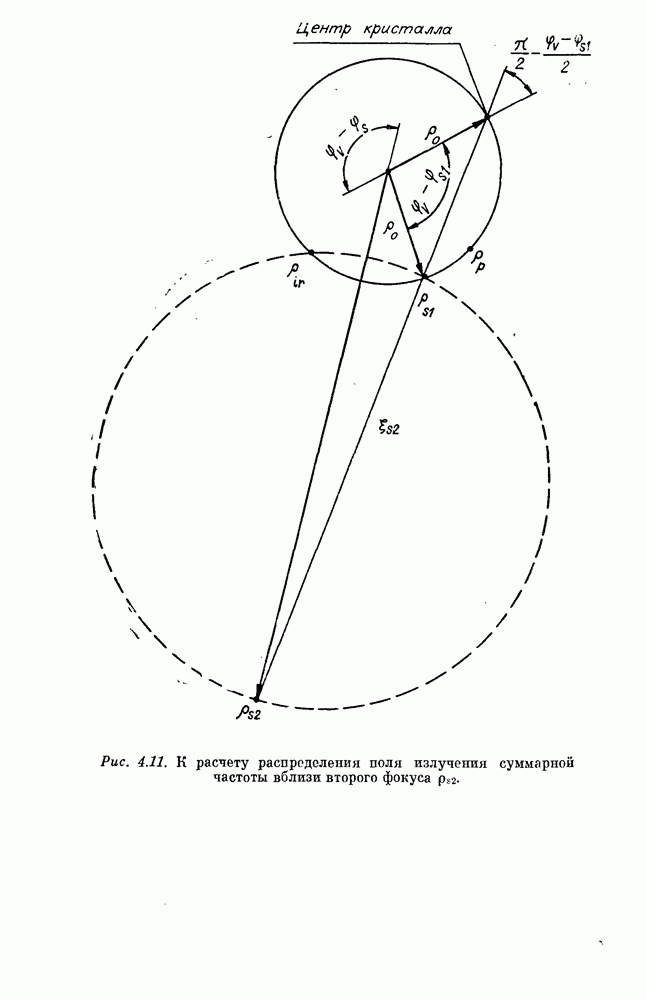
на выходной грани нелинейной среды. Дисперсионная связь  позволяет затем вычислить распределение излучения суммарной частоты в любой плоскости наблюдения
позволяет затем вычислить распределение излучения суммарной частоты в любой плоскости наблюдения  Для моделирования апертурных эффектов будем считать, что на входной границе нелинейной среды паходится диафрагма с распределенной по гауссовскому закону амплитудной прозрачностью
Для моделирования апертурных эффектов будем считать, что на входной границе нелинейной среды паходится диафрагма с распределенной по гауссовскому закону амплитудной прозрачностью

Теорема Бореля о свертке для фурье-преобразований [226] позволяет вычислить фурье-образ инфракрасной волны на входной грани нелинейной среды после диафрагмы. Используя (3.47) и  имеем
имеем

с помощью (1.126), (1.128) или (1.130), а также  и учитывая, что в каждой сигнальной волне, рожденной ИК-волной с данным
и учитывая, что в каждой сигнальной волне, рожденной ИК-волной с данным  можно найти пространственный фурье-образ (по х, у) поля суммарной частоты на выходной грани нелинейной среды
можно найти пространственный фурье-образ (по х, у) поля суммарной частоты на выходной грани нелинейной среды  . С учетом
. С учетом  пересчитываем
пересчитываем  в плоскость
в плоскость  и выполняя обратное фурье-преобразование по
и выполняя обратное фурье-преобразование по  вычисляем пространственное распределение поля суммарной частоты в плоскости наблюдения
вычисляем пространственное распределение поля суммарной частоты в плоскости наблюдения 

где введенная в [159, 160] функция разброса

Для построения теории прибора достаточно рассмотреть преобразование излучения точечного источника, т. е. сферической волны. Однако в параксиальном приближении распределение поля точечного источника в плоскости  аппроксимируется дельта-функцией. В самом деле, в смысле формирования изображения источник ведет себя как точечный, если его размеры много меньше
аппроксимируется дельта-функцией. В самом деле, в смысле формирования изображения источник ведет себя как точечный, если его размеры много меньше  но могут быть еще велики по сравнению с
но могут быть еще велики по сравнению с  Тогда дифракционная расходимость излучения такого источника еще мала и в плоскости
Тогда дифракционная расходимость излучения такого источника еще мала и в плоскости  поле заметно отличается от нуля только в самом источнике. Непосредственным вычислением можно
поле заметно отличается от нуля только в самом источнике. Непосредственным вычислением можно
убедиться, что пространственные спектры  сферической волны и
сферической волны и  -образного источника в плоскости входной грани нелинейной среды совпадают в параксиальном приближении. Сказанное означает, что сама функция разброса
-образного источника в плоскости входной грани нелинейной среды совпадают в параксиальном приближении. Сказанное означает, что сама функция разброса  в параксиальном приближении описывает распределение преобразованного излучения точечного ИК-источника.
в параксиальном приближении описывает распределение преобразованного излучения точечного ИК-источника.
В пренебрежении анизотропией  и выражение для функции разброса после перехода к полярным координатам по
и выражение для функции разброса после перехода к полярным координатам по  и интегрирования по углу принимает вид
и интегрирования по углу принимает вид

 функция Бесселя,
функция Бесселя,  определяется выражением (3.506).
определяется выражением (3.506).
Без учета внеинтегрального фазового множителя поле в двух плоскостях наблюдения  симметричпых относительно плоскости
симметричпых относительно плоскости  такой, что
такой, что 

комплексно сопряжено; а при  поле чисто действительно, аналогично распределению поля относительно фокуса идеальной линзы. При
поле чисто действительно, аналогично распределению поля относительно фокуса идеальной линзы. При

(3.526) совпадает с (3.9а) при  и с учетом различия на начало координат в этих формулах.
и с учетом различия на начало координат в этих формулах.
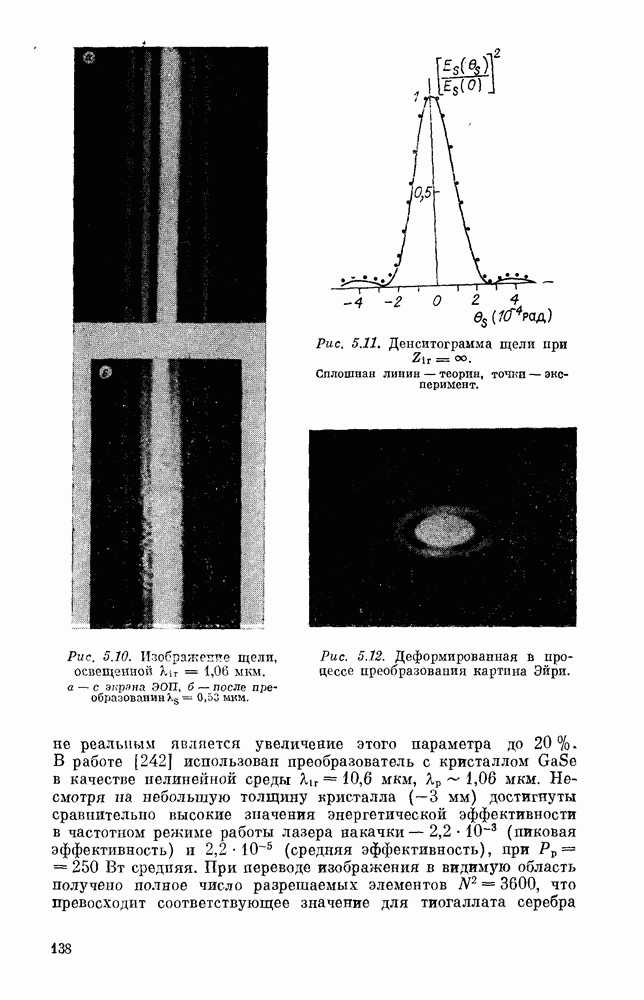
В условиях (3.53) можно выполнить интегрирование в (3.51) и получить аналитическое выражение для функции разброса 1163]:


В плоскости формирования идеального изображения  имеем
имеем

В случае слабой анизотропии членами порядка  можно пренебречь, сохранив члены порядка
можно пренебречь, сохранив члены порядка  Из (3.50) следует, что выражение для функции разброса с точностью до фазового множителя совпадает с (3.51), если в последнем сделать замену
Из (3.50) следует, что выражение для функции разброса с точностью до фазового множителя совпадает с (3.51), если в последнем сделать замену 

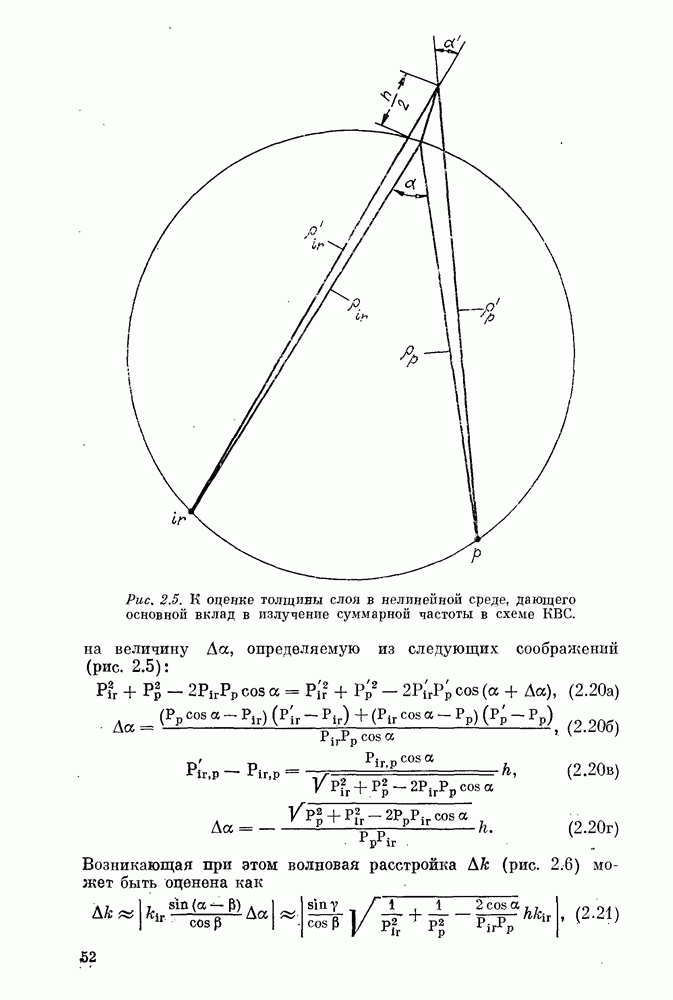
Сказанное означает, что слабая анизотропия не меняет формы распределения поля суммарной частоты, но приводит к сносу изображения в направлении х на величину 
Подробный анализ распределения поля в фокальной области проведен в работе [21,7], где предложены простые аппроксимации функции разброса, полученные заменой множителя —X в (3.51) на более простые для интегрирования множителя  или на
или на  Такие аппроксимации позволили провести приближенный анализ распределения поля суммарной частоты вблизи фокуса при произвольных расположениях ИК-источника относительно нелинейного кристалла.
Такие аппроксимации позволили провести приближенный анализ распределения поля суммарной частоты вблизи фокуса при произвольных расположениях ИК-источника относительно нелинейного кристалла.
Анализ, проведенный в настоящем параграфе, позволяет сделать следующие выводы [159—163, 180, 191, 217]:
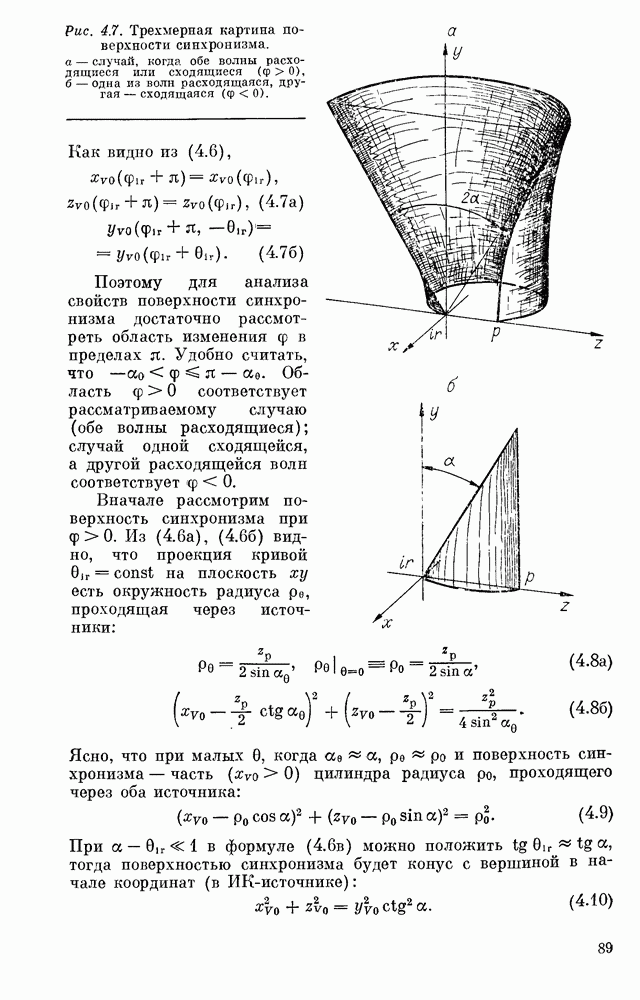
I. В пренебрежении анизотропией кристалла  при
при  в условиях
в условиях  что соответствует френелевской зоне апертурной диафрагмы, положение плоскости наблюдения z с минимальной характерной шириной функции разброса определяется формулой
что соответствует френелевской зоне апертурной диафрагмы, положение плоскости наблюдения z с минимальной характерной шириной функции разброса определяется формулой

Точка  этой плоскости, в которой яркость максимальна, дается равенством (3.23). В двух плоскостях
этой плоскости, в которой яркость максимальна, дается равенством (3.23). В двух плоскостях  расположенных на равных расстояниях от плоскости
расположенных на равных расстояниях от плоскости  поля являются взаимно комплексно сопряженными друг другу, подобно тому, как это имеет место в области фокуса идеальной линзы. В области
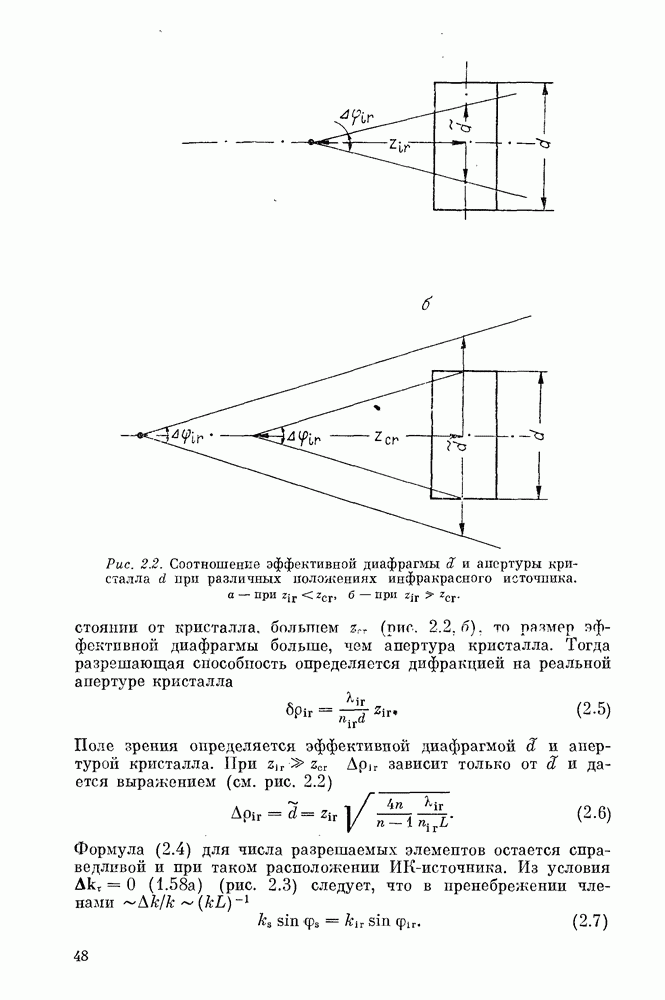
поля являются взаимно комплексно сопряженными друг другу, подобно тому, как это имеет место в области фокуса идеальной линзы. В области  разрешающая способность дается формулой (2.3), а при
разрешающая способность дается формулой (2.3), а при  размытие изображения связано только с дифракцией на диафрагме (3.47). Продольное размытие изображения также соответствует дифракции на диафрагмах
размытие изображения связано только с дифракцией на диафрагме (3.47). Продольное размытие изображения также соответствует дифракции на диафрагмах  угловой ширины синхронизма
угловой ширины синхронизма  формулу
формулу  при
при  или (3.47) при
или (3.47) при  Поле зрения при этом равно
Поле зрения при этом равно  или определяется формулой (2.6) соответственно. В фраунгофоровской зоне диафрагмы (3.47) угловое разрешение определяется дифракцией на ней, а угловое поле зрения — угловой шириной синхронизма (2.1). Число разрешаемых элементов во всех случаях одинаково и совпадает с оценкой (2.4).
или определяется формулой (2.6) соответственно. В фраунгофоровской зоне диафрагмы (3.47) угловое разрешение определяется дифракцией на ней, а угловое поле зрения — угловой шириной синхронизма (2.1). Число разрешаемых элементов во всех случаях одинаково и совпадает с оценкой (2.4).
2. Слабая анизотропия (позволяющая пренебречь членами в (3.50) и (3.54) с сохранением членов  не меняет никаких характеристик преобразователя по сравнению с изотропной нелинейной средой. Как видно из (3.50), учет анизотропии приводит лишь к сносу изображения на величину
не меняет никаких характеристик преобразователя по сравнению с изотропной нелинейной средой. Как видно из (3.50), учет анизотропии приводит лишь к сносу изображения на величину 

3. Введение небольшой положительной расстройки Д/со увеличивает эффективную угловую ширину синхронизма и, как следствие, несколько растет разрешающая способность. Оптимальное значение расстройки  При этом разрешающая способность улучшается в два раза.
При этом разрешающая способность улучшается в два раза.
4. При больших коэффициентах преобразования передаточная функция в представлении нелинейной среды меняется — вместо фактора  имеем фактор
имеем фактор  (см.
(см. 
Как показал численный анализ выражения (3.54), проведенный в работе [180], это обстоятельство практически не меняет характерного размера размытия, хотя несколько уменьшает амплитуду главного максимума  и отношение этой амплитуды к амплитуде второго максимума.
и отношение этой амплитуды к амплитуде второго максимума.
Итак, расчеты разложением по плоским волнам и с использованием подхода функций Грина всех основных характеристик схемы касательного синхронизма с накачкой в виде плоской
волны дают практически совпадающие результаты. Однако подход функций Грина имеет преимущество: он позволяет с самого начала установить аналогию НПИ с линейными оптическими системами и тем самым понять общие свойства таких преобразователей, влияние на формирование изображения различной фокусировки накачки и т. д. Для расчета конкретных характеристик можно воспользоваться хорошо разработанной теорией линейных оптических систем и тем самым резко упростить вычисления. Наконец, в таком варианте построения теории классификация искажений изображения идет в терминах обычной теории оптических приборов, что облегчает использование линейных оптических систем на входе и выходе преобразователя для требуемого в конкретных случаях улучшения изображения. Вместе с тем учет некоторых факторов в рамках разложения по плоским волнам оказывается значительно проще. Если коэффициент преобразования близок к единице, то нарушение приближеиия заданного поля по ИК-сигналу усложняет расчет несущественно (в выражении (3.50) просто меняется конкретный вид передаточной функции нелинейной среды). В то же время в подходе с использованием функций Грина весь расчет нужно начинать сначала и вместо вычисления интеграла (2.27) необходимо решить систему интегральных уравнений типа (2.27) для полей суммарной частоты и ИК-излучения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
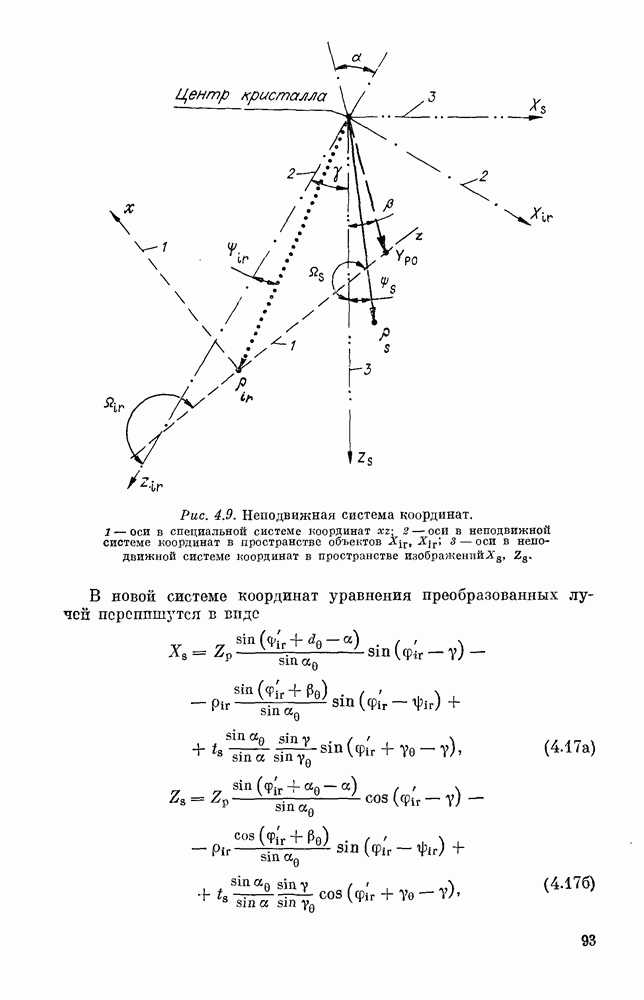
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
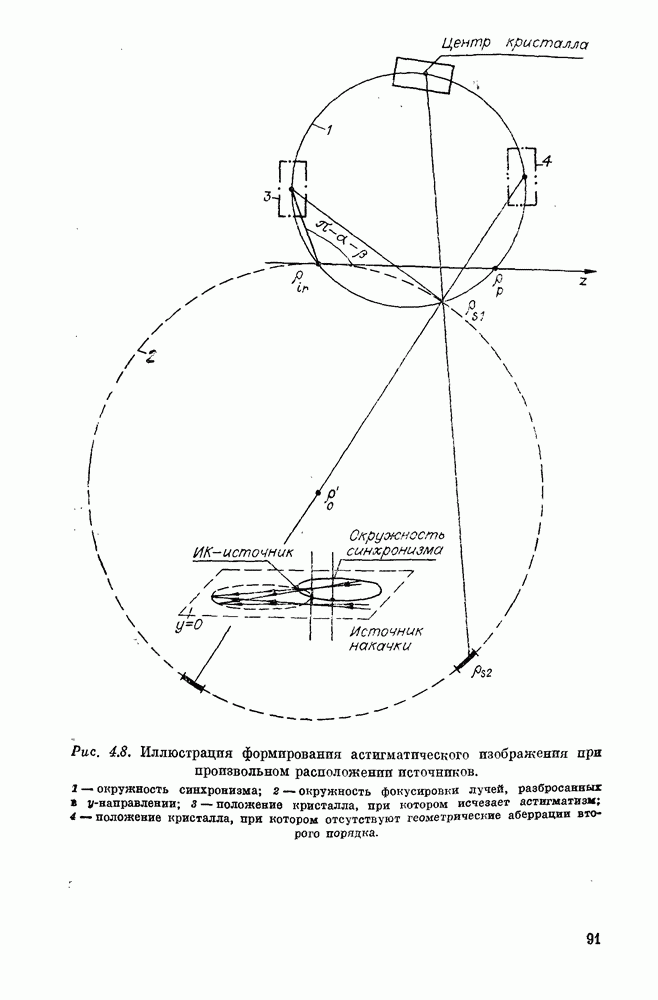
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
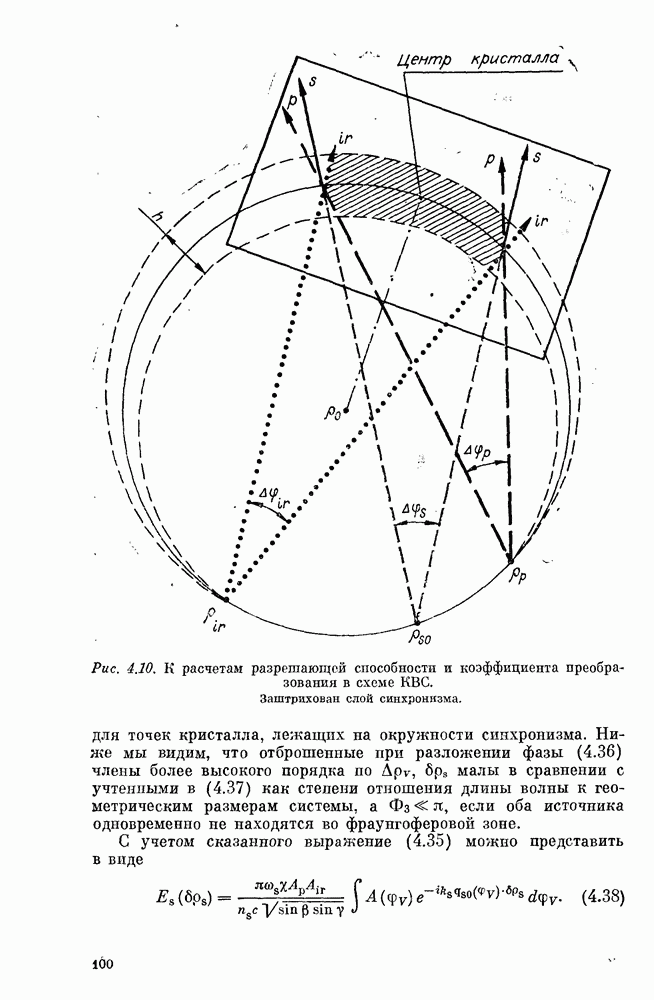
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)