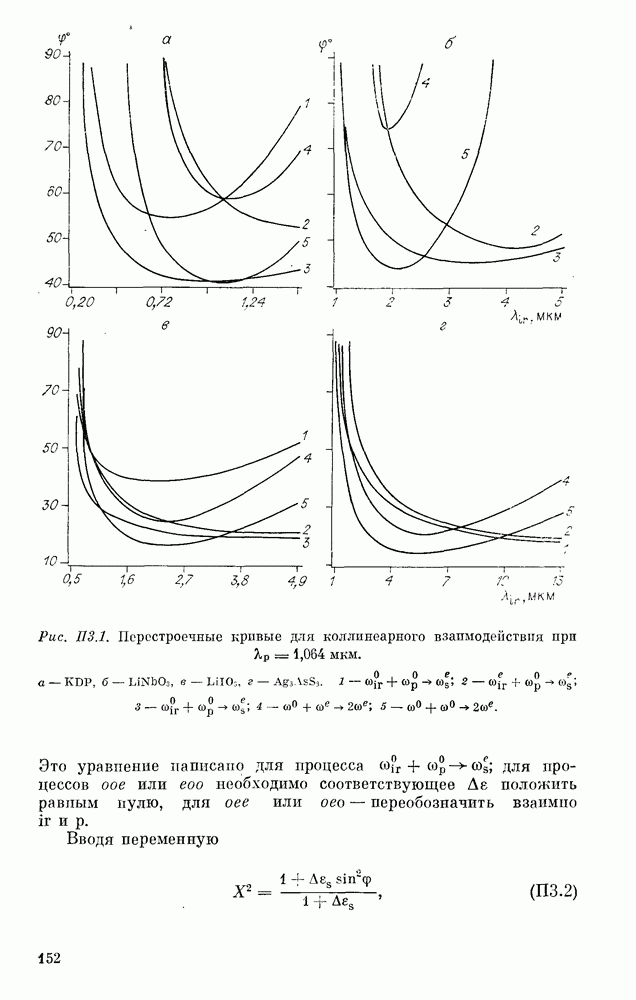
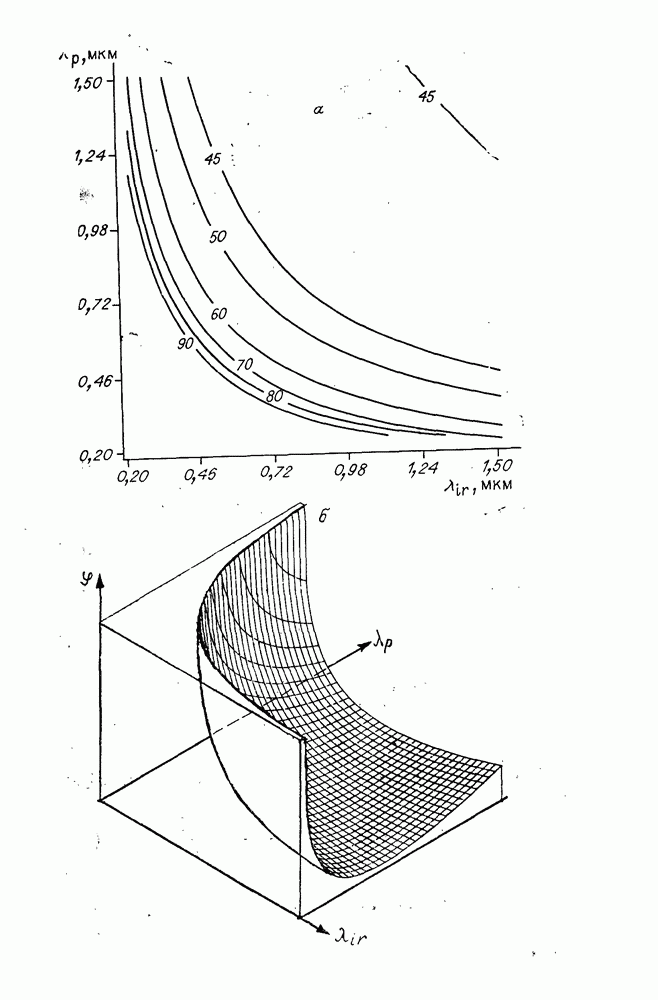
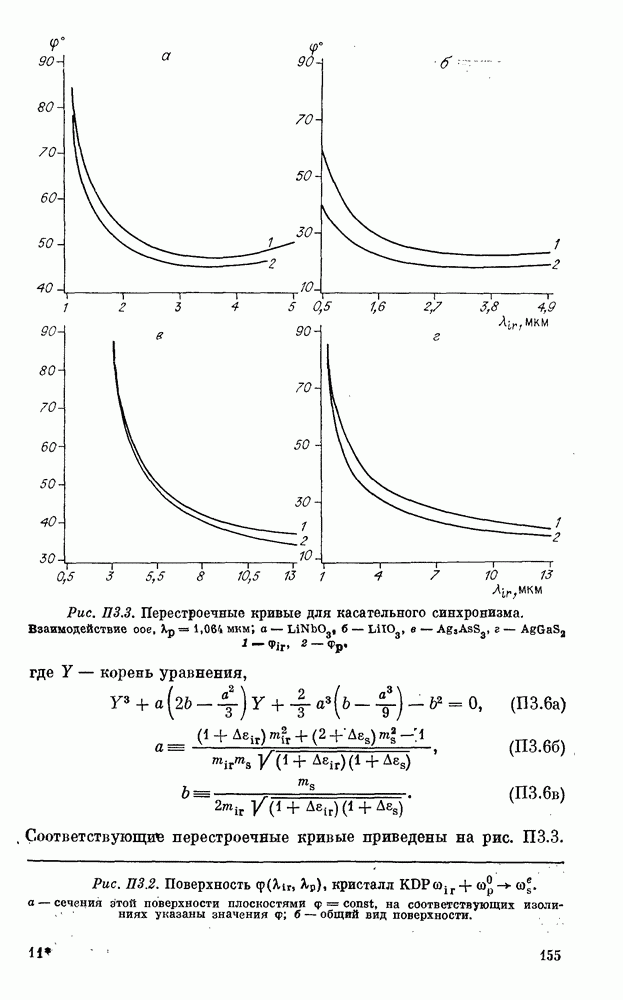
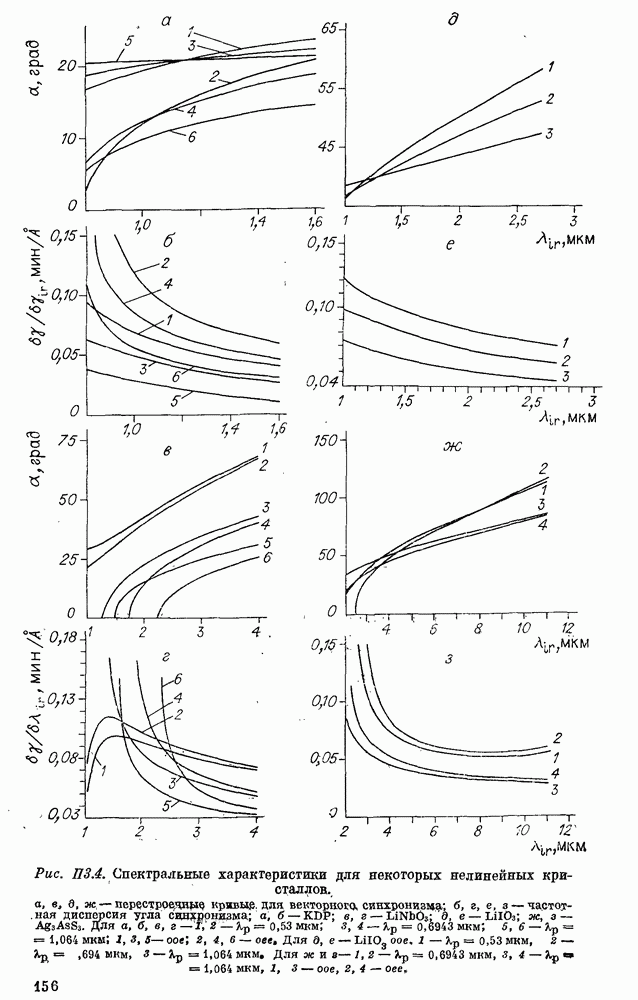
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
Материальное уравнение, устанавливая связь между поляризацией и полем, позволяет замкнуть систему уравнений Максвелла и решить задачу о пространственном и временном распределении электромагнитного поля для среды с заданными свойствами и заданными, падающими извне на среду, волнами. Последние определяют граничные условия для описывающего поле внутри среды волнового уравнения, в которое сворачиваются
уравнения Максвелла после исключения из них магнитного поля

Оптические эффекты тесно связаны с характером зависимости  от
от  Если эта зависимость линейна (см. (1.6)), то фундаментальным свойством электромагнитных волн в таких средах является принцип суперпозиции. Он позволяет любое состояние электромагнитного поля представить в виде совокупности простых решенийсвойства каждого из которых хорошо изучены. Так, в пространственно однородной среде такими решениями являются плоские волны (однородные или неоднородные), а уравпения (1.6) и (1.41) задают так называемую дисперсионную связь между частотами временных со и пространственных к колебаний поля. Эта связь существенна для линейных оптических эффектов в однородных средах (например, дифракционное расплывание пучков света и дисперсионное расплывание волновых пакетов).
Если эта зависимость линейна (см. (1.6)), то фундаментальным свойством электромагнитных волн в таких средах является принцип суперпозиции. Он позволяет любое состояние электромагнитного поля представить в виде совокупности простых решенийсвойства каждого из которых хорошо изучены. Так, в пространственно однородной среде такими решениями являются плоские волны (однородные или неоднородные), а уравпения (1.6) и (1.41) задают так называемую дисперсионную связь между частотами временных со и пространственных к колебаний поля. Эта связь существенна для линейных оптических эффектов в однородных средах (например, дифракционное расплывание пучков света и дисперсионное расплывание волновых пакетов).
Нелинейная зависимость  нарушает принцип суперпозиции, и, вообще говоря, возникает необходимость самостоятельного анализа каждой конкретной задачи. Однако нелинейные эффекты, как правило, весьма малы, по крайней мере в локальном смысле:
нарушает принцип суперпозиции, и, вообще говоря, возникает необходимость самостоятельного анализа каждой конкретной задачи. Однако нелинейные эффекты, как правило, весьма малы, по крайней мере в локальном смысле:

Это обстоятельство позволяет сделать некоторые общие для всей нелинейной оптики заключения. Например, если при  решение волнового уравнения имеет вид плоской волны, то при
решение волнового уравнения имеет вид плоской волны, то при  решение можно представить в виде квазиплоской волны, амплитуда и фаза которой мало меняются на расстояниях порядка длины волны. Еще большие возможности для общего описания нелинейно-оптических эффектов возникают в случае, когда эти эффекты малы не только в локальном, но и в интегральном по всей нелинейной среде смысле. В данном параграфе рассматривается именно такая ситуация.
решение можно представить в виде квазиплоской волны, амплитуда и фаза которой мало меняются на расстояниях порядка длины волны. Еще большие возможности для общего описания нелинейно-оптических эффектов возникают в случае, когда эти эффекты малы не только в локальном, но и в интегральном по всей нелинейной среде смысле. В данном параграфе рассматривается именно такая ситуация.
Сделаем временное фурье-преобразование обеих частей уравнения (1.41):

Здесь линейное по полю слагаемое (1.6), (1.13) выделено из  перенесено в левую часть уравнения и объединено с членом
перенесено в левую часть уравнения и объединено с членом 

Рассмотрим здесь только ту часть  , которая генерируется
, которая генерируется  в отсутствие падающих на среду волн на частотах
в отсутствие падающих на среду волн на частотах  Поэтому Ем также можно считать достаточно малым. Основная идея приближения заданного поля состоит в том, чтобы пренебречь влиянием рождающегося в среде поля
Поэтому Ем также можно считать достаточно малым. Основная идея приближения заданного поля состоит в том, чтобы пренебречь влиянием рождающегося в среде поля  на физические факторы,
на физические факторы,
породившие  Возможны два случая. Первый — когда в создании нелинейной поляризации на частоте со участвует поле той же частоты:
Возможны два случая. Первый — когда в создании нелинейной поляризации на частоте со участвует поле той же частоты:

 здесь никак нельзя считать заданным. В этом случае заданными, не зависящими от Ем, считаются все остальные факторы, участвующие в создании
здесь никак нельзя считать заданным. В этом случае заданными, не зависящими от Ем, считаются все остальные факторы, участвующие в создании  в частности сильные поля других частот. Как видно из (1.43) и (1.45), задача фактически сводится к задаче линейной оптики с заданным пространственным распределением комплексного показателя преломления. Оно определяется упомянутыми факторами, пространственное распределение которых предварительно необходимо узнать, например, решая линейную задачу о распространении электромагнитных волн других частот (отличных от
в частности сильные поля других частот. Как видно из (1.43) и (1.45), задача фактически сводится к задаче линейной оптики с заданным пространственным распределением комплексного показателя преломления. Оно определяется упомянутыми факторами, пространственное распределение которых предварительно необходимо узнать, например, решая линейную задачу о распространении электромагнитных волн других частот (отличных от  ).
).
Второй случай, не имеющий прямых аналогов в линейной оптике, связан с процессами, когда в создании не участвует  Здесь также сначала необходимо рассчитать физические факторы, генерирующие
Здесь также сначала необходимо рассчитать физические факторы, генерирующие  Например, для процессов типа генерации гармоник решить в рамках линейной оптики задачу об отражении и преломлении в нелинейном кристалле возбуждающего излучения. Затем с помощью нелинейного материального уравнения необходимо вычислить
Например, для процессов типа генерации гармоник решить в рамках линейной оптики задачу об отражении и преломлении в нелинейном кристалле возбуждающего излучения. Затем с помощью нелинейного материального уравнения необходимо вычислить  наконец, решить фактически линейное уравнение (1.43) с заданным распределенным в объеме источником
наконец, решить фактически линейное уравнение (1.43) с заданным распределенным в объеме источником  Кардинальным физическим вопросом в данном случае является вопрос о сложении волн, излучаемых источниками, находящимися в разных точках среды. Если такое сложение происходит в фазе, то нелинейный эффект накапливается. В противном случае накопление эффекта от разных частей среды отсутствует.
Кардинальным физическим вопросом в данном случае является вопрос о сложении волн, излучаемых источниками, находящимися в разных точках среды. Если такое сложение происходит в фазе, то нелинейный эффект накапливается. В противном случае накопление эффекта от разных частей среды отсутствует.
Поскольку в рассматриваемом приближении уравнение (1.43) линейпо по  то принцип суперпозиции в этом приближении снова выполняется и для понимания общей ситуации, так же как и в линейной оптике, достаточно рассмотреть отклик среды на конкретное
то принцип суперпозиции в этом приближении снова выполняется и для понимания общей ситуации, так же как и в линейной оптике, достаточно рассмотреть отклик среды на конкретное  принадлежащее к любой полной системе функций (
принадлежащее к любой полной системе функций ( -радиус-вектор точки в среде). В пространственно однородной среде с плоскими границами удобно в качестве такого распределения выбрать плоскую волну
-радиус-вектор точки в среде). В пространственно однородной среде с плоскими границами удобно в качестве такого распределения выбрать плоскую волну

Принцип суперпозиции в приближении заданного поля выполняется только по отношению к составляющим  но не по отношению к исходным физическим факторам, порождающим нелинейный эффект. Например, при генерации второй гармоники
но не по отношению к исходным физическим факторам, порождающим нелинейный эффект. Например, при генерации второй гармоники

Рис. 1.1. Волны нелинейной поляризации, рожденные двумя плоскими волнами накачки.

Рис. 1.2. К нелинейно-оптическому аналогу задачи Френеля.
в среде  двумя возбуждающими волнами с одинаковыми частотами и разными к нелинейная поляризация на двойной частоте состоит из трех волн: у первой
двумя возбуждающими волнами с одинаковыми частотами и разными к нелинейная поляризация на двойной частоте состоит из трех волн: у первой  второй
второй  третьей
третьей  (рис. 1.1). Отклик среды на эти три волны
(рис. 1.1). Отклик среды на эти три волны  аддитивен, но отнюдь не аддитивен эффект генерации гармоники по отношению к волнам возбуждающего излучения. При наличии одновременно обеих волн возникает неаддитивный член — гармоника, рожденная волной
аддитивен, но отнюдь не аддитивен эффект генерации гармоники по отношению к волнам возбуждающего излучения. При наличии одновременно обеих волн возникает неаддитивный член — гармоника, рожденная волной 
Таким образом, процедура решения состоит в следующем. Разлагаем заданное  в пространственный интеграл Фурье, находим решение
в пространственный интеграл Фурье, находим решение  для каждой фурье-компонент
для каждой фурье-компонент  (1.46) и затем вычисляем интерференцию всех
(1.46) и затем вычисляем интерференцию всех 
В итоге приходим к нелинейному аналогу задачи Френеля  Постановка этой задачи такова. Имеется полубесконечная однородная нелинейная среда II, находящаяся в области пространства
Постановка этой задачи такова. Имеется полубесконечная однородная нелинейная среда II, находящаяся в области пространства  (рис. 1.2). В этой среде распространяется волна нелинейной поляризации (1.46). Падающие из области
(рис. 1.2). В этой среде распространяется волна нелинейной поляризации (1.46). Падающие из области  электромагнитные волны на частоте со отсутствуют. Требуется найти пространственное распределение
электромагнитные волны на частоте со отсутствуют. Требуется найти пространственное распределение  в первой
в первой  и второй
и второй  средах. Граничные условия на границах сред
средах. Граничные условия на границах сред  и
и  остаются теми же, что и в линейной оптике:
остаются теми же, что и в линейной оптике:

поскольку на границе сред отсутствуют поверхностные токи с бесконечной плотностью.
Так как нелинейная поляризация определяется только формулой (1.9) и сама по себе не обязана подчиняться какому-либо уравнению типа волнового, то мы не можем заранее ограничиться ни условием поперечности, ни какой бы то ни было связью между со и  и будем считать, что
и будем считать, что  в (1.46) принимает любые значения,
в (1.46) принимает любые значения,  любые направления по отношению к
любые направления по отношению к 
Поэтому представим  в виде суммы трех слагаемых:
в виде суммы трех слагаемых:

где  компоненты поперечной (перпендикулярной
компоненты поперечной (перпендикулярной  части,
части,  и
и  — продольная (параллельная
— продольная (параллельная  часть,
часть,

 перпендикулярна
перпендикулярна  и параллельна границе раздела сред:
и параллельна границе раздела сред:

 перпендикулярна
перпендикулярна 

 соответствует случаю
соответствует случаю  -поляризации задачи Френеля в линейной оптике;
-поляризации задачи Френеля в линейной оптике;  случаю
случаю  -поляризации [1, 6—8];
-поляризации [1, 6—8];  единичные орты
единичные орты  и
и  -поляризаций.
-поляризаций.  так же как и в линейной оптике, комплексно, если в задаче имеются неоднородные волны (например,
так же как и в линейной оптике, комплексно, если в задаче имеются неоднородные волны (например,  комплексно) [8]. Поскольку принцип суперпозиции остается справедливым в данной задаче, влияние
комплексно) [8]. Поскольку принцип суперпозиции остается справедливым в данной задаче, влияние  можно рассматривать независимо друг от друга.
можно рассматривать независимо друг от друга.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ НЕЛИНЕЙНОЙ ОПТИКИ
- § 2. НЕЛИНЕЙНЫЕ МАТЕРИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПРИБЛИЖЕНИЕ ЗАДАННОГО ПОЛЯ В НЕЛИНЕЙНОЙ ОПТИКЕ
- Геометрические законы распространения волн, рожденных в попубесконечной нелинейной среде
- Соотношения амплитуд для отраженной и свободной волн в нелинейной оптике
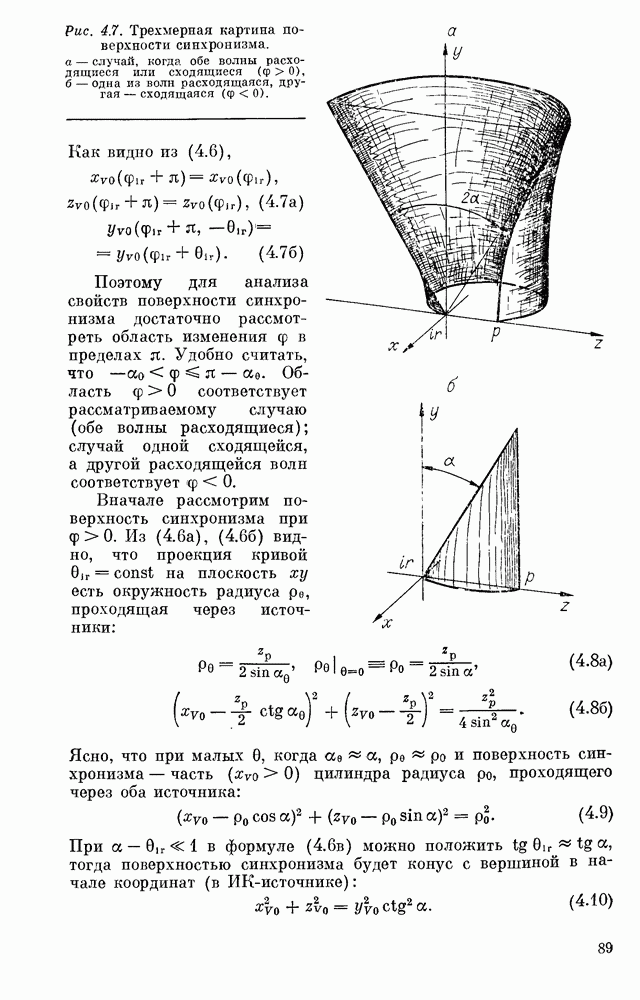
- Явления пространственной синфазности (синхронизма)
- § 4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ В КВАДРАТИЧНОЙ НЕЛИНЕЙНОЙ СРЕДЕ
- Глава 2. ОБЩИЕ СВОЙСТВА НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- § 2. ПОДХОД ФУНКЦИИ ГРИНА В НЕЛИНЕИНОИ ОПТИКЕ И ВЗАИМОДЕЙСТВИЕ ВОЛН РАЗЛИЧНОЙ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ
- § 3. ПРИБЛИЖЕНИЕ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ПРИ ВЗАИМОДЕЙСТВИИ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- § 4. ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ
- Глава 3. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 1. ОБЩИЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 2. ПРИБЛИЖЕННЫЙ МЕТОД В ДИФРАКЦИОННОЙ ТЕОРИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ ИСТОЧНИКОВ
- § 3. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА РАЗЛОЖЕНИЕМ ВЗАИМОДЕЙСТВУЮЩИХ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ. БОЛЬШИЕ КОЭФФИЦИЕНТЫ ПРЕОБРАЗОВАНИЯ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- § 5. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) ИЛИ В СХЕМЕ КАСАТЕЛЬНОГО СИНХРОНИЗМА
- Глава 4. ПРЕОБРАЗОВАНИЕ В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
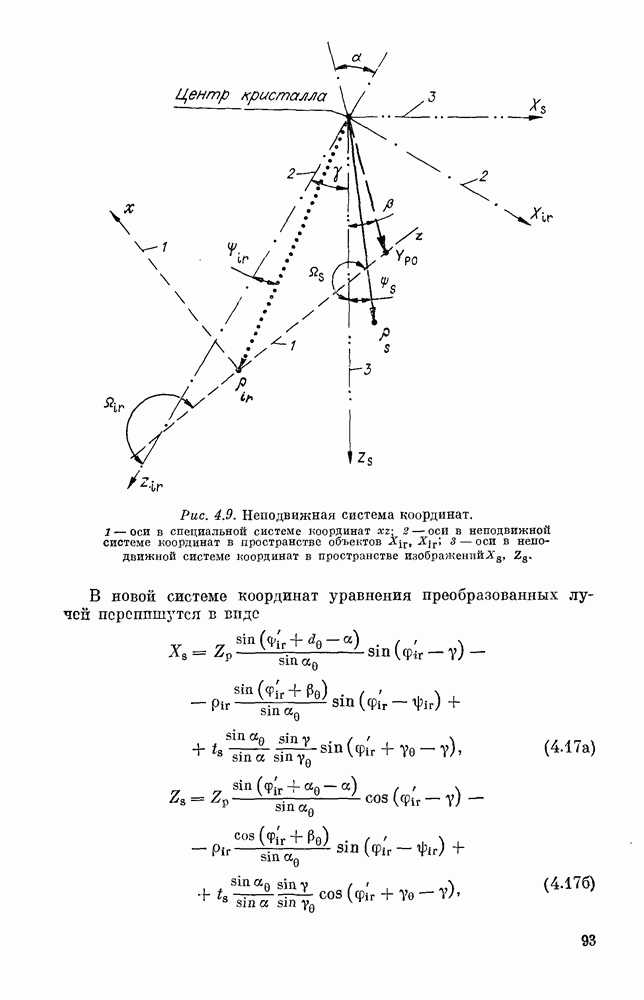
- § 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СХЕМЕ КРИТИЧНОГО ВЕКТОРНОГО СИНХРОНИЗМА
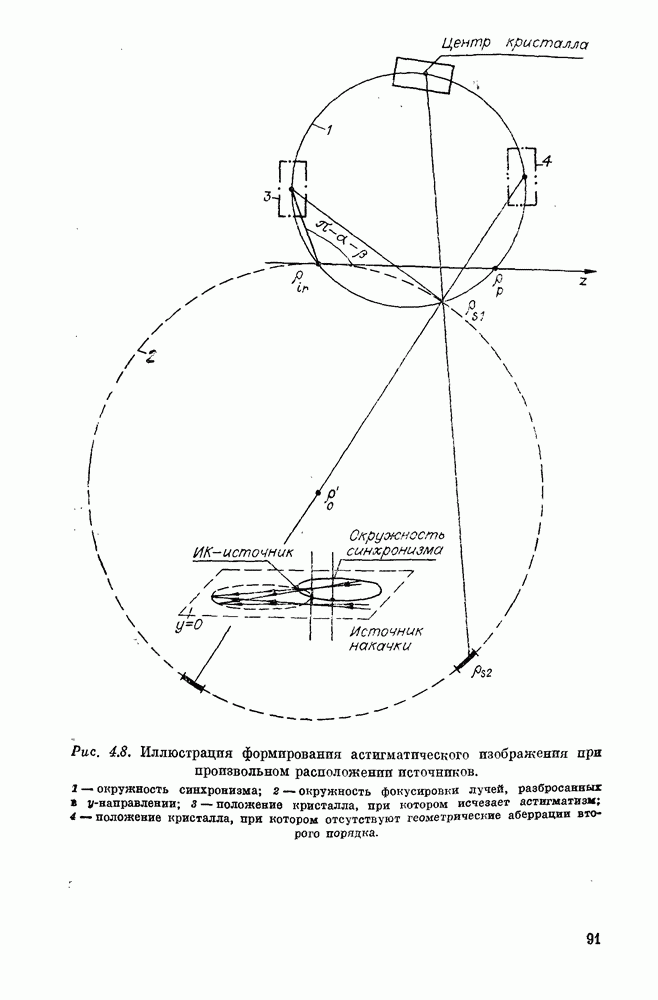
- § 2. ФОРМИРОВАНИЕ АСТИГМАТИЧЕСКОГО ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 3. ГЕОМЕТРИЧЕСКИЕ АБЕРРАЦИИ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 4. ПОЛЕ ЗРЕНИЯ ПРЕОБРАЗОВАТЕЛЯ ИЗОБРАЖЕНИЯ В СХЕМЕ КВС
- § 5. ДИФРАКЦИОННАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ НЕПЛОСКИХ ВОЛН В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ. ТОЧНО РЕШАЕМЫЕ МОДЕЛИ
- § 6. СПЕКТРАЛЬНЫЕ СВОЙСТВА СХЕМЫ КВС
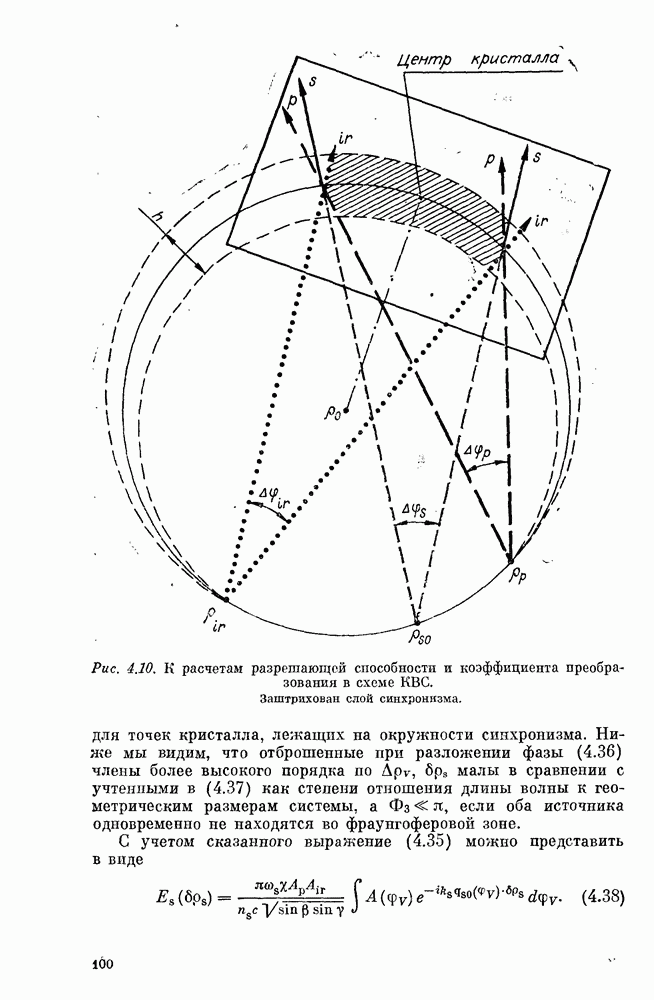
- § 7. КОЭФФИЦИЕНТ ПРЕОБРАЗОВАНИЯ (ЭФФЕКТИВНОСТЬ) В СХЕМЕ КВС
- Глава 5. ПРАКТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗЛУЧЕНИЯ
- § 1. СРАВНЕНИЕ РАЗНЫХ СХЕМ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЯ
- § 2. ПРЕОБРАЗОВАНИЕ ИНФРАКРАСНЫХ СИГНАЛОВ. ОПТИМАЛЬНАЯ ФОКУСИРОВКА
- § 3. НЕЛИНЕЙНЫЕ ИК-СПЕКТРОГРАФЫ
- § 4. ШУМЫ И ЧУВСТВИТЕЛЬНОСТЬ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРИЕМНИКОВ ИНФРАКРАСНОГО ИЗЛУЧЕНИЯ
- § 5. РЕЗУЛЬТАТЫ ПО ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ НЕЛИНЕЙНО-ОПТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ ИЗОБРАЖЕНИЯ
- ЗАКЛЮЧЕНИЕ
- Приложение 1. ПОДХОД В ТЕОРИИ ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ОСНОВАННЫЙ НА ПРИНЦИПЕ ГЮЙГЕНСА—ФРЕНЕЛЯ—КИРХГОФА
- Приложение 2. ФУНКЦИЯ ГРИНА ПАРАБОЛИЧЕСКОГО (ПАРАКСИАЛЬНОЕ ПРИБЛИЖЕНИЕ) ВОЛНОВОГО УРАВНЕНИЯ В ОДНООСНОМ КРИСТАЛЛЕ
- Приложение 3. ПЕРЕСТРОЕЧНЫЕ КРИВЫЕ (КОЛЛИНЕАРНЫЙ, КАСАТЕЛЬНЫЙ И ВЕКТОРНЫЙ СИНХРОНИЗМЫ)